Folding of Gas-Phase Polyalanines in a Static Electric Field: Alignment, Deformations, and Polarization Effects

Abstract

Monte Carlo simulations of the temperature-induced unfolding of small gas-phase polyalanines in a static, homogeneous electric field are reported, based on the AMBER ff96 force field. The peptides exhibit a structural transition from the native α-helix state to entropically favored β-sheet conformations, before eventually turning to extended coil at higher temperatures. Upon switching the electric field, the molecules undergo preferential alignment of their dipole moment vector toward the field axis and a shift of the α-β transition to higher temperatures. At higher field strengths (>10⁸ V/m) the molecules stretch and the α-β and β-coil transitions merge. A simple three-state model is shown to account for the observed behavior. Under even higher fields, density functional theory calculations and a polarizable force field both show that electronic rearrangements tend to further increase the dipole moment, polarization effects being approximately half in magnitude with respect to stretching effect. Finally a tentative (temperature, field-strength) phase diagram is sketched.

INTRODUCTION

The behavior of biological systems under electromagnetic fields has recently attracted a lot of attention (1–4), partly to address the possible damages suffered upon exposure to the many sources of radiation in our increasingly technological everyday life. Electromagnetic interactions are thought to be responsible for heating biological systems, particularly in the infrared and microwave ranges (5). These so-called nonthermal effects could alter the stability and activity of biomolecules, as was experimentally studied by several groups (6–8). Additionally, understanding the influence of electromagnetic effects on proteins could be useful in designing molecules with specific properties (9). Despite the importance of such measurements, to the best of our knowledge the effects of electromagnetic fields on the structure of biomolecules have been only poorly addressed by theory or simulation (an exception being the recent molecular dynamics study in (10), whose relevance has been questioned in (11)).

The influence of external fields on the structure and dynamics of molecular systems has been mostly investigated on water, either at the bulk level (12–16), or in low-dimensional wires (17–19) or finite clusters (20–24). In the latter case, and for small clusters having fewer than five molecules, ab initio calculations (25) have shown the preferential alignment between the dipole moments along the electric field direction as the field strength increases. Other field-induced structural transformations have been reported in clusters (22,24). In bulk (15) and confined (26) water, the easier nucleation of ice under electric fields is known as electrofreezing. Field-induced transitions in water convey the weakening of the hydrogen-bond network as the field strength increases (27,28), which is also reflected by the steady decrease in the dielectric constant (29,30). Besides water, the influence of electric fields has been addressed on various other molecular systems, including hydrates (31), liquid methanol (32), or loaded zeolites (33). In most cases, hydrogen bonds are also disrupted under high fields.

The structure of biomolecules is partly driven by long-range electrostatic forces, especially when hydrogen bonds are formed. The effects of an external field on hydrated proteins are difficult to study because of the simultaneous rearrangements of the solvent (34,35). However, measurements of secondary structures in an electric field are comparatively easier in the gas phase, as was first attempted experimentally by Antoine and co-workers (36). A review of some experimental methods to determine peptide conformations in the gas phase has been recently written by Jarrold (37). Poulain and co-workers (38) specifically investigated the finite-temperature properties of a small dipeptide (Trp-Gly) under a static electric field, for different magnitudes of the field. At low field, the peptide was found to undergo preferential alignment of its electric dipole moment along the field axis, the projection of the dipole following the Langevin-Debye equation. At high fields (above 10⁸ V/m), deviations from the Langevin law were interpreted as due to qualitative changes in the conformation (38), as made possible due to the floppiness of the molecule.

In this article, we focus on larger peptides, namely polyalanines Ala_n. These molecules are very stable in the α-helix conformation, which is associated with large electric dipole moments (also called macrodipoles) resulting from the additive contribution of nearly aligned hydrogen bonds. Individual hydrated polyalanines are expected to undergo a single helix-coil transition (39–41). However, recent experimental (42) and theoretical (43–45) investigations have suggested that β-strand conformations may be more stable than helices in an intermediate temperature range due to entropic effects. The competition between the α-helix and β-strand secondary structures is of primary importance in molecular biology, as it is responsible for the misfolding of proteins and, in the case of peptide assemblies, amyloidosis, which in turn cause fatal diseases (46–50).

Helical conformations are associated with large electric dipole moments, which essentially increase linearly with the number of amino acids. While this dipole moment is notably screened when the peptides are solvated into a polar solvent (including water), it can reach high values in the gas phase, making isolated polyalanines very sensitive to an external field. Conversely, neither β-hairpins or the random coil state are characterized by important electric dipole moments, hence the α-β or helix-coil transitions should be drastically affected by the presence of an external field.

Our goal in this article is to investigate, by means of numerical simulations, the conjugated effects of temperature, electric field, and size of polyalanines on their statistical conformations. Following our previous effort (45), we mainly use standard, nonpolarizable force fields to model these polypeptides. Combined with efficient sampling methods, this simplified approach allows us to characterize the average thermal properties, including the caloric curves. However, under the presence of high fields, the classical force-field approach may be too simplistic and fail to describe the actual electronic rearrangements of the peptide. We then also employ more accurate polarizable force fields, as well as first-principle density functional theory calculations to quantify the extent of polarization effects. The article is organized as follows. In the next section, the simulation methods are briefly outlined. Their application to Ala₈ and Ala₁₆ is then presented and discussed, before specifically studying the high field regime, where we pay a particular attention to the polarization and stretching effects. Tentative phase diagrams are finally constructed based on our simulation data. The article ends on some concluding remarks and perspectives.

METHODS

This section is devoted to the theoretical and numerical methods that have been used or developed for the problem of sampling molecular conformations in a static electric field. Methods used for studying the high field regime will be described in the subsequent section.

Model details

Our primary goal is to calculate finite temperature properties and to characterize the folding transition of small polyalanines in a broad temperature range. Even with the presently available simulation methods, the presence of a structural competition makes convergence of simulations hard to achieve unless a force field is chosen to describe the intramolecular interactions. Among the many existing biomolecular force fields, we have chosen to model the peptides using AMBER (51) with its ff96 parameters (52), as they correctly reproduce the electric dipole moments measured experimentally (38). The original partial charges of AMBER ff96 were increased with respect to their gas-phase values to compensate for polarization effects in solution. In this work, a dielectric constant of ɛ = 2 was chosen to reduce these charges. This also has the beneficial effect of minimizing the overstabilization of β-sheet structures over helices in hydrated peptides known with AMBER ff96 (53–55), while other AMBER parameters sets tend to favor α-helices (56,57).

Denoting V₀(R) the AMBER potential energy of configuration R without electric field, the total energy including the electrostatic contribution due to the field is written at the leading orders in the field strength as 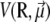with

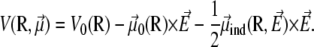(1)

In the above equation, we have separated the permanent dipole 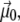which only depends on the configuration of the peptide, and the induced dipole 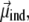which also depends on the electric field

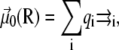(2)

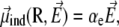(3)

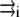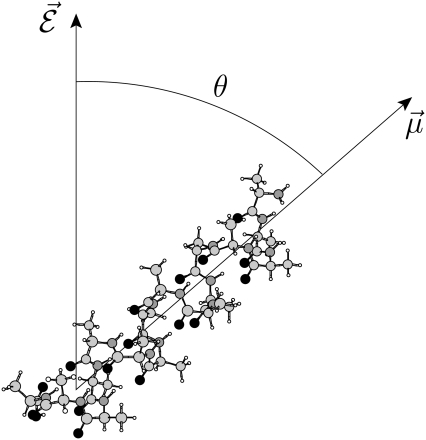
where q_i is the partial charge located at and α_e is the global electronic polarizability tensor of the molecule. This quantity weakly depends on conformation or on the orientation, and it will be neglected for sampling purposes. However, polarization effects can become important under high electric fields, and will be specifically discussed later. In the present nonpolarizable approximation, the vector 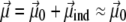no longer depends on the electric field, and the potential energy of the peptide is a function of its configuration R and orientation θ only (see Fig. 1):

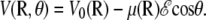(4)

This last expression will be used for sampling the configuration space of the peptide in a static electric field.

FIGURE 1.

Orientation of the helical polyalanine in the electric field. The electric dipole moment of the molecule is carried by the vector 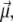while the field axis 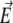is vertical in the figure plane. The angle formed by the two vectors is denoted θ.

Monte Carlo simulations in a static field

The conformational spaces of the polypeptides have been sampled with Monte Carlo (MC) simulations using the torsion angles of the peptide backbone as the only internal coordinates. The parallel tempering method (58–61) has been used to accelerate convergence of the simulations. In practice, 32 trajectories or replicas were propagated simultaneously, with one occasional exchange attempted every 10 Monte Carlo sweeps. The exchanges have been selected and performed according to the recent all-exchange strategy (62,63). The temperatures were taken as a geometric progression in the range 50–1000 K, thus providing a good overlap between energy distributions of adjacent replicas. The simulations consisted of 5 × 10⁶ Monte Carlo sweeps per replica, after 10⁶ equilibration sweeps. In absence of electric field, the results agree with our previous investigations (45) using the Wang-Landau algorithm (64,65) for joint densities of states.

For molecules in a static electric field, several simulation methods have been employed. At the most basic level, the field axis can be rigidly fixed in space, and the moves in dihedrals space would naturally change the dipole moment orientation 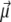with respect to 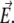Sampling the preferred orientation can be made more efficient by including a specific global rotation move, only changing the angle θ in Eq. 4. We have used this method, attempting a global rotation of the peptide once every Monte Carlo sweep. This method provides the usual statistical averages for the energy and order parameters. The multiple histogram method (66,67) can then be used to calculate the various quantities of interest as a continuous function of temperature.

Since intramolecular torsion moves and global orientational moves are decoupled when building the Markov chain, the latter can be attempted with an arbitrary probability during the Monte Carlo trajectory, much more frequently than only once in a MC sweep. In the limit of an infinite number of such moves, the statistical average of Eq. 4 over all orientations θ at temperature T is exactly given by

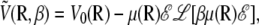(5)

where

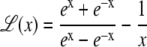(6)

is the Langevin function, and with β = 1/k_BT the inverse temperature, k_B being the Boltzmann constant. It was shown by Poulain and co-workers (38) that the projection μ_z of the electric dipole moment on the field axis correctly obeys the Langevin-Debye formula (68,69),

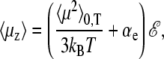(7)

where 〈μ²〉_0,T is the average square dipole of the molecule without electric field, at temperature T. The Langevin-Debye formula applies within the linear response theory framework, that is, when the field is sufficiently low in magnitude.

We should stress here that the use of Eq. 5 for the statistical average of the potential energy in the field is not equivalent to assuming that the molecule actually aligns in the field following the Langevin-Debye expression. Because the molecule is flexible, its preferred conformations will still depend on the field strength (as well as temperature).

Performing the orientational average above leads to an effective energy 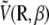which explicitly depends on temperature. Care should then be taken when attempting a replica exchange move. The acceptance probability for swapping configurations R_i and R_j initially at inverse temperatures T_i and T_j reads (70)

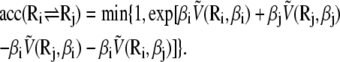(8)

The temperature dependence of the potential energy also adds corrective terms to the internal energy U(T) and, more importantly, to the heat capacity C_v(T):

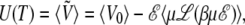(9)

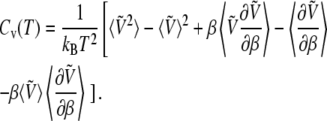(10)

In this case, it follows straightforwardly from Eqs. 5 and 6, that

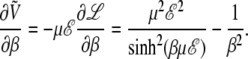(11)

The previous formulas involving the potential energy must be applied for the running statistical averages calculated on-the-fly. Statistical quantities only dependent on the configuration (but not on energy) are obtained from usual arithmetic averages.

Reweighting of zero-field histograms

In the low field limit, the interaction between the dipole moment and the electric field represented by the second term in the right-hand side of Eq. 4 can be considered as a small perturbation which mainly affects the favored orientations of the peptide. It turns out that a complete characterization of the statistical behavior of the peptide at zero field, in terms of its potential energy and dipole moment, is sufficient to provide the corresponding properties at nonzero field. The method presented here relies on the histogram reweighting approach (66,67), in which the distributions of potential energies are processed into the microcanonical density of states, allowing the subsequent calculation of statistical properties in the canonical ensemble.

At nonzero field, each configuration in phase space is characterized by its energy 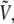which derives from V₀ and the dipole moment μ through the simple sum of Eq. 5. Any canonical property A sampled at nonzero field can be obtained from statistical averages at zero field, following a standard reweighting procedure (71),

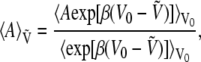(12)

which, in this case, yields

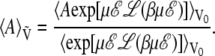(13)

Therefore, the running averages obtained at zero field can be used at finite field after correcting by the corresponding weight

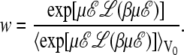(14)

Since this weight can only be estimated at the end of simulation, it is more convenient to process the energy histograms, which are obtained from a standard parallel tempering Monte Carlo simulation of the peptide without electric field. We denote by p_β (V₀, μ) the two-dimensional histograms of the potential energy V₀ and norm μ of the dipole moment, at temperature β. The standard multiple histogram method provides the configurational microcanonical density from the histograms in energy only, 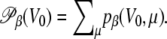Each state (V₀, μ) with probability p_β at temperature β corresponds to a different state 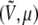also with a different probability 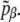The energy 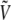is given by Eq. 5 and, according to the previous remarks, the probability 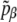should be reweighted from p_β as

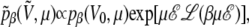(15)

and then properly normalized to keep the number of effective states constant. The multiple histogram method can then be applied to the energy distributions 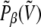obtained from summing 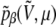on the variable μ.

Because this method is perturbative, it is expected to hold as long as the energetics of the peptide is only marginally affected by the interaction with the field. Its main interest is to avoid repeating the calculations for each new value of the electric field. As will be seen below, its predictions are rather accurate for low field strengths under ∼10⁸ V/m.

FOLDING AND STRUCTURAL TRANSITIONS IN A STATIC FIELD

Structural order parameters

Two polyalanines have been investigated with the methods described in the previous section, namely Ala₈ and Ala₁₆. As in our previous work (45), the secondary structures are characterized by the average (square) electric dipole moment 〈μ²〉 and by the end-to-end distance d between the nitrogen atom in N-ter position and the hydrogen atom from the hydroxyl group in C-ter position. Here we also use complementary order parameters, which have often been used in molecular simulation of biomolecules. The fractional helicity is defined by 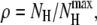where N_H is the number of helical hydrogen bonds, 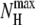being the maximum number of such bonds. A residue is considered here to be helical if its φ and ψ angles lie in the ranges [−100°, −40°] and [−67°, −7°], respectively. 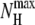is equal to 6 for Ala₈ and 14 for Ala₁₆.

The proximity of the polypeptide toward its native conformation can also be measured by a parameter χ called an overlap function. We use the definition of Veitshans and co-workers (72), which has also been adopted by Giessen and Straub in their recent study of model polyalanines (73),

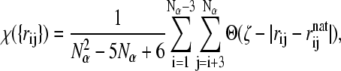(16)

where N_α denotes the number of α-carbons, and r_ij and 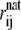are the distances between α-carbons i and j in the current configuration and in the native state, respectively. Θ is the Heaviside step function, and ζ = 0.5 Å measures how close the structure is to the native state. Similar to the heat capacity, the fluctuations in χ, that is, 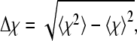turn out to be more insightful than χ itself.

In addition to these two order parameters, we have computed the average radius of gyration 〈R_g〉, which is more sensitive to the collapse transition.

Octa-alanine

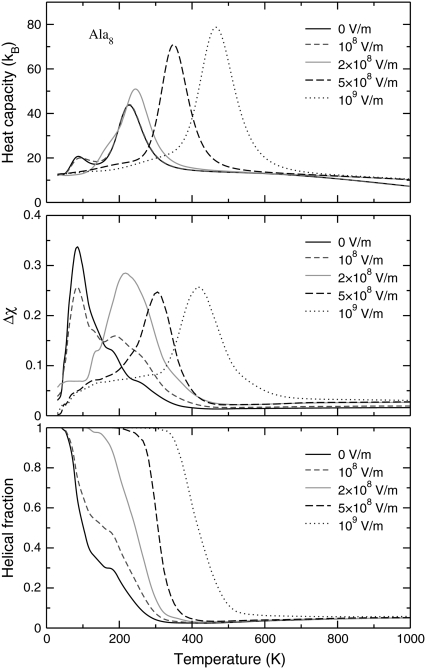
In Fig. 2, we show the variations of the heat capacity, overlap fluctuations Δχ, and helical content ρ as a function of temperature, obtained for Ala₈ under several strengths of electric field. These curves were obtained using a combination of intramolecular torsion moves, as well as occasional global rotations attempted once per MC sweep, the field axis being fixed in space.

FIGURE 2.

Variations of the canonical heat capacities (upper panel), fluctuations of the overlap function (middle panel), and helical content (lower panel) of the Ala₈ peptide as a function of temperature, for electric fields in the range 0–10⁹ V/m.

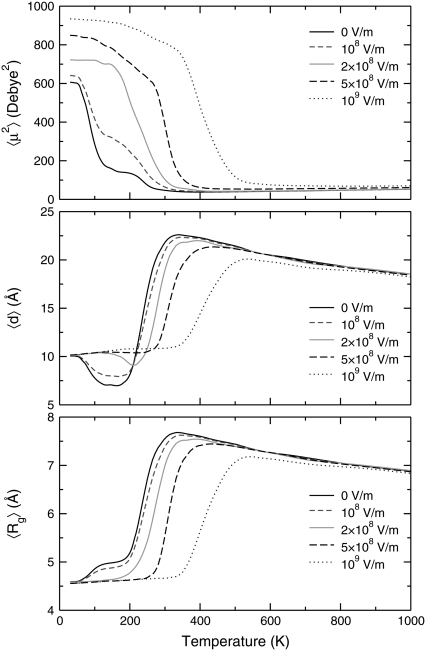
Without electric field, the heat capacity exhibits a main peak centered near 230 K, as well as a second, low-temperature peak near 90 K. These two peaks were also reported for Ala₁₂, albeit shifted to higher temperatures (45). Looking at the other order parameters, the loss in helical order is clearly associated with the low-temperature peak, and the fluctuations in the overlap function are maximum. The average electric dipole moment and the end-to-end distance, shown in Fig. 3, both drop at the same temperature. However, both the latter quantity and the gyration radius show a sharp increase at a temperature corresponding to the second heat capacity peak. In agreement with our previous study (45), we interpret these results as the manifestation of a first structural transition from α-helix to β-strand conformations, followed by a second transition from β-strand to random coil. These two transitions can be considered as the folding and the collapse transitions, respectively. The higher stability of β-conformations is due to their higher entropy (42), which can be seen in annealing simulations (45). Such entropy-driven structural transitions at low-temperatures have been previously reported in other molecular systems, particularly atomic clusters (74,75).

FIGURE 3.

Variations of the average square electric dipole moment μ² (upper panel), end-to-end distance d (middle panel), and radius of gyration R_g (lower panel) of the Ala₈ peptide as a function of temperature, for electric fields in the range 0–10⁹ V/m.

As the electric field is turned on, the peaks in the specific heat gradually shift to higher temperatures. At 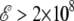V/m, the two peaks merge and the area under the peak (the latent heat associated with the transition) increases as well. The variations of all order parameters reflect the shifts in the transition temperatures. The greater thermodynamic stability of the helix conformation within an electric field is due to its strong macrodipole. Conformations with a higher β-strand character and those belonging to the random coil state have a much lower electric dipole, and their stability is not significantly enhanced in presence of the field. The greater stability of α-helices relative to the β-strand and random coil conformations is thus revealed onto the heat capacity curves. As the field becomes strong enough, the temperature range of stability for the β-conformations becomes narrower, because the β to random coil state is poorly affected by the field. As the helix-coil transition becomes single step, the transition temperature, and the latent heat both increase with the field, again reflecting the higher energetic stability of the helical state. In a first approximation, the shift in collapse temperature and the associated latent heat both vary linearly with the applied field. As long as the energy gain is itself proportional to the field, this is the expected behavior. However, this should mainly hold at sufficiently low temperature to keep the electric dipole aligned with the field.

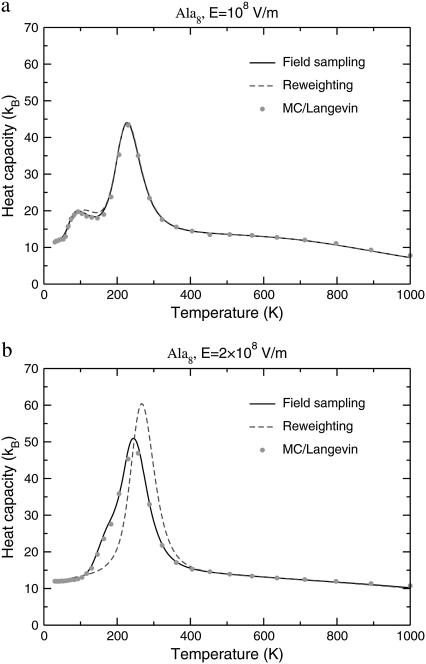
Instead of sampling the peptide conformations at fixed field, it is possible to perform the orientational average at each Monte Carlo step involving intramolecular coordinates, following the procedure outlined in the previous section. The heat capacity should then be calculated with the temperature-dependent effective potential of Eq. 5, using the formula of Eq. 10. Alternatively, the heat capacity can be also obtained by processing the joint histograms of energy and dipole moments gathered at zero field, using the reweighting formulas of Eq. 15. These calculations are illustrated in Fig. 4 for Ala₈ under field strengths of 10⁸ V/m and 2 × 10⁸ V/m.

FIGURE 4.

Variations of the canonical heat capacity of Ala₈ at field strengths (a) ℰ = 10 × 10⁸ V/m; (b) ℰ = 2 × 10⁸ V/m. In both cases, the curves obtained from direct sampling at fixed field (solid lines), reweighting from zero field sampling (dotted line), or by assuming a complete statistical orientation toward the field axis through application of the Langevin formula (circles).

At low field 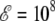V/m, the three curves agree very well with each other, showing that the main influence of the field is to align the molecule preferentially along its axis, without inducing additional deformations. However, as the field is doubled, the heat capacity curve obtained from reweighting the zero-field histograms does not show the low-temperature shoulder near 150 K that characterizes the remains of the α-β transition, as correctly reproduced by the Monte Carlo simulation using the effective Langevin potential. Instead, the specific heat displays a single peak, both the transition temperature and the latent heats being overestimated. This poor agreement indicates that the peptide undergoes not only statistical alignment toward the field axis, but also deformations which are coupled with the favored orientations. Therefore the reweighting procedure from the zero-field histograms should not be used for quantitative accuracy at fields of 2 × 10⁸ V/m and higher.

Hexadeca-alanine

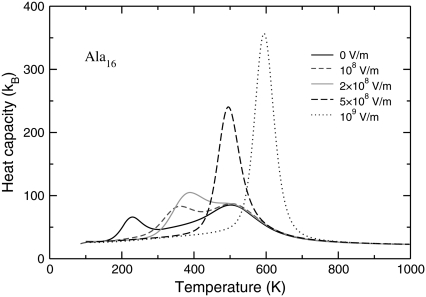
In Fig. 5, we have represented the variations of the specific heat of the Ala₁₆ polypeptide as a function of temperature. The various order parameters considered previously for Ala₈ show comparable behaviors for Ala₁₆, and are not shown for brevity.

FIGURE 5.

Variations of the canonical heat capacities of the Ala₁₆ peptide as a function of temperature, for electric fields in the range 0–10⁹ V/m.

All properties generally behave similarly as for the smaller polyalanine, but the transitions are shifted to higher temperatures, and the peaks are higher and narrower for the larger peptide. These findings are not specific to these two peptides, and a gradual evolution is observed by varying the number of alanine amino-acids between 8 and 20 (45). Both shifting and narrowing effects are well known and expected from finite-size scaling theories (76,77). As the number of amino acids grows, the polyalanine becomes increasingly stable (in both the helical and β-hairpin states) due to the increasing number of intramolecular hydrogen bonds. The decreasing importance of boundary effects is reflected on the higher unfolding transition. In three-dimensional atomic systems, phenomenological models predict that the depression in the order-to-disorder temperature grows with the inverse radius (78), and some similar behavior could be inferred here as a function of the peptide length, e.g., by computing the partition function zeros (77). The shift of the α → β transition to higher temperatures is less obvious, as it refers to a structural transition rather than an order-disorder phase change.

The sharpening of the peaks is a signature of the rounding of first-order phase transitions, as explained by Imry (79), which is consistent with well-known theories of peptide folding such as the Zimm-Bragg model (80). In the limit of infinitely long proteins, the two α → β and β → coil transitions should merge into a single helix → coil transition with a Dirac-type heat capacity peak that can only be reached at the thermodynamic limit.

In the present case of the 16-alanine peptide, the intermediate β-phase has a broader range of stability at zero field between 230 K and 500 K. Compared to Fig. 2 the effects of an external static electric field are now more important, which is due to the much larger macrodipole, namely 57 Debye instead of 24.6 Debye for Ala₈. Already for 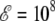V/m, the peaks of the heat capacity corresponding to the two α-β and β-coil transitions have started to merge. For 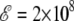V/m, the α-β peak shifts further to higher temperatures and becomes high enough to exceed the β-coil peak, making it resemble a post-melting event (81). At higher fields, only a single helix-coil transition takes place, which is characterized with a high latent heat and a still shifting transition temperature.

The stabilization of helical structures and the gradual shift of the helix-coil transition toward higher temperatures are in contrast with the destabilization of water clusters by electric fields (22,23). In the latter case, the most stable configurations are characterized by a weak dipole moment, but the liquidlike state has many isomers with a nonzero net dipole, hence they are favored in the presence of a field.

As was the case for Ala₈, the Monte Carlo simulations performed using the effective temperature-dependent Langevin potential give results in good agreement with the heat capacity curves of Fig. 5 (data not shown). The reweighting technique, on the other hand, performs only semiquantitatively for 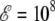V/m, and works poorly at higher fields: the deformations experienced by the molecule become significant, and can no longer be neglected.

A field-dependent three-state model

The results obtained for Ala₈ and Ala₁₆ can be rationalized using a simple multistate model. We follow here the lines of Bixon and Jortner (82), who investigated the microcanonical and canonical caloric curves of increasingly large finite systems using an harmonic approximation. We thus consider a biomolecule characterized from two or three possible states only, corresponding to the helical, β-strand, and random coil conformations. These states are characterized by their energies E_α, E_β, and E_coil, as well as their average vibrational frequencies 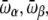and 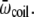The helix state is the only one to carry a dipole moment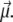

By definition, the partition function of the system at temperature T is the sum of the partition functions of each state:

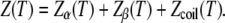(17)

In the harmonic approximation, the partition function Z_k of state k ∈ {α, β, coil} reads

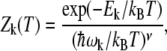(18)

where ν is the number of degrees of freedom. In the presence of an electric field ℰ, the helix state is stabilized by the interaction between the dipole moment and the field, and its energy becomes temperature-dependent, as given by Eq. 5, thus leading to

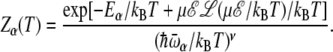(19)

Here we have assumed that the vibrational frequency does not depend on the electric field. The internal energy U(T) = −∂ ln Z/∂(1/k_BT) is thus expressed as

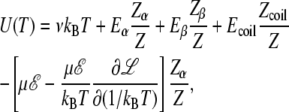(20)

where the last term in this equation accounts for the interaction with the field, including the temperature-dependent potential and statistical alignment. A rather cumbersome expression is found for the heat capacity C_v = ∂U/∂T, but it is omitted here.

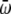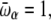
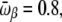
To exhibit transitions between the three states, the higher energy states must also be higher in entropy; that is, they must have lower -values. We have tested this very simple model for the following parameters, which yield clear transitions in a restricted temperature range. In reduced units (k_B = 1, ℏ = 1): E_α = 0, E_β = 5, E_coil = 20, 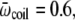and ν = 84. At zero field, these values lead to two peaks in the heat capacity located at T_α–β = 0.264 and T_β–coil = 0.615 for the α-β and β-coil transitions, respectively. The sharpness of these transitions is intimately related to the strong entropy difference arising from the lower frequencies of the β and coil states. 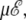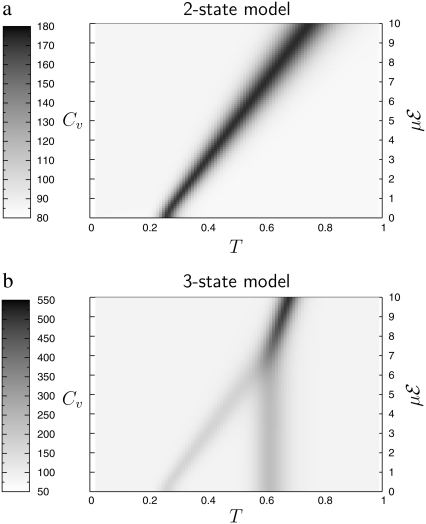As the field is turned on, the important parameter is the product which we have varied in the range, 0–10 energy units. The variations of the heat capacity with increasing temperature and for various values of 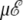are represented in Fig. 6 as contour plots, in the case of a two-state α-β, and for the more relevant three-state, α-β-coil model.

FIGURE 6.

Contour plot of the heat capacity as a function of temperature (horizontal axis) and μℰ for simple models.

In the two-state model, the α-β transition shifts linearly with the applied field, in agreement with our simulations using the all-atom AMBER force field. The height of the heat capacity peak does not increase significantly; however, the peak becomes broader, hence the latent heat globally increases with 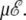In the three-state model, the β-coil transition is barely influenced by the electric field. The two heat capacity peaks merge at some critical value of the field, here for 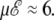Above this value, the single α-coil transition varies sharply as the field further increases, but the effect is mainly seen on the heat capacity, rather than on the transition temperature itself. Again, all these findings agree qualitatively with our simulation results, showing that the thermal behavior of small isolated polyalanines in electric field can be roughly described by a simple three-state model.

High-field deformations

This section considers two possible effects of the electric field on the polypeptides. The favorable interaction with the macrodipole tends to stretch the backbone, to maximize the dipole moment. Polarization effects further stabilize the molecules by increasing the dipole moment as the field is applied; however, their dependence on conformation may not be as significant as they are for stretching.

Stretching effects

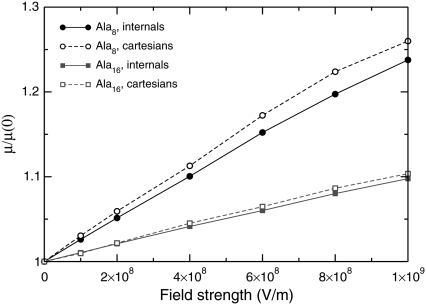
The finite-temperature Monte Carlo simulations performed using AMBER ff96 with internal torsion moves and global rotations are able to account for the statistical orientation and for possible deformations experienced by the polypeptides under electric field. We have shown in the previous section that a low field has the main consequence of aligning the molecule with respect to the field, without deforming it significantly. We have specifically studied the extent of deformations on the stable helical structures of Ala₈ and Ala₁₆. To get the maximum effect, the dipole moment was assumed to be parallel to the applied electric field. The total energy, including the interaction with the field, was locally minimized using either only the dihedral coordinates, or with the full set of Cartesian variables, thereby adapting the bond lengths and bond angles as well. The local optimizations were initiated from the lowest-energy configurations found during parallel tempering simulations in a reduced temperature range 25–150 K, and we have not carried out other specific global optimization for the peptides in electric field. The further stabilization of helices with an aligned electric field makes qualitative changes in the global minimum rather unlikely. From these minimizations, the magnitude of the dipole moment was obtained. The variations of the dipole moment relative to its value at zero field are represented in Fig. 7.

FIGURE 7.

Variations of the magnitude of the dipole moment of Ala₈ and Ala₁₆ under the stretching action of an aligned electric field, normalized by the dipole moment without field, for increasing field strength. The results obtained by local minimization using all coordinates (open symbols) or only torsion angles (solid symbols) are shown.

For both sizes, the extent of stretching is significant and exceeds 20% for Ala₈ under 10⁹ V/m. Most of the stretching effect is due to rearrangements in the backbone dihedrals, and the other internal coordinates (bond lengths and bond angles) only marginally contribute to the global stretching. Interestingly, the larger peptide stretches only half of Ala₈, in relative amounts. Since the dipole moment of Ala₁₆ is approximately twice the one of Ala₈, this shows that the two dipole moments increase with the same rate as the field is applied. This is not in contradiction with the greater effects of the field found in our simulations for the larger polypeptide, because the energetics is mainly driven by the dipole energy, which is proportional to the dipole moment, while the variations of the dipole moment itself with the field are a higher-order effect. The relatively lower effects found for the larger peptides are still somewhat surprising, considering that the entire backbone locally carries a dipole moment, thus being affected by the field. We interpret the curves of Fig. 7 as due to finite-size boundary effects, stretching of the small peptide Ala₈ being easier due the reduced number of hydrogen bonds.

Finally, the increase in the dipole moment with increasing field is initially linear, but slows down at high fields 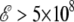V/m. This suggests further nonlinear effects due to the complex interplay between the different terms in the intramolecular energy and the interaction with the field. As a consequence, the global minimum energy approximately follows a cubic polynomial with increasing field strength, 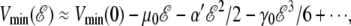where α₀ is an effective polarizability factor accounting for the stretching effects, and γ₀ the nonlinear correction.

Polarization effects

We now consider the interaction between the polypeptides and an intense electric field, discussing some aspects related to electronic polarization. The AMBER ff96 model used until now does not account for polarization effects, which may become important under extreme conditions, such as in the surroundings of ions or charged groups under a high field. The natural medium of many biological molecules, water, is highly polar, and the energy landscape of hydrated peptides is known to be affected by polarization effects (83). A lot of attention has been given recently to the development of polarizable force fields for molecular systems (84–90). Because these models are not specifically dedicated for molecules in high electric fields, they may underestimate polarization effects with respect to more sophisticated quantum mechanical calculations (91,92). Hence, we follow here a double approach, by considering first a polarizable force field, complementing some results with first-principle calculations.

Following Patel and Brooks (89,90), and consistently with some of our previous effort (93–95), we have chosen a fluctuating charges (fluc-q) framework to model polarizability effects in polyalanines. The fluc-q method has been developed by Mortier and co-workers (96) and by Rappé and Goddard (97) as the so-called charge-equilibration method. Briefly, the electrostatic energy V_Q of the molecule is written implicitly as a function of the partial charges {q_i} carried by the atoms as

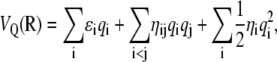(21)

where ɛ_i is the electronegativity of atom i, also equal to the opposite of the chemical potential. The parameters η_i are the hardnesses, while the cross terms η_ij depend on the distance r_ij between atoms i and j. All quantities ɛ and η are taken as adjustable parameters. Similarly as Patel and Brooks (89,90) we have chosen a simple combining rule for the hardnesses between heterogeneous elements, which has the correct asymptotic 1/r Coulomb behavior at large r:

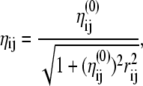(22)

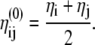(23)

The charges are calculated in practice by minimizing Eq. 21 above under the constraint of global charge neutrality, which is equivalent to solving a (N + 1) × (N + 1) linear system, with N the number of sites. We have parameterized this fluctuating charges model to mimic the AMBER ff96 charges as close as possible, for a set of conformations of the Ala₈ peptide taken from a Monte Carlo trajectory at 200 K in the helical conformation (no replica exchange attempted). In particular, we have considered the same atom types as AMBER ff96 (52); that is (for polyalanine), H, HO, H1, HC, C, CT, N, O, and OH. The values of the electronegativities and atomic hardnesses obtained from this systematic adjustment are reported in Table 1 for these atom types. They differ significantly from the values reported by Patel and Brooks (89) for the CHARMM force field, but it is important to stress that these authors parameterized their fluc-q potential based on density-functional theory calculations, while the present fitting was made to add some polarization contribution to the nonpolarizable force field without perturbing the static charges.

TABLE 1.

Atomic hardnesses η and electronegativities ɛ of the various AMBER ff96 atom types obtained by systematic least-square fitting the rigid charges for a sample of 1000 helical configurations of Ala₈ taken at 200 K

Atom type	η	ɛ	Atom type	η	ɛ
H	457.8	0	HO	3096.2	−828.9
H1	1471.5	−81.9	HC	1532.0	−287.6
C	1823.1	−1053.4	CT	2256.2	123.9
OH	2023.4	1025.5	O	3139.3	1563.3
N	1662.8	1023.6

The electronegativities are given in kcal/mol/e and the hardnesses in kcal/mol/e². The electronegativity of hydrogen attached to nitrogen (simply denoted H) was taken as the reference.

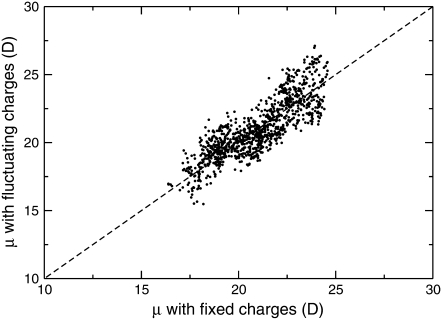
The correlation between the electric dipole moments obtained for the original AMBER ff96 fixed charges and the dipole moment obtained using the fluctuating charges is shown in Fig. 8 for the entire set of 1000 configurations.

FIGURE 8.

Correlation between the electric dipole of helical octa-alanine moments obtained with the AMBER ff96 fixed charges or with fluctuating charges, as obtained from a sample of 1000 helical configurations taken from a Monte Carlo simulation at 200 K.

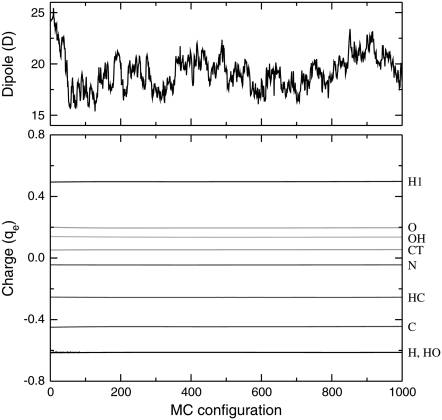
The agreement between the fixed-charges and the fluctuating-charges dipole moments is reasonably good. The behavior of the fluc-q polarizable model has been further illustrated in Fig. 9, where the variations of the norm of the dipole moment, as well as the charge averaged over identical atom types are shown versus the configuration number during the MC trajectory.

FIGURE 9.

Variations of the instantaneous electric dipole moment (upper panel) and average individual charges (lower panel) versus Monte Carlo configuration, as taken periodically along a 200 K trajectory of helical octa-alanine. The atomic charges are identified by their AMBER type, as indicated on the right of the panel.

While the dipole varies by significant amounts (from 15 Debye to ∼25 Debye), all fluctuating charges remain nearly constant for a given atom type. This surprising result tells us that the fluc-q model is able to mimic the original AMBER ff96 electrostatics, even relatively far from the equilibrium geometries.

We have used the fluc-q potential to study the influence of a high electric field on the electrostatic response. To separate the pure electronic and polarization effects from the atomic deformations, we only consider the Ala₈ and Ala₁₆ peptides in their more stable α-helix conformation at 0 K and without a field. The fluctuating charges are affected by the presence of the field, through an interaction term 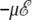in the right-hand side of Eq. 21 above. This term gives rise to effective electronegativities that are functions of the field (and the molecular geometry), but the self-consistent solution of the charges remains straightforward through matrix inversion. The charges have been determined for favorable conformations of the molecule, with its dipole moment aligned toward the field axis.

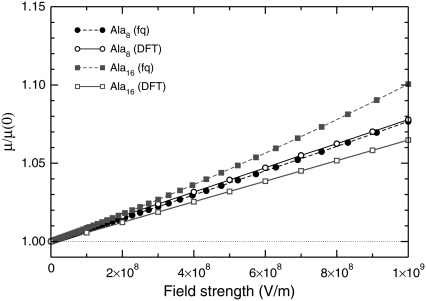
Additional density-functional theory calculations have been performed using the B3LYP hybrid functional and the 6–31+G* basis set, as available in the Gaussian03 software package (98), for electric fields in the range 0–10⁹ V/m. Again, the molecular geometry was taken as the AMBER ff96 helical minimum, and was not allowed to relax within the field. The norm of the dipole moment relative to its value without a field is represented in Fig. 10 as a function of field strength.

FIGURE 10.

Variations of the magnitude of the dipole moment of helical Ala₈ and Ala₁₆ with increasing field strength, due to electronic rearrangements only, as obtained from the fluctuating charges model (solid symbols) or from density-functional theory calculations (open symbols), for dipole moments aligned with the field. The dipole moments are normalized by their values without electric field.

Both the polarizable force field and the electronic structure calculations show that the apparent dipole is significantly increased upon applying a field, by up to 8% for Ala₈ at 10⁹ V/m. The results obtained with the present polarizable force field are in very satisfactory agreement with the density-functional theory calculations, given that no electronic structure data was included in the fitting procedure.

The marked increase in the dipole moment is a purely electronic effect, which cannot be captured by the nonpolarizable AMBER force field. Under high fields, polarization effects tend to further stabilize the peptide by increasing the dipole moment. The slopes, which measure the ratio between the polarizability and the dipole moment, are very similar for the two peptides. Considering that the dipole moment is essentially proportional to the number of alanine residues, this means that the polarizability of Ala₁₆ is approximately twice the one of Ala₈, even slightly lower, which agrees with simple additive arguments giving 100.3 ų and 198.7 ų, respectively. However, some marked deviations to the linear behavior are seen for the fluctuating charges model, which overestimates the electronic structure data by a few percents in the case of the larger peptide. Even though polarization effects are significant, they are not expected to convey a strong dependence on conformation. Therefore, the energetic balance between helices, sheets, and extended conformations should not be exceedingly affected by polarization. However, it would be interesting to calculate more specifically the polarization tensors of different secondary structures.

Structural phase diagrams

The simulation data obtained with the AMBER ff96 force field can be used to construct a phase diagram for characterizing the most stable conformation of small polyalanines as a function of both electric field and temperature. At zero field, three states are found, the α-helix state being the most stable below the folding temperature, the random coil state above the collapse temperature, and the β-strand conformation having a limited range of stability in between these two temperatures. At low field strength 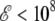V/m, the reweighting technique from the histograms in energy and dipole moment obtained at zero field can be used to determine the heat capacity curves as a continuous function of the applied field. We use this method for field strength up to 2 × 10⁸ V/m, even though its predictions above 10⁸ V/m should be only considered as semiquantitative. For higher fields, extrapolations based on our Monte Carlo simulations at 5 × 10⁸ V/m and 10⁹ V/m could also be affected by polarization effects.

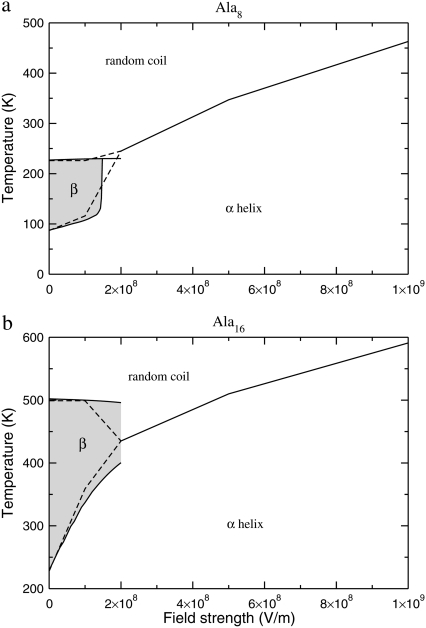
The schematic phase diagrams inferred from the simulations are shown in Fig. 11 for Ala₈ and Ala₁₆. The two polypeptides exhibit qualitatively similar diagrams, with a rather localized stability region for β-sheet conformations at moderate temperature and low electric field, separating the energetically favored α helices at lower temperatures and the entropically favored random coil states at high temperatures. Only a single-step helix-coil transition is found above ∼2 × 10⁸ V/m; however, for large peptides the α-β transition has a larger latent heat than the β-coil transition, making the two latter states harder to disentangle.

FIGURE 11.

Schematic (field strength, temperature) stability diagrams of Ala₈ (upper panel) and Ala₁₆ (lower panel). The boundaries of the shaded regions are obtained from reweighting of zero-field histograms, while the dashed lines are the results of direct simulations.

At high field strengths, the helix-coil transition temperature steadily grows with the field. Stretching effects are partly responsible for this increase, but the role of polarization should be investigated further.

The trends found in this work can be extended to larger polyalanines. First, the α-β transition should not last for very large peptides, and the increasing energetic stability of the helix conformations should make the β-conformations marginal, also without an electric field. In particular, tertiary structures composed of several helical parts could be more stable than the double-strand β-structures with a single turn at intermediate temperatures. The low net dipole moment of such tertiary structures would make them only moderately affected by the external field.

The structural phase diagrams of Fig. 11 can be interpreted differently if one varies the electric field at fixed temperature. At moderate temperature, increasing the field can lead to a β → α transition. At high temperatures, transitions from the random coil state to the α-helix can also take place upon increasing the field, in a very similar effect to the electrofreezing transition in water (15). Such transitions occur at a rather high field (above 5 × 10⁸ V/m), and could take place in the vicinity of counterions, metal ions, or other field-enhancing peptides.

CONCLUSIONS

External electromagnetic fields can have a strong influence on the structural and dynamical properties of polar molecular systems. In this article, we have investigated the thermodynamical behavior of small gas-phase polyalanines in the presence of a static and homogeneous electric field in the range 0–10⁹ V/m. Such values, albeit high, are comparable to the intensities found in the inner parts of biological molecules, e.g., ion channels (99). We have performed Monte Carlo simulations improved with all-exchanges parallel tempering, using the AMBER ff96 force field as our main model. An efficient way of sampling the flexible conformations and the various orientations together within the field was introduced by performing the statistical average over all orientations for each molecular configuration. This procedure leads to an effective temperature-dependent potential involving the Langevin function ℒ. We have also used a two-dimensional multiple histogram method where, from the correlated energies and dipole moments gathered at a series of temperatures and at zero field, the caloric curves at finite field can be calculated perturbatively. This method was found to be accurate at low fields 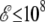V/m.

By calculating several order parameters, including the radius of gyration, the helical content, the end-to-end distance, and the fluctuations in the overlap with the native state, we have been able to characterize the combined influences of temperature and electric field on the stable conformations of octa-alanine and hexadeca-alanine. In agreement with our previous investigation (45), with experimental measurements (42) and with recent theoretical suggestions (43,44), the polyalanines were found to display a two-step unfolding transition, changing first from α-helix to β-strand conformations, then to extended coil at higher temperatures. The temperatures of these two transitions, respectively the folding and the collapse temperature, differ more for the larger peptide, but come closer to each other as the field is turned on.

Upon increasing the field strength, the macrodipole of the helical conformations stabilizes them significantly at the expense of the β-strand and random coil states. This shifts the α-β folding transition toward higher temperatures. Above some critical value of the field, the two peaks in the heat capacity merge and only a single helix-coil transition is observed. As the magnitude of the field increases, the helix is stabilized further and the collapse transition shifts to higher temperatures. The field has a stronger influence on the larger peptide, due to its larger dipole. In particular, the peak associated with the α-β transition becomes higher than the second peak, which appears as a high-temperature shoulder in an apparent post-melting phenomenon. These results could be interpreted using a simple three-state harmonic model in which the energetics of the helical state explicitly depends on the electric field according to the Langevin statistical behavior.

At low electric fields (<∼10⁸ V/m), an orientation toward the field axis takes place according to the Langevin law; hence, it is most important at low temperatures. At moderate fields, some deformations increase the macrodipole by stretching along the field, hence further stabilizing the α-helix. A specific study of this process reveals that the relative stretching is quite large in magnitude, and reaches 25% for Ala₈ under 10⁹ V/m, as measured on the dipole moment. However, stretching is not as important for the larger peptide, and it would be interesting to study specifically such effects as a function of the number of amino acids.

At high electric fields, polarization effects become more important, and we have parameterized a fluctuating charges model to mimic the fixed AMBER charges from a sample of equilibrium configurations. This polarizable model, as well as complementary density-functional theory calculations, both predict that the dipole moment increases at high field, linearly for the smaller peptide, but second-order effects are more pronounced for Ala₁₆ in the fluc-q model. These linear variations provide a direct estimate for the polarizabilities. While they are comparable in magnitude to the stretching effects, their increase with peptide size balances the decreasing stretching effects. However, and contrary to stretching, polarization effects should affect all conformations similarly. Thus, even though polarization effects should increase the macrodipole more rapidly than stretching, their influence on the structural transitions and helix/coil stability may not be so important.

Finally, based on our Monte Carlo simulations and the reweighting method developed here, we have sketched a schematic (field, temperature) structural phase diagram showing the various domains where each of the α-helix, β-strand, and random coil states is the most stable. In particular, our results suggest that electrofreezing transitions could occur at reasonably high temperatures, upon increasing the intensity of the field.

It would be interesting to characterize the global energy landscapes of the polyalanines studied here, especially for getting insight into the relaxation kinetics and pathways associated with the helix ↔ sheet interconversion. In particular, comparison with the results obtained by Mortenson and Wales (100,101) who also used AMBER ff96, albeit with different shielding parameters (including implicit solvent), would be very useful for assessing the role of the force field. The evolution of the landscape as the field is switched on and progressively increased would probably shed light onto the mechanisms affecting the relative stability of helical and sheet conformations.

The methods developed in this article could be useful for studying any molecular system in presence of an electromagnetic field. Water clusters (20–24) or water wires (17–19), for instance, would provide straightforward applications of the effective potential approach. Reweighting from zero-field histograms could also exempt us from performing explicit simulations in the weak fields' regime, thus allowing the investigation of field effects in a continuous range. This would be most valuable for dealing with larger biomolecules, for which sampling of the potential energy surface is a real concern.

The approximation of a single polarizability and dipole moment may be problematic for large molecules, whose geometrical extent may exceed the radius of convergence of the electrostatic energy. Distributed multipoles and polarizabilities would be a natural step beyond the present approach; however, their inclusion in the simulations would demand an important numerical effort. Guiding the Monte Carlo trajectories with a nonpolarizable force field, and correcting a posteriori with a proper polarizable potential, could be one way of improving the modeling along such lines (102,103). However, it would be desirable to have reference data obtained at a higher level of calculation, to assess the relevance of such potentials under intense fields.