Abstract
We propose what to our knowledge is a new technique for modeling the kinetics of voltage-gated ion channels in a functional context, in neurons or other excitable cells. The principle is to pharmacologically block the studied channel type, and to functionally replace it with dynamic clamp, on the basis of a computational model. Then, the parameters of the model are modified in real time (manually or automatically), with the objective of matching the dynamical behavior of the cell (e.g., action potential shape and spiking frequency), but also the transient and steady-state properties of the model (e.g., those derived from voltage-clamp recordings). Through this approach, one may find a model and parameter values that explain both the observed cellular dynamics and the biophysical properties of the channel. We extensively tested the method, focusing on Nav models. Complex Markov models (10–12 states or more) could be accurately integrated in real time at >50 kHz using the transition probability matrix, but not the explicit Euler method. The practicality of the technique was tested with experiments in raphe pacemaker neurons. Through automated real-time fitting, a Hodgkin-Huxley model could be found that reproduced well the action potential shape and the spiking frequency. Adding a virtual axonal compartment with a high density of Nav channels further improved the action potential shape. The computational procedure was implemented in the free QuB software, running under Microsoft Windows and featuring a friendly graphical user interface.
INTRODUCTION
In neurons and other excitable cells, voltage-gated channels open and close in response to changes in the membrane potential and thus play a critical role in the generation and propagation of action potentials. To understand neuronal function, one must obtain accurate models of ion channel gating mechanisms. The quantitative analysis of voltage-gated channels started with the work of Hodgkin and Huxley (1) on squid giant axons. Their original insight was to describe the gating mechanism in terms of independent activation and inactivation “particles”, each with first-order kinetics and voltage-dependent rate constants. For example, the Hodgkin-Huxley (HH) model of the Nav channel assumes three identical activation particles and one inactivation particle. However, experimental evidence strongly suggests that the four voltage sensors are not identical and activate cooperatively, and that the inactivation and activation processes are coupled (2–5). These features cannot be represented with a vectorial product of several independent gating particles, and one must turn to a description based on Markov models.
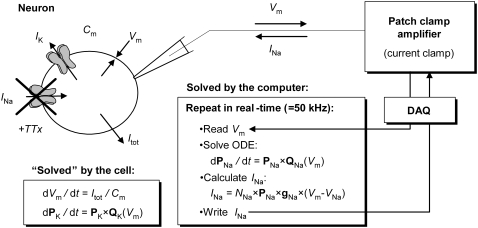
Ideally, one would determine the gating mechanism and estimate the average kinetic parameters for each channel type, across a population of neurons. However, even when this is practically possible, assembling this knowledge into a model of cellular dynamics may not reproduce the observed neuronal behavior. Factors contributing to model failure are the nonlinear dynamics of the cell (small parameter estimation errors may substantially change the cellular dynamics), and possibly a nonconvex parameter space, in which case the average estimate is not a generally acceptable solution (6). A recent technique that allows one to functionally replace a biological ion channel with a virtual conductance, and to study its effects upon cellular electrical behavior is the “dynamic current clamp” (7). In the “passive” current-clamp mode, a patch-clamp amplifier injects a current of prescribed value into the cell and simultaneously measures the membrane voltage. In contrast, the “dynamic” current clamp is a feedback loop (Fig. 1): the membrane voltage is measured, and a current is calculated according to a computational model that includes voltage dependence. This current is then injected into the cell, which in turn changes the voltage, and the whole process is repeated in real time.
FIGURE 1.
Replacing ion channel currents in functional neurons using dynamic clamp. As shown, the cell's own Na+ current is blocked with TTX, and a replacement current is injected using dynamic clamp, on the basis of a Nav kinetic model. In a real-time computational loop, the computer reads Vm from the amplifier through the digital acquisition card (DAQ), integrates the ODEs of the Nav model (shown as Markov), and calculates an output current INa and injects it into the cell. The entire construct is a hybrid biological-computational simulator: in each cycle, the cellular membrane “solves” the ODEs for Vm, IK, and other currents while the calculated INa is held constant by the D/A converter; simultaneously, the computer solves the Nav model using an effectively constant Vm, as provided by the A/D converter.
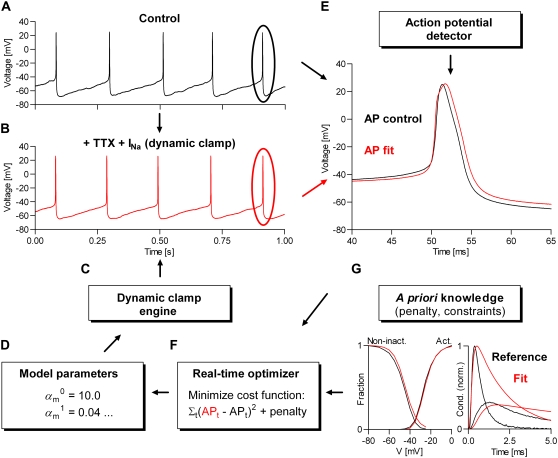
Here, we present the theoretical and computational details of what to our knowledge is a new technique—based on dynamic clamp—for real-time modeling of the kinetics of voltage-gated ion channels in a functional context. As illustrated in Fig. 2, this procedure involves several steps:
Record the “reference” action potential normally generated by the cell. If necessary, depolarize the cell to induce spiking.
Pharmacologically block the current passing through the studied channel (e.g., Nav).
On the basis of a voltage-dependent kinetic model, calculate and inject a current into the cell, using dynamic clamp. Adjust the parameters until spiking is restored, albeit with different frequency and action potential shape.
Calculate the error between the reference and the dynamic-clamp-generated action potentials.
If the error is small, then the model and its parameter values are accepted. If the error is large, choose a new set of parameters and repeat step 3. The search for optimal parameters can be automated, and prior knowledge from other experiments (e.g., previously recorded macroscopic currents) can be included in the fit.
FIGURE 2.
Real-time kinetic modeling of voltage-gated channels using dynamic clamp. The procedure is based on minimizing the difference between two action potential waveforms: one obtained under control conditions (A), and the other (B) obtained by replacing the current of the studied voltage-gated channel, using the dynamic-clamp engine (C), as shown in Fig. 1. The minimization of the cost function (the MSE between the two AP waveforms) can be done manually or programmatically (F), by changing in real time the parameters of a voltage-dependent kinetic model (D). A parameter-dependent penalty can be optionally added to the cost function, to include a priori knowledge, such as that provided by macroscopic currents (G) previously recorded from the same or other cell(s). Both the control and the fitted AP waveforms are averages of multiple consecutive spikes, detected when Vm crosses a user-defined threshold, e.g., −30 mV (E). The computation is divided between several parallel threads, but only the dynamic-clamp thread (C) runs in real time, responding within dt to any change in parameters, via manual user input, or from the optimizer.
The advantage of this new approach is that one may find a model and parameter values for a given channel type (e.g., Nav) that explain not only the biophysical properties of the channel, but also the functional behavior of a specific cell, without requiring any knowledge about the nonlinear interactions with other currents (e.g., Kv). Modeling kinetics from voltage-clamp protocols only has the potential of being very precise, but does not guarantee that the estimated parameters do, in fact, explain the observed dynamics for that very same cell; fitting the action potential should do so. Furthermore, in principle, one could repeat the experiment for other ion channel types, and functionally replace several currents one by one. At the end of the experiment, the obtained parameters will still guarantee spiking, with similar frequency and action potential shape, all for the same cell. In this way, one could even inspect the distribution of parameters across a population of cells (8).
Our results suggest that the real-time modeling technique proposed here has the practical potential to advance our understanding of how voltage-gated ion channels function and interact with each other in neurons and other excitable cells to create a large variety of dynamical behaviors. We extensively tested this procedure with computer simulations, but also with in vitro experiments on raphe neurons (9,10) patch-clamped in brainstem slices. These neurons were chosen because they spike tonically and are easy to identify, and are relatively electrotonically compact, which reduces experimental artifacts. We chose to model Nav channels because they can be fully and conveniently blocked with tetrodotoxin, but especially because they place the highest constraints on the dynamic clamp system due to their very fast kinetics and rather complex gating mechanisms. However, the same procedure can be applied to study other voltage-gated channels in neurons or in other excitable cells. We implemented the technical procedure as an extension of the freely available QuB software for electrophysiology (www.qub.buffalo.edu).
MATERIALS AND METHODS
Modeling
Kinetic models
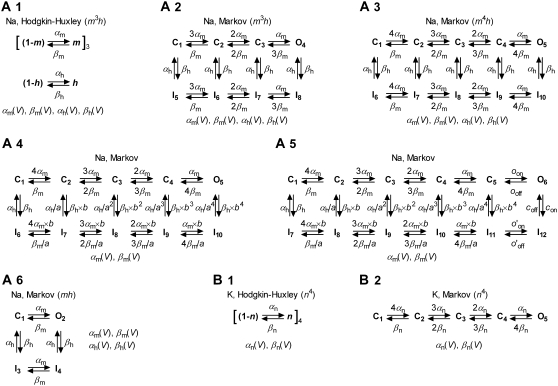
We tested both Markov and Hodgkin-Huxley models (Fig. 3). In the Markov formalism, each conformation of the ion channel is mapped into a state of the model, and the frequencies of transitions between states are quantified by rate constants. The rate constants of any Markov model can be compactly expressed as a rate matrix Q (11), of dimension NS × NS, where NS is the number of states. The Q matrix has each off-diagonal element, qij, equal to the rate constant between states i and j, and each diagonal element, qii, equal to the negative sum of the off-diagonal elements of row i, so that the sum of each row is zero. A voltage-dependent rate constant, kij, has the Eyring expression
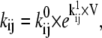 |
(1) |
where V is the transmembrane voltage, 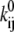 is the rate at zero membrane depolarization and
is the rate at zero membrane depolarization and 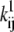 is a factor equal to δijzijF/RT, where zij is the electrical charge moving over the fraction δij of the electrical field, F is Faraday's constant, R is the gas constant, and T is the absolute temperature. The dynamics of a Markov model are described by the Kolmogorov equation:
is a factor equal to δijzijF/RT, where zij is the electrical charge moving over the fraction δij of the electrical field, F is Faraday's constant, R is the gas constant, and T is the absolute temperature. The dynamics of a Markov model are described by the Kolmogorov equation:
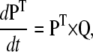 |
(2) |
where P is the (transposed) state probability vector, representing the occupancy of the NS states.
FIGURE 3.
Kinetic models of voltage-gated ion channels evaluated in this study. Hodgkin-Huxley models are a vectorial product of independent “gating particles”, each with first-order kinetics. Typically, Nav models have three identical activation particles and one inactivation particle (A1), whereas Kv models have four identical activation particles (B1). Markov models describe channels in terms of interconvertible conformational states, some conducting ionic current (the “open” states). Any HH model has a Markov equivalent (e.g., A1 and A2), but the converse is not true (e.g., Markov models A4 and A5 do not have a HH equivalent). In the Markov form, the constraints of gating-particle identity and independence are reflected by the ratio between successive steps (e.g., A2, 3αm:2αm:αm). The constraint of microscopic reversibility is implicit (in all HH models), or explicit (e.g., imposed by the a and b allosteric factors in A4). In most cases, rate constants are exponential functions of voltage, e.g., 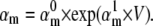
The Hodgkin-Huxley formalism describes voltage-gated ion channels in terms of independently gating “particles”, each with first-order kinetics and voltage-dependent rate constants. For a given channel, several identical particles may be required to describe a certain function, e.g., activation or inactivation. The dynamics of a HH model, e.g., of a Nav channel, can be formulated as
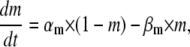 |
(3) |
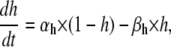 |
(4) |
where m and h are the occupancy probabilities for the activation and inactivation particles, respectively. The α and β values are the rate constants describing the gating transitions, in their standard naming convention, with Eyring voltage dependency as in Eq. 1:
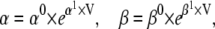 |
(5 and 6) |
although phenomenological voltage-dependent expressions are also used (1). Each HH model has a Markov equivalent, but the converse is not true, as Markov models are not limited to the same assumptions (identical and independent gating particles). The HH version of a model generally requires fewer differential equations than its Markov equivalent (e.g., two versus seven for the m3h Nav model), and therefore computes faster.
Steady-state probabilities
The steady-state probabilities of an ion channel can be calculated by setting equal to zero the differential equations describing the dynamics of the model. For a Markov model, we have
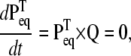 |
(7) |
where Peq is the vector of equilibrium-state probabilities. Equation 7 above can be solved for Peq as detailed in Colquhoun and Hawkes (11). For a HH model, the equilibrium occupancy probability, xeq, of a gating particle is similarly obtained by solving the equation
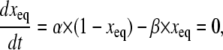 |
(8) |
with the simple solution
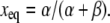 |
(9) |
When α and β have Eyring expressions, as in Eqs. 5 and 6, xeq is a sigmoidal function of voltage:
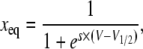 |
(10) |
where the slope, s, and the half-activation voltage, V1/2, are calculated as
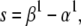 |
(11) |
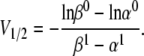 |
(12) |
The above calculations are for one gating particle only. For q identical and independent gating particles, the sigmoid in Eq. 10 is raised to the qth power.
Ionic currents
The ionic current passing through an ensemble of NC ion channels, in the Markov formulation, is calculated as
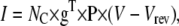 |
(13) |
where g is the vector of unitary conductances, and Vrev is the reversal voltage for the permeant ion. For a HH model, e.g., of a Nav channel, the current is
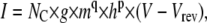 |
(14) |
where g is the unitary conductance, and q and p are the numbers of activation and inactivation particles, respectively. Including NC in the current equation is required for stochastic simulations, where the actual number of channels is important. For deterministic simulations, it may be more convenient to express the current in terms of specific conductance, gC (e.g., in nS/pF) and membrane capacitance, C (in pF), which is proportional to the membrane area:
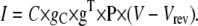 |
(15) |
In this case, g has elements equal to zero or 1, for closed or open states, respectively, being simply used to select the conducting states. Similarly, for HH models,
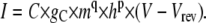 |
(16) |
In actual experiments, the capacitance of the membrane, C, can be estimated using the capacitance compensation circuits of the patch-clamp amplifier.
Cellular dynamics
The dynamic-clamp technique is practically restricted to measuring the membrane voltage in one cellular compartment (e.g., soma) and injecting a calculated current in the same compartment. For this reason, we assume here that the voltage and the modeled ion channel(s) are homogenously distributed within a single compartment. Under these conditions, the cellular dynamics are minimally described with ordinary differential equations (ODEs), one for voltage and the others for channel state probabilities. For example, to simulate the dynamics of a neuron with Nav and Kv currents, formulated as Markov models, one has to integrate the following ODEs:
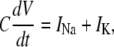 |
(17) |
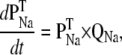 |
(18) |
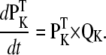 |
(19) |
Injecting currents into biological neurons using dynamic clamp is equivalent to a real-time, hybrid biological/computational simulation. Thus, the neuron “integrates” the ODEs for voltage and for its own biological ion channels, e.g., a Kv channel, whereas the computer integrates the ODEs for the modeled ion channel, e.g., a Nav channel, as illustrated in Fig. 1.
Deterministic ODE solver
Splitting the integration between the cell and the computer leads to errors. To minimize these errors, the integration step dt has to be as short as possible, and, since it takes place in real time, the computation must be fast. One of the fastest numerical integration methods is the explicit Euler. If x is the variable to be integrated (e.g., Pi or m) with dx/dt = fx(x, y, z,…), then the explicit Euler method provides the solution:
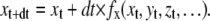 |
(20) |
The explicit Euler integration requires only one function evaluation per time step, but it also makes the largest error, proportional to dt (12), and it is the least stable.
The very fact that only the channel state probabilities have to be propagated in time, whereas the voltage has to be assumed constant between successive readings, makes it possible to use another integration method. Thus, the differential equation describing the dynamics of the state probability vector (Eq. 2) has the following analytical solution:
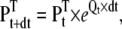 |
(21) |
where Pt and Pt+dt are the state probability vectors at time t and after a time step dt, respectively, and Qt is the rate matrix calculated using the voltage measured at time t. The assumption of constant voltage notwithstanding, this solution is exact, and it can be applied to any model, whether Markov or Hodgkin-Huxley. For a Markov model, the exponential of Qt × dt is the transition probability matrix, which can be conveniently calculated using the spectral expansion (11)
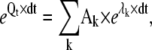 |
(22) |
where the Ak values are the spectral matrices and the λk values are the eigenvalues of the Qt matrix. For a HH model, based on the assumptions of equal and independent gating particles, the solution simplifies to
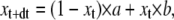 |
(23) |
where x represents the occupancy probability of a gating variable, such as m or h, and a and b are the expressions
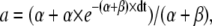 |
(24) |
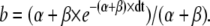 |
(25) |
The analytical solution (Eq. 21) consists of multiplying the vector of state probabilities by the transition probability matrix, and requires about the same computational effort as the Euler integration. However, for a general Markov model, it also involves computing the eigenvalues and the eigenvectors of the rate matrix Q. Clearly, this cannot be executed at each time step fast enough for a real-time application, but the matrix exponential can be calculated only once over an entire range of voltages, and the appropriate matrix can be substituted in Eq. 21, according to the value of V. This calculation will have to be repeated each time a parameter affecting Q is changed, but it can be performed outside the real-time thread.
Stochastic ODE solver
When the number of channels NC is in the thousands or hundreds, stochastic effects may become significant (13) and deterministic integration may not be accurate enough. In this case, we can use Gillespie's stochastic algorithm (14). Briefly, the lifetime of a Markov model in state i is a random variable with exponential distribution, with average equal to −1/qii. When the state randomly changes from i to j, it does so with probability
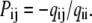 |
(26) |
Thus, to simulate the random dwelling of a Markov model, one needs to draw a sequence of random number pairs: an exponential deviate for the dwell duration and a uniform deviate to choose the next state. For an ensemble of NC channels, the descriptor of the ensemble's state is how many channels, Ni, are in each of the NS states. The average lifetime in this ensemble state is
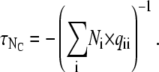 |
(27) |
This is the first random number to be drawn, an exponential deviate. Each of the Ni sets of channels can change state with probability
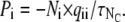 |
(28) |
This is the second random number, a uniform deviate. Thus, one channel in state i will switch to state j with probability Pij as in Eq. 26. This is the third random number, also a uniform deviate. For the new ensemble state, we make Ni := Ni – 1 and Nj := Nj + 1. The vector of state probabilities P is advanced over dt by repeatedly drawing these three random numbers, until the sum of the dwell times is ≥dt.
Gillespie's algorithm is very efficient (15). However, the average lifetime of the ensemble state is inversely proportional to the number of channels, NC. Thus, to advance the solution over dt, one will have to draw more and more random numbers as NC becomes larger, but this computation itself must take at most dt seconds in real time. For large NC, this becomes impossible. In this case, we can use Langevin's approximation (16), which is essentially solving the same deterministic ODEs, but with an added stochastic term ωt, so that dx/dt = fx(x, y, z,…) + ωt. This approximation gives different results from Gillespie's exact solution (13,16), but it is good enough when NC is large (17). Note that the stochastic integration is subject to the same kind of error as the deterministic integration, due to the assumption that the voltage is constant during dt.
Model parameters and constraints
The parameters of interest are the factors 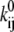 and
and 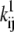 (or
(or 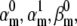 etc.), and the number of channels, NC, or the specific conductance, gC. As in any optimization problem, it is best to reduce the number of free parameters to a minimum, by enforcing constraints on the model. Some constraints arise naturally from the model itself. For example, one rate may be a multiple of another in the voltage activation pathway, and loops must be in microscopic detailed balance. Note that loop-containing Markov models that have a HH equivalent are automatically in balance. A particularly efficient way of implementing these linear constraints for Eyring rates (Eq. 1) is described in detail in (18), and we use it here whenever appropriate. The procedure involves using the singular value decomposition to obtain a reduced set of free parameters from the set of rate constants, through a logarithmic transformation of variable. For non-Eyring rates, the logarithmic transformation cannot be used, and the parameterization becomes more difficult when the model contains loops, but alternative solutions exist (19).
etc.), and the number of channels, NC, or the specific conductance, gC. As in any optimization problem, it is best to reduce the number of free parameters to a minimum, by enforcing constraints on the model. Some constraints arise naturally from the model itself. For example, one rate may be a multiple of another in the voltage activation pathway, and loops must be in microscopic detailed balance. Note that loop-containing Markov models that have a HH equivalent are automatically in balance. A particularly efficient way of implementing these linear constraints for Eyring rates (Eq. 1) is described in detail in (18), and we use it here whenever appropriate. The procedure involves using the singular value decomposition to obtain a reduced set of free parameters from the set of rate constants, through a logarithmic transformation of variable. For non-Eyring rates, the logarithmic transformation cannot be used, and the parameterization becomes more difficult when the model contains loops, but alternative solutions exist (19).
Parameter transformations
For Hodgkin-Huxley models with Eyring voltage-dependent rates (Eqs. 5 and 6), the following transformations—in addition to changing any parameter independently—simplify the manual search for optimal parameters:
- Offset V1/2 by ΔV mV, by changing the preexponential factors:
where f is a factor calculated from the relation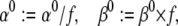
(29 and 30) 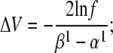
(31) - Change the slope, s, by Δs mV−1, by adding Δs/2 to the absolute value of each exponential factor:
At the same time, the preexponential factors are changed to keep V1/2 the same: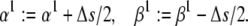
(32 and 33)
where f is calculated from the relation: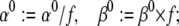
(34 and 35) 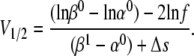
(36) - Keep the electrical charge constant but reposition the transitional complex in the electric field, by adding Δs/2 to each exponential factor:
Note that s is proportional to the total charge moved by the gating particle, and the transitional complex is positioned symmetrically in the electric field if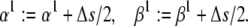
(37 and 38) 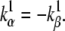 This transformation does not change the steady state;
This transformation does not change the steady state; - Make the gating process faster or slower, by changing the preexponential factors:
where f > 1 to make it faster. This transformation does not change the steady state;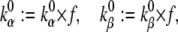
(39 and 40) - Offset the exponential voltage dependence of a single rate by ΔV mV, as follows:
where k stands for either α or β. This transformation does change the steady state.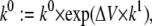
(41)
For Markov models, similar transformations may be difficult to implement in the general case, but for each specific model one may find empirical relations to obtain approximately the same results.
Real-time fitting
The principle of the real-time fitting procedure is illustrated in Fig. 2. The cost function is the sum of square errors (or the mean-square error) between the action potential waveforms, one recorded as a control and the other one obtained by injecting into the cell a current calculated according to the current set of parameters:
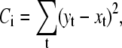 |
(42) |
where i refers to the iteration, t is the discrete time index in the waveform, and x and y are the voltage values in the fitted and in the control AP waveforms, respectively.
The real-time optimization procedure adjusts the parameters of the model—subject to constraints—as to minimize C. Although this is nothing more than curve fitting, there are some technical difficulties. Most important, the fitting curve cannot be simply calculated but it must be generated dynamically in real time (e.g., it takes 10 s of real time to simulate a 10-s time course). Second, the cost function is inherently random, due to stochastic ion channel fluctuations, voltage measurement noise, finite time resolution, and time step jitter. To reduce the effect of noise, several spikes should be collected and averaged, at the cost of increasing the fitting time.
There is no easy way to calculate analytically the gradients of the cost function. Numerical gradients could in principle be calculated, but they will be affected by the randomness of the cost function. Hence, a gradient-descent search method (18,20), although it would be very efficient, cannot be used here, unless this randomness can be reduced to acceptable levels (e.g., by averaging over many spikes, which depends on the stability of the experimental preparation). Therefore, we chose the Simplex optimization algorithm (21), as implemented in Press et al. (22), which is quite robust and relatively impervious to the randomness of the cost function. The main disadvantage of Simplex it that it becomes inefficient as it approaches the optimum. However, the very random nature of the cost function imposes a limit as to how far the convergence can be pushed, as C cannot be reduced below the inherent noise. Of course, a less stringent convergence results in less precise estimates.
Including a priori knowledge
The nonlinear interactions between ionic currents and membrane voltage result in a complicated relationship between the input parameters of the kinetic model and the cellular output. Therefore, a model tested with the dynamic clamp technique must also satisfy other a priori knowledge, if that is available. Including additional knowledge in the parameter estimation process can be accomplished by global fitting or by adding penalties to the cost function. In the first case, one can globally fit not only the action potential waveform, but other data as well, such as the steady-state activation and inactivation curves, or macroscopic currents elicited by voltage steps. Since these different data types have different noise properties and are also likely to come from different sources, their respective sums of squares must be weighted:
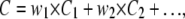 |
(43) |
where the w values are weighting factors summing to 1, which can be chosen empirically.
The objective of estimation with penalties is to find a set of parameters that best fit the data (e.g., action potentials), but which at the same time are in agreement with a prior parameter distribution. This prior distribution could be, for example, a multivariate Gaussian with mean vector μx and covariance matrix Vx. Thus, any set of parameter estimates x will have the associated probability density:
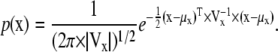 |
(44) |
The μx and Vx values can be determined from previously available data, e.g., by maximum likelihood fitting of single-channel (20,23,24) or macroscopic currents (18). From steady-state curves, μx can be determined with any fitting program, and Vx can be calculated using the method described in Colquhoun et al. (25).
For real-time fitting, the penalty can be added to the cost function in the following way:
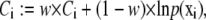 |
(45) |
where w is an empirical weighting factor. Using a penalty might be useful even when parameters are changed manually, if correlations are known to exist between them. Thus, when one parameter, 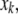 is individually changed to
is individually changed to 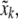 the other parameters
the other parameters 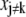 should be changed to
should be changed to 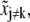 so as to maximize
so as to maximize 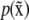 in Eq. 44. This maximization can be done numerically. If Vx is diagonal, then changing
in Eq. 44. This maximization can be done numerically. If Vx is diagonal, then changing 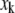 will not require any change in
will not require any change in 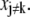 However, in the presence of cross correlations,
However, in the presence of cross correlations, 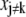 will also have to be adjusted, with the overall result that a change in one parameter is compensated by changes in the other parameters to minimize the error with respect to prior knowledge. Using prior parameter distributions has the advantage of including a priori knowledge in a computationally compact way, although these distributions may not be readily available.
will also have to be adjusted, with the overall result that a change in one parameter is compensated by changes in the other parameters to minimize the error with respect to prior knowledge. Using prior parameter distributions has the advantage of including a priori knowledge in a computationally compact way, although these distributions may not be readily available.
Experimental methods
Electrophysiology
In vitro brainstem slices (350–400 μm thick) from postnatal P0-P4 rats were perfused in aCSF containing (in mM): 124 NaCl, 25 NaHCO3, 3 KCl, 1.5 CaCl2, 1.0 MgSO4, 0.5 NaH2PO4, and 30 D-glucose, equilibrated with 95% O2/5% CO2, at room temperature (pH 7.4). Whole-cell recordings from neurons in raphe nucleus obscurus were obtained under IR-DIC visualization. For current-clamp recordings (including dynamic clamp experiments), electrodes (4–6 MOhm) were filled with a solution containing the following (in mM): 125 K-gluconate, 4 NaCl, 11 EGTA, 1 CaCl2, 10 HEPES, 4 Mg-ATP, 0.3 Na-GTP, and 4 Na-phosphocreatine, pH 7.3 (with KOH). For measuring Na+ currents with voltage steps, the K-gluconate was replaced with Cs-gluconate, prepared from CsOH and gluconic acid, and pH-adjusted with CsOH. In this case, the following blockers were added (in mM): 4 4-AP and 10 TEA-Cl in the pipette (substituting for Cs-gluconate), and 0.2 CdCl2 and 0.02 CNQX in the bath. Where necessary, Nav channels were blocked with 1–2 μM tetrodotoxin (TTX). A measured liquid junction potential of ∼10 mV for the K+-based and ∼8 mV for the Cs+-based solutions was corrected online.
Pipettes were coated with Sylgard to reduce capacitive transients, which also resulted in a more stable operation of the dynamic clamp. The series resistance error was compensated 75–80% for voltage-clamp recordings, using the 2 μs response time option of the amplifier-controlling software (Pulse 8.77, HEKA, www.heka.com), and 100% for current-clamp recordings. The value of Rs was periodically checked and the compensation was readjusted, if necessary. For voltage-clamp recordings, cells with Rs > 15 MOhm were discarded. For current-clamp experiments, Rs values as high as 40 MOhm were acceptable, but precise compensation was critical. Voltage-clamp data were digitally sampled at 100 kHz and low-pass filtered at 40 kHz. Where necessary, the capacitance of the neuronal membrane was determined as the value used to compensate the slow capacitive component, as determined automatically by the Pulse software. In some dynamic clamp experiments, an RC circuit representing a physical model of the cell was connected to the patch-clamp amplifier (model cell MC-9, from HEKA).
Computer work and data acquisition
We used the following hardware and software components: a desktop computer with a dual-processor 2.6 GHz AMD Opteron, running Windows XP Pro SP2; a National Instruments DAQ NI 6052E, controlled by the NI-DAQmx 8.1 driver (free download from www.ni.com); a HEKA EPC10 Double patch-clamp amplifier, controlled with the Pulse 8.77 software. The EPC10 features true, fast current-clamp, and allows injecting currents of maximum ±10 nA, sufficient for our application. A current offset of several pA, measured by the amplifier in the absence of any input, was corrected online with the dynamic clamp software.
Software implementation
We programmed the dynamic clamp and the real-time fitting procedure as extensions of the scripting language featured in the freely available QuB program (www.qub.buffalo.edu). A brief description of the operating procedure and examples are provided in Supplementary Material, Data S1.
RESULTS
First, we tested our dynamic clamp system with respect to integration accuracy, throughput rates and real-time performance. Next, we explored the issues of parameter identifiability and model discrimination, occurring when fitting action potentials, and determined the benefits of including additional knowledge obtained from voltage-clamp experiments. Finally, we tested the real-time fitting procedure, first in a computer simulation and then on raphé neurons.
Testing the dynamic clamp
The performance of the dynamic clamp and its suitability as a quantitative tool for modeling ion channel kinetics depend on how accurately the model is solved. Three deterministic and one stochastic integration methods were compared: the implicit back-differentiation formula implemented in the CVODE package (26), the explicit Euler (Eq. 20), the method using the transition probability matrix (Eqs. 21–25), and Gillespie's stochastic algorithm (Eqs. 26–28). The CVODE solution was run with settings for high accuracy (absolute and relative tolerances 1 × 10−6), and was used as the gold standard. A neuronal model having one Nav and one Kv channel type was simulated, with parameters chosen to produce tonic spiking. The Nav channel was formulated either as an m3h HH model (Fig. 3 A1), or as its Markov equivalent (Fig. 3 A2), and was integrated either deterministically or stochastically. The Kv channel was formulated as an n4 HH model (Fig. 3 B1), and was integrated deterministically. We also tested other models, as further described. The Euler and the matrix methods were tested both in non-real time and in real time. In the real-time case, the model was run as a self-contained computer simulation, or was interfaced with the patch-clamp amplifier, using a model cell connected as input.
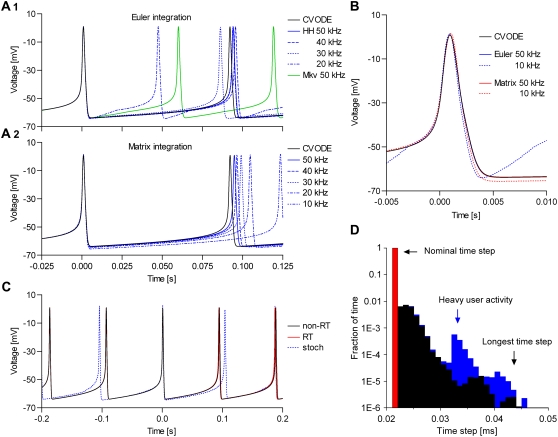
The spiking frequency and the shape of the action potential depend on the integration method, the size of the time step, and the properties of the model (Fig. 4, A and B). In general, the CVODE method was only slightly dependent on the time step, as expected. With the HH m3h Nav model, the spiking frequencies obtained with the three deterministic integration methods were approximately equal only if they were run at rates ≥50 kHz (Fig. 4, A1 and A2). Also, at 50 kHz all three methods resulted in virtually identical AP shapes (Fig. 4 B). At lower rates, Euler integration produced faster spiking and a distorted AP shape, becoming practically useless below 30 kHz (Fig. 4 A1). In contrast, the matrix integration was generally more stable, with only slightly slower spiking at lower rates, and was usable even at 10 kHz (Fig. 4 A2).
FIGURE 4.
Quantitative modeling with dynamic clamp relies on small integration errors and good real-time performance. A spiking neuronal model having one Nav and one n4 Kv channel type was integrated at different throughput rates (different dt), with the implicit back-differentiation formula in the CVODE package (used as reference), the explicit Euler (cf. Eq. 20), the transition probability matrix (cf. Eq. 21), and Gillespie's stochastic algorithm (cf. Eqs. 26–28). The spiking frequency (A) and the action potential shape (B) depend on dt and integration method. The matrix integration is more precise and stable than Euler, at all rates and with all tested Nav models. Thanks to minimal time-step jitter, a real-time simulation (C, red line) shows little difference from a non-real-time simulation (C, black line). A stochastic simulation (blue line) is considerably more irregular, like a biological experiment would be. The system runs at the nominal rate (50 kHz) ∼99% of the time, with a longest time step of ∼50 μs, and is relatively immune to heavy user activity and other simultaneous computation (D).
As expected, the Euler method had difficulty integrating the Markov form of the m3h model, with large errors even at 50 kHz (Fig. 4 A1). With more complex Markov models (e.g., the model in Fig. 3 A5), Euler failed completely. In contrast, the matrix method integrated the HH and the Markov forms with identical results, and could successfully solve the larger models. In conclusion, the dynamic clamp must be run at a frequency of ∼50 kHz, and possibly higher for models with faster kinetics. For Markov models, especially complex ones, or at lower throughput rates, the matrix integration method is the only reasonable choice. Based on these results, we recommend the matrix method for general purpose simulations, as it is accurate, stable, and fast.
Can typical models be run fast enough in a dynamic clamp configuration? Certainly. In Table 1, we list the throughput rates achieved with different models, on our test hardware configuration (see Methods). Generally, a single HH model runs at rates >75 kHz. Even more complete neuronal models, such as that proposed for respiratory neurons showing bursting behavior (27), containing three HH channels (m3h Nav + mh Nav + n4 Kv), run at 60–70 kHz. Markov models run more slowly, as there are more ODEs to be integrated, but they are still fast enough. Thus, the Markov equivalent of the m3h Nav model, having eight states and seven ODEs, runs at >60 kHz, whereas the larger model in Fig. 3 A5, having 12 states and 11 ODEs, runs at >50 kHz.
TABLE 1.
Kinetic models of voltage-gated channels can be accurately solved in real time
| Deterministic
|
Stochastic | ||||
|---|---|---|---|---|---|
| Euler integration
|
Matrix integration
|
Gillespie | |||
| HH
|
Markov
|
HH
|
Markov
|
Markov | |
| Model(s) | Maximum rate [kHz] | NC at 50 kHz | |||
| Navm3h | 79 | 62 | 77 | 61 | ∼20 |
| Navm4h | Idem | 55 | Idem | 55 | — |
| Navmh | Idem | 74 | Idem | 74 | ∼300 |
| Nav (Fig. 3A5) | — | 51 | — | 51 | — |
| Kvn4 | 81 | 73 | 81 | 73 | ∼400 |
| Kvn4 + Navm3h | 76 | 53 | 71 | 52 | — |
| Kvn4 + Nav (m3h + mh) | 70 | 47 | 64 | 47 | — |
Even a complex Nav Markov model (Fig. 3 A5) can be integrated at >50 kHz (dt < 20 μs), using the matrix method. Each case is a real-time simulation with I/O (reading Vm on one A/D channel and writing the calculated current on one D/A channel) and an R/C circuit—representing a physical model of the cell—connected to the patch-clamp amplifier. For stochastic simulations, the performance measure is the number of channels, NC, that can be integrated in the dt interval. In the absence of a model, the maximum throughput rate was limited by I/O to ∼110 kHz. These values will vary with computer performance.
The matrix integration method was only a little slower than Euler when applied to HH models, but was equally fast with Markov models. However, this was only a test for the matrix multiplication to advance the solution over dt (Eq. 21), and did not include the calculation of the transition probability matrix itself (Eq. 22). For Markov models, this matrix must be computed over a whole range of voltages, whenever a kinetic parameter is changed. We found that this calculation takes between a few hundred milliseconds and a few seconds, depending on the size of the model and on the range and discretization of the voltage. For example, it takes only a couple of seconds to calculate the matrix corresponding to the large Nav model shown in Fig. 3 A5, over a voltage range from −80 to 50 mV, with a discretization step of 0.1 mV. In fact, the accuracy was just as good even with a 0.5-mV discretization, which takes less than half a second. Note that this matrix computation takes place outside the real-time dynamic clamp loop, and only adds a little delay to the system's response to a user-input change in parameter values, without altering the integration time step. This delay is short enough, considering the human reaction time.
These tests cover a useful range of models, and can be used to predict the maximum throughput rates for other models, when using deterministic integration. We also tested the limits of stochastic integration with Gillespie's algorithm. In this case, the test measure is not the maximum rate, but the maximum number of channels that can be integrated within dt. With more channels than this maximum, the real-time required to advance the stochastic solution exceeds—probabilistically—the prescribed dt. To carry out this test, a spiking neuronal model was simulated, where one channel type was integrated stochastically, and the other(s) were integrated deterministically. The results are presented in Table 1. With the Markov equivalent of the m3h Nav model, the maximum number of channels that could be integrated at a throughput rate of 50 kHz was ∼20, but it reached ∼300 for the mh equivalent. Note that these numbers would be larger if only the stochastic channel was computed. For those applications requiring larger numbers, our software offers the choice of using Langevin's approximation, which runs at a speed comparable to deterministic simulations.
Real-time performance
Our dynamic clamp implementation runs under Microsoft Windows, which is not a real-time operating system, and it is therefore subject to time-step jitter. Practically, jitter means that occasionally some computational cycles will take longer to execute—in real time—than the prescribed dt. With the Euler integration, the actual duration of the time step, which can be read from the computer clock, can be used in Eq. 20. Thus, the effect of a longer dt is only a correspondingly larger integration error, although extremely long time steps may still bring the integration to a halt. With the matrix integration method, it is more difficult to take advantage of knowing the actual dt, as, for efficiency reasons, the transition matrix is precalculated for a given dt. However, the time-step jitter should have reasonably small effects, provided that the fraction of larger steps is small, and that the worst-case step is short.
By taking advantage of the multiprocessor architecture, we obtained a real-time performance comparable to that reported for real-time systems (28,29), in terms of jitter, and may have even exceeded it, in terms of throughput rates (see Table 1). Thus, a real-time simulation shows little difference from its non-real-time counterpart (Fig. 4 C, red line versus black line). An experiment involving a biological cell would certainly show more irregularity, due to inherent ion channel stochasticity and fluctuations in the measured membrane voltage. We illustrate this situation with a simulation in which the m3h Nav model is integrated stochastically (NC = 1000), and the n4 Kv model is integrated deterministically (Fig. 4 C, blue line). Notice the irregular interspike interval. Certainly, the time-step jitter affecting our dynamic clamp system is not only small, but will have effects that are an order of magnitude below those caused by biological and experimental noise.
The real-time performance of the software is summarized by the histogram of the actual time steps taken over a 2-min interval (Fig. 4 D). Thus, the longest time step was ∼50 μs, and the percentage of time steps longer than the nominal dt was <1%. It is very important to note that the performance was not affected much by graphical user activity or by other computation taking place in parallel with the dynamic clamp, such as calculating the transition probability matrix, the steady-state curves, or the macroscopic currents. In conclusion, the most important factors affecting the performance are the maximum throughput rate and the integration errors, and to a lesser extent the variability of the time-step. Taken together, these results suggest that our dynamic clamp system is fast enough to accurately run models of realistic complexity, either deterministically or stochastically. The numbers listed here can only improve as faster processors become available, and with some further code optimization.
Parameter identifiability
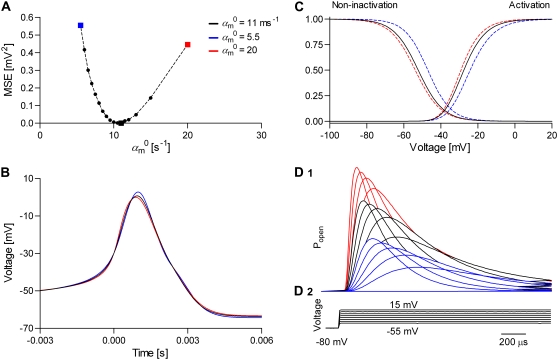
Our modeling goal is to find—for a given model—those parameters that best explain the data, according to some optimality criterion, such as minimum sum of square errors, or maximum likelihood. Under ideal conditions, i.e., noiseless, unlimited data, how many parameters can be uniquely identified from fitting action potentials? We answered this question empirically, with a simple experiment: using the automated fitting procedure (Fig. 2), we optimized all parameters of the model except one, which was held constant at different values. The rationale is that if all parameters can be uniquely identified, then we expect the plot of the cost function versus the value of the fixed parameter to show a single minimum. On the contrary, if parameters are degenerate, the cost function would be a flat line (a continuum of solutions), or would have multiple and identical minima (discrete solutions).
We tested the parameter identifiability for the m3h Nav model, but the same principles would apply to other kinetic models. Note that, for the purpose of parameter estimation, the HH and the Markov representations of the same model are equivalent. With all rates simple exponential functions of voltage, cf. Eqs. 5 and 6, the m3h model has nine free parameters: 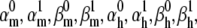 and g. In general, it may be tempting to reduce the number of free parameters by making equal the exponential factors for the same transition (e.g.,
and g. In general, it may be tempting to reduce the number of free parameters by making equal the exponential factors for the same transition (e.g., 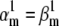 ), but doing so resulted in poor fits to our own voltage-clamp data recorded from raphe neurons. For this test, we fixed
), but doing so resulted in poor fits to our own voltage-clamp data recorded from raphe neurons. For this test, we fixed 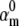 (the activation rate at zero depolarization) and optimized the other eight parameters.
(the activation rate at zero depolarization) and optimized the other eight parameters.
We found that the m3h model has a unique set of parameters for a given action potential. Thus, the cost function had a single minimum, corresponding to the true value of 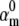 (Fig. 5 A). However, the cost function was rather shallow: changing the fixed parameter by a factor of 2 could be compensated by the free parameters so as to result in almost identical AP shapes (Fig. 5 B). These waveforms differed by a root mean-square (RMS) of <1 mV, which is comparable to membrane voltage fluctuations measured in real experiments. In contrast to the small differences in AP shape, the activation and inactivation steady-state distributions changed significantly with the value of the fixed parameter, especially with respect to V1/2 (Fig. 5 C). The responses to voltage steps also changed significantly, in terms of time course and maximum conductance (Fig. 5 D).
(Fig. 5 A). However, the cost function was rather shallow: changing the fixed parameter by a factor of 2 could be compensated by the free parameters so as to result in almost identical AP shapes (Fig. 5 B). These waveforms differed by a root mean-square (RMS) of <1 mV, which is comparable to membrane voltage fluctuations measured in real experiments. In contrast to the small differences in AP shape, the activation and inactivation steady-state distributions changed significantly with the value of the fixed parameter, especially with respect to V1/2 (Fig. 5 C). The responses to voltage steps also changed significantly, in terms of time course and maximum conductance (Fig. 5 D).
FIGURE 5.
Model parameters are theoretically identifiable from the action potential but practical identifiability requires additional information. First, a spiking neuronal model with one m3h Nav and one n4 Kv channel type was simulated. The resulting action potential waveform (B, black line), steady-state curves (C, black lines) and macroscopic currents (D1) calculated in response to a voltage-clamp protocol (D2) were registered as reference. Then, one parameter (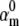 ) of the Nav model was fixed at different values, and the other kinetic and conductance parameters of the Nav model were optimized using the real-time optimizer. The cost function was the MSE between the reference and the fitting action potential waveforms. The MSE value of the best fit had a minimum at the true value of
) of the Nav model was fixed at different values, and the other kinetic and conductance parameters of the Nav model were optimized using the real-time optimizer. The cost function was the MSE between the reference and the fitting action potential waveforms. The MSE value of the best fit had a minimum at the true value of 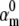 (A), indicating that a unique solution exists. The spike corresponding to the best fit (B, red and blue lines)—as obtained with different
(A), indicating that a unique solution exists. The spike corresponding to the best fit (B, red and blue lines)—as obtained with different 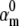 fixed values—differed little from the reference spike, but the steady-state curves (C, red and blue lines) and the macroscopic timecourses (D1, red and blue lines) differed significantly from their corresponding references.
fixed values—differed little from the reference spike, but the steady-state curves (C, red and blue lines) and the macroscopic timecourses (D1, red and blue lines) differed significantly from their corresponding references.
This test indicates that adding macroscopic currents or steady-state distributions to the action potential fit should improve parameter identifiability in practical terms, i.e., in the presence of noise. For models assuming independent and identical gating particles (i.e., Hodgkin-Huxley), steady-state distributions can be calculated with Eq. 10. However, even supposing that these assumptions are true in reality, it may be impossible to reconstruct the steady-state curves from experimental data, when the measured current depends on both activation and inactivation. The alternative is to construct approximate distributions, using a voltage-clamp protocol such as that shown in Fig. 6 A. Thus, the peak current during the first voltage segment is used as a measure of activation, whereas the peak current during the second segment is used as a measure of noninactivation.
FIGURE 6.
Theoretical steady-state distributions may not be approximated well from experimental voltage-clamp data. (A1–A3) We simulated the response of an m3h Nav model to a voltage-clamp protocol (A3) typically used to determine the voltage dependency of steady-state activation and inactivation, for 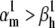 (A1), and for
(A1), and for 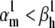 (A2). In both cases, for the same value of
(A2). In both cases, for the same value of 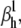 the
the 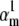 and
and 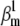 values were chosen so that
values were chosen so that 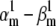 remained constant, which left unchanged the theoretical steady-state curves (B, black lines), calculated according to Eq. 25. Experimental steady-state curves were constructed by plotting the normalized peak conductance versus voltage (e.g., A1 and B, red circles). In this example, the two sets of experimental steady-state curves are quite different from each other (B, red and blue lines), and different from the theoretical curves (B, black lines). In each case (A1 and A2), the time to reach the peak conductance during the activation step is a different function of voltage (C).
remained constant, which left unchanged the theoretical steady-state curves (B, black lines), calculated according to Eq. 25. Experimental steady-state curves were constructed by plotting the normalized peak conductance versus voltage (e.g., A1 and B, red circles). In this example, the two sets of experimental steady-state curves are quite different from each other (B, red and blue lines), and different from the theoretical curves (B, black lines). In each case (A1 and A2), the time to reach the peak conductance during the activation step is a different function of voltage (C).
How good can these approximations be, relative to the theoretical steady-state curves? We answer with a practical example, by simulating the response of an m3h Nav model to the voltage-clamp protocol shown in Fig. 6 A3. The response is shown for two cases: 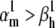 (Fig. 6 A1), and
(Fig. 6 A1), and 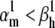 (Fig. 6 A2). Note that in each case we chose
(Fig. 6 A2). Note that in each case we chose 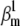 and
and 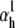 so as to preserve the charge, and hence to keep the theoretical curves unchanged (see Eqs. 37 and 38). A comparison between the theoretical and the two sets of approximate distributions indicates significant differences (Fig. 6 B), especially in activation. Differences are also notable in the time-to-peak, plotted as a function of voltage (Fig. 6 C). These results strongly suggest that, when used as an additional fit criterion, steady-state curves should be calculated from a simulation in response to the same voltage-clamp protocol as that used for the experimental data. Failure to do so may easily result in estimation errors, e.g., underestimation of the activation charge or V1/2.
so as to preserve the charge, and hence to keep the theoretical curves unchanged (see Eqs. 37 and 38). A comparison between the theoretical and the two sets of approximate distributions indicates significant differences (Fig. 6 B), especially in activation. Differences are also notable in the time-to-peak, plotted as a function of voltage (Fig. 6 C). These results strongly suggest that, when used as an additional fit criterion, steady-state curves should be calculated from a simulation in response to the same voltage-clamp protocol as that used for the experimental data. Failure to do so may easily result in estimation errors, e.g., underestimation of the activation charge or V1/2.
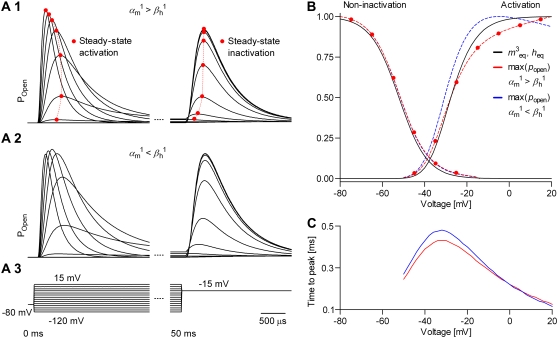
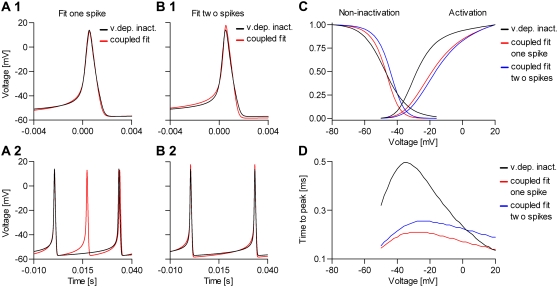
Model discrimination
When the model itself is not known, one needs to be able to compare different models and select the best one. For example, one may want to test whether inactivation is intrinsically voltage-dependent or is coupled to the activation process (2), or to estimate the number of steps in the activation pathway, by comparing m4h, m3h, and m2h models (30). Under ideal conditions, can these models be discriminated on the basis of fitting action potentials? To answer this question empirically, we simulated with one type of model and fitted with the other(s). For the first test, data were simulated with the Markov model shown in Fig. 3 A3, which features voltage-dependent inactivation, and were fitted with the model shown in Fig. 3 A4, which has voltage-independent inactivation, but coupled to the activation process. For the second test, data were simulated with the m4h model and were fitted with m3h or m2h. The tests were run by fitting either a single spike or two consecutive spikes. Fitting two spikes effectively adds the constraint that the model should match the data in terms of spiking frequency, although it cannot be easily applied to experimental data, when the interspike interval is variable.
The results of the first test indicate that the model with voltage-dependent inactivation (Fig. 3 A3) can be theoretically distinguished from the model with inactivation coupled to activation (Fig. 3 A4), as shown in Fig. 7, A and B. However, the differences are probably too small to matter in practical experiments, unless additional information is considered (Fig. 7, C and D). Thus, when fitting a single spike, the second model was capable of a good fit to data simulated with the first model (Fig. 7 A1), but could not reproduce the spiking frequency (Fig. 7 A2). In contrast, when fitting over two consecutive spikes, the AP shapes were more different (Fig. 7 B1), but the spiking frequency was correct (Fig. 7 B 2). In contrast to the small differences in AP shape, the two models differed significantly in terms of steady-state distributions (Fig. 7 C) and time-to-peak plots (Fig. 7 D). Likewise, the results of the second test (not shown) indicate that the m2h, m3h, and m4h models are theoretically distinguishable from each other, but the differences in AP shape were small. In contrast, the steady-state distributions and the time-to-peak plots were significantly different, and can help to discriminate these models in practice.
FIGURE 7.
Models with and without voltage-dependent inactivation can be discriminated. We simulated a spiking neuron having one Nav channel type with voltage-dependent inactivation rates (cf. Fig. 3 A3) and one n4 Kv channel type. The Nav channel was then replaced by a model with voltage-independent inactivation rates (cf. Fig. 3 A4), and optimal parameters were found with the real-time optimizer. As cost function, we used the shape of one single spike (A) or two consecutive spikes (B), which effectively enforces a match of the spiking frequency. The coupled model could not exactly reproduce the spike simulated with the uncoupled model, especially when fitting two spikes, but differences were small. More obvious was the mismatch between the different sets of steady-state curves (C), and between the time-to-peak plots (D, cf. Fig. 6 C). Similar results were obtained when comparing models with different numbers of activation particles (voltage sensors)—see text.
Improving parameter identifiability and model discrimination
Taken together, the previous results strongly suggest that, as expected, extra information should be added to the action potential fit to significantly improve parameter identifiability and model discrimination. Exactly what data are necessary depends on the specific model and parameter values. At the minimum, one could use a voltage-clamp protocol like the one shown in Fig. 6. The macroscopic currents recorded in response to this protocol contain both stationary and transient information. While these currents can be fitted directly, it is more efficient to condense this information into activation and inactivation steady-state plots, time-to-peak plots, and time courses at a few voltages. These data representations, together with the action potential waveform, make the components of the cost function, C (cf. Eq. 43)
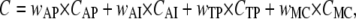 |
(46) |
where the terms indexed by AP, AI, TP, and MC stand for the components of the cost function (weight and mean-square error) calculated from the action potential, activation and inactivation steady-state curves, time-to-peak plots, and macroscopic currents, respectively.
To determine the sensitivity of the cost function to parameter values, we first simulated a spiking model having an m3h Nav and an n4 Kv channel type. Multiple trials were then simulated, with the parameters of the Nav model uniformly randomized within a range containing the reference values. For each trial, the voltage-clamp protocol shown in Fig. 6 was used to calculate the steady-state and time-to-peak curves, and the macroscopic time courses corresponding to voltage steps from −80 to −30 mV and from −80 to 0 mV, normalized to the maximum current value of the two. Furthermore, we calculated the RMS difference between each of the randomized trials and the reference trial separately for AP, steady state, time to peak, and macroscopic currents. We selected only those trials that resulted in spiking. Out of these, we further selected those with an AP RMS of <3 mV, steady-state RMS of <0.03, time-to-peak RMS of <0.03 ms, or macroscopic (normalized) current RMS of <0.03. These RMS values represent ∼3% of the range of the cost function variable (e.g., voltage or probability) for each component.
The AP component of the cost function changed little even when parameters were changed two- or even fourfold, as indicated by the correlation plots in Fig. 8 A (black circles). Some parameters appeared to be correlated, e.g., 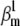 and
and 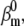 or to have a narrower range, e.g.,
or to have a narrower range, e.g., 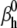 and
and 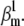 In comparison, the timecourse component was more sensitive to parameter values (Fig. 8 A, red circles). Clearly, fewer trials met the selection criteria in this case (there are fewer red circles than black circles), and over a narrower parameter range, e.g.,
In comparison, the timecourse component was more sensitive to parameter values (Fig. 8 A, red circles). Clearly, fewer trials met the selection criteria in this case (there are fewer red circles than black circles), and over a narrower parameter range, e.g., 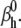 The activation and inactivation steady-state and the time-to-peak components were also more sensitive to parameter values than the AP (results not shown). Interestingly, there was no apparent correlation between the four components of the cost function, as indicated by the plots in Fig. 8 C. This suggests that these criteria are orthogonal and should be used together. Their intersection will effectively result in estimates with higher precision, as is generally the case with global fitting. We also checked the sensitivity of the spiking frequency to each parameter, and found that for this particular model and parameter values, only
The activation and inactivation steady-state and the time-to-peak components were also more sensitive to parameter values than the AP (results not shown). Interestingly, there was no apparent correlation between the four components of the cost function, as indicated by the plots in Fig. 8 C. This suggests that these criteria are orthogonal and should be used together. Their intersection will effectively result in estimates with higher precision, as is generally the case with global fitting. We also checked the sensitivity of the spiking frequency to each parameter, and found that for this particular model and parameter values, only 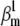 changed it somewhat predictably (Fig. 8 B).
changed it somewhat predictably (Fig. 8 B).
FIGURE 8.
Action potentials of similar shape can be obtained with different parameter sets. We simulated a spiking neuron having one m4h Nav and one n4 Kv channel type. For each simulation trial, parameters were uniformly randomized around some reference values (A and B, green circles). The randomization ranges were as shown for each graph. Shown are the spiking trials with MSE < 3 × 3 mV2 from the reference action potential waveform (A and B, black circles), and the spiking trials with MSE < 0.03 × 0.03 from the reference normalized time courses at −30 and 0 mV (A, red circles). Some parameters appear correlated, notably 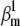 with
with 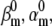 or
or 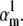 The spiking frequency (fAP) can depart considerably from the reference (∼30 Hz), and is mostly correlated with
The spiking frequency (fAP) can depart considerably from the reference (∼30 Hz), and is mostly correlated with 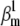 (B). There is no apparent correlation between the MSE for AP shape (MSEAP), steady-state (MSEAI), time-to peak (MSETP), or time course (MSETC) (C), which suggests that all these criteria should be simultaneously used in a global fit to improve the precision of the estimates.
(B). There is no apparent correlation between the MSE for AP shape (MSEAP), steady-state (MSEAI), time-to peak (MSETP), or time course (MSETC) (C), which suggests that all these criteria should be simultaneously used in a global fit to improve the precision of the estimates.
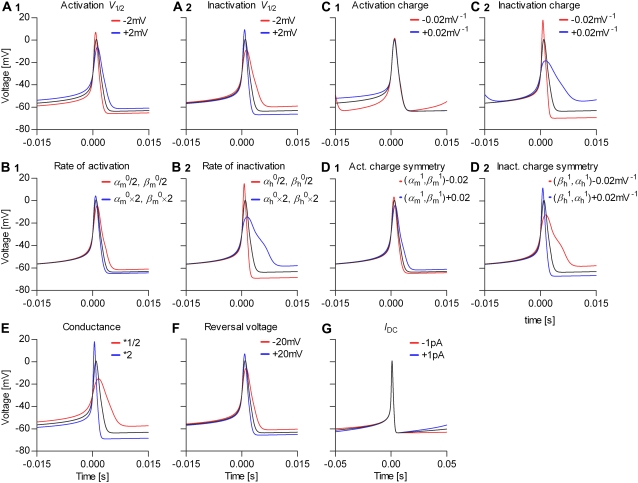
Effects of parameter transformations on the shape of the action potential
Even when the free parameters have a unique solution, the real-time optimizer may still get trapped in a local minimum, if started too far from the global solution. Also, some experimental variables may change if it takes too long to reach convergence. To improve the chance of finding the global minimum and to shorten the time, one must carefully choose the parameter starting point. For this, it is important to know how to change the model so as to obtain a desired change in the shape of the action potential. Of course, this extends to all fitting criteria, such as steady-state curves and macroscopic currents, but changing these is more intuitive. Having this information, it is easier to manually adjust parameters toward a better starting point for the automated fitting routine. We applied this sensitivity analysis to the parameters of the m3h Nav model, and to a few other biophysical variables. The kinetic parameters of the model were changed indirectly, through the transformations specified by Eqs. 29–41. The results apply only to this particular Nav model and parameter values, and are valid only in the context of the accompanying Kv model, but some general principles can be extracted.
We found that different parameters had specific effects on the action potential shape, as illustrated in Fig. 9. However, there was some ambiguity, confirming the results of previous experiments (Fig. 5). Thus, the width and height of the spike were simultaneously affected by the activation V1/2 (Fig. 9 A1), but also by the Na conductance (Fig. 9 E). Likewise, the inactivation V1/2 (Fig. 9 A2) and the Na reversal potential (Fig. 9 F) had comparable effects. Also, the rate of (in)activation (Fig. 9, B1 and B2) and the position of the (in)activation charge in the electrical field (Fig. 9, D1 and D2) had similar effects. This ambiguity can be resolved only by inspecting other properties of the model, e.g., the steady-state distributions and the macroscopic time courses. For example, the (in)activation V1/2 is a parameter of the (in)activation steady-state curve, but the conductance and the reversal voltage are not. Together with the AP shape, these properties of the model should indicate which parameters should be adjusted.
FIGURE 9.
Parameter transformations change the action potential shape and the spiking frequency in a predictable way. We simulated a spiking neuron having one m4h Nav and one n4 Kv channel types (black line in each graph), then we applied several transformations to the parameters of the Nav model (rate factors) (A–D), and to the Na conductance (E), Na reversal voltage (F), and injected offset current (G), as indicated (red and blue lines).
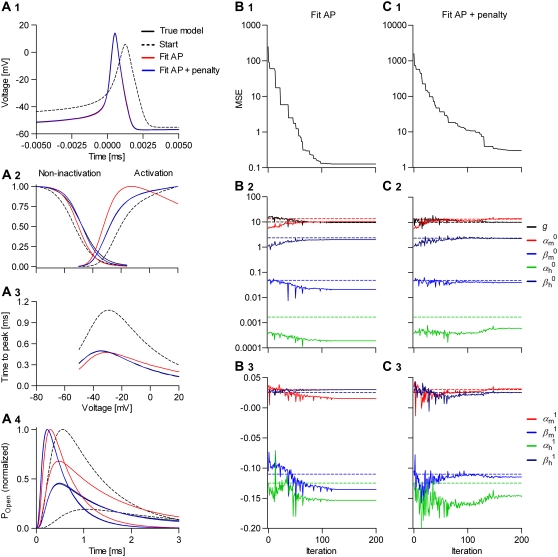
Testing the real-time fitting in a computer simulation
To test the optimizer in controlled conditions, a spiking neuron having one m4h Nav and one n4 Kv channel type was simulated. The parameters of the Nav model were then randomly changed from their reference values, so as to preserve spiking but to significantly change the shape of the action potential and the steady-state and transient properties of the model. From this point, we let the optimizer find the best fit, with the expectation that it will converge onto the reference values. The free parameters to be optimized were the eight rate factors (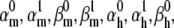 and
and 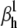 ) and the conductance, g. The cost function was the mean-square error (MSE) calculated from the AP shape, or from the AP shape together with the activation and inactivation steady-state curves, time-to-peak plots, and the normalized macroscopic time courses at −30 and 0 mV. In the second case, the four components were weighted in a ratio 2 × 10−4:1:1:1. The steady-state distributions were calculated according to the experimental voltage-clamp protocol. For the macroscopic time courses, the starting-state probabilities were calculated as the equilibrium distribution at the holding voltage (−80 mV).
) and the conductance, g. The cost function was the mean-square error (MSE) calculated from the AP shape, or from the AP shape together with the activation and inactivation steady-state curves, time-to-peak plots, and the normalized macroscopic time courses at −30 and 0 mV. In the second case, the four components were weighted in a ratio 2 × 10−4:1:1:1. The steady-state distributions were calculated according to the experimental voltage-clamp protocol. For the macroscopic time courses, the starting-state probabilities were calculated as the equilibrium distribution at the holding voltage (−80 mV).
When the cost function was calculated only from the action potential, the optimizer found a set of parameters that accurately reproduced the shape of the action potential (Fig. 10 A1), but not necessarily the other properties of the model, especially the steady-state activation curve (Fig. 10 A2) and the macroscopic time courses (Fig. 10 A4). In contrast, the solution found by global fitting explained very well not only the AP shape (Fig. 10 A1) but all the other properties of the model (Fig. 10, A2–A4). One exception was the steady-state inactivation curve, which indicated a slight underestimation of the electrical charge (i.e., 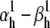 ). It turned out that this was a local minimum that trapped the optimizer. After manually increasing the inactivation charge, the optimizer easily found the global minimum (results not shown).
). It turned out that this was a local minimum that trapped the optimizer. After manually increasing the inactivation charge, the optimizer easily found the global minimum (results not shown).
FIGURE 10.
Convergence of the automated fitting procedure: a simulation study. We simulated a spiking neuron having one m4h Nav and one n4 Kv channel type (A, black lines). Then we randomized the kinetic parameters and the conductance of the Nav model, and from this starting point (A, dashed lines), we let the real-time optimizer find the best fit. As cost function, we used either the AP shape (B), or the AP shape and the steady-state curves, time-to-peak plots, and normalized time courses at −30 and 0 mV (C). The progress of the optimization (the MSE) is illustrated with an example in each case (B1 and C1). The true parameter values are indicated by the interrupted lines in B2, B3, C2, and C3.
Even with global fitting, the optimized parameters were not exactly the same as the reference values. This is not surprising, considering both the sensitivity results (Fig. 8) and the relative inefficiency of the Simplex optimizer near convergence. Certainly, optimizing nine free parameters of a model with highly nonlinear dynamics is not an easy problem, and it took ∼100–150 iterations to reach convergence. Generally, adding constraints improves the solution. Constraints such as those used in the second experiment (Fig. 10 C), which do not change the number of free parameters, slowed the convergence a little (Fig. 10 C1). On the other hand, constraints such as microscopic reversibility or scaled rates, which reduce the number of free parameters (18,19), would make convergence faster. We also tested the optimizer with the Nav model integrated stochastically. In this case, the spike shape and the interspike intervals were irregular. Despite the added stochasticity, we obtained similar results (not shown) by increasing the number of spikes to be collected and averaged for each evaluation of the cost function.
Testing the real-time fitting in neurons
The results so far are based on computer simulations of a neuronal model that minimally consists of Nav and Kv channel types. In reality, the kinetics of Nav channels are finely tuned to interact with the multitude of other ionic currents expressed by the neuron to generate action potentials of specific shape and frequency (31). Since not just any Nav model, with an arbitrary set of parameters, will make the neuron spike, we had to construct a preliminary Nav model from whole-cell voltage-clamp data. As shown in Table 1, it is possible to accurately run Markov models that are more complex and more realistic than the traditional Hodgkin-Huxley model. However, our goal here was to test the technique, and thus the widely known and better understood HH model seemed more appropriate.
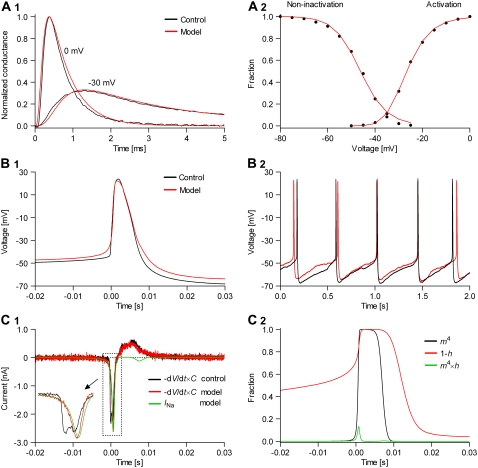
The m4h Nav model fitted well the voltage-clamp data (Fig. 11 A, red lines), and better than the m3h model (results not shown). Instead of fitting the entire set of macroscopic currents elicited by the voltage-clamp protocol shown in Fig. 6 A3, we chose to globally fit only the normalized macroscopic currents raised by voltage steps from −80 to −30 mV, and from −80 to 0 mV (Fig. 11 A1), and the steady-state curves (Fig. 11 A2). The rationale was that this condensed information is visually more intuitive and it is more likely to be used as prior knowledge in a modeling experiment. We verified that this combination of transient and steady-state data provided enough information for a unique parameter solution. The curve fitting was done with the same real-time optimizer (cf. Fig. 10), but without including the action potential component in the cost function (cf. Eq. 46).
FIGURE 11.
Nav channels in raphe neurons can be functionally replaced with dynamic clamp. Whole-cell macroscopic currents were recorded in response to the voltage-clamp protocol shown in Fig. 6 A3, and steady-state curves were constructed as explained in the legend to Fig. 6. The currents elicited by −30 and 0 mV steps (A1), together with the steady-state curves (A2) were globally fitted with an m4h Nav model (red lines). The estimated parameters are 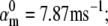
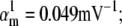
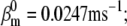
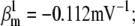

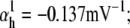
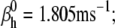 and
and 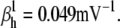 (B) A current-clamp recording of a tonically spiking raphe neuron (black traces). After bath application of TTX, a current is injected with dynamic clamp, using the m4h Nav model with the above kinetic parameters and a conductance of 16 nS/pF (A and B, red lines). (C1) The current flowing through the membrane (black and red traces) and calculated from the model (green trace). (C2) The time courses of activation (m4), inactivation (1 − h), and open probability (m4 × h). The real-time integration rate was 50 kHz.
(B) A current-clamp recording of a tonically spiking raphe neuron (black traces). After bath application of TTX, a current is injected with dynamic clamp, using the m4h Nav model with the above kinetic parameters and a conductance of 16 nS/pF (A and B, red lines). (C1) The current flowing through the membrane (black and red traces) and calculated from the model (green trace). (C2) The time courses of activation (m4), inactivation (1 − h), and open probability (m4 × h). The real-time integration rate was 50 kHz.
The m4h Nav model and the above estimated parameter values (see Fig. 11 legend) were tested in tonically spiking raphe neurons. Characteristic for these neurons is a relatively broad action potential (4–5 ms; Fig. 11 B1, black trace), a regular spiking pattern (2–3 Hz; Fig. 11 B2, black trace), and a strong after-hyperpolarization. For each analyzed cell, we recorded the firing pattern in the current clamp mode (i.e., the control), then bath-applied TTX, which fully blocked Na+ channels in these neurons, as verified with voltage steps. Upon TTX application, some cells ceased firing, whereas others switched to a Cav channel-based spiking behavior (data not shown). Using the dynamic clamp, we then tried to restore the spiking pattern, in terms of action potential shape and firing frequency. We started with a zero nS/pF conductance (cf. Eq. 16), and increased it until spiking was initiated (in initially silent neurons), and then until the slope of the voltage during the rising phase approximately matched the control.
With the m4h model and the kinetic parameters obtained from voltage-clamp data we were able to generate action potentials in virtually all of the cells we tried (>20). In most cells, the shape of the action potential was an almost perfect match for the control, as illustrated by the example shown in Fig. 11 B1 (red trace). The overall spiking pattern was also remarkably similar to the control, in terms of regularity, frequency, and after-hyperpolarization (Fig. 11 B2, red trace). However, one obvious difference characterizes the onset of the action potential, when the voltage rises slowly in the model but takes a sharp upturn in the control. This difference makes the activation threshold of the model appear more positive than the control. This is not true, in fact, considering that the two traces were aligned with respect to the point where they cross a −30-mV threshold. On the other hand, the reduction in the after-hyperpolarization between the control and the model is a real difference, but it is largely due to a cellular run-down in some outward current, which we could not prevent.
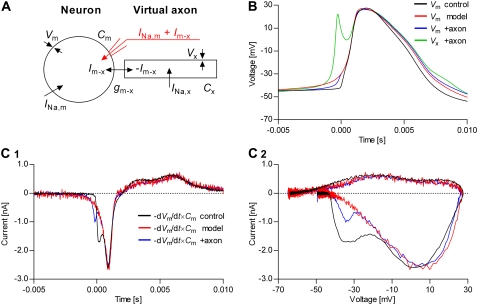
The current flowing through the membrane during the action potential, calculated as 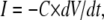 where C is the estimated membrane capacitance, is shown in Fig. 11 C1 (control, black trace; model, red trace). The minus sign is used to follow the convention that a depolarization is caused by a negative (inward) current. Also shown is the current injected in the cell, as calculated according to the Nav model (INa, green trace). Note that C, and consequently I, are only estimates. In fact, I in this figure was adjusted by an arbitrary factor, to match INa, since the only current likely to flow during the rising phase of the action potential is through Nav channels. Also note that the control current has a more abrupt rising initially, and reaches a peak value, after which it follows approximately the same trajectory as the model current. The time courses followed by activation (m4), inactivation (1 − h), and open probability (m4 × h) during the action potential are shown in Fig. 11 C2. It is remarkable that the maximum open probability reached by the Nav model is <0.15. Given that value, the overlap between the control and the model currents—at least during the later phase—suggests that the conductance of the model was appropriate. Of course, a model with a different set of rates might reach a different open probability, and thus it will require a different conductance to give the same current.
where C is the estimated membrane capacitance, is shown in Fig. 11 C1 (control, black trace; model, red trace). The minus sign is used to follow the convention that a depolarization is caused by a negative (inward) current. Also shown is the current injected in the cell, as calculated according to the Nav model (INa, green trace). Note that C, and consequently I, are only estimates. In fact, I in this figure was adjusted by an arbitrary factor, to match INa, since the only current likely to flow during the rising phase of the action potential is through Nav channels. Also note that the control current has a more abrupt rising initially, and reaches a peak value, after which it follows approximately the same trajectory as the model current. The time courses followed by activation (m4), inactivation (1 − h), and open probability (m4 × h) during the action potential are shown in Fig. 11 C2. It is remarkable that the maximum open probability reached by the Nav model is <0.15. Given that value, the overlap between the control and the model currents—at least during the later phase—suggests that the conductance of the model was appropriate. Of course, a model with a different set of rates might reach a different open probability, and thus it will require a different conductance to give the same current.
Next, we tested the automated real-time fitting. The results presented in Fig. 12 illustrate the ability of the real-time optimizer to find a set of parameters that simultaneously explains not only the action potential shape (Fig. 12 A), but also the steady-state (Fig. 12 C) and the macroscopic currents (Fig. 12 D). In the cost function, the above three components were weighted in a 1 × 10−4:1:1 ratio. We started the optimizer with parameters that were intentionally changed from the voltage-clamp-derived values, to test the ability to converge. Thus, starting from a set of kinetic parameters that produced action potential, steady-state curves, and normalized macroscopic currents (Fig. 12, A, C, and D, respectively, red dotted lines) that were significantly different from their controls, the optimizer converged in <10 min (40–50 iterations) to a solution of good precision (Fig. 12 B). In this example, the five free parameters to be optimized were the theoretical half-activation and inactivation voltages, the rates of activation and inactivation, and the conductance. Optimizing these parameters is equivalent to optimizing 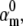
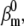
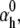
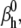 and g, but using a more intuitive parameter space. Similar results were obtained when all nine parameters of the model were optimized (i.e.,
and g, but using a more intuitive parameter space. Similar results were obtained when all nine parameters of the model were optimized (i.e., 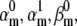 etc., and g), but convergence was slower (results not shown).
etc., and g), but convergence was slower (results not shown).
FIGURE 12.
Automated real-time fitting of action potentials. Nav channels in a raphe neuron were blocked with TTX and functionally replaced with dynamic clamp, using an m4h model. Then, the real-time fitting procedure was started, to globally fit the action potential shape (A), the steady-state curves (C), and the normalized macroscopic currents (D), using a 1 × 10−4:1:1 weighting. The initial set of parameters generated spikes, but of different shape than the control (A, red dotted line), and produced different steady-state (C, red dotted lines) and macroscopic currents (D, red dotted lines). The free parameters to be optimized were the theoretical activation and inactivation V1/2, the activation and inactivation rates, and the conductance. An accurate solution (A, C, and D, red solid lines) was found in <10 min (B). The parameters corresponding to the solution were: 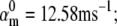
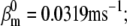
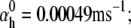
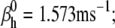 and
and 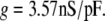 The
The 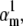
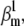
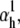 and
and 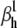 factors were not optimized, and were the same as in Fig. 11. The real-time integration rate was 50 kHz.
factors were not optimized, and were the same as in Fig. 11. The real-time integration rate was 50 kHz.
The control and fit action potentials were virtually identical from −20 mV to the peak, and back down to −20 mV (Fig. 12 A). However, as in the experiment shown in Fig. 11, the fit action potential rises more slowly at the onset than the control. Apparently, the optimizer tried to compensate this by making the rate of activation faster (about twofold) than the voltage-clamp data would require (Fig. 12 D; see legend for parameter values). The steady-state inactivation curve corresponding to the fit is shifted from the control data by a few millivolts in the positive direction. This result is remarkable, as our voltage-clamp data obtained from raphe neurons indicate that the inactivation curve of Nav channels may shift in time in the negative direction (32,33). Thus, the inactivation data used as control in Fig. 12 C may contain some bias. Also as in Fig. 11, there was a strong rundown of the after-hyperpolarization during the 10–15 min elapsed since recording the control action potential. However, this rundown has not affected the fit, as the calculation of the cost function was restricted between −10 and +7 ms from the point where the voltage crosses the −30 mV detection threshold.
Generally, a couple of practical problems were encountered when running the automated real-time fitting. First, some parameter sets were not able to generate spiking at all, whereas others locked the membrane voltage in a depolarized plateau. The solution was to incorporate into the optimizer a time-out mechanism to detect both silent and above-the-threshold periods of a certain duration (e.g., 5 and 0.2 s, respectively), and reject those parameter sets. In the case of the plateau, it was also necessary to reset the model, i.e., to reinitialize the state probabilities to values corresponding to a subthreshold equilibrium (i.e., −80 mV); otherwise the voltage remained locked at the plateau value. Second, excessively large conductance values, as sometimes proposed by the optimizer, resulted in ringing. The solution to this problem was to scan the detected action potential for ripples, and reject that parameter set if necessary. We implemented a simple but effective ripple detector that searches for a local minimum (of user-defined depth and width) immediately after the threshold crossing point.
Adding a virtual axonal compartment
What remains to be explained now is the abrupt rise of the voltage at the onset of the action potential in the control, compared to the slower rise obtained with the Hodgkin-Huxley model and the set of parameters directly derived from voltage-clamp data, or obtained with the real-time fitting procedure. We hypothesize that this is a short-coming of the single-compartment assumption, traditionally made in dynamic-clamp experiments, whereby Nav channels are located only in the soma, whereas in reality Nav channels are distributed not only in the soma but also along the axon. Probably no other type of kinetic model or parameter combination would work in the single-compartment paradigm. We tested this hypothesis by using the dynamic clamp to add to the neuron the simplest possible—yet physically plausible—model of an axonal compartment, populated only with Nav channels in high density.
According to the schematic shown in Fig. 13 A, a current INa,m flows into the neuronal soma through somatic Na channels, whereas a current INa,x flows into the virtual axon through axonal channels. Whenever there is a difference between the somatic and axonal voltages (Vm and Vx, respectively), a current flows between the two compartments, with intensity 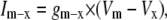 where gm−x is the electrical conductance between the two compartments. The somatic voltage, Vm, is measured by the patch-clamp amplifier, whereas the axonal voltage, Vx, is calculated by the dynamic clamp, by solving the differential equation
where gm−x is the electrical conductance between the two compartments. The somatic voltage, Vm, is measured by the patch-clamp amplifier, whereas the axonal voltage, Vx, is calculated by the dynamic clamp, by solving the differential equation 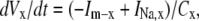 where Cx is the axonal capacitance. Thus, the current injected in the neuron is the sum between INa,m and Im−x.
where Cx is the axonal capacitance. Thus, the current injected in the neuron is the sum between INa,m and Im−x.
FIGURE 13.
Adding a virtual axon to the neuron explains the abrupt voltage rising. An axonal compartment was modeled as shown in the schematic (A), populated only with a high density of Nav channels. (B) The voltage rises faster in the axon (green trace) than in the soma (blue trace), due to the higher density of Nav channels. The difference in voltage causes a depolarizing current to flow into soma, which makes the somatic voltage (blue trace) rise more abruptly than it does without an axon (red trace), although not as fast as the control (black trace). (C) The current that flows through the somatic membrane during an action potential is shown as a function of time (C1) or voltage (C2). The current obtained without axon has only one component (red traces). In contrast, both the control (black traces) and the current produced when an axon is added (blue traces) show two components. The following values were used: Cm = 20 pF; Cx = 1 pF; gm-x = 0 (no axon) or 10 nS (plus axon); gNa,x = 0 or 100 nS/pF; and gNa,m = 12.46 or 9.76 nS/pF. Both somatic and axonal Nav channels were modeled as m4h Hodgkin-Huxley, using separate models, with kinetic parameters as in Fig. 11. The real-time integration rate was 40 kHz.
The virtual axon significantly sharpened the onset of the action potential, as illustrated in Fig. 13 B. Thus, the model action potential obtained with the virtual axon (Fig. 13 B, blue trace) is approximately halfway between the control (black trace) and the model action potential without axon (red trace), in terms of how fast the voltage rises. The cause for the faster rising of the somatic voltage is easy to explain: the high density of Nav channels in the axon allows the axonal voltage Vx to rise (more) abruptly. Then, the positive difference between Vx and Vm causes a depolarizing current to flow into the soma, until the two voltages are again equalized. Thus, the sharpening effect of the axonal compartment is approximately confined to the initial rising phase. This is also illustrated in Fig. 13 C, where the current flowing through the somatic membrane is plotted as a function of time (Fig. 13 C1) or voltage (Fig. 13 C2). One can easily imagine that further adjusting the axonal model or its parameter values may result in an even better action potential shape.
DISCUSSION
Currently, sophisticated techniques exist, such as model-based maximum likelihood fitting of single-channel (20,23) or macroscopic (18,34–36) currents, that can be used to extract kinetic parameters from voltage-clamp data and to discriminate between different models (36–39). Studying ion channels in the isolation provided by the voltage-clamp paradigm is ideal from a biophysical perspective. However, this analysis is biased toward those data features that are prominent in such experiments (i.e., the exponential distribution of single-channel dwell times, or the exponential relaxation of macroscopic currents), and it may overlook some model properties that play an important functional role but do not manifest strongly in the data. As a result, an optimal model selected on the basis of voltage-clamp data alone may fail to explain the observed cellular dynamics.
The strength of the new methodology presented here is that realistic biophysical models of voltage-gated ion channels can be tested and fitted in a functional context, in neurons and other excitable cells. Using the dynamic clamp, different kinetic models can be functionally tested, and parameters can be estimated with good accuracy, in real time, by fitting action potential waveforms. A priori knowledge, derived from voltage-clamp data or from any other experiment, can and should be incorporated to constrain the fit and to improve the solution. The result is that a good model would not only satisfy the existing biophysical constraints (e.g., the number of kinetic states and their interconnectivity) but would also explain the electrical activity of the cell (e.g., action potential shape and spiking frequency), without requiring any information about the other ionic currents.
The real-time fitting technique was demonstrated here with an application to modeling the kinetics of Nav channels in tonically spiking raphé neurons. Starting from a Nav m4h model and a parameter set obtained from whole-cell voltage-clamp experiments, we could make these neurons spike, after blocking Na+ currents with TTX, by injecting a model-based current with dynamic clamp (Fig. 11). Considering the real complexity of Nav kinetics (2,5,40–44), it is quite surprising that a basic Hodgkin-Huxley model with all rates simple exponential functions of voltage could reproduce the action potential shape and the spiking pattern with such remarkable accuracy. To our knowledge, this is the first time the dynamic clamp technique has been used to reconstruct in such detail the action potential in mammalian central neurons, by using a kinetic model of Na+ channels derived from voltage-clamp data, and further improving it by real-time fitting (Fig. 12). Future studies are necessary to include in the Nav model other features, such as deactivation or recovery from inactivation, that were not covered here.
It is convenient to model neuronal dynamics assuming a spherical cellular geometry and a spatially and kinetically homogeneous channel distribution. For dynamic clamp studies, this paradigm is not only convenient but apparently was the only choice until now, probably due to computational limitations imposed by the available software. In contrast, according to experimental evidence, the neuron may express several Nav channel types, differentially distributed in the soma and in the axon (31,45,46), and possibly with different activation thresholds (47). Our own current-clamp data indicate clearly the presence of two components in the inward current flowing during the rising phase of the action potential (Fig. 11 C1), suggesting that the action potential is initiated in the axon. We reported here the first attempt at modeling the function of Nav channels located within the axon, using dynamic clamp. Thus, together with the model for somatic Nav channels, a model of a single axonal compartment populated with a high density of Nav channels (Fig. 13 A) is enough to produce action potentials featuring a significantly more abrupt onset (Fig. 13 B), and a two-component inward current, approaching the characteristics of action potentials normally generated by raphe neurons.
The performance of the dynamic clamp technique as a quantitative tool for modeling the kinetics of voltage-gated channels depends on several factors. Most importantly, it should be able to accurately integrate realistic—often very complex—kinetic models. In this sense, we made a significant advance by using the transition probability matrix of the ion channel model to advance the state probabilities, thus integrating the equations of dynamics. This method is much more accurate than the traditional Euler integration (see Fig. 4), but also very fast, allowing to solve, for example, Markov models with 12 states at >50 kHz (Table 1). These integration rates are critical for modeling voltage-gated channels with fast kinetics, such as Nav channels. For example, in raphe neurons the voltage during the action potential rises from −30 to +20 mV in ∼1 ms. Within this interval, the voltage is sampled 50 times, if the rate is 50 kHz. Correspondingly, the maximum error in reading the voltage is only 1 mV. In contrast, running at lower rates, e.g., 10 kHz, would be unacceptable, as the kinetics of Nav channels would change dramatically over a 5-mV range.
Equally important is the advance we made in terms of software implementation. To date, most efforts in writing dynamic-clamp software have focused on real-time operating systems (28,29,48) or on real-time hardware (49), with few—and relatively slow—Windows implementations (50). The reason for adopting a real-time operating system, generally at the price of sacrificing a convenient graphical user interface, is the need for consistent real-time performance. However, we have demonstrated here that recent advances in hardware and software have made it possible to achieve quasi-real-time performance under the Windows operating system (Fig. 4), using off-the-shelf dual-processor computers and low-cost National Instruments data acquisition cards. Our software exploits the dual-processor architecture to run the dynamic-clamp computational thread simultaneously with a sophisticated graphical user interface featuring, for example, real-time display of data and model parameters (Data S1). Faster computers will allow solving yet more complex models, whereas computer systems with several processors will further improve the real-time and the multitasking performance.
Fitting kinetic models with our software can be accomplished in two ways: 1), manually, by changing the parameters of the model one by one, or by changing phenomenological properties of the model, such as half-activation voltage or inactivation time constant; or 2), automatically, by running a Simplex optimizer, with user-defined free parameters and cost function. We found that manually adjusting the properties of the model (cf. Eqs. 29–41) can be very efficient, depending on the model type, starting parameters, and data complexity. Very helpfully, the software recalculates the properties of the model, and overlays the calculated curves over the reference experimental data (Data S1). On the other hand, we found the automated fitting to be successful (Fig. 12), though critically dependent on several factors. Most important is the stability of the preparation, since any change in the properties of any other channel involved in the cellular dynamics, or in the electrical properties of the patch, may prevent finding the correct solution. Hence, the duration of the experiment has to be kept to a minimum. Furthermore, the choice of initial parameter values must be reasonable, and should generate spiking; otherwise the optimizer has no information about where to search next.
The dynamics of excitable cells can be rather complex, from spontaneous action potentials to bursts of activity (27). Here, we have focused on action potentials, as the most basic dynamic behavior, but the technique can be applied to bursting behavior, and can be extended to more complex experimental protocols. Note that bursts of activity cannot be averaged in the same way as action potentials, due to intrinsic stochasticity. The solution is to fit not the waveform per se, but features of the waveform, such as burst length, intraburst spiking frequency, etc. Extracting these features is not too computationally expensive, and our own tests showed that it can be done in real time. Besides quantitative modeling, the dynamic-clamp technique can also be used as a hybrid simulator, when one part of the model—the one presumably unknown—is integrated by the cell, whereas the other is integrated by the computer.
SUPPLEMENTARY MATERIAL
To view all of the supplemental files associated with this article, visit www.biophysj.org.
Acknowledgments
We thank our colleagues, particularly Drs. Joel Tabak of Florida State University and Mirela Milescu, Andrew Plested, Arthur Sherman, and Christopher Thomas of the National Institutes of Health (NIH), for numerous and fruitful discussions and for critical reading of the manuscript. Dr. Ruli Zhang of NIH helped with experimental procedures. Dr. Robert Butera and Ivan Raikov of Georgia Tech and Dr. John White and Jonathan Bettencourt of Boston University provided technical advice on dynamic clamp. The dynamic clamp software was developed with contributions from Chris Nicolai and John Bannen, from the laboratory of Dr. Frederick Sachs of the State University of New York at Buffalo.
This work was supported by the Intramural Research Program of the National Institute of Neurological Disease and Stroke, NIH.
Murtaza Z. Mogri's present address is Dept. of Bioengineering, Stanford University, Stanford, CA.
Editor: Toshinori Hoshi.
References
- 1.Hodgkin, A. L., and A. F. Huxley. 1952. A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 117:500–544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Bean, B. P. 1981. Sodium channel inactivation in the crayfish giant axon: must channels open before inactivating? Biophys. J. 35:595–614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Cha, A., P. C. Ruben, A. L. George, Jr., E. Fujimoto, and F. Bezanilla. 1999. Voltage sensors in domains III and IV, but not I and II, are immobilized by Na+ channel fast inactivation. Neuron. 22:73–87. [DOI] [PubMed] [Google Scholar]
- 4.Bezanilla, F. 2000. The voltage sensor in voltage-dependent ion channels. Physiol. Rev. 80:555–592. [DOI] [PubMed] [Google Scholar]
- 5.Armstrong, C. M. 2006. Na channel inactivation from open and closed states. Proc. Natl. Acad. Sci. USA. 103:17991–17996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Taylor, A. L., T. J. Hickey, A. A. Prinz, and E. Marder. 2006. Structure and visualization of high-dimensional conductance spaces. J. Neurophysiol. 96:891–905. [DOI] [PubMed] [Google Scholar]
- 7.Sharp, A. A., M. B. O'Neil, L. F. Abbott, and E. Marder. 1993. Dynamic clamp: computer-generated conductances in real neurons. J. Neurophysiol. 69:992–995. [DOI] [PubMed] [Google Scholar]
- 8.Schulz, D. J., J. M. Goaillard, and E. Marder. 2006. Variable channel expression in identified single and electrically coupled neurons in different animals. Nat. Neurosci. 9:356–362. [DOI] [PubMed] [Google Scholar]
- 9.Jacobs, B. L., and E. C. Azmitia. 1992. Structure and function of the brain serotonin system. Physiol. Rev. 72:165–229. [DOI] [PubMed] [Google Scholar]
- 10.Richerson, G. B. 2004. Serotonergic neurons as carbon dioxide sensors that maintain pH homeostasis. Nat. Rev. Neurosci. 5:449–461. [DOI] [PubMed] [Google Scholar]
- 11.Colquhoun, D., and A. G. Hawkes. 1995. A Q-matrix cookbook: how to write only one program to calculate the single-channel and macroscopic predictions for any kinetic mechanism. In Single Channel Recording. B. Sakmann and E. Neher, editors. Plenum Press, New York. 589–636.
- 12.Butera, R. J., and M. L. McCarthy. 2004. Analysis of real-time numerical integration methods applied to dynamic clamp experiments. J. Neural Eng. 1:187–194. [DOI] [PubMed] [Google Scholar]
- 13.Chow, C. C., and J. A. White. 1996. Spontaneous action potentials due to channel fluctuations. Biophys. J. 71:3013–3021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Gillespie, D. 1977. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 81:2340–2361. [Google Scholar]
- 15.Cao, Y., H. Li, and L. Petzold. 2004. Efficient formulation of the stochastic simulation algorithm for chemically reacting systems. J. Chem. Phys. 121:4059–4067. [DOI] [PubMed] [Google Scholar]
- 16.Fox, R. F. 1997. Stochastic versions of the Hodgkin-Huxley equations. Biophys. J. 72:2068–2074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Mascagni, M. V., and A. S. Sherman. 1998. Numerical methods for neuronal modeling. In Methods in Neuronal Modeling: From Ions to Networks. C. Koch and I. Segev, editors. MIT Press, Cambridge, MA. 569–606.
- 18.Milescu, L. S., G. Akk, and F. Sachs. 2005. Maximum likelihood estimation of ion channel kinetics from macroscopic currents. Biophys. J. 88:2494–2515. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Colquhoun, D., K. A. Dowsland, M. Beato, and A. J. R. Plested. 2004. How to impose microscopic reversibility in complex reaction mechanisms. Biophys. J. 86:3510–3518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Qin, F., A. Auerbach, and F. Sachs. 1996. Estimating single channel kinetic parameters from idealized patch-clamp data containing missed events. Biophys. J. 70:264–280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Nelder, J. A., and R. Mead. 1964. A simplex method for function minimization. Comput. J. 7:308–313. [Google Scholar]
- 22.Press, W. H., S. A. Teukolsky, W. T. Vetterling, and B. P. Flannery. 1992. Numerical Recipes in C. Cambridge University Press, Cambridge, MA.
- 23.Colquhoun, D., A. G. Hawkes, and K. Srodzinski. 1996. Joint distributions of apparent open times and shut times of single ion channels and the maximum likelihood fitting of mechanisms. Philos. Trans. R. Soc. Lond. A. 354:2555–2590. [Google Scholar]
- 24.Qin, F., A. Auerbach, and F. Sachs. 2000. A direct optimization approach to hidden Markov modeling for single channel kinetics. Biophys. J. 79:1915–1927. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Colquhoun, D., C. J. Hatton, and A. G. Hawkes. 2003. The quality of maximum likelihood estimates of ion channel rate constants. J. Physiol. 547:699–728. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Cohen, S. D., and A. C. Hindmarsh. 1996. CVODE, a stiff/nonstiff ODE solver in C. Comput. Phys. 10:138–143. [Google Scholar]
- 27.Butera, R. J., J. Rinzel, and J. C. Smith. 1999. Models of respiratory rhythm generation in the pre-Bötzinger complex. I. Bursting pacemaker neurons. J. Neurophysiol. 82:382–397. [DOI] [PubMed] [Google Scholar]
- 28.Butera, R. J., C. G. Wilson, C. A. DelNegro, and J. C. Smith. 2001. A methodology for achieving high-speed rates for artificial conductance injection in electrically excitable biological cells. IEEE Trans. Biomed. Eng. 48:1460–1470. [DOI] [PubMed] [Google Scholar]
- 29.Dorval, A. D., D. J. Christini, and J. A. White. 2001. Real-time LINUX dynamic clamp: a fast and flexible way to construct virtual ion channels in living cells. Ann. Biomed. Eng. 29:897–907. [DOI] [PubMed] [Google Scholar]
- 30.Baranauskas, G., and M. Martina. 2006. Sodium currents activate without a Hodgkin-and-Huxley-type delay in central mammalian neurons. J. Neurosci. 26:671–684. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Bean, B. P. 2007. The action potential in mammalian central neurons. Nat. Rev. Neurosci. 8:451–465. [DOI] [PubMed] [Google Scholar]
- 32.Fernandez, J. M., A. P. Fox, and S. Krasne. 1984. Membrane patches and whole-cell membranes: a comparison of electrical properties in rat clonal pituitary (GH3) cells. J. Physiol. 356:565–585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Hanck, D. A., and M. F. Sheets. 1992. Time-dependent changes in kinetics of Na+ current in single canine cardiac Purkinje cells. Am. J. Physiol. 262:1197–1207. [DOI] [PubMed] [Google Scholar]
- 34.Celentano, J. J., and A. G. Hawkes. 2004. Use of the covariance matrix in directly fitting kinetic parameters: application to GABAA receptors. Biophys. J. 87:276–294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Moffatt, L. 2007. Estimation of ion channel kinetics from fluctuations of macroscopic currents. Biophys. J. 93:74–91. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Gurkiewicz, M., and A. Korngreen. 2007. A numerical approach to ion channel modelling using whole-cell voltage-clamp recordings and a genetic algorithm. PLoS Comput. Biol. 3:1633–1647. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Csanády, L. 2006. Statistical evaluation of ion-channel gating models based on distributions of log-likelihood ratios. Biophys. J. 90:3523–3545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Kienker, P. 1989. Equivalence of aggregated Markov models of ion-channel gating. Proc. R. Soc. Lond. B. Biol. Sci. 236:269–309. [DOI] [PubMed] [Google Scholar]
- 39.Bruno, W. J., J. Yang, and J. E. Pearson. 2005. Using independent open-to-closed transitions to simplify aggregated Markov models of ion channel gating kinetics. Proc. Natl. Acad. Sci. USA. 102:6326–6331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Patlak, J. 1991. Molecular kinetics of voltage-dependent Na+ channels. Physiol. Rev. 71:1047–1080. [DOI] [PubMed] [Google Scholar]
- 41.Kuo, C. C., and B. P. Bean. 1994. Na+ channels must deactivate to recover from inactivation. Neuron. 12:819–829. [DOI] [PubMed] [Google Scholar]
- 42.Raman, I. M., and B. P. Bean. 1997. Resurgent sodium current and action potential formation in dissociated cerebellar Purkinje neurons. J. Neurosci. 17:4517–4526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Magistretti, J., and A. Alonso. 1999. Biophysical properties and slow voltage-dependent inactivation of a sustained sodium current in entorhinal cortex layer-II principal neurons: a whole-cell and single-channel study. J. Gen. Physiol. 114:491–509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Raman, I. M., and B. P. Bean. 2001. Inactivation and recovery of sodium currents in cerebellar Purkinje neurons: evidence for two mechanisms. Biophys. J. 80:729–737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Castelli, L., G. Biella, M. Toselli, and J. Magistretti. 2007. Resurgent Na+ current in pyramidal neurones of rat perirhinal cortex: axonal location of channels and contribution to depolarizing drive during repetitive firing. J. Physiol. 582:1179–1193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Kole, M. H., S. U. Ilschner, B. M. Kampa, S. R. Williams, P. C. Ruben, and G. J. Stuart. 2008. Action potential generation requires a high sodium channel density in the axon initial segment. Nat. Neurosci. 11:178–186. [DOI] [PubMed] [Google Scholar]
- 47.Colbert, C. M., and D. Johnston. 1996. Axonal action-potential initiation and Na+ channel densities in the soma and axon initial segment of subicular pyramidal neurons. J. Neurosci. 16:6676–6686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Raikov, I., A. Preyer, and R. J. Butera. 2004. MRCI: a flexible real-time dynamic clamp system for electrophysiology experiments. J. Neurosci. Methods. 132:109–123. [DOI] [PubMed] [Google Scholar]
- 49.Kullmann, P. H. M., D. W. Wheeler, J. Beacom, and J. P. Horn. 2003. Implementation of a fast 16-bit dynamic clamp using LabView-RT. J. Neurophysiol. 91:542–554. [DOI] [PubMed] [Google Scholar]
- 50.Pinto, R. D., R. C. Elson, A. Szucs, M. I. Rabinovich, A. I. Selverston, and H. D. I. Abarbanel. 2001. Extended dynamic clamp: controlling up to four neurons using a single desktop computer and interface. J. Neurosci. Methods. 108:39–48. [DOI] [PubMed] [Google Scholar]