Three-Dimensional FRET Reconstruction Microscopy for Analysis of Dynamic Molecular Interactions in Live Cells

Abstract

Analysis of cellular pathways requires concentration measurements of dynamically interacting molecules within the three-dimensional (3D) space of single living cells. Förster resonance energy transfer (FRET) microscopy from widefield, from confocal, and potentially from superresolution microscopes can access this information; however, these measurements are distorted by the inherent 3D blurring of optical imaging, spectral overlap of fluorophores, and detection noise. We propose a mathematical model of these processes and demonstrate, through simulation, how these distortions limit the dynamic range and sensitivity of conventional FRET microscopy. Using this model, we devise and validate a new approach (called 3D-FRET stoichiometry reconstruction, 3DFSR) for reconstructing 3D distributions of bound and free fluorescent molecules. Previous attempts to reconstruct 3D-FRET data relied on sequential spectral unmixing and deconvolution, a process that corrupts the detection statistics. We demonstrate that 3DFSR is superior to these approaches since it simultaneously models spectral mixing, optical blurring, and detection noise. To achieve the full potential of this technique, we developed an instrument capable of acquiring 3D-FRET data rapidly and sensitively from single living cells. Compared with conventional FRET microscopy, our 3D-FRET reconstruction technique and new instrumentation provides orders of magnitude gains in both sensitivity and accuracy wherein sustained high-resolution four-dimensional (x,y,z,t) imaging of molecular interactions inside living cells was achieved. These results verify previous observations that Cdc42 signaling is localized to the advancing margins of forming phagosomes in macrophages.

INTRODUCTION

Understanding the molecular basis of cellular function requires that the spatial and temporal organization of cellular pathways be measured precisely inside living cells. Accordingly, Förster resonance energy transfer (FRET) microscopy is emerging as a powerful tool for imaging the dynamics of protein interactions comprising these pathways within living cells. These methods hold the promise of measuring the concentrations of bound and free molecules inside cells, thereby providing the information necessary for mathematical modeling of the molecular pathways controlling cell function. However, the capability of FRET microscopy to report accurately the concentration of bound and free molecules is impaired by the combined effects of spectral mixing, optical blurring, and detection noise. Methods have been developed to quantify the relative concentrations of interacting proteins via FRET-induced changes in the fluorescence spectrum (1–3), fluorescence polarization (4), and fluorescence lifetime (5); however, these methods all suffer from optical distortions and imperfect sectioning. Although confocal microscopes have reduced z axis blurring relative to conventional widefield microscopes, they have seen only partial success in quantitative live-cell FRET microscopy because of reduced signal/noise ratios (SNR), cumbersome instrument parameters, and signal instability (6). These limitations have driven the advancement of instrumentation, but image analysis and reconstruction algorithms for quantitative FRET measurements are lacking.

In the analysis of cellular pathways, the goal of FRET microscopy is to convert fluorescence signals from donor- and acceptor-tagged molecules into concentrations of bound and free proteins. The imperfect sectioning and blurring of the three-dimensional (3D) distribution of fluorescence signals in widefield and confocal microscopes, however, complicates the interpretation of fluorescence intensities as concentrations. This complication has motivated the use of fluorescence lifetime microscopy (FLIM) and the development of spectral-based ratiometric methods for FRET analyses. In FLIM, the donor's lifetime can be used to estimate the apparent FRET efficiency by dividing the donor lifetime in the presence of acceptor by its natural lifetime (5). For spectral approaches, relative concentrations of bound and free fluorescent proteins can be expressed as ratios of D-A complex (or the product of the FRET efficiency, E, times the apparent concentration of D-A complex, E[DA]) to total donor [D] or total acceptor [A] (1). These lifetime and concentration ratio images are easy to interpret since they distinguish changes in concentration from changes in cell thickness, which are otherwise poorly resolved due to out-of-focus light (1,2,7). To move from these informative yet inadequate ratiometric descriptions toward concentration estimates, reassignment of out-of-focus light by image reconstruction techniques is needed.

Image reconstruction can significantly reverse blurring distortions and reduce noise in both 3D widefield and confocal images (8). These reconstruction techniques make use of prior knowledge of sample properties such as positivity and of the microscope's optical performance as described by the point spread function (PSF). The PSF describes the spatial redistribution of light produced by the microscope when imaging an infinitely small point source. For both widefield and confocal microscopes the PSF is anisotropic, being much longer (hence lower resolution) along the z axis than in the x and y directions. Imaging of intricate objects in these microscopes results in the redistribution of fluorescence signals emanating from each point within the object to the PSF distribution. The 3D image acquired by the microscope is then the superposition of all redistributed (blurred) points of the object. This process is described mathematically by the convolution of the original object and the PSF. Convolution results in a distorted correspondence between the distribution of signal collected in the image and the distribution of fluorophore in the object. This problem cannot be directly inverted to estimate the original object from the blurred microscopy data. Rather, a number of iterative reconstruction algorithms have been devised to generate improved estimates of the original object, including maximum likelihood estimation by entropy maximization (MLE-EM) (9,10), least squares minimization by steepest and conjugate gradient descents (10), the iterative constrained Tikhonov-Miller (ITCM) algorithm (11), and conjugate gradient minimization of maximum a posteriori (MAP) functionals (12). All of these techniques produce improved estimates of fluorophore distribution while retaining the quantitative nature of the microscopy data. These algorithms are formulated in terms of log-likelihood functionals, which account for the statistical properties of the detection noise and for the imaging distortions described by the PSF. Minimization of these functionals provides improved estimates for the distribution of fluorophores that gave rise to the data. The quality of these estimates depends on the noise level of the data, the spatial frequencies sampled during data acquisition, and the spatial frequencies transferred by the microscope's PSF.

These conventional approaches, however, do not apply to FRET microscopy and microscopy involving spectrally overlapping fluorescence signals. In these cases, multiple images of the same sample must be collected at various combinations of excitation and emission wavelengths. The resulting data are a linear combination of fluorescence signals from the various fluorophores (engaged in FRET or not) within the sample. Direct reconstruction of these data by existing techniques would provide improved estimates of the mixed fluorescence signals but not the concentrations of the individual fluorophores therein. The fact that FRET microscopy is composed of spectrally overlapping signals and linear coupling between the fluorescence processes of the donor and acceptor motivates the development of a combined 3D reconstruction and spectral unmixing approach.

We applied maximum likelihood methods to achieve reconstruction suitable for 3D-FRET microscopy data. Direct minimization of these log-likelihood functionals to data corrupted by either Gaussian or Poisson noise was problematic. However, a solution using alternating functionals applied directly to the data and to a spectrally unmixed version of the data provided sensitive and accurate estimation of the concentrations of donors [D], acceptors [A], and donor-acceptor complexes [DA] (or the product of the FRET efficiency E and [DA]). In particular, we propose a matrix model to describe the effects of spectral overlap, optical distortion, and noise on the formation of 3D-FRET microscopy data. This model was used to devise an approach for 3D-reconstruction of FRET microscopy data (3D-FRET stoichiometry reconstruction; 3DFSR) capable of obtaining deconvolved, ML estimates of the concentrations of [D], [A], and E[DA]. Furthermore, simulations suggest 3DFSR is highly robust against noise and significantly improves concentration estimation for both widefield and confocal microscopy while outperforming conventional reconstruction approaches such as deconvolution followed by spectral unmixing. 3DFSR imaging was validated by both simulation and measurements in living cells. Construction of a novel microscope capable of multiplexed detection allowed sensitive and rapid acquisition of four-dimensional (4D)(x,y,z,t) FRET data in living cells. The combined application of this instrument and 3DFSR allowed sustained 4D imaging of small G-protein signaling by measurement of the concentrations of interacting fluorescent Cdc42 and fluorescent effector domain (P21-binding domain; PBD) within a single living cell.

THEORY

Model for 3D image formation of multispectral and FRET microscopy data

Estimation of fluorophore concentrations from fluorescence microscopy data is complicated by three effects: 1), overlapping excitation and emission spectra of multiple fluorophores; 2), blurring due to contributions of fluorescence from neighboring points in the image; and 3), noise associated with detection of fluorescence. The first two effects can be modeled mathematically by matrix operations and the third by appropriate probability distributions.

Spectral mixing of FRET fluorescence

In microscopy, images generated with excitation and emission combinations can be used to estimate the quantities of fluorophores in a sample even if the excitation and emission spectra of the fluorescent molecules overlap. In this case, the spectral mixing in the microscope is described by a system of linear equations in which the elements of the mixing matrix A describe the excitation and emission contributions of each fluorophore in vector x to each voxel in vector y

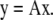(1)

This linear system of equations can be solved by obtaining a least squares solution with or without constraints on x (13). In the absence of constraints, this solution can be obtained by multiplying both sides of Eq. 1 by the inverse of A (for square A, determined) or by the Moore-Penrose pseudoinverse of A (for an overdetermined A, e.g., having more rows than columns). Alternatively, iterative methods have been devised to maintain the nonnegativity of x (14). Recent work by Neher and Neher (7) has shown that Eq. 1 can be extended to include FRET-based processes. In fact, the equations of FRET stoichiometry (1) that describe the fractions of interacting donors and acceptors as apparent FRET efficiencies and the acceptors/donors molar ratio can be written in a matrix form to generate A. FRET stoichiometry uses three images obtained with three combinations of donor and acceptor excitation and emission: I_A (acceptor excitation, acceptor emission), I_D (donor excitation, donor emission), and I_F (donor excitation, acceptor emission). Four calibration constants are obtained from pure samples of acceptor (α), donor (β), and a donor-acceptor linked construct (γ and ξ) of known FRET efficiency. α and β correct for spectral crossover of donor and acceptor into the I_F image to allow estimation of sensitized emission (SE or the fluorescence from the acceptor due to energy transfer from the donor) (1,2,15):

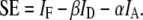Second, γ scales the acceptor excitation to donor excitation and ξ scales the sensitized emission (16) to donor emissions allowing estimates of the fraction of donors in complex times the FRET efficiency (the apparent donor FRET efficiency, E_D), the fraction of acceptors in complex with donors times the FRET efficiency (the apparent acceptor FRET efficiency, E_A), and the molar ratio of acceptors to donors (R_M). With the definition of SE, the equations of FRET stoichiometry (1) can be written as

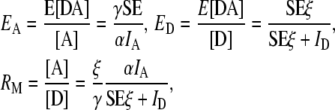where [D] and [A] are the total concentration of donor and acceptor, and E[DA] is the FRET efficiency times the concentration of donor-acceptor complex. Note that we now set the term ξ/γ of the original derivation of FRET stoichiometry to ξ since the ratio is unnecessary (17). Given these equations, we can write the matrix form of FRET stoichiometry for A in (Eq. 1) as (16)

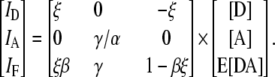In this case, application of A⁻¹ provides the unconstrained maximum likelihood (least squares) estimate identical to that provided by FRET stoichiometry for the spatially distorted concentrations of [D], [A], and E[DA] if the noise in images I_D, I_A, and I_F was Gaussian. In microscopy, however, the detection statistics tend to follow Poisson distribution; however, no analytical or numerical solutions have been proposed for that case.

Blurring

Blurring can be described as the probability (p_b,v) that photons emanating from voxel b with intensity y in the object plane will be detected in voxel v of the imaging plane with intensity z (10),

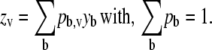(2)

The probabilities p_b are obtained from the instrument-specific PSF. Alternatively, Eq. 2 can be written as a matrix operation as in Eq. 1 where the voxels of the image are arranged into a vector y and the probabilities p_b are arranged in a corresponding matrix P. Restating Eq. 2 as a matrix operation we have

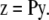(3)

Direct inversion or factorization of P to obtain a deblurred estimate of y is not feasible because its structure makes it difficult to obtain a sufficiently accurate P⁻¹ (10), or P⁻¹ computed by discrete Fourier transforms may not exist for microscopy (12). As such, algorithms for deblurring seek to find a better estimate of y via iterative methods with positivity constraints on y and an assumed noise model. Examples include the Richardson-Lucy (RL) algorithm (for Poisson noise (9)) and the ITCM inversion (for Gaussian noise (11)). Furthermore, the addition of regularization functional can reduce the influence of noise and stabilize the solutions for y. Algorithms for reconstructing imaging data have been extensively studied in the areas of medical and satellite imaging as well as 3D microscopy (10,12). However, little research exists on the 3D estimation of multiple fluorophores from a mixture of fluorescence spectral components encountered in the case of 3D-FRET microscopy.

Detection noise

The detection of photons in light microscopy introduces noise into the data. This process can be described by drawing data g from a noise distribution N that has an expectation value given by the blurred distribution of fluorescence arriving at the detector and constant background signal (b) (12)

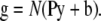Commonly, the RL algorithm based on entropy maximization (EM) can be used to deblur the image (estimate y) when N is given by the Poisson noise model (9,11). In particular, the RL algorithm iteratively estimates y by computing a search direction d, which is then multiplied by y to generate an improved y. This process continues until a fixed number of iterations is reached or a quality factor is exceeded. A limitation of this approach is that the EM form of this algorithm is slow to converge. The RL algorithm can be accelerated by techniques which scale the step size of each iteration by testing changes in the log-likelihood functional for various possible step sizes (overrelaxation) (9) or by approximation of the step size from the log-likelihood functional itself for conjugate gradient methods (12). The form of these overrelaxed algorithms is

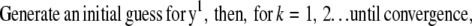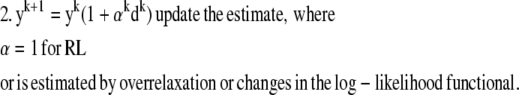For conjugate gradient, step 1 includes the previous search direction.

Model for FRET microscopy

Taken together, the spectral mixing, blurring, and noise operations give the following model for FRET microscopy:

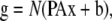(4)

where as before, x is the concentration of fluorophore in each voxel. This model can be directly extended to multispectral imaging for determined or overdetermined systems by simply changing the matrix A. In general, g is composed of multiple images corresponding to various excitation and emission combinations and would require matrix P to contain multiple PSFs corresponding to the excitation and emission configurations in the corresponding elements of g.

3D-FRET reconstruction

The goal for reconstruction of FRET microscopy data is to estimate the vector x, which contains the 3D concentrations of bound and free fluorophores that gave rise to the data vector g. As mentioned above, there are numerous examples in the literature of image reconstruction approaches that seek to reconstruct x while neglecting the spectral mixing described by the matrix A. Conversely, the subject of spectral unmixing while neglecting blurring, has been extensively studied (13,14). To date, a combined method for image reconstruction that estimates the 3D fluorophore concentration in the presence of spectral mixing and blurring has yet to be reported. Attempts to approximate this procedure have included deconvolution to the blurred data followed by spectral unmixing (18) or classification of chromosomes labeled with mixtures of dyes based on color (19). Alternatively, x could be reconstructed from spectrally unmixed data; however, this would be an inferior approach since the unmixing process corrupts the detection statistics, which must be accurately modeled in the reconstruction process.

The log-likelihood functional

Estimation of x from Eq. 4 represents an ill-posed inverse problem that must be solved by iterative methods. Unlike Eq. 1, which can be inverted by direct application of the inverse or pseudoinverse of A, Eq. 4 involves convolution from multiplication of matrix P and is therefore ill posed. Generally, image reconstruction algorithms strive to find the most likely value of x given the data, either by direct application of maximum likelihood (ML) methods or by MAP approaches that seek the most likely posterior density of x given the data g (ML) or the most likely density of x given the data g and prior distribution p(x) to regularize the solution (MAP) (12). For ML, we seek a solution for x with posterior density p(x|g), which can be found by

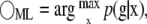(5)

or in the case of prior information about the distribution of x (e.g., p(x)), we seek

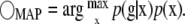(6)

Obtaining the ML or MAP estimates from the above equations is equivalent to defining a likelihood functional based on the assumed noise model and for MAP an additional penalty functional. The prior probability p(x) can be given by various functionals that will penalize roughness in the result to various degrees (12). We chose the entropy prior for p(x) for regularization and easy implementation in the reconstruction algorithm; however, other choices such as Good's roughness are possible (20). To make this mathematical problem tractable, it is common to minimize the negative logarithm of the log-likelihood functional.

The ML and MAP log-likelihood functional for inverting Eq. 4 for 3DFSR or any data for which the component mixtures can be represented by a linear matrix operation is given for Poisson noise (MLP, MAPP) or Gaussian noise (MLG, MAPG), when assuming an entropy prior for p(x) without prior information about the object, are

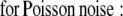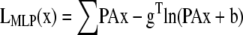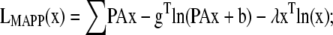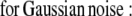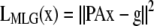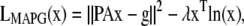where λ controls the influence of the regularization term. Note that the terms that contain dot products (e.g., x^Tln(x) and g^Tln(PAx)) result in the sum of the product of the vector elements.

Minimizing these functionals can be accomplished by determining the argument x at which their gradient d vanishes. For simplicity, we omit the background term b from the gradients. Background can be accounted for by adding b to each instance of the forward projection PAx (e.g., PAx + b) in the subsequent equations or by subtracting b in the case where A⁻¹ is applied to the data (e.g., A⁻¹(g − b)).

For MLP,

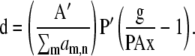For MLG,

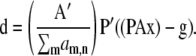At first glance, it appears that a modified form of the RL algorithm could be used for the MLP case:

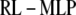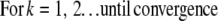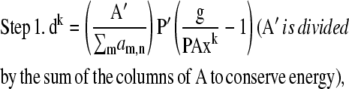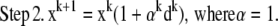Alternatively, steepest descent or conjugate gradient algorithms could be used, with the hope of obtaining faster convergence.

Surprisingly, we found that FRET data were poorly reconstructed by EM or steepest descent minimization of the MLP, MAPP, MLG, and MAPG functionals. This was true in both the presence and absence of noise when the algorithm was started with uniform images set to the mean value of each unmixed estimate (Supplementary Material, Fig. S1). In these cases, localized FRET signals embedded within non-FRET regions were poorly recovered both spatially and spectrally. This observation correlated with the spatial component of the gradient (d) being very shallow for localized FRET signals embedded within larger non-FRET volumes, whereas the spectral components of d dominated in these areas. We reasoned that data unmixed by A⁻¹ could be used to generate gradients sensitive to the spatial reconstruction while eliminating the spectral component of the gradient. This by itself, however, would return us to the original problem of reconstructing with the incorrect noise model. Preservation of the statistical properties of the ML and MAP formalisms requires that we optimize the likelihood functionals given above. To improve the performance, one could imagine using spectrally unmixed estimates to generate a better initial guess or to incorporate a second functional to estimate x in areas where d is insensitive to the spatial component of the gradient. Of these two approaches, we found that the latter approach gave superior robustness against noise. This led us to the following objective functionals for the Poisson noise case:

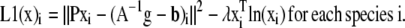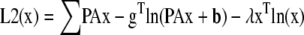with gradients (omitting b),

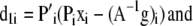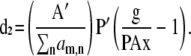Note that we include the index i to distinguish each molecular species (e.g., E[DA], [D], and [A]) contained within the vector x or cognate A⁻¹g.

The application of A⁻¹ to the data corrupts the noise distribution; however, this corruption will tend toward a zero-mean distribution for full A or a Poisson distribution for A approaching the identity matrix. Since we are concerned with the case of FRET, there will always be off-diagonal terms in A motivating the unbiased least squares functional for L1, rather than a biased Poisson functional.

We minimized these functionals by alternating between a bounded steepest descent for L1 and EM for L2. One could imagine designing the algorithm to use bounded steepest descent for both functionals; however, in the case of Poisson noise, the estimation of step size is considerably more complicated and requires substantial computational effort (21). For this reason, we chose to implement an EM step with overrelaxation. Neglecting the regularization terms for simplicity, the algorithm can be written as a steepest descent step along d₁ for each unmixed image i, followed by an overrelaxed EM step along d₂. When large overrelaxation factors are applied in the second EM step, the estimated values for x will be displaced by small offsets. To ensure that x remains close enough to the previous value for the next step along d₁, we applied a second round of EM with no overrelaxation (e.g., α = 1). Owing to the negative terms in matrix A, a second set of constraints was also imposed on the algorithm to ensure E[DA] ≤ [D] and E[DA] ≤ [A]. This constraint is physically meaningful as well, since E ranges from zero to one and the concentration of complex must always be less than or equal to the concentration of the total bound and free donors and acceptors.

A second approach that we tried was to start the reconstruction by first minimizing L1 for some number of iterations and then use these estimates to start the minimization of L2. This approach was successful in generating good reconstructions; however, it created the problem of needing to determine the number of required iterations for L1 minimization before passing the estimates to the L2 minimization. Furthermore, we found that noise propagated into the estimates faster using this approach than with the alternating L1 and L2 reconstruction, further motivating the alternating reconstruction approach.

The 3DFSR algorithm for Poisson noise, neglecting regularization terms for simplicity is given as

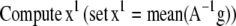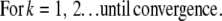For each species (i) in x:

Step

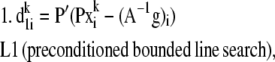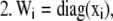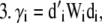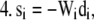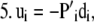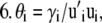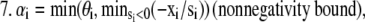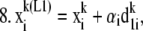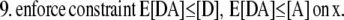If x_E[DA] > x_D, then x_E[DA] = x_D.

If x_E[DA] > x_A, then x_E[DA] = x_A.

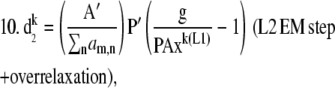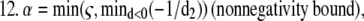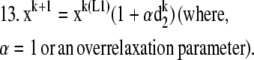If α < 1.1, refine estimate for L1 step (L2 EM refinement):

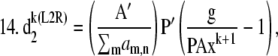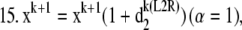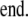Termination of the iterations can be accomplished by monitoring changes in the quality factor between the estimates and the data such as the mean-square error (MSE) or Cizar's I-divergence (22). For this work, we used a fixed number of iterations or plotted the MSE for evaluating the convergence of the algorithm.

Overrelaxation parameter

Acceleration of this algorithm could be accomplished by estimating the step size, by numerical overrelaxation techniques based on approximate changes in the likelihood functional, or by estimating the maximum of the likelihood functional by the steepest descent or conjugate gradient approaches. For the multispectral model, both strategies are somewhat complicated and computationally costly. Thus, to allow reconstruction of real data sets with reasonable computation times for our unoptimized computer programs, we took advantage of the robust nature of the MLP-EM step to allow assignment of overrelaxation parameters for α from an alternating sequence of numbers >1 but ≤8. This approach has been used previously in conventional maximum likelihood reconstruction and found to give comparable performance (23,24) to the overrelaxation method of Holmes and Lui (9). Infeasible solutions were constrained by subjecting the choice for α to a nonnegativity bound of the forward projected images during reconstruction (step 12 in the 3DFSR algorithm) in a method similar to that proposed by Kaufman (10). For 3DFSR reconstructions this approach appeared to work well, in that few differences were observed when comparing with nonoverlaxed reconstructions of the same data carried out for more iterations. However, we expect that more precise means for estimating the EM step size or alternative algorithms for maximizing L2 such as Verveer's method (21) will be needed for optimal implementation of 3DFSR.

Photobleaching correction

In the widefield microscope, the effects of photobleaching during acquisition can be corrected by equalizing the photon flux in successive planes. This is possible since the PSF for the widefield microscope has the property of summing to a fixed value in each xy plane. Thus, the integral of the fluorescence intensity in each xy plane will remain constant in the absence of photobleaching provided that the image is wide enough in the x and y dimensions to encompass the fluorescence emanating from the object with cone angle given by the PSF. When imaging tissue culture cells spread on glass, this requirement is often met. For example, a 1.33 NA objective with half-cone angle of 60° imaging a field of 45 μm would include the majority of fluorescence ∼6 μm above and below an 8-μm-tall, 20-μm-diameter cell centered in the image volume.

In the case of FRET, the photobleaching rates do not map directly to each image. Since FRET modifies the excited state lifetime of a fluorescent molecule, it also modifies the rate of irreversible photobleaching such as reactivity with molecular oxygen. Each bound or free species, therefore, bleaches with its individual rate, and bleaching corrections must be applied to the unmixed signals. Although previous photobleaching correction methods neglect this well-described feature of FRET, we implemented a simple and effective method. The photon flux emanating from each donor, acceptor, or complex species (indexed by i) can be measured as

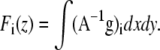These decays can then be mixed by multiplication with A, then normalized and used to divide each plane of the data (I_A, I_D, and I_F) to correct for photobleaching as

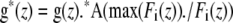where “.” denotes element-wise multiplication or division and the F_i elements comprise the vector to the right of A.

This approach is valid if the z axis collection is faster than the overall dynamics of complex formation and dissolution.

MATERIALS AND METHODS

Computation

The computer simulations and algorithm development were carried out in using MATLAB 7.3 (The Mathworks, Natick, MA) and the DIPImage toolbox for MATLAB (http://www.diplib.org/, Quantitative Imaging Group, Delft University of Technology, Netherlands) in the Linux operating system (OpenSUSE 10.0, Novell, Waltham, MA). The computer was a custom-built dual-Athlon (AMD) machine with 5 GB RAM. The MATLAB function for 3DFSR can be found at http://sitemaker.umich.edu/4dimagingcenter/3dfsr.

Simulation of images

Images were simulated by creating arbitrary distributions of [D], [A], and E[DA] in oversampled 3D images by binary operations on spherical objects created with the “rr” function in DIPImage. These binary spheres were then added, subtracted, and scaled to form the test object shown in Fig. 1 as well as other test objects, which included spherical shells and other structures not shown in the figures. A simulated PSF was convolved with the test object, and the resulting image was resampled to achieve the stated sampling frequencies. Detection noise was simulated by scaling the blurred results and passing them to the DIPImage “noise” function, which used the blurred images as expectation values to generate the measured image drawn from Poisson or Gaussian distributions. The mean SNR was defined as the square root of the mean of the blurred image over the domain of the original object. This is a functional definition which allows assignment of a single number to the SNR for a complex object and is useful for comparing simulated images since they always have the same 3D structure.

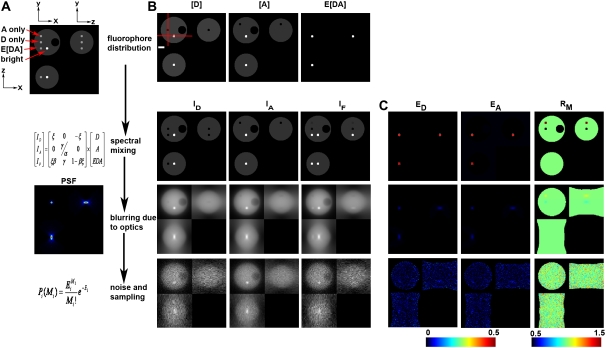
FIGURE 1.

Model of 3D-FRET data. (A) A model of a 4.5-μm-diameter yeast cell with three distinct distributions of donor ([D]), acceptor ([A]), and donor-acceptor complex times FRET efficiency (E[DA]) was generated. (B) Spectral mixing of fluorescence from each fluorescent species (via multiplication with matrix A) gave rise to the fluorescence distributions detected in each imaging channel. These spectral mixtures were blurred by the imperfect detection of the optical microscope (e.g., multiplication with matrix P). Here, blurring was modeled using a PSF simulated for the widefield epifluorescence microscope. To simulate detection noise, the blurred distributions were used as expected values E to obtain measured value M from a Poisson distribution. Asymmetric 3D data acquisition (resulting voxel dimensions were 67 nm, 67 nm, 201 nm) was simulated by resampling the model simulated after convolution. (C) The apparent FRET efficiencies E_A (E[DA]/A) and E_D (E[DA/D]) and the molar ratio R_M ([A]/[D]) were calculated from the corresponding rows of images to demonstrate the impact of spectral mixing, blurring, and noise on the resolution of the apparent FRET efficiencies and R_M images. Red lines in B indicate the axes used for making the xz and xy slices. The xy slice was taken from the central plane. Scale bar is 1 μm.

Image display

All images were displayed as xy, xz, and yz slices either with the conventional “gray” color map in MATLAB or with a modified color map called “jetb”. Jetb was created by changing the lower end of the commonly used “Jet” color map to black instead of dark blue (see color bars in the figures). The 3D surface display in Fig. 7 used the MATLAB isosurface, isocaps, and patch functions to create a “green” surface mapping the surface of the cell, “gray” mapping the distribution of yellow fluorescent protein (YFP)-Cdc42, and pseudocolor showing the distribution of E[DA] complexes.

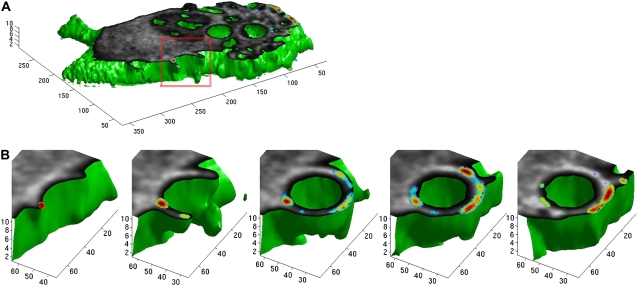
FIGURE 7.

3DFSR enabled 4D(x,y,z,t) imaging of dynamic molecular association within a living cell. 3D images of a bone marrow-derived macrophage internalizing an IgG-coated 5 μm bead were collected at 30 s intervals and reconstructed by 30 iterations of 3DFSR. Surface reconstruction (green) shows the surface of the cell, which was sliced open near the middle focal plane to reveal the concentrations of [A] (YFP-Cdc42, in gray) and the concentration of E[DA] (E × [YFP-Cdc42/CFP-PBD] in pseudocolor) (A). (B) Time series of the reconstructed forming phagosome indicated that Cdc42 was active at the advancing edges of the forming phagosome.

Cells, constructs, and transfection

COS7 cells were obtained from the American Type Culture Collection (Manassas, VA) and maintained at 37°C under 5% CO₂ in Dulbecco's Modified Eagle Medium supplemented with 10% heat-inactivated fetal bovine serum, 100 units/ml penicillin, and 100 μg/ml streptomycin. Cell culture reagents were products of Invitrogen (Carlsbad, CA). Approximately 2.5 × 10⁵ cells per coverslip were plated and transfected the day before imaging using FuGene-6 according to the manufacturer's recommended protocol (Roche Diagnostics, Indianapolis, IN). Murine bone marrow-derived macrophages were prepared as described (25) and transfected using the Amaxa Nucleofector system (Amaxa, Gaithersburg, MD). The target particles for phagocytosis were low-refractive index silica beads coated with streptavidin (Bang's Labs, Fishers, IN, NA = 1.43–1.46). These beads were opsonized for phagocytosis by incubation of 1.4 × 10⁶ beads with 8 μg polyclonal antistreptavidin immunoglobulin G (IgG) (Abcam, Cambridge, MA) in phosphate buffer saline with 1% bovine serum albumin at 37°C for 30 min.

The YFP-Rac2(V12), YFP-Cdc42, cyan fluorescent protein (CFP)-PBD, YFP-CFP, CFP-N1, and YFP-N1 plasmids were previously described (26). All YFP molecules were actually monomeric citrine containing the Q69M (pH desensitizing) and A206K (monomeric) mutations.

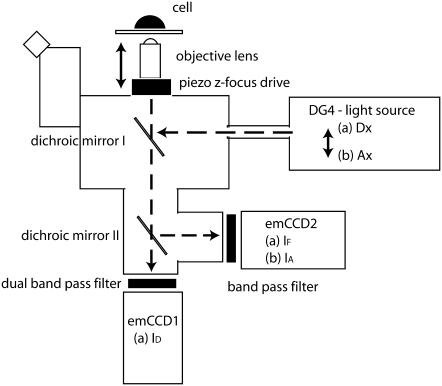
Imaging and the 4D-FRET microscope

Imaging was performed on a custom-built microscope (called the 4D-FRET microscope, Fig. 4) consisting of a Nikon TE 2000 inverted microscope body, equipped with a “stage up kit” to allow insertion of a custom-built mechanical positioner for positioning two dichromatic reflectors in the optical path below the objective. These beam splitters could be independently aligned and adjusted. The top mirror (86006bs, Chroma Technology, Rockingham, VT) reflected epifluorescence excitation launched from a liquid light guide connected to a DG4 fast switching light source (Sutter Instrument, Novato, CA). The lower mirror (535AF26) transmitted YFP fluorescence, allowing it to pass through the microscope body and tube lens and 2.5× Nikon magnifying lens to electron multiplying charge coupled device (emCCD) camera1 (Cascade II, Roper Scientific, Tucson, AZ) while reflecting CFP emission through a custom-built optical path containing a Nikon tube lens and 2.5× magnifying lens fitted to the rear dovetail of the microscope body. Light from this path was imaged onto a second identical emCCD detector (camera2). Filter wheels from Prior Scientific (Rockland, MA) were mounted between the 2.5× magnifying lens and cameras by modifying the magnifying lens holder to mount directly to the filter wheel assembly. These lens holders were also shortened to allow image formation at the plane of the CCD chip. Excitation filters were S436/10x for CFP and S492/18x for YFP and emission filters were S465/30m and S535/30m for CFP and YFP, respectively (Chroma Tech). A 60× Plan Apo (violet corrected) water-immersion objective (NA 1.2) with correction collar (Nikon) was used for imaging. Focus was controlled by moving this objective with a PIFOC (Physik Instruments, Kartsruhe, Germany). A motorized xy stage (Prior) positioned samples, which were held at 37°C in a Leiden chamber mounted in a heated microstage and regulated by a CL-100 temperature controller (Harvard Apparatus, Holliston, MA). The microscope was controlled by MetaMorph v6.5.3 (Universal Imaging, Malvern, PA). “Device Streaming” in MetaMorph was employed to maximize data acquisition rates through efficient coordination of the cameras, piezo focus, and DG4.

FIGURE 4.

Diagram of the 4D-FRET microscope. The 4D-FRET microscope was an inverted microscope optimized for rapid acquisition of three or four fluorescence images at multiple planes of focus. Broken lines indicate light paths. A water-immersion objective lens with correction collar minimizes spherical aberration in live samples. The z focus is controlled by a piezo drive that moves the objective lens. A fast light source switched rapidly between two illuminations: (a) donor excitation (Dx) and (b) acceptor excitation (Ax). The switching of wavelengths and the z axis movement of the piezo device are the only moving parts and both require 1–10 ms to change. Excitation light is reflected onto the sample by dichromatic beamsplitter I. Sample fluorescence passes through beamsplitter I to a second dichromatic beamsplitter contained within the microscope via custom-built optics and optomechanics. Dichromatic beamsplitter II transmits CFP emission to emCCD1 while reflecting the YFP emission to emCCD2. When illumination a is in place, emCCD1 records the I_D image and emCCD2 simultaneously records the I_F image. When illumination b is in place, emCCD2 records I_A. Device streaming was used to switch illumination and move the z focus (requiring a total of ∼10 ms) during the read time after each exposure, and the next image is captured. The cameras are frame-transfer and run synchronously in streaming mode.

Image processing for 3DFSR of real data

Images from the two cameras were registered using an in-house program that used the MATLAB Image Toolbox to create a projective transform from images of small beads. This transform was then applied to rotate, translate, and scale each image from camera 1 onto camera 2. Displacement was generally less than two pixels in the xy plane. Images were corrected for camera bias level by subtracting the mean of ∼30 images collected from each camera with the illumination blocked. The subtracted images were then corrected for exposure time before analysis by 3DFSR. Simulated PSFs were used for reconstruction of the data. Other than a small degree of astigmatism in the reflected image on camera 2 (likely originating from poor flatness of the dichromatic reflector) good agreement was observed between theoretical and measured PSFs.

RESULTS AND DISCUSSION

Blurring limits the accuracy and sensitivity of FRET microscopy

The model equation (Eq. 4) was used to simulate widefield FRET imaging of a single cell containing a defined arrangement of [D], [A], and E[DA]. A model cell was constructed to simulate a 4.5-μm-diameter spherical yeast cell with [D] and [A] at equal concentration in the cytosol, a 1.4-μm-diameter empty vacuole, four 400-nm-diameter compartments containing equal concentrations of [D] only, [A] only, [DA] only (with E = 0.50), and a bright compartment with [D] and [A] at 10× cytosolic concentration (Fig. 1 A). The compartments were centered on the middle z section and aligned in rows to allow easy production of xy, xz, and yz slices through all compartments. Together, the images [D], [A], and E[DA] form the vector x in Eq. 4. Other tested arrangements of the organelles did not alter the results significantly (data not shown).

The spectral mixing of the model object was accomplished by multiplication with the matrix A to generate the I_A, I_D, and I_F images of the cell (Fig. 1 A, second row). The parameters for A were taken from a microscope in our lab (α = 0.026, β = 0.657, γ = 0.037, and ξ = 0.245). In the absence of blurring, each of the compartments is clearly visible in the spectrally mixed images indicating that spectral mixing is not the limiting factor in the detection of FRET signals (Fig. 1, B and C, “spectral mixing” row). Indeed, if this process is reversed in the absence of noise by the application of A⁻¹ (e.g., FRET stoichiometry), the original object can be recovered and the E_D, E_A, and R_M terms return the correct estimates (Fig. 1 B, corresponding row). Corruption of the data by blurring and noise cannot be reversed by simple matrix multiplication. Importantly, when neglecting noise and blurring, the accuracy to which unmixing can recover the donor, acceptor, and complex distributions will be limited only by the accuracy to which A can be determined.

Blurring of FRET data results in severe spatial averaging of localized FRET signals. Blurring by matrix P simulated by convolving the spectrally mixed estimates with a simulated PSF (imaging parameters NA = 1.2, λ_ex = 434 nm, λ_em = 480 nm) using fast Fourier transforms. We focused on widefield microscopy since most live-cell FRET microscopy experiments have been performed on such instruments. In this work a single PSF was used; however, different PSFs for each color channel could be modeled as well. The sampling frequency was reduced to typical microscopy voxel dimensions of 67 nm × 67 nm × 201 nm. After blurring, the 400 nm compartments are barely visible in the I_A, I_D, and I_F images (Fig. 1 A, third row), indicating that the blurring greatly impairs detection of spectrally mixed signals. Furthermore, if FRET stoichiometry is applied to these data even in the absence of noise by multiplying by A⁻¹ and computing E_D, E_A, and R_M, the 400 nm compartments show E_D, E_A, and R_M values far from the original object. In fact, the apparent efficiencies (E_D and E_A) estimated from the blurred images were more than an order of magnitude below their values in the original images (blurred E_A and E_D = 0.026, original = 0.50). These effects are a result of the spatial averaging occurring between the cytosol and the FRET signal or high or low ratios in the 400 nm compartments. The principal effect of blurring is a redistribution of the fluorescence signals, thereby reducing the expected measured “concentrations” of fluorophores by “mixing” neighboring distributions even though they may be distinct in the original object. In the absence of spectral mixing, each signal could still be independently observed; however, when combined with spectral mixing, the spatial averaging induced by imaging severely limits the detection of FRET signals localized within a volume of non-FRET signals.

In addition to spectral mixing and optical blurring, detection noise significantly degrades FRET signals. Detection noise was simulated by drawing from a Poisson distribution with the expected mean values for each voxel defined by the spectrally mixed and spatially blurred images (Fig. 1 A, bottom). Even moderate detection noise (mean SNR for I_D = 10.4, I_A = 24.9, I_F = 10.3) was sufficient to make the various compartments nearly undetectable in the I_A, I_D, and I_F images. Furthermore, unmixing these estimates with A⁻¹ did very little to recover these compartments as seen by E_D, E_A, and R_M values at or below the limit of visual detection (Fig. 1 B, bottom row). Together, the combined effects of spectral mixing, blurring, and detection noise severely impaired the detection of subcellular FRET signals, as demonstrated for this model. This model represents a realistic FRET imaging situation in which localized interactions are hidden within delocalized signals from noninteracting molecules. The situations encountered in real FRET microscopy may be more or less challenging depending on the strength of the interaction and the cellular morphology.

3DFSR outperforms independent deconvolution and spectral unmixing

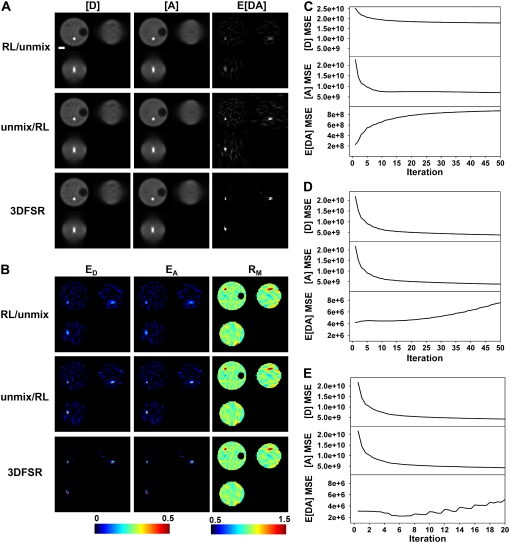
What is the best algorithm to recover the local concentrations of bound and free donors and acceptors in a sample? To address this question, we used the simulated cell in Fig. 1 to compare the performance of 1), RL-deconvolution followed by unmixing; 2), unmixing followed by RL-deconvolution; and 3), 3DFSR reconstruction. Each algorithm was run overrelaxed and unregularized for a fixed number of iterations, and the MSE between the original object and the estimated object were calculated for [D], [A], and E[DA] (Fig. 2). RL-deconvolution followed by unmixing gave poor reconstruction of the FRET-positive compartment (Fig. 2 A). In particular, the reconstruction of the spectrally mixed signals produced improved estimates of I_D, I_A, and I_F; however, unmixing by multiplication with A⁻¹ showed that the FRET-positive compartment was dim (Fig. 2 A and E[DA]) and that the E[DA] image contained many spurious signals. Furthermore, the apparent efficiencies (Fig. 2 B, E_D, and E_A) showed a FRET-positive compartment well below the expected value of 0.50 and showed many spurious FRET signals in the range of 0.10–0.20. Additionally, the MSE (Fig. 2 C) for the [D] and [A] estimates showed different convergence trajectories and optima despite [D] and [A] having nearly identical structure. Furthermore, E[DA] diverged from the original object because of spurious signals appearing in E[DA]. Despite the apparent divergence in the MSE, some reconstruction of the FRET-positive organelle was still obtained. This can be seen when comparing the last rows of Fig. 1, A and B, with the first rows of Fig. 2, A and B.

FIGURE 2.

Comparison of reconstruction techniques for noisy FRET data. Images were simulated from the model (with SNR I_D = 10.4, I_A = 24.9, I_F = 10.3, for Poisson statistics), and three reconstruction approaches were applied to obtain estimates of [D], [A], and E[DA] (A) and E_D, E_A, and R_M (B). Reconstruction with the overrelaxed RL algorithm followed by unmixing (RL/unmix) produced images that showed poor reconstruction of the FRET-positive compartment and many spurious signals in the cytosol (seen in the E[DA], E_D, and E_A images). Spectral unmixing before reconstruction by the RL algorithm (unmix/RL) produced estimates of E[DA] that showed improved reconstruction of the FRET-positive compartment; however, numerous spurious signals were also observed in E[DA], E_D, and E_A. 3DFSR outperformed direct application of the RL algorithm and produced excellent reconstruction of the [D], [A], and E[DA] concentrations as seen by the FRET-positive compartment approaching the expected FRET efficiency of 0.50 (dark red color in E_D and E_A) and the lack of spurious signals in E[DA], E_D, and E_A. The MSE between the reconstructed and simulated [D], [A], and E[DA] images indicated the convergence of the estimates to the original object for RL/unmix (C), unmix/RL (D), and 3DFSR (E). Scale bar is 1 μm. Slices are from the same planes as in Fig. 1.

Unmixing followed by RL-deconvolution performed better than the reverse approach. In particular, the FRET-positive organelle gave E_A and E_D values well above those obtained by RL/unmix approach (compare Fig. 2 B top and middle rows). Furthermore, the MSE values for this approach were improved over the RL/unmix approach as seen by the similar trajectories for the [A] and [D] estimates and by the slowed divergence for E[DA] (Fig. 2 D). However, many spurious signals were evident in the E[DA], E_D, and E_A images (Fig. 2, A and B, middle rows). These spurious signals, which were observed in both the RL/unmix and unmix/RL approaches, arose from the biased Poisson functional applied to data whose noise statistics were altered by multiplication with A⁻¹ and were no longer Poisson distributed. The appearance of spurious FRET signals was alarming since it suggests that incorrect application of deconvolution to FRET data could give rise to false-positive signals. Attempts to reduce the appearance of these signals by regularization with the entropy prior or filtering approaches gave only marginal improvements in performance (data not shown). Another limitation of this approach was seen when examining simulated cells with more complex distributions of [D], [A], and E[DA]. In those cases, the estimates of [D], [A], and E[DA] would lose correspondence from each other due to different rates of convergence depending on object complexity (data not shown). This problem could not be resolved by switching to the unbiased Gaussian functional. These observations motivated the derivation of the joined likelihood functionals for 3DFSR.

Our first approach to 3DFSR was to minimize the MLP or MLG likelihood functionals either by an RL-like EM algorithm (MLP-EM) or by steepest descent (MLG-SD). These approaches gave poor spatial reconstruction and inaccurate spectral assignment of the [D], [A], and E[DA] of the FRET-positive compartment even in the absence of noise (Fig. S1). Further investigation revealed that this behavior reflected the relative magnitudes of the spatial and spectral components of the gradient. In particular, if nearly diagonal matrices were used for A, the spatial deconvolution gave good reconstruction of each object, but as the nondiagonal components of A were increased, the reconstruction of the FRET-positive organelle suffered. Alternatively, in cases where the blurring was reduced or eliminated by setting the PSF to a delta function, accurate spectral unmixing was possible. These observations lead us to conclude that early in the reconstruction, the simultaneous optimization of spectral and spatial components of the gradient may be inefficient for minimization of the objective functionals. We concluded that the reconstruction performance should be improved if one of the spatial or spectral gradient components could be held constant while progress was made along the other component. Since there is no obvious way to hold the spatial part of the reconstruction constant, we decided to use the inverse of A to hold the spectral part constant to allow progress along the spatial direction (e.g., in the likelihood functional L1).

Alternating optimization of the L1 and L2 functionals by 3DFSR provided accurate reconstruction of the FRET-positive compartment while effectively suppressing spurious signals. In particular, 3DFSR was able to accurately recover the factor of 20 loss in both the peak value for the E[DA] (Fig. 2 A, bottom row) and the apparent FRET efficiency, as seen by the 0.50 values estimated in both the E_D and E_A images (Fig. 2 B, bottom row). Calculation of the MSE between the estimates and original objects showed good convergence for [D] and [A] and a superior convergence for E[DA]. The MSE for E[DA] (Fig. 2 E) increased at later iterations, owing to a large number of small deviations in the E[DA] estimate. However, these small deviations were largely negligible, as can be seen in the E[DA] and E_D and E_A images (Fig. 2, A and B). The reduced number of iterations needed for convergence was a result of 3DFSR taking effectively two or three steps at each iteration: one for the steepest decent minimizing L1 and one for the overrelaxed EM step minimizing L2 and possibly a third nonoverrelaxed EM step to refine the L2 estimate before the start of the next iteration.

Including the entropy prior helped suppress the spurious noise, stabilize the solution for E[DA], and further decrease the MSE (data not shown). Estimating the regularization parameters is difficult, however, and will require future work. If the regularization parameters are chosen too large, the reconstructed results become more homogenous, resulting in lower effective concentrations for highly localized signals. Alternatively, if the regularization parameters are chosen too small, the solution returns to the unregularized solution.

3DFSR provides improved sensitivity for the detection of interacting molecules from noisy data

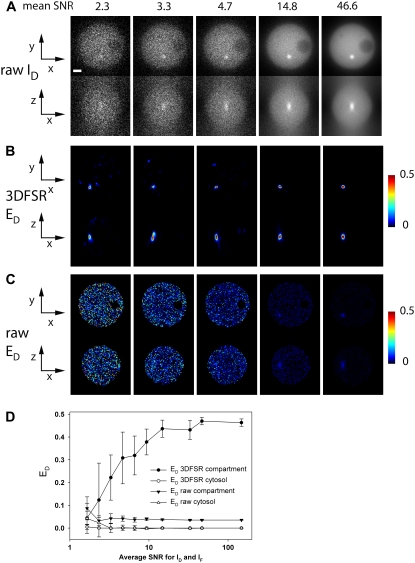
To gauge the sensitivity of 3DFSR for recovering localized or weak FRET signals from noisy data, we varied the noise by varying the number of photons used to generate images with 3× oversampling along the z axis. These images were then reconstructed with 15 iterations of 3DFSR or analyzed directly by FRET stoichiometry (Fig. 3). For FRET stoichiometry, the FRET-positive organelle was undetectable at intermediate levels of noise (disappearing near SNR = 10). In contrast, 3DFSR recovered the organelle from very noisy data (SNR = 2.3, Fig. 3, B and C). Even at this noise level, the contrast of the E_D signal in the reconstructed image surpassed that seen in the SNR = 14.8 image computed by conventional FRET stoichiometry. Repeating these experiments with 10 stochastic realizations of the simulated noise for each noise level showed that 3DFSR had a weak dependence on noise level for images with average SNRs above 10 and for images with SNR below 10, there was a nearly log-linear relationship between SNR and the average E_D value recovered from the FRET-positive organelle (Fig. 3 D). This decrease in the recovered FRET efficiency reflected two effects of noise on the reconstruction. The first effect was that the shape of the FRET-positive organelle was poorly reconstructed from low SNR images. Typically, this resulted in a narrower organelle for which less of the volume of the FRET-positive organelle would be filled (compare Fig. 3 B SNR = 2.3 and SNR = 46.6); hence, we recovered a lower average E_D signal. The second effect reducing E_D average came from occasional poor reconstruction of the FRET-positive compartment (particularly for SNR 2.3 and 3.3) resulting in E[DA] and hence E_D values even in the center of the organelle <0.50. No false positives, e.g., FRET signals emerging from the noise, were observed. Together, these measurements indicate that 3DFSR can significantly improve the sensitivity of FRET microscopy in the widefield microscope by approximately an order of magnitude.

FIGURE 3.

3DFSR improves accuracy and sensitivity over conventional FRET microscopy at all noise levels. Data simulated with various noise levels were reconstructed with 15 iterations of 3DFSR. 3DFSR provided accurate reconstruction of the FRET-positive compartment as seen by the E_D signals approaching 0.50 (A), whereas direct application of FRET stoichiometry only allowed detection of the FRET-positive compartment at high SNR (SNR ∼14.8). (D) The mean and standard deviations from 10 realizations for the FRET-positive compartment and a region in the cytosol indicated that 3DFSR could accurately recover the FRET signal in the compartment (solid circles) while correctly suppressing noise to zero (open circles), whereas conventional FRET stoichiometry measured the FRET-positive compartment to be well below the expected 0.50 at all SNR levels (solid triangles) and gave cytosol signals near zero (open triangles). Diminishing values of E_D with decreasing SNR correlated with smaller size of the reconstructed FRET-positive compartment. Scale bar is 1 μm. xy and xz slices are from the same planes as in Fig. 1.

Oversampled images (3×) were used to illustrate the impact of noise on reconstruction of a resolution limit sized object. Since the subcelluar organelles had an initial diameter of only 400 nm, we decided to use oversampled (e.g., 67 nm rather than 201 nm spacing along the z axis) images to better visualize the impact of noise on the reconstruction of these compartments. The oversampling added a degree of improved reconstruction over sampled data, but this improvement was largely due to the 3× increase in number of photons or the ∼1.7× increase in SNR.

The SNR needed for accurate reconstruction of FRET signals will depend on many factors, including the distribution of the [DA] complexes within the cell, backgrounds of free [D] and [A], as well as the instrument parameters. For these data, accurate estimation of E[DA] can be obtained by 3DFSR for data with SNR ≥10. Nonetheless, these data represent a challenging problem, with only one out of 4 × 10⁴ photons originating from E[DA] versus [A] + [D]. E[DA] distributions of greater abundance or larger volume will be easier to recover by 3DFSR. However, it is conceivable that some biological systems will have highly localized interactions with only a small subset of donor and acceptor proteins participating in the interaction. In these cases, the higher SNRs or greater z axis oversampling (effectively increasing SNR) will be needed to detect the interaction accurately. With improved optical sectioning, such as in a confocal microscope, the degree of spatial averaging will be reduced, thereby improving detection of [DA] complexes, albeit also requiring higher axial sampling.

Instrumentation for live-cell 4D(x,y,z,t) FRET microscopy of protein interactions

Given the excellent performance of 3DFSR in response to noise, we constructed an instrument capable of collecting data fast enough to limit distortions due to cellular movement and sensitive enough to avoid excessive photobleaching. The widefield instrument, referred to as the 4D-FRET microscope, used two cameras and custom optics to allow simultaneous imaging of both donor and acceptor fluorescence (Fig. 4). The detection of the FRET signal could thus be multiplexed such that during illumination at the donor excitation maximum, camera 1 recorded I_D while camera 2 simultaneously recorded I_F (which would otherwise require a separate exposure). The illumination could then be switched to the acceptor excitation maximum and I_A could be recorded on camera 2 (camera 1 could record either a blank image or a third fluorophore). By taking advantage of the rapid switching of the DG4 and efficient hardware control afforded by “device streaming” in the MetaMorph software, we were able to collect 3D stacks of images 512 × 512 × 30 planes ×4 wavelengths in ∼2 s repeatedly. Furthermore, this efficient coordination combined with high quantum efficiency (QE) emCCD cameras (QE ∼90%) and on-chip em-amplification allowed small numbers of photons to overcome the read noise, enabling in minimal exposure of the cells to excitation light. In turn, this allowed sustained imaging, image sampling with minimal photobleaching and phototoxicity (e.g., Fig. 7).

3DFSR accurately reconstructs the distributions of fluorophores and their interactions

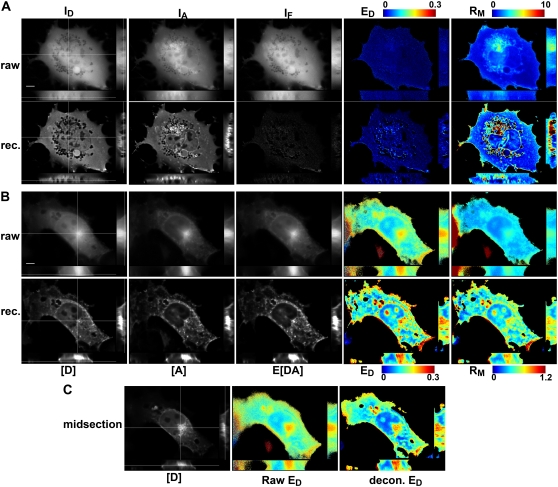
The performance of 3DFSR was tested in live cells by two approaches. The first test was to determine if 3DFSR could reconstruct the concentrations of identically distributed [D], [A], and E[DA] in the presence or absence of FRET. For this test, cells expressing free CFP and YFP (which have identical cytosolic distributions but do not show FRET (26)) were imaged at multiple focal planes, and 30 iterations of 3DFSR were applied to the data. Direct application of FRET stoichiometry indicated no interaction (as seen by E[DA], E_D, and E_A ∼0) and a uniform molar ratio (Fig. 5 A). 3DFSR produced deblurred estimates for [D] and [A] while accurately reconstructing E[DA] and, therefore, E_D and E_A near zero (Fig. 5 A). Furthermore, the R_M image remained as uniform as the nonreconstructed result (Fig. 5 A), confirming that 3DFSR reproduced the expected identical distribution of [D] and [A] in the cytosol. The holes that appear in the R_M image arose from subcellular compartments in which the reconstructed [D] and [A] signals dropped below the masking level. Similar results were consistently observed in at least nine cells, indicating the robustness of 3DFSR at reconstructing the distribution of [D] and [A] in the absence of FRET without generating false positives. In this test, we also observed that 3DFSR was robust in that large deviations in the [D]/[A] ratio between adjacent structures did not create false-positive FRET signals. An example can be seen in Fig. 5 A, where a projection from an adjacent cell expressing only acceptor crosses into the center cell expressing both donor and acceptor. This jump in acceptor/donor ratio was enhanced in the R_M image by 3DFSR, but this abrupt change did not affect the E[DA] or E_D estimates.

FIGURE 5.

3DFSR provides improved 3D resolution while accurately estimating E_D, E_A, and R_M for uniformly distributed bound and free molecules. The concentrations of [D], [A], and E[DA] were reconstructed by 3DFSR from widefield images of live cells expressing uniform free CFP and YFP (A) or a linked CFP-YFP molecule (B). 3D stacks of I_D, I_A, and I_F from cells expressing free CFP and YFP were used for direct calculation of FRET stoichiometry (top row, E_D and R_M, E_A images were very similar to E_D). Thirty iterations of 3DFSR (including photobleaching correction) produced improved estimates of [D] and [A], whereas the reconstructed estimates for E[DA] and E_D indicated no complex. Furthermore, R_M was precisely maintained. Cells expressing a linked construct demonstrated a uniform E_D of ∼0.37 and R_M ∼1.0. 3DFSR (including photobleaching correction) generated improved estimates for [D], [A], and E[DA] and accurately returned ratio images with values of 0.37 and 1.0 in all planes. The effects of FRET-enhanced photobleaching and its correction can be observed by comparing the raw E_D and reconstructed E_D in (B). Scale bar is 5 μm.

The second test was to determine if 3DFSR could accurately reconstruct uniform FRET signals. Here, cells displaying a uniform FRET efficiency of 0.37 throughout their cytosol were obtained by expressing a covalently linked donor and acceptor molecule whose FRET efficiency was known from fluorescence lifetime (1). Direct application of FRET stoichiometry to the raw data gave uniform images for E_A, E_D, and R_M in each xy plane. However, a small, but decreasing gradient was observed along the z axis for both the E_D and R_M images, indicating that photobleaching of the acceptor occurred at a nonnegligible rate during data acquisition (Fig. 5 B). The accelerated photobleaching in the presence of FRET is consistent with the acceptor molecule spending more time in the excited state, leading to accelerated photobleaching (5). Application of 3DFSR, which included the photobleaching correction, accurately produced sharpened images of [A], [D], and E[DA]. Furthermore, 3DFSR recovered the correct and uniform proportions of each species as seen by the E_D = 0.37, E_A = 0.37 (not shown), and R_M = 1.0 throughout the 3D space of the cell (Fig. 5 B). This result was representative of the nine cells analyzed. The intensity variations that can be seen in the E_D image (Fig. 5 B) can be attributed to noise in the nonregularized nature of the reconstruction. Also, the gradient induced by photobleaching was eliminated. This was unrelated to the noise enhancement.

To examine the performance of 3DFSR in the case where donor and acceptor distributions are distinct or only partially overlapping, we turned to our previously established FRET system for detecting the activation of small Rho-family GTPases. In particular, Rac2 and Cdc42 bind a domain from PAK1 called “P21-binding domain” (PBD) when in their activated, GTP-bound forms (26,27). Activating mutations in Rac2 (e.g., Rac2(V12)) impairs its ability to hydrolyze GTP to GDP, promoting its high affinity state for PBD and exposing a C-terminal membrane tethering domain that targets this protein to plasma membrane, nuclear envelope, and other internal membranes (27,28). Thus, cells cotransfected with YFP-Rac2(V12) and CFP-PBD have a largely membrane-bound YFP-Rac2(V12) distribution and a cytosolic CFP-PBD distribution except where YFP-Rac2(V12) recruits CFP-PBD to the membrane, resulting in a FRET signal (26). In cells expressing YFP-Rac2(V12) and free CFP, a pair which should not produce FRET, direct application of FRET stoichiometry showed no FRET in the cytosol and a nonhomogenous R_M image (Fig. 6 A, top row). 3DFSR of these same cells reconstructed E[DA] near zero, as expected, and recovered much of the distributions of YFP-Rac2(V12) and CFP, as can be seen by the enhanced contrast in the R_M image (Fig. 6 A, bottom row). Although the YFP-Rac2(V12) localization to the nuclear envelope was nearly undetectable in the I_A image of Fig. 6 A, after 3DFSR, the nuclear envelope localization was clearly evident (as are numerous other small vesicles). No false-positive FRET signals were observed over nine reconstructions of different cells. For cells expressing YFP-Rac2(V12) and the binding domain CFP-PBD, direct application of FRET stoichiometry recovered strong FRET signals on internal and plasma membranes; however, the contrast of the E_D and R_M images was poor (Fig. 6 B top row, E_A not shown) due to the blurring along the z axis. 3DFSR reconstruction of these cells yielded sharp reconstructions of the membrane-associated YFP-Rac2(V12), partially cytoplasmic CFP-PBD distributions, and membrane-associated YFP-Rac2(V12)/CFP-PBD complexes (Fig. 6 B, bottom row). These results were consistent over the five cells examined.

FIGURE 6.

3DFSR accurately reconstructed the 3D distribution of interacting proteins with overlapping but different distributions. (A) In cells expressing YFP-Rac2(V12) and CFP, the raw 3D images I_D, I_A, and I_F showed YFP-Rac2(V12) distributed in the cytosol and partly on internal membranes. The E_D image indicated no FRET, and R_M indicated modest differences in the distribution of the two proteins. 3DFSR estimates (A, rec.) showed improved 3D resolution of the concentrations of [D] indicating CFP localized to the cytosol and [A] indicating YFP-Rac2(V12) was predominately localized to the nuclear envelope and intracellular membranes. After reconstruction, no interaction between CFP and YFP-Rac2(V12) was observed (E[DA] and E_D = 0). Furthermore, the contrast of the R_M image was greatly increased, indicating the improved accuracy of 3DFSR in recovering the distributions of YFP-Rac2(V12) relative to free CFP. (B) A cell expressing YFP-Rac2(V12) along with interaction partner CFP-PBD indicated FRET on plasma membrane and internal membranes by direct FRET stoichiometry. The 3DFSR reconstructed YFP-Rac2(V12)/CFP-PBD complex (E[DA]) predominantly localized to intracellular membranes and plasma membrane, indicating that Rac2(V12) recruited CFP-PBD to these membranes. Again, the R_M image displayed an improved dynamic range after 3DFSR. (C) A midsection slice through the E_D image demonstrates that 3DFSR improves optical sectioning. The midsection 3DFSR E_D slice reveals structures distinct from the E_D slice taken lower in the reconstructed stack in B; however, the raw E_D image at the midsection appears nearly identical to the raw E_D from lower in the raw stack in B. Scale bar is 5 μm.

In addition to improving the contrast of these images, 3DFSR improved the z axis sectioning of the FRET and ratio images. In cells expressing YFP-Rac(V12) + CFP-PBD, the conventional FRET stoichiometry images E_A and E_D appeared very similar at several z planes (compare raw E_D in Fig. 6 B with 6 C). However, in 3DFSR reconstructed images, the contrast in the apparent efficiency images (E_A and E_D) and R_M image was significantly improved. Furthermore, individual z sections appeared more distinct than in nonreconstructed data. This effect can be seen in the distinct appearance between two planes after 3DFSR reconstruction (compare images of decon. E_D in Fig. 6 B with 6 C). The improved contrast along the z axis demonstrates that 3DFSR improves the recovery of individual z sections and helps overcome a long-standing problem with the poor contrast and z sectioning observed in apparent efficiency and ratio images obtained from widefield FRET microscopy.

4D imaging of dynamic protein interactions mediating signal transduction by 3DFSR

The goal of this work was to improve estimation of the 3D concentrations of bound and free molecules relative to morphological structures within single living cells. This was achieved by 3DFSR combined with the optimized instrumentation of the 4D-FRET microscope. Previously, we had shown by FRET that the small GTPase, Cdc42, was activated and found in complex with PBD during phagocytosis (26). The interaction between YFP-Cdc42 and CFP-PBD localized near the leading edge of the forming phagosome, producing weak signals that could only be observed when the phagosome was in the correct focal plane and phagosome extension moved in a direction parallel to the coverglass. Using 3DFSR, we were able to capture the complete morphology of the forming phagosome and the 3D distributions of molecular interactions within the cell. The improved 3D resolution and sensitivity afforded by 3DFSR allowed detection of the localized and transient interactions between YFP-Cdc42 and CFP-PBD. Slices through the center of the cell before phagocytosis indicated that YFP-Cdc42 was bound to CFP at ruffles forming near the leading edge of the cell (Fig. 7 A). Furthermore, display slices through the phagosome showed that YFP-Cdc42 interacted with CFP-PBD at the advancing margins of the forming phagocytic cup (Fig. 7 B), consistent with our earlier observations. These measurements demonstrate that 3DFSR and improved instrumentation enable sensitive detection of dynamic protein interactions within living cells.

3DFSR improves confocal FRET microscopy

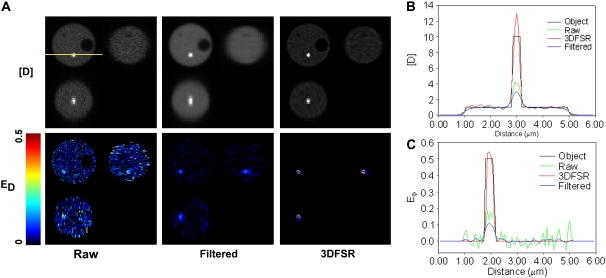
Why bother with image reconstruction if one can simply use a confocal microscope? Although the confocal microscope greatly reduces blurring along z axis, it cannot perfectly image the concentrations of localized interacting proteins. This can be seen when the model was blurred with a theoretical confocal PSF (Fig. 8 A). In particular, the concentration of complex (E[DA]) in the FRET-positive organelle is reduced by the blurring, whereas the concentrations of [D] and [A] in the larger cytosolic volume were largely unaffected. This effect decreased E_D to a value of ∼0.15 rather than 0.50 (Fig. 8 C). The same effect can be seen for the bright organelle whose concentration for [D] is reduced by averaging with its neighbors (Fig. 8 B). By including Poisson noise typical of live-cell confocal experiments (SNR for I_D = 4.7, I_A = 11.4, I_F = 4.4), we observed that even with the moderate blurring in the confocal, the FRET-positive organelle was difficult to detect (E_D image in Fig. 8 A), albeit much better than in widefield data (compare with Fig. 3 C). 3DFSR was able to reverse the blurring to provide concentration estimates that closely matched the original distributions of [D], [A], and E[DA] and therefore accurately recovered the E_D image (Fig. 8): a factor of ∼3.5 over confocal alone. The ability of 3DFSR to simultaneously improve the estimation of molecular concentration and suppress noise is a property of the deblurring with the correct statistical model and this improvement cannot be accomplished by any linear or nonlinear filtering techniques. Indeed, low-pass filtering suppressed the noise-induced degradation of the estimates (as seen in E_D, Fig. 8, A and C); however, this comes at the cost of reduced resolution (Fig. 8, A and B) and reduced accuracy in the estimation of molecular concentrations (Fig. 8 C). Wavelet-based denoising can somewhat preserve resolution while suppressing noise (29); however, this technique cannot reverse blurring or improve concentration estimation. This is in sharp contrast with the results achieved by 3DFSR, which include suppression of noise and improvements in resolution and concentration estimation. Additionally, it is possible that the combination of 3DFSR with wavelet-based denoising may yet provide superior image reconstruction (29).

FIGURE 8.

3DFSR improves confocal data and is superior low-pass filtering. Images of the model yeast cell were simulated by blurring with a confocal PSF and Poisson detection noise (mean SNR ∼7). (A) Analysis by conventional FRET stoichiometry on the raw data illustrates that the distribution of [D] and detection of E_D were just above the noise. Low-pass filtering with a Gaussian blur (σ = 67 nm) suppressed noise at the expense of resolution (as can be seen in [D]) and accuracy as seen in E_D. Alternatively, six iterations of 3DFSR recovered accurately the E_D signal while suppressing noise and improving resolution. A three-pixel-wide line scan (position shown by the yellow line in the [D] image) provides a comparison between the original object, FRET stoichiometry applied to the raw data, FRET stoichiometry applied to low-pass filtered data, and 3DFSR for either [D] (B) or E_D (C).

3DFSR implementation and applications

Although the algorithm for 3DFSR presented here provides substantial advances, its deployment in MATLAB/DIPImage is not very efficient. Typical reconstruction times for 30 iterations of 3DFSR on images 512 × 512 × 25 were 5–10 h, running on a single core of an Athlon CPU (such as for the data in Figs. 5 and 6). 3DFSR requires 7.5 times as many convolutions per iteration as conventional MLE deconvolution of a single image, indicating that about an 8× increase in computational power will be needed for 3DFSR to run at a similar rate. There is no obvious way to decrease the number fast Fourier transformations required by 3DFSR, indicating that acceleration will require deployment in a multiprocessor environment with more efficient computer code. Another possibility for accelerating the algorithm was alluded to in the methods section, in which a partly deconvolved initial guess for the 3DFSR algorithm was generated by first deconvolving with the unmixed likelihood functional (L1). This process is analogous to ITCM reconstruction and should allow faster generation of an initial approximation that can then be refined by 3DFSR.

This work demonstrates that FRET microcopy and likely also other multispectral data can benefit significantly from image reconstruction. The extension of 3DFSR to multispectral microscopy techniques such as chromosome painting and multispectral FISH should only require replacing the matrix A with the appropriate matrix. Three-dimensional reconstruction of multispectral data consisting of many wavelength measurements will be challenging with the current algorithm since the computational cost will scale linearly with the number of recorded wavelengths and the number of fluorescent species to be estimated. Nonetheless, for 3D-FRET or 3D-multispectral microscopy the number of spectral images is usually minimized to allow rapid data collection, and for FRET it has been argued that the collection of broad regions of the donor and acceptor spectrum improves the detection of FRET signals over the collection of numerous wavelengths (7).

What are the possible fluorophore pairs that can be used with 3DFSR? Although we have not explored this in detail, an examination of A and some simulations provides some clues. In the extreme case where a donor and acceptor have essentially no spectral overlap (such as Sapphire and mCherry), A will be nearly diagonal (except for the upper right corner). Here, 3DFSR will have little work in terms of spectral unmixing, and deburring operations will dominate. Importantly, the step size for each (L2) iteration of 3DFSR is constrained over the entire model, and thus, the convergence rates for [A], [D], and E[DA] will be more similar than with independent deconvolutions. Alternatively, for donors and acceptors that display large degrees of spectral overlap (e.g., green fluorescent protein and YFP), the mixing matrix A will be full and less well conditioned. Here, 3DFSR will outperform any approaches that utilize sequential unmixing and reconstruction operations. However, it is important to point out that as the spectral overlap between the fluorophores increases, higher SNR input images will be needed to obtain results equivalent to those from a system with spectral overlap. The CFP and YFP data presented in this work represent an intermediate case of spectral mixing that was successfully reconstructed by 3DFSR. More work will be needed to precisely define how the relationship among noise, spectral overlap, and the accuracy of determining A affect the performance of 3DFSR. The figure of merit defined for noise by Neher and Neher (7,13) should be a valuable tool for that endeavor.

As with any FRET technique, fluorescence components present in the sample (e.g., autofluorescence) but omitted from the analysis can give rise to false-positive FRET signals. It is possible to extend 3DFRSR to include extra fluorescent components by expanding the matrix A, the spectral measurement vector g, and the estimation vector x. Such modifications may improve detection of FRET signals in the presence of competing fluorescence signals.

3DFSR will be most useful for measuring highly localized protein interactions. Such interactions are frequently encountered in signal transduction and in the interactions of host cells with viruses and bacteria. In these cases, localized FRET signals are embedded in larger volumes of non-FRET signals, and only approaches that limit or reassign out-of-focus light will be able to improve the detection and quantification of FRET in these structures. This advantage, combined with the robustness of 3DFSR against noise, makes this technique useful for imaging localized and dynamic structures in live cells that may otherwise be undetectable by spectral FRET microscopy (e.g., FRET stoichiometry) or by fluorescence lifetime measurements in widefield microscopes. These gains, however, come at the cost of needing more images and hence increased illumination leading to photobleaching and potential phototoxicity in live-cell experiments. The impact of increased data acquisition in live cells may be somewhat offset by the robustness of 3DFSR against noisier input data and therefore allow shorter image exposures and faster acquisitions than used in z stack collections for widefield or confocal FRET images. The main disadvantage of 3DFSR is that it requires that the data be collected faster than the movement of subcellular structures or the formation and dissolution of the FRET complex. If this cannot be achieved, distortions will propagate across the z planes in the reconstructed data. Importantly, this was not a factor in the imaging of Cdc42 activation during the phagocytosis presented here. Hence, 3DFSR will be most useful for localized and dynamic interactions when additional data acquisition and computational efforts can be afforded.

In widefield FRET microscopy, interpretation of sensitized emission images is confounded by variations in the sensitized emission intensity arising from variations in cell thickness (due to poor sectioning along the z axis) and changes in the local concentrations of donors and acceptors. Although 3DFSR reassigns out-of-focus light, interpretation of E[DA] while neglecting [D] and [A] distributions could still be ambiguous since bright regions could arise from formation of more D-A complexes or simply the accumulation all three species. This ambiguity is resolved by calculation of the apparent efficiencies since they reflect the fraction of bound molecules. Although FLIM can used to measure E_D (or to even separate [DA]/[D] from E), R_M and E_A are usually not recovered, leaving ambiguities in the interpretation of molecular associations. FRET stoichiometry and 3DFSR data are easily converted into apparent efficiencies and, therefore, are useful for measuring bimolecular associations in situations of variable cell thickness and donor/acceptor ratios. In an in vivo binding experiment, FRET stoichiometry was used to generate a titration curves for the binding of acceptor and donors (e.g., E_A and E_D) at acceptor/donor ratios ranging from 10⁻² to 10² (26). Similar performance would be expected for 3DFSR, provided exposure times were varied to maintain sufficient SNR in I_A, I_D, and I_F.

3DFSR provides a foundation for reconstruction of FRET data obtained by superresolution microscopy. For superresolution microscopy techniques such as 4Pi (30), stimulated emission depletion (STED) (31), and structured illumination microscopy (32,33), reconstruction schemes are very important to deal with harmonic sidebands (4Pi), noisy data (STED), and image reassembly (structured illumination). These reconstruction approaches are of the same form as the 3DFSR approach presented here. Although instrumentation for FRET microscopy does not yet exist for these modalities, such experiments are likely to become feasible, and reconstruction approaches will be needed.

3DFSR brings FRET microscopy one step closer to quantitative analysis of cellular pathways. 3DFSR provides orders of magnitude improvement for both sensitivity and accuracy in the detection of localized FRET signals for widefield microscopy and smaller, although significant gains (factors of 2–5), for confocal microscopy. These gains when combined with novel instrumentation allowed attainment of one of the long-standing goals of FRET microscopy: sustained, sensitive, and accurate measurement of submicron localized molecular interactions throughout the 3D space of living cells. This is evidenced by sustained 4D imaging of the signal transduction of Cdc42 during phagocytosis, which may otherwise be missed or inaccurately measured by conventional FRET approaches. Furthermore, the improvements in concentration estimation can be combined with methods for calibrating fluorescence in terms of actual molar concentrations (34). This combination will facilitate the measurement of parameters needed for quantitative modeling of the chemistries occurring in real cellular pathways by partial and ordinary differential equation models. Additionally, application of 3DFSR to the analysis of protein interactions inside living cells requires only a modest investment in instrumentation and computational resources, which should make it a widely available technique for cellular pathway analysis.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.