Molecular Dynamics and Principal Components Analysis of Human Telomeric Quadruplex Multimers

Abstract

Guanine-rich DNA repeat sequences located at the terminal ends of chromosomal DNA can fold in a sequence-dependent manner into G-quadruplex structures, notably the terminal 150–200 nucleotides at the 3′ end, which occur as a single-stranded DNA overhang. The crystal structures of quadruplexes with two and four human telomeric repeats show an all-parallel-stranded topology that is readily capable of forming extended stacks of such quadruplex structures, with external TTA loops positioned to potentially interact with other macromolecules. This study reports on possible arrangements for these quadruplex dimers and tetramers, which can be formed from 8 or 16 telomeric DNA repeats, and on a methodology for modeling their interactions with small molecules. A series of computational methods including molecular dynamics, free energy calculations, and principal components analysis have been used to characterize the properties of these higher-order G-quadruplex dimers and tetramers with parallel-stranded topology. The results confirm the stability of the central G-tetrads, the individual quadruplexes, and the resulting multimers. Principal components analysis has been carried out to highlight the dominant motions in these G-quadruplex dimer and multimer structures. The TTA loop is the most flexible part of the model and the overall multimer quadruplex becoming more stable with the addition of further G-tetrads. The addition of a ligand to the model confirms the hypothesis that flat planar chromophores stabilize G-quadruplex structures by making them less flexible.

INTRODUCTION

Telomeric DNA occurs at the ends of eukaryotic chromosomes. Its function is to protect the genome from degradation, chromosomal fusions, and recombination (1). In vertebrates it consists of the guanine-rich tandem repeats d(T₂AG₃)_n, and in normal human somatic cells is ∼5–8 kb in length (2). It is in duplex form for most of this length, with the exception of the 3′ terminal 150–200 nucleotides, that comprise a single-stranded overhang (3). Due to the inability of DNA polymerase to fully copy the 3′ ends, telomeric DNA progressive shortens during replication (4). This does not occur in cancer cells and the “end-replication problem” is overcome by the expression of the enzyme telomerase, which adds hexanucleotide repeats to the 3′ end of the single-stranded DNA, thereby preventing shortening of telomeres.

Single-stranded G-rich telomeric sequences at the end of chromosomes can fold into intramolecular quadruplex structures, that involve G-tetrad building-blocks held together by Hoogsteen basepairing (5), making the resulting quadruplex structures extremely stable. Although their formation is likely to be hindered by single-strand binding proteins, and by telomerase itself, G-quadruplexes may play a role in telomere regulation (4). It has also been established experimentally that small molecule-induced stabilization of G-quadruplexes can inhibit the enzyme telomerase, leading to telomere shortening and cell death in neoplastic cells (6,7). This approach is currently being developed as a selective therapeutic strategy in human cancer. Identification of several proteins specific for G-quadruplexes has given credence to the importance of these structures and the roles that they might play in both telomere maintenance and other biological processes (8–16).

The folding and formation of short (up to four repeat) telomeric G-quadruplex structures have been studied extensively by a variety of biophysical, structural, and chemical probe methods. The crystal structure of a four-repeat human telomeric sequence d[AG₃(T₂AG₃)₃], crystallized from a potassium ion environment, shows that it forms an intramolecular G-quadruplex structure in which all four phosphate backbone strands are parallel to each other and the tetrads stabilized by the presence of K⁺ ions in the central cavity (17). Several NMR solution studies on this and related sequences (18–23) have shown distinct topologies involving anti-parallel backbone arrangements, both for d[AG₃(T₂AG₃)₃] itself in sodium solution and for this 22-mer with the addition of stabilizing flanking sequences in potassium solution. In these topologies the connecting lateral and diagonal loops are positioned such as to restrict access to the terminal G-tetrad planes compared to the more open arrangement in the parallel structure (17). The crystal structure of the human telomeric sequence has connecting loops on the side of the G-quadruplex, away from the G-tetrad planes. Such an arrangement has broad implications for the design of new quadruplex stabilizing ligands. The three TTA sequences that link the core G-tetrads are folded to form loops and project outward in a propeller-like manner connecting the top of one strand with the bottom of the other, thus maintaining the parallel arrangement and the integrity of the G-quadruplex (Fig. 1, b and d).

FIGURE 1.

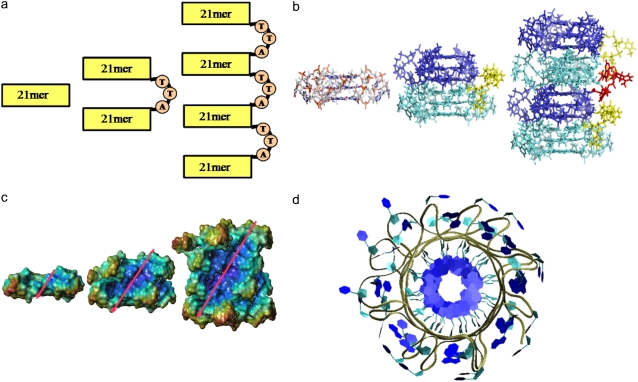
Schematic showing the construction of higher order human telomeric DNA quadruplexes. (a) Cartoon and (b) stick representations of the construction of the 45-mer from two 21-mer units (cyan and blue), connected together by a TTA loop in a 5′ → 3′ orientation (yellow). Two 45-mer units can be joined by a TTA loop (red) to form a 93-mer. (c) Surface representation of 21-mer, 45-mer, and 93-mer models. The values of rise and rotation between successive G-tetrads results in the generation of grooves (whose direction is indicated by diagonal arrows), which are retained in the higher order models. (d) Top view of model 4 highlighting its propeller-like appearance.

All structural studies reported to date on telomeric G-quadruplexes have been on short sequences with not more than four telomeric repeats. Higher-order arrangements with several G-quadruplex repeats are at least feasible in vivo because they are allowed as a consequence of the length of the telomeric DNA single-stranded overhang. However, there is no data at present on the structural properties of G-quadruplex repeats, so their structural features can only been estimated at present, based on the existing crystal and NMR structures. Such models will also provide insight into ways of improving small-molecule ligands and in the design of new ones that can stabilize these structures.

We have used molecular modeling methods to build models of G-quadruplex arrays of dimer and tetramer structures formed from extended human telomeric DNA, to ascertain whether such repeats are stable, and then to analyze the conformations and stability of these multimer quadruplexes, their component quadruplex units, the G-tetrads, and the TTA loops. All-atom molecular dynamics (MD) simulations in explicit solvent have been used. The solvent-accessible terminal G-tetrad planes, known to bind quadruplex stabilizing ligands have also been examined. The relative free energies of loop conformations have been estimated using molecular mechanics and the Poisson-Boltzmann surface area (MM-PBSA) approximation. Principal components analysis has been used to describe the inherent dynamic motions of G-quadruplex structures and has identified several concerted principal motions, mainly in the loop regions.

The study has also been used to validate the AMBER methodology and its force-field for quadruplex DNA simulations. Comparisons with crystallographically-derived geometries have shown that there are no significant perturbations of G-tetrad geometry or of the ions in the central channel, by contrast with earlier simulations. These are well-established problems that have been extensively documented (24–27), and arise in large part from the particular challenges to simulations posed by the electrostatic environment of quadruplex DNA, which are a consequence of the combination of the charges on the phosphate ions around the exterior of quadruplex structures, and their central cation-containing ion channel.

METHODS

Quadruplex model building

The crystal structure (17) of the 22-mer human telomeric DNA d[AG₃(T₂AG₃)₃] (PDB code 1KF1) was used as the primary unit for the construction of the higher-order models. It consists of three stacks of guanine tetrads connected by TTA loops. The extreme 5′ adenine base was first removed to generate a 21-mer. The 45-mer human telomeric DNA model (model 1) was then constructed using two 21-mer units (Fig. 1, a and b). The two units were positioned end-to-end (3′ → 5′) and rotated 30° relative to each other. This 30° twist was taken from the original crystallographic analysis (17), and is the twist angle found between two consecutive stacked quadruplexes. The rise and rotation of G-tetrads between the two units was kept at values observed in the crystal structure, and were positioned at an optimal separation of 3.5 Å. The two units were then joined by a TTA loop that had been extracted from the crystal structure. The final 45-mer model was subjected to molecular mechanics energy minimization (3 × 1000 steps steepest descent and conjugate gradient) to relieve any steric clashes within the structure.

A second 45-mer human telomeric DNA model (model 2) was also constructed with a pseudo-intercalation ligand binding site introduced between the two 21-mer units. The binding site was constructed by breaking the phosphate backbones and separating the two units in the model so that the distance between the two guanine tetrads increased from 3.5 Å to 7.0 Å. The sugar-phosphate backbones were reconnected and molecular-mechanics energy minimization (3 × 1000 steps steepest descent and conjugate gradient) was used to relieve any resulting steric distortions while retaining the intercalation geometry between guanine tetrads by means of appropriate positional restraints. A third model (model 3) was generated where a potential G-quadruplex stabilizing ligand was docked in the pseudo-intercalation site generated in model 2.

The model of the four-quadruplex repeat 93-mer human telomeric DNA (model 4) was generated by taking two 45-mer units, positioning them and joining them in a manner analogous to that described above. The resultant model was subjected to a similar protocol of molecular mechanics energy minimization procedures. The models are shown in Figs. 1 and 2.

FIGURE 2.

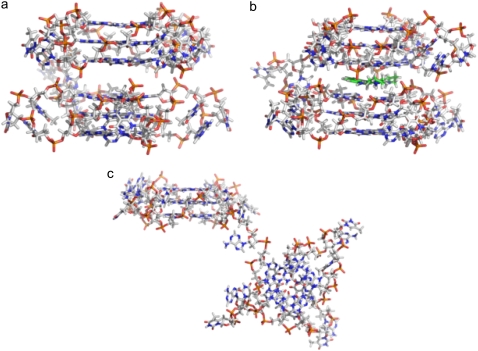
Stick representations of model 2 and model 3. (a) Model 2 with a pseudo-intercalation site can be generated by increasing the stacking distance between the two 21-mer units in model 1 from 3.5 Å to 7.0 Å. (b) Ligand molecule (green) can be docked in the pseudo-intercalation site to generate model 3. (c) Average structure of model 2 calculated from the 15 ns simulation. The overall structure of the model is distorted; however, the two individual quadruplex units (21-mer) retain their structures.

Ligand modeling

A molecular model of an acridine molecule (BSU6039) identified previously by us as a quadruplex-binding ligand (28,29), was constructed, minimized, and partial charges calculated semi-empirically using MOPAC (30) from the Insight II suite software (www.accelrys.com). The ligand was minimized and docked in the pseudo-intercalation site in model 2 with the AFFINITY docking program (www.accelrys.com) to generate model 3, using the systematic grid docking method available with AFFINITY, and with the quadruplex structure kept fixed. This approach has been validated previously in our earlier studies on the rational design of quadruplex ligands (31,32). The G-tetrads were kept frozen in their original conformation throughout the docking procedures. We consider this to be a valid approximation because the G-tetrad platform has been shown previously by a number of experimental and simulation studies (17–28) to be exceptionally stable and structurally rigid; this assumption was subsequently borne out by the results of the simulation studies. The program uses an automated approach to identify those ligand positions exhibiting high interaction energies within the binding site. The final conformation of the ligand complex was then subjected to a further 500 steps of unrestrained molecular mechanics energy minimization. The XLEAP module in the AMBER 9.0 suite (33) was then used to set up the complex for further molecular dynamics simulations. The force-field parameters for the ligands were extrapolated from the existing values for analogous groups in the AMBER ff99 (34) and CFF force fields (35,36).

Molecular dynamics simulations

The x-ray structure has shown a vertical alignment of consecutive K⁺ ions along the axis within the central core of the complex, mid-way between each G-tetrad. The ions were retained in the positions observed in the crystal structure (17). The models were then solvated in a periodic TIP3P water box (37) of dimensions whose boundaries extended at least 10 Å from any solute atom. Additional positively-charged K⁺ counterions were included in the system to neutralize the charge on the DNA backbone. These maintained consistency with the crystallization conditions and hence simulated a uniform K⁺ ionic environment. The counterions were automatically placed by the LEAP program throughout the water box at grid points of negative Coulombic potential. The final system had net zero charge.

The simulation protocols were consistent for all of the systems. Each system was equilibrated with explicit solvent molecules by 1000 steps of minimization and 220 ps of molecular dynamics at 300 K. The entire systems were kept constrained, while allowing the ions and the solvent molecules to equilibrate. The systems were then subjected to a series of dynamics calculations in which the constraints were gradually relaxed, until no constraints at all were applied. The final production run was carried out without any restrain on the complex for 15 ns and coordinates were saved after every 10 ps for analysis of their trajectories.

All calculations were carried out with the SANDER module of AMBER 9.0, and with the SHAKE algorithm (38) enabled for hydrogen atoms, with a tolerance of 0.0005 Å and a 2-fs time step. The SHAKE feature constrains the vibrational stretching of hydrogen bond lengths and effectively fixes the bond distance to the equilibrium value. A 10 Å nonbonded Lennard-Jones cut-off was used and the nonbonded pairs list updated every 20 steps. The Particle-Mesh Ewald summation (39) term was used for all simulations with the charge grid spacing at ∼1.0 Å. The trajectories were analyzed using the PTRAJ module available in the AMBER 9.0 suite and visualized by means of the VMD program (40).

MM-PBSA calculations

Free energies were calculated using the MM-PBSA method. The electrostatic contribution to the solvation free energy was calculated using the Delphi program (41). Free energies were estimated by averaging the configurations that were collected at 20 ps intervals for energetic analysis during the last 5 ns of the MD simulation. This included the cations present within the electronegatively-charged central channel. These are considered to be an integral part of the structure and are required to be included in the MM-PBSA calculations to obtain meaningful results (25). The AMBER parm99 charge set and Bondi radii were used (42). The K⁺ radius was kept at 2.025 Å, based on a study by Hazel et al. (43). All other calculations were carried out using internal scripts distributed with the AMBER 9.0 suite. The solute entropic contribution was estimated with the Nmode program, using snapshots collected every 250 ps.

An attempt also was made to identify free energies contributed by different segments within the quadruplex, and was split into tetrad stems, loops and linker loops. The free energies of the individual segments were calculated independently using the programs in the AMBER 9.0 suite.

Principal components analysis

Reducing the dimensionality of the data obtained from molecular dynamics simulations can help in identifying configurational space that contains only a few degrees of freedom in which anharmonic motion occurs. Principal components analysis (PCA) is a method that takes the trajectory of a molecular dynamics simulation and extracts the dominant modes in the motion of the molecule (44–47). These pronounced motions correspond to correlated vibrational modes or collective motions of groups of atoms in normal modes analysis (48). The overall translational and rotational motions in the MD trajectory are eliminated by a translation to the average geometrical center of the molecule and by a least squares fit superimposition onto a reference structure (45). The configurational space can then be reconstructed using a simple linear transformation in Cartesian coordinate space to generate a 3 N × 3 N covariance matrix. Diagonalization of the covariance matrix generates a set of eigenvectors that gives a vectorial description of each component of the motion by indicating the direction of the motion. The eigenvector describing the motion has a corresponding eigenvalue that represents the energetic contribution of that particular component to the motion. Projection of the trajectory on a particular eigenvector highlights the time-dependent motions that the components perform in the particular vibrational mode. The time-average of the projection shows the contribution of components of the atomic vibrations to this mode of concerted motion (47).

PCA was carried out using the PCAZIP software (49) on i), all-atom quadruplex models 1 and 3 containing 1463 (45-mer) and model 4 3023 (93-mer) atoms; and on ii), backbone-only atoms of model 1 and 3 containing 269 (45-mer) and model 4 comprising of 557 (93-mer) nonsolvent atoms (Table 1). Molecular dynamics trajectories of corresponding atoms were extracted using the PTRAJ program and analysis carried out for the last 5 ns (10–15 ns) using 500 frames.

TABLE 1.

Summary of the simulations together with numbers of atoms and rmsd values (Å)

		Environment
Simulations	Timescale	DNA (backbone)	Waters	Rmsd, Å (all)	Rmsd, Å (backbone)
45-mer	15 ns	1463 (269)	22,889	3.80	2.93
45-mer(empty binding site)	15 ns	1463 (269)	21,764	12.66	11.27
45-mer(+ BSU6039)	15 ns	1463 (269)(+70)	22,961	3.68	2.90
93-mer	15 ns	3023 (557)	36,692	3.52	2.72

Other Computational Details

All structural diagrams were prepared using the VMD program (40). All graphs were plotted using the Xmgrace program (http://plasma-gate.weizmann.ac.il/Grace/) and the arrows representing the magnitude and direction of eigenvectors were calculated using in-house scripts.

RESULTS

Structural stability of the models

The root mean-square deviation (rmsd) over the course of the simulation can be used as a measure of the conformational stability of a structure or a model during that simulation. Here we are interested in examining the conformational stability of the higher-order G-quadruplex structures from telomeric DNA and to observe the dynamic effects of the G-quadruplex ligand BSU6039 on such higher order structures.

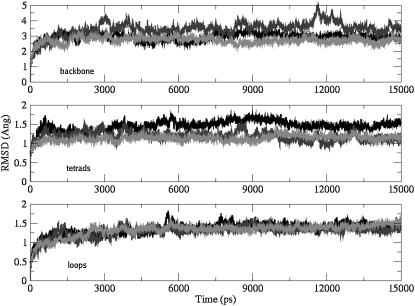
Fig. 3 compares the rmsd of the models over the course of the simulation to the initial reference structure. Each plot shows the rmsd from the all-atom model (black), backbone-only atoms (green), and G-tetrads (red). A jump in rmsd is observed within the first nanosecond, which is a consequence of relaxation of the starting model. The trajectory was stabilized over the time course, with relatively small fluctuations in the models. As evident from the plots, the rmsds of the all-atom models are higher than that of the backbone alone. The backbone atoms are stabilized earlier during the course of the simulation and the higher rmsd of an all-atom model is a result of the wobbling effect of the nucleotide bases. Each G-tetrad is held together in a co-planar array with eight hydrogen bonds, which is the major factor contributing to these tetrads being the most stable moieties in the models.

FIGURE 3.

Plots following the stability of the models during the dynamics runs. Rmsd plots calculated from all-atoms (black), backbone-only atoms (light gray), and G-tetrads (dark gray) for (a) model 1 (45-mer), (b) model 2 (45-mer with empty binding site), (c) model 3 (45-mer with ligand in binding site) and (d) model 4 (93-mer). The tetrads are the most stable subsegment. The rmsds of G-tetrads from individual 21-mer units are plotted for model 2 (gray shades) in (b).

All the models are stable over the course of the simulation except model 2 (Fig. 3 b; Table 1). The rmsd of the 45-mer in the absence of the ligand in the pseudo-intercalation site (model 2) was extremely high, suggesting distortion of the structure from its starting conformation (Fig. 2 c). Close examination of the structure showed that the two quadruplex units were remarkably stable independently, as evident by their individual rmsds (Table 2). Displacement of the ligand from the pseudo-intercalation site results in the loss of the π-π stacking interactions that holds the two quadruplex units together. As a result, the quadruplexes behave as two independent subunits connected together by a TTA linker loop. The TTA linker loop also looses all of its original conformational features and becomes extended, thereby explaining the higher rmsd observed for this system.

TABLE 2.

Rmsd values (Å) for quadruplex units

Segments	Model 145-mer	Model 245-mer (EBS)*	Model 345-mer (+ BSU6039)	Model 493-mer
Tetrads
Quadruplex 1 (A)	1.44	1.32	1.30	1.18
Tetrad 1	1.62	1.51	1.24	1.48
Tetrad 2	1.61	1.34	1.53	1.12
Tetrad 3	1.11	1.13	1.13	0.96
Quadruplex 2 (B)	1.18	1.11	1.09	1.08
Tetrad 4	1.41	1.57	1.22	1.10
Tetrad 5	1.06	0.86	1.06	0.79
Tetrad 6	1.15	0.91	1.01	1.37
Quadruplex 3 (C)	–	–	–	0.98
Tetrad 7	–	–	–	1.14
Tetrad 8	–	–	–	0.94
Tetrad 9	–	–	–	0.88
Quadruplex 4 (D)	–	–	–	1.16
Tetrad 10	–	–	–	1.28
Tetrad 11	–	–	–	0.96
Tetrad 12	–	–	–	1.24
Individual loops
Quadruplex 1
Loop LA1	1.34	1.55	1.51	1.51
Loop LA2	1.39	0.84	1.28	1.13
Loop LA3	1.57	1.53	1.25	1.67
TTA Linker Loop 1	1.36	3.91	1.74	1.11
Quadruplex 2
Loop LB1	1.39	1.20	1.19	1.43
Loop LB2	1.10	1.65	1.37	1.66
Loop LB3	1.30	1.49	1.12	1.47
TTA Linker Loop 2	–	–	–	0.95
Quadruplex 3
Loop LC1	–	–	–	1.81
Loop LC2	–	–	–	1.23
Loop LC3	–	–	–	1.15
TTA Linker Loop 3	–	–	–	1.10
Quadruplex 4	–	–	–	0.94
Loop LD1	–	–	–	1.33
Loop LD2	–	–	–	0.74

^*Empty binding site.

We have also analyzed the stability of the subsegments of the models. Table 2 summarize the rmsds of individual quadruplexes, G-tetrads, loops within the quadruplexes, and the TTA linker loops that join individual quadruplexes together. The flexibility of the TTA linker loop is highlighted when comparing the TTA linker loop in model 1 and model 3. The higher rmsd value observed for the TTA linker loop in model 3 can be attributed to the presence of the ligand molecule in the pseudo-intercalation site. The alkyl side chains of the ligand molecule are mobile and the model needs to adjust to their high mobility. The TTA linker loop can accommodate their flexibility by adjusting its conformation to stabilize the model. This also results in the rotary motion observed in the principal components analysis (see below).

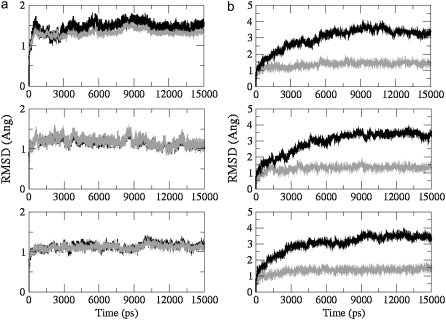
Fig. 4 compares the rmsds of different subsegments between the models. Model 2 has not included in the analysis because of the instability of the overall model. The rmsd values of all subsegments are within the comparable range. The most stable subsegments belong to model 4, suggesting that multiple G-tetrad stacks enhance the overall stability of the model. Rmsd plots of all-atom versus backbone-only atoms again show the highly stable nature of the G-tetrads (Fig. 5 a). However, this is not the case for the loops where the differences are large enough to identify the wobbling effect of nucleoside bases to be the main contributor to the higher rmsd values (Fig. 5). There are only small differences between the rmsd values observed for an all-atom model and the backbone-only models for the G-tetrads.

FIGURE 4.

Rmsd plots comparing different subsegments between models. Backbone atoms (top), G-tetrads (middle), and TTA loops (bottom). The pattern of stability observed between different subsegments is consistent with model 4 (93-mer; light gray) being most stable, followed by model 3 (45-mer + ligand; dark gray) and then model 1 (45-mer; black).

FIGURE 5.

Rmsd plots of all-atoms (black) versus backbone-only atoms (gray) for the (a) G-tetrads and for the (b) TTA loops, calculated from the 15ns simulations of model 1 (top), model 3 (middle), and model 4 (bottom).

Conformation of the G-tetrads

The planar arrangement of the G-tetrads with their extensive network of Watson-Crick and Hoogsteen basepairing is maintained throughout the 15 ns simulation runs. The geometry of the consecutive G-tetrad stacking as observed in the crystal structures, measured by rise and twist, is also retained in models 1, 3, and 4. The models retain a stacking geometry of 12 G-tetrads per turn, similar to the G-tetrads in the parallel-stranded crystal structure. They are slightly under-wound when compared to canonical B-form (10.5 bases per turn) and A-form (11 bases per turn) DNA (50). Very minor variations in geometry are observed during the course of the simulation, for example, the average N2–N7 distance and O6-N1 bonds lengthen up to 0.2 Å (Table 3). The average phosphate-phosphate distance is also slightly increased during the simulations, by up to 0.4 Å (Table 3).

TABLE 3.

Mean distances (Å) calculated from the simulations, averaged over all G-tetrads and over all nucleotides

Distance	X-ray (22-mer)	45-mer	45-mer (+ BSU6039)	93-mer
N2…N7	2.82	2.95	2.94	2.93
O6…N1	2.86	2.97	2.96	2.96
P…P	6.45	6.89	6.86	6.87

Conformation of the TTA loops

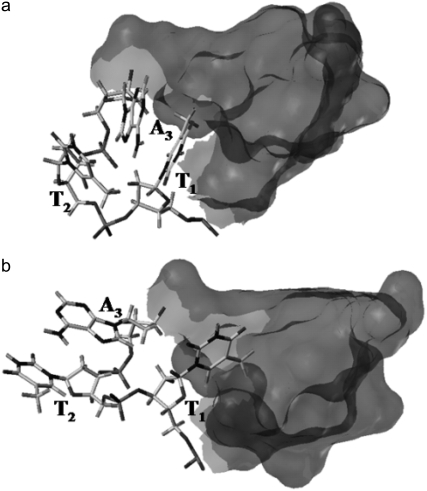
The TTA loops (with nucleotides labeled T₁, T₂, and A₃) in the models are arranged diagonally, external to the guanine tetrads in a propeller-like manner and are consistent with the generation of a parallel stranded G-quadruplex. The A₃ nucleotide in each TTA sequence is swung back such that it intercalates between T₁ and T₂ and makes stacking interactions with T₁ (Fig. 6 a). Stabilization of the loop may also come from hydrogen-bonding interactions of the central thymine T₂ with the adjacent adenine A₃ (Thy O4–Ade N6) and T₁ (Thy O4–Thy O2). Comparison between the starting conformations of the loops with their time-averaged structures from the MD simulation shows major conformational changes in some of the loop structures. The Thy(T₁)–Ade(A₃) stacking is disrupted. T₁ then slides into the groove created by the stacking of the G-tetrads (Fig. 6 b). T₁ also optimizes the network of hydrogen bonds with guanines in the tetrads (Thy O4–Gua N2). Comparison of the calculated average loop structure with that observed in the crystal structure indicated that in the absence of constrains the adenine (A₃) base flips to stack over the second thymine (T₂) via π-π stacking interaction (Fig. 6 b). This increases the distance between thymine T₁ and the adenine A₃ phosphate groups from 8 Å (x-ray) to 10.8 Å (simulations). However, some of the loops in the models also retain their starting conformation.

FIGURE 6.

Conformations adopted by the TTA loop during the simulations. (a) The TTA loop in the crystal structure or starting conformation in which the thymine T₁ is stacked with adenine A₃. (b) Time-averaged structure of the TTA loop adopting another conformation where thymine T₂ and adenine A₃ are flipped outward and base stacked. The thymine T₁ slides deeper into the groove and makes hydrogen-bond interactions with the G-tetrads. The partial structure of the G-tetrads is represented as gray surface.

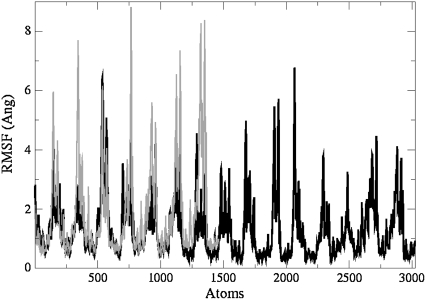
Nevertheless, the conformational changes observed in the loops do not have any impact on the structure of the central G-tetrads core. These results are in agreement with the reported rmsd values that indicate greatest stability for the central G-tetrads in a quadruplex, followed by the loops (41). This is also confirmed by the rms fluctuation plots calculated from the first eigenvector (Fig. 7) in which atoms 1–1463 (model 1; black) are superimposed over atoms 1–3023 of model 4 (blue). Large fluctuations indicated by sharp peaks belong to the loops, with much smaller fluctuations observed for the tetrads. Peaks would be observed at identical positions indicating concerted fluctuations within the models. Higher fluctuation for model 1 indicates that it is more flexible than model 3 and model 4. This is also confirmed by the cumulative eigenvalues (see below).

FIGURE 7.

All-atom rms fluctuation versus atom number for model 1 (black) and model 4 (gray) simulations calculated from the first eigenvector. The pattern shows the position of atoms in loops as sharp peaks interspaced by low fluctuating atoms from the G-tetrads. Peaks at identical position relate to the corresponding atom in different models.

MM-PBSA calculations

Free energies calculated using MM-PBSA methodology can be used to study quadruplex models and provide a semiquantitative estimate of their stability (25). Models with lower free energies are expected to be more stable than those with higher values. Previous studies investigating different conformations of the loops have carried out separate free energy calculations on the tetrad core (tetrad stems) and loop regions (25,43). We have adopted a similar approach, of calculating the total free energy G_total for the models simulated with MD in explicit solvent. G_total was further subdivided into tetrad stem, loop, and TTA linker loop contributions, to study the individual energetic contributions by these subsegments. However, the different nature of the propeller loops in our simulations should be kept in mind. Furthermore, it should be noted that the free energies reported here should be considered as relative values for the comparison of structures rather than absolute values (that could be compared with experimental values). Results from the simulations are summarized in Table 4. The solute entropic contribution was not included in the free energy values in Table 4, although the solvent entropy is implicitly taken into account in the solvation energy term. This is because the entropic contribution is the least accurately calculated component of the free energy (43). It should also be noted that the difference between the calculated free energies for the models is very small and within the margins of error for the free energy calculations.

TABLE 4.

Free energies (kcal/mol) calculated using MM-PBSA methodology (last 5 ns) for the whole system (total) and subsegments including individual loops and TTA linker loops

G	Model 145-mer	Model 245-mer (EBS)*	Model 345-mer (+ BSU6039)	Model 493-mer
Total	−7853.68	−7813.73	−8033.61	−15,623.70
Quadruplex 1 (A)	−2413.17	−2399.86	−2392.24	−2415.63
Loops 1
LA1	−371.66	−374.13	−367.74	−368.35
LA2	−372.36	−368.44	−371.52	−371.84
LA3	−369.49	−367.42	−370.04	−369.33
TTA Linker Loop 1	−369.67	−308.11	−365.31	−366.58
Quadruplex 2 (B)	−2439.23	−2447.22	−2434.97	−2435.41
Loops 2
LB1	−370.71	−371.36	−370.40	−371.42
LB2	−372.14	−366.43	−370.58	−368.67
LB3	−368.33	−371.20	−368.55	−371.45
TTA Linker Loop 2	–	–	–	−365.74
Quadruplex 3 (C)	–	–	–	−2441.07
Loops 3
LC1	–	–	–	−372.15
LC2	–	–	–	−375.09
LC3	–	–	–	−367.63
TTA Linker Loop 3	–	–	–	−364.10
Quadruplex 4 (D)	–	–	–	−2437.93
Loops 4	–	–	–	−372.22
LD1	–	–	–	−373.58
LD2	–	–	–	−371.40

Free energy values do not include the solute entropy.

^*Empty binding site.

The free energy values for various subsegments in the different models are remarkably similar. That for model 2 is higher than the value calculated for model 1. This has its basis in the distortion of model 2, which would offer a molecular surface that is more amenable to solvation. This distortion is a consequence of the disruption of the π-π stacking interactions that holds the two quadruplex units together. The TTA linker loop that joins the two quadruplex units together also looses its structure (Fig. 2 c) exposing the bases to solvent. However, the individual quadruplex units are stable and their energetic contributions are comparable to corresponding subsegments in other models. This distortion is not observed in model 1 where the π-π stacking is strong between the adjacent tetrads and also in model 3 where the π-π stacking in the pseudo-intercalation site is compensated for by the planar aromatic acridine chromophore. Additional structural stability is also provided by the centrally protonated nitrogen atom in the ligand molecule. It is also interesting to note the difference in energies between model 1 and model 3, which is the more energetically stable of the two. The stabilization of model 3 is brought about by the presence of ligand (BSU6039), which also contributes toward the energetic component of the model. Even though the MM-PBSA method does not provide accurate, or absolute binding energies, the large difference in calculated energy between ligand-free and ligand-bound models give confidence to the use of this method. This also gives credence to the experimental identification of 3,6 di-substituted acridines and other molecules that bind to quadruplex DNA in this manner, as G-quadruplex stabilizers and telomerase inhibitors (51).

The free energies of all the loops are also similar except for the TTA linker loop in model 2, which is higher because of its distorted structure. To minimize errors in estimating the free energies of different subsegments, we have calculated free energies individually for various subsegments and not extrapolated them, as described previously (25). The different conformations adopted by the loops during the course of the simulation results in a 9 kcal/mol difference in free energy between the loops within a single quadruplex unit (Table 4). The total free energy of the G-quadruplex molecules does not reflect the stability of individual loop conformations.

Model 4 (the 93-mer) comprising four quadruplex units, is the most stable structure. The presence of positively charged cations within the central core, π-π stacking interactions and hydrogen bonding network all contribute to the higher stability. The energetics of individual quadruplex units within the 93-mer is very similar suggesting that the overall contribution to the model is a direct result of the contribution from individual units.

PCA

To identify the overall patterns of motions in the quadruplex models, we have used principal components analysis (i.e., essential dynamics). By calculating the eigenvectors from the covariance matrix of a simulation and then filtering the trajectories along each of the different eigenvectors, it is possible to identify the dominant motions observed during a simulation by visual inspection. A large portion of the overall fluctuations of the macromolecules can often be accounted for by a few low-frequency eigenvectors with large eigenvalues (48). If the motions are similar, the eigenvectors and eigenvalues coming from individual trajectories should be similar to each other.

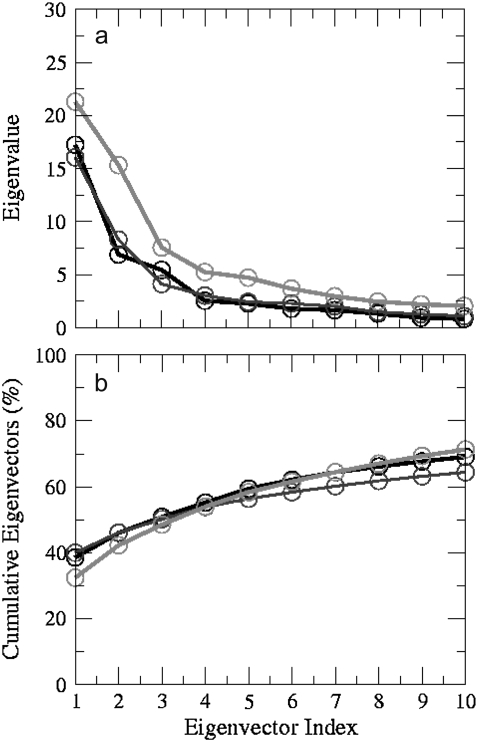
Principal components analysis was applied to the backbone atoms in model 1, 3, and 4. Such analysis showed that the first two eigenvectors account for >40% of all the motion in model 1, 3, and 4 (Fig. 8). We have visualized this motion of the top two eigenvectors by using “porcupine” plots (52,53) that show the direction and magnitude of selected eigenvectors for each of the backbone atoms. Although there might be differences between the simulations with respect to the motions sampled, it is evident that the G-tetrads form the least and the loops the most flexible of the subsegments in the models.

FIGURE 8.

(a) Eigenvalue versus eigenvector index (10 nm²) and (b) cumulative eigenvalues (%) derived from principal components analysis of trajectories of all atoms for the first 10 eigenvectors of model 1 (black), model 3 (dark gray), and model 4 (light gray) simulations. The concerted motion specified by first five eigenvectors can account for ∼60% of the overall motion.

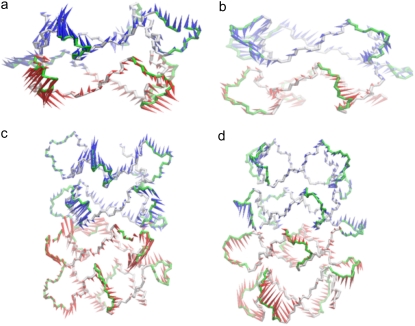
The top two principal components for model 1 (the 45-mer) are illustrated in Fig. 9, a and b. The most prominent motions observed in the top two eigenvectors are the movement of the loops. The propeller loops attached to the upper tetrad unit move in opposite direction to the loops attached to the lower unit. This motion is reversed in the second component. The thymine-adenine stack in each loop maintains its adopted conformation and moves as a single unit in a concerted manner instead of individual wobbling of bases. However, the motions of different loops in the model are independent of each other.

FIGURE 9.

Porcupine plots of the (a) first and (b) second eigenvectors for simulation of model 1 and (c) first and (d) second eigenvectors for simulations of model 4. The models are shown as a backbone trace. The arrows attached to each backbone atom indicate the direction of the eigenvector and the size of each arrow shows the magnitude of the corresponding eigenvalue. Each 21-mer unit is colored in an alternating fashion of red and blue. The motion in eigenvector 2 is opposite to that observed in eigenvector 1. The arrows summarize the direction of motion of the loops.

The top two principal components for model 3 (45-mer + BSU6039) are illustrated in Fig. 10, a–c. The presence of a ligand in the pseudo-intercalation site changes the internal motion of the model, such that the motion observed in the first component is a rotary motion. The top half of the model moves in a clockwise direction and the lower half moves in an anticlockwise direction. The loops in this component also exhibit the same motion. This is visualized more clearly from the top in Fig. 10 b. The most prominent motion that is observed in the second component is that of the loops. It is similar to the motion of loops that have been observed in the first component in model 1. We note that the motion of the loops is not the primary motion for model 3. This may suggest that the ligand in the pseudo-intercalation site is able to stabilize the model by reducing the motion of the loops to a lower component.

FIGURE 10.

Porcupine plots of (a) first and (c) second eigenvectors for simulation of model 3. (b) Top view of the motion described by the first eigenvector. The models are shown as a backbone trace. The arrows attached to each backbone atom indicate the direction of the eigenvector and the magnitude of the corresponding eigenvalue. Each 21-mer unit is colored in an alternating fashion of red and blue. The TTA linker loop is colored as yellow arrows. The arrows summarize the direction of motion. The motion in the first eigenvector correspond to rotary motion of the top tetrad unit (blue) in clockwise direction relative to the bottom tetrad (red) in an anticlockwise direction. The motion exhibited by the second eigenvector in (c) is identical to that observed for the first eigenvector in models 1 and 4.

The top two principal components for model 4 (the 93-mer) are illustrated in Fig. 9, c and d. The motion of the loops dominates the motion in the model in both of the components, albeit in the opposite direction, similar to that observed in model 1. The loops also move as a single unit in a concerted manner. However, their motion is independent of any subsegment in the model.

Stability of the models

Two structural features have been analyzed to examine the quality of the simulations, G-tetrad hydrogen-bonding geometry, and K⁺ positions in the central cation channels of the structures. The time-averaged structures for the three simulated structures do not show any bifurcated hydrogen bonding patterns between guanine N1, N7, and O6 atoms, and comparison with the G-tetrad hydrogen-bonding in the parallel quadruplex crystal structure (17) shows remarkably little deviation from the experimental observations (Fig. 11). The plots of the G-tetrad hydrogen-bond distances (between guanine N1-O6 and N2-N7 atoms), during the course of the simulations show that the hydrogen bonds are extremely stable and are maintained throughout all of the simulation runs (Fig. 12).

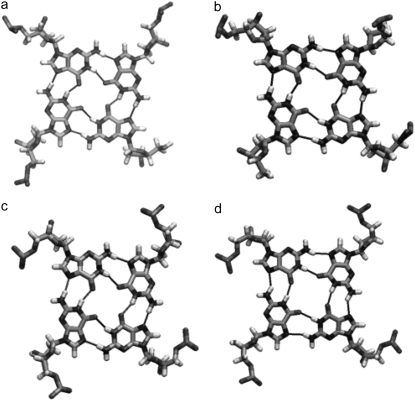
FIGURE 11.

The G-tetrad geometries of (a) the 3′ terminal G-tetrad in the parallel-stranded propeller-loop crystal structure, (b) the 45-mer, (c) the 45-mer + BSU6039, and (d) the 93-mer. For (b–d) these are the averaged G-tetrads for each structure, averaged over the 15 ns simulation times. The thin black lines indicate hydrogen bonding arrangements.

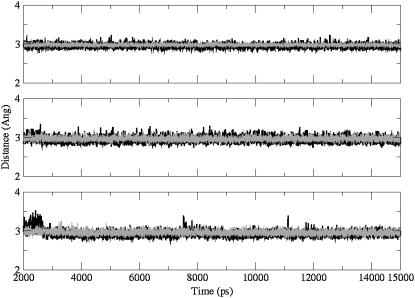
FIGURE 12.

Plots of minimum interatomic distances between guanine N1-O6 (gray) and N2–N7 (black) atoms in the G-tetrads, during the course of the 15 ns simulations, (top) 45-mer, (middle) 45-mer + BSU6039, and (bottom) 93-mer, throughout the 15 ns simulation runs.

The positions of the K⁺ ions within the cation channels are stable and the overall approximately linear arrangements, typically observed in quadruplex crystal structures (17), are retained (Fig. 13). There is no evidence of ions having high mobility and exiting the channels during the simulations. The radius of the ions had been reduced from 2.68 Å to 2.025 Å based on a previous quadruplex simulation study in this laboratory (34). The ions with the modified radius stabilize the central negatively charged channel and do not move out of the channel as reported in some of the early quadruplex simulations (26,27).

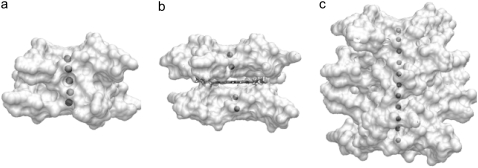
FIGURE 13.

Time-averaged structures from the 15 ns simulations, highlighting the position of K⁺ ions within (a) the 45-mer, (b) the 45-mer + BSU6039, and (c) the 93-mer. Each quadruplex is shown in solvent-accessible surface representation, with views into the central channel, and the ions colored gray.

DISCUSSION

G-quadruplex structures have been reported for telomeric DNA sequences from a number of different species including vertebrates and protozoan ciliates (17–23,54,55). Some of these structures have been shown to be highly polymorphic, even for closely-related sequences, and especially for the human telomeric repeat quadruplexes (17–23). Thus there has been intense debate over the biological relevance of the different polymorphic structures. Two principal types of fold have been reported for intramolecular (unimolecular) quadruplexes based on the study of human telomeric sequences in K⁺ solution, the all-parallel propeller loop crystal structure (17), and propeller-edge-edge folds that have been subsequently determined by NMR techniques (20–23). These latter studies show that the nature of the quadruplex formed by a repeating region of human telomeric DNA is heavily dependent on the exact core sequence and the flanking region chosen for study. These NMR studies have used the human telomeric sequence, sometimes with variable flanking regions, mutated sequences (d[T₂G₃(T₂AG₃)₃A] and d[A₃(AG₃(T₂AG₃)₃)AA]) to obtain interpretable NMR spectra. The topology of the 4-repeat species in physiological K⁺ solution is thus still controversial, and it is likely that multiple species do occur, with only small perturbations (for example, the addition of stable extra flanking basepairs (20–23) or dense packing (17,56)), able to push the equilibrium to either antiparallel or parallel topologies.

This study has shown that molecular modeling of quadruplex dimers and tetramers can produce stereochemically plausible structures. These take account of a notable feature of the crystal structure of the 22-mer intramolecular quadruplex (17), the large planar surface area presented by the G-tetrad faces at the 3′ and 5′ ends, which facilitates the continuous stacking of G-tetrads. The propeller loop arrangement in the all-parallel dimer and tetramer models allow the G-tetrad faces to remain completely unobstructed by loop bases and thereby allows efficient quadruplex stacking, a key feature in these higher-order unimolecular models. This topology is much simpler than those suggested for oligomers of the antiparallel structural models (20), and suggests an obvious pathway for folding and unfolding of G-quadruplex multimer structures formed from longer telomeric sequences, without the formation of knots. Alternative models for end-to-end multimer formation have been proposed using one of the NMR solution (3 + 1) antiparallel solution structures (20). These would necessarily differ from the 45-mer and 93-mer models in loops arrangements and strand orientation. The NMR structures have capping sequences at the ends, such as 3′-TAT, and to effectively pack to form an end-to-end multimer, the TAT triad would have to collapse on the G-tetrad from the adjacent quadruplex. This would require the rearrangement of two residues (TA) from the 3′ linker that join the two quadruplex units together. Furthermore, the presence of a lateral loop between the two units would also act as a barrier to effective stacking, and we therefore consider such models to be less plausible than those presented here. The parallel-stranded propeller-loop topology enables effective stacking of successive quadruplex units to be achieved without significant energy penalty, because the propeller loops offer no obstruction to the stacking of G-tetrads. The arrangement of the propeller loops on the sides of the G-tetrad stacks provide accessible interfaces for interactions with proteins, nucleic acids, and small molecules, which would provide additional stability and efficient packing.

The simulated structures retain the key features of quadruplexes as observed in crystal structures, namely propeller loops and G-tetrad geometry. The pattern of K⁺ ions is retained within the central cation channels, with each ion in an anti-prismatic bipyramidal arrangement, as found in the parallel intramolecular crystal structure (17). These conservations of structure give one confidence that molecular dynamics simulations on DNA quadruplexes, at least on the relatively restricted timescales used here, will result in undistorted structures, and thus can be used as semiquantitative predictive tools. It is also apparent that the AMBER ff99 force field is adequate for this purpose, although some adjustment of cation ionic radii may be required, as has been done here.

Loop flexibility

The free energies calculated using the MM-PBSA methodology for the quadruplex units and individual loops in the various models are comparable within and between each quadruplex, indicating that each repeating unit is behaving in a similar manner. The MM-PBSA method correctly predicts the G-tetrad stem to be the most stable moiety in each quadruplex. The patterns of concerted motion also highlight loop flexibility and that their mobility is independent of any other structural subsegment. During the entire simulations, neither the pairing of the guanines, nor the stacking geometry of the G-tetrads was modified by the linking topology of the external loops. Some changes in loop conformations were observed, relaxing from the crystallographic conformations. It was observed, for example, that the adenine base in a loop can flip and then stack on the middle thymine, resulting in a change in the conformation of some of the loops. The second thymine of each loop is frequently positioned at the tip of the loop such that it can interact in a variety of ways with other molecules. The loops thus form the most flexible part of the quadruplex models, suggesting that they could actively interact with small molecules. The majority of studies of small molecule-quadruplex binding have emphasized the role of G-tetrad stacking with planar chromophores (31,32,50,51), and the paucity to date of detailed structures of these complexes has hindered considerations of the role of the loops and their flexibility in ligand recognition and binding. The crystal structure of the complex between the porphyrin TMPyP4 and a bimolecular quadruplex formed from a two-repeat human telomeric DNA sequence (57) has shown that the TTA loops can change conformation from that observed in the native human intramolecular quadruplex crystal structure (17), to interact directly with one of the two bound porphyrin molecules.

In general, the dynamic behavior of groups within biological molecules consists of thermal fluctuations and collective motions that may be related directly to their function. Principal components analysis using essential dynamics algorithms can illuminate these motions, and has been used here to filter the most prominent motions in the models generated from the less correlated ones. The first five eigenvectors can account for the majority of the motions in the models analyzed here (∼60%). It is apparent that model 1 is the most flexible of the three, followed by model 3 and then model 4. This is in accord with what would be expected from the degree of base-stacking between the units. The difference in flexibility between model 1 and model 3 is also consistent with experimental findings that small molecules are able to bind to quadruplexes, resulting in more stable structures (51). The reduced flexibility of model 4 is interesting, and suggests that longer telomeric structures when folded into a four-unit structure are stiffened by the greater number of stacking interactions between the G-tetrads. The principal components analysis also shows differences in the pattern of fluctuations for loops and the G-tetrads. Fluctuations can be mapped from model 1 onto model 4 showing that the corresponding principal component in both the models is identical. The nucleotides in the loops exhibit wobbling effects and the switch in stacking between first thymine-adenine to middle thymine-adenine can be visualized clearly (Fig. 6, a and b). Both of the observed conformations seem to be favorable for interaction with proteins, other TTA loops, and DNA/RNA by standard base-base interactions. These loops can extend laterally up to ∼12 Å from the G-tetrad core. In particular we note that the conformations that the loops adopt via the two different stacking arrangements of the TTA bases could be involved potentially in specific hydrogen bonding interactions with other nucleic acids because the conformation of the TAT interface matches that of A-form RNA (Fig. 14). We find that this heteroduplex closely matches the published structure (58,59) containing the sequence r(AUA) (PDB id 219D) with a rms deviation of 1.7 Å for all six nucleotides. It also matches a commonly found AUG mismatch TAT:AUG (60,61) where the mismatched guanine N2 is available for specific hydrogen bonding with either main chain or side chain residues. This suggests that the loops forming a regular array on the exterior of a telomeric quadruplex superstructure may interact with other molecules, for example proteins, telomerase RNA, or duplex DNA telomeric sequences involved in higher order telomere structure such as D- or t-loops (2).

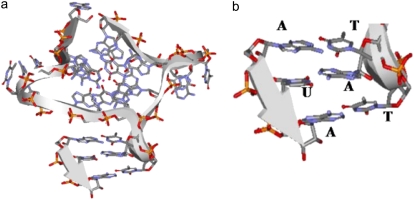
FIGURE 14.

A schematic ribbon representation of a trinucleotide RNA from a RNA/DNA heteroduplex of sequence r(AUA) PDB id 219D, (a) positioned adjacent to the TTA loop of the crystal structure and (b) enlarged view of the T₁A₃T₂:AUA interactions.

Quadruplex dimer and tetramer features

Computational studies have been carried out previously on quadruplexes in telomeric DNA (24–27). However, possible structures for higher order human telomeric sequences have not been studied in detail, although these are likely to be of relevance to studies on ligand binding to telomeres in cells, where the local environment is a densely packed one. It is well-established that ligands containing planar groups are effective quadruplex stabilizers (31,32,51). The models presented here suggest that these ligands can bind to the single-stranded telomeric DNA overhang in an intercalative-like manner between dimers comprising two individual quadruplex units, as in the 45-mer model. Formation of the binding site would not disrupt any hydrogen bonds or alter the core structure. At the same time, enough space is generated for a planar ligand molecule to move in and out of the binding site. The simulated removal of the ligand from the binding site results in the distortion of the complex; these simulations have not directly explained why the two individual quadruplex units do not collapse on one another to generate a conformation similar to that of model 1. It is likely that the motions required in the linker loop structure to achieve this are not accessible within the 15 nsec timescale of this simulation, and the structure is thus unable to refold to generate a conformation that allows efficient stacking of G-tetrads.

To date there have been only a small number of biophysical studies carried out on the quadruplexes formed by more than four telomeric DNA repeats (62–64), and none on small-molecule complexes. G4 “nanowires” have been reported, which contain large numbers of continuously-stacked G-tetrads (65–67)—these are not strictly comparable to the structures formed by telomeric DNA repeats. It appears that for long telomeric DNA repeats, sequence length has effects on the thermal stability of the intramolecular G-quadruplex formed that depend on the details of the solution conditions (62–64). Multimer telomeric sequences whose repeat number is a multiple of four are more ordered than other sequences (63) and their rigidity increases with sequence length. The 45-mers and 93-mer modeling in the simulations presented here, have stacking interactions between G-quadruplex units, and structural stability (as judged by the calculated free energies) that are proportional to the increase in G-tetrad stacking on going from one to two to four stacked quadruplex units. The models do tend to become more rigid with increased stacking, in accord with the experimental observations. Circular dichroism studies suggest (64) that the human telomeric 8-mer DNA repeat, which is analogous to the 45-mer model developed here, is in a mixture of parallel and anti-parallel conformations in K⁺ solution conditions, and thus by analogy with studies on individual 4-repeat quadruplexes (56), may well be in a parallel conformation in crowded solution conditions, as in a cellular environment.