Hydration Dependence of Active Core Fluctuations in Bacteriorhodopsin

Abstract

We used neutron scattering and specific hydrogen-deuterium labeling to investigate the thermal dynamics of isotope-labeled amino acids and retinal, predominantly in the active core and extracellular moiety of bacteriorhodopsin (BR) in the purple membrane and the dynamical response to hydration. Measurements on two neutron spectrometers allowed two populations of motions to be characterized. The lower amplitude motions were found to be the same for both the labeled amino acids and retinal of BR and the global membrane. The larger amplitude dynamics of the labeled part, however, were found to be more resilient than the average membrane, suggesting their functional importance. The response to hydration was characterized, showing that the labeled part of BR is not shielded from hydration effects. The results suggest that the inhibition of high-amplitude motions by lowering hydration may play a key role in the slowing down of the photocycle and the proton pumping activity of BR.

INTRODUCTION

The highly complex structure of biological macromolecules is reflected in their dynamical behavior over a time domain of several orders of magnitude from 10⁻¹⁴ to 10¹ s (1). Internal protein motions in the 0–25 meV range result in a range of conformations for the protein molecule and play an important role in biological activity (2,3).

Neutron scattering may be used to elucidate functional protein dynamics (4–6). Thermal neutron energies are, by definition, of the same magnitude as those of thermal internal motions of proteins. The accessible motions span an energy range from ∼0.1 to 10 meV and have characteristic times between the nano- to picosecond. Incoherent neutron scattering has been used as an effective tool for the investigation of the average dynamics in biological macromolecules. The incoherent scattering from hydrogen nuclei largely dominates the protein signal; H-atoms in the time and length scale of the experiments effectively reflect the motions of the groups to which they are bound (4). Neutrons also discriminate between different isotopes of an element. The incoherent signal from deuterium, for example, is much lower than that of hydrogen. Specific H/²H labeling allows the study of local dynamics in the part of a protein structure in which the hydrogens have been preserved whereas the deuterated parts are effectively masked. Energy-resolved, elastic incoherent neutron scattering provides access to atomic mean-square displacements (MSD), 〈u²〉, as a function of temperature. MSD as defined here probe the full displacement of the hydrogen atoms in the length-timescale defined by the spectrometer momentum-energy transfer resolution.

Several models have been proposed for protein dynamics and the motions explored by incoherent neutron scattering. The free energy of the protein atoms has been represented by a multidimensional energy landscape as a function of conformational coordinates (3,7). The biologically active form is not unique, and a protein can assume a large number of nearly isoenergetic conformations with only small structural differences between them. At low temperatures, protein atoms vibrate harmonically within their substates. As the temperature increases, sufficient energy is provided to cross from one well to another, which gives rise to diffusive nonvibrational dynamics. A simplified model, the double-well model, has been applied to neutron scattering data on myoglobin (8), where a dynamical transition has been observed. Once the transition temperature has been passed in the model, atoms can jump between states of different energy. Molecular dynamics simulations of myoglobin have shown that the diffusive motions seen in neutron scattering experiments result from rigid-body motions of the protein side chains (9). The concept of force constants has been introduced by Zaccai and colleagues (6,10). It consists of the determination of the slope of the MSD values with respect to the temperature, which refers to a force constant 〈k〉 in the harmonic region and an effective force constant 〈k′〉 in the nonharmonic region.

Bacteriorhodopsin (BR) in the purple membrane (PM) of Halobacterium salinarum is a prominent and extensively studied example of a light-active membrane transport protein (11); its thermal motions have been investigated by neutron scattering ((12–14) and references therein). BR is organized with lipids in a two-dimensional lattice, which has been named PM (15). PM can easily be isolated from the archaebacterium and is extremely stable. Absorption of one photon by the BR-bound chromophore (retinal) leads to its isomerization and initiates a photocycle, which results in translocation of one proton from the cytoplasm to the extracellular medium. Several photointermediates of the photocycle (J, K, L, M, N, and O) have been revealed by spectroscopy. Structures of the BR ground state and several photointermediates have been identified from numerous diffraction studies. In addition, structural changes during the photocycle, which are coupled to proton transfer, have been resolved (for reviews see (16,17)). The retinal is covalently bound to Lys216 via a protonated Schiff base that divides the proton pathway into a cytoplasmic and an extracellular half. The M intermediate of the BR photocycle has been divided into two substates, M1 and M2 (18,19). The Schiff base is only deprotonated in the M intermediate, and a change in accessibility from the extracellular to the cytoplasmic half is necessary for proton release and uptake (18,20). The retinal-binding pocket, particularly rich in aromatic residues, plays an important role in the irreversible transition during the photocycle and is constituted of 21 amino acids, which are close enough to be in van der Waals contact with the retinal (21). Amino acids in the binding pocket are conserved in other retinal proteins and constrain retinal motions during photoisomerization (22,23), whereas others influence the proton pumping efficiency (24). For example, spectroscopic studies have revealed that Trp182 plays a role in the early photocycle stages, and a strong interaction between this residue and the retinal has been demonstrated (25,26). Molecular dynamics simulations have shown the impact of Trp86 on the retinal planarity (27).

The relationship between BR structure-dynamics and activity as reflected in the photocycle and proton pumping has been explored by dynamical studies of PM. A protein is only active if it adopts its particular three-dimensional structure and if all internal motions attached to its function can be accomplished. Both activity and dynamics are sensitive to hydration and temperature, and so these two parameters have been developed into effective tools for the study of dynamics-activity relationships. Based on this, Zaccai (28) has suggested a hypothesis that the close packing of PM in a cooled or dry state would inhibit the motions necessary to fulfill the BR photocycle and the proton pumping across the membrane. Several incoherent neutron scattering studies support the hypothesis that a global soft environment obtained through temperature and hydration, which allows larger diffusive thermal motions, is required to ensure the functioning of BR (29–32). The dynamical heterogeneity of the membrane and its dependence on hydration and temperature has been divided into two different categories of motions: 1), the “high-amplitude” motions exhibiting smaller frequency and higher amplitude motions (maximum of 2 Ų at 300 K for hydrated PM) and 2), a population of “low-amplitude” motions at a higher frequency and smaller amplitudes ≤〈u²〉 values of 1 Ų (33). From the hydration dependence of the photocycle and pumping characteristics of BR, a correlation has been made to the thermal motions (14). It has been demonstrated that a global fluidity is necessary for the functioning of BR and that the particular response to hydration of the different populations of motions can be correlated to the functional behavior of BR (32). Local dynamics of the active core and extracellular moiety of BR, measured by neutron scattering in a hydrogen-deuterium-labeled sample, have elucidated the dynamical heterogeneity of the protein (34). In the hydrated state, a decreased flexibility in terms of the MSD of the labeled amino acids and retinal compared to the global membrane has been reported. The retinal-binding pocket is considered to be a proton valve between the extracellular and cytoplasmic parts of BR, participating in the control of stereospecific selection of retinal conformations to accomplish the pumping function.

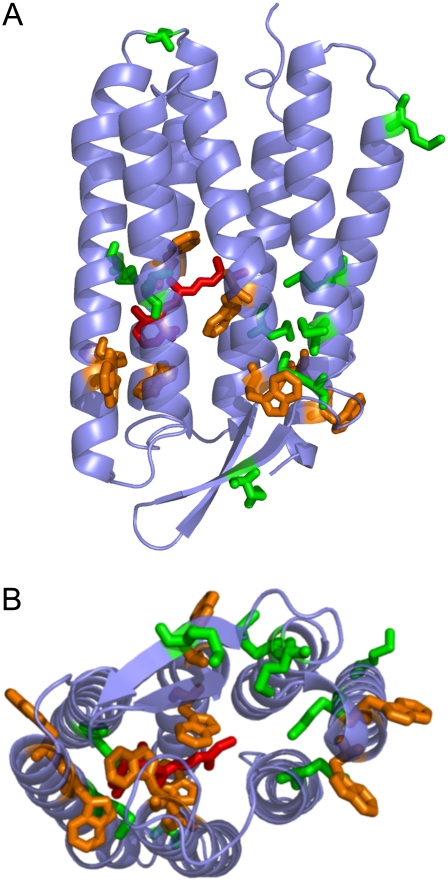
In our study, we contribute new insight to the question of how a back flip of the proton (return of the proton toward the cytoplasmic side) is possibly prevented through the aid of thermal motions. A labeled, specifically hydrogenated PM sample, constituted of fully deuterated PM containing hydrogenated amino acids methionine, tryptophan, and retinal, was produced for elastic incoherent neutron scattering measurements. The distribution of the labeled groups is shown in Fig. 1; they are located mainly in the retinal-binding pocket and the extracellular half of the protein and therefore probe the thermal motions of the key region involved in proton translocation of BR. Four of the eight tryptophan residues and three of the nine methionines are in the retinal pocket. All of the labeled residues, apart from three methionines in loops, are in the extracellular α-helices. We investigated whether a distinctive population of motions can be defined in the labeled part, and how it responds to hydration compared to the global membrane motions. We focused on the rigidity/flexibility of the system by the calculation of effective force constants. The work was performed in the context of the question: How do local thermal motions relate to specific protein activity?

FIGURE 1.

Distribution of labeled amino acids in the SH-PM sample (Protein Data Bank entry 1QHJ (59)). The labeled retinal (red), methionine (green), and tryptophan (orange) residues are in stick representation. The figure was created using Pymol (63). (A) The cytoplasmic side (C-terminus) is at the top of the figure; the extracellular side is at the bottom. (B) Represents the view seen from the extracellular side of BR.

MATERIALS AND METHODS

Sample preparation

Natural abundance PM (H-PM) and specifically hydrogen-deuterium labeled PM (SH-PM) were isolated in 150-mg quantities from Halobacterium salinarum cells. H-PM was obtained from the cell cultures as described previously (35,36). Deuterated medium was prepared according to Patzelt and colleagues (37). The bacteria were adapted in several steps to the deuterated medium. On average, the stationary phase of the culture growth was reached after 10 to 14 days. Deuterated PM containing hydrogenated methionine, tryptophan, and retinal (SH-PM) was prepared by adding 2.5 mM of methionine and 0.5 mM of tryptophan as previously described (34); the retinal negative Jw5-strain was used and hydrogenated all-trans-retinal was added during culture growth. Special care was taken, as the hydrogenated retinal had to be added at defined, increasing steps to ensure BR production. A total of 2 μM of retinal was added at six equally spaced steps during the growth process until the stationary phase was reached.

The process of PM isolation did not differ for natural abundance and deuterated cultures, except for the sucrose density gradient, which is described elsewhere (32). For fully hydrogenated PM, a linear 25–45% (weight/weight) gradient was prepared, whereas a 40–60% gradient was required for deuterated PM. Typically, equilibrium was reached after 14 h of centrifugation in 35 mL volumes at 100,000 g and 8°C. The buoyant density was 1.18 g/cm³ for the H-PM and ∼1.26 g/cm³ for the SH-PM. The purple band was collected, and the sucrose was removed by dialysis overnight against 10 L H₂O. Water was renewed once after a few hours of dialysis. The specific H labeling of the required amino acids and retinal was verified by mass spectrometry (results not shown).

All neutron scattering experiments were carried out in D₂O, and sample preparation was identical for both types of PM. H₂O was replaced with D₂O by three centrifugation-resuspension steps. After the last centrifugation step, the D₂O-washed pellet (∼150–180 mg BR) was layered in an aluminum sample holder (beam area, 4 × 3 cm²; path length, 0.5 mm). Rapid, partial drying was achieved with silica gel in a desiccator at room temperature until the final D₂O content reached ∼0.5 mg/mg PM (measured by weighing). Final equilibration to the required hydration level was achieved by replacing the silica gel by a saturated solution of an appropriate salt (NaBr for 57%, NaCl for 75%, KCl for 86%, and KNO₃ for 93% relative humidity (RH) (38)) in D₂O, which defined the RH. The dry sample was obtained by complete desiccation over silica gel. The SH-PM sample was measured at all hydration states on both instruments; the H-PM sample was not measured at 57% RH on IN16. Each equilibration proceeded for 7–9 days, until the weight of the sample and sample holder did not vary by >0.3 mg. The sample holder was sealed with an indium ring and closed.

The container was placed in a cryostat during neutron experiments, and its weight was checked before and after the experiment to verify there was no hydration loss. After the experiments, the total amount of water in the H-PM samples was estimated by weighing before and after complete drying over silica gel. The following values were found in D₂O/g H-PM: 0.011 for 0% RH, 0.11 for 75% RH, 0.15 for 86% RH, and 0.32 for 93% RH.

Elastic incoherent neutron scattering

Neutrons are scattered by atomic nuclei, and the incoherent scattering neutron cross section of the hydrogen atom is much larger than that of other elements usually present in biological systems. It is also ∼40× larger than that of its stable isotope deuterium, which makes the investigation of local protein motions possible by hydrogen-deuterium labeling. In our labeled sample (SH-PM), hydrogen atoms corresponded to 10% of the total number of hydrogen atoms in PM. The incoherent scattering cross section of SH-PM was divided approximately as follows: 72% corresponded to the labeled hydrogenated groups (12% retinal, 30% methionine, 30% tryptophan), 20% to the ²H in the protein, and 7% to lipid ²H. All of the amino acids were within the helical regions of the protein except for three of the nine methionines, which corresponded to 10% of the scattering contribution. The contribution of the retinal and labeled residues located in the retinal pocket was 37%; 62% of the scattering cross section came from the extracellular side.

The neutron scattering experiments were performed on the backscattering instruments INI6 (λ = 6.27 Å, energy resolution ΔE = 0.9 μeV, full width at half maximum) and IN13 (λ = 2.23 Å, energy resolution ΔE = 8 μeV, full width at half maximum) at the Institut Laue-Langevin in Grenoble, France.

The sample containers were placed in a cryostat with an orientation of 135°C between the incident neutron beam and the sample plane and taken to 20 K at a rate of 2 K/min. The data collection time depended on the instrument and on the nature of the sample to ensure good counting statistics.

Data were collected on the unlabeled (labeled) sample on IN16 for 15 min (28) every 3 K from 20 K to 320 K. On IN13, data collection time was set at 20 min (39) for temperatures ≤200 K, after which the counting time was doubled. The chosen stepwidth was 5 K. On each instrument, the empty sample holder was measured for subtraction. Raw data were corrected for scattering by the empty sample container and for absorption, which takes the orientation of the sample holder into account. The correction for detector efficiency was performed with the elastic scattering from the sample itself at 20 K, which is expected to be constant with angle for a purely incoherent scatterer. Bragg reflections from the aluminum sample holder and coherent scattering from the sample itself were identified and discarded in the analysis. The corrected data were grouped to an averaged temperature step of 10 K. Error calculation was performed based on the statistical error of the intensities and the monitors following Poisson's law.

In the Gaussian approximation, the elastic incoherent scattering intensity measured at a certain temperature (T), I_el,T(Q,ω = 0) (where ℏQ, ℏω are momentum and energy transfer, respectively), can be expressed as follows:

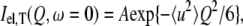(1)

where 〈u²〉 is the atomic MSD and A is a constant. The approximation is similar to the Guinier approximation in small-angle scattering and is valid for 〈u²〉 Q² ≤ ∼2 (33).

The MSD were calculated from the linearized form of Eq. 1. The 〈u²〉-value corresponds to the full amplitude of the motions and describes the spatial extent of the atomic displacement. The error evaluation of the linear fit (and therefore of the MSD) assumed weighted statistical errors around each intensity data point, and was calculated in a graphics program (Igor Pro 5.0.1.0l; WaveMetrics, Lake Oswego, OR). The MSD values were then plotted as a function of absolute temperature T.

The MSD of the “high-amplitudes” motions, corresponding to a maximum length scale of 2.2 Å, were derived from the IN16 data. For H-PM, the logarithm of the normalized intensity was linear with the square of the wave vector Q² from 0.2 Å⁻² ≤ 1.6 Å⁻², and the analysis was performed in the entire range. For the SH-PM, the range had to be reduced at higher temperatures because of a coherent scattering peak from the deuterated lipids, visible around Q = 1.4 Å⁻¹, which broadened with increasing temperatures. From 30 to 100 K, the same Q range was used for the specifically labeled samples as for the wild-type PM (0.2 Å⁻² < Q² < 1.6 Å⁻²). Between 100 and 175 K, this was reduced to 0.2 < Q² < 1.3 Ų; between 175 and 300 K, it was reduced to 0.2 < Q² < 0.9 Ų. The approach is valid because extending the Q-range was found to not change the calculated MSD but to reduce the error on its calculation.

The “low-amplitudes” motions were extracted from Q = [2.0;4.2] Å⁻¹ (Q = [2.0;3.71] Å⁻¹) on IN13 for the SH-PM (H-PM), corresponding to a maximum length scale of 0.5 Å. The Gaussian approximation was still valid in the larger Q-region chosen for the labeled SH sample. A direct comparison between the 〈u²〉 values of the SH-PM and H-PM still was justified, because the change of the Q-range did not modify the MSD values but did lead to an improvement of the fit quality.

Effective force constants 〈k′〉 values were calculated from the temperature scans (〈u²〉 versus temperature T plots) (6). They were defined as resilience values and calculated as 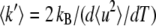with the Boltzmann constant k_B = 1.38 10⁻²³ J/K and 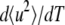expressed in m²/K.

For high-amplitude motions, the slopes of the MSD versus the temperature data were calculated in the regions 20–130 K, 160–250 K, and 260–310 K, and effective force constants were calculated (〈k₁〉_HA, 〈k₂′〉_HA and 〈k₃′〉_HA, respectively). Slopes also were calculated from 20 to 230 K for the low amplitudes. The fit regions were chosen with respect to the breaks observed in MSD as a function of temperature. As the transition covers a broad temperature range, care was taken to reduce the linear fit to a region where the amplitudes followed a linear behavior.

RESULTS

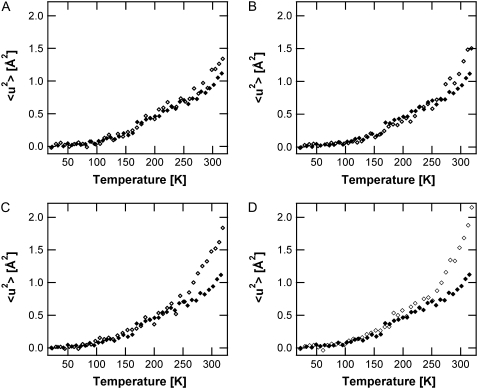
The SH-PM high-amplitude MSD are presented for five different hydration states, including 0%, 57%, 75%, 86%, and 93% RH in Fig. 2. Two breaks in the MSD as a function of temperature can be distinguished. The first, present at all hydration states, is situated at 130 ± 10 K, and previously has been attributed to methyl rotations (39,40). A hydration-dependent transition is located at 250 ± 5 K, which is clearly observable only at hydration states >57% RH. The 〈u²〉 values show no significant differences depending on hydration state between 20 and 250 K. Diffraction measurements have shown that <250 K, excess water in the sample forms ice, and only two layers stay in contact with the PM (41). PM samples with 86% and 93% RH, therefore, have the same hydration level <250 K. On further heating >250 K, the hydration dependence of the MSD becomes significant and the amplitudes increase to higher values with increasing hydration.

FIGURE 2.

Hydration-dependence of the functional core high-amplitude motions. SH-PM mean-square displacements derived from IN16 data at 57% RH (A), 75% RH (B), 86% RH (C), and 93% RH (D), shown as open diamonds. In every panel, the 〈u²〉 values of the dry SH-PM (solid diamonds) are also shown for comparison.

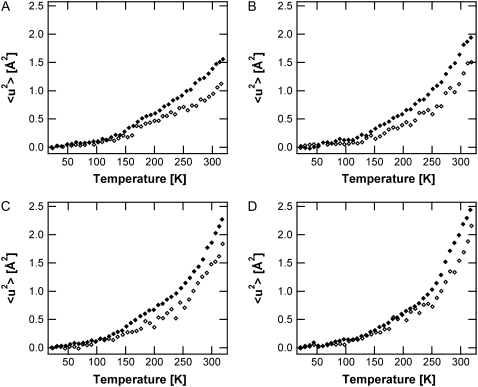
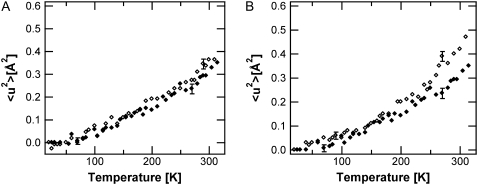
In Fig. 3, the high-amplitude 〈u²〉 values of the SH-PM sample are compared to those of H-PM for 0%, 75%, 86%. and 93% RH. Below the first break, a similar behavior is visible for the labeled and unlabeled membranes. Above 130 K, the 〈u²〉 values for global PM increase much faster with respect to the temperature than for the unlabeled sample. Like the H-PM, the labeled retinal and amino acids display a hydration-dependent transition at 250 K.

FIGURE 3.

Mean-square displacements of the high-amplitude motions (IN16 data) for SH-PM (open diamonds) and H-PM (solid diamonds) at 0% RH (A), 75% RH (B), 86% RH (C), and 93% RH (D).

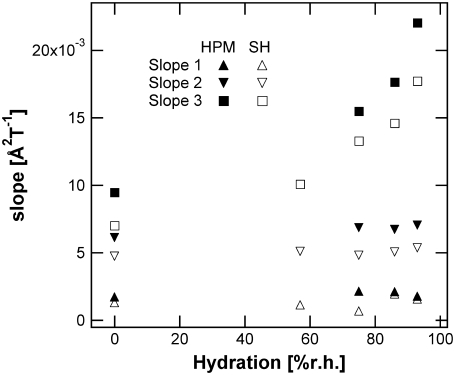
We calculated slopes and effective force constants from the elastic temperature scans of the high-amplitude MSD to compare the resilience or rigidity of the different parts of the membrane (Table 1). Fig. 4 represents (d 〈 u² 〉 /dT) values for the high-amplitude motions of H-PM and SH-PM in the three different temperature regions, 20–130 K, 160–250 K, and 260–310 K, from which effective force constants were calculated (〈k₁〉_HA, 〈k₂′〉_HA, and 〈k₃′〉_HA, respectively). The first two temperature regions do not show any hydration dependence for either sample. In the harmonic region (slope 1), the inverse of the slope directly corresponds to a force constant, and it can be regarded as an effective force constant in the nonharmonic regions (slopes 2 and 3) as diffusive motions emerge (6). The most important difference between the force constants was found in the intermediate temperature region. The SH-PM has a 〈k₂′〉_HA-value that is 30% higher than that of H-PM. Although SH-PM and H-PM 〈k₁〉_HA values differ, the large error on the small slope makes it difficult to comment on this result. The 〈k₃′〉_HA-value depends on the hydration state of the sample and decreases with increasing hydration. Hydration changes influence 〈k₃′〉_HA effective force constants for both H-PM and SH-PM, but the resilience remains higher for the labeled groups at all hydration states.

TABLE 1.

Effective force constants derived from the high-amplitude motions (IN16 data)

	〈k1〉HA	〈k2′〉HA	〈k3′〉HA
Hydration	All	All	75	86	93
SH-PM	2.4 ± 0.7	0.55 ± 0.06	0.21 ± 0.03	0.19 ± 0.01	0.16 ± 0.01
H-PM	1.4 ± 0.2	0.41 ± 0.01	0.18 ± 0.01	0.16 ± 0.01	0.13 ± 0.01

〈k₁〉_HA, 〈k₂′〉_HA, and 〈k₃′〉_HA values were calculated in the temperature regions 20–130 K, 160–250 K, and 260–310 K, respectively.

FIGURE 4.

Slope of the high-amplitude motions for the H-PM (solid symbols) and the SH-PM (open symbols). Slope 1 corresponds to a temperature region between 20 K and 130 K, slope 2 between 160 K and 250 K, and slope 3 between 260 K and 310 K.

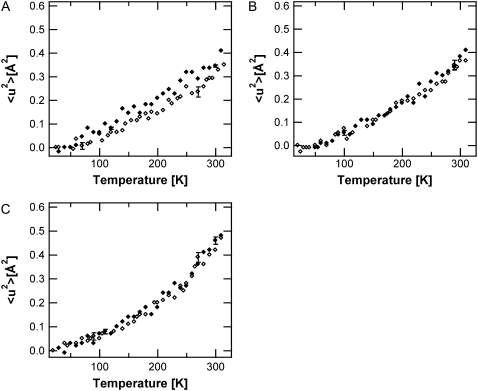
Fig. 5 represents low-amplitude MSD population-dependence on temperature of the labeled sample. One dynamical transition is observed at 240 ± 10 K in the high RH values. This transition is clearly discernible only at 86% RH, not at 0% RH, and barely at 57% RH. Moreover, a comparison with H-PM demonstrates that the labeled part and the global membrane exhibit an identical dynamical behavior in the IN13 length-timescale of the low-amplitude MSD (Fig. 6). In the case of the low-amplitude motions, the slope for the 〈u²〉 values versus temperature in the harmonic region from 20 to 230 K is (1.25 ± 0.2) × 10⁻³ Ų/K for labeled and unlabeled PM. This corresponds to a force constant of 〈k₁〉_SA = 2.2 ± 0.2 N/m.

FIGURE 5.

SH-PM low-amplitude mean-square displacements extracted from IN13 measurements. Open diamonds represent 〈u²〉-values obtained at 57% RH (A) and 86% RH (B). In both panels, the dry SH-PM is shown as solid diamonds for comparison.

FIGURE 6.

Mean-square displacements of the low-amplitude motions (IN13 data) for SH-PM (open symbols) and H-PM (solid symbols) at 0% RH (A), 57% RH (B), and 86% RH (C). The data of the unlabeled PM are from a previous study (32).

DISCUSSION

The relative water content in the samples at a defined RH condition was similar for the SH and unlabeled samples. Therefore, we could compare MSD values for the same hydration states.

The two motion populations observed in our study correspond, respectively, to thermal motions localized in a time window <100 ps for the high Q data set and <1 ns for the small Q data set. In the small Q-range, high- and low-amplitude motions contribute to the motions. Because the populations displayed a distinct difference in MSD values, increasing the Q-range allowed the essentially separate observation of the low-amplitude motions, in a way similar to that in small-angle scattering in the case of a mixture of particles, with a distinct size difference (33).

A striking feature in our study is that only the high-amplitude motions differ significantly between the SH-PM and H-PM samples. The low-amplitude motions are similar, indicating that, on average, they are independent of both the location in the protein and of the residue type. The high-amplitude MSD, corresponding to low-frequency modes, jumps between conformational substates or diffusive motions, primarily express the functional requirement for rigid and soft parts in the structure.

In the low-temperature region, the force constant values, 〈k₁〉_HA and 〈k₁〉_SA, are not significantly different for the global membrane and the selected protein part. At 130 K, the break is observable only for the high-amplitude motions, which supports the hypothesis that they arise from movements such as methyl group rotations.

Between 140 and 240 K in the second dynamical region, the 〈k₂′〉_HA values differ significantly between SH-PM and the average membrane. High-amplitude motions are liberated in both cases without a change in low-amplitude fluctuations. The environment of the labeled amino acids appears to be decoupled from the rest and shows its own thermal dynamical behavior. Another explanation could be that the H-PM MSD values increase more steeply with respect to temperature than the labeled sample because the former has an increased contribution to the scattering from methyl groups. Methyl groups contribute 34% to the scattering in the case of H-PM, whereas only 11% comes from the methionine methyl group in the SH-PM. The effective resilience of the labeled groups, tryptophan, methionine, and retinal in the intermediate temperature region is ∼30% higher than the membrane average (Table 1).

Two observations can be made for the effective force constants, 〈k₃′〉. First, the 〈k₃′〉_HA-value of the labeled part and that of the average membrane again become closer. The resilience, although decreasing significantly for the labeled groups and for the average membrane, still remains higher by ∼20% for the labeled groups. The second observation concerns the effective force constants of the low- and high-amplitude motions. Mobility is enhanced in the lipid, loop, and surface regions and in the labeled part of the protein studied in this article, which is not shielded from hydration effects. Water molecules are mainly localized around the lipid headgroups and on the surface (42), and the presence of specific water molecules within the proton channel has been established (43). At ∼240–250 K, both low- and high-amplitude motion populations in the membrane globally, in the active core and in the extracellular moiety of BR react to the flexibility introduced by surrounding water molecules through the increase of the RH. The data on the hydration dependence of the labeled amino acids and retinal presented in our study clearly demonstrate that the 250 K dynamical transition is also present in the specifically labeled part of the protein. This conclusion was not apparent in a previous study by Réat and colleagues (34). The transition is also evident in both low- and high-amplitude motions.

A closer look at the force constants reveals that the largest differences appear in the temperature region where the protein is not yet fully active—between 130 and 240 K. This is the same temperature range in which different photointermediates can be trapped. The K-intermediate, the first state possible to trap, can accumulate <150 K (44,45). BR can accumulate in the M-intermediate of the photocycle at 240 K (46), about the same temperature below which proton-pumping activity is no longer detectable. The structural changes associated with the first photointermediates mainly involve the vicinity of the retinal-binding pocket (45,47). The high force constants measured between 130 and 240 K for the retinal and its neighboring tryptophan and methionine residues (located mainly in the core and extracellular moiety of BR) suggest a blocking of the structural rearrangements, which are required to continue the photocycle. This is substantiated by NMR and crystallographic data in which characteristic structural changes in the retinal environment have been examined; the uptilt of C13 of the retinal in the M-intermediate was clearly demonstrated in the work of Luecke and colleagues (48). In the NMR data gathered by Patzelt et al. (49), the photoisomerization of the retinal from the all-trans to the 13-cis,15-anti form and the thermal isomerization of the all-trans to the 13-cis,15-syn form show functionally important structural differences. In particular, the direction of the NOH dipole of the Schiff base is changed on photoisomerization from down (extracellular) to up (cytoplasmic), but remains stable on thermal isomerization. Therefore, only the light energy absorbed in photoisomerization places the proton into a potentially energetically unfavorable environment. The transfer of the Shiff base proton to Asp85 would then lead to the relaxation of the Schiff base by deprotonation; after which the proton can leave to the outside but not return to the nitrogen. Structural rearrangements and thermal relaxations of the photocycle can be completed only above the temperature at which the force constants of the high-amplitude motions again become similar for the global membrane and labeled part. Note that, in Table 1, the difference between SH-PM and H-PM in the temperature region 130–250 K is increased compared with that >250 K, where the differences are barely outside errors for all humidity conditions.

A complex image of the potential valve dynamics emerges in that specific resilience values in the retinal and labeled amino acids are needed to inhibit or allow motions, which either block or ensure the vectorial proton transfer. Above the 250 K transition temperature, the photocycle becomes predominantly dependent on hydration effects. The distortion of the photocycle upon a change in hydration was revealed (50), and nonharmonic motions were correlated to characteristics of the photocycle and proton pumping (32). It should be noted that dehydration is not the only reason for the a slow photocycle; it is also slowed in perfectly hydrated mutants such as D96N (51).

The force constants underlying the thermal motions (20–200 pN/Å) are of the same order of magnitude as the forces explored by atomic force microscopy on PM samples (52,53). The surface structure of BR has been explored by atomic force microscopy, and an applied force of 200 pN was able to bend away the E-F loop by 2 Å (54). Interestingly, if the applied force was <100 pN, the created deformations were negligible; in the context of our study, this observation suggests that the loop-bending caused by this smaller force might still be in the limit of thermal fluctuations and so has no net effect. The effective force constants of the thermal fluctuations represent an average value of the entire protein or the labeled part and are certainly higher than what can be expected for the flexible loop regions. BR helices have been pulled off the membrane in pairs by applying forces ∼350 pN (55). The ruptured bonds correspond to inter- and intrahelix hydrogen-bonding and interaction with lipids and so are considerably higher than the bending forces. To pull off lipids, a force of only 25 pN is sufficient, as the interactions are smaller due to the fluid-like lipid behavior. This suggests that the force constants derived from thermal motions of lipids should be much smaller than those of the protein should. Indeed, quasielastic incoherent neutron scattering on lipid bilayers have characterized fast in-plane and out-of-plane motions of lipid chains and molecules with amplitudes ≤3 Å (55,56). Lipid dynamics in PM were found to achieve 〈u²〉 values ∼4 Ų at high RH and room temperature with an effective force constant of 0.1 N/m (57).

Electron microscopy studies have indicated that BR is most rigid in the middle of the membrane near the retinal-binding pocket (58). An asymmetric distribution of temperature factors over the protein has been demonstrated with larger values in the cytoplasmic than in the extracellular region for both ground state and intermediate structures (49,59–61). In molecular dynamics simulations, the fluctuations of the helix extremities in the cytoplasmic half of BR appeared twice as large as those in the extracellular half (62). Our neutron scattering measurements quantified the lesser flexibility of the retinal and labeled amino acid residues on the angstrom-nanosecond length and timescales.

Our hypothesis of how thermal motions help to prevent the back flip of the protonated Schiff base emerged, as follows. The flexibility of the retinal-binding pocket and the photocycle are both sensitive to hydration effects. The inhibition of high-amplitude motions by lowering hydration could then be the key for the low-hydration slowing of the photocycle and the pumping activity.