Comparative Energy Measurements in Single Molecule Interactions

Abstract

Single molecule experiments have opened promising new avenues of investigations in biology, but the quantitative interpretation of results remains challenging. In particular, there is a need for a comparison of such experiments with theoretical methods. We experimentally determine the activation free energy for single molecule interactions between two synaptic proteins syntaxin 1A and synaptobrevin 2, using an atomic force microscope and the Jarzynski equality of nonequilibrium thermodynamics. The value obtained is shown to be reasonably consistent with that from single molecule reaction rate theory. The temperature dependence of the spontaneous dissociation lifetime along with different pulling speeds is used to confirm the approach to the adiabatic limit. This comparison of the Jarzynski equality for intermolecular interactions extends the procedure for calculation of activation energies in nonequilibrium processes.

INTRODUCTION

Single molecule investigations can uniquely address some problems considered difficult in traditional test-tube approaches by providing excellent specificity, temporal resolution, and requiring very small quantities of reactants (1–7). While single molecule experiments have provided new insights into the dynamics, structure, and mechanical function, obtaining quantitative information on the interaction energies remains a challenge for many molecular configurations. The response of the single molecule to an applied force is measured in all the available techniques such as the atomic force microscope (AFM), optical tweezers, or biomembranes (1–7). Because the force and molecular extension are usually applied in an irreversible manner (i.e., finite velocity), the mean values of the bond energy corresponding to the work done are nonequilibrium values, and comparison to theoretical models of the protein structure are difficult. However, recent theoretical results such as the Jarzynski equality (JE) provide a basis for extending nonequilibrium experimental results to the reversible limit (8–12). In the JE, the equilibrium free energy (ΔG) is calculated using the expression (8,9)

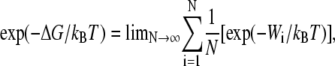(1)

where N is the number of independent experimental repetitions and W_i is the work done found from the applied force and corresponding extension of the single molecule system. In using Eq. 1, there is considerable concern (13–16) that such a reconstruction of ΔG might be limited by the finite number N of the experimental repetitions. The JE has been verified experimentally for single molecule RNA linked to beads with RNA-DNA hybrid linkers using optical tweezers (17,18). A free energy reconstruction of the unfolding free energy barrier for the I27 domain of titin using the JE has also been recently reported (19). To our knowledge, this work is the first experimental probe of the JE for intermolecular interactions, which would allow application to a wider range of biological systems.

For measuring the single molecule interaction energies, we use a model system of two exocytotic/synaptic proteins syntaxin 1A (Sx1A) and synaptobrevin 2 (Sb2) which are involved in vesicular fusion and neurotransmitter release at the synapse (20–22). Their interaction has been subject to single molecule investigations using the AFM (23,24), and fluorescence resonance energy transfer (25,26). The cytoplasmic tail sequences of Sb2 (amino acids 1–94 of rat Sb) and Sx1A (amino acids 1–266 of rat Sx1A) are used. The interacting segments consist of α-coils from the amino-acid sequence 27–94 in Sb2 and 190–266 in Sx1A, which form a coiled-coil when brought into contact with each other (20–26). The lengths of the α-coils are much smaller than their persistence length (27) and therefore can be considered as relatively rigid rods.

Here, for the first time (to our knowledge), we quantitatively compare interaction energies obtained for two interacting single proteins using the different theoretical approaches of single molecule reaction rate theory (28–32) and the JE (8,9). Next, we independently confirm the JE by checking the convergence of the free energy with the rate of applied force. We also utilize the temperature dependence of the bond lifetime to verify the approach to the reversible limit in the application of the JE. Additionally, we use a pointlike six histidine linker to attach the proteins to the probes. The linker undergoes negligible extensions on force application and therefore allows an unambiguous calculation of the protein interaction energy. This work extends the application of JE to interacting molecules and generalizes the procedure for calculation of activation energies in nonequilibrium processes. Our approach, applied here to exocytotic/synaptic proteins, opens prospects for rigorous comparison of experimental results to theoretical modeling of protein interactions.

METHODS

Recombinant proteins

Recombinant Sb2 and Sx1A were produced using modified pET vectors, leading to their cytoplasmic domains (rat sequence aa1-94 for Sb2 and aa1-266 for Sx1A) being tagged with six histidines (H6) at their C-termini (24). The proteins were then purified using nickel-Sepharose beads (Qiagen, Germantown, MD), and quantified using the Bradford reagent (Pierce Biotechnology, Rockford, IL) and bovine serum albumin as a standard. To determine their purity, the proteins were subjected to 15% SDS-PAGE in combination with the silver-stain technique. Densitometry of silver-stained gels, performed using ChemiDoc XRS gel documentation system (BioRad Laboratories, Hercules, CA), indicated that purified recombinant proteins represent 84–97% of the total protein content.

For SDS-PAGE analysis followed by Western blotting, the proteins were loaded at 1 μg per lane. We then tested the membranes using monoclonal antibodies against Sx1 syntaxin 1 (clone 78.2; Synaptic Systems, Göttingen, Germany, or clone HPC-1; Sigma-Aldrich, St. Louis, MO), and against Sb2 (clone 69.1; Synaptic Systems). Enhanced chemiluminescence (Amersham Pharmacia, Sunnyvale, CA) was used to detect the single immunoreactive bands with appropriate molecular weights.

Functionalization of cantilevers and glass coverslips

Triangular silicon nitride cantilevers (320-μm-long) with integral tips and glass coverslips (cat. No. 12-545-82-12CIR-1D; Fisher Scientific, Pittsburgh, PA) were coated with nickel films (thickness ∼ 150 nm) using a thermal evaporator. After nickel film deposition and partial film oxidation in air, the tips were functionalized with recombinant proteins by incubating tips in a solution containing proteins for 3 h at room temperature. Nickel-coated glass coverslips were functionalized with recombinant proteins for 1 h at room temperature. After incubation with recombinant proteins, the tips and coverslips were rinsed three times with internal solution, and then kept separately submersed in this internal solution in a humidified chamber at +4°C until used in experiments up to 6 h later. Internal solution contained: potassium-gluconate, 140 mM; NaCl, 10 mM; and HEPES, 10 mM (pH = 7.35). Before experiments, the glass coverslips were mounted on the metal disk AFM sample holders.

The presence of Sx1A on the functionalized cantilever tips and Sb2 on the functionalized glass coverslips was determined by indirect immunochemistry, as previously described (24). Here, we used mouse monoclonal antibodies against Sx1 (clone HPC-1, 1:500) and Sb2 (1:500). Cantilevers and coverslips were incubated with the primary antibodies for 1 h at room temperature, and then followed by triple wash with internal solution. Next, the TRIC-conjugated goat anti-mouse antibodies were applied and incubated for 1 h at room temperature followed by a triple washout in internal solution. Visualization for immunochemistry was done using an inverted microscope (TE 300; Nikon, Melville, NY) equipped with wide-field epifluorescence (100-W xenon arc lamp; Opti-Quip, Highland Mills, NY), and standard rhodamine/TRITC) filter set (Chroma Technology, Brattleboro, VT).

Force-distance curves

We used a Nanoscope E and associated equipment (Digital Instruments, Santa Barbara, CA) in force spectroscopy mode. All experiments were carried out in a fluid cell that maintained the hydration and osmotic properties of the sample. Force was calibrated using spring constants, usually ranging from 10 to 16 mN/m, which was determined for each cantilever using its thermal spectrum (33). The bending of the cantilever was taken into account in the calculation of the extension as described in the text (34). The piezoelectric tube extension, including nonlinearities, was calibrated interferometrically for all the force loading rates used (35). The experiments were carried out at 24°C, 14°C, and 4°C in temperature-controlled rooms containing the entire experimental setup.

Specificity of the interaction between Sx1A and Sb2 was confirmed using the light chain of Botulinum neurotoxin type B, which cleaves Sb2 and thus reduces the probability of interactions between Sx1A and Sb2 (24). As previously described, we verified the coiled-coil nature of the bonding between Sx1A and Sb2 and the role of the extension using synthetic cognate peptides encoding for parts of the rat Sx1A sequence, either aa178–200 or aa215–235 (24).

RESULTS AND DISCUSSION

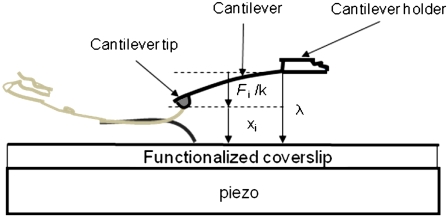
A schematic of the experimental setup used is shown in Fig. 1. The tips of microfabricated AFM cantilevers were nickel-coated and exposed to air. The resulting tips containing Ni²⁺ were then functionalized with a recombinant exocytotic/synaptic protein Sx1A conjugated to six consecutive histidine molecules (H6) tag at its C-terminus. Nickel-plated coverslips, after oxidation, were functionalized with recombinant Sb2 conjugated to an H6 tag at its C-terminus. This attachment procedure allows the free interaction of the N-termini of the two proteins. The Ni²⁺-H6 attachment is relatively pointlike (having negligible extensions) and comparatively rigid, with mean rupture forces of 525 ± 41 pN as in Liu et al. (24), which is much larger than the force required to rupture the Sx1A-Sb2 molecular interaction. This pointlike attachment of the proteins removes ambiguities such as the role of the long flexible linkers in the force-extension measurements. Immunochemistry was used to confirm the functionalization of the cantilever tips and coverslips (24).

FIGURE 1.

Schematic of experimental setup. Recombinant syntaxin 1A and synaptobrevin 2 cytoplasmic tails are attached to the cantilever tip and coverslip, respectively, through a Ni²⁺-six histidine residue coordination at the C-termini of these proteins. The picture is not to scale. The piezo is used to first move the coverslip up toward the cantilever tip to bring about the interaction and then down to exert force on the intermolecular bond. The work parameter λ is the distance from the bottom of the cantilever holder to the top of the coverslip, x_i is the extension of the bound intermolecular complex, and F_i/k is the distance bent by the tip of a cantilever of spring constant k in response to a force F_i.

The Sx1A functionalized cantilever tips and Sb2 functionalized coverslips were then loaded into a fluid cell containing internal saline (24). The experiment is first done at a room temperature of 24°C. The coverslip was raised toward the cantilever using the piezo, until they came into contact for 0.5 to 3 s, allowing the Sx1A-Sb2 intermolecular binding. Then the piezo was used to lower the coverslip away from the cantilever, thereby increasing the work parameter λ, the distance between the cantilever holder and the coverslip, at a constant velocity of v = dλ/dt = 1.447 μm/s. This corresponds to a rate of applied force, dF/dt = k × v = 21.1 nN/s, where k is the cantilever spring constant. The applied force causes the sequential rupture of the bonds leading to an increase in the cantilever tip-coverslip distance. The corresponding extension of the bound intermolecular system is x_i = λ − F_i/k, where F_i/k is the distance bent by the cantilever of spring constant k due to the force of magnitude F_i on its tip. The initial value of λ on contact of the tip and coverslip is set equal to zero. A typical force versus extension curve with the sequence of interactions is shown in Fig. 2 a. Here, the line ab is due to direct contact between the coverslip and the cantilever tip. The section cde was confirmed to be specific to this interaction, as it was absent when both or either the cantilever tip or the coverslip remained unfunctionalized. We also checked that the specific interactions were greatly reduced 1), by the competitive displacement in the presence of soluble forms of Sx1A or Sb2; and 2), when using Botulinum Toxin type B which cleaves Sb 2 (for details, see (24)). The increasing extension from c as the coverslip moves further away from the cantilever tip with increasing λ leads to increased application of the force on the intermolecular bond until it ruptures at point d and the cantilever returns to its free equilibrium position e. The segment de is the force necessary to rupture the Sx1A-Sb2 bond which, in the example shown, is 242 pN. The net extension to the point of rupture can be calculated from the distance moved by the coverslip from point c to d, and subtracting from it the rupture force divided by spring constant, which is the decrease in tip-coverslip separation distance due to the bending of the cantilever tip from the applied force at rupture. The experiment is repeated 54 times and a histogram of the force and extension required to rupture the bond is developed as shown in Fig. 2, panels b and c, respectively. From the histogram, the mean ± SE values of rupture force and extension were found to be 252 ± 10 pN and 22.2 ± 1.0 nm, respectively, consistent with our earlier measurements reported in Liu et al. (24), where a different and much larger number of repetitions (N = 456) were used.

FIGURE 2.

(a) A typical force curve obtained for the intermolecular interaction of the syntaxin 1A-synaptobrevin 2 pair. The force on the cantilever tip is plotted as a function of the distance moved by the coverslip. The segment de represents the bond rupture force. The net intermolecular extension to the point of rupture can be calculated from the distance moved by the piezo from point c to d, and subtracting from it the rupture force divided by the spring constant, which is the decrease in tip-coverslip separation distance due to the bending of the cantilever tip from the applied force at rupture. The segment ab is due to direct contact between the cantilever tip and coverslip. (b) Force and (c) extension histograms at the point of rupture for the intermolecular interaction of the syntaxin 1A-synaptobrevin 2 pair. The arrowheads on the histogram show mean values.

Next the rate of change of the work parameter, dλ/dt is modified by moving the coverslips at different velocities v, and for each velocity the above experiments are repeated and the force and corresponding extensions are measured. This is repeated for different velocities v from 40 nm/s to 3875 nm/s. The corresponding dF/dt ranged between 500 pN/s and 52,000 pN/s. This complete series of experiments done at 24°C (297 K) for the different dF/dt were also repeated at two other temperatures, 14°C (287 K) and 4°C (277 K).

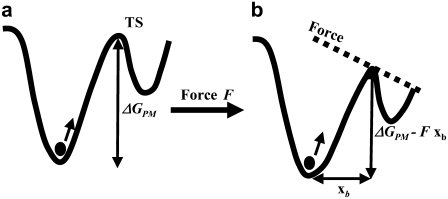
The results of the single molecule force spectroscopy, the mean rupture force as a function of the rate of applied force dF/dt, and temperature can be used to obtain the spontaneous dissociation lifetime and the corresponding activation energy barrier using a phenomenological model (PM) (28). The PM model for the behavior of a bound single molecule system under the application of a force has been adapted from classical chemical reaction rate theory. Without application of the force, the bound system, represented as a solid circle at the bottom of a potential well in Fig. 3 a, thermally escapes over the transition state at the top of the barrier. The rate of escape is given by the thermal energy of the system. On application of the force F, the energy barrier is lowered to ΔG_PM-Fx_b, where x_b is the width of the barrier as shown in Fig. 3 b. Note that the force is assumed to be applied along the direction of the bond. In cases where there is a constant angle θ between the bond axis and the force, a factor cosθ is included in the value of x_b. This lowering of the barrier due to the force leads to a decrease of the lifetime of the bond as seen from the equation

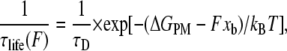(2)

where τ_D is the inverse of the thermal attempt frequency. In these single molecule experiments, the backward reaction rate after complete rupture of the intermolecular bonds is zero as the reactants are rapidly pulled apart to effectively infinite separation. Then Eq. 2 leads to

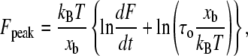(3)

where F_peak is the peak value in the measured force distribution and τ₀ is the lifetime for the spontaneous dissociation of the intermolecular bonds when the applied force is F = 0. When many bonds are broken in sequence for the zipper-type, coiled-coil interaction relevant here (24), the lifetime τ_o represents the lifetime for the dissociation of all the bonds.

FIGURE 3.

(a) The bound state is represented by the solid circle at the bottom of the potential well. (b) The lowering of the energy barrier due to the application of the force.

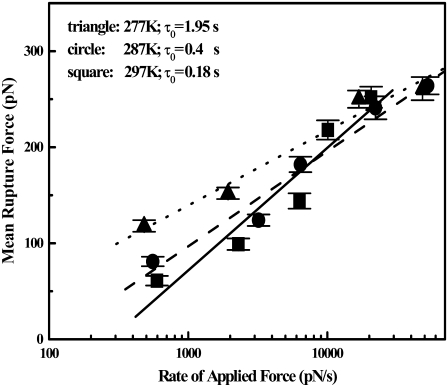
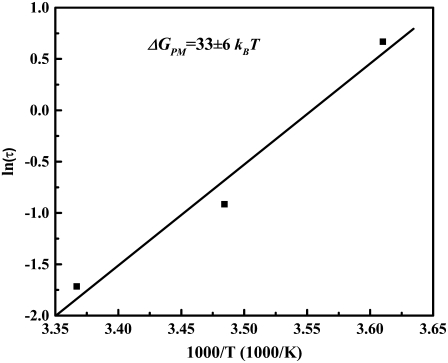
We can apply the experimental results to the PM of single molecule reaction rate theory to obtain the activation free energy ΔG_PM. In Fig. 4, the measured values F_peak are plotted against dF/dt. Based on Eq. 3, the spontaneous dissociation lifetime τ_o can be calculated from the intercept and the slope in Fig. 4. The values of τ_o are 0.18, 0.4, and 1.95 s at the three different temperatures 297 K, 287 K, and 277 K, respectively. Knowing the lifetime τ_o at the three different temperatures, one can use Eq. 2 (setting F = 0) to solve for the ΔG_PM (30). This is done graphically by plotting ln(τ_o) versus (1/T) as shown in Fig. 5 from the slope ΔG_PM = 33 ± 6 k_BT. Here, the linear temperature dependence of τ_D can be neglected in Eq. 2, given the presence of the exponential term.

FIGURE 4.

The mean rupture force as a function of the rate of applied force dF/dt, for three different temperatures of 277 K, 287 K, and 297 K, are shown as triangles, circles, and squares, respectively. The corresponding best-fit straight lines are indicated as dotted, dashed, and solid lines. Based on the phenomenological model, the mean lifetime τ_o of the bound system under zero force is found from the intercept and the slope of the lines to be 1.95, 0.4, and 0.18 s, respectively. Points indicate mean ± SE values.

FIGURE 5.

The natural logarithm of the mean lifetime τ_o of the bound system plotted as a function of inverse temperature. From the slope, the activation energy ΔG_PM can be found based on the phenomenological model.

Next, we compute the ΔG_JE for the intermolecular interaction using the JE. From the applied force and corresponding extension measured in Fig. 2 a, we can calculate the work done on the single molecule system according to 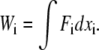Here, W_i measures the work done from the bound state at x_i = 0 to the unbound state at the point of rupture. The force is assumed to act along the axis of the bond. The distribution of W_i values obtained from the force-extension measurements obtained at a pulling velocity v = 40 nm/s are shown in Fig. 6 a. The JE is now applied to all the W_i. The procedure is repeated for the force-extension curves obtained for other pulling velocities. In Fig. 6 b, the values of the ΔG obtained by applying the JE are shown as a function of the reciprocal of the pulling velocity for the different dF/dt at the three different experimental temperatures. At each temperature, the decreasing value of ΔG with decreasing pulling velocity can be observed. This results from the slower rate of rupture of the intermolecular bonds at the lower pulling velocities. To recognize the approach to the reversible limit, the total time to rupture the intermolecular bonds needs to be compared to a characteristic timescale which is given here by the bond lifetime at that particular temperature. In the case of 297 K, for experiments at a pulling velocity of 1447 nm/s (N = 54), the average time to rupture the intermolecular interaction is 0.027 s, which is much smaller than the lifetime 0.18 s of the interaction, resulting in a large ΔG. However, in experiments done at a pulling velocity of 40 nm/s (N = 53) done at the same temperature, the average time to rupture the intermolecular interactions is 0.43 s, which is much larger than the spontaneous lifetime of the interaction. Thus, at the two lowest pulling velocities where all the intermolecular bonds are ruptured slowly in comparison to the lifetime, the ΔG has a horizontal asymptote, suggesting the approach to the adiabatic limit. The value of ΔG_JE at the lowest pulling velocity is 49 ± 5 k_BT. Although the JE is valid at all pulling speeds, the number of repetitions N has to be large at pulling speeds with intermolecular rupture times much smaller than that of the characteristic lifetime of the bound system. The systematic error, resulting from an inadequate number of repetitions N, will lead to larger values of ΔG (8–16) at the larger pulling speeds. At the lower temperatures of 277 K and 287 K, the adiabatic limit is not achieved in the experiment for our number of repetitions (N is 44 and 42, respectively), even at the lowest pulling velocity, due to the corresponding respective longer lifetimes of 1.95 s and 0.4 s. Note that the related Crooks fluctuation theorem (11,12) cannot be applied here, as reverse binding is not possible after rupture of the intermolecular bond.

FIGURE 6.

(a) The distribution of W_i obtained from the force extension curves recorded at a pulling velocity of 40 nm/s for experiments done at 297 K. (b) Values of ΔG plotted as a function of the reciprocal pulling velocity using the JE for three different temperatures. For experiments at 297 K (squares), the asymptotic behavior of ΔG_JE approaches the adiabatic limit at low pulling velocities. At lower temperatures of 277 K (triangles) and 287 K (circle), the adiabatic limit is not achieved due to the longer lifetimes. The lines connecting the data points can be used as an aid to the eye. Points indicate mean ± SE values.

Next, we discuss the difference in the values of ΔG obtained with the phenomenological reaction rate theory and the values using the JE. One explanation for the larger values of ΔG_JE over ΔG_PM resides in the assumption that the force acts along the axis of the bond in the calculation of W_i used in the computation of ΔG_JE. Reconciling the mean values would lead to an angle of 48° between the direction of applied force and the bond axis rather than the zero degrees assumed initially. Perhaps this angle represents the average opening angle between the proteins as they are pulled apart. A second but smaller factor in the difference in the two values can be attributed to the neglect of the role of the entropy in the use of PM. Deviations between the two approaches can also be explained due to the approximations in the PM. It has recently been pointed out that the PM is a special case of the analytical form of the interaction of the applied force and curvature of the free energy landscape of the bond (31), and a concern that the PM can lead to very large values of τ_o has been noted. To explore this, we have independently measured the lifetime of the bond at zero force by applying constant forces with the help of a second piezo attached to the coverslip in Fig. 1. We obtained a value of τ_o = 0.11 ± 0.02 s at 297 K consistent within errors of the 0.18 ± 0.06 s from the PM model (errors are derived from that of the slope and intercept in Fig. 4). Other emerging models (36) are not applicable to the experiment, due to our use of our pointlike linkers to attach the proteins. The possible alternative use of long flexible linker could still lead to the uncertainty associated with the opening angle due to the more rigid nature of the coiled-coil interacting molecules studied here. There is additional concern that the flexible linker might introduce uncertainties associated with the entropic work necessary to extend the linker. Nonetheless, future work will be necessary to completely reconcile the interaction energies obtained through the two methods.

In conclusion, we have provided a quantitative comparison of two methods for the experimental determination of activation free energies for the disassembly of a pair of interacting single proteins. A model system of exocytotic/synaptic proteins Sx1A and Sb2 attached with pointlike linkers is used to study the rupture force and the extension of the bound system at different rates of applied force and at three different temperatures. These studies allow independent determinations of the ΔG by applying the JE and from phenomenological models of the modification of the energy barrier due to an applied force. The two methods are compared and reasonable agreement was found within the uncertainties of the experiment. This extends the effectiveness of the JE to single molecule experiments involving a pair of interacting molecules and techniques based on AFM. Additionally, the suggested method will facilitate rigorous comparison of experiment to physical modeling of protein interactions.