Abstract
Absorbance difference spectra associated with the light-induced formation of functional states in photosystem II core complexes from Thermosynechococcus elongatus and Synechocystis sp. PCC 6803 (e.g.,  ) are described quantitatively in the framework of exciton theory. In addition, effects are analyzed of site-directed mutations of D1-His198, the axial ligand of the special-pair chlorophyll PD1, and D1-Thr179, an amino-acid residue nearest to the accessory chlorophyll ChlD1, on the spectral properties of the reaction center pigments. Using pigment transition energies (site energies) determined previously from independent experiments on D1-D2-cytb559 complexes, good agreement between calculated and experimental spectra is obtained. The only difference in site energies of the reaction center pigments in D1-D2-cytb559 and photosystem II core complexes concerns ChlD1. Compared to isolated reaction centers, the site energy of ChlD1 is red-shifted by 4 nm and less inhomogeneously distributed in core complexes. The site energies cause primary electron transfer at cryogenic temperatures to be initiated by an excited state that is strongly localized on ChlD1 rather than from a delocalized state as assumed in the previously described multimer model. This result is consistent with earlier experimental data on special-pair mutants and with our previous calculations on D1-D2-cytb559 complexes. The calculations show that at 5 K the lowest excited state of the reaction center is lower by ∼10 nm than the low-energy exciton state of the two special-pair chlorophylls PD1 and PD2 which form an excitonic dimer. The experimental temperature dependence of the wild-type difference spectra can only be understood in this model if temperature-dependent site energies are assumed for ChlD1 and PD1, reducing the above energy gap from 10 to 6 nm upon increasing the temperature from 5 to 300 K. At physiological temperature, there are considerable contributions from all pigments to the equilibrated excited state P*. The contribution of ChlD1 is twice that of PD1 at ambient temperature, making it likely that the primary charge separation will be initiated by ChlD1 under these conditions. The calculations of absorbance difference spectra provide independent evidence that after primary electron transfer the hole stabilizes at PD1, and that the physiologically dangerous charge recombination triplets, which may form under light stress, equilibrate between ChlD1 and PD1.
) are described quantitatively in the framework of exciton theory. In addition, effects are analyzed of site-directed mutations of D1-His198, the axial ligand of the special-pair chlorophyll PD1, and D1-Thr179, an amino-acid residue nearest to the accessory chlorophyll ChlD1, on the spectral properties of the reaction center pigments. Using pigment transition energies (site energies) determined previously from independent experiments on D1-D2-cytb559 complexes, good agreement between calculated and experimental spectra is obtained. The only difference in site energies of the reaction center pigments in D1-D2-cytb559 and photosystem II core complexes concerns ChlD1. Compared to isolated reaction centers, the site energy of ChlD1 is red-shifted by 4 nm and less inhomogeneously distributed in core complexes. The site energies cause primary electron transfer at cryogenic temperatures to be initiated by an excited state that is strongly localized on ChlD1 rather than from a delocalized state as assumed in the previously described multimer model. This result is consistent with earlier experimental data on special-pair mutants and with our previous calculations on D1-D2-cytb559 complexes. The calculations show that at 5 K the lowest excited state of the reaction center is lower by ∼10 nm than the low-energy exciton state of the two special-pair chlorophylls PD1 and PD2 which form an excitonic dimer. The experimental temperature dependence of the wild-type difference spectra can only be understood in this model if temperature-dependent site energies are assumed for ChlD1 and PD1, reducing the above energy gap from 10 to 6 nm upon increasing the temperature from 5 to 300 K. At physiological temperature, there are considerable contributions from all pigments to the equilibrated excited state P*. The contribution of ChlD1 is twice that of PD1 at ambient temperature, making it likely that the primary charge separation will be initiated by ChlD1 under these conditions. The calculations of absorbance difference spectra provide independent evidence that after primary electron transfer the hole stabilizes at PD1, and that the physiologically dangerous charge recombination triplets, which may form under light stress, equilibrate between ChlD1 and PD1.
INTRODUCTION
While all of the photosynthetic reaction centers share considerable similarity in the nature and arrangement of their redox cofactors, only that of photosystem II (PS-II) is able to generate a reduction potential that is positive enough to oxidize water to molecular oxygen. While the mechanistic details of the water splitting and of the primary electron and hole transfer reactions in PS-II are not fully understood, recent progress in the x-ray crystallographic structure determination (1,2) has resulted in a 3.0 Å resolution crystal structure (2) that provides the basis for detailed calculations of optical spectra.
The following scheme of primary reactions was established for PS-II by various spectroscopic techniques (recent reviews are given in (3,4)). Optical excitation of the reaction center, either directly or via excitation energy transfer from the core antennae CP43 and CP47 generates a state commonly referred to as P* which donates an electron to the pheophytin of the electron transfer active D1-branch, PheoD1 and a state  is formed. The electron is transferred further to the plastoquinone QA and the hole via a tyrosine, TyrZ, to the manganese cluster, where the water-splitting reaction takes place. Under light stress, a triplet state 3P680 may be generated in the reaction center by charge recombination of
is formed. The electron is transferred further to the plastoquinone QA and the hole via a tyrosine, TyrZ, to the manganese cluster, where the water-splitting reaction takes place. Under light stress, a triplet state 3P680 may be generated in the reaction center by charge recombination of 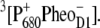 Although the overall reaction scheme is clear, the molecular identities of some of the functional states and the mechanistic and kinetic details are not.
Although the overall reaction scheme is clear, the molecular identities of some of the functional states and the mechanistic and kinetic details are not.
It is still not entirely clear whether electron transfer at physiological temperatures starts at the accessory chlorophyll of the D1-branch ChlD1 or at the special-pair chlorophyll PD1 or both. On the one hand there are recent reports by Groot et al. (5) and Holzwarth et al. (6) who inferred independently from femtosecond IR studies and pump-probe experiments in the visible spectral region, respectively, that the primary electron transfer at physiological temperatures occurs between ChlD1 and PheoD1. However, the reported timescale for the pheophytin reduction differs by a factor of 4–5. Whereas Groot et al. report a 600–800 fs time constant, that of Holzwarth et al. is 3 ps.
In contrast, Novoderezhkin et al. (7), based on a fit of linear and time-resolved nonlinear optical spectra, using an exciton model including charge transfer (CT) states, concluded that the primary charge-separated state is an intra special-pair CT state that either is directly optically excited or populated within 100 fs by exciton relaxation from the core pigments. This idea seems to be in line with studies of Krausz et al. (8), who detected a long wavelength excited state capable of charge separation. One difference between the two CT states is that the one of Novoderezhkin et al. is broadened inhomogeneously whereas the one of Krausz was shown to be homogeneously broadened (8). In more recent work, Novoderezhkin et al. (9) concluded that two parallel electron transfer pathways exist, one starting from an intra dimer CT state of the special-pair and one at ChlD1, where the relative importance of the two pathways is determined by the specific realization of disorder in site energies.
A key idea about the identity of the primary electron donor in PS-II came from van Brederode, van Grondelle, and co-workers (10–12), who found that in bacterial reaction centers there is ultrafast electron transfer from the excited state of the accessory bacteriochlorophyll (BA) of the L-branch. Electron transfer from BA* is an order-of-magnitude faster than electron transfer from the low energy exciton state of the special pair. However, in bacterial reaction centers the slow pathway is dominant because of the large energy gap between the low energy special-pair exciton state and the remaining excited states that gives rise to an equilibrated excited state population that is localized at the special pair. The fact that the excited states of the PS-II reaction center are much closer in energy, as seen, e.g., from the absorption spectrum, led van Brederode and van Grondelle(12) to suggest that the fast side pathway in bacterial reaction centers might be the dominant one in PS-II.
Very much related to the question of the identity of the primary electron donor is the extent to which P* is a delocalized excited state of the core pigments, as assumed in the multimer model, or an excited state, that is localized on a particular pigment, the primary electron donor. In the original multimer model proposed by Durrant et al. (13) all of the pigments, in the absence of excitonic couplings, had the same mean transition energy (site energy). In such a model, all of the exciton states are delocalized over a number of core pigments, where the extent of delocalization and the energy and population of a particular exciton state depend on the particular realization of static disorder, caused by slow conformational motion of the protein. As the coupling between the two special-pair chlorophylls is the largest in all multimer models (13–17), the lowest exciton state contains a considerable contribution from the special-pair chlorophylls.
In contrast to these traditional multimer models, we have recently suggested an exciton model with blue-shifted site energies of the special-pair pigments and a red-shifted site energy of ChlD1 (named AccD1 in (18)) that results in a high degree of localization of the lowest exciton state on the latter, a second lowest exciton state with a large contribution from the pheophytin PheoD2 of the inactive D2-branch and where only the third lowest exciton state is the low-energy exciton state of the special pair. This model explains 11 independent optical spectra of the D1-D2-cytb559 complexes, including difference spectra with chemically modified, oxidized, and reduced pigments and pigments in the triplet state (18). In a recent work of Novoderezhkin et al. (9), similar site energies were inferred.
The D1-D2-cytb559 complexes unfortunately contain neither the manganese cluster nor the primary quinone electron acceptor QA. Consequently, it is not possible to investigate with this material the whole sequence of primary and secondary electron transfer reactions. In addition, because of the rather harsh isolation procedure of the D1-D2-cytb559 complexes, it cannot be excluded that the transition energies of the reaction center pigments might be different from those in core complexes. This point has been raised ever since D1-D2-cytb559 preparations became available (see, e.g., (3) and references therein). We will provide evidence in this work that the D1-D2-cytb559 complexes represent a valid model system for the reaction center pigments in PS-II core complexes, as concerns the transition energies of the pigments. The only modification with respect to our proposed site energies of D1-D2-cytb559 complexes concerns ChlD1, the site energy of which is red-shifted in core complexes and less inhomogeneously distributed.
A major difficulty in interpreting optical experiments on PS-II core complexes is that the bands of the reaction center pigments strongly overlap each other as well as the bands of the pigments in the core antenna subunits, CP43 and CP47. Therefore it is difficult in such a complex to excite particular states of the reaction center. An alternative is to measure optical difference spectra of core complexes in which particular reaction center pigments have been converted into a different electronic state. The optical difference spectrum reveals only those pigments that are coupled to the pigment that has undergone a change in electronic state. As the couplings between the reaction center pigments and the pigments in the CP43 and CP47 subunits are weak, the difference spectra provide direct information about the reaction center pigments of PS-II core complexes without interference from the antenna pigments. The combination of optical difference spectroscopy with site-directed mutagenesis, in which amino-acid residues in the local environment of certain chlorophylls are replaced, provides valuable information regarding the transition energies of these pigments located at the sites of mutation.
Analysis of triplet minus singlet (T-S) and 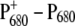 difference spectra on wild-type and mutants of the axial ligands of the special-pair chlorophylls of Synechocystis sp. PCC 6803, provided evidence that electron transfer starts at ChlD1 and that the hole stabilizes at PD1 at low temperatures (19). In addition, recent experiments on mutants with changes in the local environment of ChlD1 have provided direct evidence that the charge recombination triplet is localized on ChlD1 at low temperatures (20).
difference spectra on wild-type and mutants of the axial ligands of the special-pair chlorophylls of Synechocystis sp. PCC 6803, provided evidence that electron transfer starts at ChlD1 and that the hole stabilizes at PD1 at low temperatures (19). In addition, recent experiments on mutants with changes in the local environment of ChlD1 have provided direct evidence that the charge recombination triplet is localized on ChlD1 at low temperatures (20).
We present in this work an independent verification of the molecular identities of the states P*, 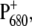 and 3P680 from exciton calculations of wild-type difference spectra at low temperature and comparison with experimental data. It is demonstrated that the exciton model developed previously for D1-D2-cytb559 complexes (18) explains these wild-type spectra as well as the difference spectra measured on mutant core complexes.
and 3P680 from exciton calculations of wild-type difference spectra at low temperature and comparison with experimental data. It is demonstrated that the exciton model developed previously for D1-D2-cytb559 complexes (18) explains these wild-type spectra as well as the difference spectra measured on mutant core complexes.
An important question is: Do the experimental and theoretical studies at cryogenic temperatures reflect the same primary reactions that occur in the living cell, i.e., at physiological temperatures? There is a remarkable change of several difference spectra with increasing temperature (21). At low-temperature, multiple bands are visible in the 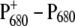 difference spectrum, whereas at room temperature just a single bleaching band at 680 nm appears (22), the source of the spectroscopic term
difference spectrum, whereas at room temperature just a single bleaching band at 680 nm appears (22), the source of the spectroscopic term 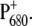 This strong overlap of different bands at physiological temperatures is a major obstacle in identifying functional states.
This strong overlap of different bands at physiological temperatures is a major obstacle in identifying functional states.
We show in this work that the identity of the functional states does not change significantly as a function of temperature. Rather the temperature dependence of the dielectric constant and of the site energies of ChlD1 and PD1 are responsible for the temperature dependence of the difference spectra involving 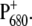 This change in site energies, however, does not alter the exciton model, in that the lowest excited state is still localized at ChlD1. However, in the case of the T-S spectrum, more than one triplet state contributes at higher temperatures.
This change in site energies, however, does not alter the exciton model, in that the lowest excited state is still localized at ChlD1. However, in the case of the T-S spectrum, more than one triplet state contributes at higher temperatures.
The work presented here is organized in the following way. We first summarize the theoretical methods and our earlier exciton model for the reaction center pigments in PS-II (18). We next present calculations of difference spectra of wild-type and mutant core complexes, that identify the functional states. We describe the temperature dependence of the wild-type difference spectra and provide a discussion of 1), the necessary revision of the multimer model; 2), an identification of functional states at physiological temperatures; and 3), functional implications of our exciton model.
THEORETICAL METHODS
The theoretical methods were described in detail in our recent report on D1-D2-cytb559 complexes (18). We provide below a short summary and concentrate on some new aspects. We used the recent 3.0 Å structure of PS-II (2) to calculate the excitonic couplings between the reaction center pigments by the ab initio TrEsp method, developed previously (23), that combines the accuracy of the ab initio transition density cube method (24) with the simplicity of the semiempirical transition monopole method (25). We use the TrEsp atomic transition charges determined from a fit of the electrostatic potential of the transition density calculated with time-dependent density functional theory, with a B3LYP exchange correlation-functional and a 6-31G* basis set (23). (Note that the TrEsp charges for chlorophyll a are given in the Supplementary Material of (23) and those of pheophytin a in this article's Supplementary Material, Data S1.) The transition charges were rescaled to yield an effective transition dipole moment of 4.4 D for Chl a and 3.4 D for Pheo. (Please note that the effective dipole strength of Chl a was chosen in accordance with the empty cavity analysis of chlorophyll dipole strengths in different solvents by (26), which resulted in a vacuum dipole strength of 4.6 D. The reduction to 4.4 D takes into account the change in excitonic coupling by screening and local field effects by the dielectric environment. The reduction was chosen somewhat smaller than obtained recently from electrostatic calculations on the pigments of the FMO-protein (41) to take into account the closer distance and hence less screening in the PS-II reaction center. The effective dipole strength of 3.4 D for Pheo a was estimated on the basis of the value for Chl a and the optical dipole strengths measured for Chl a and Pheo a in an ether solvent (27).) Much to our surprise, the coupling between PD1 and PD2 was drastically reduced compared to the coupling obtained previously (18) from structural data with lower resolution and the transition monopole charges of Chang (25). Judging from the structural data, considerable wavefunction overlap can be expected between the two special-pair chlorophylls PD1 and PD2. This overlap results in a Dexter-type exchange coupling, in addition to Förster-type Coulomb coupling obtained by the TrEsp method. To estimate the exchange contribution we refitted the eleven D1D2-cytb559 spectra, studied previously (18), taking the special-pair coupling as well as the site energies as fit parameters. The coupling was allowed to vary between 60 cm−1 and 240 cm−1. We obtained the same optimal site energies as previously (18) and an optimal special-pair coupling of 140–170 cm−1. In parallel, we performed quantum chemical calculations of the excited state energies and transition dipole moments of the special-pair monomers and the whole dimer (unpublished). The short-range coupling was extracted by comparing the monomer and dimer results, using an effective two-state Hamiltonian. The short-range coupling obtained was smaller than that inferred from the fit. However, agreement with the fitted value was obtained after moving the two Chls closer together, within the error limits of the crystallographic structure (J. Biesiadka, 2007, private communication). The excitonic couplings used in the calculations are given in Table 1.
TABLE 1.
Ab initio excitonic couplings, obtained using the TrEsp method (23), in units of cm−1
| PD2 | ChlD1 | ChlD2 | PheoD1 | PheoD2 | ChlzD1 | ChlzD2 | |
|---|---|---|---|---|---|---|---|
| PD1 | 150 (239) | −42 (−17) | −53 (−81) | −6 (−4) | 17 (16) | 1 (1) | 1 (1) |
| PD2 | −60 (−82) | −36 (−10) | 21 (20) | −3 (−4) | 1 (1) | 1 (1) | |
| ChlD1 | 7 (12) | 47 (71) | −4 (−5) | 3 (3) | 0 (0) | ||
| ChlD2 | −5 (−5) | 35 (64) | 0 (0) | 2 (2) | |||
| PheoD1 | 3 (3) | −4 (−4) | 0 (0) | ||||
| PheoD2 | 0 | −4 (−4) | |||||
| ChlzD1 | 0 (0) |
The following effective dipole strengths have been assumed: 4.4 D for Chls and 3.4 D for Pheos. For the coupling between PD1 and PD2 additional short-range exchange contributions were included as described in the text. The values in parentheses were obtained using a point dipole approximation.
For comparison, we also show in Table 1 the point dipole couplings (numbers in brackets). The largest deviations between the TrEsp couplings and the point dipole approximation, except for the special-pair coupling discussed above, are obtained for the coupling between the special-pair and the accessory chlorophylls. Whereas in point dipole approximation the special-pair chlorophyll of one branch couples more strongly to the accessory chlorophyll of the other branch, in TrEsp the couplings to the accessory chlorophyll of both branches are similar.
The energies and oscillator strengths of the exciton states, obtained from the couplings in Table 1 and the site energies by a diagonalization procedure, determine the positions and intensities of optical bands of the reaction center. The homogenous line shape follows from the coefficients of the exciton states and the spectral density of the pigment-protein coupling which was extracted previously from fluorescence line-narrowing spectra and the temperature dependence of the absorption spectrum (16,18). The local transition energies of the pigments were determined from a fit of the optical spectra of D1-D2-cytb559 complexes (18).
In the calculation of the difference spectra, the absorbance spectrum is calculated twice, first with all of the pigments and second without those pigments which are oxidized, reduced, or transformed into the triplet state. In the case of a reduced or oxidized pigment, electrochromic shifts of the transition energies of the remaining pigments are taken into account as described in detail previously (18). Briefly, the electrochromic shift is calculated from the Coulomb interaction of the excess charge of the reduced or oxidized pigment with the change in permanent dipole moment 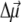 between ground and excited states of the neutral pigment. The excess charge was evenly distributed over the π-atoms of the conjugated rings of the reduced or oxidized pigment. The simplest approximation for the orientation of
between ground and excited states of the neutral pigment. The excess charge was evenly distributed over the π-atoms of the conjugated rings of the reduced or oxidized pigment. The simplest approximation for the orientation of 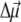 for Chl a is to assume that it is aligned along the NB-ND axis (18), in crystallographic notation (where NB and ND correspond to N21 of ring A, N23 of ring C, respectively, in IUPAC nomenclature (29)). From Stark spectra an angle of 20° between
for Chl a is to assume that it is aligned along the NB-ND axis (18), in crystallographic notation (where NB and ND correspond to N21 of ring A, N23 of ring C, respectively, in IUPAC nomenclature (29)). From Stark spectra an angle of 20° between 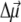 and this axis was reported (30). We find the best agreement with experimental difference spectra if we assume that the
and this axis was reported (30). We find the best agreement with experimental difference spectra if we assume that the 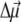 vector is rotated in plane by 15° with respect to the NB → ND direction toward NC (N22 of ring B in IUPAC nomenclature (29)). We assume the same orientation of the
vector is rotated in plane by 15° with respect to the NB → ND direction toward NC (N22 of ring B in IUPAC nomenclature (29)). We assume the same orientation of the 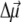 vector for the two Pheos. In the calculation of electrochromic shifts, an effective dielectric constant εeff = 2 (18) was used at cryogenic temperatures as a screening factor of the Coulomb interaction. At higher temperatures εeff was allowed to increase, reflecting additional conformational motion of the protein that is frozen out at low temperatures.
vector for the two Pheos. In the calculation of electrochromic shifts, an effective dielectric constant εeff = 2 (18) was used at cryogenic temperatures as a screening factor of the Coulomb interaction. At higher temperatures εeff was allowed to increase, reflecting additional conformational motion of the protein that is frozen out at low temperatures.
Static disorder in optical transition energies has been taken into account by a Monte Carlo method as before (18), assuming independent variations of site energies according to a Gaussian distribution function. A full width at half-maximum Δinh = 200 cm−1 for all pigments, except for ChlD1, gave the best agreement with experimental data. We note, however, that any value for Δinh that lies within 180 cm−1 as assumed earlier (18) and 220 cm−1 gives very similar results. The Δinh for ChlD1 had to be reduced to 120 cm−1 to describe the difference spectra of core complexes.
In summary, of all the parameters, only two, 1), the site energy of ChlD1 and 2), the width of the inhomogeneous distribution function of the site energy of ChlD1 were allowed to vary freely to fit the low temperature experimental data. In addition, in the case of the calculation of temperature dependence of the difference spectra, a temperature-dependent site energy of ChlD1 and PD1 and a temperature-dependent εeff had to be assumed.
RESULTS
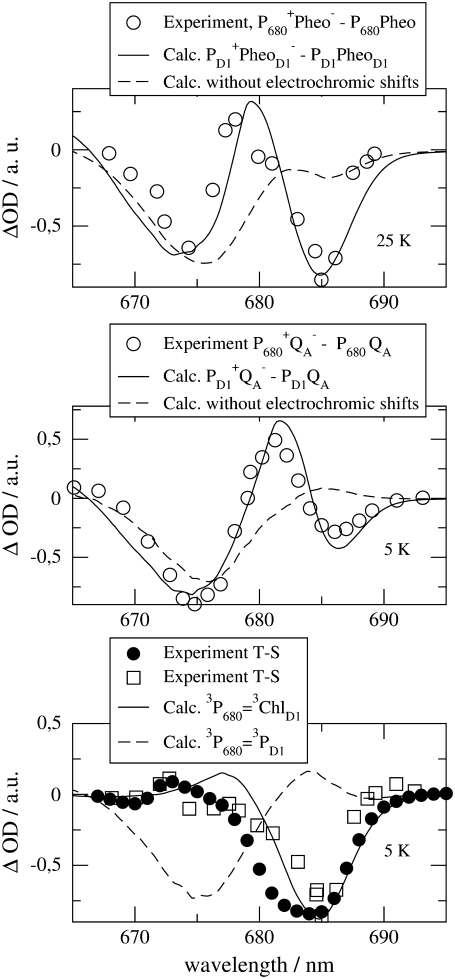
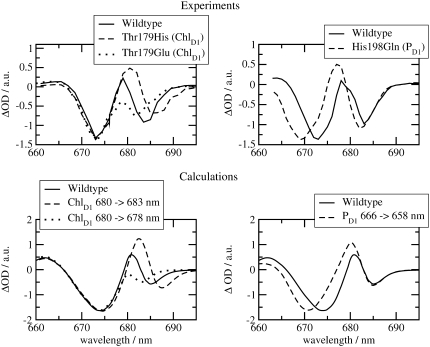
Three calculated optical difference spectra are compared in Fig. 1 with experimental spectra measured by Hillmann et al. (21) on core complexes of Thermosynechococcus elongatus, the same PS-II core complex for which the three-dimensional structure was recently determined (2). The site energy of the accessory chlorophyll of the D1-branch, ChlD1, was red-shifted by 4 nm from 678 nm in D1-D2-cytb559 complexes (18) to 682 nm in PS-II core complexes.
FIGURE 1.
Experiments (21) and calculations of optical difference spectra of PS-II core complexes from Thermosynechococcus elongatus. The calculations were performed using the site energies determined previously (18), except for ChlD1 which was shifted by 4 nm to the red. The corresponding wavelengths assigned to each pigment are PD1, 666 nm; PD2, 666 nm; ChlD1, 682 nm; ChlD2, 667 nm; PheoD1, 672 nm; and PheoD2, 675 nm. The two experimental T-S spectra (bottom panel) were obtained for singly (open squares) and doubly (solid circles) reduced QA. In the latter case it is also possible that QA has dissociated from the core complex.
In the calculation of the difference spectrum (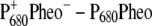 ) in the upper part of Fig. 1 it was assumed that the electron is localized at the pheophytin of the D1-branch, PheoD1, and the hole resides at the special-pair chlorophyll of the same branch, PD1. The first assumption is justified by the fact that electron transfer occurs only along the D1-branch (31,32) and the second one, suggested earlier from difference spectra measured on mutant core complexes (19), was verified by considering different possibilities of hole stabilization as discussed in detail further below. The experimental and calculated spectra show two bleachings, one at ∼675 nm and one at ∼685 nm. When the electrochromic shifts are neglected, only a single bleaching at ∼675 nm is obtained, whereas the one at 685 nm vanishes. The strongest electrochromic shift of 5.6 nm to the blue was calculated for the accessory chlorophyll of the D1-branch, ChlD1.
) in the upper part of Fig. 1 it was assumed that the electron is localized at the pheophytin of the D1-branch, PheoD1, and the hole resides at the special-pair chlorophyll of the same branch, PD1. The first assumption is justified by the fact that electron transfer occurs only along the D1-branch (31,32) and the second one, suggested earlier from difference spectra measured on mutant core complexes (19), was verified by considering different possibilities of hole stabilization as discussed in detail further below. The experimental and calculated spectra show two bleachings, one at ∼675 nm and one at ∼685 nm. When the electrochromic shifts are neglected, only a single bleaching at ∼675 nm is obtained, whereas the one at 685 nm vanishes. The strongest electrochromic shift of 5.6 nm to the blue was calculated for the accessory chlorophyll of the D1-branch, ChlD1.
The two bleachings are also seen in the experimental and calculated (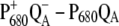 ) spectrum in the middle part of Fig. 1. In the calculated spectrum, the low energy bleaching also vanishes if no electrochromic shifts are included. However, the amplitude of the low energy bleaching is smaller than the bleaching of the high energy one, whereas in the
) spectrum in the middle part of Fig. 1. In the calculated spectrum, the low energy bleaching also vanishes if no electrochromic shifts are included. However, the amplitude of the low energy bleaching is smaller than the bleaching of the high energy one, whereas in the 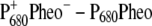 spectrum discussed above, the low energy bleaching is stronger. Of those pigments undergoing site energy shifts, ChlD1 shifts largest, by 3.3 nm to the blue. This shift, however, is only approximately half of that calculated for
spectrum discussed above, the low energy bleaching is stronger. Of those pigments undergoing site energy shifts, ChlD1 shifts largest, by 3.3 nm to the blue. This shift, however, is only approximately half of that calculated for 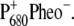 The best agreement between the experimental and calculated spectra is obtained by assuming that the hole is localized at PD1, as suggested earlier (19). The spectra for alternative placement of the cation in the state
The best agreement between the experimental and calculated spectra is obtained by assuming that the hole is localized at PD1, as suggested earlier (19). The spectra for alternative placement of the cation in the state  including
including 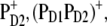 and
and 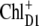 are shown in Fig. 2 and give less satisfying agreement with the experimental data.
are shown in Fig. 2 and give less satisfying agreement with the experimental data.
FIGURE 2.
Calculation of 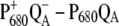 difference spectrum using different assumptions for the localization of the cation in the
difference spectrum using different assumptions for the localization of the cation in the 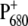 state, in comparison with experimental data (21). For
state, in comparison with experimental data (21). For 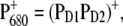 0.5 elementary positive charges were put on both special-pair chlorophylls for the calculation of electrochromic shifts. For better comparison with experimental data, the calculated spectra were scaled such that their low energy bleaching gets equal in magnitude (the unscaled spectra are shown in Data S1).
0.5 elementary positive charges were put on both special-pair chlorophylls for the calculation of electrochromic shifts. For better comparison with experimental data, the calculated spectra were scaled such that their low energy bleaching gets equal in magnitude (the unscaled spectra are shown in Data S1).
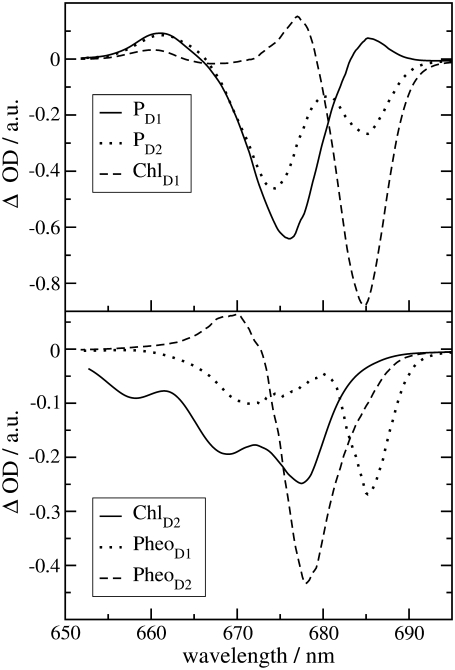
The experimental and calculated T-S spectra in the lower part of Fig. 1 show a main bleaching at ∼684 nm. We note that the position of this bleaching is red-shifted by ∼3 nm with respect to the one reported for D1-D2-cytb559 complexes (33). The experimental spectra were measured for two different states of QA, singly (squares) and doubly (solid circles) reduced, giving rise to two different widths of the main bleaching. The reason for the difference is unclear and indicates larger conformational disorder of the protein for doubly reduced QA. In the calculations, the triplet state was assumed to be localized at ChlD1, in agreement with recent mutant spectra (20), discussed below. An alternative assignment of the triplet state as 3PD1 yields a main bleaching at 675 nm (dashed curve) in strong contradiction with the experimental data. T-S spectra calculated assigning the triplet state to any other pigment in the reaction center are shown in Fig. 3 and also do not fit the experimental data of Fig. 1.
FIGURE 3.
T-S spectra at 5 K calculated assuming the triplet state to be localized on the respective reaction center pigments, as indicated in the legends.
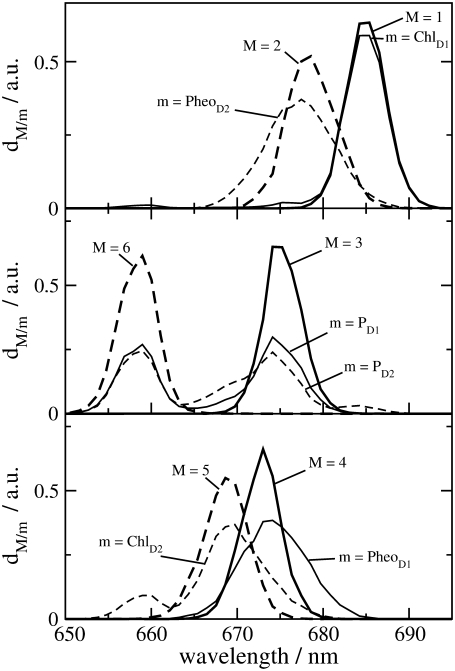
The density of exciton states
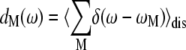 |
(1) |
is compared in Fig. 4 with the exciton states pigment distribution
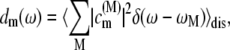 |
(2) |
where ωM is the transition frequency between the ground state and the Mth exciton state, 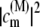 is the probability that pigment m is excited in the Mth exciton state, and 〈…〉dis denotes an average over disorder in site energies. The very similar shape of dM=1(ω) and
is the probability that pigment m is excited in the Mth exciton state, and 〈…〉dis denotes an average over disorder in site energies. The very similar shape of dM=1(ω) and 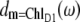 shows that the lowest exciton state M = 1 at ∼685 nm is dominated by ChlD1. The next higher exciton state M = 2 has large contributions from PheoD2 and minor contributions from other pigments (ChlD2, PD1, PD2, PheoD1). As seen in the middle part of Fig. 4 the special-pair chlorophylls PD1 and PD2 form two delocalized exciton states M = 3 at ∼675 nm and M = 6 at ∼658 nm.
shows that the lowest exciton state M = 1 at ∼685 nm is dominated by ChlD1. The next higher exciton state M = 2 has large contributions from PheoD2 and minor contributions from other pigments (ChlD2, PD1, PD2, PheoD1). As seen in the middle part of Fig. 4 the special-pair chlorophylls PD1 and PD2 form two delocalized exciton states M = 3 at ∼675 nm and M = 6 at ∼658 nm.
FIGURE 4.
Density of exciton states dM(ω) (Eq. 1) and exciton states pigment distribution dm(ω) (Eq. 2) for the six strongly coupled reaction center pigments.
One might get the impression that it is easy to detect the special-pair exciton states. However, Fig. 4 just considers the distribution of different pigments over the exciton states but not the oscillator strengths of the latter which determines the probability of an optical transition. According to our calculations, ∼80% of the oscillator strength of the special pair is in the lower dimer state at 675 nm. Further, when interpreting optical difference spectra where a pigment was converted to a different electronic state one also has to take into account that this pigment does not participate in the delocalization of exciton states anymore. This effect is seen in the T-S spectra in Fig. 3. The positions of the main bleachings obtained by assuming the triplet to be localized on PD1, PD2, and ChlD1 agree with the peak positions of the corresponding dm(ω) in Fig. 4. However, the relative intensities of the minor peaks are different. Moreover, the high energy exciton transition of the special pair seen in 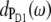 and
and 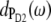 at ∼658 nm is not seen as a bleaching in the 3PD1-PD1 and 3PD2-PD2 spectra. Instead a positive band appears at ∼662 nm. This band is due to the monomer absorption band of the special-pair pigment that remains in its singlet state, while the other pigment is in the triplet state. As the monomer band is broader (due to the missing resonance energy transfer narrowing) and more intense than the high energy exciton band of the special pair, the latter is completely covered. We also note that the maximum of the monomer band is shifted by 4 nm to the blue with respect to the wavelength of 666 nm corresponding to the local site energies of PD1 and PD2. This shift is caused by the larger oscillator strengths of the low-energy exciton state which in the difference spectrum diminishes the low energy side of the monomer band. Another interesting result is that the 3PD1-PD1 and 3PD2-PD2 spectra differ at long wavelengths. Obviously there is a mixing between the excited states of the special-pair chlorophyll PD2 and ChlD1 that redistributes oscillator strength. In that sense, although qualitatively true, it is too simple to speak about the exciton states of the special pair.
at ∼658 nm is not seen as a bleaching in the 3PD1-PD1 and 3PD2-PD2 spectra. Instead a positive band appears at ∼662 nm. This band is due to the monomer absorption band of the special-pair pigment that remains in its singlet state, while the other pigment is in the triplet state. As the monomer band is broader (due to the missing resonance energy transfer narrowing) and more intense than the high energy exciton band of the special pair, the latter is completely covered. We also note that the maximum of the monomer band is shifted by 4 nm to the blue with respect to the wavelength of 666 nm corresponding to the local site energies of PD1 and PD2. This shift is caused by the larger oscillator strengths of the low-energy exciton state which in the difference spectrum diminishes the low energy side of the monomer band. Another interesting result is that the 3PD1-PD1 and 3PD2-PD2 spectra differ at long wavelengths. Obviously there is a mixing between the excited states of the special-pair chlorophyll PD2 and ChlD1 that redistributes oscillator strength. In that sense, although qualitatively true, it is too simple to speak about the exciton states of the special pair.
In the case of ChlD2 and the two pheophytins (lower part of Fig. 3), the positions of the main bleachings in the T-S spectra are shifted with respect to the peaks of the respective dm(ω) in Fig. 4. Obviously the change in excitonic couplings that occurs when one pigment goes to the triplet state becomes even more important in this case. For example, the function 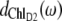 shows that ChlD2 contributes most strongly to an exciton state at 670 nm, whereas the main bleaching of the 3ChlD2-ChlD2 spectrum occurs at 677 nm. The excitonic coupling obviously redistributes oscillator strength between PheoD2 and ChlD2 in the singlet spectrum. We note that the 3PheoD2-PheoD2 closely resembles the difference spectrum measured by Germano et al. (33) for exchange of PheoD2 by a chemically modified pheophytin, the absorbance of which is blue-shifted. Due to the strong blue shift this pigment is effectively decoupled from the other pigments and the absorbance difference (except for the strongly blue-shifted monomer absorption of the exchanged pheophytin) becomes very similar to the T-S spectrum calculated here.
shows that ChlD2 contributes most strongly to an exciton state at 670 nm, whereas the main bleaching of the 3ChlD2-ChlD2 spectrum occurs at 677 nm. The excitonic coupling obviously redistributes oscillator strength between PheoD2 and ChlD2 in the singlet spectrum. We note that the 3PheoD2-PheoD2 closely resembles the difference spectrum measured by Germano et al. (33) for exchange of PheoD2 by a chemically modified pheophytin, the absorbance of which is blue-shifted. Due to the strong blue shift this pigment is effectively decoupled from the other pigments and the absorbance difference (except for the strongly blue-shifted monomer absorption of the exchanged pheophytin) becomes very similar to the T-S spectrum calculated here.
The strong bleaching at 685 nm in the 3PheoD1-PheoD1 spectrum (lower part of Fig. 3) reflects the redistribution of oscillator strength between ChlD1 and PheoD1, which in first approximation form an excitonic hetero dimer. Due to the “inline” geometry of transition dipole moments, a considerable part of the oscillator strength is distributed to the low energy exciton state. Because of the large difference in site energies of ∼200 cm−1 the energy of this state is close to the excitation energy of ChlD1, despite a considerable redistribution of oscillator strength (an effect discussed in detail in Fig. 3 of (34)). The upper exciton state is close in energy to the site energy of PheoD1, explaining the position of the high energy bleaching in the difference spectrum. Finally, we note that the difference spectrum measured by Germano et al. (33) after replacing both pheophytins can be understood by taking into account that in D1D2-cytb559 complexes the site energy of ChlD1 is blue-shifted by 4 nm. For a more detailed discussion of this and other difference spectra of D1D2-cytb559 complexes, we refer to our previous article (18).
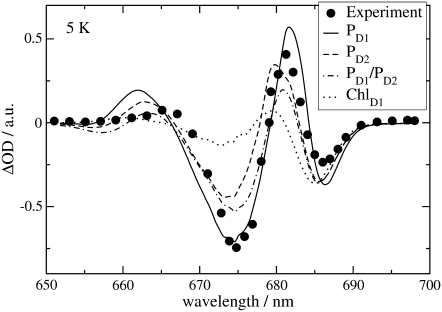
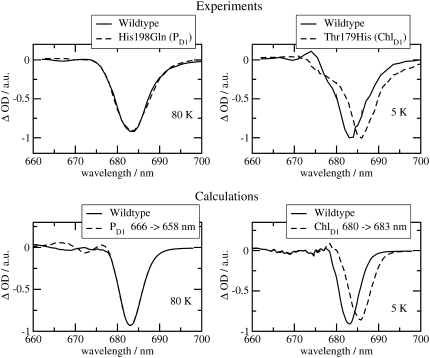
The 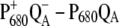 spectra of wild-type and mutants of Synechocystis sp. PCC 6803 are shown in Fig. 5. The axial ligand D1-His198 of the special-pair chlorophyll PD1 was replaced by a glutamine in the D1-His198Gln mutant, whereas the D1-Thr179, which overlies the accessory chlorophyll ChlD1, was replaced with a His or a Glu in the D1-Thr179 mutants. It has been proposed (2) that a water molecule, hydrogen-bonded to D1-Thr179, is the axial ligand of ChlD1. The experimental spectra (19,20) are shown in the upper part and the calculations in the lower part of this figure. The site energy of ChlD1 was shifted from 682 in T. elongatus to 680 nm to describe the spectral position of the low-energy bleaching in the wild-type of Synechocystis sp. PCC 6803.
spectra of wild-type and mutants of Synechocystis sp. PCC 6803 are shown in Fig. 5. The axial ligand D1-His198 of the special-pair chlorophyll PD1 was replaced by a glutamine in the D1-His198Gln mutant, whereas the D1-Thr179, which overlies the accessory chlorophyll ChlD1, was replaced with a His or a Glu in the D1-Thr179 mutants. It has been proposed (2) that a water molecule, hydrogen-bonded to D1-Thr179, is the axial ligand of ChlD1. The experimental spectra (19,20) are shown in the upper part and the calculations in the lower part of this figure. The site energy of ChlD1 was shifted from 682 in T. elongatus to 680 nm to describe the spectral position of the low-energy bleaching in the wild-type of Synechocystis sp. PCC 6803.
FIGURE 5.
Experiments (19,20) (upper part) and calculations (lower part) of wild-type and mutant 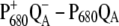 spectra of Synechocystis sp. PCC 6803 at 80 K. In the calculations of the mutant spectra, the site energy of the pigment at the mutation site was shifted with respect to its wild-type value as indicated in the legends.
spectra of Synechocystis sp. PCC 6803 at 80 K. In the calculations of the mutant spectra, the site energy of the pigment at the mutation site was shifted with respect to its wild-type value as indicated in the legends.
The shift of the low energy bleaching of the ChlD1 mutant, where Thr179 was replaced by His on the left half of Fig. 5, can be explained by shifting the site energy of ChlD1 by 3 nm to the red in the calculation of the mutant spectrum. The blue shift of the same band that is measured when Thr179 is replaced by Glu can be reproduced by assuming a 2-nm blue shift of the site energy of ChlD1 in the calculation. These mutations and site energy shifts do not effect the high energy absorbance band at ∼673 nm.
However, the latter is shifted by the mutation of the axial ligand of PD1 as shown in the right half in Fig. 5. Upon changing His198 to Gln, a blue shift of the high energy bleaching results, a shift that is explained by assuming an 8-nm blue shift of the site energy of PD1 in the calculations. An important experimental and theoretical result here is that a local change at ChlD1 changes only the low energy bleaching in the spectrum and a local change at PD1 influences mainly the high-energy bleaching.
The T-S spectra of the same wild-type and mutants are compared in Fig. 6 with the calculations. In agreement with experiment, a local change at PD1 does not influence the spectrum, whereas a red shift of the experimental and calculated bleaching occurs for the ChlD1 D1-Thr179His mutant. The same 3-nm red shift of the site energy of ChlD1 was assumed as in the calculations of the 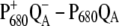 spectrum of this mutant in Fig. 5.
spectrum of this mutant in Fig. 5.
FIGURE 6.
Experiments (19,20) (upper part) and calculations (lower part) of wild-type and mutant T-S spectra of Synechocystis sp. PCC 6803. In the calculations of the mutant spectra, the site energy of the pigment at the mutation site was shifted with respect to its wild-type value as indicated in the legends.
The temperature dependence of the experimental T-S spectrum of wild-type Synechocystis sp. PCC 6803 (19) is compared in Fig. 7 with the calculations. The site energy of ChlD1 was varied with temperature in accordance with our previous analysis of D1-D2-cytb559 reaction centers (18), and the analysis of core complexes of T. elongatus below. As in our previous analysis, it was assumed that there is a thermal equilibrium of the triplet state occupation at 3ChlD1 and 3PD1. From the fit of the spectra in Fig. 7 we infer a free energy difference between the two triplet states of 11 meV, a value that is very close to the 10 meV determined for D1-D2-cytb559 complexes (18) and in between the 8 meV (35) and the 13 meV (36) determined from FTIR and EPR studies, respectively, on D1D2-cytb559 complexes.
FIGURE 7.
Experiments (19) and calculations of the temperature dependence of T-S spectra of Synechocystis sp. PCC 6803. The site energy of ChlD1 was assumed to change with temperature, corresponding to wavelengths of 680 nm at 77 K and 678 nm at 150 K.
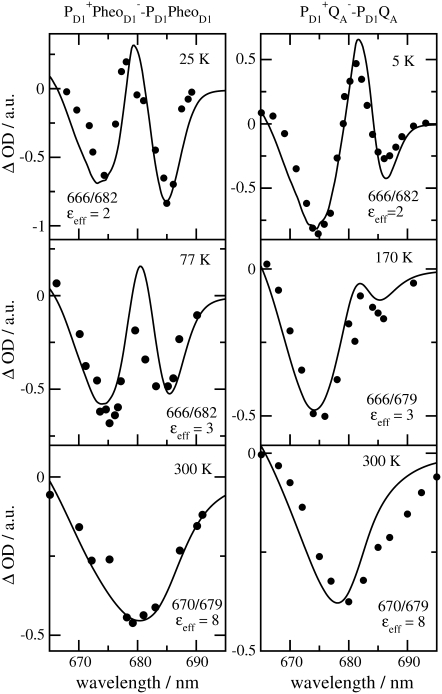
Finally we examined the temperature dependence of the 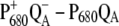 and
and 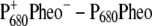 difference spectra of T. elongatus. The calculated spectra are compared in Fig. 8 with the experimental data (21). A temperature dependence was assumed for the site energy of ChlD1 and PD1 and for the dielectric constant εeff used in the calculation of electrochromic shifts. The site energy shift of ChlD1 with temperature is as described in the previous calculations on D1-D2-cytb559 reaction center spectra (18), whereas the site energy shift of PD1 is new. Due to these temperature dependencies and the increase in homogeneous broadening with increasing temperature, the double bleaching at low temperatures is transformed into a single negative peak at 680 nm at physiological temperature.
difference spectra of T. elongatus. The calculated spectra are compared in Fig. 8 with the experimental data (21). A temperature dependence was assumed for the site energy of ChlD1 and PD1 and for the dielectric constant εeff used in the calculation of electrochromic shifts. The site energy shift of ChlD1 with temperature is as described in the previous calculations on D1-D2-cytb559 reaction center spectra (18), whereas the site energy shift of PD1 is new. Due to these temperature dependencies and the increase in homogeneous broadening with increasing temperature, the double bleaching at low temperatures is transformed into a single negative peak at 680 nm at physiological temperature.
FIGURE 8.
Temperature dependence of the 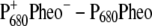 (left half) and the
(left half) and the 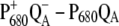 (right half) spectra of T. elongatus. The calculations (solid lines) are compared with experimental data (solid circles) (21). The temperature-dependent wavelengths corresponding to the site energies of PD1 and ChlD1 (PD1/ChlD1) and the dielectric constants (εeff) are shown as well at each temperature.
(right half) spectra of T. elongatus. The calculations (solid lines) are compared with experimental data (solid circles) (21). The temperature-dependent wavelengths corresponding to the site energies of PD1 and ChlD1 (PD1/ChlD1) and the dielectric constants (εeff) are shown as well at each temperature.
DISCUSSION
Revision of the multimer model
The calculation of optical difference spectra of WT and mutant core complexes shows that the exciton Hamiltonian that we proposed previously for D1-D2-cytb559 complexes (18) also applies to the reaction center pigments of PS-II core complexes. The only difference in the excited state energies between these two preparations involves ChlD1. Its site energy is even more red-shifted in core complexes and its inhomogeneous width is smaller than that of the other pigments. A consequence of the red shift is an even stronger localization of the lowest excited state of the reaction center on ChlD1 as seen by the almost identical functions 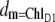 and dM=1 in Fig. 4. At low temperatures there is an ∼10 nm gap between this lowest excited state and the lowest energy exciton state of the special pair. The experiments and calculations on the various mutants in Figs. 5 and 6 provide a direct proof of this assignment. The fact that in the exciton theory just one site energy (that of the pigment with the mutated protein environment) had to be shifted to explain the mutant spectra, shows that the mutation was indeed local and did not lead to a large conformational change of the protein.
and dM=1 in Fig. 4. At low temperatures there is an ∼10 nm gap between this lowest excited state and the lowest energy exciton state of the special pair. The experiments and calculations on the various mutants in Figs. 5 and 6 provide a direct proof of this assignment. The fact that in the exciton theory just one site energy (that of the pigment with the mutated protein environment) had to be shifted to explain the mutant spectra, shows that the mutation was indeed local and did not lead to a large conformational change of the protein.
A close inspection of the experimental 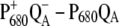 wild-type and His198Gln mutant spectra in the upper-right panel of Fig. 5 shows that changing the environment of PD1 leads, besides the dominating shift of the 673 nm band, to a slight shift of the long wavelength band at 683 nm. At first glance, the latter could be caused by a changed contribution of PD1 in the lowest exciton state, i.e., by the excitonic coupling between ChlD1 and PD1. However, in this case, we would expect also a shift of the 673 nm band, if the environment of ChlD1 is changed, a shift that is seen neither in the experiment nor in the calculations in the upper- and lower-left panels of Fig. 5, respectively. We take the absent shift and the fact that the calculations of the His198Gln mutant spectra in the lower-right panel of Fig. 5 do not reproduce the slight shift at long wavelengths seen in the experiment (upper right panel) as evidence that the site energy of ChlD1 is slightly blue-shifted in the His198Gln mutant. This result is in line with the fact that the site energy of ChlD1 is found to react more sensitively in different preparations than those of the other pigments.
wild-type and His198Gln mutant spectra in the upper-right panel of Fig. 5 shows that changing the environment of PD1 leads, besides the dominating shift of the 673 nm band, to a slight shift of the long wavelength band at 683 nm. At first glance, the latter could be caused by a changed contribution of PD1 in the lowest exciton state, i.e., by the excitonic coupling between ChlD1 and PD1. However, in this case, we would expect also a shift of the 673 nm band, if the environment of ChlD1 is changed, a shift that is seen neither in the experiment nor in the calculations in the upper- and lower-left panels of Fig. 5, respectively. We take the absent shift and the fact that the calculations of the His198Gln mutant spectra in the lower-right panel of Fig. 5 do not reproduce the slight shift at long wavelengths seen in the experiment (upper right panel) as evidence that the site energy of ChlD1 is slightly blue-shifted in the His198Gln mutant. This result is in line with the fact that the site energy of ChlD1 is found to react more sensitively in different preparations than those of the other pigments.
Whereas a replacement of Thr179 by His leads to a red shift of the site energy of ChlD1, a replacement by Glu results in a blue shift. The reason for the red shift might be the stronger dispersive interaction (37–39) between the strongly polarizable π-electrons of His and ChlD1 and the blue shift might be caused by the charge density coupling (40–43) between the ground and excited states of ChlD1 and the negative charge on Glu, assuming a standard protonation state of this residue.
Interestingly, a replacement of His by Gln in the PD1 mutant leads to a site energy shift of 8 nm to the blue, whereas replacing Thr by His in the ChlD1 mutant just results in a 3-nm red shift. The reason for the different magnitudes might be in the strong distance-dependence of the dispersive interaction and the fact that the His at PD1 is an axial ligand, whereas in the case of ChlD1 the His might still be connected via a water molecule, i.e., further away than the one at PD1.
The evidence for the excited state structure of the reaction center pigments provided by the experiments and this exciton theory is so strong, that we feel a revision of the multimer model of PS-II is necessary. The two essential changes are 1), the lowest excited state of the reaction center is localized at ChlD1; and 2), the low-energy exciton state of the special pair absorbs at 6–10 nm to shorter wavelengths (higher energy).
Except for our exciton model (18) and the recent model of Novoderezhkin (9), in all previous exciton models, mostly of the multimer type, i.e., assuming the same (mean) site energies of all pigments, there are considerable contributions from the excited states of the special-pair chlorophylls PD1 and PD2 in the lowest exciton state. Even in the multimer calculations of Prokhorenko and Holzwarth (15), who correctly predicted the primary electron donor at low temperatures from calculations and comparison with their photon echo data, the lowest excited state is dominated by PD1 and PD2, an assignment that is in contrast with this study. In an earlier article of Novoderezhkin et al. (7), different site energies were proposed for the reaction center pigments, based on fits of linear as well as nonlinear optical spectra. However, the lowest excited state still had large contributions from the special pair and therefore could not explain the experiments described here. These results demonstrate how difficult it is to find an exciton model of PS-II that has predictive power. On the one hand, nonlinear spectra contain more information about the system, but on the other hand, it is more difficult to describe these spectra as more parameters are needed than for the description of linear spectra. In that respect, mutant experiments are ideally suited to check an exciton Hamiltonian, since no new parameters are involved and just one site energy needs to be shifted, if the mutation indeed is local.
In our calculations, the spectral density J(ω) just contains the low-frequency protein modes. The inclusion of the high-frequency intramolecular modes of the pigments described in the literature (7,9) gives rise to a large reorganization shift of the exciton energies that, we believe, might not be real for the following reason: The shift depends on the delocalization of exciton states (9). By including the high-frequency modes into the spectral density that is transformed into the exciton basis, one neglects the fact that the delocalization of those transitions that involve excitation of intramolecular vibrations is much weaker than for the 0→0 transitions, due to the small Franck-Condon factors of the former. We think, a proper inclusion of intramolecular vibrations would necessitate incorporating them as separate states in the exciton Hamiltonian that is diagonalized. Since we expect mainly corrections in the high-frequency wing of the spectra, where, in addition, higher electronic excitations like Qx occur, we have neglected theses modes, for simplicity.
The assignment of the site energies in our earlier study (18) on the D1-D2-cytb559 complexes was verified by calculations of a large number of additional spectra and comparison with experimental data. In the case of core complexes, we have to rely on a few difference spectra, namely the three spectra calculated here and the 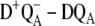 difference spectra presented elsewhere (19), where D represents the carotenoid or the peripheral Chlz on the D2-side of the reaction center. Fortunately, these difference spectra can be described at least qualitatively by the site energies determined earlier for D1-D2-cytb559 complexes (18). In the case of
difference spectra presented elsewhere (19), where D represents the carotenoid or the peripheral Chlz on the D2-side of the reaction center. Fortunately, these difference spectra can be described at least qualitatively by the site energies determined earlier for D1-D2-cytb559 complexes (18). In the case of 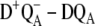 difference spectra we actually performed the calculations of the mutant spectra first, before one of us (E.S.) determined experimentally the predicted curve, proving that the low energy electrochromic band shift in the
difference spectra we actually performed the calculations of the mutant spectra first, before one of us (E.S.) determined experimentally the predicted curve, proving that the low energy electrochromic band shift in the 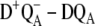 difference spectra is due to ChlD1 (20).
difference spectra is due to ChlD1 (20).
We will have to await a structural study with higher resolution to calculate the excitonic coupling within the special pair with greater precision. The value of 150 cm−1, inferred from refitting the D1-D2-cytb559 spectra, can only be understood by including a Dexter type exchange contribution, which, however, depends critically on the positions of the atoms. Applying a point dipole approximation also leads to a large excitonic coupling, but such an approximation is not valid for the small interpigment distance in this case, as shown in our TrEsp calculations (see Table 1). There is currently no direct experimental measure of the value of the excitonic coupling in the special pair. The high energy exciton component has a rather small oscillator strength and therefore is not easy to detect. Inspection of the calculated 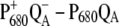 spectra in the lower part of Fig. 5 reveals a small positive band at ∼662 nm. A similar band is found in the experiment on the wild-type complexes in the upper part of this figure at 665 nm and may reflect the electrochromically shifted monomer band of PD2 that becomes visible upon oxidation of PD1. To resolve this band more clearly, experiments with polarized light on oriented samples will be performed. Direct extraction of the excitonic coupling from the relative positions of the monomer and exciton bands will still be difficult, since in a dimer of closely packed chlorophylls like PD1 and PD2, in addition to the excitonic coupling, the shift of the monomer and exciton energies by the charge density and dispersive coupling, and by mixing with charge transfer states, has to be taken into account.
spectra in the lower part of Fig. 5 reveals a small positive band at ∼662 nm. A similar band is found in the experiment on the wild-type complexes in the upper part of this figure at 665 nm and may reflect the electrochromically shifted monomer band of PD2 that becomes visible upon oxidation of PD1. To resolve this band more clearly, experiments with polarized light on oriented samples will be performed. Direct extraction of the excitonic coupling from the relative positions of the monomer and exciton bands will still be difficult, since in a dimer of closely packed chlorophylls like PD1 and PD2, in addition to the excitonic coupling, the shift of the monomer and exciton energies by the charge density and dispersive coupling, and by mixing with charge transfer states, has to be taken into account.
A higher resolution structural study might also help to identify the charge transfer states and their influence on the excited state properties. From nonconventional Stark spectra it was suggested that the low energy exciton state is mixed with a charge transfer state (44). Experimental evidence at cryogenic temperatures, indicating that charge separation occurs upon long wavelength excitation (8), could also reflect a low-lying CT state. In our calculations we find indirect evidence regarding CT states from the fact that two site energies (ChlD1 and PD1) change with temperature. This change could reflect a temperature-dependent dephasing of the quantum mechanic mixing of an exciton and a CT state (45).
Identification of functional states at physiological temperatures
We have provided independent evidence that at low temperatures the lowest excited state is localized at ChlD1 (Fig. 4), that the hole is stabilized at PD1 (Fig. 2) and that the triplet is localized at ChlD1 (bottom panel of Figs. 1 and 3). These conclusions agree with those inferred earlier from mutant spectra (19) measured at 5 K. We have recently presented evidence (18) that, if PD1 were the primary electron donor at low temperature, that there would be a much stronger temperature dependence of the primary electron transfer rate than has been detected in D1-D2-cytb559 reaction centers (46–48). As in core complexes, the site energy of ChlD1 is even more red-shifted, the mechanism of primary charge separation at low temperature remains the same: The excitation energy is funneled to ChlD1 forming the state P* = ChlD1* and charge separation leads to the primary radical pair 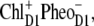 after which the hole is stabilized at PD1, where the state
after which the hole is stabilized at PD1, where the state 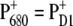 is formed.
is formed.
The situation is more complicated at physiological temperatures. The calculations of the temperature dependence of the difference spectra in Fig. 8 suggest that the identity of the state 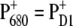 is the same at all temperatures. This finding is in agreement with pulsed EPR studies by Zech et al. (49), which determined a distance of 27.4 ± 0.3 Å between the negative charge on
is the same at all temperatures. This finding is in agreement with pulsed EPR studies by Zech et al. (49), which determined a distance of 27.4 ± 0.3 Å between the negative charge on 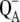 and the positive charge on
and the positive charge on 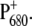 Given this distance, one cannot conclude whether the cation resides on PD1 or PD2. However, cation localization on ChlD1 or ChlD2 can be excluded as can a distribution of the cationic state over all four Chls.
Given this distance, one cannot conclude whether the cation resides on PD1 or PD2. However, cation localization on ChlD1 or ChlD2 can be excluded as can a distribution of the cationic state over all four Chls.
To describe the temperature dependence of the spectra in Fig. 8, it was necessary to assume 1), an increase of the dielectric constant εeff from about 2 to 8 as the temperature is increased from below to above 170 K; and 2), a shift of the site energies of PD1 and ChlD1 around this temperature.
The internal dielectric constant of proteins reflects, on the one hand, the possible degree of orientation of its polar side chains and its amide backbone dipoles in response to an electric field. In addition to this orientational polarization there is the polarization of electron clouds often termed ε∞ since it remains the only contribution if the frequency of the field is very high. The value ε∞ is given by the square of the refractive index. For typical organic solvents, ε∞ ≈ 2. The orientational polarization of a polar solvent is influenced by the temperature. Below the glass transition temperature at ∼200 K (50) the orientational degrees of freedom are frozen out, causing a sudden drop of the dielectric constant around this temperature (51). Such a transition is also expected in proteins (50,52–57), explaining the low value of 2–3 for εeff at low temperatures inferred in this study.
Information about conformational protein dynamics at different temperatures (55,56) was obtained from measurements and calculations on a charge recombination reaction in bacterial reaction centers, occurring in the 100-ms time range. Below the glass transition temperature, the restricted conformational motion led to a wide distribution of electron transfer rates that became much narrower above this temperature. Below 100 K, no change of the distribution was found, indicating that the conformational dynamics of the protein does not change further below 100 K. In our calculations we find a slight increase of εeff from 2 at 25 K to 3 at 77 K. This increase could reflect a thermal-activated barrier crossing in the rugged landscape of the protein, as detected by monitoring spectral diffusion in hole burning (58) and photon echo (59) experiments at cryogenic temperatures. On the other hand, using εeff = 2 in the calculation of the 77 K spectrum in Fig. 8 still describes the experiment qualitatively (as shown in the supporting information). Therefore, our evidence for an increase of εeff at <100 K is much weaker than for the εeff = 8 at 300 K. Without the latter, the room temperature spectra could not even be qualitatively described.
Whereas the free rotation of polar solvent molecules results in large values for the dielectric constant at ambient temperatures, as in liquid water (ε = 80), in a protein, the polar side chains and the amide backbone cannot rotate freely but are constrained by intramolecular forces. These constraints and the smaller density of polar groups lead to a much smaller high-temperature dielectric constant of proteins. The value εeff = 8 obtained from our calculation of the room temperature spectra is practically identical with the εeff = 7 inferred (60) from electrochromic shift calculations of chlorophylls around the secondary electron acceptor in photosystem I at room temperature. The same εeff = 8 as in this study was determined from the electric field strength measured inside an α-helix in water at 273 K (61).
The inferred temperature dependence of the site energies of ChlD1 and PD1 in Fig. 8 might reflect a mixing of exciton states with charge transfer states, as noted above. It was more straightforward to allow for a temperature dependence of the site energy than to explicitly include the CT states into the calculation of optical spectra. At present, there is no theory that can include all three aspects: a dynamic localization of excited states (45), and lifetime broadening and vibrational sidebands of exciton transitions (16). Due to the strong coupling of a CT state to the vibrations, a temperature-dependent localization of the mixed excitonic/CT state can be expected (45). A first attempt to include a CT state into the calculation of optical spectra of PS-II reaction centers was provided by Novoderezhkin et al. (7,9). In this approach, the coupling of the CT state to the vibrations was assumed to be larger by only a factor of 1.6 than the exciton-vibrational coupling of an excited state without CT character and so no dynamic localization needed to be included. However, this choice of parameters seems questionable because of the large permanent dipole moment of a CT state that should give rise to a much larger coupling to the protein vibrations of a CT state. A challenge for future theory development will be to allow for a direct calculation of the influence of CT states on the position of optical bands of oligomer complexes at different temperatures.
One important difference between low and high temperatures is that the state P* at high temperatures will be formed not only by the lowest exciton state localized at ChlD1, but the thermal energy kT is sufficient to substantially populate higher exciton states, in particular the low energy exciton state of the special pair and in principle electron transfer could start from both pigments, ChlD1 and PD1. To quantify the contributions from the different pigments to P* we assume, as in our previous model (18), that exciton relaxation between the six core pigments is fast compared to primary electron transfer and therefore that the electron transfer rate constant can be described as
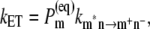 |
(3) |
where 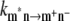 is the intrinsic rate constant for creation of the primary radical pair m+n− and
is the intrinsic rate constant for creation of the primary radical pair m+n− and 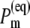 is the (quasi) equilibrium population of the local excited state of pigment m,
is the (quasi) equilibrium population of the local excited state of pigment m,
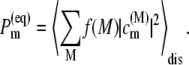 |
(4) |
Here the Boltzmann factor 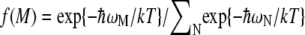 describes the thermal population of the Mth exciton state,
describes the thermal population of the Mth exciton state, 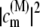 is the quantum mechanical probability to find pigment m excited in the Mth exciton state, and 〈···〉dis denotes an average over static disorder in site energies.
is the quantum mechanical probability to find pigment m excited in the Mth exciton state, and 〈···〉dis denotes an average over static disorder in site energies.
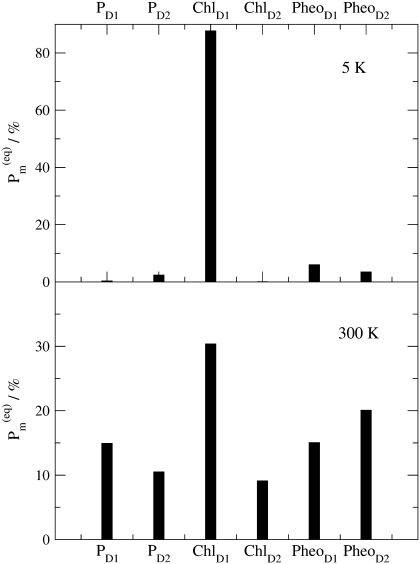
In Fig. 9 the thermal populations 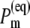 defined above are shown for two different temperatures. At 5 K practically only ChlD1 contributes to the equilibrated population of exciton states that represents the state P*. At physiological temperature there is still a 30% contribution by ChlD1, however the remaining pigments also contribute significantly. The contribution by PD1 is ∼15% and the smallest contributions of 8% is due to ChlD2.
defined above are shown for two different temperatures. At 5 K practically only ChlD1 contributes to the equilibrated population of exciton states that represents the state P*. At physiological temperature there is still a 30% contribution by ChlD1, however the remaining pigments also contribute significantly. The contribution by PD1 is ∼15% and the smallest contributions of 8% is due to ChlD2.
FIGURE 9.
Equilibrated population of local excited states 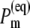 (Eq. 4) at T = 5 K (upper part) and T = 300 K (lower part).
(Eq. 4) at T = 5 K (upper part) and T = 300 K (lower part).
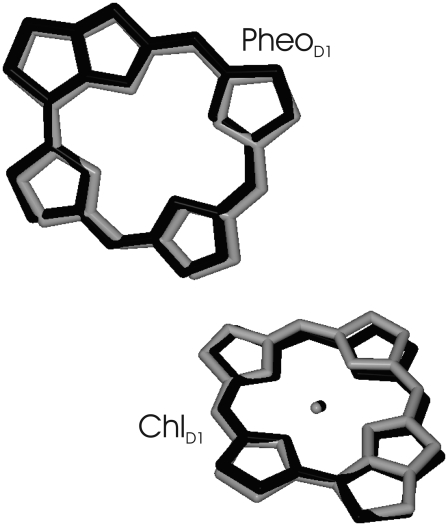
It is still an open question as to why in the bacterial reaction center the electron transfer starting at the accessory bacteriochlorophyll is one order-of-magnitude faster than the one starting at the special pair (10,11). However, from the nearly perfect overlay of ChlD1/PheoD1 in PS-II reaction centers and in the homologous bacterial reaction centers, as shown in Fig. 10, it is likely that the electron transfer coupling matrix elements in the two reaction centers are similar. Therefore it seems not unlikely, despite uncertainties of other factors like the driving force of the process, that, in PS-II, subpicosecond electron transfer can also occur starting at ChlD1. The present finding, that at room temperature the excited state is mostly localized on ChlD1, strongly suggests that this electron transfer pathway dominates in PS-II. From calculations of the time-dependent fluorescence decay of PS-II core complexes and comparison with experimental data (62), we obtained additional evidence for the presence of ultrafast primary electron transfer (63).
FIGURE 10.
Overlay of accessory (bacterio-) chlorophylls and pheophytins of the electron transfer active branch of PS-II (shaded) and the bacterial reaction center (solid). The overlay was determined from a minimization of the mean-square deviation in positions of equivalent atoms of the two molecules using the program VMD (75).
Considering that the electron hole is stabilized at PD1, it is likely that this pigment has the highest HOMO level of the reaction center pigments. Furthermore, from the blue-shifted transition energy of PD1, it follows that the LUMO of PD1 is higher than that of ChlD1. Therefore, an excited electron at ChlD1 is transferred energetically downhill only to PheoD1, which has a higher oxidation potential (64) and therefore a lower LUMO. As the accessory chlorophyll in the D2 branch, ChlD2, contributes mostly to an exciton state at ∼668 nm; even at room temperature, this excited state is only weakly populated. This asymmetry in the excited state energies of the two accessory chlorophylls might be one of the factors that leads to unidirectional electron transfer in PS-II.
FUNCTIONAL IMPLICATIONS
The particular challenge in the evolution of the oxygenic photosystems was to find a way to use water as a proton and electron source. The reduction potential of the O2/2H2O couple at pH 6 is ∼880 mV versus NHE, larger than the reduction potentials measured for chlorophyll in most solvents. A confluence of factors was therefore necessary to allow the special-pair chlorophylls and also the accessory chlorophylls to be substantially more oxidizing than the potential required for water oxidation. One of these is the protein environment (65). Another factor is the degree of delocalization of the cationic state. Whereas the hole is localized on one of the two special-pair chlorophylls in PS-II (66), most likely on PD1 according to mutant experiments at low temperatures (18) and these calculations, it is more delocalized (67) over both special-pair pigments in the bacterial reaction center, which does not have as severe constraints as in PS-II on the reduction potential of the primary donor.
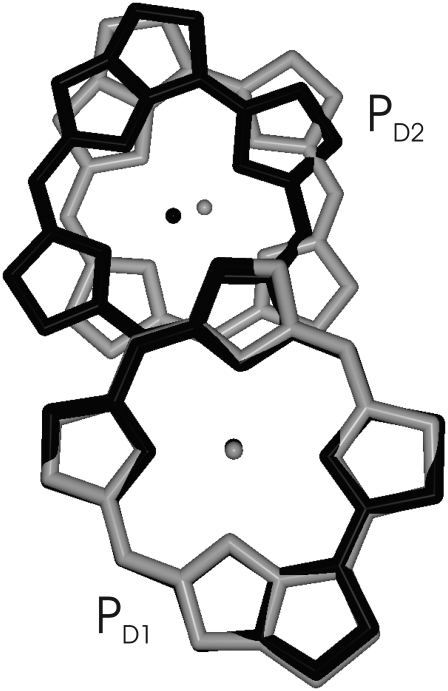
It is interesting to note that although the overall arrangement of pigments is very similar in the two reaction centers, an important difference is the mutual orientation of the two special-pair chlorophylls, as seen in Fig. 11. Whereas there is a remarkable overlay of two rings in the bacterial reaction center, this π-stacking interaction is disrupted in PS-II by an in-plane tilt of the macrocycle. It is likely that this tilt was needed to localize the hole state. As noted by Rutherford and Faller (68), the monomeric nature of the 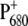 state was probably a key element in the evolution of PS-II that allowed it to reach a high enough reduction potential to drive the splitting of water. Another interesting observation is that the higher the resolution of the crystal structure data of PS-II became, the smaller the distance got, between the two special-pair pigments in the crystallographic models. It seems that it is a rotation rather than a translation that has localized the state
state was probably a key element in the evolution of PS-II that allowed it to reach a high enough reduction potential to drive the splitting of water. Another interesting observation is that the higher the resolution of the crystal structure data of PS-II became, the smaller the distance got, between the two special-pair pigments in the crystallographic models. It seems that it is a rotation rather than a translation that has localized the state 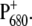
FIGURE 11.
Overlay of the special pair (bacterio-) chlorophylls of PS-II (shaded) and the bacterial reaction center (solid). The overlay was determined from a minimization of the mean-square deviation in positions of equivalent atoms of the two molecules using the same program as in Fig. 10.
The reduction potentials of the reaction center chlorophylls in PS-II are so high that the usual photoprotection mechanism, i.e., the quenching of the physiologically dangerous triplet state populations of the chlorophylls by carotenoids would not work, as the carotenoids would simply be oxidized by the chlorophylls. Consequently, no carotenoids are found within van der Waals contact of the four strongly coupled reaction center chlorophylls in PS-II. An alternative mechanism concerns the quenching of triplets by 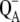 (69). As proposed by Noguchi (70) this quenching mechanism might be the reason why the triplets equilibrate between PD1 and ChlD1, simply because the triplets at ChlD1 can be quenched efficiently because of its proximity to
(69). As proposed by Noguchi (70) this quenching mechanism might be the reason why the triplets equilibrate between PD1 and ChlD1, simply because the triplets at ChlD1 can be quenched efficiently because of its proximity to 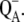 Nevertheless, the mean in vivo lifetime of a PS-II reaction center is only approximately one-half hour at high light intensity (71,72). During that time the D1-polypeptide is irreversibly damaged and is subsequently replaced by a new polypeptide. At least two different possibilities are discussed for the molecular mechanism behind the photodamage (72). One possibility is an oxidation of pigments (or parts of the protein) by the highly oxidizing
Nevertheless, the mean in vivo lifetime of a PS-II reaction center is only approximately one-half hour at high light intensity (71,72). During that time the D1-polypeptide is irreversibly damaged and is subsequently replaced by a new polypeptide. At least two different possibilities are discussed for the molecular mechanism behind the photodamage (72). One possibility is an oxidation of pigments (or parts of the protein) by the highly oxidizing 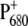 and a subsequent degradation of the unstable cationic states. Another possibility (70,72,73) is that QA becomes doubly reduced and doubly protonated and leaves its binding pocket in the protein. Now, the chlorophyll triplets can no longer be quenched by
and a subsequent degradation of the unstable cationic states. Another possibility (70,72,73) is that QA becomes doubly reduced and doubly protonated and leaves its binding pocket in the protein. Now, the chlorophyll triplets can no longer be quenched by 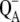 and their lifetime increases by two orders of magnitude (69). The chlorophyll triplets react with triplet oxygen to form the highly reactive singlet oxygen which damages the D1-protein. In both cases, the unidirectional electron transfer in photosystem II is of physiological relevance, because it confines triplet formation and the creation of oxidizing equivalents to the D1-branch, thereby limiting photophysical damage to this branch. An additional mechanism to prevent oxidative damage probably is the controlled hole transfer from
and their lifetime increases by two orders of magnitude (69). The chlorophyll triplets react with triplet oxygen to form the highly reactive singlet oxygen which damages the D1-protein. In both cases, the unidirectional electron transfer in photosystem II is of physiological relevance, because it confines triplet formation and the creation of oxidizing equivalents to the D1-branch, thereby limiting photophysical damage to this branch. An additional mechanism to prevent oxidative damage probably is the controlled hole transfer from 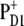 to cytb559 via CarD2 (20) and a subsequent charge recombination with reduced QB (74). In addition, based on calculations of excitation energy and primary electron transfer in PS-II core complexes, we have proposed that for closed reaction centers the rate constant for primary electron transfer slows down to an extent that a considerable part of the excitation energy remains in the antenna and the subsequently formed triplet states of the Chls are quenched there by the antenna carotenoids (63).
to cytb559 via CarD2 (20) and a subsequent charge recombination with reduced QB (74). In addition, based on calculations of excitation energy and primary electron transfer in PS-II core complexes, we have proposed that for closed reaction centers the rate constant for primary electron transfer slows down to an extent that a considerable part of the excitation energy remains in the antenna and the subsequently formed triplet states of the Chls are quenched there by the antenna carotenoids (63).
SUPPLEMENTARY MATERIAL
To view all of the supplemental files associated with this article, visit www.biophysj.org.
Acknowledgments
We thank E. M. Madjet for calculating the transition charges of pheophytin.
This work was supported by the Deutsche Forschungsgemeinschaft through Sonderforschungsbereich No. 498 (grant No. TP A6 to E.S. and No. TP A7 to T.R.). B.A.D. gratefully acknowledges financial support from the National Research Initiative of the United States Department of Agriculture Cooperative State Research, Education and Extension Service, grant No. 2003-35318-13589.
Editor: José Onuchic.
References
- 1.Ferreira, K. N., T. M. Iverson, K. Maghlaoui, J. Barber, and S. Iwata. 2004. Architecture of the photosynthetic oxygen-evolving center. Science. 303:1831–1838. [DOI] [PubMed] [Google Scholar]
- 2.Loll, B., J. Kern, W. Saenger, A. Zouni, and J. Biesiadka. 2005. Towards complete cofactor arrangement in the 3.0 Å resolution structure of photosystem II. Nature. 438:1040–1044. [DOI] [PubMed] [Google Scholar]
- 3.Renger, G., and A. R. Holzwarth. 2005. Primary electron transfer. In Photosystem II: The Light-Driven Water Plastoquinone Oxidoreductase. T. Wydrzynski and K. Satoh, editor. Springer, Dordrecht, The Netherlands.
- 4.Diner, B. A., and F. Rappaport. 2002. Structure, dynamics, and energetics of the primary photochemistry of photosystem II of oxygenic photosynthesis. Annu. Rev. Plant Biol. 53:551–580. [DOI] [PubMed] [Google Scholar]
- 5.Groot, M. L., N. P. Pawlowicz, L. J. G. W. Van Wilderen, J. Breton, I. H. M. Van Stokkum, and R. van Grondelle. 2005. Initial electron donor and acceptor in isolated photosystem II reaction centers identified with femtosecond mid-IR spectroscopy. Proc. Natl. Acad. Sci. USA. 102:13087–13092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Holzwarth, A. R., M. G. Müller, M. Reus, M. Nowaczyk, J. Sander, and M. Rögner. 2006. Kinetics and mechanism of electron transfer in intact photosystem II and in the isolated reaction center: pheophytin is the primary electron donor. Proc. Natl. Acad. Sci. USA. 103:6895–6900. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Novoderezhkin, V. I., E. G. Andrizhiyewskaya, J. P. Dekker, and R. Van Grondelle. 2005. Pathways and timescales of primary charge separation in the photosystem II reaction center as revealed by a simultaneous fit of time-resolved fluorescence and transient absorption. Biophys. J. 89:1464–1481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Krausz, E., J. L. Hughes, P. Smith, R. Pace, and S. P. Årsköld. 2005. Oxygen-evolving photosystem II core complexes: a new paradigm based on the spectral identification of the charge separating state, the primary acceptor and assignment of low-temperature fluorescence. Photochem. Photobiol. Sci. 4:744–753. [DOI] [PubMed] [Google Scholar]
- 9.Novoderezhkin, V. I., J. P. Dekker, and R. Van Grondelle. 2007. Mixing of exciton and charge-transfer states in photosystem II reaction centers: modeling of stark spectra with modified Redfield theory. Biophys. J. 93:1293–1311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Van Brederode, M. E., M. R. Jones, F. Van Mourik, I. H. M. Van Stokkum, and R. Van Grondelle. 1997. A new pathway for transmembrane electron transfer in photosynthetic reaction centers of Rhodobacter sphaeroides not involving the excited special pair. Biochemistry. 36:6855–6861. [DOI] [PubMed] [Google Scholar]
- 11.Van Brederode, M. E., F. Van Mourik, I. H. M. Van Stokkum, M. R. Jones, and R. Van Grondelle. 1999. Multiple pathways for ultrafast transduction of light energy in the photosynthetic reaction center of Rhodobacter sphaeroides. Proc. Natl. Acad. Sci. USA. 96:2054–2059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Van Brederode, M. E., and R. Van Grondelle. 1999. New and unexpected routes for ultrafast electron transfer in photosynthetic reaction centers. FEBS Lett. 455:1–7. [DOI] [PubMed] [Google Scholar]
- 13.Durrant, J. R., D. R. Klug, S. L. S. Kwa, R. van Grondelle, G. Porter, and J. P. Dekker. 1995. A multimer model for P680, the primary electron donor of photosystem II. Proc. Natl. Acad. Sci. USA. 92:4798–4802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Leegwater, J. A., J. R. Durrant, and D. R. Klug. 1998. Exciton equilibration induced by phonons: theory and application to PS II. J. Phys. Chem. B. 102:5378–5386. [Google Scholar]
- 15.Prokhorenko, V., and A. R. Holzwarth. 2000. Primary processes and structure of the photosystem II reaction center: a photon echo study. J. Phys. Chem. B. 104:11563–11578. [Google Scholar]
- 16.Renger, T., and R. A. Marcus. 2002. On the relation of protein dynamics and exciton relaxation in pigment-protein complexes: an estimation of the spectral density and a theory for the calculation of optical spectra. J. Chem. Phys. 116:9997–10019. [Google Scholar]
- 17.Barter, L. M. C., J. R. Durrant, and D. R. Klug. 2003. A quantitative structure-function relationship for the photosystem II reaction center: supermolecular behavior in natural photosynthesis. Proc. Natl. Acad. Sci. USA. 100:946–951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Raszewski, G., W. Saenger, and T. Renger. 2005. Theory of optical spectra of photosystem II reaction centers: location of the triplet state and the identity of the primary electron donor. Biophys. J. 88:986–998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Diner, B. A., E. Schlodder, P. J. Nixon, W. J. Coleman, F. Rappaport, J. Laverge, W. F. J. Vermaas, and D. A. Chisholm. 2001. Site-directed mutations at D1-His198 and D2-His197 of photosystem II in Synechocystis PCC 6803: sites of primary charge separation and cation and triplet stabilization. Biochemistry. 40:9265–9281. [DOI] [PubMed] [Google Scholar]
- 20.Schlodder, E., T. Renger, G. Raszewski, W. J. Coleman, P. J. Nixon, R. O. Cohen, and B. A. Diner. 2008. Site-directed mutations at D1-Thr179 of photosystem II in Synechocystis sp. PCC 6803 modify the spectroscopic properties of the accessory chlorophyll in the D1-branch of the reaction center. Biochemistry. 47:3143–3154. [DOI] [PubMed] [Google Scholar]
- 21.Hillmann, B., K. Brettel, F. van Mieghem, A. Kamlowski, W. A. Rutherford, and E. Schlodder. 1995. Charge recombination in photosystem II. 2. Transient absorbance difference spectra and their temperature dependence. Biochemistry. 34:4814–4827. [DOI] [PubMed] [Google Scholar]
- 22.Doering, G., H. H. Stiel, and H. T. Witt. 1967. A second chlorophyll reaction in the electron chain of photosynthesis-registration by the repetitive excitation technique. Z. Naturforsch. 22:639–644. [DOI] [PubMed] [Google Scholar]
- 23.Madjet, M. E., A. Abdurahman, and T. Renger. 2006. Intermolecular Coulomb couplings from ab initio electrostatic potentials: application to optical transitions of strongly coupled pigments in photosynthetic antennae and reaction centers. J. Phys. Chem. B. 110:17268–17281. [DOI] [PubMed] [Google Scholar]
- 24.Krüger, B. P., G. D. Scholes, and G. R. Fleming. 2005. Calculation of couplings and energy transfer pathways between pigments of LH2 by the ab-initio transition density cube method. J. Phys. Chem. B. 4:744–753. [Google Scholar]
- 25.Chang, J. C. 1977. Monopole effects on electronic excitation interaction between large molecules. I. Application to energy transfer in chlorophylls. J. Chem. Phys. 67:3901–3909. [Google Scholar]
- 26.Knox, R. S., and B. Q. Spring. 2003. Dipole strengths in the chlorophylls. Photochem. Photobiol. 77:497–501. [DOI] [PubMed] [Google Scholar]
- 27.Houssier, C., and K. Sauer. 1970. Circular dichroism and magnetic circular dichroism of the chlorophyll and protochlorophyll pigments. J. Am. Chem. Soc. 92:779–791. [Google Scholar]
- 28.Reference deleted in proof.
- 29.Moss, G. 1988. Nomenclature of tetrapyrroles, recommendations 1986. Eur. J. Biochem. 178:277–328. [DOI] [PubMed] [Google Scholar]
- 30.Krawczyk, S. 1991. Electrochromism of chlorophyll-a monomer and special pair dimer. Biochim. Biophys. Acta. 1056:64–70. [Google Scholar]
- 31.Shkuropatov, A. Y., R. A. Khatypov, T. S. Volshchukova, V. A. Shkuropatova, T. G. Owens, and V. A. Shuvalov. 1997. Spectral and photochemical properties of borohydride-treated D1–D2-cytochrome b-559 complex of photosystem II. FEBS Lett. 420:171–174. [DOI] [PubMed] [Google Scholar]
- 32.Shkuropatov, A. Y., R. A. Khatypov, V. A. Shkuropatova, M. G. Zvereva, T. G. Owens, and V. A. Shuvalov. 1999. Reaction centers of photosystem II with a chemically modified pigment composition: exchange of pheophytins with 131-deoxo-131-hydroxy-pheophytin a. FEBS Lett. 450:163–167. [DOI] [PubMed] [Google Scholar]
- 33.Germano, M., A. Y. Shkuropatov, H. Permentier, R. de Wijn, A. J. Hoff, V. A. Shuvalov, and H. J. van Gorkom. 2001. Pigment organization and their interactions in reaction centers of photosystem II: optical spectroscopy at 6K of reaction centers with modified pheophytin composition. Biochemistry. 40:11472–11482. [DOI] [PubMed] [Google Scholar]
- 34.Renger, T., J. Voigt, V. May, and O. Kühn. 1996. Dissipative exciton motion in a chlorophyll a/b dimer of the light-harvesting complex of photosystem II: simulation of pump-probe spectra. J. Phys. Chem. 100:15654–15662. [Google Scholar]
- 35.Noguchi, T., Y. Inoue, and K. Satoh. 1993. FT-IR studies on the triplet state of P680 in the photosystem II reaction center: triplet equilibrium within a chlorophyll dimer. Biochemistry. 32:7186–7195. [DOI] [PubMed] [Google Scholar]
- 36.Kamlowski, A., L. Frankemoller, A. van der Est, D. Stehlik, and A. R. Holzwarth. 1996. Evidence for delocalization of the triplet state 3P680 in the D1D2cytb559 complex of photosystem II. Ber. Bunsenges. Phys. Chem. 100:2045–2051. [Google Scholar]
- 37.Heinz, H., U. W. Suter, and E. Leontidis. 2001. Simple and accurate computations of solvatochromic shifts in π→π* transitions of aromatic chromophores. J. Am. Chem. Soc. 123:11229–11236. [DOI] [PubMed] [Google Scholar]
- 38.Bayliss, N. S. 1950. The effect of the electrostatic polarization of the solvent on electronic absorption spectra in solution. J. Chem. Phys. 18:292–296. [Google Scholar]
- 39.Longuet-Higgens, H. C., and J. A. Pople. 1957. Electronic spectral shifts of nonpolar molecules in nonpolar solvents. J. Chem. Phys. 27:192–194. [Google Scholar]
- 40.Eccles, J., and B. Honig. 1983. Charged amino-acids as spectroscopic determinants for chlorophyll in vivo. Proc. Natl. Acad. Sci. USA. 80:4959–4962. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Adolphs, J., and T. Renger. 2006. How proteins trigger excitation energy transfer in the FMO complex of green sulfur bacteria. Biophys. J. 91:2778–2797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Müh, F., M. E. Madjet, J. Adolphs, A. Abdurahman, B. Rabenstein, H. Ishikita, E.-W. Knapp, and T. Renger. 2007. Alpha-helices direct excitation energy flow in the Fenna-Matthews-Olson protein. Proc. Natl. Acad. Sci. USA. 104:16862–16867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Adolphs, J., F. Müh, M. E. Madjet, and T. Renger. 2008. Calculation of pigment transition energies in the FMO protein: from simplicity to complexity and back. Photosynth. Res. 95:197–209. [DOI] [PubMed] [Google Scholar]
- 44.Frese, R. N., M. Germano, F. L. de Weerd, I. H. M. van Stokkum, A. Y. Shuropatov, V. A. Shuvalov, H. J. van Gorkom, R. van Grondelle, and J. P. Dekker. 2003. Electric field effects on the chlorophylls, pheophytins, and β-carotenes in the reaction center of photosystem II. Biochemistry. 42:9205–9213. [DOI] [PubMed] [Google Scholar]
- 45.Renger, T. 2004. Theory of optical spectra involving charge transfer states: dynamic localization predicts a temperature dependent optical band shift. Phys. Rev. Lett. 93:188101(1)–188101(4). [DOI] [PubMed] [Google Scholar]
- 46.Greenfield, S. R., M. Seibert, Govindjee, and M. R. Wasielewski. 1997. Direct measurements of the effective rate constant for primary charge separation in isolated photosystem II reaction centers. J. Phys. Chem. B. 101:2251–2255. [Google Scholar]
- 47.Greenfield, S. R., M. Seibert, Govindjee, and M. R. Wasielewski. 1999. Time-resolved absorption changes of the pheophytin Qx band in isolated photosystem II reaction centers at 7 K: energy transfer and charge separation. J. Phys. Chem. B. 103:8364–8374. [Google Scholar]
- 48.Groot, M. L., F. van Mourik, C. Eickelhoff, I. H. M. van Stokkum, J. P. Dekker, and R. van Grondelle. 1997. Charge separation in the reaction center of photosystem II studied as a function of temperature. Proc. Natl. Acad. Sci. USA. 94:4389–4394. [DOI] [PMC free article] [PubMed] [Google Scholar]
-
49.Zech, S. G., J. Kurreck, H.-J. Eckert, G. Renger, W. Lubitz, and R. Bittl. 1980. Pulsed EPR measurements of the distance between
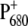 and
and 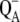 in photosystem II. Biophys. Chem. 12:83–91.17000146 [Google Scholar]
in photosystem II. Biophys. Chem. 12:83–91.17000146 [Google Scholar] - 50.Nienhaus, G. U., H. Frauenfelder, and F. Parak. 1991. Structural fluctuations in glass-forming liquids: Mössbauer spectroscopy on iron in glycerol. Phys. Rev. B. 43:3345–3350. [DOI] [PubMed] [Google Scholar]
- 51.Yu, I. S. 1993. Electrodeless measurement of RF dielectric constant and loss. Meas. Sci. Technol. 4:344–348. [Google Scholar]
- 52.Parak, F., E. W. Knapp, and D. Kucheida. 1982. Protein dynamics: Mössbauer spectroscopy on deoxymyoglobin crystals. J. Mol. Biol. 161:177–194. [DOI] [PubMed] [Google Scholar]
- 53.Smith, J., K. Kuczera, and M. Karplus. 1990. Dynamics of myoglobin: Comparison of simulation results with neutron scattering spectra. Proc. Natl. Acad. Sci. USA. 87:1601–1605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Rasmussen, B. F., A. M. Stock, D. Ringe, and G. A. Petsko. 1992. Crystalline ribonuclease A loses function below the dynamical transition at 220 K. Nature. 357:423–424. [DOI] [PubMed] [Google Scholar]
- 55.McMahon, B. H., J. D. Müller, C. A. Wraight, and G. U. Nienhaus. 1998. Electron transfer and protein dynamics in the photosynthetic reaction center. Biophys. J. 74:2567–2587. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Kriegl, J. M., and G. U. Nienhaus. 2003. Structural, dynamic, and energetic aspects of long-range electron transfer in photosynthetic reaction centers. Proc. Natl. Acad. Sci. USA. 101:123–128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Fenimore, P. W., H. Frauenfelder, B. H. McMahon, and R. D. Young. 2004. Bulk-solvent and hydration-shell fluctuations, similar to α- and β-fluctuations in glasses, control protein motions and functions. Proc. Natl. Acad. Sci. USA. 101:14408–14413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Zollfrank, J., J. Friedrich, J. Vanderkooi, and J. Fidy. 1991. Conformational relaxation of a low-temperature protein as probed by photochemical hole burning. Biophys. J. 59:305–312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Leeson, D. T., and D. A. Wiersma. 1995. Real time observation of low-temperature protein motions. Phys. Rev. Lett. 74:2138–2141. [DOI] [PubMed] [Google Scholar]
- 60.Dashdorj, N., W. Xu, P. Martinsson, P. R. Chitnis, and S. Savikhin. 2004. Electrochromic shift of chlorophyll absorption in photosystem I from Synechocystis sp. PCC 6803: a probe of optical and dielectric properties around the secondary electron acceptor. Biophys. J. 86:3121–3130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Lockhart, D. J., and P. S. Kim. 1992. Internal Stark effect measurement of the electric field at the amino terminus of an α-helix. Science. 257:947–951. [DOI] [PubMed] [Google Scholar]
- 62.Miloslavina, Y., M. Szczepaniak, M. G. Müller, J. Sander, M. Nowaczyk, M. Rögner, and A. R. Holzwarth. 2006. Charge separation kinetics in intact photosystem II core particles is trap-limited. A picosecond fluorescence study. Biochemistry. 45:2436–2442. [DOI] [PubMed] [Google Scholar]
- 63.Raszewski, G., and T. Renger. 2008. Light-harvesting in photosystem II core complexes is limited by the transfer to the trap: can the core complex turn into a photoprotective mode? J. Am. Chem. Soc. 130:4431–4446. [DOI] [PubMed] [Google Scholar]
- 64.Watanabe, T., and M. Kobayashi. 1991. Electrochemistry of Chlorophylls in Chlorophylls. H. Scheer, editor. CRC Press, Boca Raton, FL.
- 65.Ishikita, H., W. Saenger, J. Biesiadka, B. Loll, and E.-W. Knapp. 2006. How photosynthetic reaction centers control oxidation power in chlorophyll pairs P680, P700, and P870. Proc. Natl. Acad. Sci. USA. 103:9855–9860. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Rigby, S. E. J., J. H. A. Nugent, and P. J. O'Malley. 1994. ENDOR and special triple resonance studies of chlorophyll cation radicals in photosystem 2. Biochemistry. 33:10043–10050. [DOI] [PubMed] [Google Scholar]
- 67.Müh, F., F. Lendzian, R. Mason, J. C. Williams, J. P. Alenn, and W. Lubitz. 1985. Pigment-protein interactions in bacterial reaction centers and their influence on oxidation potential and spin density distribution of the primary donor. J. Phys. Chem. B. 106:3226–3236. [Google Scholar]
- 68.Rutherford, A. W., and P. Faller. 2002. Photosystem II: evolutionary perspectives. Philos. Trans. R. Soc. Lond. B Biol. Sci. 358:245–253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Van Mieghem, F., K. Brettel, B. Hillmann, A. Kamlowski, A. W. Rutherford, and E. Schlodder. 1995. Charge recombination reactions in photosystem II. 1. Yields, recombination pathways, and kinetics of the primary pair. Biochemistry. 34:4789–4813. [DOI] [PubMed] [Google Scholar]
- 70.Noguchi, T. 2002. Dual role of triplet localization on the accessory chlorophyll in the photosystem II reaction center: photoprotection and photodamage of the D1 protein. Plant Cell Physiol. 43:1112–1116. [DOI] [PubMed] [Google Scholar]
- 71.Kim, J. H., J. A. Nemson, and A. Melis. 1993. Photosystem II reaction center damage and repair in Dunaliella salina (green alga). Plant Physiol. 103:181–189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Barber, J. 1994. Molecular basis of the vulnerability of photosystem II to damage by light. Aust. J. Plant Physiol. 22:201–208. [Google Scholar]
- 73.Vass, I., S. Styring, T. Hundal, A. Koivuniemi, E.-M. Aro, and B. Andersson. 1991. Reversible and irreversible intermediates during photoinhibition of photosystem II: stable reduced QA promote chlorophyll triplet formation. Proc. Natl. Acad. Sci. USA. 89:1408–1412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Buser, C. A., B. A. Diner, and G. W. Brudvig. 1992. Photooxidation of cytochrome b559 in oxygen-evolving photosystem II. Biochemistry. 31:11449–11459. [DOI] [PubMed] [Google Scholar]
- 75.Humphrey, W. W., A. Dalke, and K. Schulten. 1996. VMD—visual molecular dynamics. J. Molec. Graphics. 14:1–33. [DOI] [PubMed] [Google Scholar]