Cortical Mechanisms of Smooth Eye Movements Revealed by Dynamic Covariations of Neural and Behavioral Responses

Abstract

SUMMARY

Neural activity in the frontal eye fields controls smooth pursuit eye movements, but the relationship between single neuron responses, cortical population responses, and eye movements is not well understood. We describe an approach to dynamically link trial-to-trial fluctuations in neural responses to parallel variations in pursuit and demonstrate that individual neurons predict eye velocity fluctuations at particular moments during the course of behavior, while the population of neurons collectively tiles the entire duration of the movement. The analysis also reveals the strength of correlations in the eye movement predictions derived from pairs of simultaneously recorded neurons and suggests a simple model of cortical processing. These findings constrain the primate cortical code for movement, suggesting that either a few neurons are sufficient to drive pursuit at any given time or that many neurons operate collectively at each moment with remarkably little variation added to motor command signals downstream from the cortex.

INTRODUCTION

One central mystery in systems neuroscience is how a population of cortical neurons collectively enables dynamic behavior. Smooth pursuit eye movement is a dynamic oculomotor behavior engaged when primates attempt to keep their fovea pointed at a target that is moving in space (Krauzlis, 2004). The appropriate cortical population for pursuit behavior is a group of neurons in the pursuit region of the frontal eye fields (FEF_SEM) of the macaque monkey. These neurons respond preferentially during smooth tracking in a given direction (Gottlieb et al., 1994; Tanaka and Lisberger, 2002b). Electrical microstimulation of the FEF_SEM both drives smooth eye movements and increases the gain of the eyes' response to target motion (Gottlieb et al., 1993; MacAvoy et al., 1991; Tanaka and Lisberger, 2001, 2002a, 2002b). The robustness of pursuit eye movements and their strong link to neural activity in the FEF_SEM make this an excellent area in which to test hypotheses about how the structure of a cortical population response relates to real-time dynamic behavior.

The inherent variability of neural activity might limit the behavioral impact of individual neurons. All cortical neurons, including those thought to drive pursuit, respond differently with each presentation of a stimulus and subsequent movement (Tolhurst et al., 1983; Shadlen and Newsome, 1998). Measurements of large ensembles of cortical motor neurons during continuous behavior suggest that neural variation is so potent that movement is only possible by pooling large numbers of neurons (Carmena et al., 2005; Lee et al., 1998; Maynard et al., 1999; Paninski et al., 2004a). Crucially, each attempt to pursue a moving target is also unique, suggesting that some aspects of neural variation may reflect behavioral variation. Recent work has successfully linked preparatory cortical dynamics to motor variation (Churchland et al., 2006a, 2006b; Riehle and Requin, 1993). The present paper elucidates an impressive link between variation in pursuit behavior and the concurrent variation in single neurons in the FEF_SEM.

A link between neural and behavioral variation might arise under one of two population architectures, for fundamentally different reasons. If a population is quite small, or “sparse,” then each individual neuron makes a measurable contribution to behavior; such architecture has been proposed in motor regions of the avian song system (Hahnloser et al., 2002). Alternatively, if the active population is quite large, then only signals that are common across neurons are likely to propagate; such a scheme has been proposed to underlie the representation of motion direction in area MT (Shadlen et al., 1996). Here, we combine our measurements of the trial-by-trial covariation of neural and behavioral responses with measurement of the degree to which variation is shared across pairs of concurrently active neurons in the FEF_SEM, enabling us to constrain the architecture of the population underlying movement variation.

To understand the relationship between behavioral variation and the activity of single neurons, we used linear systems analysis to derive a filter that represents the transformation between deviations from the “average” spiking activity of single neurons in the FEF_SEM and simultaneous deviations from the mean eye velocity (Halliday et al., 1995; Paninski et al., 2004b). We found that the trial-by-trial variation in responses of single cortical neurons in the behaving macaque can precisely encode behavioral dynamics in single trials. Each neuron can predict the evoked eye movement over a short temporal interval, and different neurons tile the entire duration of eye movement. We also found small but significant correlations between the trial-by-trial predictions of eye velocity for pairs of simultaneously recorded neurons, implying some common drive for behavior. Finally, we used a computational model of signal pooling to demonstrate that the combination of neuron-behavior and neuron-neuron correlations in our data could result from decoding a tiny neural population with a reasonable level of variation added downstream, or from a larger neural population with remarkably little variation added downstream. Taken together, our analysis of a cortical population during behavior challenges traditional understandings of the oculomotor circuit and establishes rigorous criteria for exploring circuit architecture.

RESULTS

Neural and Behavioral Variation Expressed as Residuals

To elicit a set of highly stereotyped behaviors, we trained two male monkeys to fixate on a target directly in front of them and then to track the target when it was displaced a short distance to one side and moved in the opposite direction at constant velocity across the original position of fixation. This stimulus induces smooth acceleration of the eyes ∼100 ms after target motion begins, followed by sustained smooth pursuit near the velocity of the target. Though the eye movement response to step-ramp target motion is quite stereotyped, animals show considerable variation in the latency to move, the magnitude of acceleration, and the final tracking velocity (Figure 1A); however, each motor response is unique.

Figure 1. A Typical Example of Neural and Behavioral Variation.

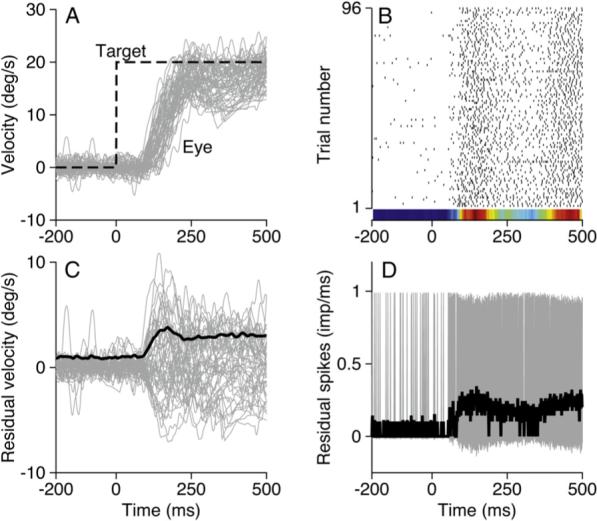
(A) The gray area shows superimposed eye movements in response to 95 presentations of identical target motion. The dashed black line indicates target velocity as a function of time.

(B) Raster showing the responses of a single neuron during the eye movements shown in (A); each black tick indicates one spike. The peristimulus time histogram is plotted as a colored strip below the rasters; red and blue correspond to the peak and nadir of activity.

(C) Gray area and black trace show the residuals of eye velocity derived from the data in (A) and their standard deviation as a function of time.

(D) The gray area and black trace show the residual spikes as a function of time and their standard deviation.

Single-neuron activity recorded in the FEF_SEM during repeated responses to the same target motion likewise shows a stereotyped profile with subtle trial-to-trial variation. On every trial in the raster of Figure 1B, the neuron was relatively silent before the eyes began to move and was generally active during tracking. For this example neuron, activity was most vigorous in two intervals, one at the beginning of the movement, and one toward the end of the illustrated interval. Even in the face of this consistency, there is considerable variation in the precise number and timing of spikes on individual trials. The variation appears to be random in the sense that the raster does not suggest any consistent drift in the neural response across the duration of the experiment (from bottom to top of the raster). As a result, we are confident that we can consider the response to be stationary across the 30 min required to collect 95 repetitions of this and seven other target motions.

To examine behavioral and neural variation in more detail, we plotted the residuals of eye movement and firing rate, defined as the difference between the response on each individual trial and the mean across trials. The residuals of eye velocity (Figure 1C, gray traces) reach maxima of about ± 5°/s, about twice the magnitude of the standard deviation of the original traces (black trace) and considerably smaller than the 15−20°/s of eye velocity in the original traces. Inspection of Figure 1C and more detailed quantitative analysis confirm that the residuals form a continuous distribution that is fairly uniform across the part of the trial that contains smooth tracking. While some of the variation no doubt arises from the alignment of the trials on the onset of target motion, all of our findings remain when we realign the trials to minimize this variation. Similarly, all our findings obtain when we perform our analysis on the eye position trace rather than on eye velocity records (data not shown).

We obtained an analogous representation of the variation in firing rate by starting with a binary representation of each trial. In each 1 ms wide bin, the neural activity took on a value of one or zero depending on whether or not a spike occurred in that bin. To compute the residuals of firing rate, we subtracted the average activity across trials (the peristimulus time histogram) from the binary representations of the neural activity on each trial. When the residuals from all 95 trials are superimposed (Figure 1D), the spikes from individual trials cannot be resolved, but it is possible to see important trends. On each individual trial, there is a low probability in any 1 ms bin that a spike will have occurred. When a spike is present, it takes the gray traces up to a value of one minus the mean across trials. In most bins, however, a spike will not have occurred, so that the value of the residual is the inverse of the mean firing rate (−〉fr〉). At higher resolution (data not shown), it becomes clear that the top and botolution tom of the gray region ride, as expected, along 1 − 〉fr〉 and −〉fr〉. This and other analyses were done with a bin size of 1 ms. Altering the bin size did not change the nature of our results (data not shown).

Figure 1 illustrates that there is a reasonable degree of trial-by-trial variation in both smooth eye movements and neural activity when the monkey tracks the same target motion repeatedly. The heterogeneity provides a substrate for asking whether there is a relationship at the level of individual trials between neural and behavioral variation.

Correlations between Neural and Behavioral Variation

Figure 2A shows a description of the “neuron-behavior correlation,” defined as the trial-by-trial correlation between the residual firing rate and the residual eye velocity (Gerstein and Perkel, 1972; Vaadia et al., 1995). In this correlation map, the color of each pixel represents the value of Pearson's correlation coefficient r(e(t₁), ρ(t₂)) where e(t₁) is the set of residuals of eye velocity across all trials, ρ(t₂) is the set of residuals of firing rate across across all trials, and t₁ and t₂ represent the times within each trial along the y and x axes. To make the trends in the data more readily apparent, we've smoothed the residual spike train with a Gaussian function (σ = 20 ms).

Figure 2. The Covariation between Spikes and Eye Movements for an Example Neuron.

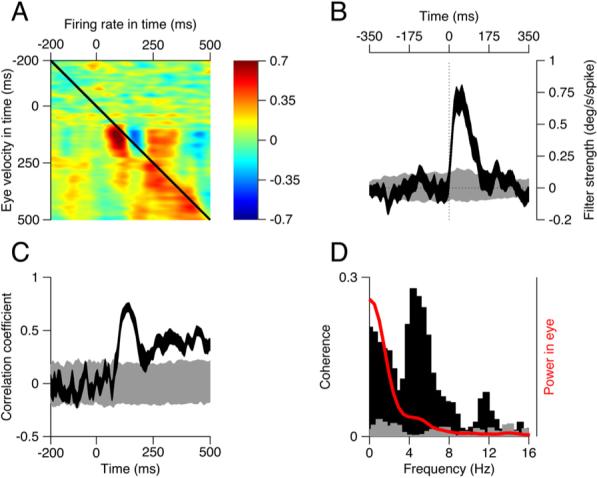
(A) The neural-behavior correlations as a function of time. Each pixel shows the correlation coefficient between the eye velocity and the firing rate at times given by the position of the x and y axes.

(B) The black trace shows the filter that describes the relationship between residual eye velocity and spikes as a function of time elapsed from a spike. Negative and positive values of time correspond to changes in eye velocity that precede or follow the spike. The gray trace shows the corresponding filter derived from shuffled trials. Filters are based on 40% of the trials.

(C) The black and gray traces plot the correlation coefficient between the actual and predicted residuals as a function of time, for the filters obtained from the actual and shuffled data, respectively. Correlations are based on the 60% of the data not used to generate the filter.

(D) The black and gray histograms plot the coherence of the normal and shuffled filters in (B) as a function of frequency. The red curve shows the normalized power in the residual eye velocity. The width of each ribbon shows the standard deviation derived from 150 draws from the data.

The upper-left corner of Figure 2A represents the period of fixation before the target starts to move (cf. Figure 1A) and is mottled green and blue, corresponding to the limited variation in both the eyes' velocity and the neural response. During the initiation of pursuit (t = 100−200 ms), there is a strong positive correlation between the residual firing rate and the residual eye movement 10−20 ms later. The correlation appears as the red peak with a dark core just below the black diagonal line. The correlation map also contains a wide region of positive correlations at later times in the response and a blue strip indicating strong negative correlation just to the right of the strongest positive correlation. The hotspots in the correlation map of Figure 2A suggest that the neuron's response across trials does covary with the animal's behavior.

A better analysis of whether there is a trial-by-trial relationship between the variation of neural responses and eye movements starts by deriving a relationship between residual spiking and residual movement. We now outline a linear systems approach that models the eye velocity residuals on each trial as a linear filter of the spiking residuals. This approach makes few assumptions about what the neuron encodes and can capture relationships between spiking residuals and any linear combination of the parameters of movement residuals. We will argue in the Discussion and Supplemental Data that, similar to filters derived from reverse correlation in sensory systems, the filter derived here provides a linear approximation of “what the neuron encodes” that can be extrapolated beyond residuals to the complete behavior. The use of residuals restricts the analysis to a small range of eye movements, allowing us to approximate the nonlinear relationship between spiking and movement.

The filter in Figure 2B (black curve) was derived by cross-correlating the residuals in the eye velocity with the residuals in the spike train (Experimental Procedures) for the example neuron; it is related to the average value along the diagonals of Figure 2A (Brenner et al., 2000). The filter shows the time course of the variation in eye velocity that is correlated with the occurrence of one “extra” spike above the mean in our example neuron. The shape of the filter suggests that, following each extra spike, the eye increases its velocity over a duration of ∼130 ms, with a peak response of ∼0.75°/s The time where the filter peaks, 57 ms after the extra spike, represents the time, probabilistically speaking, when the influence of an extra spike will be felt most strongly. The filter was corrected for the first-order correlations in the spike train by dividing the filter by the power spectrum of the spike train in the frequency domain (Experimental Procedures); correcting for correlations in the eye movement yielded a similar filter, reflected about the zero-lag point. The actual filter (black curve) is clearly different from a filter derived from the same data after the trial order had been shuffled (gray curve). Shuffling controls for correlations that might arise from the general pattern of activity across trials (Brody, 1999).

The filter in Figure 2B allows us to assess the magnitude and statistical significance of the relationship between neural and behavioral variation and provides a model of how an additional spike in this cell influences the behavior. Next, to determine what percent of the behavioral variation can be accounted for by this neuron's firing at each moment in the trial, we used the filter to predict the time course of the residual eye velocity for each test trial. We then computed the trial-by-trial correlation between actual and predicted residual eye velocity as a function of time (Figure 2C, black ribbon). Here, the black ribbon is visible only when the correlations were statistically different (p < 0.0002) from the analysis based on shuffled trials (gray ribbon). For this cell, the correlations were small and mostly nonsignificant before the onset of pursuit. They rose rapidly around the initiation of pursuit, reached values as high as 0.7 for an interval of 20 ms duration, and were greater than 0.6 for an interval of over 50 ms. For the example neuron, the time of the greatest correlations between actual and predicted residuals of eye velocity corresponds well to the time when the neuron fired most vigorously, and the time course of the correlations was closely related to the time course of average firing rate for this neuron (compare to the raster in Figure 1B).

The time domain analysis in Figures 2B and 2C suggests that qualitatively different portions of the eye movement—such as initiation versus steady-state pursuit—may be encoded differentially by this FEF_SEM neuron. To examine such selectivity more quantitatively, we plotted the coherence of the movement and firing rate residuals (Figure 2D), or the correlation as a function of frequency. Importantly, coherence is corrected for first-order correlations in both the spike train and the eye movement. Like our other measures of covariance, the coherence of the filter derived from the residuals of firing rate and eye velocity (black bars) was different than shuffled data (gray bars). The coherence has two major peaks: one peak is at frequencies below 4 Hz, where residual eye movements (red curve) have the most power; the other peak is at ∼6 Hz and probably corresponds to the initiation of pursuit, expressed as a small deflection at ∼6 Hz in the power spectrum of the variation in eye velocity (red curve). Qualitative examination of the spectrogram of eye movement variation confirmed this intuition (data not shown). The difference in the relative size of these two peaks in the eye movement and the coherence suggests that variation in the responses of the example neuron preferentially encoded variation in the more rapid changes in the eye movement, such as the initiation of pursuit.

Like r², the metric of coherence reveals the fraction of variance explained, but as a function of frequency; thus, the magnitude of coherence should be similar to the square of the correlation coefficient. If the coherence were 1, there would be a perfect trial-by-trial correspondence between the neural and behavioral variation. For the example unit, over the frequency range that contained most of the power in the eye movement residuals (0−8 Hz), the coherence averaged 0.25. Thus, the frequency domain analysis indicates that the filters account for about 25% of the variation in the actual residual eye velocities, in good agreement with the values of r² obtained from the time domain analysis across the interval of pursuit (100−500 ms) (Figure 2C).

Figure 2 illustrates that we can describe comprehensively, on a trial-by-trial basis, the dynamic nature of the correlation between the variations in the activity of one neuron and the associated behavior. The correlations can be seen equally clearly in time and frequency domain representations of our data.

Temporal Heterogeneity in the Strength of the Neuron-Behavior Relationship and the Mean Neural Activity

Population data confirmed the patterns seen in our example cell. Of 141 neurons in our sample, 105 yielded filters that were statistically different from filters based on shuffled data. Figure 3A plots the distribution of the peak values across time of the correlation between neuron and behavior (r_NB) for each neuron in the sample. For the neurons with statistically significant versus nonsignificant filters (black versus gray bars), the peak value of r_NB averaged 0.41 (range 0.18−0.76, SD 0.15) versus 0.23 (range 0.07−0.43, SD 0.08). The correlations between actual and predicted residuals were significantly different for neurons with significant versus nonsignificant filters (t test, p < 10 ⁹). Average coherence between 0 to 10 Hz confirmed data analyzed in the time domain: 0.15 (SD 0.10) versus 0.11 (SD 0.08) for neurons with significant versus nonsignificant filters (Wilcoxon rank-sum, p < 0.02). As expected, many neurons had values of coherence that peaked between 0 and 10 Hz (data not shown), in good agreement with the range of frequencies found in the eye movement residuals.

Figure 3. Timing of Maximum Responses and Neuron-Behavior Correlations across the Population of FEF_SEM Neurons.

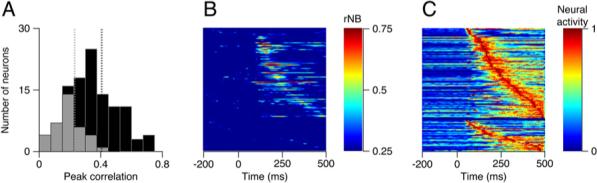
(A) Distributions of peak magnitude of correlations between predicted and actual eye variation for cells with significant (black) and nonsignificant (gray) filters.

(B) A color map showing the time course of the neuron-behavior correlation. Each line shows the quality of one neuron's prediction of eye velocity in time with neurons ordered from top to bottom according to the time of the peak correlation.

(C) The color-coded normalized peristimulus time histogram for each cell in the population, again ordered according to the latency to the peak firing rate. In (B) and (C), the horizontal black line divides the population into neurons with significant (top) and nonsignificant filters.

Across the duration of the trial, each neuron had a distinct moment when it best predicted the residual eye movements. Collectively, the population tiled the duration of the trial. Figure 3B diagrams these findings: each neuron is represented by one horizontal line in the plot, color represents r_NB as a function of time, and neurons are arranged by the latency to peak correlation. Similarly, each neuron's peak activity came at different moments during tracking, and collectively, the population tiles the trial. Each line of Figure 3C plots the PSTH of one neuron as a color code, and the neurons are aligned from top to bottom according to the time of the peak activity (red). The neurons averaged 64.37 ms (SD 40.93) spent at or above 80% of their peak rate.

The similar tiling across the trial led us to ask whether the cells most active at a given time also best predicted the behavioral variation at that time. The mean correlation between the two time courses was r = 0.40 (SD 0.35). Further, neurons with larger peak values of neuron-behavior correlation also tended to have a better correspondence between the time courses of the average response and the neuron-behavior correlation. The strength of the neuron-behavior correlation (Figure 3A) predicted the size of the correlation between neuron-behavior correlation and the PSTH (r = 0.54, p < 10⁻¹⁰).

Our population analysis in Figure 3 demonstrates three key features of the data. First, individual neurons can reliably encode trial-to-trial fluctuations in behavior. Second, they do so at particular moments in the trial, collectively tiling the entire duration of movement. Finally, the temporal patterns of the neuron-behavior correlations derived from analysis of residuals reflect the mean firing patterns of the neurons themselves, which similarly tile the duration of movement.

Filter Shapes Suggest an Orthogonal Basis Set for Movement Commands

The shape of the filters can be thought of as the “feature” that best describes the relationship between the residuals of neural activity and the attendant behavior. Of the 105 filters that were statistically significant, 66 could be classified visually according to their shape into three classes: 18 had a single, positive-going lobe (Figure 4A), 40 were biphasic (Figure 4B), and 8 were triphasic, with a large negative deflection (Figure 4C). Each filter shape suggests a different role in encoding smooth eye movement. A single lobed filter describes an integrator: a neuron whose activity is related to a pulse of eye velocity. The width of the filter reflects the downstream smoothing of the impulse provided by a single spike in the neuron. A biphasic positive-going filter emerges if spikes are associated with a transition from lower to higher eye velocity, i.e., eye acceleration. Finally, a triphasic filter with a downward deflection implies that a spike is associated with an increase in the rate of change of the acceleration, or “jerk.”

Figure 4. Properties of Filters for the Population of FEF_SEM Neurons.

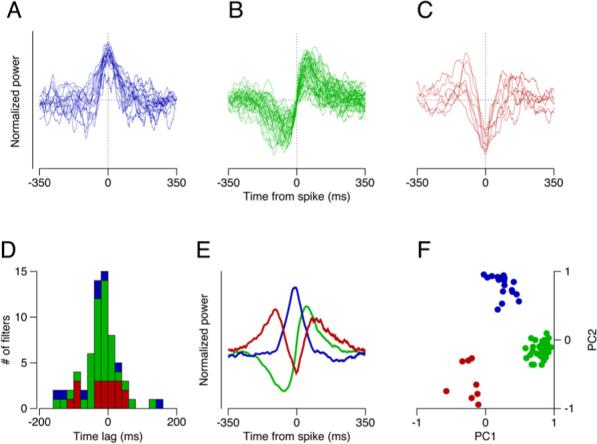
(A–C) Superimposed filters of three different shapes that were prevalent among our sample of neurons. Filters were categorized by eye, normalized, and shifted in time so that all had the same time of maximum influence.

(D) Distribution of latencies from the time of spike occurrence to the time of maximal influence of each filter. Histogram bars are color coded to match the shapes in (A)–(C).

(E) The first three principal components obtained by principal component analysis of the aligned filters.

(F) Projections onto the first and second principal components are plotted on the x and y axes for each filter included in (A)–(C), with the points color coded according to their initial grouping by eye.

The latency and width of the filter provide another way to classify the data. We estimated the latency of each filter as the time from the extra spike to the “moment of maximal influence,” defined as the time of the peak of a single or tri-lobed filter and the zero crossing for a biphasic filter. The distribution of time lags from the occurrence of an extra spike to the moment of maximal influence had a single peak centered close to zero (Figure 4D), implying that some neurons caused eye movement while others responded to sensory inputs. There was no difference in time lag among the three filter types, and the mean latency from the spike to the moment of maximum influence was–0.93 ms (SD 54.9 ms). The spread about a latency of zero for each shape of filter demonstrates that there was no relationship between the shape of a filter and the time of its maximum influence. The filter width was on the order of 150−350 ms, reflecting the fact that even the residuals of smooth eye velocities are highly correlated in time.

To confirm our method of filter clustering, we aligned the filters by eye as described above and performed principal component analysis on the full set of time-shifted filters from the 66 neurons with classifiable filters. Most of the variance could be attributed to three principal components that had the shapes seen visually in our three groups of filters (Figure 4E). The projections on to the first two principal components (Figure 4F) yielded three groups of filters that conformed to our initial qualitative classification, illustrated by the different colored symbols. Our choice of alignment allowed us to explain more of the variance (40%) than we were able to explain by randomly distributing our latencies across the filters in the population (36% [SD 0.6%]). This small improvement reflects the ceiling set by noise in the data.

Neuron-Neuron and Neuron-Behavior Correlations for Example Pairs of FEF_SEM Neurons

We now turn to analysis of the correlations between different neurons that are active at the same time. Our data set included recordings from 104 pairs of neurons, made on the same or different electrodes. Differences in directional tuning reduced our data set to 52 pairs where the neurons were sufficiently active during the same set of eye movements. We plot data for one direction of motion in two example pairs, both recorded on separate electrodes (Figure 5). The rasters have been color coded: in Figure 5D, the neurons show similar profiles of activity across the response; however, the temporal heterogeneity we described earlier is especially clear in Figure 5A.

Figure 5. Correlations between Two Simultaneously Recorded Pairs of Units.

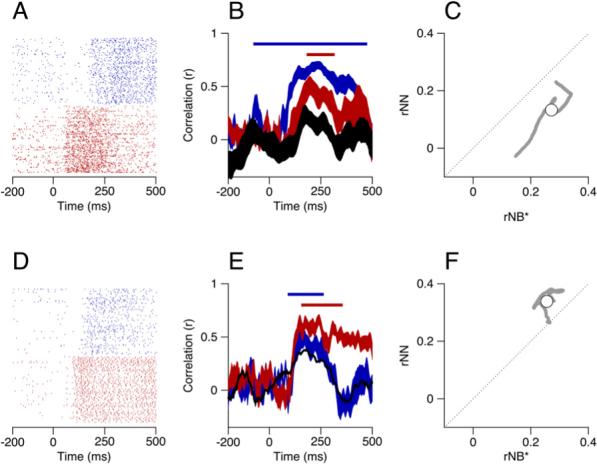
(A and D) Rasters showing the neural activity, where the two colors show responses of the two neurons in each example pair.

(B and E) The neuron-behavior correlation (r_NB) and neuron-neuron correlation (r_NN) as a function of time. Red and blue ribbons show the correlation between the actual residuals of eye velocity and those predicted from the spike train residuals and the filters for the two neurons. The black ribbon shows the trial-by-trial correlations between the predicted residuals of eye velocity for the two neurons. The ribbons show means ± one standard deviation; for clarity, only the mean is shown for the black trace in (E). The colored bars atop the functions correspond to the times where each r_NB was 1.5 SD or more away from on the results of analysis based on shuffled trials.

(C and F) Comparison of the product of the neuron-behavior correlations for the two neurons in the each pair, r_NB*, and the neuron-neuron correlations (r_NN). Gray points plot the data for each individual time point, and open symbols show averages across the analysis interval.

For each pair of neurons, we computed the trial-by-trial correlation between the eye velocity predictions of their individual filters as a function of time (black ribbons in Figures 5B and 5E). Crucially, this measurement, which we refer to as the neuron-neuron correlation (r_NN), allowed us to transform the neural activity directly into the relevant behavioral space. For both pairs illustrated in Figure 5, this estimate of neuron-neuron correlations showed a peak that corresponded in time to the peaks of the neuron-behavior correlations for the individual neurons.

To examine the relationship between neuron-neuron and neuron-behavior correlations, we restrict our analysis to the time when the correlation between the predicted and actual eye movement variation for both cells in the pair were significantly different from shuffled controls (blue and red bars in Figures 5B and 5E). We used the product of the neuron-behavior correlations for the two neurons in the pair (r_NB*) to estimate the collective strength of the prediction from each individual neuron. For identical neurons operating in the absence of any other noise sources, we expect the product of the neuron-behavior correlations (r_NB*) to equal the neuron-neuron correlations (r_NN) (Medina and Lisberger, 2007). Figures 5C and 5F plot our estimate of r_NN against r_NB* for each time in the period of overlap (gray points). As the time points in our analysis are not independent, we take the mean across time for each pair of neurons as our final measurement, plotted as a white circle.

Neuron-Neuron and Neuron-Behavior Correlations for a Population of FEF_SEM Neurons

Given the temporal heterogeneity of neural activity in our data set, recordings for only 22 directions of motion from 11/104 pairs of neurons had more than 20 simultaneous milliseconds of excellent predictive power for movement variation. We summarize the relationship between r_NN and r_NB* for these 22 data sets as separate symbols in Figure 6A. We could not resolve a significant difference (pairwise t test, p = 0.07) between the means of the distributions of r_NB* (mean: 0.14+0.07 SD), and r_NN (mean: 0.18 + 0.11 SD), nor were the two significantly correlated (r = 0.29, p = 0.20).

Figure 6. Properties of Neuron-Neuron Correlations across the Population of Paired Recordings.

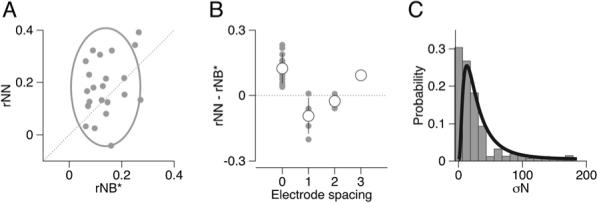
(A) We plot neuron-neuron (r_NN) correlation versus the product of neuron-behavior correlations for each pair of neurons (r_NB*) for 22 data sets from 11 FEF_SEM neurons. The gray ellipse is centered at the means with major and minor axis lengths representing 2 SD.

(B) The difference, r_NN–r_NB* plotted as a function of the distance between the electrodes used to record the two neurons. Gray and white circles show individual data sets and means; error bars show SDs. An electrode spacing of zero means both units were recorded on a single electrode.

(C) Distribution of variance of the predictions of eye velocity residuals. Gray histogram summarizes values for each time in the analysis interval for each data set. Black curve shows a log-normal fit to the distribution.

To investigate the source of the considerable variance across our pairs, we first plotted the difference between r_NN and r_NB* for each of our 22 data sets as a function of the distance between the electrodes used to record from the two members of the pair (Figure 6B). Pairs of neurons recorded on the same electrode (zero on x axis) accounted for almost all values for r_NN-r_NB* greater than zero. Two reasons might explain why this analysis could yield different results for pairs recorded on the same versus different electrodes: either because the values of r_NN might be higher than the average for the population, because of the anatomical proximity, or lower values of r_NB* might be an artifact of the decreased signal to noise resulting from superposition of waveforms. Our data showed that the value of r_NN for units recorded on the same versus different electrodes was 0.24 (0.88) versus 0.12 (0.11), which were different (t test, p = 0.01). However, The value of r_NB* for units recorded on the same versus different electrodes was 0.11 (0.56 SD) versus 0.17 (0.07 SD); the two just missed being significantly different (t test, p = 0.05). Thus, neurons recorded on the same electrode simply tend to be more correlated.

A major goal of analyzing neural and behavioral variations is to shed light on the nature of the neural population that drives movement. We now turn to one final feature of the data that will prove to be necessary to understand the population: the variance of the magnitude of the predicted eye velocity residual from each individual cell. We performed this analysis only for the overlapping intervals of significant neuron-behavior correlations in the 22 data sets used for Figure 6. Figure 6C shows that the distribution of the magnitude of the trial-by-trial variance in the predicted eye movements (gray bars) is well fit with a log-normal distribution with mean and standard deviation of 25.40 and 2.28 (black curve). Our population is thus comprised of neurons whose trial-by-trial variations in spiking encode vastly different levels of behavioral variation.

Computational Analysis of the Relationship between Neuron-Neuron and Neuron-Behavior Correlations in Our Neuron Sample

So far, we have provided a set of measurements that relate variations in neural activity in the FEF_SEM to the ongoing dynamics of behavior. Specifically, we demonstrated that variation in the responses of individual neurons can encode different aspects of movement fluctuations at different times, and we measured the degree to which pairs of neurons copredict movement dynamics. To understand how a population of neurons might give rise to behavioral fluctuations, we have built a simple generative model of movement variation. Parameters in the model are fixed on the basis of our data: its units show the same level of response variation recorded in our neuronal sample and the same mean and variance of neuron-neuron correlations. We then varied the parameters we cannot measure, namely the amount of variation added to the behavioral response in processing that occurs downstream from the FEF_SEM and the number of FEF_SEM neurons involved in generating the movement. For each parameter value, we analyzed the output from the model to see what ranges of those parameters would be compatible with our measures of neuron-behavior correlation.

Figure 7A schematizes our model. We created a population of units whose drive varies according to a log-normal distribution: σ_N = 25.40 (2.28 SD). The responses of all units in the population are decoded by summation, after which additional “downstream” variation (η) is added. The population had the same level of neuron-neuron correlations as found in our sample (r_NN = 0.18 [0.11 SD]). For each value of η and number of units, we measured the neuron-behavior correlations as we did in our data and computed their product for each pair of neurons in the model neural population (r_NB*). While we have assumed that the population is decoded by summation, similar results would obtain if we had decoded by averaging the population response. Our model is static and therefore addresses only the properties of the active population at any instant. Even though different neurons may be involved at different times, we assume that any given subset of neurons behaves analogously at all times during the trial.

Figure 7. A Generative Model of the Sources of Motor Variation and Neuron-Behavior Correlations.

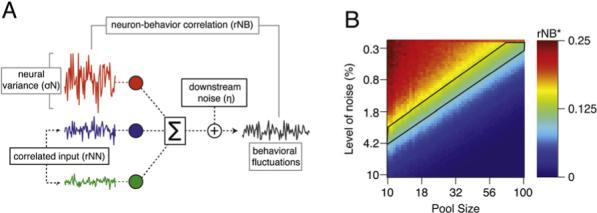
(A) A schematic of the model. The colored traces show the activity of three model units. The population activity is summed, and then variation is added downstream (η) to create behavioral output with fluctuations.

(B) Color map showing the product of the pairwise correlation between two units (r_NB*) as a function of the number of neurons in the pool and the amount of variation added downstream. The area outlined in black corresponds to the ranges of variation added downstream and pool size that led to values of r_NB* in agreement with our data.

The color plot in Figure 7B shows that the fluctuations of any one neuron have a large effect on the fluctuations in the pooled output for the model, and r_NB* can be larger than r_NN if the number of neurons is small and no noise is added downstream (top, left corner of plot). As the pool size increases, however, the effect of any one neuron on the summed output goes down, and r_NB* approaches the value of r_NN that was built into the model (0.18), as expected for this class of models (Shadlen et al., 1996; Medina and Lisberger, 2007). If the size of the pool is fixed (any vertical line), then r_NB* decreases as the magnitude of downstream variation increases. The biologically realistic portion of the plot is shown by the area bounded in black lines, which corresponds to the measured level of r_NB* across pairs of neurons in our population, or 0.14 (0.07 SD). Of course, our conclusions could be affected somewhat by experimental errors in estimating the mean r_NN from our relatively small sample of neuronal pairs. However, the good agreement between our estimates of r_NN and those found for other cortical areas implies that our estimates are not wrong by much, so that the effect on the details of Figure 7 would not be large (Lee et al., 1998; Zohary et al., 1994).

Taken together, our modeling and our data imply that the size of the relevant neural population and the magnitude of variation added downstream from the FEF_SEM play against one another. Our experimental observations could result either from a large (n > 100) pool of neurons in the FEF_SEM with little variation added downstream or from a very small pool of neurons with considerable variation added downstream. Either scenario would challenge fundamental assumptions about the way a population of-cells might operate to generate behavioral fluctuations, or behavior itself.

DISCUSSION

How might activity in a population of cortical neurons give rise to behavior? Recordings from single units during repeated attempts at the same movement tend to be quite variable; consequently, most previous studies have focused on the relationship between the average neural activity and an average behavior. Such an analysis leaves open the question of whether the neural variation represents biological noise that the system must overcome to drive coherent movement or whether the observed neural fluctuations represent a true behavioral drive. Our findings favor the latter situation: individual neurons are highly correlated with the behavior at specific times during the trial. They can encode different aspects of the behavior, suggesting that different cortical neurons play fundamentally different roles in driving behavior. Comparison of the neuron-behavior correlations with the correlation in behavioral commands across pairs of neurons reveals much about the architecture of the cortical circuit for control of smooth eye movements from the frontal eye fields. There is an interesting tradeoff between the number of neurons that are involved in generating behavior at any given time and the amount of noise added to motor commands downstream of this particular motor area. We come to the surprising conclusion that either a small handful of neurons are involved in cortical control of pursuit eye movements at any given moment or remarkably little noise is added downstream from the frontal eye fields.

We obtained our results through a series of novel methods. First, we adapted a technique that is commonly used in sensory physiology to build a robust set of neural filters, where filters for different neurons could predict different aspects of the motor fluctuations at different times in the trial. Second, we developed an understanding of the neuron-neuron correlations by evaluating the relationship between the eye movements predicted by the two neurons in each pair, rather than by correlating the spike count of the neurons. Third, we exploited a method previously developed for financial market analysis to simulate a population of model neurons with the same mean and variance of neuron-neuron correlations as we found in our data (Hirschberger et al., 2007).

We have computed the relationship between the residuals of firing rate and eye velocity, but we think that the results of our analysis also speak to the relationship between the net firing rate and the full movement. For a linear system, this assumption is true by definition. To the degree that the system is nonlinear, the assumption will be only an approximation (see Supplemental Data). Crucially, as a linear approximation to a nonlinear system, the performance of our models serves as a lower bound. We expect that a more complete nonlinear model would account for still more of the variation in behavior (e.g., Paninski et al., 2004b). Thus, we believe that our measurements provide a conservative probe for the contribution of a neuron's overall activity to the net movement.

Two Possible Neural Architectures for a Cortical Sensory-Motor System

What manner of cortical population drives smooth pursuit eye movements? Our computational modeling was consistent with either of two scenarios: (1) very few neurons contribute at any given time but considerable variation is added downstream from the FEF_SEM or (2) at least 100 neurons contribute at any given time and essentially no variation is added downstream. We find both ideas challenging to a traditional understanding of noisy and distributed cortical function.

The latter explanation of little variation added downstream from the cortex appeals primarily because it is hard to imagine few neurons in the mammalian cortex participating in a behavior at any one time (Shadlen and Newsome, 1998). An architecture involving many neurons suggests that the population activity underlying the transformation from vision to action involves two components. One component is the “noise,” which may follow from the biophysics of individual cell membranes. The second component is reflected in the existence of correlated neural variation, which gives rise to a “common drive” for eye movement. Because only the common drive is preserved when the population activity is pooled, it propagates through the sensory-motor system. Thus, our finding that a single extra spike in a single neuron has a correlate in the eye movement would imply that such “extra spikes” must be common across neurons. Our measurements of the common drive, expressed as the similarity between the eye movements predicted from coactive neurons, are sufficient to confirm this intuition. This two-component architecture has been analyzed for perceptual decisions, with similar conclusions (Shadlen et al., 1996; Zohary et al., 1994).

If there were a direct transformation between common drive in the FEF_SEM and behavior, then strong neuron-behavior correlations such as we have found is precisely what we ought to have predicted. It is striking that neurons far from the muscles, in the mammalian cortex, behave as if the downstream motor system can faithfully transmit their common drive. Our data may reflect the remarkable fidelity possible within such a circuit-level framework. The notion of a highly reliable motor system downstream from the FEF_SEM is compatible with our laboratory's previous suggestion that variation in pursuit originates largely in upstream sensory areas (Osborne et al., 2005, 2007).

Still, our data do not allow us to reject the hypothesis of a population where only a few neurons contribute to the trial-to-trial fluctuations in movement. Our theoretical analysis suggests a strong test for such a population: if the neuron-behavior correlations were larger than would be expected given the level of neuron-neuron correlations, then we would be forced to conclude that only a few neurons comprise the essential part of the population. In fact, the neuron-behavior correlations (r_NB*) we obtained were commensurate on average with the neuron-neuron correlations (r_NN). However, either of two scenarios would still allow the conclusion that only a few neurons drive behavior at any given time. First, we would have concluded that the neural population was small if we had considered only neurons recorded on different electrodes: neuron-behavior correlations there were greater than would be expected from common drive. Second, equality of r_NN and r_NB* would occur if the presence of variation downstream from the FEF_SEM reduced the effective correlation between neural and behavioral variation. Because we cannot estimate such downstream noise, the number of neurons in the population remains undefined, and we can neither prove nor disprove the existence of a numerically restricted population that generates movement variation.

The Form and Utility of a Temporally Restricted Population Architecture Generating Movement Variation

While the absolute size of the population that generates movement variation is inaccessible, the temporal tiling of activity and distinct patterns our neurons encode gives us a glimpse into the space in which the FEF_SEM operates. A temporally restricted source for movement variation has a number of advantages. First, it would allow the cortex to exercise modulation and voluntary control over different aspects of motor behavior on a fine temporal scale, allowing different neurons that mediate pursuit to have special influences at different times; the orthogonal nature of the filters for our sample of FEF_SEM neurons supports this notion. Second, it would enable excellent temporal control over long-term plasticity and learning (Fiete et al., 2004). Pursuit learning is exquisitely sensitive to time, and both the direction of target motion and the time when target motion changes can be learned well (Carey et al., 2005; Medina et al., 2005). We propose that neurons that can encode specific features of movement with high fidelity over restricted time intervals are likely to be involved preferentially in learning. Changing a small set of neurons is likely to be more efficient than synchronously modulating thousands and may underlie our remarkable ability to learn new motor behaviors rapidly while still retaining old skills.

We find the features of cells in the proposed cortical population to be particularly interesting when contrasted with our laboratory's findings in the cerebellum (Medina and Lisberger, 2007). Located between the FEF_SEM and the muscles, Purkinje cells in the flocculus have responses that are temporally stereotyped across the population. Both the neuron-behavior correlations and the average neural activity reach peaks during the initiation of pursuit and are sustained at lower levels during steady-state tracking. Thus, at any moment, all Purkinje cells make qualitatively similar contributions to movement. In contrast, at any moment, FEF_SEM neurons may contribute differentially to movement. In the domain of direction, Purkinje cells are almost exclusively tuned to cardinal directions, while neurons in the FEF_SEM are tuned across all possible eye movement directions. Finally, all Purkinje cells seem to be related to a linear combination of mainly smooth eye velocity and eye acceleration, while the three filter shapes in our FEF_SEM population imply that different neurons encode distinct features of movement along their preferred directions. The stereotyped responses of the Purkinje cells may serve to transform the temporally distributed and spatially oriented movement commands from the cerebral cortex into coordinates appropriate for the muscles. The more diverse pattern of responses of FEF_SEM neurons may be critical for highly specific control of movement on the basis of cortical plans.

Recent work in motor control in songbirds and representation of visual stimuli provides evidence that ethologically relevant stimuli and behaviors can be quite sparsely represented, with remarkable sensitivity and precision; here, we provide complementary evidence for temporally sparse coding in a similarly relevant behavioral space (Hahnloser et al., 2002; Theunissen, 2003; Vinje and Gallant, 2000). Because smooth pursuit is considerably slower than most behaviors, temporal sparseness in pursuit-related populations of neurons ought be more restricted than in songbird motor nuclei, which drive a less temporally correlated set of behaviors. We think that the utility of a sparse population organization for the generation of behavior ought accommodate many behaviors, no matter their specific coding demands.

The Role of the FEF_SEM in Driving Behavior

Both microstimulation (Gottlieb et al., 1993) and lesion studies (Keating, 1991) provide strong evidence that the FEF_SEM plays a causal role in determining the parameters of eye movements. While not unique in this respect, activity in the FEF_SEM is likely necessary for normal pursuit dynamics. Thus, the presence of an impressive correlation between neuronal and behavioral variation could reflect the causal role of the FEF_SEM as a highly precise command for movement. However, neuron-behavior correlations also could arise from the corollary discharge inputs that likely contribute to the responses of neurons in the FEF_SEM (Wurtz and Sommer, 2004). The latencies of our filters do not resolve this issue, partly because the lag from the spike to the time of maximum influence is broadly distributed around zero and partly because the autocorrelations in the pursuit response limit our ability to resolve the precise latency of the neuron-behavior correlations. Therefore, we cannot exclude the possibility that FEF_SEM neurons play no causal role in determining behavior, even though they are high-fidelity encoders of variation in the movement, a finding that would be fascinating in its own right. However, we think that the other evidence of a causal role for neurons in the FEF_SEM renders this conclusion unlikely.

Linear Systems Analysis of Continuous Oculomotor Behavior

Many have noted that cortical neurons, both sensory and motor, are inherently variable. Our experiments quantify the degree to which variation reflects signal rather than noise, in the sense that it encodes the trial-to-trial deviations in behavior. Neurons in the FEF_SEM are thus in agreement with studies suggesting that small numbers of spikes can encode significant information (Luna et al., 2005; Osborne et al., 2004) and that variation in continuous motor behavior is unlikely to reflect true “noise” (Maye et al., 2007). By linking single “extra” spikes to behavioral consequences, we extend the analyses established in the sensory domain into the realm of movement.

Linear systems analysis of motor systems offers a number of special challenges. The method we used to analyze the covariation of neural firing and behavior is adapted from techniques traditionally used to describe the relationship between neural firing and a sensory stimulus (Chichilnisky, 2001; Dayan and Abbott, 2005; Nagel and Doupe, 2006; Rieke et al., 1999; Wu et al., 2006). In the sensory system, such an analysis is greatly aided by the experimenter's ability to present exactly the same stimulus repeatedly and to contrive the stimulus to minimize temporal autocorrelations. In the motor system, the behavior varies outside of experimenter control from trial to trial, and the motor response is inescapably correlated across time. By and large, meaningful filters cannot be extracted from strongly correlated stimuli or movements (but see Sharpee et al., 2004). The residual movements that remain after subtracting the mean eye movement were considerably less correlated in time. We therefore opted to restrict our analysis to the residuals, a choice that allowed us to obtain filters that correctly predicted a significant fraction of the trial-to-trial variation. Nonetheless, the slow nature of smooth eye movements means that, despite our efforts to correct for autocorrelations, our filters are probably wider than the actual influence of each cell on its immediate downstream targets. We thus think of the filters not as models of FEF_SEM neurons per se, but rather of the entire downstream cascade that follows an FEF_SEM spike.

By design, our analysis of the relationship between cortical spikes and behavioral dynamics made one simplifying assumption: that the downstream cascade was inaccessible and best modeled holistically. However, our analysis provides the kernel of a way in which we can do better. In sensory cortex, the transformation of stimulus representation across brain regions has been nicely modeled by incorporating different areas into a cascade of linear/nonlinear systems (Rust et al., 2006). Similarly, as we seek to understand behavioral dynamics, we can estimate the downstream noise by working backward from the periphery. If we model the relationship between motor neurons and behavior in the same way as we did the relationship between the FEF_SEM and behavior, for example, then we can extend our model of the FEF_SEM by fitting it not to the behavior, but to the drive the motor neurons provide to behavior. Similarly, we anticipate that we can leverage the measurements in this report to understand the relationship between upstream areas, such as the population of motion-sensitive cells in area MT, and behavior. Mapping the cascade of transformations between different populations of neurons and concurrent behavioral dynamics will allow a deep understanding of the way those populations interact, ultimately allowing us to move as well as we do.

EXPERIMENTAL PROCEDURES

Two male monkeys (Macaca mulatta) were used in experiments approved by the Institutional Animal Care and Use Committee of UCSF. All experimental procedures were in accordance with the National Institutes of Health Guide for the Care and Use of Laboratory Animals. Eye position was monitored using the scleral search coil technique, while the head was held stationary using custom hardware (Ramachandran and Lisberger, 2005). The eye coil and hardware were previously implanted during sterile surgery with the monkey under isoflurane anesthesia. Both monkeys had been trained to smoothly track visual targets for a juice reward. Targets always moved at 20°/s in one of eight evenly spaced directions. Monkeys had to maintain their gaze within a small window (0.75° during fixation, and 2°−3° during target movement) for at least 500 ms (up to 1100 ms) to receive a small fluid reward.

Up to five quartz-shielded tungsten electrodes were lowered simultaneously into the caudal region of the frontal eye fields using a microdrive (Thomas Mini-Matrix 05, Thomas Recording, Giessen, Germany). When feasible, we sought to record from multiple single units simultaneously, both on the same and on different electrodes. Electrical signals were amplified and digitized for on-line spike sorting using template matching of waveforms that crossed a user-defined threshold (Plexon MAP, Plexon Inc., Dallas, TX). Waveforms were considered to reflect the activity of a single source if they were distinct from the noise and had no refractory period violations, defined as two or more threshold crossings within 1 ms. Additionally, during off-line sorting, when plotted as projections onto the first and second principal components, recordings were considered to comprise single units only if they formed clusters distinct from both noise and other units over the duration of the experiment (usually>45 min of continuous data acquisition). After sorting, waveforms were converted to timestamps with 1 ms precision for analysis.

We studied the smooth component of the monkey's pursuit of a moving target. The movement period was defined as 200 ms of fixation before the onset of target motion and 500 ms after the target began to move. Velocity traces were generated by digitally differentiating the position traces with a balanced difference algorithm; traces were digitally smoothed with a zero-phase 25 Hz 2-pole Butterworth filter. Saccades show up as large deflections in the velocity trace and were removed so as not to dominate the trial-to-trial variations: saccades were marked initially with a threshold-crossing algorithm, described previously, and each trial was examined by eye using custom software (Schoppik and Lisberger, 2006). The velocity trace then was interpolated between saccade beginning and end. We restricted our initial analysis of the relationship between behavioral and neural variation to the eye movements along the single best direction of the neuron, determined by the direction that had the greatest number of spikes overall. When the preferred direction was along an oblique axis, we analyzed the radial eye velocity. There was little jitter in the time of movement onset, so we defined the onset of target motion as the beginning of the behavior.

Each neuron's raster was examined by eye, to exclude units that were not strongly responsive during the eye movement or whose responses changed qualitatively over the duration of the experiment. A minimum of 15 repeats of pursuit in a single direction was necessary for inclusion; on average, we had 80 (SD 53) repetitions of each trial in our data sets. A total of 141 single units met our criteria for inclusion in the analysis (97 and 44 from monkeys Cb and Gu). As we could resolve neither qualitative nor quantitative differences between data from the two monkeys, data from both were analyzed as a unified population.

Although a smoothed estimate of firing rate was not needed for our data analyses, we did use one for display purposes. For these figures, we smoothed the binary spike train for that experiment using a Gaussian filter with a standard deviation of 20 ms (Figure 2A) or windowed the data with a 10 ms square window to estimate the peristimulus time histogram (Figures 1B and 3C).

Modeling the Relationship between the Residuals in Spikes and Eye Movements

We derive a linear filter that related the variation in neural firing to the variation in eye movement responses on a trial-by-trial basis. The residual variation was generated by subtracting the mean eye trajectory across all trials from the eye's trajectory on each trial, and similarly for the spike train. Filters were then generated by cross-correlating the residuals of firing rate and eye velocity on each trial and taking the average across trials. To avoid over-fitting, we used a cross-validation technique, randomly selecting a subset of data to generate the filter and using the remaining trials to test the performance of the filter. The split that minimized both the variance in the estimate of the filter and the variance in the prediction quality was 40% filter generation and 60% test trials. To generate confidence intervals on the filter, we repeated the reconstruction procedure 150 times with different trials assigned for filter generation or testing. To quantify the null hypothesis, that there was no relationship between trial-by-trial neural and behavioral variation, we generated a separate filter after shuffling the neural responses across trials. This procedure is conceptually similar to the “shuffle” or “shift-predictor” used to estimate the effect of a repeated stimulus on correlations between neurons (Brody, 1999).

Specifically, we began with the following model of the transfer function between eye movement residuals and spikes:

$$e_i\left(t\right)-\stackrel{‒}{e}\left(t\right)=D\left(\tau \right)\otimes ({\rho }_i\left(t\right)-\stackrel{‒}{\rho }\left(t\right))$$ (1)

where e_i(t) and ρ_i(t) are the eye speed and the spike train on trial i, and ē(t) and $\stackrel{‒}{\rho }\left(t\right)$ are the mean eye movement and mean neural response, respectively. Our model assumes that there exists some linear filter, D(τ) that allows us to convert the residual spike variation into the residual eye movement. To estimate D(τ), we begin with the following equation:

$$Q_{e\rho }\left(t\right)=\frac{1}{n}\sum _{i=1}^n[(e_i\left(t\right)-\stackrel{‒}{e}\left(t\right))\otimes ({\rho }_i\left(t\right)-\stackrel{‒}{\rho }\left(t\right))]$$ (2)

Q_eρ is the filter we have generated and is some approximation of the true filter D(τ).Q_eρ differs from D(τ) by the autocorrelation of the spike train (Theunissen et al., 2000). To correct for correlations in the spike train, we divided the filter in the frequency domain by the power spectrum of the residual spike train:

$$D\left(\tau \right)=\frac{1}{2\pi }{\int }_{-\infty }^{\infty }d\omega \frac{\sum _{i=1}^n{Q}_{e_i{\rho }_i}\left(\omega \right)}{\sum _{i=1}^n{Q}_{{\rho }_i{\rho }_i}\left(\omega \right)}{e}^{i\omega t}$$ (3)

where D(τ) is the decorrelated filter, and Q_eiρi(ω) and Q_ρiρi(ω) are the Fourier domain representations of the filter from Equation 2 and the power spectrum of the spike train, respectively. Equation 3 states that the true eye movement reconstruction filter can be estimated by weighting the power in the raw filter by the power in the spike train. Because the spike train has a relatively narrow autocorrelogram, the majority of its power lies above 50 Hz. Consequently, the denominator of Equation 3 acts as a low-pass filter.

By convention, we call the filter we have generated the “reverse” filter, as it allows us to predict eye movements using spike trains. To generate the “forward” filter, which predicts spike trains from eye movements, we must correct for the autocorrelations in the eye movement. We replaced the denominator in Equation 3 with the power spectrum of the residual eye movements. Noise in the estimate of the power spectrum tends to overwhelm the signal in the filter, and so we smoothed the spectrum using an exponential filter with a rapid dropoff ( ∼2.5 Hz). The cutoff for smoothing was set at the frequency where the power in the spectrum of the shuffled residual eye movements (our estimate of a noise spectrum) overlapped the power in the spectrum of the residual eye movements. The mean dot-product between the forward filter flipped about the zero-lag point and the reverse filter was 0.91 (SD 0.05), supporting the conclusion that, despite a different denominator, the two filters ought be equivalent. We thus focus the description of our results on the “reverse” filter, which needed no additional smoothing.

Lastly, we computed the coherence of the filter:

$$C\left(\omega \right)=\frac{{\left(Q_{e\rho }\left(\omega \right)\right)}^2}{Q_{ee}\left(\omega \right)\ast Q_{\rho \rho }\left(\omega \right)}$$ (4)

where Q_xx(ω) is iconic for

$$\sum _{i=1}^n{Q}_{x_i{x}_i}\left(\omega \right).$$

Coherence describes the percent of variance in the data accounted for as a function of frequency and, thus, is similar to the definition of r², which is the square of Pearson's correlation coefficient (Brillinger, 2001). Importantly, with two terms in the denominator, the coherence corrects for autocorrelations in both the eye movement residuals and the spike train residuals.

We defined a filter as “significant” if a two-sided t test showed that the total power in the filter was significantly different from the total power in the filter derived from randomly shuffled data. The value of α was adjusted by the number of draws, so that our criterion for significance became p < 0.0003. In monkeys Cb and Gu, 74/97 and 31/44 neurons yielded filters that were significant, respectively. By convolving the successfully derived filters with the residuals of the spike trains on each test trial, we generated predictions that could be compared directly with the residual eye velocity on each trial. We measured the filter performance by calculating Pearson's correlation coefficient for the predicted versus actual residuals, at each at each point in time.

Data and Analysis of Paired Recordings

Our data set included 104 simultaneously recorded pairs of neurons, (84 and 20 from monkeys Cb and Gu), with 26 pairs recorded on the same electrode. As the neurons rarely had overlapping preferred directions, we extended our analysis to include the complete set of eight directions of motion. We defined our time window for analysis as the time in the trial when the correlation between predicted and actual fluctuations (the filter performance) was at least 1.5 SD greater than the performance of a random filter. We restricted our pairwise analysis to directions of motion where both cells in a pair had at least 20 ms of overlap in their analysis windows. Of 104 pairs, 52 had at least one direction where both neurons had significant filters, and of those, 11 had overlapping analysis windows in a total of 22 directions.

To measure the strength of the relationship between pairs of units, we computed the filter as in Equation 3, direction by direction, for each neuron in the pair, for 50 runs in each direction. We then used the filter to generate a set of predicted fluctuations in eye movements and measured the correlation between predictions from each neuron in the pair. We also measured the neural variance as the absolute magnitude of the predicted fluctuation.

Computational Analysis

Our population model consisted of simulating the relationship between each member of a set of random variables (the neurons) and the sum of the set (the behavior). Each random variable consisted of 2500 draws from a standard normal distribution, which were then scaled. The scaling of each variable (the neural variance) was determined by a draw from a log-normal distribution with mean and standard deviation determined from our data, as described in the previous section. We constrained our covariance matrix so that its mean and standard deviation matched the values from pairs of neurons. To do so, we generate a matrix, F, such that the properties of FF^T matched the mean and standard deviation of the pairwise correlations measured in the previous section (Hirschberger et al., 2007). For display purposes, each set of parameters was simulated 50 times, and the mean result is presented.

We used standard statistical methodology to describe our data. Correlation coefficients were evaluated using Pearson's method. To compare normally distributed data, we used t tests, paired when appropriate; non-normally distributed data were compared with the Wilcoxon rank-sum test. All code was written using MATLAB (Mathworks, Natick, MA) and is available, along with all relevant data, at http://keck.ucsf.edu/~schoppik/.

Supplementary Material

sup data

SUPPLEMENTAL DATA

The Supplemental Data for this article can be found online at http://www.neuron.org/cgi/content/full/58/2/248/DC1/.