Five-dimensional neuroimaging: Localization of the time-frequency dynamics of cortical activity

Abstract

The spatiotemporal dynamics of cortical oscillations across human brain regions remain poorly understood because of a lack of adequately validated methods for reconstructing such activity from noninvasive electrophysiological data. In this paper, we present a novel adaptive spatial filtering algorithm optimized for robust source time-frequency reconstruction from magnetoencephalography (MEG) and electroencephalography (EEG) data. The efficacy of the method is demonstrated with simulated sources and is also applied to real MEG data from a self-paced finger movement task. The algorithm reliably reveals modulations both in the beta band (12–30 Hz) and high gamma band (65–90 Hz) in sensorimotor cortex. The performance is validated by both across-subjects statistical comparisons and by intracranial electrocorticography (ECoG) data from two epilepsy patients. Interestingly, we also reliably observed high frequency activity (30–300 Hz) in the cerebellum, though with variable locations and frequencies across subjects. The proposed algorithm is highly parallelizable and runs efficiently on modern high performance computing clusters. This method enables the ultimate promise of MEG and EEG for five-dimensional imaging of space, time, and frequency activity in the brain and renders it applicable for widespread studies of human cortical dynamics during cognition.

1 Introduction

Magnetoencephalography (MEG) and electroencephalography (EEG) are functional neuroimaging techniques with millisecond time resolution (Hämäläinen et al., 1993). Traditionally, MEG and EEG have been used to study evoked responses, i.e., activity that is both time-locked and phase-locked to a stimulus or task. These analyses assume a model of neural activity in which responses are additive and/or phases are reset (Hanslmayr et al., 2007). However, it has been well-known that ongoing MEG/EEG oscillations can be suppressed in response to a stimulus or task since the earliest EEG research (Berger, 1930); this possibility is not accounted for by the evoked model. Furthermore, the across-trial jitter inherent in responses to even simple stimuli have been shown to be sufficient to markedly reduce the amplitude of averaged responses (Michalewski et al., 1986); this effect becomes even more pronounced for higher frequency bands. Averaging also assumes trial-to-trial phase locking, which may not be valid for many complex cognitive paradigms.

Another approach to interpreting MEG and EEG data is to quantify oscillatory aspects of the signals using time-frequency methods. Typically, modulations of oscillatory activity are described as event-related spectral power changes (Pfurtscheller and Aranibar, 1977; Pfurtscheller and Neuper, 1992; Makeig, 1993). By comparing the power of neural activity to a quiescent baseline, these types of analyses reveal induced responses, i.e., activity that is time-locked but not necessarily phase-locked. Additionally, the power change may be negative, termed an event-related desynchronization (ERD), or positive, termed an event-related synchronization (ERS). Analyses of ERD and ERS overcome many of the limitations of evoked response analyses. However, most MEG/EEG time-frequency analyses are conducted on the sensor signals without source localization, providing only vague information as to which brain structures generated the activity of interest.

Several source reconstruction algorithms, each employing a different set of assumptions, have been proposed to overcome the ill-posed inverse problem. Source reconstructions from MEG data can be classified as either parametric or tomographic. Parametric methods include equivalent current dipole (ECD) fitting techniques; they often require knowledge about the number of sources and their approximate locations and poorly model sources with a large spatial extent.

Tomographic methods reconstruct source activity at each voxel (3-D location) in the brain. Spatial filtering techniques avoid the high number of parameters and the nonlinear iterative search required by ECD analysis. Nonadaptive spatial filtering techniques, which include minimum-norm-based methods such as sLORETA (Pascual-Marqui, 2002), use sensor geometry to construct the weights for the spatial filter. Adaptive techniques, on the other hand, additionally use sensor data to create a custom filter depending on signal characteristics. It has been shown that a class of adaptive spatial filters known as beamformers (Van Veen and Buckley, 1988) have the best spatial resolution and performance amongst existing tomographic methods (Darvas et al., 2004; Sekihara et al., 2005).

Spatial filtering methods have the potential to compute electromagnetic source images in both the time and frequency domains (Robinson and Vrba, 1999; Gross et al., 2001; Sekihara et al., 2001; Jensen and Vanni, 2002; Dalal et al., 2004). Techniques such as the synthetic aperture magnetometry (SAM) beamformer have been employed to examine either the time course of neural sources or the spatial distribution of power within a specific frequency band (Robinson and Vrba, 1999). However, published studies typically employ SAM to generate static fMRI-style images using a large bandwidth and wide time window—effectively discarding the temporal resolution advantage of magne-toencephalography. Only a few studies have attempted time-frequency analysis in source space (Singh et al., 2002; Cheyne et al., 2003; Brookes et al., 2004; Gaetz and Cheyne, 2006; Jurkiewicz et al., 2006). These reports describe a method in which a single set of beamformer weights are first computed over a wide time window and frequency range; time-frequency decompositions are then computed from the reconstructed time series for a few locations of interest. However, as we show in this paper, weights computed from unfiltered or wideband data may be inherently biased towards resolving low-frequency brain activity due to the power law of typical electrophysiological data. Additionally, responses of shorter duration or outside the fixed time window used to generate the weights may not be adequately captured.

In this paper, we propose a novel adaptive spatial filtering algorithm that is optimized for time-frequency source reconstructions from MEG/EEG data. Performance of this algorithm will first be evaluated with simulated data. Then we will demonstrate the method with real finger movement data, validated with group statistics and intracranial recordings. The proposed algorithm enables accurate reconstruction of five-dimensional brain activity from MEG and EEG data, thereby realizing the ultimate promise of MEG- and EEG-based neuroimaging.

2 Methods

2.1 Definitions and Problem Formulation

Throughout this paper, plain italics indicate scalars, lowercase boldface italics indicate vectors, and uppercase boldface italics indicate matrices.

We define the magnetic field measured by the mth detector coil at time t as b_m(t) and a column vector b(t) ≡ [b₁(t); b₂(t),…, b_M(t)]^T as a set of measured data, where M is the total number of detector coils and the superscript T indicates the matrix transpose. The second-order moment matrix of the measurement is denoted R, i.e., R ≡ 〈b(t)b^T (t)〉, where 〈·〉 indicates the ensemble average over trials. When 〈b(t)〉 = 0, R is also equal to the sample covariance matrix. In practice, the covariance is estimated over a subset of latencies, t ≡ [t₁; t₂,…,t_N], that represents samples from a desired time window of length N. Defining B(t) ≡ [b(t₁),b(t₂),…,b(t_N)], the covariance estimate then becomes R(t) ≡ 〈B(t)B^T (t)〉.

We assume that the sensor data arises from elemental dipoles at each spatial location r, represented by a 3-D vector such that r = (r_x, r_y, r_z). The orientation of each source is defined as a vector η (r) ≡ [β^x, β^y, β^z], where β^x, β^y, and β^z are the angles between the moment vector of the source and the x, y, and z axes, respectively.

We define $l_m^{\varsigma }\left(\mathit{r}\right)$ as the output of the mth sensor that would be induced by a unit-magnitude source located at r and pointing in the ζ direction. The column vector l_ζ(r) is defined as ${\mathit{l}}_{\varsigma }\left(\mathit{r}\right)\equiv {\left[l_1^{\varsigma }\left(\mathit{r}\right),l_2^{\varsigma }\left(\mathit{r}\right),\mathrm{\cdots },l_M^{\varsigma }\left(\mathit{r}\right)\right]}^T$. The lead field matrix, which represents the sensitivity of the whole sensor array at r, is defined as L(r) ≡ [l_x(r); l_y(r); l_z(r)]. The lead field vector for a unit-dipole oriented in the direction η is defined as l(r, η) where l(r, η) ≡ L(r) η (r).

2.2 Conventional Adaptive Spatial Filtering

This section reviews an adaptive spatial filter called the minimum variance (MV) scalar beamformer, also referred to as the synthetic aperture magnetometry (SAM) beamformer (Robinson and Vrba, 1999). An adaptive spatial filter estimate of the source moment ŝ(r, t) is given by

$$\widehat{s}\left(\mathit{r},t\right)={\mathit{w}}^T\left(\mathit{r}\right)\mathit{b}\left(t\right)$$ (1)

where w (r) is the weight vector.

The MV scalar beamformer weight vector w (r) is calculated by minimizing w^T (r)R(t) w(r) subject to l^T (r, η) w(r) = 1. The solution is known to be (Robinson and Vrba, 1999):

$$\mathit{w}\left(\mathit{r}\right)=\frac{{\mathit{R}}^{-1}\left(\mathit{t}\right)\mathit{l}\left(\mathit{r},\mathit{\eta }\right)}{{\mathit{l}}^T\left(\mathit{r},\mathit{\eta }\right){\mathit{R}}^{-1}\left(\mathit{t}\right)\mathit{l}\left(\mathit{r},\mathit{\eta }\right)}.$$ (2)

Finally, in the absence of a priori orientation information from, e.g., MRI, an optimal orientation η_opt(r) must be determined. The typical approach to determining η_opt is to compute the solution that maximizes output power with respect to η (Sekihara and Scholz, 1996). Our approach is to compute the solution that maximizes output SNR (Sekihara et al., 2004):

$${\mathit{\eta }}_{\mathit{\text{opt}}}\left(\mathit{r}\right)=\underset{\mathit{\eta }}{\text{max}}\frac{{\mathit{l}}^T\left(\mathit{r},\mathit{\eta }\right){\mathit{R}}^{-1}\left(\mathit{t}\right)\mathit{l}\left(\mathit{r},\mathit{\eta }\right)}{{\mathit{l}}^T\left(\mathit{r},\mathit{\eta }\right){\mathit{R}}^{-2}\left(\mathit{t}\right)\mathit{l}\left(\mathit{r},\mathit{\eta }\right)}$$ (3)

As shown in Sekihara et al. (2004), the solution for η_opt is υ₃, the eigenvector corresponding to the minimum eigenvalue of:

$${\left[{\mathit{L}}^T\left(\mathit{r}\right){\mathit{R}}^{-1}\left(\mathit{t}\right)\mathit{L}\left(\mathit{r}\right)\right]}^{-1}\left[{\mathit{L}}^T\left(\mathit{r}\right){\mathit{R}}^{-2}\left(\mathit{t}\right)\mathit{L}\left(\mathit{r}\right)\right]{\mathit{\upsilon }}_j={\gamma }_j{\mathit{\upsilon }}_j,$$ (4)

The estimated source power ${\widehat{P}}_s\left(\mathit{r},\mathit{t}\right)$ can be computed from the weights w and covariance R(t):

$${\widehat{P}}_s\left(\mathit{r},\mathit{t}\right)=\langle \widehat{s}{\left(\mathit{r},\mathit{t}\right)}^2\rangle =\langle \left[{\mathit{w}}^T\left(\mathit{r}\right)\mathit{B}\left(\mathit{t}\right)\right]\left[{\mathit{B}}^T\left(\mathit{t}\right)\mathit{w}\left(\mathit{r}\right)\right]\rangle ={\mathit{w}}^T\left(\mathit{r}\right)\mathit{R}\left(\mathit{t}\right)\mathit{w}\left(\mathit{r}\right)$$ (5)

The sensor noise power σ²(t) may be obtained from calibration measurements of the MEG system or estimated by computing the minimum eigenvalue of R(t). Then, the power of projected sensor noise ${\widehat{P}}_N$ may be estimated by replacing R(t) with σ²(t)I:

$${\widehat{P}}_N\left(\mathit{r}\right)={\mathit{w}}^T\left(\mathit{r}\right)\left[{\mathit{\sigma }}^2\left(\mathit{t}\right)\mathit{I}\right]\mathit{w}\left(\mathit{r}\right)={\mathit{\sigma }}^2\left(\mathit{t}\right){\mathit{w}}^T\left(\mathit{r}\right)\mathit{w}\left(\mathit{r}\right)$$ (6)

Often, one is interested in the change in power from a control (i.e., baseline) time window to an active time window, i.e., adual-condition paradigm. These windows are denoted as vectors of time samples, t_con and t_act, respectively. In this case:

$${\widehat{P}}_{\mathit{\text{con}}}\left(\mathit{r}\right)={\widehat{P}}_s\left(\mathit{r},{\mathit{t}}_{\mathit{\text{con}}}\right)={\mathit{w}}^T\left(\mathit{r}\right){\mathit{R}}_{\mathit{\text{con}}}\mathit{w}\left(\mathit{r}\right)$$ (7)

$${\widehat{P}}_{\mathit{\text{act}}}\left(\mathit{r}\right)={\widehat{P}}_s\left(\mathit{r},{\mathit{t}}_{\mathit{\text{act}}}\right)={\mathit{w}}^T\left(\mathit{r}\right){\mathit{R}}_{\mathit{\text{act}}}\mathit{w}\left(\mathit{r}\right)$$ (8)

where R_con ≡ R(t_con), the covariance of the control window, and R_act ≡ R(t_act), the covariance of the active window.

In order to improve numerical stability and ensure an appropriately matched baseline period, the same orientation η_opt(r) and w(r) must be used to compute ${\widehat{P}}_{\mathit{\text{act}}}\left(\mathit{r}\right)\text{and}{\widehat{P}}_{\mathit{\text{con}}}\left(\mathit{r}\right)$. This ensures that the magnitude of sources are comparable between the active and control periods; it also decreases the likelihood of resolving false sources. Thus, η_opt(r) and w(r) may be computed using the average covariance of the active and control periods, i.e., by substituting R = (R_act + R_con)/2. Note that t_con must be the same length as t_act.

The contrast between ${\widehat{P}}_{\mathit{\text{act}}}\text{and}{\widehat{P}}_{\mathit{\text{con}}}$ can then be expressed as a pseudo-t difference ${\widehat{P}}_{\mathit{\text{act}}}-{\widehat{P}}_{\mathit{\text{con}}}$ or an F-ratio ${\widehat{P}}_{\mathit{\text{act}}}/{\widehat{P}}_{\mathit{\text{con}}}$. If the contribution of projected sensor noise is subtracted, the ratio becomes $F=\left({\widehat{P}}_{\mathit{\text{act}}}-{\widehat{P}}_N\right)/\left({\widehat{P}}_{\mathit{\text{con}}}-{\widehat{P}}_N\right)$. In this paper, we will use the noise-corrected F-ratio expressed in units of decibels:

$$F_{dB}=10{\text{log}}_{10}\frac{{\widehat{P}}_{\mathit{\text{act}}}-{\widehat{P}}_N}{{\widehat{P}}_{\mathit{\text{con}}}-{\widehat{P}}_N}.$$ (9)

2.2.1 Time-Frequency Extension of Conventional Beamformers

It is often desirable to compute contrasts for multiple activation windows and possibly multiple baseline windows, relative to specific experimental or cognitive events. The resulting contrasted spectrogram is a time-frequency representation of source events. In order to obtain such a representation from the conventional beamformer, one may directly compute the spectrogram of the source time series from Equation 1, contrasting it with the spectrogram of the control period (Singh et al., 2002; Cheyne et al., 2003).

Another approach is to apply the weights w(r) computed above—with R estimated from long time windows t_act and t_con spanning the entire duration of interest—to a new set of covariance estimates generated from filtered and segmented data. First, the data is passed through a filter bank and partitioned into several overlapping active segments, τ_act[n], and a control segment, τ_con, where the subscript n refers to the index of the time window. (These windows are shorter than t_act and t_con.) Then, covariances are computed for each resulting time-frequency window, yielding ${\tilde{\mathit{R}}}_{\mathit{\text{act}}}\left(n,f\right)\equiv \mathit{R}\left({\mathit{\tau }}_{\mathit{\text{act}}}\left[n\right],f\right)\text{and}{\tilde{\mathit{R}}}_{\mathit{\text{con}}}\left(f\right)\equiv \mathit{R}\left({\mathit{\tau }}_{\mathit{\text{con}}},f\right),$ where f corresponds to the index of the frequency band. Power maps may be computed directly by replacing R_act and R_con with ${\tilde{\mathit{R}}}_{\mathit{\text{act}}}\left(n,f\right)\text{and}{\tilde{\mathit{R}}}_{\mathit{\text{con}}}\left(f\right):$, respectively:

$${\widehat{P}}_{\mathit{\text{con}}}\left(\mathit{r},n,f\right)={\mathit{w}}^T\left(\mathit{r}\right){\tilde{\mathit{R}}}_{\mathit{\text{con}}}\left(f\right)\mathit{w}\left(\mathit{r}\right)$$ (10)

$${\widehat{P}}_{\mathit{\text{act}}}\left(\mathit{r},n,f\right)={\mathit{w}}^T\left(\mathit{r}\right){\tilde{\mathit{R}}}_{\mathit{\text{act}}}\left(n,f\right)\mathit{w}\left(\mathit{r}\right)$$ (11)

$${\widehat{P}}_N\left(\mathit{r},n,f\right)={\sigma }^2\left(n,f\right){\mathit{w}}^T\left(\mathit{r}\right)\mathit{w}\left(\mathit{r}\right)$$ (12)

Finally,

$$F_{dB}\left(\mathit{r},n,f\right)=10{\text{log}}_{10}\frac{{\widehat{P}}_{\mathit{\text{act}}}\left(\mathit{r},n,f\right)-{\widehat{P}}_N\left(\mathit{r},n,f\right)}{{\widehat{P}}_{\mathit{\text{con}}}\left(\mathit{r},n,f\right)-{\widehat{P}}_N\left(\mathit{r},n,f\right)}.$$ (13)

However, while spectrograms may be constructed from the conventional beamformer in this fashion, the weights are still optimized for the wide t_act and t_con windows used to compute w(r). MEG/EEG spectra follows the power law, implying that weights generated from unfiltered data are inherently biased towards low-frequency activity.

2.3 Frequency-Dependent Weight Computation

Therefore, in order to better resolve low-amplitude, high-frequency activity, one approach is to calculate a different set of weights for each frequency band:

$$\mathit{w}\left(\mathit{r},f\right)=\frac{{\mathit{R}}^{-1}\left(f\right){\mathit{l}}^T\left(\mathit{r},\mathit{\eta }\right)}{\mathit{l}\left(\mathit{r},\mathit{\eta }\right){\mathit{R}}^{-1}\left(f\right)\mathit{l}\left(\mathit{r},\mathit{\eta }\right)}$$ (14)

where R(f) is the sample covariance matrix generated from B(t) filtered for the frequency band of interest, and η = η _opt(r, f), i.e., the optimum orientation computed using R(f). The corresponding power at each voxel for each frequency band is:

$${\widehat{P}}_s\left(\mathit{r},f\right)={\mathit{w}}^T\left(\mathit{r},f\right)\mathit{R}\left(f\right)\mathit{w}\left(\mathit{r},f\right)$$ (15)

Again, the powers of an active window and a control window may be computed as follows:

$${\widehat{P}}_{\mathit{\text{con}}}\left(\mathit{r},f\right)={\widehat{P}}_s\left(\mathit{r},{\mathit{t}}_{\mathit{\text{con}}},f\right)={\mathit{w}}^T\left(\mathit{r},f\right){\mathit{R}}_{\mathit{\text{con}}}\left(f\right)\mathit{w}\left(\mathit{r},f\right)$$ (16)

$${\widehat{P}}_{\mathit{\text{act}}}\left(\mathit{r},f\right)={\widehat{P}}_s\left(\mathit{r},{\mathit{t}}_{\mathit{\text{act}}},f\right)={\mathit{w}}^T\left(\mathit{r},f\right){\mathit{R}}_{\mathit{\text{act}}}\left(f\right)\mathit{w}\left(\mathit{r},f\right)$$ (17)

The time-frequency representation may be computed either from the source time series, or, as shown here, by using w(r; f) from Equation 14 and replacing R(f) from Equation 15 with${\tilde{\mathit{R}}}_{\mathit{\text{act}}}\left(n,f\right)\text{and}{\tilde{\mathit{R}}}_{\mathit{\text{con}}}\left(f\right):$

$${\widehat{P}}_{\mathit{\text{con}}}\left(\mathit{r},f\right)={\mathit{w}}^T\left(\mathit{r},f\right){\tilde{\mathit{R}}}_{\mathit{\text{con}}}\left(f\right)\mathit{w}\left(\mathit{r},f\right)$$ (18)

$${\widehat{P}}_{\mathit{\text{act}}}\left(\mathit{r},n,f\right)={\mathit{w}}^T\left(\mathit{r},f\right){\tilde{\mathit{R}}}_{\mathit{\text{act}}}\left(n,f\right)\mathit{w}\left(\mathit{r},f\right)$$ (19)

$${\widehat{P}}_N\left(\mathit{r},n,f\right)={\sigma }^2\left(n,f\right){\mathit{w}}^T\left(\mathit{r},f\right)\mathit{w}\left(\mathit{r},f\right)$$ (20)

$$F_{dB}\left(\mathit{r},n,f\right)=10{\text{log}}_{10}\frac{{\widehat{P}}_{\mathit{\text{act}}}\left(\mathit{r},n,f\right)-{\widehat{P}}_N\left(\mathit{r},n,f\right)}{{\widehat{P}}_{\mathit{\text{con}}}\left(\mathit{r},n,f\right)-{\widehat{P}}_N\left(\mathit{r},n,f\right)}.$$ (21)

This formulation accounts for amplitude differences between different frequency bands, but its performance may be degraded in the presence of activity that is more transient. Sources that are active only briefly may not be adequately captured. Similarly, the spatial filters may not be optimized for sources that change position and orientation over time. Lastly, when analyzing long epochs, this method might be prone to sources active at different latencies interfering with each other. For example, if one source has an early response, and another nearby source becomes active later in the same frequency band, then generating weights from the covariance of the whole interval may result in degraded reconstruction and poor separation of the two sources.

2.4 Proposed Time-Frequency Optimized Beamforming

To overcome the above mentioned limitations, we propose that a custom set of weights w(r, n, f) be generated from the sample covariances ${\tilde{\mathit{R}}}_{\mathit{\text{act}}}\left(n,f\right)$ corresponding to each time-frequency window. As in the approaches described above, the data is first passed through a filter bank and subsequently segmented into overlapping active windows, τ_act[n], and control windows, τ_con[n]. For optimum time-frequency resolution and beamformer performance, it is desirable to choose larger time windows for lower frequencies and narrower time windows for higher frequencies.

$$\mathit{w}\left(\mathit{r},n,f\right)=\frac{{\mathit{R}}^{-1}\left(n,f\right)\mathit{l}\left(\mathit{r}\right)}{{\mathit{l}}^T\left(\mathit{r}\right){\mathit{R}}^{-1}\left(n,f\right)\mathit{l}\left(\mathit{r}\right)}$$ (22)

where $\mathit{R}\left(n,f\right)=\left[{\tilde{\mathit{R}}}_{\mathit{\text{act}}}\left(n,f\right)+{\tilde{\mathit{R}}}_{\mathit{\text{con}}}\left(f\right)\right]/2.$ Then,

$${\widehat{P}}_{\mathit{\text{con}}}\left(\mathit{r},n,f\right)={\mathit{w}}^T\left(\mathit{r},n,f\right){\tilde{\mathit{R}}}_{\mathit{\text{con}}}\left(f\right)\mathit{w}\left(\mathit{r},n,f\right)$$ (23)

$${\widehat{P}}_{act}\left(\mathit{r},n,f\right)={\mathit{w}}^T\left(\mathit{r},n,f\right){\tilde{\mathit{R}}}_{act}\left(n,f\right)\mathit{w}\left(\mathit{r},n,f\right)$$ (24)

$${\widehat{P}}_N\left(\mathit{r},n,f\right)={\sigma }^2\left(n,f\right){\mathit{w}}^T\left(\mathit{r},n,f\right)\mathit{w}\left(\mathit{r},n,f\right)$$ (25)

$$F_{dB}\left(\mathit{r},n,f\right)=10{\text{log}}_{10}\frac{{\widehat{P}}_{\mathit{\text{act}}}\left(\mathit{r},n,f\right)-{\widehat{P}}_N\left(\mathit{r},n,f\right)}{{\widehat{P}}_{\mathit{\text{con}}}\left(\mathit{r},n,f\right)-{\widehat{P}}_N\left(\mathit{r},n,f\right)}.$$ (26)

Finally, the estimated power of overlapping segments are averaged to improve numerical stability and better capture transitions in source activity. The procedure is summarized in Figure 1.

Fig. 1.

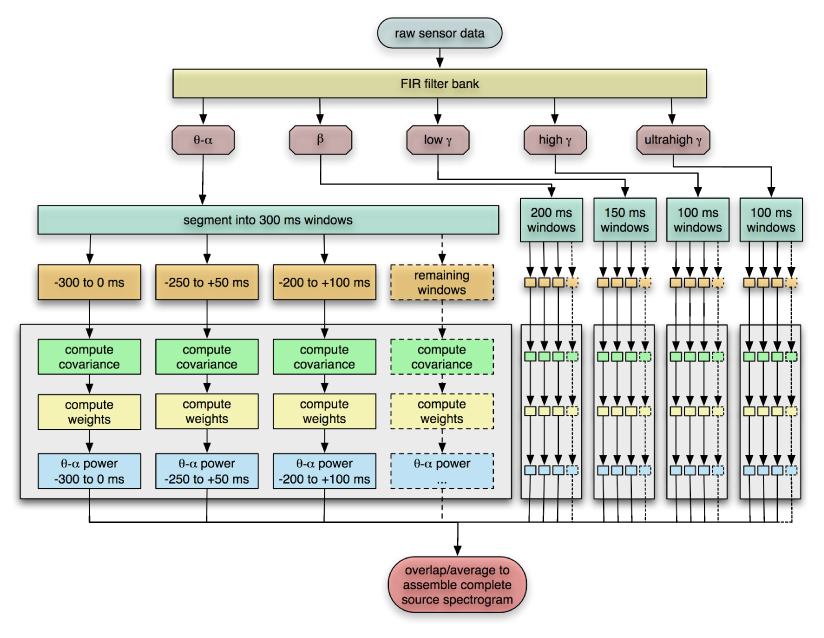
Algorithm for optimal time-frequency beamforming. Processing of the combined θ-α band is shown in detail; each of the other frequency bands has a similar workflow. Note that the algorithm is highly parallel and well-suited to run on high performance computing clusters.

The computational load of the algorithm scales linearly with the number of time-frequency bins. In practice, hundreds of weight vectors must be computed to assemble a complete source spectrogram and would require dozens of CPU hours to complete. However, since the result for each time-frequency window is essentially an independent computation, the time-frequency array is well-suited for running on a parallel computing cluster. We used the shared computing cluster at the California Institute for Quantitative Biomedical Research to generate the results shown in this paper; the total running time for generating images for all time-frequency windows is less than 20 minutes when the cluster is unloaded and all windows can be processed on approximately 300 nodes simultaneously. Upon conclusion of the cluster run, the results were assembled and visualized with a development version of our NUTMEG neuromagnetic source reconstruction toolbox (Dalal et al., 2004), freely available from http://bil.ucsf.edu.

The filter bank approach provides an inherent potential advantage over FFT and wavelet-based techniques, since frequency bins can be of variable size and customized according to the experimenter’s hypothesis. For example, it has been suggested that the spectral peak of high gamma activity may vary across subjects and even within an individual (Crone et al., 2001a; Edwards et al., 2005); therefore, those bands may be defined with a larger bandwidth. We chose to follow traditional MEG/EEG power band definitions as best as possible for the experiments presented here: 4–12 Hz (theta-alpha), 12–30 Hz (beta), 30–55 Hz (low gamma), and 65–90 Hz (high gamma). Additionally, we defined ultrahigh frequency bands at 90–115 Hz, 125–150 Hz, 150–175 Hz, and 185–300 Hz. The power line frequency (60 Hz) and harmonics (120 Hz and 180 Hz) were avoided to reduce noise.

The length of the time windows and width of the frequency bands must be chosen to ensure that stable and well-conditioned estimates of the covariance matrices are produced. The parameters used in this paper were determined with this in mind, but may need to be adjusted for other MEG systems or data characteristics. See the Supplementary Methods online for an exploration of the effect of time window length and bandwidth on performance of the proposed algorithm.

2.5 Across-Subjects Statistics

The significance of activations across subjects was tested with statistical nonparametric mapping (SnPM) (http://www.sph.umich.edu/ni-stat/SnPM/). SnPM does not depend on a normal distribution of power change values across subjects and allows correction for familywise error of testing at multiple voxels and time-frequency points. The detailed rationale and procedures of SnPM statistics of beamformer images are described elsewhere (Singh et al., 2003). In short, time-frequency beamformer images for each subject were first spatially normalized to the MNI template brain using SPM (http://www.fil.ion.ucl.ac.uk/spm). The three-dimensional average and variance maps across subjects were calculated at each time-frequency point. he variance estimates can be noisy for a relatively low number of subjects, so the variance maps were smoothed with a 20×20×20 mm Gaussian kernel. From this, a pseudo-t statistic was obtained at each voxel, time window, and frequency band. In addition, a distribution of pseudo-t statistics was also calculated from 2^N permutations of the original N datasets (subjects). Each permutation consisted of two steps: 1) inverting the polarity of the power change values for some subjects (with 2^N possible combinations of negations), and 2) finding the current maximum pseudo-t value among all voxels and time windows for each frequency band. Instead of estimating the significance of each non-permuted pseudo-t value from an assumed normal distribution, it is then calculated from the position within the distribution of these maximum permuted pseudo-t values. The comparison against maximum values effectively corrects for the familywise error of testing multiple voxels and time windows.

2.6 Numerical Experiments

2.6.1 Data Generation

Numerical experiments were conducted to evaluate the proposed method and compare it with existing methods. The sensor configuration of the 275-channel CTF Omega 2000 biomagnetic measurement system (VSM MedTech, Coquitlam, BC, Canada) was used. Data were simulated and processed using a development version of NUTMEG (Dalal et al., 2004).

Fifty trials of simulated data were generated, spanning −750 ms to 1000 ms per trial, sampled at 1200 Hz. Two 77 Hz sine wave sources were synthesized and placed at (10, 50, 60) mm and (15, 60, 75) mm¹; the phases of each source were assigned randomly and varied between each other and each trial. The sine waves were windowed such that they represented ERS activity and were not simultaneously active; one source was active from 50 ms to 300 ms, while the other was active from 350 ms to 550 ms. A third 19 Hz source was placed at (25, 30, 100) mm, active from −750 ms to 50 ms and from 600 ms to 1000 ms to simulate ERD activity.

A sensor lead field was calculated with 5 mm grid spacing using a single-layer multiple sphere volume conductor as the forward model (Huang et al., 1999) and the Omega 2000’s sensor geometry with respect to a real subject’s head-shape. Spontaneous MEG recordings from a human subject (“brain noise”) were added to the generated data such that the signal-to-noise (SNR) was equal to 1. The SNR was defined as the ratio of the Frobenius norm of the simulated data matrix to that of the brain noise matrix.

2.6.2 Data Processing

Covariances for use with the beamformers were generated by creating a lattice of time-frequency windows. The original data were first passed through a bank of 200th-order finite impulse response (FIR) bandpass filters and subsequently split into 29 overlapping temporal windows with a step size of 25 ms for all bands. In our filter design, we chose to follow traditional MEG/EEG power band definitions as best as possible. Theta-alpha band was defined as 4–12 Hz with 300 ms windows, beta band 12–30 Hz with 200 ms windows, low gamma 30–55 Hz with 150 ms windows. Additionally, five high gamma bands were defined, avoiding the 60 Hz power line frequency and its harmonics: 65–90 Hz, 90–115 Hz, 125–150 Hz, 150–175 Hz, 185–300 Hz, all with 100 ms windows. Finally, sample covariances were calculated for this matrix of time-frequency windows and averaged over trials:

$${\tilde{\mathit{R}}}_{\mathit{\text{act}}}\left(n,f\right)=\langle {\mathit{B}}_f\left({\mathit{\tau }}_{\mathit{\text{act}}}\left[n\right]\right){\mathit{B}}_f^T\left({\mathit{\tau }}_{\mathit{\text{act}}}\left[n\right]\right)\rangle$$ (27)

Spatial filter weights were computed for each time-frequency window, and an F_dB(r; n; f) space-time-frequency power map was assembled as described earlier.

For comparison, the data was processed in three additional ways. In the first way, which we will term the “broadband” approach, the simulated data were processed with a conventional minimum variance beamformer; i.e., a single weight was computed from unfiltered data using one large active window and a corresponding large control window (Equation 2). In this case, 0 ms to 500 ms was chosen as the active window, and −600 ms to −100 ms was chosen as the control window. This weight was then applied to the sample covariances for each time-frequency window to calculate estimated power and contrasted with the estimated power of the control period to generate the final space-time-frequency representation.

The second way was a frequency-dependent beamformer approach (Equation 14). The original simulated data was passed through the same filter bank as with our proposed method. However, instead of segmenting into several time windows, the single large active window with a corresponding control window was chosen as for the broadband approach. Thus, weights were computed for filtered data corresponding to each frequency band. Again, 0 ms to 500 ms was chosen as the active window, with −600 ms to −100 ms as the control window. Weights, powers, and the final power map were generated as with the other two techniques.

Finally, the data was analyzed with sLORETA (Pascual-Marqui, 2002) as a representative of minimum norm source reconstruction techniques. As sLORETA is a nonadaptive spatial filter dependent only on sensor configuration, the same set of weights was applied to the sample covariances for each time-frequency window. The estimated power and contrast with a control period was performed as described above with the beamformer techniques (Equation 13).

2.7 Finger Movement Data

2.7.1 Subjects

Data was collected from 12 right-handed volunteers (6 females and 6 males, mean age 29.2 years, age range 22–38 years). The participants were screened for potentially confounding health conditions and medications. The study protocol was approved by the UCSF Committee on Human Research.

2.7.2 Data Acquisition and Processing

Data was acquired with a 275-channel CTF Omega 2000 whole-head MEG system from VSM MedTech (Coquitlam, BC, Canada) with a 1200 Hz sampling rate. All post-processing and analysis were performed using a development version of NUTMEG (Dalal et al., 2004). A digital filter was used to high-pass the data at 1 Hz. Trials containing eyeblink and movement artifacts were manually rejected.

Subjects were instructed to press the response button with their right index finger (RD2) at a self-paced interval of approximately four seconds, acquiring 100 trials. In a subsequent block, the subjects completed the same task with their left index finger (LD2) instead.

The data was processed as in the above simulation, but with 50 ms window step size due to the length of the epochs. For the broadband and frequency-domain methods, the active window was chosen to be −250 ms to 250 ms relative to the button press, with −950 ms to −450 ms as the baseline. These windows were chosen based on typical results in the literature (Pfurtscheller and Neuper, 1992; Jurkiewicz et al., 2006) and our laboratory’s extensive unpublished clinical data.

As with the simulations, a multiple sphere head model was calculated for each subject at 5 mm resolution based on individual head shape and relative sensor geometry. Spectral power changes were statistically tested across subjects with the SnPM method described above, with p < 0:05 as the threshold for significant activity.

2.8 Intracranial Recordings

Preoperative MEG data and corresponding intracranial electrocorticograms (ECoG) were obtained from two patients undergoing surgical treatment for intractable epilepsy. Intracranial electrodes were implanted in these patients for preresection seizure localization and functional mapping of critical language and motor areas. The study protocol, approved by the UCSF and UC Berkeley Committees on Human Research, did not interfere with the ECoG recordings made for clinical purposes and presented minimal risk to the subjects. Upon informed consent, the experiments were conducted while the patient was alert and on minimal medication. The implants consisted of an 8×8 grid of platinum-iridium electrodes (Ad-Tech Medical, Racine, WI) placed over the left frontotemporal region (Figure 2(a)). The electrodes had a 2.3 mm contact diameter and a center-to-center spacing of 10 mm. Electrodes with an impedance greater than 5 kΩ or exhibiting epileptiform activity were rejected from further analyses. An electrode in the corner of the electrode grid was selected as the reference. Data was collected with an EEG amplifier (SA Instrumentation, San Diego, CA) sampling at 2003 Hz with 16-bit resolution. As with the MEG experiment, patients were asked to move their right index finger (RD2) at a self-paced interval of approximately four seconds for a total of 100 trials. Both patients had corresponding MEG recordings acquired one day prior to their grid implants. The recordings were conducted identically as with the healthy volunteers (see above).

Fig. 2.

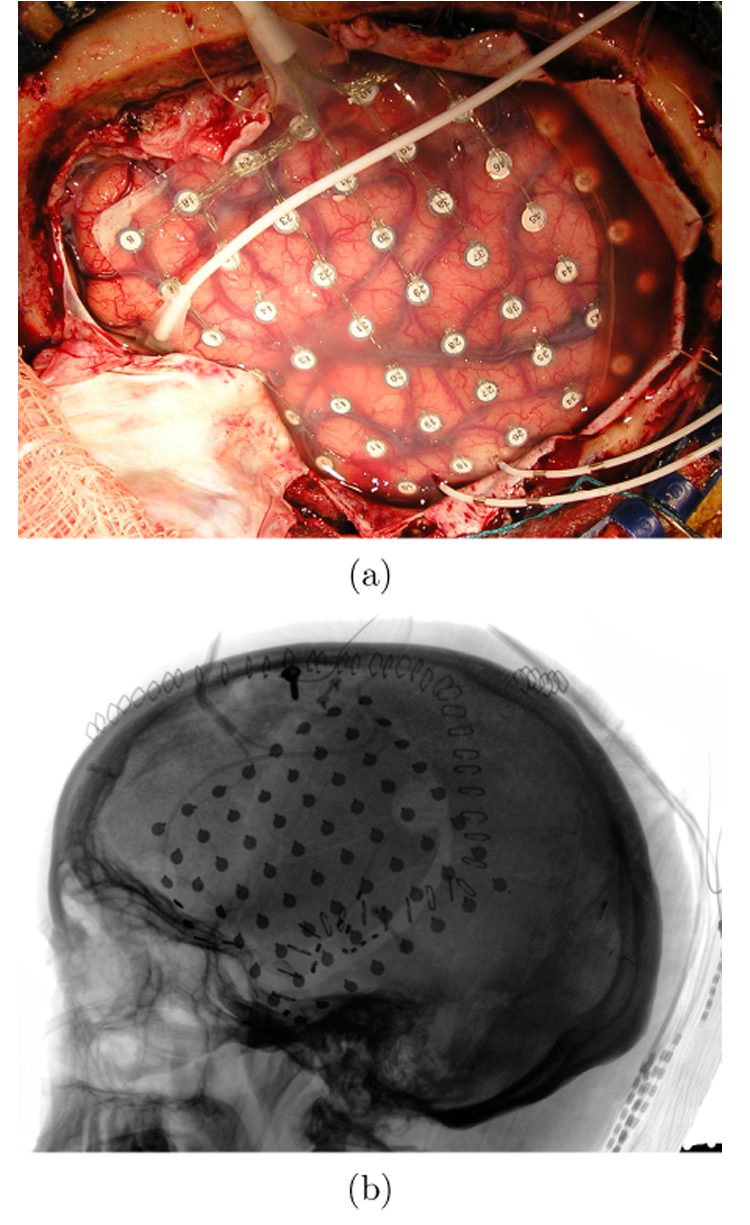
(a) Example of a typical frontotemporal ECoG montage in an intractable epilepsy patient. The implant consists of an 8×8 electrode grid with 10 mm center-to-center spacing between electrodes. (b) Lateral X-ray radiograph of the same patient showing electrode locations. The surgical photograph was used to annotate the locations of visible electrodes on an MRI rendering, while the coordinates of hidden electrodes were found using X-ray backprojection to the MRI-derived brain surface (Dalal et al., 2007).

Electrodes were localized on individual subject MRIs using visual identification of landmarks on intraoperative photographs and backprojection from postimplant X-rays as described in Dalal et al. (2007) (Figure 2). Time-frequency analyses of ECoG data were performed using the event-related spectral perturbation (ERSP) method (Makeig, 1993). Time courses for the power of single trial data were generated for each frequency band using a Gaussian filter bank and the Hilbert transform (Edwards, 2007); after averaging across trials, the power time courses were divided by the mean baseline spectrum to generate the ERSP. These results were converted to decibels and then rebinned into the same time-frequency windows used to analyze the MEG data for ease of comparison. Electrodes were localized on individual subject MRIs using visual identification of landmarks on intraoperative photographs and backprojection from postimplant X-rays as described in Dalal et al. (2007) (Figure 2).

Time-frequency analyses of ECoG data were performed using the event-related spectral perturbation (ERSP) method (Makeig, 1993). Time courses for the power of single trial data were generated for each frequency band using a Gaussian filter bank and the Hilbert transform (Edwards, 2007); after averaging across trials, the power time courses were divided by the mean baseline spectrum to generate the ERSP. These results were converted to decibels and then rebinned into the same time-frequency windows used to analyze the MEG data for ease of comparison.

3 Results

3.1 Numerical Experiments

The sLORETA method produced relatively blurry results for all three simulated sources, with peaks on the periphery of the defined volume of interest in each case (see Figure 3). The reconstructions were not of sufficiently high fidelity to appreciably distinguish the spectrograms of the different sources. Several regularization parameters were tested with similar results.

Fig. 3.

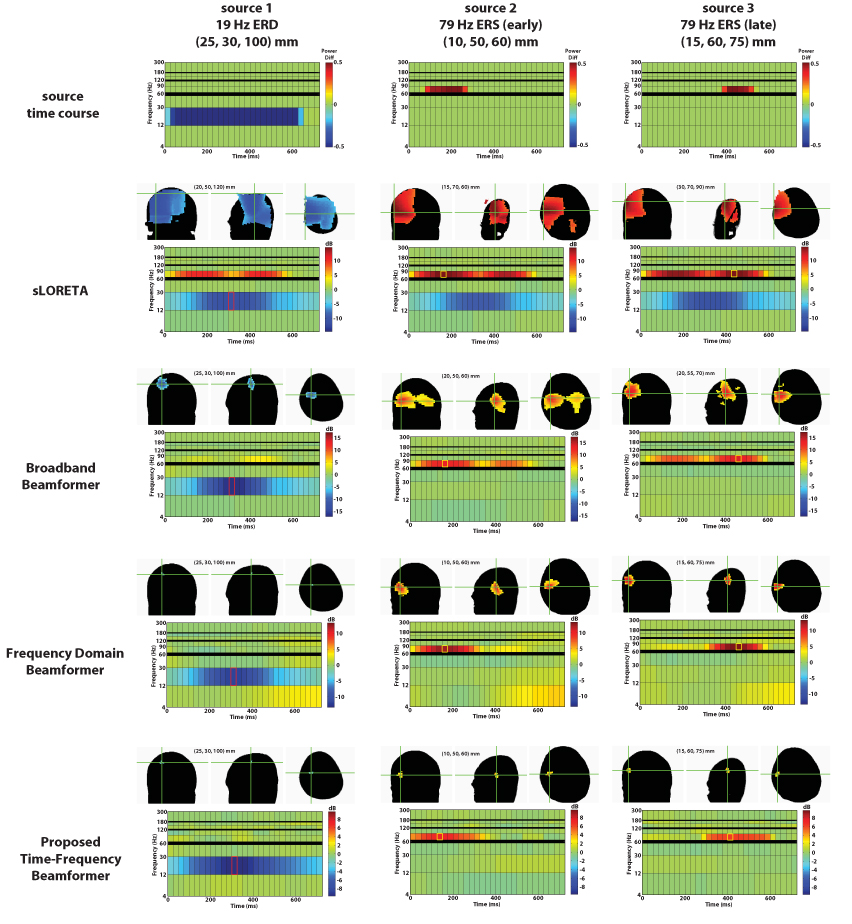
At top is the spectrogram corresponding to the three simulated sources. In the rows below are the reconstruction results using sLORETA, the broadband beamformer, the frequency domain beamformer, and the proposed time-frequency beamformer. In each of those panels, the crosshairs mark the spatiotemporal peak for the reconstructed source, with the corresponding spectrogram shown below it. The time-frequency window plotted on the MRI is highlighted on the spectrogram. The functional maps are thresholded at 50% of the maximum power (in dB) for the beamformer variants and 75% for sLORETA.

The broadband beamformer correctly placed the peak of beta ERD at (25, 30, 100) mm. (See Figure 3.) However, the spatiotemporal extent of both high gamma ERS sources were not as cleanly resolved. The first source was placed at (20, 50, 60) mm peaking over 150–175 ms, while the second source was placed at (20,55,70) mm, peaking over 450–475 ms. Additionally, the spatial extent of all sources was blurred.

The frequency domain beamformer found the correct location of the beta ERD, resolving a more focal peak than the broadband beamformer. (See Figure 3.) It also found the correct locations for both high gamma ERS sources. However, the activation was spatially blurred and attenuated for the high gamma ERS sources, especially over 300–350 ms when one source tapers off and other tapers on. Additionally, the spatiotemporal extent of all three sources was compromised. The spectrogram computed for (15,60,75) mm shows contamination from the (10,50,60) mm source and vice versa.

Finally, we applied our proposed technique to the data. (See Figure 3.) As expected, the beta ERD was accurately resolved. Both high gamma ERS sources were accurately localized and their temporal extents accurately captured. Virtually no contamination between the two source locations were observed on their respective spectrograms. This method provided the best reconstruction of the simulated data.

3.2 Finger Movement Data

The characteristic beta band power decrease in contralateral sensorimotor cortex was observed and reached statistical significance across subjects for all three beamformer variants. (See Figure 4 for corresponding MNI coordinates and corrected p values for right index finger movement.) However, only low-amplitude early time windows near −400 ms were significant for the broadband beamformer. In contrast, significant contralateral activation was observed over −500 ms to 250 ms with both the proposed time-frequency beamformer and the frequency-domain beamformer, although results were more spatially focal for the proposed method. Additionally, both of these methods revealed significant beta band power decreases in ipsilateral sensorimotor cortex and ipsilateral secondary somatosensory cortex approximately 0 ms to 200 ms after movement onset.

Fig. 4.

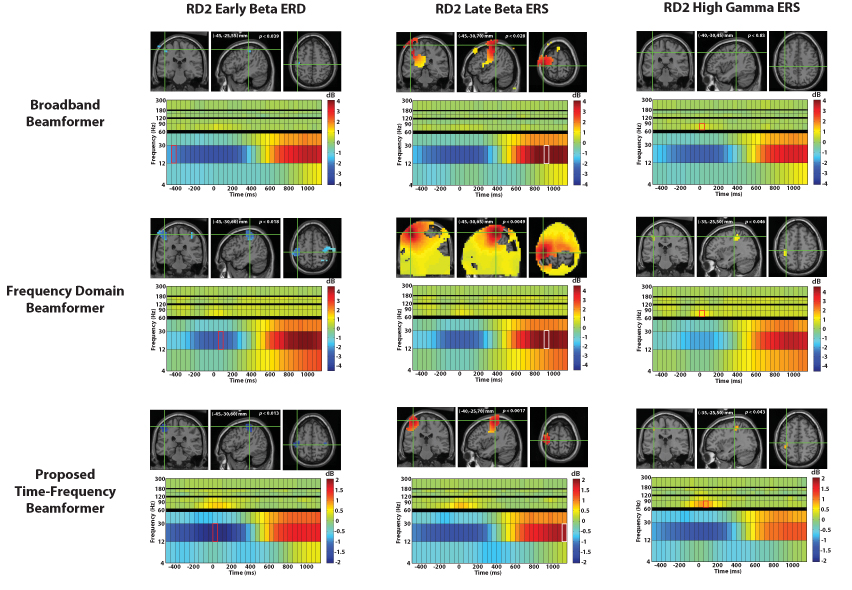
Shown above are the grand average reconstruction results for right index finger movement using the broadband beamformer, the frequency domain beamformer, and the proposed time-frequency beamformer. The functional maps are superimposed on the MNI template brain and are statistically thresholded at p < 0:05 (corrected). In each of the panels, the crosshairs mark the spatiotemporal peak for the reconstructed source, with the corresponding spectrogram shown below it. The functional map plotted on the MRI corresponds to the time-frequency window highlighted on the spectrogram. Note that the frequency-domain beamformer localized peaks similar to the other methods, but grossly overestimated the statistically significant spatial extent of the late beta ERS, likely due to a large baseline shift of inactive voxels.

The contralateral decrease in beta power was followed by a significant contralateral beta rebound for all three methods. Again, the time-frequency beamformer performed the best, with a relatively focal activation area. The broadband beamformer revealed a peak in sensorimotor cortex, but the spatial extent of the activation extended into areas both implausibly deep as well as outside the brain. The frequency-domain beamformer placed the peak nearby, but grossly overestimated the statistically significant spatial extent, apparently due to a large baseline shift evident in voxels distant from motor cortex. The time-frequency beamformer depicts a relatively focal activation in contralateral sensorimotor cortex. (Individual results for many subjects also showed an ipsilateral beta rebound, but this did not reach statistical significance across subjects.) It also found an increase in beta power peaking at (5,− 5,65) mm (MNI coordinates, p < 0.038, corrected), corresponding to activation of the supplementary motor area (SMA) (not shown).

Interestingly, both the frequency-domain beamformer and the time-frequency beamformer localized a focal, statistically significant high gamma (65–90 Hz) peak in sensorimotor cortex. This activity was found to be more spatially focal and temporally bound to the movement. No significant high gamma activity was observed with the broadband beamformer.

Similarly, the proposed technique revealed similar activity for left index finger movement (Figure 5). The typical beta band desynchronization and late rebound as well as high gamma activity were found in right sensorimotor cortex, reaching statistical significance across subjects.

Fig. 5.

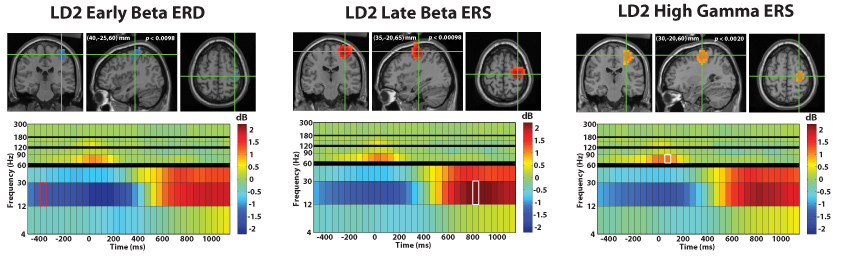
Shown above are the grand average reconstruction results for left index finger movement using the proposed time-frequency beamformer, superimposed on the MNI template brain. The functional maps are superimposed on the MNI template brain and are statistically thresholded at p < 0:05 (corrected). In each panel, the crosshairs mark the spatiotemporal peak for the reconstructed source, with the corresponding spectrogram shown below it. The functional map plotted on the MRI corresponds to the time-frequency window highlighted on the spectrogram.

Activation of the cerebellum was also found in 9 of 12 healthy volunteers and in both of the patients. (See Figure 6.) While the spatiotemporal extent and particular frequency content of cerebellar activations exhibited considerable variability across subjects and did not reach statistical significance in our across-subject analyses with whole-brain multiple comparison correction, we did observe that our method found consistent high-frequency sources in the cerebellum in either the 65–90 Hz or 90–115 Hz bands. Examples of distinct cerebellar responses from two subjects are shown in Figure 6; see Figure 7 for responses from the two patients.

Fig. 6.

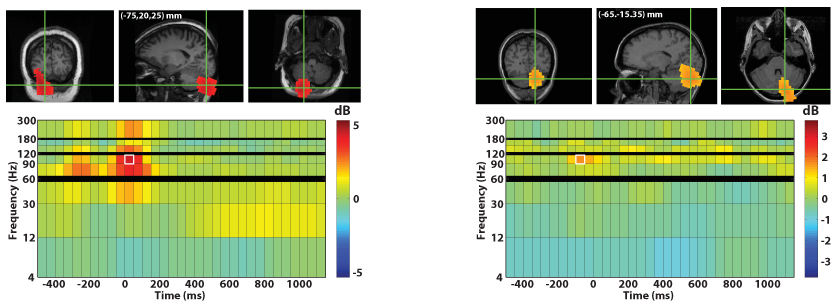
Above, examples of cerebellum activation for finger movement in two subjects. Above left are the results for RD2 movement in one subject. Above right are the results for LD2 movement in a different subject. Both functional maps are thresholded at 75% of the maximum power (in dB).

Fig. 7.

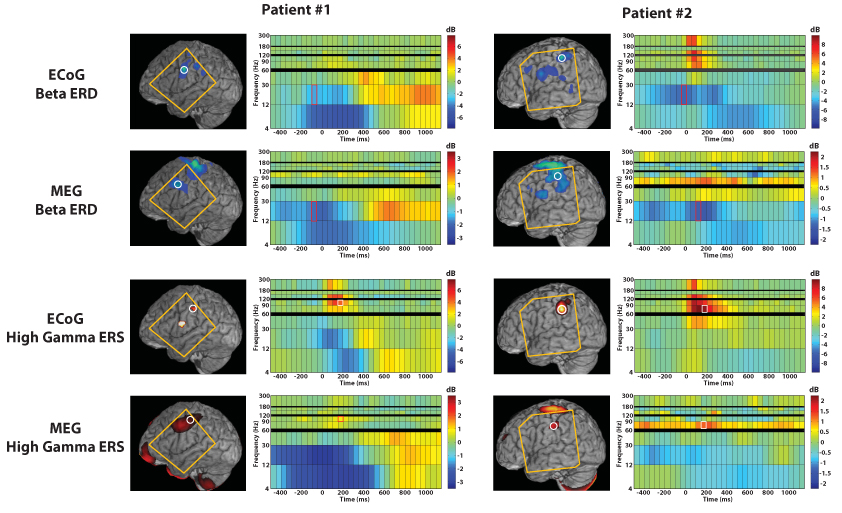
Shown above are the right finger (RD2) movement activity for two intractable epilepsy patients, using both time-frequency analyses from an 8×8 intracranial electrode grid and the corresponding results from preoperative magnetoencephalography and the proposed time-frequency beamformer. The spectrogram corresponds to the circled spatial location, while the functional maps show the spatial extent of activation for the indicated time window and frequency band. The orange outline indicates the region covered by the intracranial electrode grid. Note that MEG reveals strong primary motor cortex and cerebellum activity, but these areas were not covered with electrodes in either patient; instead, lower-amplitude secondary activations are compared between the two methods.

3.3 Intracranial Recordings

As shown in Figure 7, several locations showing ECoG activity during the right finger movement task were also found with the proposed MEG time-frequency beamformer method and exhibited fairly similar spectrogram patterns. Table 1 lists the coordinates of each peak in the grid coverage area for beta and high gamma activations for both patients. MEG peaks were found between 2.8 mm and 10.4 mm from eight ECoG peaks, while two adjacent electrodes showing low-amplitude beta ERD and one electrode showing high gamma ERS did not have corresponding MEG activations.

Table 1.

The above table lists ECoG electrode locations with activity in the beta and high gamma bands and the nearest peaks found from the MEG time-frequency beamformer reconstruction. Note that coordinates given are in each patient’s native MRI space (rather than MNI coordinates) in order to accurately characterize Euclidean distances between ECoG and MEG peaks, given in the last column.

Patient	Band	ECoG Coords (mm)	MEG Coords (mm)	Difference (mm)
1	beta	−50.6, 3.8, 28.2	−45.8, −1.2, 25.5	7.5
1	beta	−55.2, 13.2, 9.4	−50.3, 13.8, 15.3	7.7
1	beta	−54.9, −0.7, 20.6	−50.8, −1.1, 25.4	6.3
1	beta	−57.7, −5.1, 0.0	-	-
1	beta	−57.7, 0.6, 7.7	-	-
1	high gamma	−54.9, −0.7, 20.6	−51.0, −3.1, 30.0	10.4
1	high gamma	−53.7, 20.3, 3.9	-	-
2	beta	−56.9, −24.4, 30.6	−51.3, −28.9, 36.7	9.5
2	beta	−58.3, 2.0, 14.1	−61.0, 0.3, 8.9	6.1
2	beta	−55.0, −33.7, 33.3	−51.2, −27.5, 32.0	7.4
2	high gamma	−64.4, −26.4, 23.5	−66.2, −24.5, 22.5	2.8

Note that the MEG reconstruction for both patients show the largest-amplitude beta desynchronization and high gamma synchronization in left primary motor cortex and the cerebellum in accordance with the across-subjects analyses above, but these areas were not covered by the ECoG grid in either patient; therefore, the ECoG analyses show only lower-amplitude secondary areas of activation which tend to result in blurrier MEG activations. Nevertheless, the ECoG analyses supported the validity of MEG reconstructions of these secondary activations, taking into account the 1 cm spacing and cortical surface placement of the ECoG grid as well as spatiotemporal blurring inherent to the beamformer technique.

4 Discussion

We have shown that, with our novel time-frequency optimized beamformer techniques, MEG can resolve sources of transient power changes across multiple frequency bands, including high gamma activity. The method was validated with across-subjects statistics and intracranial recordings.

Some secondary activity revealed by the ECoG analyses was not observed with the MEG source reconstructions; these sources may have activated a small cortical region and/or were not optimally oriented for detection by MEG sensor arrays. Additionally, MEG source reconstructions for any given voxel are linear combinations of activity from multiple nearby sources due to spatiotemporal blur and may explain minor spectrogram differences as compared to ECoG. The degree of spatial blur depends on various factors, especially SNR as well as the true spatial extent of the sources.

Adaptive spatial filter weights computed in the traditional manner from unfiltered or wideband data are inherently biased towards resolving low-frequency brain activity due to the power law of typical electrophysiological data. By creating a set of weights customized for each time-frequency window, higher frequency sources may be characterized with much greater fidelity. Additionally, segmenting the data into time windows can better capture the temporal extent of oscillatory modulations as well as allow for sources to change position and orientation. This is particularly important for experiment designs with long interstimulus intervals that yield several hundred milliseconds of data per epoch.

In using our proposed method, care must be taken to choose window lengths and bandwidths that ensure stable and well-conditioned covariance estimates. Optimal parameters will vary considerably depending on the type of experiment, background noise level, number of sensors, and number of trials. Too few time samples or too little bandwidth would result in poor covariance estimates and severely degrade performance of the beamformer reconstruction (Brookes et al., 2007). As we demonstrated in the Supplementary Methods section (available online), a compromise must be made between bandwidth and time window length. The ultimate parameter choice, then, must be driven by experimental hypotheses. It must be considered that real sources are unlikely to stay active for several hundreds of milliseconds at a time, making extremely narrow bandwidths impractical. Conversely, a source at a given location may generate a power increase in one band simultaneously with a power decrease in another band (as with common gamma power increase commonly observed in tandem with beta power decrease); performance would suffer if both events were contained by a single wide frequency band. Finally, total data length (the product of time window length with number of trials) had a direct impact on performance. Therefore, experiments should be designed with the duration of hypothesized activations and bands of interest in mind, increasing the number of trials acquired as necessary.

Noise is known to significantly impact the performance of minimum-norm-based methods by increasing localization bias and decreasing spatial resolution (Greenblatt et al., 2005; Sekihara et al., 2005), and this likely explains the presented sLORETA results; ultimately, the regularization parameters and method are critical in the presence of noise. Perhaps a similar approach to the proposed method can be taken; i.e., regularization parameters can be customized for different time-frequency segments, creating a hybrid adaptive-nonadaptive source reconstruction technique. This requires additional investigations beyond the scope of this paper.

ECoG has been shown to clearly resolve high gamma (>60 Hz) activity and suggests it is more spatiotemporally focal than lower-frequency activity (Crone et al., 1998, 2001a,b; Edwards et al., 2005; Canolty et al., 2006). Recently, high gamma activity has been gaining attention in the MEG/EEG literature as well (Kaiser et al., 2002; Hoogenboom et al., 2006; Vidal et al., 2006; Siegel et al., 2006; Osipova et al., 2006). While increases in high gamma power may coincide with decreases in beta power in many cases, high gamma may be a better indicator of task-specific neural processing in local cortical circuits since it is found to be more focused spatially and temporally. The hand motor data we present in this paper supports this hypothesis. Additionally, many studies have recently shown that high gamma activity is positively correlated with the hemodynamic response measured by functional MRI (fMRI) (Logothetis et al., 2001; Mukamel et al., 2005; Niessing et al., 2005; Brovelli et al., 2005; Hoogenboom et al., 2006; Lachaux et al., 2007). Finally, higher frequency bands may be less likely to be temporally correlated even if they are simultaneously active, and may thereby naturally circumvent the known limitation of beamformer techniques to resolve highly temporally correlated sources (Sekihara et al., 2002).

Other ECoG studies also show motor ERS in bands greater than 60 Hz (Ohara et al., 2000; Pfurtscheller et al., 2003) and even up to 200 Hz (Leuthardt et al., 2004; Brovelli et al., 2005; Crone et al., 2006) in the same region we observed with our MEG technique. Additionally, the postmovement beta rebound has been observed in both ECoG (Pfurtscheller et al., 1996; Sochůrková et al., 2006) and MEG (Jurkiewicz et al., 2006).

Our method suggested activations in the cerebellum for most of the healthy subjects and both epilepsy patients, though it did not reach statistical significance across subjects, likely due to individual variability in precise location, latency, and frequency. We speculate that both the sensor configuration and existing head models are not optimized for accuracy in the cerebellar region. Currently available MEG sensor arrays may not provide adequate coverage that far down the head with normal subject positioning. Furthermore, evidence from fMRI studies (Grodd et al., 2001; Hülsmann et al., 2003; Thickbroom et al., 2003; Dhamala et al., 2003; Dimitrova et al., 2006) suggests that the anterior cerebellum may be the most active, placing the neural generators fairly distant from the sensors and significantly lowering the SNR of the signals. Additionally, the strategy employed by individual subjects in pacing their finger movements may have introduced variability in the quality and extent of activation due to the cerebellum’s role in timing and rhythm (Ivry and Keele, 1989; Dhamala et al., 2003; Lotze et al., 2003). Finally, existing MEG/EEG head models focus on cerebral hemispheres and do not explicitly account for the structure of the cerebellum or its role in generating signals. As such, they may introduce large lead field inaccuracies in the region of the cerebellum, severely degrading the performance of spatial filtering techniques. Perhaps more sophisticated models based on boundary element modeling (BEM) or finite element modeling (FEM) are needed to improve fidelity in the cerebellum and other deep brain structures.

Previous MEG/EEG studies have suggested coherence between the cerebellum and cerebral cortex in the alpha and beta bands (Gross et al., 2002; Pollok et al., 2005). However, the activations found in this study suggest that the cerebellum may exhibit oscillatory activity at much higher frequencies that are not necessarily coherent with other locations, in accordance with speculation by Niedermeyer (2004) and the classic experiments of Adrian (1935), Dow (1938), Ten Cate and Wiggers (1942), and Pellet (1967). The use of space-time-frequency methods for analyzing MEG/EEG data may finally allow the cerebellum’s electrical activity to be independently studied noninvasively.

In addition to the hand motor data presented in this paper, other MEG studies by our group show that our method can reveal more complex cognitive processes related to learning, decision-making, and memory (Dalal et al., 2005; van Wassenhove and Nagarajan, 2006; Hinkley, 2007; Guggisberg et al., 2007; van Wassenhove and Nagarajan, 2007).

The technique we propose can be customized according to the preferences of the experimenter. For example, the frequency bands and time windows can be adjusted depending on the expected SNR and trial-to-trial variability of the experiment. Any typical filter type can be used to construct the filter banks; an experimenter may prefer to substitute filters with different properties than we have chosen or even wavelet-based filters. Finally, since the power of the active windows, control window, and noise are preserved in the final results, the contrast type may be selected by the end user. Rather than an F-ratio contrast, a t-test (difference) or the uncontrasted power time course may be selected instead.

This type of analysis does yield a large amount of information—a time-frequency spectrogram for every spatial location implies five dimensions of output data! Therefore, we have implemented an interactive time-frequency viewer into our software package NUTMEG to help make navigation of the results more intuitive. Future directions may include developing factor analysis techniques to help mine the rich output afforded by five-dimensional space-time-frequency analyses.