A data-driven model of the generation of human EEG based on a spatially distributed stochastic wave equation

Abstract

We discuss a model for the dynamics of the primary current density vector field within the grey matter of human brain. The model is based on a linear damped wave equation, driven by a stochastic term. By employing a realistically shaped average brain model and an estimate of the matrix which maps the primary currents distributed over grey matter to the electric potentials at the surface of the head, the model can be put into relation with recordings of the electroencephalogram (EEG). Through this step it becomes possible to employ EEG recordings for the purpose of estimating the primary current density vector field, i.e. finding a solution of the inverse problem of EEG generation. As a technique for inferring the unobserved high-dimensional primary current density field from EEG data of much lower dimension, a linear state space modelling approach is suggested, based on a generalisation of Kalman filtering, in combination with maximum-likelihood parameter estimation. The resulting algorithm for estimating dynamical solutions of the EEG inverse problem is applied to the task of localising the source of an epileptic spike from a clinical EEG data set; for comparison, we apply to the same task also a non-dynamical standard algorithm.

Introduction

The human brain represents one of the most complex systems known in nature; its elementary constituents, the neurons, encode, process and relay information predominantly by electrical pulses, known as action potentials. The electrical activity of large assemblies of neurons gives rise to electromagnetic fields which can be detected outside the head. The electrical fields can be observed as weak voltages by electrodes attached to the skin and connected to differential amplifiers, giving rise to the electroencephalogram (EEG) (Nunez 1981).

EEG time series contain a considerable amount of detailed information on brain activity; they are known to possess high temporal resolution, while the spatial resolution is much poorer, resulting from the fact that the measurement of the EEG voltages at the surface does not directly permit localisation of the sources of these voltages inside the head. These sources are commonly modelled by current dipoles, forming a time-dependent distribution over all electrically active parts of the brain. To which extent the field of a single dipole can be detected by a given pair of electrodes will depend not only on the position, but also on the direction of the dipole. Moreover, each pair of electrodes will record a superposition of the fields of all current dipoles that have suitable positions and directions.

If detailed information about the activity at particular sites of the cortex or within deeper structures is required, it is usually necessary to attach electrodes directly to the brain tissues in question, i.e. to resort to invasive methods. As an alternative to invasive approaches one could try to estimate the time-dependent distribution of source currents from the EEG time series data by appropriate numerical procedures; this task represents the inverse problem of EEG generation.

Numerous methods have been developed for the purpose of estimating approximative solutions of this inverse problem (Baillet et al. 2001); a class of these methods is based on solving underdetermined equation systems by constrained least-squares techniques, employing Tikhonov regularisation (Neumaier 1998; Hansen et al. 2000). In the case of the inverse problem of EEG generation one of these approaches has become known as “Low-Resolution Electromagnetic Tomography” (LORETA) (Pascual-Marqui et  al. 1994; Pascual-Marqui 2002). Generally these methods are instantaneous, i.e. they are applied repeatedly to the data recorded at each point of time, without taking the information into account which is encoded in the temporal order of the available data.

It can easily be seen that by ignoring the temporal order a huge amount of information is neglected. The temporal order of the data directly reflects the dynamics of the sources, which plays no role in instantaneous methods. Recently, methods have been developed which aim at solving the inverse problem of EEG generation by exploiting temporal information (Galka et al. 2004a, b; Yamashita et al. 2004).

As soon as temporal information is analysed, the dynamics of the sources becomes an additional object of investigation. The dynamics of neural assemblies has been studied and modelled by a large number of authors, and a wide variety of models have been developed, ranging from substructures of individual neurons on one extreme to neural masses of billions of neurons on the other extreme (Lopes da Silva et al. 1974; Freeman 2000; Robinson et al. 2003; Sotero et al. 2007). For the case of neural masses it is natural to apply a continuum approximation, although for the purpose of numerical computations, it will finally be necessary to apply again a discretisation step, which, however, is unrelated to the actual neural constituents of brain tissue.

The task of relating models for the dynamics of neural masses, possibly represented by stochastic differential equations, to actual EEG data in a quantitative framework poses considerable mathematical and computational challenges, and research in this field is still at an early stage. In this paper we will formulate a particular linear model, a stochastic variant of a standard damped wave equation, and demonstrate how this model can be employed for modelling EEG data. This approach will lead to a linear state space (LSS) model which describes the generation of the EEG by the primary current density vector field; for the inverse direction, i.e. for the estimation of the primary current density from the EEG, a generalised variant of Kalman filtering will be employed. After fitting the LSS model to the data, estimates for the time-dependent primary currents density can be obtained. Furthermore, the fitting process itself provides also estimates for the parameters of the model, which is attractive since it provides a data-based justification for the corresponding parameter values.

The focus of this paper lies on methodology; after presenting and discussing the model and the estimation algorithm, a practical example will also be presented, but it will serve only for the purpose of demonstrating the practicability of the proposed methodology.

The results reported in this paper are based on earlier work (Galka et al. 2004a; Yamashita et al. 2004) which we intend to extend and update with respect to a number of points. In particular we now discuss a damped wave equation as a generalised continuous-time model, serving as a basis for deriving the discretised state space model to be used in the actual implementations. The discretised state space model will be formulated in a different way than in the earlier papers; this will allow us to add moving-average (MA) terms to the dynamics, leading to a more powerful model. The modified state space representation offers a very efficient implementation of this generalised predictive model.

As another generalisation we will propose a new model for the state-adaptive covariance within the Kalman filter, to be termed “state space GARCH”; such models were introduced in Galka et al. (2004b), but in that paper we had not yet been able to estimate the additional model parameters within the maximum-likelihood framework. This has become possible now through several modifications and improvements, enabling us to present for the first time a case of successful application of state space GARCH modelling to clinical EEG data.

Furthermore, with respect to the actual implementation, we have considerably improved the numerical procedures for nonlinear maximisation of likelihood, such that parameter estimates of better quality can be obtained; as a result, the direct comparison with LORETA via information criteria such as AIC and BIC now demonstrates that the dynamical model offers a much superior description of the data, as compared to LORETA.

Methodology for modelling

Stochastic damped wave equation model

Let the unobserved primary current density vector field be denoted by j(r,t), where r and t denote space and time, respectively. j(r,t) shall be defined as a 3-dimensional column vector. In the linear approximation, the dynamics in a spatially extended passive medium can be described by stochastic partial differential equations, such as the damped linear wave equation

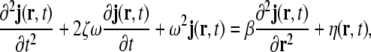1

where 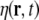denotes a stochastic driving noise term, and ζ, ω and β denote model parameters; ω represents a frequency, while ζ represents a damping coefficient.

Equation 1 expresses the dynamics for continuous time (and continuous space), therefore the simultaneous presence of a stochastic term and of time derivatives creates certain mathematical difficulties; since we will next introduce temporal, and also spatial, discretisations, we will ignore these difficulties; see Jazwinski (1970) for a thorough discussion.

Discretised wave equation: local model

In practical work, the volume of brain is discretised into a rectangular grid of N_vvoxels, and also the wave equation is transformed into a discrete-time dynamical model; the resulting model for the evolution of the primary current density j(v,t) (where v = 1, …, N_v labels voxels, and t = 1, …, N_t denotes time, measured in units of the sampling time) represents a linear state space (LSS) model. The local vectors j(v,t) are collected (stacked) into a global state vector 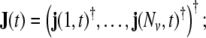the dimension of J(t) is given by N_J = 3N_v. At the level of an individual voxel, the equation for the evolution of the state is given by a 3-variate autoregressive (AR) model

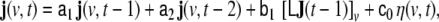2

where the discrete Laplacian is defined as

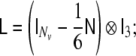3

here 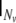denotes the N_v-dimensional identity matrix, and 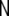denotes the neighbourhood matrix of the voxel set, i.e. a N_v × N_v matrix with N_ij = 1 if voxels i and j are spatial neighbours, and N_ij = 0 otherwise. The symbol ⊗ denotes Kronecker multiplication. Comparing with Eq. 1, replaces the operator 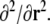The product 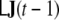represents a vector with the same dimension as J(t−1); by the notation we denote those 3 elements of this vector which correspond to voxel v.

The elements of the AR state transition matrices 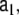and 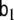are model parameters and may depend on the voxel index v; however, here we choose a simpler model where these matrices are defined as

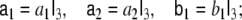4

here 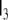denotes the 3-dimensional identity matrix. The parameters a₁, a₂ and b₁ are regarded as global parameters, i.e. they do not depend on the voxel index v. Through the discretisation of Eq. 1 they are related to the parameters ζ, ω and β by

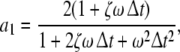5

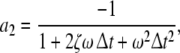6

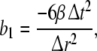7

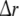where and denote the temporal and spatial discretisation units, respectively. However, since for the parameters ζ, ω and β no reliable values are available, it is recommended to estimate a₁, a₂ and b₁ directly from EEG data; this will be discussed below in sections “Spatiotemporal Kalman filtering and parameter estimation” to “Information criteria for model comparison”.

In Eq. 2 we have expressed the driving noise term as 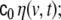here we assume for the covariance matrix of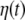

8

(where the symbol denotes expectation); consequently all cross-correlations between the components of the driving noise term are described by the additional input gain matrix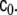 In this paper, is modelled as where c₀ is another global parameter of the model.

Moving-average terms and state space representation

The local model of Eq. 2 represents an AR model of second order, denoted as AR(2); it can be further generalised by adding a moving-average (MA) term:

9

where the additional MA parameter matrix is modelled in the same way as i.e. 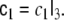This model is denoted as ARMA(2,1). More generally, ARMA(p,q) models for arbitrary model orders p and q may be defined, but in this paper we will only explore the ARMA(2,1) case.

It is well known, that ARMA models of arbitrary order can be reformulated as linear state space (LSS) models (Akaike 1974; Deistler 2006); for the model of Eq. 9 a corresponding LSS model is given by

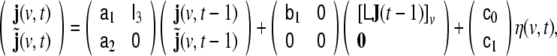10

Among the four possible formulations for the state transition matrix, here we have chosen the left companion form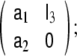 often, the upper companion form, 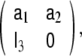is used instead, however, it has the disadvantage that the MA parameters need to be incorporated into the observation equation, instead of the dynamical equation, as shown in Eq. 10, where the MA parameters remain with the stochastic term of the model.

As can be seen from Eq. 10, in this model the state space is 6-dimensional, i.e. the original 3-dimensional primary current density vector j(v,t) has been augmented by a vector 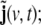by this augmentation the second-order AR component of the model has been reformulated as a first-order AR model, as it is required in a LSS model. The additional state component can be interpreted as a stochastic variable corresponding to a one-step-ahead prediction of the primary current density vector, (Akaike and Nakagawa 1988).

A LSS model consists of two equations, a dynamical equation, given by Eq. 10, and an observation equation. In this case, the observation equation simply redefines the first three state components, j(v,t), to be the observation, while the additional state components, 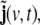are not observed. Note, however, that this problem has its intrinsic physical observation equation, as will be shown below in section “Observation equation”.

Discretised wave equation: global model

The set of local LSS models, as defined by Eq. 10 for each voxel, corresponds to a global LSS model

11

where J(t) is the global state vector defined in section “Discretised wave equation: local model”, and 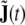collects in the same way all the additional state components 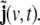The global state transition matrices are given by

12

The Laplacian, Eq. 3, arises here, because we have limited dynamical interactions between voxels to nearest neighbours, and we have defined the corresponding coupling parameter b₁ to be global, i.e. not to depend on the voxel index. Since we have limited these interactions to first-order, there is no Laplacian term for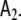

In Eq. 11, the global vector of the stacked driving noise terms 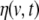has been denoted by H(t) (“capital eta”), and the input gain and MA matrices are given by

13

In this model, most elements of the parameter matrices 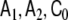and 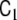are zero, i.e. the matrices are sparse. This model design considerably simplifies numerical model fitting, since it allows us to decompose the high-dimensional global model into the voxel-wise low-dimensional local models and to work only on the level of these local models most of the time, hence avoiding time- and memory-consuming operations on huge matrices. The local models are coupled by the neighbourhood terms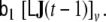

We note that choosing a non-zero value of the parameter b₁ has the important benefit of ensuring observability of the global LSS model (Kalman et al. 1969; Galka et al. 2004a); it is precisely this property which renders it possible to estimate state components from the subspace which is inaccessible to direct inversion of Eq. 15.

Spatial whitening

If the high-dimensional global state estimation problem is to be decomposed into a set of coupled local low-dimensional state estimation problems, also the covariance matrix of the global driving noise vector H(t) is required to be diagonal. This, however, is a very strong assumption, which usually is not justified. describes very fast interactions and instantaneous correlations between the voxels, and it has been observed (Galka et al. 2004a) that the possibility for such correlations is essential for successful modelling of real EEG data.

In order to save the convenient decomposition approach, it has been suggested (Galka et al. 2004a; Yamashita et al. 2004) to define, as an approximation, a non-diagonal 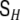with a particular form given by

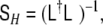14

where denotes again the Laplacian matrix of Eq. 3. Since and 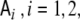commute, this ansatz is equivalent to assuming that after replacing J(t) by 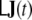in Eq. 11, the correspondingly transformed covariance matrix will indeed be diagonal. We call the transformation 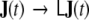“spatial whitening” and will from now on denote by J(t) exclusively the spatially whitened global state vector, and the diagonal covariance matrix of the transformed global driving noise by Note that no additional model parameter should be added to the definition of 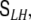since the corresponding degree of freedom has already been allocated to the parameter c₀ in Eq. 13.

Observation equation

As mentioned above, any LSS model needs an observation equation. For the inverse problem of EEG generation, the observation equation is given by

15

where Y(t) denotes the vector of observations, i.e. the EEG voltages, with dimension N_y, 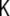denotes an observation matrix of dimension N_y × N_J, and 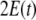denotes a vector of observational noise of dimension N_y, assumed to be gaussian and white, for which we define the covariance matrix We model this matrix as 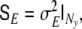i.e. we assume that the same amount of noise is present in each EEG electrode.

The observation matrix is known as lead field matrix; it can approximately be calculated for given head model and electrode locations by the “boundary element method” (Ary et al. 1981; Pascual-Marqui et al. 1994; Riera et al. 1998). In this paper we use a lead field matrix obtained by the method of Riera et al. (1998).

Since usually the number of EEG electrodes N_y is much smaller than the number of voxels N_v, solving Eq. 15 for Y(t) directly is impossible. By employing techniques such as pseudo-inversion and regularisation, as employed in the Low Resolution Electromagnetic Tomography (LORETA) method (Pascual-Marqui et al. 1994; Pascual-Marqui 2002), a unique solution may be obtained, but still a large subspace of the state space will remain inaccessible. For practical work this fact has the effect that there exist many different primary current densities which are consistent with a given set of EEG voltages. Dynamical analysis by LSS modelling provides an alternative to pseudo-inversion and regularisation.

Two more remarks need to be added. First, due to the spatial whitening transform, discussed in section “Spatial whitening”, we are using a transformed state space instead of the original. When we move from states to observations, this transformation needs to be undone, such that the observation matrix which we are using, is no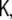t but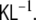

Second, we mentioned in section “Moving-average terms and state space representation” that when rewriting the ARMA model into a LSS model, an observation equation is automatically contributed; on the global level, it defines j(v,t) as observation, while 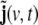remains unobserved. Here, we have to merge this observation equation with the physical observation equation, Eq. 15, so we observe the first part of the augmented state vector, J(t) through Eq. 15—thereby reducing its dimension considerably—while the additional part 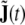remains unobserved; this can be achieved formally by augmenting the lead field matrix by a matrix of zeros of appropriate size.

State space GARCH

In principle, the dynamical model, as it has been described in sections “Discretised wave equation: local model” to “Observation equation”, is sufficient for estimating inverse solutions from EEG data by LSS modelling; however, we would like to add a further generalisation. So far, the model for the dynamics and for the stochastic driving noise is completely stationary, since all its main properties are encoded in constant parameters. Six model parameters have been defined so far: a₁, a₂, b₁, c₀, c₁ and 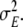A further limitation of the model is that these parameters are the same for all voxels, i.e. they are global parameters.

Now we choose to allow c₀ and c₁, or more precisely the corresponding matrices 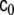and 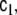to change with time, thereby providing more flexible modelling of the stochastic component of the dynamics; furthermore we allow these changes to occur at each voxel independently, thereby and become not only time-dependent, but also voxel-dependent. For this purpose we define a “second-level” dynamical system, following the example of generalised autoregressive conditional heteroscedasticity (GARCH) modelling, a famous method for modelling financial and econometric time series (Engle 1982; Bollerslev 1986); but in contrast to standard GARCH modelling, here we formulate a GARCH variant which can be applied to LSS models, to be abbreviated as SSGARCH. At voxel v, the model is given by

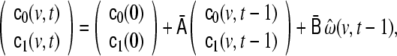16

where the parameter matrices are defined by

17

This model can be regarded as an AR(1) model for 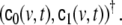Higher AR model order, as well as MA terms, are also possible, but according to our experience they seem to offer little additional benefit. The model of Eq. 16 consists of three terms:

• a constant term 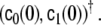corresponding to the parameters c₀ and c₁ in the case without SSGARCH; if all other SSGARCH model parameters are zero, the stationary case is retrieved by these two parameters;

• an AR term, adding a 2 × 2 parameter matrix α_ij, i,j = 1,2, to the set of parameters;

• a driving noise term, adding a 2 × 2 parameter matrix β_ij, i,j = 1,2, to the set of parameters.

The driving noise term requires a driving noise input, denoted by which presents a problem, since in a standard GARCH model this noise term would be provided by the innovations, i.e. the residuals of the predictions of the data. In contrast, in the SSGARCH case this driving noise needs to be local at each voxel site, directly in state space. Since by definition no data directly from state space is available, the innovations cannot be used directly, and an estimator for “state space innovations” needs to be defined. A simple estimator was introduced in Galka et al. (2004b); here we use an improved estimator that was recently proposed in Wong et al. (2006), given by

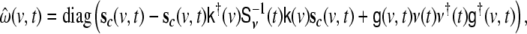18

where we have defined the covariance matrix 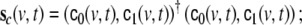by 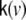those 3 columns within the lead field matrix are denoted which map the state at voxel v to the observations, i.e. the EEG electrodes; also 3 further columns of zeros are added, representing those state components which remain unobserved, such that 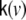has size N_y × 6. denotes the innovations vector and the corresponding innovation covariance matrix. denotes the local Kalman gain matrix at voxel v. The algebraic expression on the right-hand side of Eq. 18 provides a square matrix, therefore we define the noise estimates for the individual state components 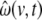as the diagonal values of this matrix.

This estimator provides estimates of the squared state prediction errors (“state space innovations”), not of the state prediction errors themselves, but we have found that the dynamical model of SSGARCH can be driven well by these squared estimates, if the model parameters are appropriately optimised.

Note that the additional model parameters of SSGARCH, c₀(0), c₁(0), α_ij and β_ij, are global parameters, such that the total number of model parameters remains small. In order to reduce it further, in this paper we have chosen to use non-zero values only for c₀(0), c₁(0), α₁₁ and β₁₁, while the other α_ij and β_ij were kept at zero. Future work may investigate whether these omitted parameters would play an important role within SSGARCH modelling.

Spatiotemporal Kalman filtering and parameter estimation

The dynamical model, as presented so far, depends on a number of parameters, which shall be collected in a parameter vector

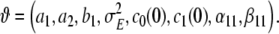19

The dimension of 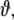i.e. the number of model parameters, shall be denoted as Fitting the model to data corresponds to estimating values for these parameters. For any given set of estimates the LSS model of Eqs. 11 and 15 can be solved iteratively by Kalman filtering; at each time point, two steps are performed. The Kalman filter iterates in forward direction (i.e. in the direction of time) through the data, producing predictions of states and observations (first step), and then corrects these predictions after comparison with the actual observations (second step). The corrected predictions of states are known as filtered state estimates; they serve as starting points for the state prediction step at the next time point.

It is obvious that an algorithm for modelling time series data by predictions will necessarily have to exploit information that is contained in the temporal ordering of the data, including the direction of time, i.e., information that is ignored by non-dynamical methods like LORETA. An efficient implementation of Kalman filtering for high-dimensional state spaces, known as spatiotemporal Kalman filtering, has been presented in Galka et al. (2004a); its core idea is to replace a single (3N_v)-dimensional filtering problem by a set of N_v coupled 3-dimensional filtering problems, each of which is localised at a single voxel, corresponding to the local models of Eq. 10.

Each application of the Kalman filter to a given time series can be regarded as a mapping of the time series to a corresponding innovation time series, representing those components of the data which are non-predictable within the chosen model. From these innovations and their corresponding covariance matrix, a logarithmic likelihood can be computed as

20

Maximisation of this log-likelihood represents a non-convex optimisation task, whence numerical nonlinear optimisation needs to be performed. The design of a suitable optimisation methodology is of crucial importance; the quality of the obtained solution can be assessed in various ways. Most prominently, the ability of the model to predict the data serves as a measure of model quality; the better the predictions, the larger the (logarithmic) likelihood. Poor parameter choices will reveal themselves immediately by poor performance of the Kalman filter; even if the model is very simple and therefore incapable of good predictions, the Kalman filter should still be able to track the data, like in a random-walk predictor. Experience has shown that the Kalman filter is very robust against poor model choice, if appropriate parameters are chosen.

Furthermore, the local structure of the likelihood function in a neighbourhood around the obtained solution can be analysed by the local Hessian matrix; if all its eigenvalues are negative, the solution is indeed a maximum, while some positive and some negative eigenvalues would indicate a saddle point.

With respect to these ways of assessment of solutions, we have found an iterative sequence of Broyden–Fletcher–Goldfarb–Shanno (BFGS) secant method steps and Nelder–Mead simplex method steps to provide solutions of sufficient quality, within the limitations of the chosen model class (Dennis and Schnabel 1983). It seems to be particularly beneficial to limit some of the optimisation steps to subsets of parameters, such as the dynamical parameters a₁, a₂, b₁, the driving noise covariance/MA parameters c₀(0), c₁(0), the SSGARCH dynamics parameters α₁₁, β₁₁ and the observation noise covariance parameter

However, we note that so far no results on the topology of the log-likelihood function Eq. 20 are known to us, such that we cannot rule out the possibility that our optimisation procedure will only provide local maxima, instead of global maxima. This limitation is shared with other applications of numerical nonlinear optimisation in contemporary science, e.g. protein folding. The risk of getting caught in local maxima could possibly be reduced by introducing stochastic elements into the optimisation procedure, such as simulated annealing; but such approach would be expensive with respect to computational time consumption.

On the other hand, since we know that we are employing a massively simplified model structure, we believe that we do not depend critically on finding globally optimal parameters; we expect that in practice a good local maximum will be as useful as the global maximum. For practical application there is also the need for a trade-off between the quality of the solution and the computational time consumption. Depending on the time series length N_t, the number of EEG channels N_y and the number of voxels N_v, our optimization procedure may still consume several hours of CPU time. Typical values of our analyses are N_t = 512, N_y = 18 and N_v = 3564.

Information criteria for model comparison

When different models are fitted to the same data set, a comparison of their performance is required, in order to decide which model provides a superior description of the data; the log-likelihood itself is not well suited for this purpose since it will typically favour models with many parameters; the more data-adaptive parameters a model has, the better it will fit the data. In order to prevent overfitting and provide a measure of model quality that can be compared even between unrelated model classes, information criteria like the Akaike Information Criterion (AIC) (Akaike 1974) or the Bayesian Information Criterion (BIC) (Schwarz 1978) have been defined:

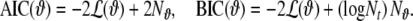21

These measures correct (−2) times the log-likelihood by a penalty term for the number of model parameters; for BIC this penalty term is larger than for AIC, and increases with increasing time series length N_t. Also for the LORETA method similar quantities can be defined, such as the Akaike Bayesian Information Criterion (ABIC) (Akaike 1980), which can be directly compared with the AIC (Galka et al. 2004a; Yamashita et al. 2004). Despite its name, the ABIC contains the same penalty term 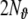as the AIC, not the penalty term of BIC. Therefore, if we intend to compare ABIC to BIC, we should replace this penalty term by the corresponding penalty term from BIC. The resulting quantity will, for simplicity, be denoted as “BBIC”, ignoring for the moment the awkward double appearance of “Bayesian” in this acronym.

An application example

We will now present an example of the application of the modelling algorithm discussed in this paper so far. We choose a short multivariate time series, selected from a clinical EEG recording. Inverse solutions will be computed for this data set using LORETA and LSS modelling.

Description of time series data

The selected time series is a clinical EEG recording, recorded from a 9-year old awake male patient suffering from Rolandic epilepsy. The data is shown in Fig. 1. The length of the chosen data set was 2.0 s; the sampling rate was 256 Hz. Electrode positions correspond to the clinical 10–20 system; electrical reference potential of the data was the average of the F3 and F4 electrodes, while for further analysis the data was converted to average reference. In order to remove the redundancy from the data set, resulting from including the reference potential, the data from the PZ electrode was discarded after the change of reference. Furthermore the data was standardised to zero-mean unit-variance, as follows : after removing the mean from each channel, the standard deviation of the concatenated time series of all channels was computed and its inverse was used as a normalisation factor.

Fig. 1.

EEG time series data from an awake epilepsy patient with eyes closed; electrode labels according to the clinical 10–20 system are indicated on the vertical axis. The data is shown in average reference representation

No filtering was applied, except for careful removal of a 50 Hz hum noise component and two of its higher harmonics (at 100 and 106 Hz). In Fig. 1 it can be seen that in the selected time interval, at about t = 1.4 s, a pronounced epileptic spike-wave event had occurred, visible in most electrodes. Furthermore, the occipital electrodes O1 and O2 display a clear alpha oscillation, as it is typical of the awake closed-eyes state.

Method of analysis

The time series, as shown in Fig. 1, was analysed by LORETA and by the LSS modelling algorithm, as proposed in this paper. A voxel set based on the Montreal Neurological Institute average brain model was employed (Mazziotta et al. 1995), consisting of 3,546 voxels covering the grey-matter brain tissues of the model brain, including cortex and basal ganglia, but excluding the cerebellum. Voxel grid spacing was 7 mm in all directions; the voxel set was layered into 18 horizontal slices.

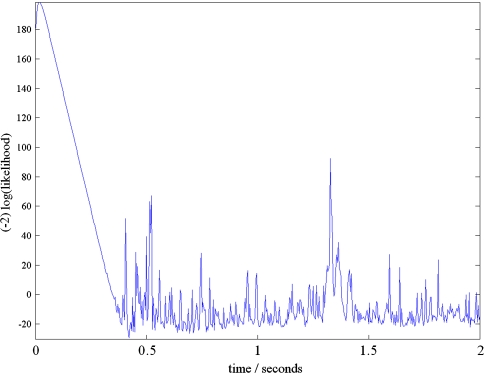
The Kalman filter needs to converge to its steady state, i.e. a transient has to die out. We can estimate the length of this transient by plotting the incremental log-likelihood versus time; in other words, we plot the term which is summed over in Eq. 20. A typical result is shown in Fig. 2; note that here (−2) times the log-likelihood is displayed, which is the quantity needed in the definition of AIC and BIC. The transition from the transient to the steady state after about 0.39 s, corresponding to about 100 sample points, can be seen clearly. Therefore, during optimisation and model comparison we omit the contributions to the log-likelihood within the first 100 samples. Since LORETA is a non-dynamical algorithm, it is not affected by transients; nevertheless, in order to keep model comparisons referring to precisely the same data set, we omit the same interval from the evaluation of ABIC and BBIC for LORETA.

Fig. 2.

Contributions to (−2) times the logarithm of the likelihood as function of time, for linear state space modelling of the data shown in Fig. 1

Results: model

Numerical maximisation of likelihood (or, equivalently, minimisation of AIC or BIC) yields a LSS model with parameters a₁ = 1.610, a₂ = −0.637, b₁ = −1.786 × 10⁻², c₀(0) = 7.238 × 10⁻¹³, c₁(0) = −6.009 × 10⁻⁴, α₁₁ = 0.102 and β₁₁ = −100.442. We note that for the given values of a₁ and a₂ the AR state transition matrix 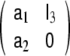has two real eigenvalues 0.909 and 0.701 (each of them threefold, strictly speaking), therefore the AR dynamics is stable; also the SSGARCH dynamics is stable, since its AR parameter α₁₁ does not exceed unity.

Furthermore the observation noise covariance parameter 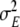assumes a very small value; it was a major weakness of the solutions reported in Galka et al. (2004a) that was allowed to assume comparatively large values. Such results correspond to the case of a sizable fraction of the power in the data representing purely observational noise; while this could be true, it seems unlikely for standard EEG, and in time series modelling we should altogether aim at describing as much power in the data as possible by predictable dynamics, while keeping the power to be attributed to unpredictable noise as low as possible. Therefore, during the numerical optimisation procedure, was kept at a very small value while the other model parameters were fitted, and only after they had assumed stable values was 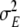itself optimised.

The values of AIC and BIC, corresponding to the final maximum-likelihood result, were −4812.0735 and −4779.8859, respectively. Note that these are both logarithmic quantities, so they may easily assume negative values for suitably scaled data; but only differences of these quantities are relevant. For comparison, the corresponding results for LORETA are ABIC = 15337.11 and BBIC = 15345.15; since AIC and ABIC (and likewise BIC and BBIC) can be directly compared, it is obvious that the dynamical model provides a far superior description of the data. These results all refer to a data set of 412 sample points length, since the first 100 points were reserved for the transient of the Kalman filter.

We also mention that if we omit the SSGARCH part of the model, i.e. set α₁₁ = β₁₁ = 0, we obtain AIC = −4716.4521 and BIC = −4692.3114. This result demonstrates that the SSGARCH part of the model actually contributes to improving the likelihood, resp. the AIC/BIC; the first paper discussing SSGARCH (Galka et al. 2004b) had not yet succeeded to achieve such improvement.

Results: inverse solution

For the given time series data, the LSS modelling step produces an estimate of the unobserved states, i.e. an inverse solution. It consists of current density vectors for each voxel and each time point; time points within the transient are discarded. Vectors consist of x, y and z components, and in general the direction of the estimated vectors at a given voxel will change with time. The same is true for inverse solutions estimated by LORETA. Here we ignore these time-varying directions and focus on the modulus of the vectors.

We discuss the inverse solutions both with respect to space and time. To begin with space, Fig. 3 shows a set of 9 horizontal slices of the voxel set; these are slices 8–16 out of a total of 18 slices, where slice numbers increase from the bottom to the top (vertex) of the head (slice numbers are given in the lower left corner of each subfigure). For both LORETA (left) and LSS (right), the moduli of the estimated vectors are displayed in a colour code which represents zero and small values by blue and green, while large values are represented by yellow and red. The mapping of the colours to the values of the estimated moduli was chosen differently for LORETA and for LSS modelling, such that in both cases the full range of colour was employed; at most time points, LORETA values were considerably smaller than LSS values.

Fig. 3.

Spatial distribution of moduli of estimated primary current density vectors for the data shown in Fig. 1, as estimated by LORETA (left set of subfigures) and LSS modelling (right set of subfigures). The figure shows the estimates at time t = 1.4 s, corresponding to the peak of the epileptic spike visible in the data. The subfigures represent 9 horizontal cross sections (slices) through a brain model, where slice numbers are given in the lower left corner; slice numbers increase towards the top of the head (vertex). Vector moduli are colour-coded with blue and green representing small values, while yellow and red represent large values. The mapping of the colours to the values of the moduli was chosen differently for LORETA and for LSS modelling, such that in both cases the full range of colour was employed

Figure 3 displays the inverse solutions at a fixed point of time which was chosen to coincide with the peak of the epileptic spike that occurred at a time of around 1.4 s. As can be seen, both LORETA and LSS locate the origin of this spike in the left hemisphere; for LSS the maximum of the corresponding activity is well localised in an area of slice 15, corresponding to the postcentral gyrus. In the same area also LORETA finds strong activity; however, in the LORETA solution this activity extends far downwards into temporal cortex, until slices 8–10, where a second focus of strong activation can be seen.

In Fig. 4 we show the time series of the moduli of the estimated vectors at these two locations (slice 15, left postcentral gyrus; slice 9, left superior temporal gyrus), corresponding to the apparent foci of activity during the epileptic spike. By comparing the LORETA (left) and LSS (right) results, it can be clearly seen that LSS moduli are larger than LORETA moduli. Furthermore, it can be seen that also LSS finds increased activation at the temporal cortex location; however, while for LORETA the peak modulus amplitude at the two locations is approximately equal, for LSS it is considerably stronger in the postcentral gyrus than in the superior temporal gyrus. This result shows that the differences between the LORETA and LSS inverse solutions are not limited to a general change of modulus scale; there are, in addition, qualitative differences of the activation maps, which, in this case, correspond to a different conclusion on the probable origin of the epileptic spike.

Fig. 4.

Time series of moduli of estimated primary current density vectors for the data shown in Fig. 1, as estimated by LORETA (left pair of subfigures) and LSS modelling (right pair of subfigures). The figure shows the estimates at a voxel within slice 9, corresponding to the left superior temporal gyrus (top pair of subfigures) and a voxel within slice 15, corresponding to left postcentral gyrus (bottom pair of subfigures). For the LSS results, the first 0.39 s have been omitted, since these estimates are affected by the transient of the Kalman filter

The motivation for introducing the SSGARCH generalisation into the model is given by the lack of local flexibility in the stationary state space model. Sudden large values in the data cannot be predicted well by the model, such that large innovations result. In principle, the Kalman filter can, through its two-step structure, adapt to this situation, but only if the corresponding driving noise covariance parameters are sufficiently large. The purpose of the SSGARCH dynamics is to increase these covariance parameters at the appropriate time, and in particular at those voxels that have, via the lead field matrix, a strong influence on the given pattern of innovations. This will immediately reduce the following innovations and thereby improve the likelihood. It will also have an immediate effect on the estimated states themselves, since these will become considerably larger, with respect to moduli, at the corresponding set of voxels. Larger local driving noise covariance will necessarily lead to larger state estimates; this effect contributes much to the qualitative differences which we find between LORETA and LSS. A LSS model without SSGARCH would also outperform LORETA, due to its ability to exploit temporal information; but it would lack local flexibility, and therefore its state estimates would differ less from the LORETA estimates; this was demonstrated clearly, both for simulated and real data, in Galka et al. (2004a).

Note that from the qualitative differences between the LORETA and LSS inverse solutions we cannot infer which of the two comes closer to the unobserved truth; it is still possible that, for a sufficiently unfavourable situation, both solutions may completely miss the true distribution of activation. So far, this remains an inherent caveat applying to all work on inverse solutions based on EEG or MEG time series data. All that can be inferred from our analysis, is that LSS provides a much superior description of the data, in terms of the maximum-likelihood or minimum-AIC/ABIC/BIC/BBIC criterion. Further work needs to investigate whether and to which extent these superior models provide useful and reliable information about the sources of the human EEG. In this paper, the application to epileptic spikes has only served as an example of a potential area of application.

Conclusion

In this paper we have presented an approach for dynamical modelling of EEG time series, with the particular aim of obtaining an estimate of the spatial distribution of the primary current vector field which is assumed to be the source of the electromagnetic fields that are represented by the EEG; such estimate provides a solution to the inverse problem of EEG generation.

Following earlier work (Galka et al. 2004a, b; Yamashita et al. 2004), we have chosen an approach based on linear state space modelling, where the state space is closely related to physical space, namely a discretisation of those parts of brain volume which are occupied by grey-matter tissue. The dynamical aspect of the model is given by the assumption that the electrical activity of this tissue can be described by a linear stochastic damped wave equation; discretisation of this equation with respect to space and time naturally leads to a state space model.

The inverse problem of EEG generation represents a twofold estimation problem; first, a model of the dynamics and of the observation needs to be estimated, and second, given this model, the actual inverse solution needs to be estimated. The second problem requires inversion of a highly underdetermined observation equation, a task which the LORETA method solves by regularised pseudo-inversion; here we have argued that Kalman filtering, based on state space modelling, provides a natural and powerful alternative, since it has, in theory, the potential of removing or at least reducing the underdetermination by using dynamical information. For practical work we recommend an approximative algorithm which we have called spatio-temporal Kalman filtering (Galka et al. 2004a).

The first of the two estimation problems can be expressed as a problem of parameter estimation through maximisation of likelihood or, preferably, minimisation of an information criterion, such as AIC or BIC; the application of the maximum-likelihood method and its extensions to estimating parameters of state space models is well established in statistical data analysis (Kitagawa and Gersch 1996; Durbin and Koopman 2001). Luckily, the close relationship between state space and physical space simplifies the problem, since it renders it possible to estimate the observation matrix (known as the lead field matrix) from first principles, i.e. through electromagnetic modelling; this decreases massively the number of model parameters to be estimated by numerical optimisation. It would, however, remain possible, and possibly advisable, to estimate certain parameters required by this electromagnetic modelling, such as tissue conductivities, within the maximum-likelihood framework; so far, the conductivity values used for estimating the lead field matrix are standard values taken from literature.

There remain various other issues that require further work. Perhaps the main issue concerns the improvement of the model. In time series modelling it is intended to remove all correlations, both instantaneous and dynamical (i.e., involving time delays), from the data by building a predictive model; if the model is optimal, the prediction errors, also known as innovations, will consist of featureless, and therefore unpredictable, white noise. The innovations need to be white, since any structure in the power spectrum could be employed for designing an improved predictor. In turn, improved predictors would reduce the amplitude of the innovations and thereby, according to Eq. 20, increase the likelihood.

Due to the obvious fact that the dynamical model, as described in sections “Discretised wave equation: local model” to “Spatial whitening”, is massively oversimplified, with respect to what is known about “true” brain dynamics, we cannot expect “perfect” predictions and truly white innovations. Nevertheless, by introducing generalisations into the model, we can hope to remove further structure from the innovations, render them “whiter” and improve the likelihood. The SSGARCH part of the model is an attempt to provide such generalisation, not by improving the predictor term of the model, i.e. the deterministic part of the dynamics, but by improving the driving noise term, i.e. the stochastic part of the dynamics. In a recent study on the decomposition of univariate time series a similar SSGARCH model has been shown to perform well in improving the likelihood (Wong et al. 2006). The situation of modelling a full multivariate EEG time series is more demanding, and it is not obvious how precisely a SSGARCH model needs to be defined for optimal results. The detailled SSGARCH model, as described in section “State space GARCH”, will probably still require further modifications, before it may approach optimal performance.

Other open issues concern the stability of the Kalman filter and the computational time consumption of the numerical estimation of model parameters. If the Kalman filter iteration is applied “out-of-sample”, there is a risk of gradual divergence of the state estimates, a behaviour which in the current state of the algorithm needs to be countered by refitting the model parameters. The model fitting itself tends to be time-consuming, since the spatiotemporal Kalman filter needs to iterate twice through all voxels for each time point (Galka et al. 2004a); currently, due to the large number of voxels, each full Kalman filter iteration over a time series of a few hundred time points will consume several minutes of CPU time. In a numerical optimisation scheme, the Kalman filter iteration has to be repeated many times, before the parameter estimates converge.

There exist approaches to the inverse problem of EEG generation which employ different source models than LORETA and LSS, such as the scalar model of ELECTRA (Grave de Peralta Menendez et al. 2000). While this approach would reduce the state space dimension by a factor of three, it would not offer an easy way to significantly reduce the high computational time consumption of the parameter fitting step of the LSS approach, since this time consumption is mainly caused by the large number of voxels; due to the use of the spatio-temporal Kalman filtering algorithm, we are already avoiding the problem of huge state space dimension. The high computational time consumption of LSS stands in marked contrast to instantaneous methods, such as LORETA or ELECTRA, which offer the advantage of the availability of fast and efficient implementations.

In this paper, we do not discuss the problems of Kalman filter stability and of computational time consumption further, but we would like to mention them as topics for future research.

We briefly mention another possible generalisation of the method. In contemporary brain research, stimuli are commonly applied to subjects while recording their EEG, such that stimulus responses (known as “event-related potentials”, ERP) can be investigated. From a dynamical systems perspective, stimuli correspond to the presence of a known external input signal to the system; such input signal provides additional information which can also be included into the model. In the common case of a block design, this input signal would correspond to a time series of zeros, corresponding to absence of stimulus, and ones, corresponding to presence of stimulus. This time series could be made available to each voxel, and additional model parameters could be defined for its contribution to the prediction of local states. However, since we expect, that different brain areas react differently to a given stimulus, these additional parameters should not be global, but should depend on the voxel index; within the current implementation of this method, optimisation of such a large set of model parameters would be impracticable. Therefore, alternative approaches need to be developed for incorporating stimulus information into this class of high-dimensional state space models.

Finally, we mention that in this paper we have limited the presentation and discussion to methodological aspects; the application example, i.e. the estimation of the sources of an epileptic spike in an EEG time series from an awake patient, has served only for the purpose of demonstrating the practicability of the proposed algorithm and introducing a potential field of application. In order to assess the potential usefulness and reliability of inverse solutions estimated by LSS modelling and to compare them with other competing algorithms, such as LORETA, extended studies on data bases of clinical EEG time series will be required.