Abstract
In everyday life we often encounter situations in which we can expect a visual stimulus before we actually see it. Here, we study the impact of such stimulus anticipation on the actual response to a visual stimulus. Participants were to indicate the sex of deer and cattle on photographs of the respective animals. On some trials, participants were cued on the species of the upcoming animal whereas on other trials this was not the case. Time frequency analysis of the simultaneously recorded EEG revealed modulations by this cue stimulus in two time windows. Early  spectral responses
spectral responses  displayed strongest stimulus-locking for stimuli that were preceded by a cue if they were sufficiently large. Late
displayed strongest stimulus-locking for stimuli that were preceded by a cue if they were sufficiently large. Late  responses displayed enhanced amplitudes in response to large stimuli and to stimuli that were preceded by a cue. For late responses, however, no interaction between cue and stimulus size was observed. We were able to explain these results in a simulation by prestimulus gain modulations (early response) and by decreased response thresholds (late response). Thus, it seems plausible, that stimulus anticipation results in a pretuning of local neural populations.
responses displayed enhanced amplitudes in response to large stimuli and to stimuli that were preceded by a cue. For late responses, however, no interaction between cue and stimulus size was observed. We were able to explain these results in a simulation by prestimulus gain modulations (early response) and by decreased response thresholds (late response). Thus, it seems plausible, that stimulus anticipation results in a pretuning of local neural populations.
Keywords: Beta, Gamma, Gain, Threshold, EEG, Vision
Introduction
Our environment is constantly changing. However, in most cases these changes do not come as a surprise. We usually make predictions to know in advance what might happen in the next moment (Bar 2007). How is such anticipatory activity integrated with the upcoming stimuli? Can we identify different modes of such integration processes?
As a plausible correlate for such integration between sensory information and information stored in memory, high frequency (20–90 Hz) brain activity has been suggested (Herrmann et al. 2004b). These authors have argued, that high frequency oscillatory brain activity is enhanced if sensory input matches with stored object templates. In such a case, it is assumed that feedback from the locus of the match to earlier stages of visual processing results in activity reverberating within the visual system. Current findings suggest that such reverberating activity can be measured from the scalp (Herrmann et al. 2004a; Morup et al. 2006) as stimulus-locked, so called evoked γ responses (usually 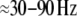 at a latency around
at a latency around 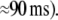 Several authors also reported later amplitude modulations of high frequency brain activity (Tallon-Baudry et al. 1996, 1998; Lachaux et al. 2005; Gruber et al. 2002; Gruber and Müller 2005; Keil et al. 2001; Busch et al. 2006a; Hoogenboom et al. 2006; Sederberg et al. 2003). These later, so called induced γ responses have been interpreted as being related to later stages of perceptual processing (Herrmann et al 2004b) in which more abstract, high level object representations are available (Tallon-Baudry and Bertrand 1999).
Several authors also reported later amplitude modulations of high frequency brain activity (Tallon-Baudry et al. 1996, 1998; Lachaux et al. 2005; Gruber et al. 2002; Gruber and Müller 2005; Keil et al. 2001; Busch et al. 2006a; Hoogenboom et al. 2006; Sederberg et al. 2003). These later, so called induced γ responses have been interpreted as being related to later stages of perceptual processing (Herrmann et al 2004b) in which more abstract, high level object representations are available (Tallon-Baudry and Bertrand 1999).
Evoked γ responses are usually regarded as being dominated by low level sensory processes (Basar et al. 2001; Karakaş and Başar 1998) that can be modulated by attention (Busch et al. 2006b; Tiitinen et al. 1993; Debener et al. 2003). Consequently, modulations of evoked γ responses by several physical characteristics of a stimulus have been reported (Busch et al. 2004; Fründ et al. 2007a; Schadow et al. 2007). In these studies, evoked γ responses could mainly be characterized as a transient period during which ongoing activity was locked to the onset of the stimulus. How can such early responses be modulated by the anticipation of the identity of a stimulus? Obviously these responses cannot start to lock to the stimulus before it is actually being presented. An alternative could be to silently pretune the neural populations involved in processing the stimulus by changing their response gain (Salinas and Sejnowski 2001; Chance et al. 2002). In this case, the impact of a stimulus on these populations should be enhanced, leading to an interaction of stimulus parameters and stimulus anticipation.
Due to their longer latency to the stimulus, induced γ responses could be shaped by feedback to a much larger extend than evoked γ responses. If such feedback were purely excitatory, it would usually result in a decrease of the response threshold in the target neural populations. In contrast, if the (excitatory) feedback were balanced by inhibition this would result in a modulation of response gain in the target population (Chance et al. 2002). Both these effects have been observed in animal experiments (Reynolds and Chelazzi 2004). Furthermore, signals at high-level visual areas display invariance to size and translation (e.g. Desimone et al. 1984). Thus, one might expect that the effects of feedback from high level visual areas are relatively independent of the size of a stimulus.
Some studies have investigated EEG correlates of cue processing (Fan et al. 2007; Lai and Mangels 2007; Luck et al. 1994; Martinez et al. 2006; Yamaguchi et al. 2000). However, these studies focused on the effect of spatial cues and the spread of the effects of spatial cues along spatially extended objects (Martinez et al. 2006). In addition, only one of these studies (Fan et al. 2007) analyzed their data with respect to spectral dynamics. Unfortunately, these authors did not clearly differentiate between stimulus locked, evoked responses and amplitude modulated, induced responses. Thus, the precise relation between high frequency electroencephalographic responses and cue directed attention can still be sharpened.
In the current study, we investigated evoked and induced electroencephalographic responses from human participants. On some trials, the participants were cued about the category of the stimulus before it appeared on the screen, on other trials this was not the case. In addition, stimuli were presented at different sizes. This enabled us to differentiate stimulus-related from cue-related responses. We expected early responses to show the signatures of gain modulation. This should manifest in an enhanced modulation by the cue for large stimuli. In contrast, we expected later responses to show signatures of both the abovementioned types of feedback. As outlined above, such responses should show threshold modulation (from purely excitatory feedback) as well as gain modulation (due to balance by inhibition). Feedback effects originate from areas which display more invariant responses with respect to physical stimulus features. Thus, we expected later responses to be affected by the cue irrespective of the size of the stimuli. The data were compared to a simple model of neural population responses.
Methods
Participants
Twelve healthy volunteers participated in the current study after giving their written informed consent. All participants had normal or corrected to normal vision and reported being free of current or past neurologic or psychiatric disorders. Participants received money or course credits for their participation. The experiments were conducted in accordance with the Declaration of Helsinki and the local ethics committee of the University of Magdeburg.
Experimental procedure
During the experiment, participants observed a set of pictures of male and female cattle and deer. For every combination of species and sex a total of 66 different color photographs were presented on a medium gray background. These 66 different photographs were scaled to either 545 × 470 pixels (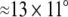 visual arc) or 170 × 131 pixels (
visual arc) or 170 × 131 pixels (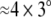 visual arc) to yield either large or small stimuli, respectively. This resulted in a total of 528 different stimuli (2 species × 2 sexes × 66 photographs × 2 sizes). Participants judged the sex of the depicted animals under two different conditions. In one block they were naive about the species of the upcoming animal (uncued trials); in another block, participants were cued on the species of the upcoming animal 500 ms before the onset of the animal’s photograph (cued trials). The cue consisted of the name of the species and was presented in bold letters at the center of the screen. On 80% of the cued trials the cue was valid, meaning that the presented animal was indeed the same as indicated by the cue. There were only few invalid trials (20% of the cued trials). Thus, only uncued and validly cued trials were analyzed.
visual arc) to yield either large or small stimuli, respectively. This resulted in a total of 528 different stimuli (2 species × 2 sexes × 66 photographs × 2 sizes). Participants judged the sex of the depicted animals under two different conditions. In one block they were naive about the species of the upcoming animal (uncued trials); in another block, participants were cued on the species of the upcoming animal 500 ms before the onset of the animal’s photograph (cued trials). The cue consisted of the name of the species and was presented in bold letters at the center of the screen. On 80% of the cued trials the cue was valid, meaning that the presented animal was indeed the same as indicated by the cue. There were only few invalid trials (20% of the cued trials). Thus, only uncued and validly cued trials were analyzed.
Cueing the species of the animals rather than the sex allowed us to induce preparation for the visual analysis of the images rather than motor preparation. However, information about the species of the animals is beneficial because it cues the sex defining feature (antlers for deer, udder for cattle).
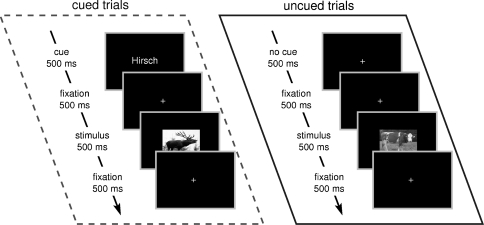
Stimuli were presented for 500 ms with an inter stimulus interval varying randomly between 2,000 and 3,000 ms. Participants responded by pressing a button with one hand if the animal was male and pressing another button with the other hand if the animal was female. Response hands were counterbalanced across participants. Participants were instructed to fixate a small black fixation cross at the center of the screen during the whole experiment and to avoid eye blinks. A schematic illustration of the paradigm can be found in Fig. 1.
Fig. 1.
Illustration of the experimental procedure. In cued trials (dashed box), participants received a written cue 500 ms before stimulus onset. This was not the case for uncued trials (solid box)
Data acquisition
During data acquisition, participants sat in an electrically shielded and sound attenuated room (IAC, Niederkrüchten, Germany). The stimulation monitor was placed outside the cabin behind an electrically shielded window. All devices inside the cabin were battery operated to avoid line frequency interference (50 Hz in Germany). The electroencephalogram (EEG) was measured from 62 scalp locations according to an extended 10–20 system. The nose served as reference. Electrooculographic activity was measured from one electrode below the orbital rim and another electrode lateral from the right eye in order to detect artifacts due to eye movements. Activity was measured using sintered Ag/AgCl electrodes mounted in an elastic cap (Easycap, Falk Minow Services, Munich, Germany) and amplified by means of a Brain Amp amplifier (Brain Products, Munich, Germany). Electrode impedances were kept below 5 kΩ. The EEG signals were filtered between 0.02 and 500 Hz and stored on a computer hard disk at a rate of 1 kHz for offline analysis. Digitized EEG data were transferred to a computer outside the recording cabin by means of a fiber optic cable. An additional digital high-pass filter with a cutoff frequency of 0.5 Hz was applied offline to reduce slow shifts in the baseline. An automatic artifact rejection was computed which excluded trials from further analysis if the standard deviation within a moving 200 ms time window exceeded 40 μV in any channel. The automatic artifact rejection was supplemented by visual inspection to ensure that only trials without artifacts were included in the subsequent analysis.
Data analysis
A time frequency representation of the EEG signals was derived using a complex valued wavelet transform (Herrmann et al. 2005). The wavelet transform was computed by convolving the raw EEG signal with a set of scaled and translated versions of a complex modulated gaussian. At 40 Hz the wavelet had a time resolution of 2σt = 50 ms and a frequency resolution of 2σf = 13 Hz. The exact time frequency resolution of the wavelet depended on the analyzed frequency. The wavelets were normalized to have unit energy. From the wavelet transformed data three quantities were derived: (i) the amount of evoked activity, that is the absolute value of the wavelet transform applied to the averaged evoked potential, (ii) the total activity, which is the average modulus of the wavelet transform applied to the single trials, and (iii) the strength of stimulus-locking. Stimulus-locking was quantified by a time frequency version of the so called mean resultant length (Fisher 1993) as has been done before (e.g. Tallon-Baudry et al. 1996; Fründ et al. 2007c). A stimulus-locking value of 1 indicates perfect locking across trials, while a stimulus-locking value of 0 indicates a constellation in which the phases exactly cancel out each other, as it is the case for a uniform distribution of phases across trials. This resulted in a representation of the responses from every participant in the plane spanned by time and frequency. These planes were transformed to a dB-scale in case of evoked and total responses indicating the change relative to a baseline that extended from 200 to 100 ms before the onset of the stimulus. Stimulus-locking was related to the same baseline by simply subtracting the average stimulus-locking from this time window.
As response frequencies vary considerably, but rather consistently between individuals (Fründ et al. 2007c), we decided to analyze oscillatory activity at peak frequencies. For the analysis of early activity, these individual response frequencies were selected as the maximum in a time window between 60 and 160 ms. For the analysis of late activity, individual response frequencies were selected from a time window between 200 and 300 ms after the onset of the stimulus. As we were looking for stimulus-locked and/or amplitude modulated responses in the gamma band, we initially determined response frequencies from a range of 25–90 Hz. In this frequency range, no stimulus-locked responses exceeded the noise level. However, very consistent modulations of stimulus-locked activity could be observed in the beta band. Therefore, evoked activity was analyzed with individual response frequencies determined from a frequency range between 15 and 25 Hz.
The impact of the two factors size (large versus small stimuli) and cue (valid cue versus no cue) on EEG measures was tested by means of an analysis of variance (ANOVA) for repeated measurements. For the ANOVA, data were pooled across channels from a posterior region of interest (channels O1, O2, Oz, P3, P4, Pz, P7, P8, PO3, PO4, POz, P5, P6, P1, P2).
Simulation
The results from the EEG analysis were compared to a simple model of gain modulated cells. This model consisted of an array of 100 × 100 units—each of which was described by an input–output mapping given by a Naka–Rushton function (Naka and Rushton 1966; Wilson 1999)—relating output strength y and input strength x in the form
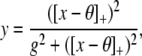 |
1 |
where θ is a threshold that determines the minimum value, for which the unit will respond at all. Here, [·]+ denotes rectification. The parameter g is inversely related to the gain of the input/output relation. Smaller gs result in stronger increases in output strength with increasing input. Naka–Rushton functions are usually regarded as a good approximation to the input/output behavior of neural processing elements (e.g. Wilson 1999, p. 19). Note that there are no interconnections between the different units. Therefore, this model can make predictions about changes in the input/output behavior of neural populations but not about their interconnections.
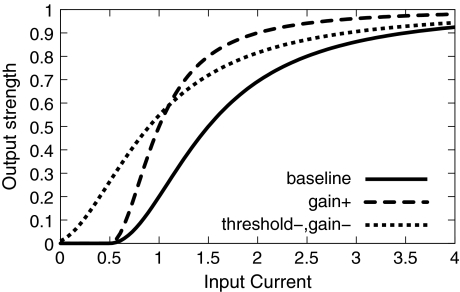
To simulate the effects of different modes of processing, the parameters g and θ in Eq. 1 were varied. As a baseline condition reflecting the no cue condition of the EEG experiment, these values were arbitrarily set to 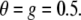 We will refer to this condition as the baseline condition (see Fig. 2). The cue condition of the EEG experiment could in principle be modeled by either increased gain or decreased threshold. Our simulation was intended to reveal which of the two mechanisms simulates the EEG data more closely. To simulate increased gain due to stimulus anticipation, we set g = 0.25 for a subset of units, keeping θ constant (gain+ condition in Fig. 2). The mechanism of decreased threshold was simulated by setting θ = −0.1 while at the same time setting g = 1 to simulate balanced input (Chance et al. 2002) (threshold−, gain− condition in Fig. 2). Both these modulations were performed on a subset of 30 × 30 cells in the total array of model neurons. The effect of gain and threshold modulations on the response properties of the underlying populations is illustrated in Fig. 3. Stimuli could either be presented inside or outside the modified region.
We will refer to this condition as the baseline condition (see Fig. 2). The cue condition of the EEG experiment could in principle be modeled by either increased gain or decreased threshold. Our simulation was intended to reveal which of the two mechanisms simulates the EEG data more closely. To simulate increased gain due to stimulus anticipation, we set g = 0.25 for a subset of units, keeping θ constant (gain+ condition in Fig. 2). The mechanism of decreased threshold was simulated by setting θ = −0.1 while at the same time setting g = 1 to simulate balanced input (Chance et al. 2002) (threshold−, gain− condition in Fig. 2). Both these modulations were performed on a subset of 30 × 30 cells in the total array of model neurons. The effect of gain and threshold modulations on the response properties of the underlying populations is illustrated in Fig. 3. Stimuli could either be presented inside or outside the modified region.
Fig. 2.
Different types of input–output mappings used in the simulation. “Baseline” refers to the simulation of the no cue condition of the EEG experiment, “gain+” corresponds to the condition with increased gain, and “threshold−, gain−” corresponds to the condition with decreased gain and threshold, both reflecting different possible implementations of the cue condition of the EEG experiment
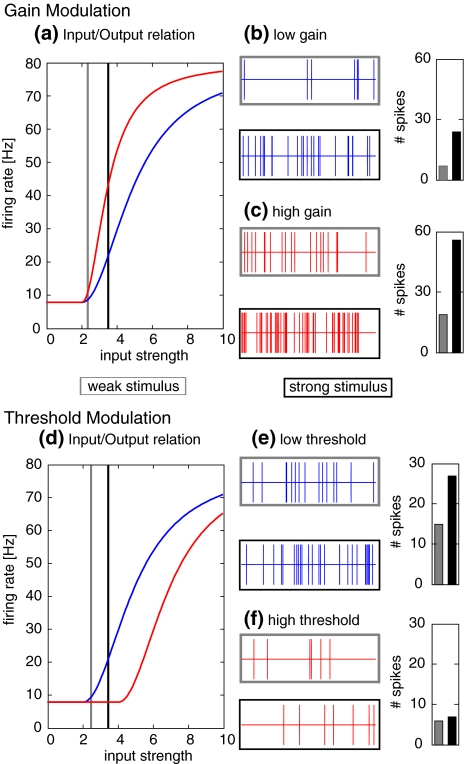
Fig. 3.
Effects of gain and threshold modulation. (a) Two different response functions that differ in gain. The blue curve has a lower gain, the red curve has a higher gain. (b) Example responses for a poisson spike process with low gain response function. Gray box: weak input corresponding to the gray vertical line in part (a). Black box: stronger input corresponding to the black vertical line in part (a). On the right, the corresponding spike counts are illustrated as bars. (c) Example responses for a poisson spike process with high gain. Remaining conventions are like in (b). (d) Two different response functions that differ in threshold. The blue curve has a lower threshold, the red curve has a higher threshold. (e) Example responses for a poisson spike process with low threshold. Gray box: weak input corresponding to the gray vertical line in part (d). Black box: stronger input corresponding to the black vertical line in part (d). (f) Example responses for a poisson spike process with high threshold. Remaining conventions are like in (e)
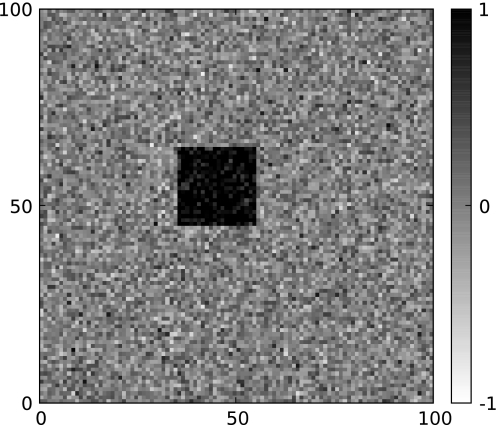
For all 100 × 100 pixels, Gaussian white noise with standard deviation σ = 0.25 served as input data x. In order to simulate the effect of a stimulus, a value of 1 was added to the noise either for a square region of 20 × 20 (large stimulus) or 10 × 10 pixels (small stimulus). This is illustrated in Fig. 4 for a large stimulus. Pixels that are set to 1 can be thought of as matches between sensory input and the structure of the receptive field of the respective unit. Gaussian white noise with standard deviation σ = 0.25 was added to each pixel. The input and output strength can be though of as spike counts of averaged local field potentials. More technical details of the simulation can be found in the appendix.
Fig. 4.
An example of an input stimulus to the simulation. The large (20 × 20 pixels) stimulus is presented in white noise
Results
Modulations of high frequency spectral EEG components were observed in two time windows. An early modulation was found between 15 and 25 Hz in a time interval between 60 and 160 ms, and a later modulation was found between 30 and 90 Hz in a later time window between 200 and 300 ms. In the following we will describe these modulations in more detail.
Early modulation
Although previous studies have reported stimulus related modulations in the γ frequency range (e.g. Busch et al. 2004, 2006b; Tallon-Baudry et al. 1996; Spencer et al. 2004), the current data did not contain any systematic responses at frequencies above 30 Hz.
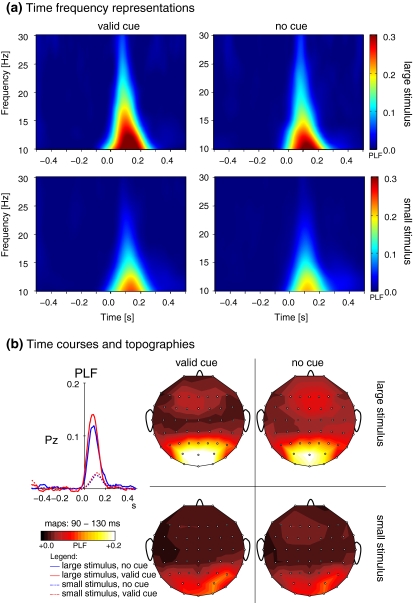
In contrast, modulations were observed in the β frequency range (15–25 Hz). In this frequency range, most participants elicited a response peak in the time frequency planes that was concentrated in time as well as in frequency (see Fig. 5). Averaging across different participants smeared these relatively concentrated peaks across multiple frequencies (Fig. 6a). As these responses were mainly defined by locking to the stimulus, we will here focus on effects on stimulus-locking. Stimulus-locking in the β frequency range was strongly enhanced in response to large stimuli as compared to small stimuli (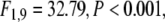 see Fig. 6). In addition, stimulus-locking was stronger in cued trials as compared to uncued trials (
see Fig. 6). In addition, stimulus-locking was stronger in cued trials as compared to uncued trials (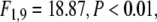 cued versus uncued for large stimuli: t10 = 4.38, P < 0.001, cued versus uncued for small stimuli: t10 = 3.43, P < 0.01). This effect was particularly salient for large stimuli (size × cue interaction,
cued versus uncued for large stimuli: t10 = 4.38, P < 0.001, cued versus uncued for small stimuli: t10 = 3.43, P < 0.01). This effect was particularly salient for large stimuli (size × cue interaction, 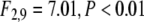 ). We also compared at what time after stimulus onset stimulus-locking was most pronounced between the different conditions. These response latencies were strongly modulated by the size of the presented stimulus, with shorter latencies for large stimuli (large stimuli: 77 ± 12 ms, small stimuli: 110 ± 21 ms, F1,9 = 30.69, P < 0.001, see also Fig. 6b). As can be inferred from the topographic maps displayed in 6b, stimulus-locking was constrained to electrodes over the occipital region.
). We also compared at what time after stimulus onset stimulus-locking was most pronounced between the different conditions. These response latencies were strongly modulated by the size of the presented stimulus, with shorter latencies for large stimuli (large stimuli: 77 ± 12 ms, small stimuli: 110 ± 21 ms, F1,9 = 30.69, P < 0.001, see also Fig. 6b). As can be inferred from the topographic maps displayed in 6b, stimulus-locking was constrained to electrodes over the occipital region.
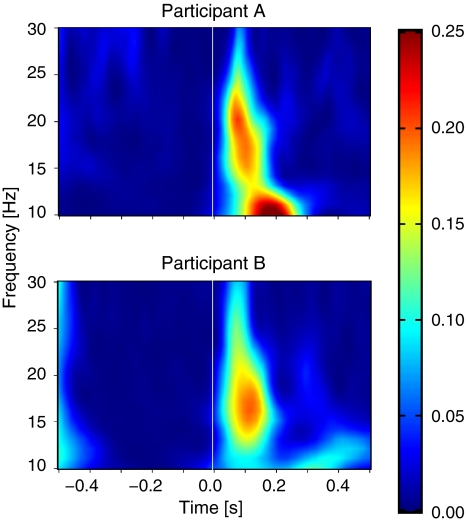
Fig. 5.
Early stimulus-locking in the β band in two single participants. Top: a participant with a relatively high response frequency. Bottom: a participant with a relatively low response frequency. Note that averaging these responses results in a smeared broad band response like in Fig. 6a
Fig. 6.
Early stimulus locking (PLF-values) in the β band. (a) Time frequency representations of stimulus locking in response to cued (left) and uncued (right) large stimuli (upper row) and small stimuli (lower row). (b) Time courses (left) and topographic maps of stimulus-locking in the β band. Maps are arranged in the same way as the time frequency representations in part (a). Note that the cue related increase in stimulus-locking is much more pronounced in response to large stimuli (solid lines/upper rows) than in response to small stimuli (dotted lines/lower rows)
Late modulation
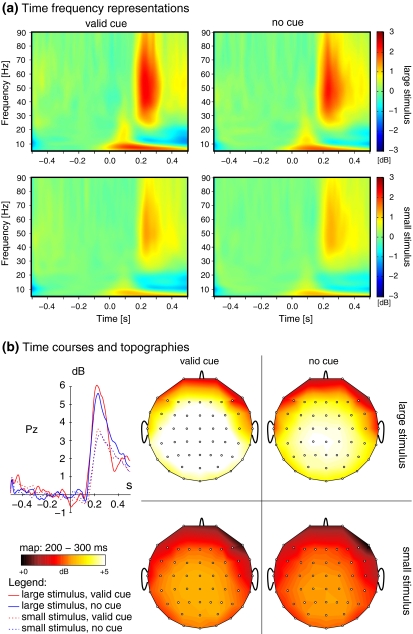
A clear response in total γ activity was observed about 200–300 ms after stimulus onset. As Fig. 7a shows, this response was clearly separated from lower frequency activity. However, the amplitude increase that was captured by the total activity extended over a fairly broad range of frequencies in all but one participant (similar to Fig. 7a). This late response was significantly stronger in response to large stimuli as compared to small stimuli (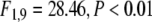 ). In addition to this strong modulation, a small but consistent modulation of total γ activity by the presence or absence of the cue was observed (F1,9 = 8.01, P < 0.05, cued versus uncued for large stimuli: t10 = 3.6, P < 0.01, cued versus uncued for small stimuli: t10 = 6.30, P < 0.001). In contrast to the early response, this cue effect was relatively independent of the size of the stimuli (no significant size × cue interaction, F2,9 = 2.11, ns). This late spectral response was relatively similar across a wide region of the scalp (see Fig. 7b).
). In addition to this strong modulation, a small but consistent modulation of total γ activity by the presence or absence of the cue was observed (F1,9 = 8.01, P < 0.05, cued versus uncued for large stimuli: t10 = 3.6, P < 0.01, cued versus uncued for small stimuli: t10 = 6.30, P < 0.001). In contrast to the early response, this cue effect was relatively independent of the size of the stimuli (no significant size × cue interaction, F2,9 = 2.11, ns). This late spectral response was relatively similar across a wide region of the scalp (see Fig. 7b).
Fig. 7.
Late stimulus related spectral amplitude modulations (dB-scale) in the γ band. (a) Time frequency representations of total γ activity in response to cued (left) and uncued (right) large stimuli (upper row) and small stimuli (lower row). (b) Time courses (left) and topographic maps of total γ activity. Maps are arranged in the same way as the time frequency representations in part (a). Note that cue related increases are—albeit weak—observed irrespective of stimulus size
Simulation results
Neural responses can be modulated with respect to their threshold (i.e. at which level of input does a neuron start to fire) and their gain (i.e. how fast does the output rate increase with increasing input). We simulated a population of 100 × 100 neural units in order to find out which of the two mechanisms is more likely involved in the generation of our EEG effects. In a subset of this population, threshold and/or gain were modified. In addition, a subset of the simulated populations (not necessarily overlapping) received input, simulating that a stimulus excited the receptive fields of the cells. In Fig. 4 such an input pattern is shown. Fig. 2 displays input–output relations of the simulated populations for different threshold–gain constellations. The solid line labeled “baseline” represents a baseline condition reflecting the no cue condition of the EEG experiment. To simulate pretuning of neural populations, we increased the gain of the input–output relation. Thus, without a sufficiently strong stimulus this should not change the behavior of the populations. However, if a stimulus is presented the responses of this population should increase much faster. This is evident from the increased slope of the dashed curve in Fig. 2 labeled “gain+”. Finally, we added a third condition which is mainly characterized by a shift in the response threshold towards weaker inputs. This is labeled “threshold−, gain−” in Fig. 2. In addition, and to match the experimental results, the gain of the input–output relation for this condition had to be reduced.
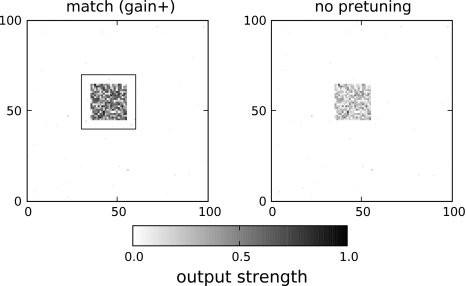
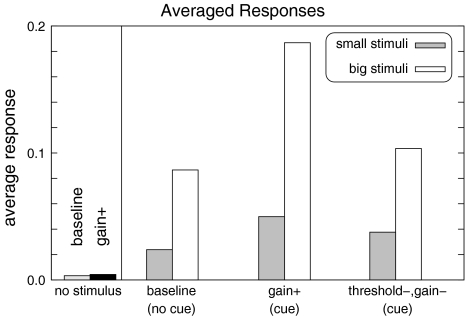
The responses of the model to the stimulus presented in Fig. 4 for two different conditions are displayed in Fig. 8. It can be observed that responses are enhanced if the locus of pretuning matches that of the stimulus. No response enhancement is observed if gain+ pretuning is applied to an area that does not match the stimulus. In order to allow a more rigorous comparison we replotted average responses across the whole array in Fig. 9. In the absence of a stimulus, the anticipatory modulation does not seem to make any difference in the large scale response (see the bars labeled “no stimulus” in Fig. 9). This is in accordance with the situation observed before the stimulus was presented. Without any modulation, the model displays higher responses for large stimuli as compared to small stimuli (“baseline” in Fig. 9). For gain+ modulation, however, a strong enhancement of the responses is observed if the stimulus matches the modulation of the populations. Similar to the stimulus-locking data in the β band, this enhancement is particularly salient for large stimuli. In the threshold−, gain− condition, an enhancement of the responses can also be observed. However, now the response enhancement is rather similar for large and small responses, resembling the total responses observed in the γ band.
Fig. 8.
Responses of the model under different conditions. Left: the area of pretuning (gain+ condition) matches the input area, right: there is no pretuning at all. The area of pretuning is marked by a thin black line
Fig. 9.
Barplot of the simulation responses under different conditions. The gain+ and threshold−, gain− conditions resemble the early β and late γ responses, respectively
Discussion
In the present study, we investigated high-frequency spectral responses to natural images with respect to stimulus anticipation. We observed both, stimulus-locking and total amplitude responses in our data. Stimulus anticipation effects were observed for the stimulus-locking of spectral responses in the β band primarily for large stimuli. In contrast, total γ responses were modulated by size and stimulus anticipation relatively independently. These results have qualitative counterparts in a model of gain modulated population responses.
Spectral responses at high frequencies
In the current experiment, we observed stimulus-locked responses in the β range that depended on bottom-up and anticipatory modulation resembling what had previously been reported as an interaction of bottom-up and top-down processes for stimulus-locked γ responses (Busch et al. 2006b). In contrast to these earlier results, the frequency of the stimulus-locked responses was much lower—nearly half that of previous reports. The most obvious difference between these previous reports and the current report comes from the stimulus material. Previous reports on stimulus-locked spectral responses often used rather simple stimulus configurations like geometrical shapes (Busch et al. 2004; Fründ et al 2007b) or gratings (Bodis-Wollner et al. 2001; Busch et al. 2006b; Fründ et al. 2007a; Schadow et al. 2007) and observed response frequencies between 30 and <90 Hz. Other studies that applied more complex stimuli (Busch et al. 2006a; Gruber and Müller 2005; Lachaux et al. 2005; Tallon-Baudry et al. 1997; Vidal et al. 2006) either did not observe stimulus-locked γ responses at all, or did not find these responses to be modulated by experimental manipulations. Our results are in line with these findings in that we did not find any stimulus-locked γ responses at all. The properties that would be expected for a stimulus-locked γ response, dependence on size (Busch et al. 2004; Fründ et al. 2007c) and an interaction between size and attention (Busch et al. 2006b), were found in a somewhat lower frequency range in the β band. A possible interpretation for this might be that the stimulus-locked response has shifted its frequency. Such downward shifts with increasing stimulus complexity have been proposed by several authors (Chen and Herrmann 2001; Olufsen et al. 2003; von Stein and Sarntheim 2000). These authors argue that in order to integrate information from remote cortical areas, the information that is integrated needs to be carried by spectral components of lower frequency. For instance Busch et al. (2004) observed a decrease in response frequency if the size of the evoking stimulus increased, although this effect was not significant. In a recent study, Fründ et al. (2008) found slightly lower response frequencies for stimuli with higher pixel-wise entropy. It is thus conceivable that the frequency of stimulus-locked oscillations is adapted to the demands of a particular perceptual task. The determinants of such frequency shifts are yet unclear. More experimental work is needed to identify the determinants of such frequency shifts.
The observed late enhancement of spectral power in the γ band (see Fig. 7) is consistent with previous reports in terms of frequency and latency (Busch et al. 2006a; Gruber and Müller 2005; Rodriguez et al. 1999; Tallon-Baudry et al. 1997). Such responses that consist of a power enhancement that is not accompanied by any stimulus-locking have been termed induced γ responses (Basar-Eroglu et al. 1996; Tallon-Baudry and Bertrand 1999). They seem to play a pivotal role for a wide variety of cognitive phenomena such as attention (Fries et al. 2001), memory (Gruber and Müller 2005; Howard et al. 2003; Sederberg et al. 2003), object recognition (Tallon-Baudry and Bertrand 1999), gestalt perception/binding (Uhlhaas and Singer 2006), multistable perception (Mathes et al. 2006), and associative learning (Miltner et al. 1999). Models of visual perception have associated such induced γ responses with the refinement of an initial coarse categorization of sensory input (Herrmann et al. 2004b; Körner et al. 1999) or with the activation of an associative network representing the semantic categorization of a stimulus (Tallon-Baudry and Bertrand 1999). These interpretations would suggest induced γ responses to be relatively independent of physical stimulus factors. Here we demonstrate, that this is not the case. In contrast, induced γ responses highly depended on the size of the stimulus. However, in contrast to the evoked responses (Busch et al. 2006b) the top-down effect imposed by the cue did not seem to interact with this size modulation.
Gain and threshold modulation
We simulated two different types of modulations of the input–output relation of neural processing units. In one condition, the gain of the model units was modulated, while in another condition, the threshold and the gain of the units was modulated. In the first case, global responses were dependent on the size of the stimuli, while in the second case, global responses were independent of stimulus size. These findings are remarkably similar to the EEG data. The anticipatory modulation of the evoked spectral response depends on the size of the stimulus, while this is not the case for the induced spectral response. These simulation results seem to suggest that the anticipation of a stimulus initially results in an increase of the gain of neural populations. This is consistent with the similarity between the evoked response and the behavior of the simulation in the “gain+” condition with increased input gain. The similarity between the induced response and the “threshold−, gain−” condition of the simulation seems to suggest that the induced response originated from a combined decrease of both, input gain and firing threshold.
In the current model, the gain and threshold modulations were generated by changing the respective model parameters. The biophysical mechanisms that could underlie these modulations are still under debate. Threshold modulations can be explained rather straightforward; excitatory inputs decrease the threshold, inhibitory inputs increase the threshold (Chance et al. 2002). The crucial point is about gain modulation which requires multiplicative interactions between neurons. Shunting inhibition, which drives the membrane potential closer to the cell’s resting potential rather than depolarizing or hyperpolarizing the cell, has been discussed as a possible implementation of multiplication/division of neural responses (Carandini and Heeger 1994). It has however been pointed out, that this mechanism cannot account for such effects in the context of spiking neurons (Koch 1999, p. 23). Two alternative mechanisms to implement gain modulation have been discussed. The first of these mechanisms is based on the effects of background activity of a cell (Chance et al. 2002). If this background activity consists of strong excitatory input which is balanced by strong inhibitory input, the gain of the input–output relation of that cell is diminished (Chance et al. 2002). These authors have derived an equation for the input–output relation of a leaky integrate and fire neuron (Abbott and Chance 2005). Using this equation for our simulation yielded qualitatively similar results. The noise that comes with such balanced input has recently been shown to account for contrast normalization in the primary visual cortex of cats (Finn et al. 2007). A second mechanism that could implement gain modulation is synchrony of inhibitory cells (Tiesinga et al. 2004). Cells that receive highly synchronous inhibitory input appear to have a higher input gain than cells for which the inhibitory input is temporally uncorrelated. This latter mechanism is in good accordance with the fact that the signals described in the current report show temporal structure—they are relatively concentrated in the spectral domain. Thus, in conclusion, different mechanisms exist that could implement a modulation of gain in a neural system. Although we cannot decide which particular mechanism implemented the gain modulation in the current data, it seems plausible that the observed effects (at least for evoked activity) can be explained as modulation of the input gain of the underlying cells. In contrast, the increase in induced high frequency activity seems to be consistent with a general increase in feedback activity that is in part driving the target cells closer to the threshold, in part reducing the input gain of the neural populations.
Relation to neural population models
The current model does not explicitly simulate individual spikes. Instead, it considers responses that are pooled across a group of cells. Dynamics of such models have been discussed by several authors (David and Friston 2003; Freeman 1975; Jansen and Rit 1995; Jirsa and Haken 1997; Nunez and Srinivasan 2006; Robinson et al. 1997, 1998, 2001; Rennie et al. 2000). Although these models incorporate a nonlinear response function similar to the one in Eq. 1, they typically emphasize dynamical aspects that arise if different populations of neurons interact. In the current paper we completely disregarded any dynamical properties of the neural populations. This enabled us to study the impact of the response function in separation. Indeed, it was possible to explain certain aspects of the experimentally observed responses simply by changes in the response function. In this way, the current approach complements the above dynamical models. It remains to be investigated, how transient changes of the response function change the dynamics of interacting neural populations.
Relation of anticipatory effects to cueing
In the literature about cueing there is a controversy as to whether the anticipatory effect of a cue triggers a change of the perceptual efficiency (e.g. Luck et al. 1994) or alters information selection at later stages of processing (Eckstein et al. 2002; Shimozaki et al. 2003). The interpretation of the cueing effect on stimulus-locking in the β frequency range as gain modulation is compatible with the former idea. This is in accordance with data that suggest effects of attention as early as the C1 (Khoe et al. 2005). However, the relatively late effects on induced high frequency power seem more consistent with the latter idea that (at least part of) the perceptual process is completed when processing is altered by the cue. Thus, it seems plausible that valid cueing facilitates the transmission of neural signals from early processing stages to late processing stages (Lai and Mangels 2007). These authors argue that this improved transmission results in stronger signals at these later stages which result in possible behavioral benefits. In a spatial cueing experiment, Fan et al. (2007) observed increased γ band power after cueing spatial locations. Our data suggest, that similar effects can be observed in relation to more semantic cueing such as observed in contextual cueing (Chun 2000).
Conclusion
We demonstrated that cueing triggers different aspects of high frequency responses. An early stimulus-locked response that was most pronounced in the β frequency band seemed consistent with pretuning the gain of neural populations. In addition, a later increase in induced γ activity was interpreted as an increase in feedback activity.
Appendix: Implementation of the model
Local processing is modeled as a mapping 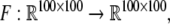 that maps a stimulus
that maps a stimulus 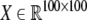 on a spatial pattern
on a spatial pattern 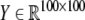 of neural activity. Measurement of the EEG (data shown in Fig. 9) is modeled by a linear form
of neural activity. Measurement of the EEG (data shown in Fig. 9) is modeled by a linear form 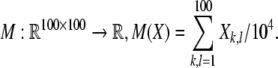 Interactions between stimulus driven and internal processes were modeled by either varying the stimulus X or the mapping F. The stimulus consisted of a field of real values X = {Xk,l}, where
Interactions between stimulus driven and internal processes were modeled by either varying the stimulus X or the mapping F. The stimulus consisted of a field of real values X = {Xk,l}, where 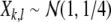 if
if 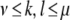 . Otherwise,
. Otherwise, 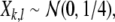 where
where 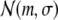 indicates a normal distribution with expectation value m and standard deviation σ. For large stimuli we set ν = 35, μ = 55, for small stimuli, we set ν = 40, μ = 50. The mapping
indicates a normal distribution with expectation value m and standard deviation σ. For large stimuli we set ν = 35, μ = 55, for small stimuli, we set ν = 40, μ = 50. The mapping 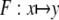 as given by Eq. 1, was applied to every element of X in order to obtain the simulated neural activity Y. The parameters g and θ in Eq. 1 were allowed to vary with space, thus
as given by Eq. 1, was applied to every element of X in order to obtain the simulated neural activity Y. The parameters g and θ in Eq. 1 were allowed to vary with space, thus 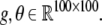 The baseline condition corresponds to
The baseline condition corresponds to 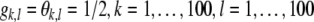 . In the gain+ condition, we set gk,l = 1/4 for
. In the gain+ condition, we set gk,l = 1/4 for 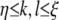 . In the threshold−, gain− condition, we set
. In the threshold−, gain− condition, we set 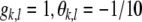 for
for 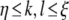 . If stimuli were modeled to be presented inside the modified region, we set η = 30, ξ = 60. If stimuli were modeled to be presented outside the modified region, we set η = 60, ξ = 90.
. If stimuli were modeled to be presented inside the modified region, we set η = 30, ξ = 60. If stimuli were modeled to be presented outside the modified region, we set η = 60, ξ = 90.
Acknowledgements
This study was supported by the German Research Foundation (DFG, Grant HE3353/2-2). The authors acknowledge the funding by the Bernstein Group for Computational Neuroscience, Magdeburg. The authors would like to thank Christian Grasmé and Toralf Neuling for help with the data acquisition.
Contributor Information
Ingo Fründ, Email: ingo.fruend@ovgu.de.
Christoph S. Herrmann, Email: christoph.herrmann@ovgu.de
References
- Abbott LF, Chance FS (2005) Drivers and modulators from push–pull and balanced synaptic input. Prog Brain Res 149:147–155 [DOI] [PubMed]
- Bar M (2007) The proactive brain: using analogies and associations to generate predictions. TRENDS Cogn Sci 11(7):280–289 [DOI] [PubMed]
- Basar E, Schürmann M, Başar-Eroglu C, Demiralp T (2001) Selectively distributed gamma band system of the brain. Int J Psychophysiol 39:129–135 [DOI] [PubMed]
- Basar-Eroglu C, Struber D, Schurmann M, Stadler M, Basar E (1996) Gamma-band responses in the brain: a short review of psychophysiological correlates and functional significance. Int J Psychophysiol 24(1–2):101–112 [DOI] [PubMed]
- Bodis-Wollner I, Davis J, Tzelepi A, Bezerianos T (2001) Wavelet transform of the EEG reveals differences in low and high gamma responses to elementary visual stimuli. Clin Electroencephalogr 32(3):139–144 [DOI] [PubMed]
- Busch NA, Debener S, Kranczioch C, Engel AK, Herrmann CS (2004) Size matters: effects of stimulus size, duration and eccentricity on the visual gamma-band response. Clin Neurophysiol 115(8):1810–1820 [DOI] [PubMed]
- Busch NA, Herrmann CS, Müller MM, Lenz D, Gruber T (2006a) A cross-laboratory study of event-related gamma activity in a standard object recognition paradigm. NeuroImage 33:1169–1177 [DOI] [PubMed]
- Busch NA, Schadow J, Fründ I, Herrmann CS (2006b) Time-frequency analysis of target detection reveals an early interface between bottom-up and top-down processes in the gamma-band. NeuroImage 29(4):1106–1116 [DOI] [PubMed]
- Carandini M, Heeger DJ (1994) Summation and division by neurons in primate visual cortex. Science 264(5163):1333–1336 [DOI] [PubMed]
- Chance FS, Abbott LF, Reyes AD (2002) Gain modulation from background synaptic input. Neuron 35:773–782 [DOI] [PubMed]
- Chen AC, Herrmann CS (2001) Perception of pain coincides with the spatial expansion of electroencephalographic dynamics in human subjects. Neurosci Lett 297(3):183–186 [DOI] [PubMed]
- Chun MM (2000) Contextual cueing of visual attention. TRENDS Cogn Sci 4(5):170–178 [DOI] [PubMed]
- David O, Friston KJ (2003) A neural mass model for MEG/EEG: coupling and neuronal dynamics. NeuroImage 20:1743–1755 [DOI] [PubMed]
- Debener S, Herrmann CS, Kranczioch C, Gembris D, Engel AK (2003) Top-down attentional processing enhances auditory evoked gamma band activity. NeuroReport 14(5):683–686 [DOI] [PubMed]
- Desimone R, Albright TD, Gross CG, Bruce C (1984) Stimulus-selective properties of inferior temporal neurons in the macaque. J Neurosci 4(8):2051–2062 [DOI] [PMC free article] [PubMed]
- Eckstein MP, Shimozaki SS, Abbey CK (2002) The footprints of visual attention in the posner cueing paradigm revealed by classification images. J Vision 2(1):25–45 [DOI] [PubMed]
- Fan J, Byrne J, Worden MS, Guise KG, McCandliss BD, Fossella J, Posner MI (2007) The relation of brain oscillations to attentional networks. J Neurosci 27(23):6197–6206 [DOI] [PMC free article] [PubMed]
- Finn IM, Priebe NJ, Ferster D (2007) The emergence of contrast-invariant orientation tuning in simple cells of cat visual cortex. Neuron 54(1):137–152 [DOI] [PMC free article] [PubMed]
- Fisher N (1993) Statistical analysis of circular data. Cambridge Universtity Press, New York
- Freeman WJ (1975) Mass action in the nervous system. Academic Press, New York
- Fries P, Reynolds JH, Rorie AE, Desimone R (2001) Modulation of oscillatory neuronal synchronization by selective visual attention. Science 291:1560–1563 [DOI] [PubMed]
- Fründ I, Busch NA, Körner U, Schadow J, Herrmann CS (2007a) EEG oscillations in the gamma and alpha range respond differently to spatial frequency. Vision Res 47(15):2086–2098 [DOI] [PubMed]
- Fründ I, Busch NA, Schadow J, Körner U, Herrmann CS (2007b) From perception to action: phase-locked gamma oscillations correlate with reaction times in a speeded response task. BMC Neurosci 8(27) [DOI] [PMC free article] [PubMed]
- Fründ I, Schadow J, Busch NA, Körner U, Herrmann CS (2007c) Evoked gamma oscillations in human scalp EEG are test–retest reliable. Clin Neurophysiol 118(1):221–227 [DOI] [PubMed]
- Fründ I, Busch NA, Schadow J, Gruber T, Körner U, Herrmann CS (2008) Time pressure modulates electrophysiological correlates of early visual processing. PLoS One 3(2):e1675 [DOI] [PMC free article] [PubMed]
- Gruber T, Müller MM (2005) Oscillatory brain activity dissociates between associative stimulus content in a repetition priming task in the human EEG. Cereb Cortex 15(1):109–116 [DOI] [PubMed]
- Gruber T, Müller MM, Keil A (2002) Modulation of induced gamma band responses in a perceptual learning task in the human EEG. J Cogn Neurosci 14(5):732–744 [DOI] [PubMed]
- Herrmann CS, Lenz D, Junge S, Busch NA, Maess B (2004a) Memory-matches evoke human gamma-responses. BMC Neurosci 5(13) [DOI] [PMC free article] [PubMed]
- Herrmann CS, Munk MH, Engel AK (2004b) Cognitive functions of gamma-band activity: memory match and utilization. TRENDS Cogn Sci 8(8):347–355 [DOI] [PubMed]
- Herrmann CS, Grigutsch M, Busch NA (2005) EEG oscillations and wavelet analysis. In: Handy TC (ed) Event-related potentials—a methods handbook, MIT Press, pp 229–259
- Hoogenboom N, Schoffelen JM, Oostenveld R, Parkes LM, Fries P (2006) Localizing human visual gamma-band activity in frequency, time and space. NeuroImage 29(3):764–773 [DOI] [PubMed]
- Howard MW, Rizzuto DS, Caplan JB, Madsen JR, Lisman J, Aschenbrenner-Scheibe R, Schulze-Bonhage A, Kahana MJ (2003) Gamma oscillations correlate with working memory load in humans. Cereb Cortex 13:1369–1374 [DOI] [PubMed]
- Jansen BH, Rit VG (1995) Electroencephalogram and visual evoked potential generation in a mathematical model of coupled cortical columns. Biol Cybern 73:357–366 [DOI] [PubMed]
- Jirsa VK, Haken H (1997) A derivation of a macroscopic field theory of the brain from the quasi-microscopic neural dynamics. Physica D 99:503–526 [DOI]
- Karakaş S, Başar E (1998) Early gamma response is sensory in origin: a conclusion based on cross-comparison of results from multiple experimental paradigms. Int J Psychophysiol 31:13–31 [DOI] [PubMed]
- Keil A, Müller MM, Gruber T, Wienbruch C, Elbert T (2001) Human large-scale oscillatory brain activity during an operant shaping procedure. Cogn Brain Res 12:397–407 [DOI] [PubMed]
- Khoe W, Mitchell JF, Reynolds JH, Hillyard SA (2005) Exogenous attentional selection of transparent superimposed surfaces modulates early event-related potentials. Vision Res 45(24):3004–3014 [DOI] [PubMed]
- Koch C (1999) Biophysics of computation. Oxford University Press, New York
- Körner E, Gewaltig MO, Körner U, Richter A, Rodemann T (1999) A model of computation in neocortical architecture. Neural Networks 12:989–1005 [DOI] [PubMed]
- Lachaux JP, George N, Tallon-Baudry C, Martinerie J, Hugueville L, Minotti L, Kahane P, Renault B (2005) The many faces of the gamma band response to complex visual stimuli. NeuroImage 25:491–501 [DOI] [PubMed]
- Lai G, Mangels JA (2007) Cueing effects on semantic and perceptual categorization: ERPs reveal differential effects of validity as a function of processing stage. Neuropsychologia 45:2038–2050 [DOI] [PMC free article] [PubMed]
- Luck SJ, Hillyard SA, Mouloua M, Woldorff MG, Clark VP, Hawkins H (1994) Effects of spatial cuing on luminance detectability: psychophysical and electrophysiological evidence for early selection. J Exp Psychol Hum Percept Perform 20(4):887–904 [DOI] [PubMed]
- Martinez A, Teder-Sälejärvi W, Vazquez M, Molholm S, Foxe JJ, Javitt DC, Di Russo F, Worden MS, Hillyard SA (2006) Objects are highlighted by spatial attention. J Cogn Neurosci 18(2):298–310 [DOI] [PubMed]
- Mathes B, Strüber D, Stadler MA, Basar-Eroglu C (2006) Voluntary control of Necker cuber reversals modulates the EEG delta-and gamma-band response. Neurosc Lett 402(1–2):145–149 [DOI] [PubMed]
- Miltner WHR, Braun C, Arnold M, Witte H, Taub E (1999) Coherence of gamma-band EEG activity as a basis for associative learning. Nature 397(6718):434–436 [DOI] [PubMed]
- Morup M, Hansen LK, Herrmann CS, Parnas J, Arnfred SM (2006) Parallel factor analysis as an exploratory tool for wavelet transformed event-related EEG. NeuroImage 29(3):938–947 [DOI] [PubMed]
- Naka KI, Rushton WA (1966) S-potentials from colour units in the retina of fish. J Physiol, London 185:584–599 [DOI] [PMC free article] [PubMed]
- Nunez PL, Srinivasan R (2006) Electric fields of the brain, 2nd edn. Oxford University Press, New York
- Olufsen MS, Whittington MA, Camperi M, Kopell N (2003) New roles for the gamma rhythm: population tuning and preprocessing for the beta rhythm. J Comput Neurosci 14(1):33–54 [DOI] [PubMed]
- Rennie CJ, Wright JJ, Robinson PA (2000) Mechanisms of cortical electrical activity and emergence of gamma rhythm. J Theor Biol 205:17–35 [DOI] [PubMed]
- Reynolds JH, Chelazzi L (2004) Attentional modulation of visual processing. Annu Rev Neurosci 27:611–647 [DOI] [PubMed]
- Robinson PA, Rennie CJ, Wright JJ (1997) Propagation and stability of waves of electrical activity in the cerebral cortex. Phys Rev E 56(1):826–840 [DOI]
- Robinson PA, Wright JJ, Rennie CJ (1998) Synchronous oscillations in the cerebral cortex. Phys Rev E 57(4):4578–4588 [DOI]
- Robinson PA, Rennie CJ, Wright JJ, Bahramali H, Gordon E, Rowe DL (2001) Prediction of electroencephalographic spectra from neurophysiology. Phys Rev E 63(021903) [DOI] [PubMed]
- Rodriguez E, George N, Lachaux JP, Martinerie J, Renault B, Varela FJ (1999) Perception’s shadow: long distance synchronization of human brain activity. Nature 397:430–433 [DOI] [PubMed]
- Salinas E, Sejnowski TJ (2001) Gain modulation in the central nervous system: where behavior, neurophysiology, and computation meet. Neuroscientist 7:430–440 [DOI] [PMC free article] [PubMed]
- Schadow J, Lenz D, Thaerig S, Busch NA, Fründ I, Rieger JW, Herrmann CS (2007) Stimulus intensity affects early sensory processing: visual contrast modulates evoked gamma-band activity in human EEG. Int J Psychophysiol 66(1):28–36 [DOI] [PubMed]
- Sederberg PB, Kahana MJ, Howard MW, Donner EJ, Madsen JR (2003) Theta and gamma oscillations during encoding predict subsequent recall. J Neurosci 23(34):10809–10814 [DOI] [PMC free article] [PubMed]
- Shimozaki SS, Eckstein MP, Abbey CK (2003) Comparison of two weighted integration models for the cueing task: linear and likelihood. J Vision 3(3):209–229 [DOI] [PubMed]
- Spencer KM, Nestor PG, Perlmutter R, Niznikiewicz MA, Klump MC, Frumin M, Shenton ME, McCarley RW (2004) Neural synchrony indexes disordered perception and cognition in schizophrenia. Proc Natl Acad Sci USA 101(49):17288–17293 [DOI] [PMC free article] [PubMed]
- Tallon-Baudry C, Bertrand O (1999) Oscillatory gamma activity in humans and its role in object representation. TRENDS Cogn Sci 3(4):151–162 [DOI] [PubMed]
- Tallon-Baudry C, Bertrand O, Delpuech C, Pernier J (1996) Stimulus specificity of phase-locked and on-phase-locked 40 Hz visual responses in human. J Neurosci 16(13):4240–4249 [DOI] [PMC free article] [PubMed]
- Tallon-Baudry C, Bertrand O, Delpuech C, Pernier J (1997) Oscillatory γ-band (30–70 hz) activity induced by a visual search task in humans. J Neurosci 17(2):722–734 [DOI] [PMC free article] [PubMed]
- Tallon-Baudry C, Bertrand O, Peronnet F, Pernier J (1998) Induced γ-band activity during the delay of a visual short-term memory task in humans. J Neurosci 18(11):4244–4254 [DOI] [PMC free article] [PubMed]
- Tiesinga PH, Fellous JM, Salinas E, José JV, Sejnowski TJ (2004) Inhibitory synchrony as a mechanism for attentional gain modulation. J Physiol (Paris) 98:296–314 [DOI] [PMC free article] [PubMed]
- Tiitinen H, Sinkkonen J, Reinikainen K, Alho K, Lavikainen J, Näätänen R (1993) Selective attention enhances the auditory 40-Hz transient response in humans. Nature 364:59–60 [DOI] [PubMed]
- Uhlhaas PJ, Singer W (2006) Neural synchrony in brain disorders: relevance for cognitive dysfunctions and pathophysiology. Neuron 52(1):155–168 [DOI] [PubMed]
- Vidal JR, Chaumon M, O’Regan JK, Tallon-Baudry C (2006) Visual grouping and the focusing of attention induce gamma-band oscillations at different frequencies in human magnetoencephalogram signals. J Cogn Neurosci 8(11):1850–1862 [DOI] [PubMed]
- von Stein A, Sarntheim J (2000) Different frequencies for different scales of cortical integration: from local gamma to long range alpha/theta synchronization. Int J Psychophysiol 38:301–313 [DOI] [PubMed]
- Wilson HR (1999) Spikes, decisions and actions. Dynamical foundations of neuroscience. Oxford University Press, New York
- Yamaguchi S, Yamagata S, Kabayashi S (2000) Cerebral asymmetry of the “top-down” allocation of attention to global and local features. J Neurosci 20(RC72):1–5 [DOI] [PMC free article] [PubMed]