Walking the Interactome for Prioritization of Candidate Disease Genes

Abstract

The identification of genes associated with hereditary disorders has contributed to improving medical care and to a better understanding of gene functions, interactions, and pathways. However, there are well over 1500 Mendelian disorders whose molecular basis remains unknown. At present, methods such as linkage analysis can identify the chromosomal region in which unknown disease genes are located, but the regions could contain up to hundreds of candidate genes. In this work, we present a method for prioritization of candidate genes by use of a global network distance measure, random walk analysis, for definition of similarities in protein-protein interaction networks. We tested our method on 110 disease-gene families with a total of 783 genes and achieved an area under the ROC curve of up to 98% on simulated linkage intervals of 100 genes surrounding the disease gene, significantly outperforming previous methods based on local distance measures. Our results not only provide an improved tool for positional-cloning projects but also add weight to the assumption that phenotypically similar diseases are associated with disturbances of subnetworks within the larger protein interactome that extend beyond the disease proteins themselves.

Introduction

At the time of this writing, over 1500 Mendelian conditions whose molecular cause is unknown are listed in the Online Mendelian Inheritance in Man (OMIM) database.¹ Additionally, almost all medical conditions are in some way influenced by human genetic variation. The identification of genes associated with these conditions is a goal of numerous research groups, in order to both improve medical care and better understand gene functions, interactions, and pathways.² Most current efforts at disease-gene identification involving linkage analysis or association studies result in a genomic interval of 0.5–10 cM containing up to 300 genes.^3,4 Sequencing large numbers of candidate genes remains a time-consuming and expensive task, and it is often not possible to identify the correct disease gene by inspection of the list of genes within the interval.

A number of computational approaches toward candidate-gene prioritization have been developed that are based on functional annotation, gene-expression data, or sequence-based features.^5–14 Recent high-throughput technologies have produced vast amounts of protein-protein interaction data,¹⁵ which represent a valuable resource for candidate-gene prioritization, because genes related to a specific or similar disease phenotype tend to be located in a specific neighborhood in the protein-protein interaction network.¹⁶ However, to date, relatively simple methods for exploring biological networks have been applied to the problem of candidate-gene prioritization, including the search for direct neighbors of other disease genes¹⁷ and the calculation of the shortest path between candidates and known disease proteins.^11,18

In this work, we have investigated the hypothesis that global network-similarity measures are better suited to capture relationships between disease proteins than are algorithms based on direct interactions or shortest paths between disease genes. We have defined 110 disease-gene families comprising genetically heterogeneous disorders, cancer syndromes, and complex (polygenic) diseases, and we have constructed an interaction network based on a total of 258,314 experimentally verified or predicted protein-protein interactions. We demonstrate that random walk and the related diffusion-kernel method—both of which capture global relationships within an interaction network—are greatly superior to local distance measures within the interaction network and also outperform other previously published methods. We have made our algorithm freely available on the web, and we also provide predictions for 287 loci from 80 of the disease-gene families described in this work.

Material and Methods

Disease-Gene Families

A total of 110 disease-gene families were defined, on the basis of entries in the Online Mendelian Inheritance in Man (OMIM) database,¹ for genetically heterogeneous disorders in which mutations in distinct genes are associated with similar or even indistinguishable phenotypes; cancer syndromes comprising genes associated with hereditary cancer, increased risk, or somatic mutation in a given cancer type; and complex (polygenic) disorders that are known to be influenced by variation in multiple genes. Additionally, we used domain knowledge and literature or database searches to select all genes clearly associated with the disorder at hand. The 110 families contained a total of 783 genes with 665 distinct genes (Some genes were members of more than one disease family), whereby the largest family contained 41 genes and the smallest only three genes. On average, each family contained seven genes. A complete listing of the disease-gene families with links to the corresponding entries in the OMIM database is given as Table S1, available online.

Protein-Protein Interaction Data

The protein-protein interaction (PPI) network is represented by an undirected graph with nodes representing the genes and edges representing the mapped interactions of the proteins encoded by the genes. To construct the network, five protein-protein interaction datasets from human, Mus musculus, Drosophila melanogaster, Caenorhabditis elegans, and Saccharomyces cerevisiae were downloaded from Entrez Gene¹⁹ on the 1st of July 2007. These datasets comprise interactions extracted from HPRD,²⁰ BIND,²¹ and BioGrid²². Additional interactions were extracted from IntACT,²³ and DIP.²⁴ Protein interactions were mapped to the genes coding for the proteins, and redundant interactions stemming from multiple data sources were removed. Interactions from the four nonhuman species were mapped to homologous human genes identified by Inparanoid²⁵ analysis with a threshold Inparalog score of 0.8. If both interaction partners could be mapped to human proteins, the interaction was used.

We also used data from STRING,²⁶ which is a comprehensive dataset containing functional links between proteins on the basis of both experimental evidence for protein-protein interactions as well as interactions predicted by comparative genomics and text mining. STRING uses a scoring system that is intended to reflect the evidence of predicted interactions. For the present study, we included interactions with a score of at least 0.4, which corresponds to a medium-confidence network²⁷ (Table 1).

Table 1.

Networks Tested in this Work

Network	Number of Interactors	Number of Interactions
Human	9169	35,910
Mapped:
Worm	684 (146)	831 (768)
Mouse	1412 (78)	1972 (853)
Fruitfly	2176 (590)	4930 (4,613)
Yeast	1557 (441)	33,396 (32,855)
Total Human and Mapped	10,231	74,885
STRING	12,594	209,089
All Data Sources	13,726	258,314
All Data Sources Excluding Text-Mining Data	11,673	133,612

“Mapped” indicates protein-protein interaction data mapped to orthologous human proteins. The number of new interactors/interactions that were added to the interaction network by mapping is shown in parentheses.

“All Data Sources” denotes the STRING data, human, and mapped interactions.

Disease-Gene Prediction

The general idea of the approach is depicted in Figure 1. The details of how the ranks were obtained are given below.

Figure 1.

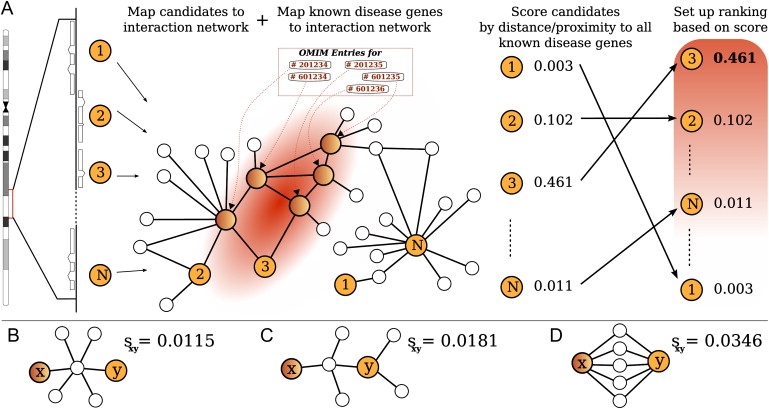
Disease-Gene Prioritization

(A) All candidate genes contained in the linkage interval are mapped to the interaction network, as are all previously known disease genes of the family in question. Our method then assigns a score to each of the candidate genes, with investigation of the relative location of the candidate to all of the known “disease genes” by the use of global network-distance measures. The genes in the linkage interval are ranked according to the score in order to define a priority list of candidates for further biological investigation.

(B–D) Each of the three subnetworks displays a different configuration consisting of the same number of nodes. The global distance between a hypothetical disease gene (x) and a candidate gene (y) is different in each case. In (B), proteins x and y are connected via a hub node with many other connections, so that the global similarity (s_xy) is less than in (C), where x and y are connected by a protein with fewer connections than those of the hub. On the other hand, nodes that are connected by multiple paths (D) receive a higher similarity than do nodes connected by only one path. Note that the shortest path between x and y is identical in each case (B–D), so that distance measures relying on such local information cannot differentiate between these three types of connection. In particular, the approach taking only direct interactions with gene x into account would identify gene y as a candidate in none of the three cases.

Random Walk

The random walk on graphs²⁸ is defined as an iterative walker's transition from its current node to a randomly selected neighbor starting at a given source node, s. Here, we used a variant of the random walk in which we additionally allow the restart of the walk in every time step at node s with probability r. Formally, the random walk with restart is defined as:

$${\mathbf{p}}^{t+1}=(1-r\text{)}\mathbf{W}{\mathbf{p}}^t+r{\mathbf{p}}^0$$

where W is the column-normalized adjacency matrix of the graph and p^t is a vector in which the i-th element holds the probability of being at node i at time step t.

In our application, the initial probability vector p⁰ was constructed such that equal probabilities were assigned to the nodes representing members of the disease, with the sum of the probabilities equal to 1. This is equivalent to letting the random walker begin from each of the known disease genes with equal probability. Candidate genes were ranked according to the values in the steady-state probability vector p^∞. This was obtained at query time by performing the iteration until the change between p^t and p^t+1 (measured by the L₁ norm) fell below 10⁻⁶.

Diffusion Kernel

The diffusion kernel K of a graph G is defined as K = e^−βL, where, intuitively, β controls the magnitude of the diffusion. The matrix L is the Laplacian of the graph, defined as D − A, where A is the adjacency matrix of the interaction graph and D is a diagonal matrix containing the nodes' degrees.²⁹ With the use of K, the rank for each candidate gene j was assigned in accordance with its score defined as

$$\mathit{score}\left(j\right)=\sum _{i\in \text{disease gene family}}{\mathbf{K}}_{\mathit{ij}}$$

For a sufficient small β the diffusion kernel can be seen as a lazy random walk consisting of transitions to one of each of the current node's neighbors with probability of β, whereby the walker remains at the current node i with a probability of 1 − d_iβ (with d_i being the degree of node i). The column vector j of the matrix K then represents the steady-state probability vector of the random walk when starting at node j.

Other Methods

For comparison with previously published methods, we have implemented screens of candidate genes in a linkage interval for direct interactions (DI) with other known disease-family proteins,¹⁷ whereby genes are predicted as potential disease genes if they have a direct interaction to known disease genes. We implemented a ranking of candidate genes according to the single shortest path (SP) to any known disease protein in the family (comparable to the CPS method in ¹⁸).

Furthermore, we ranked the genes in our test set with PROSPECTR, which uses a variety of sequence-based features, such as gene length, to train an alternating decision tree to rank genes in the order of likelihood of involvement in disease.¹³ Additionally, the internet implementation of ENDEAVOUR¹⁰ was used to test the genes listed in Table 2.

Table 2.

Performance of Five Candidate-Gene-Prioritization Methods on Seven Recently Identified Monogenic Disease Genes

Family	Gene	Rankings
		Random Walk	ENDEAVOUR	SP	DI	SQ
Nephronophthisis	GLIS237	100	43	100	100	3∗
ARVD	JUP38	1∗	1∗	1∗	2	67
RP	TOPORS39	23	69	20∗	100	56
RP	NR2E340	2	2	18	100	1∗
Noonan Syndrome	RAF141	1∗	3	4	4	42
Brachydactyly	NOG42	1∗	5	1∗	1∗	34
CMT4H	FGD443	13	2∗	27	100	9
Mean Enrichment		25.9∗	18.4	17.2	12.8	10.9

Results of random walk, two local network algorithms, ENDEAVOUR,¹⁰ and the sequence analysis program PROSPECTR¹² for the prediction of recently published genes causing monogenic diseases within artificial linkage intervals containing 100 genes.

“SP” denotes ranking according to shortest path.

“DI” denotes ranking according to direct interaction with a known disease protein.

“SQ” denotes ranking by sequence analysis with PROSPECTR.

“ARVD” denotes arrhythmogenic right ventricular dysplasia.

“RP” denotes retinitis pigmentosa.

“CMT4H” denotes Charcot-Marie-Tooth type 4H.

^∗indicates best performance.

Performance Measurement

For each disease gene we defined the artificial linkage interval to be the set of genes containing the first 100 genes located nearest to the disease gene according to their genomic distance on the same chromosome. In order to measure the performance of the whole optimization and training procedure, leave-one-out cross-validation was used for each disease-gene family. If a ranking method gives the actual disease gene the highest ranking and it is sequenced first, there is an enrichment of 50-fold. In general, the formula is Enrichment = 50/(rank) for an interval of 100 genes. For the present analysis, disease genes for which no interaction data were available were given a rank of 100 (and therefore an enrichment score of 0.5). No correction was made for intervals within which some proteins had no interaction data. If a particular method assigns an identical score to more than one gene, we assume the worst case, in which the true disease gene is the last to be sequenced from the set of equally ranked genes.

Another measure of performance of the algorithm is the receiver-operating characteristic (ROC) analysis, which plots the true-positive rate (TPR) versus the false-positive rate (FPR) subject to the threshold separating the prediction classes. The TPR/FPR is the rate of correctly/incorrectly classified samples of all samples classified to class +1. For evaluating rankings of disease-gene predictions, ROC values can be interpreted as a plot of the frequency of the disease genes above the threshold versus the frequency of disease genes below the threshold, where the threshold is a specific position in the ranking.¹⁰ In order to compare different curves obtained by ROC analysis, we calculate the area under the ROC curve (AUROC) for each curve.

Results

In this work, we constructed an interaction network based on a total of 35,910 interactions between human proteins as well as 38,975 mapped interactions from four other species. Additionally predicted protein interactions from the STRING database²⁶ were used (Table 1). We adapted a global distance measure based on random walk with restart (RWR) to define similarity between genes within this interaction network and to rank candidates on the basis of this similarity to known diseases genes. Intuitively, the RWR algorithm calculates the similarity between two genes, i and j, on the basis of the likelihood that a random walk through the interaction network starting at gene i will finish at gene j, whereby all possible paths between the two genes are taken into account. In our implementation, we let the random walk start with equal probability from each of the known disease-gene family members in order to search for an additional family member in the linkage interval (Figure 1). For comparison, we also implemented a similar global search algorithm based on the diffusion kernel (DK), which conceptually performs a different type of random walk calculated by matrix exponentiation (see Material and Methods for mathematical details). In order to compare the performance of global and local network search algorithms, we implemented two previous methods based on searching for disease genes among direct-interaction partners of candidate genes and searching for the single shortest path to a known disease gene, and we also utilized PROSPECTR, a previously described sequence-based ranking system.¹³ We tested our method on 86 genetically heterogeneous disorders in which mutations in distinct genes are associated with similar or even indistinguishable phenotypes; 12 cancer syndromes comprising genes associated with hereditary cancer, increased risk, or somatic mutation in a given cancer type; and 12 complex (polygenic) disorders that are known to be influenced by variation in multiple genes. For every such family, we then performed leave-one-out cross-validation (see Material and Methods).

Using the network containing all interactions (including text-mining data) and the RWR technique, we ranked all genes of 43 disease-gene families first (50-fold enrichment). For instance, all genes of Hirschsprung disease (six genes), Waardenburg syndrome (six genes), adrenoleukodystrophy (five genes), and limb-girdle muscular dystrophy (14 genes) families were ranked first. On average, we achieved an enrichment score of 44-fold for all 783 disease genes using all data sources including the text-mining component of STRING. Similar but slightly inferior results were obtained for the other global search method based on the DK. Leaving out text mining data, the RWR achieved a mean enrichment of 27-fold for all 110 disease families. The best results were obtained for families of heterogeneous monogenic diseases. However, there was an especially clear advantage for the RWR and DK methods for polygenic disorders and cancer families compared to the other methods, although the overall performance of all methods was somewhat less than with the monogenic disorders (Figure 2A).

Figure 2.

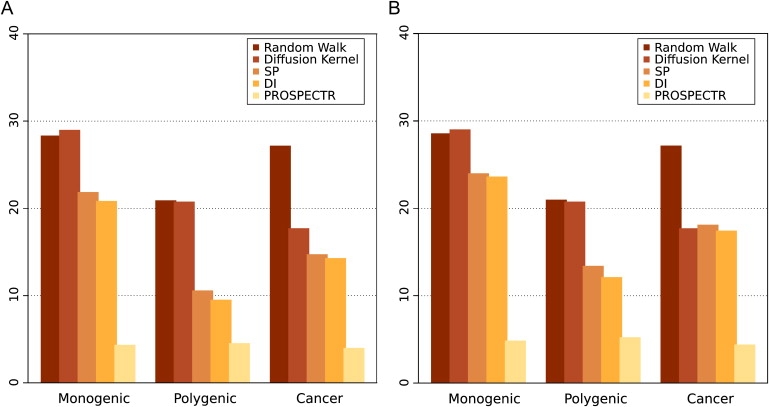
Cross-Validation Results

Enrichment analyses for the all-interactions network without STRING text-mining data are shown. Genes within an artificial linkage interval containing 100 genes were ranked according to the methods indicated. The mean enrichment reflects the position of the true disease gene in the prioritized list and is thereby related to the amount of time saved by the sequencing of candidate genes in the order calculated by the respective algorithm (see Material and Methods). Two different methods for evaluating genes with equal scores were evaluated.

(A) If multiple genes receive the same score, the worst case is assumed whereby the true disease gene is the last to be sequenced.

(B) If multiple genes receive the same score, each gene is given the mean rank of all tied genes. The complete list of results for each disease-gene family is available in Table S2.

The above comparison (Figure 2A) was performed by assumption of the worst case for genes with equal scores, i.e., that the true disease gene is sequenced last among the set of equally ranked genes. In the complete network (without text-mining data), genes have an average of 22.9 direct neighbors. There is a mean path length of 3.7 between random pairs of genes. Therefore, there are a lot of direct interactions, and nodes are rarely far apart in the interactome. One consequence of this for methods such as DI and SP is that it is not very unlikely to observe interactions that are unrelated to the disease gene family. In 61% of the cases in which the DI method correctly identified the true disease gene, it additionally identified other unrelated genes with a direct interaction to a known disease gene. On the other hand, in only 1.4% of the cases in which the true disease gene was ranked in first place by the RWR method was another, unrelated gene also given the same score. Therefore, the RWR method is better able to discriminate among genes within a dense network of interactions. However, even if all genes with equal scores are assigned the mean rank, our method clearly outperforms the methods based on local distance measures (Figure 2B).

We additionally used ROC analysis to compare the various methods shown in Figure 2A, confirming the performance advantage of RWR and DK analysis compared to the local interaction screens (DI, SP) and a sequence-based analysis (Figure 3A).

Figure 3.

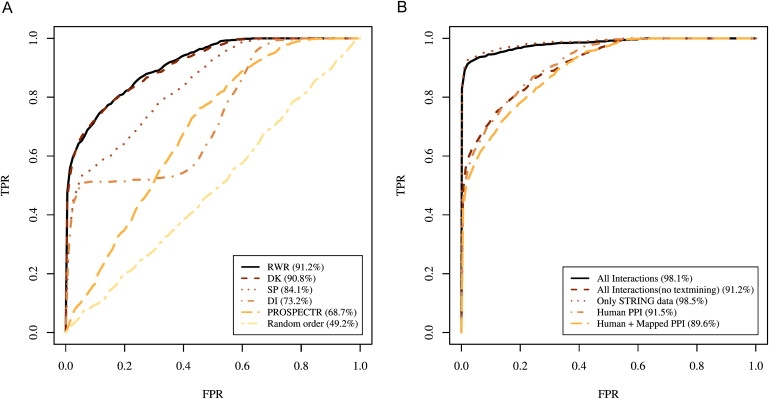
Cross-Validation Results

Rank ROC curves were generated for the 110 disease-gene families described in this work. The methods used to calculate the individual ROC curves are indicated in the figure. Intuitively, the area under the ROC curve (AUROC) reflects the false-positive rate needed to achieve various levels of sensitivity, with a perfect classifier having an AUROC of 100% and a random classifier having an AUROC of 50%. For comparison, we excluded disease genes with no interaction data, which were 15 genes in the all-data-sources network, 63 genes in the same network without text-mining data, 35 genes in the STRING network, 114 with the human and mapped data, and 139 in the human network.

(A) Comparison of different methods for the all-interactions network without STRING text-mining data. The curve labeled “random order” displays the results obtained by the sequencing of genes within the linkage interval at random, i.e., without use of any prioritization method.

(B) Comparison of different data sources with RWR analysis.

We then used ROC analysis to compare the performance of RWR using interaction networks constructed from several different data sources. Because the different data sources cover different numbers of genes, we included only those genes for which interaction data was available in the ROC analysis (768 of 783 genes for all data sources, 720 of 783 genes for all data sources except text mining, 748 of 783 genes for the STRING network, 669 of 783 genes for the human and mapped data, and 664 of 783 genes for the human data).

Present estimates suggest that only about 10% of all human protein-protein interactions have been described.³⁰ The choice of data source to use for proteome analyses essentially amounts to a choice between coverage and accuracy. Protein-protein interactions are often evolutionarily conserved,³¹ suggesting the mapping of interactions between orthologous proteins in other organisms to the human interactome. Additionally, text mining has been used as one of the components of STRING to predict protein-protein interactions.²⁷ Although these computational techniques increase the coverage of proteins and interactions, they presumably come at the cost of reducing the overall accuracy of the data by introducing false-positive interactions. Mapping interactions from four other species increased the number of genes included in the human PPI network by over 1000 additional genes (cf. Table 1). The performance of this mapped network was only slightly inferior to the network with only human data used, but given the higher coverage it could be preferable for searching for novel disease genes (Figure 3B). The network with only medium-confidence STRING data used showed the best performance of all networks, but fewer genes are covered in this network than in the complete network (cf. Table 1).

The highest area under the ROC curve (AUROC) was 98% with text mining and 91% without (Figure 3B). The improved performance of the network including literature data confirms previous observations¹⁰ that testing gene-prioritization methods on known disease genes might introduce a bias because a given gene is likely to be intensively studied in the years following its identification as a human disease gene. This “previous-knowledge bias” means that methods relying on text mining or targeted experimental studies on individual genes may perform better on historical training data (such as the 110 disease-gene families described above) than in a prospective setting in which novel disease genes are sought.

In order to simulate the real-life search for an unknown novel disease gene, we therefore chose seven disease genes that were discovered in 2007 and belong to some of the families investigated in this work. The identification of the disease associations of these genes was published subsequent to the creation date of the STRING database we used, so that we expect minimal publication bias. We tested these seven genes as above and also tested the performance of ENDEAVOR,¹⁰ which has outperformed all other previously published methods. RWR achieved a mean enrichment of 26-fold, which was superior to the results of all other methods (Table 2).

Figures 4 and 5 display the interaction networks associated with two disease-gene families for which the RWR ranked each disease gene (red) in first place. For comparison, unrelated genes that mistakenly receive the highest rank by the SP method are shown in yellow. For the protein-interaction network associated with bare lymphocyte syndrome type 1 (Figure 4), it is apparent that the disease genes are connected to one another by multiple paths, comparable to Figure 1D, whereas the unrelated genes are connected to the true disease genes by single paths only. As noted above, current databases of human protein interactions are far from complete. This is clearly problematic for predictions based upon direct interactions with disease genes, because a lack of direct interactions to disease genes will automatically result in a false-negative prediction. On the other hand, our method appears to be more tolerant of incomplete data. For instance, the disease-gene family for Stickler syndrome comprises COL2A1, COL9A1, COLA11, and COL11A2. Collagen XI is a heterotrimeric molecule consisting of alpha 1, alpha 2, and alpha 3 collagen chains; in cartilage, it assembles with collagens II and IX to produce an extensive network of thin, heterotypic collagen fibrils.³² However, these interactions are not currently listed in the protein-interaction databases used for our study. Nonetheless, the RWR method made the correct predictions on the basis of a dense network of other interacting proteins between the disease genes (again comparable to Figure 1D). On the other hand, the unrelated genes that mistakenly receive the highest rank by the SP method themselves have numerous other interaction partners, so that a single path to a single true disease gene is not weighted highly by the RWR method (Figure 5).

Figure 4.

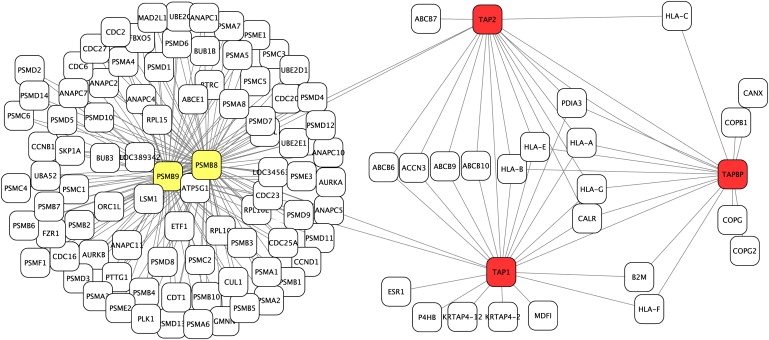
Bare Lymphocyte Syndrome Type 1 Protein-Interaction Network

The protein-interaction network associated with bare lymphocyte syndrome type 1, which comprises the genes TAP1, TAP2, and TAPBP. Each of these genes is shown in red. The DI and SP methods additionally identified the unrelated genes PSMB8 and PSMB9 (shown in yellow) as potential disease genes because they each have an interaction with one of the true disease genes. The RWR method ranks the true disease genes higher because each true disease gene has interactions with two other family members and because there is a dense net of proteins that connect the disease genes via paths with two interactions. All proteins connected to the correct or incorrect candidates by a single interaction are additionally displayed. The graphic was generated with Cytoscape.⁴⁴

Figure 5.

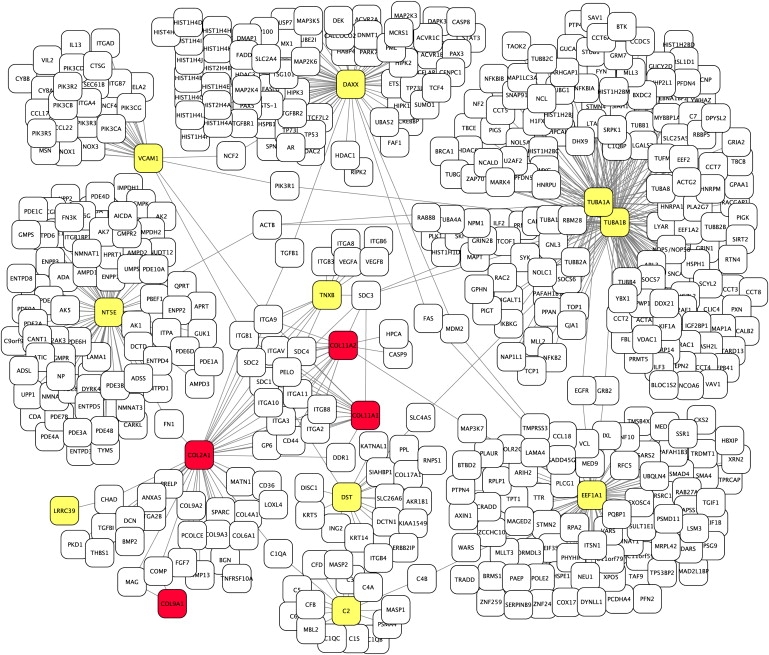
Stickler Syndrome Protein-Interaction Network

The protein-interaction network associated with Stickler syndrome comprises the genes COL2A1, COL9A1, COL11A1, and COL11A2. There is no direct path between any pair of disease genes. Therefore, the DI method will not make any correct prediction. A number of false predictions of the SP method are shown in yellow. Most of these genes have a large number of direct interactions with other proteins, so that the weight of any single interaction is small in the RWR and DK methods. Each of them has a single path of length 2 with one of the true disease genes. In contrast, the true disease genes each have multiple paths of length 2 with other disease genes and therefore receive a correspondly high score from the RWR and DK methods. For instance, the genes COL11A1, COL11A2, and COL2A1 are connected to one another by 14 other genes. The graphic was generated as in Figure 4.

Discussion

Several approaches have been published for the prioritization of candidate disease genes, which included functional as well as sequence-based methods. However, the emerging amounts of protein-protein interaction data have only sparsely been used for this problem, by investigation of either the direct interactions to other disease genes^10,17,33 or the shortest-path distance to known disease genes.¹⁸ In this work, we have presented a novel method for candidate-gene prioritization based on the random walk method, which we use to calculate a score reflecting the global similarity of candidate genes to known members of a disease-gene family (Figure 1).

There are a number of issues to consider when comparing the results of different methods for computational disease-gene prediction or prioritization. Given the cost and effort involved in characterizing novel disease genes, prospective comparisons on large numbers of disease loci have not been performed. Therefore, most groups have measured the performance of their algorithms by using collections of known disease genes. That is, a disease-gene family is defined, and the method is tested on each of the members of the family in turn by use of the remaining members of the family as positive examples. In this context, we feel it is important to create a realistic test scenario. We have defined artificial linkage intervals containing 100 genes around each of the disease genes being tested in order to simulate the situation facing positional-cloning projects. It is less appropriate to use some number of genes chosen at random, as was done to test some other methods,¹⁰ because of the tendency of similar genes to cluster in chromosomal neighborhoods. For instance, genes in the same metabolic pathway show statistically significant genomic clustering as compared to randomly chosen genes.³⁴ Additionally, we found that proteins coded by genes in the contiguous intervals around disease genes are located in greater proximity to the corresponding disease-gene family members in the PPI network than are proteins coded by randomly chosen genes; comparison of mean shortest-path distance from genes other than the disease gene within the 100-gene artificial interval with the corresponding mean distance among 100 randomly chosen genes showed a small but highly significant difference: 3.46 for the ”interval genes” and 3.58 for the randomly chosen genes, corresponding to a p value of 2.2 × 10⁻¹⁶ (data not shown).

Another important issue lies in the definition of the disease-gene families. In this work, we have defined 110 disease-gene families by using both the OMIM database¹ and domain knowledge (D.H., P.N.R.) (see Table S1). We claim that this is the largest publicly available list of disease-gene families available for the testing of gene-prioritization methods. Also important is the range of disease-gene families and of genes for which a given method is applicable. In general, methods based on sequence analysis¹³ have no restrictions. Methods based on functional annotation^5–12 have no restrictions but will presumably function poorly for novel disease genes for which little or no functional annotations are available. Especially as more protein-protein interaction data becomes available, we expect that methods using this type of data will become ever more accurate in their prediction of novel disease genes. Some of these methods are limited to genes having direct interactions with other known disease genes.^17,33 Our method can only be used for genes for which protein-protein interactions are known or predicted, but it does not require direct interactions. Thus, with our method, no prediction was possible for 15 of the 783 genes tested. Many disease-gene families as currently defined contain but two or three members (see Table S1). Our method was tested with families as small as three members, meaning that two genes at a time were used as positive examples. Other published methods have been tested with the use of larger families (for instance, ENDEAVOUR¹⁰ was tested with families of eight or more genes), so it is unclear how these methods will perform for smaller disease-gene families.

Therefore, we claim that we have used a realistic and biologically relevant testing strategy to measure the performance of our methods. We have shown that the two global distance measurements (RWR, DK) clearly outperform two local network-search methods (DI, SP) and the sequence-based method PROSPECTR.¹³ Additionally, we used a panel of recently identified monogenic disease genes to compare RWR with both the local network search methods and PROSPECTR, as well as with ENDEAVOUR.¹⁰ We expect the influence of publication of functional data concerning these new disease genes to be minimal, because their discovery was published subsequent to the version of the STRING database we used. Although no single method was superior for all of the genes tested, our RWR method outperformed all other methods on average (Table 2).

It has recently become clear that networks pervade all aspects of human health and that a network approach to the analysis of cellular functions affected by genes and gene products, rather than just a list of ”disease genes,” will be necessary for the understanding of disease mechanisms³⁵ and that proteins mutated in phenotypically similar diseases might form highly interlinked subnetworks within the larger protein interaction network.³⁶ In this work, we have shown that network algorithms that measure not only direct and shortest-path interactions but also take the global structure of the interactome into account have a clear performance advantage in the prioritization of candidate disease genes. We suggest that this supports the assumption that phenotypically similar diseases are associated with disturbances of subnetworks within the protein interactome and that exploration of global network structures with appropriate graph-theoretic algorithms will become an important resource for understanding of the biology of disease.

We have developed GeneWanderer, a freely available implementation of all four network algorithms. Scientists involved in positional-cloning projects can search for novel genes related to one of the 110 disease-gene families described here or can provide their own disease-gene family. They can then use our algorithm to rank genes in a linkage interval in order to prioritize candidate genes for sequencing. Many of the 110 disease-gene families analyzed in this work also contain loci with currently unidentified genes. On the GeneWanderer homepage, we provide predictions for 287 such loci from 80 disease-gene families extracted from the Morbid Map of OMIM.¹

Supplemental Data

Supplemental Data include two tables and can be found online at http://www.ajhg.org/.

Web Resources

The URLs for data presented herein are as follows:

• GeneWanderer, http://compbio.charite.de/genewanderer

• Online Mendelian Inheritance in Man, http://www.ncbi.nlm.nih.gov/Omim/