Genetic Flip-Flop without an Accompanying Change in Linkage Disequilibrium

Main Text

In a recent issue of the American Journal of Human Genetics, Lin et al.¹ showed that a change in linkage disequilibrium (LD) between a causal (B) and the observed (A) variants can lead to a reversal of genetic effect between two studies (a flip-flop). In this report, we show that a flip-flop can occur without a change in LD, even under simple noninteractive models. Further, we examine interactive models that allow for a flip-flop to take place under linkage equilibrium (LE). We provide specific conditions for the form of A and B interaction that permits a zero LD flip-flop, examine the behavior of allelic variance in the case of quantitative traits, and discuss potential implications of the findings for association mapping.

First, we consider a binary trait, $\mathcal{Y}:\{{\mathcal{Y}}_D,{\mathcal{Y}}_N\}$, where ${\mathcal{Y}}_D$ indicates a condition, such as the presence of disease. As in Lin et al.,¹ we will assume that the trait is influenced by two genetic variants, A:{A₁,A₂} (observed locus) and B:{B₁,B₂} (unobserved locus), and that there is no confounding. For simplicity, we disregard dominance effects, thereby allowing an essentially haploid treatment of the problem.² The two-locus penetrance values are given by M and population frequencies of the haplotypes are given by P (see Table 1). This uses the notation ${\mu }_{A_i{B}_j}=\mathrm{Pr}\left({\mathcal{Y}}_D\right|A_i,B_j)$ for the entries of M. Among those with a particular allele, the expected proportion of individuals who will develop the condition is

$${\mu }_{A_1}=\mathrm{Pr}\left({\mathcal{Y}}_D\right|A_1)=\frac{{\mu }_{A_1{B}_1}{p}_{A_1{B}_1}+{\mu }_{A_1{B}_2}{p}_{A_1{B}_2}}{p_{A_1{B}_1}+p_{A_1{B}_2}}$$ (1)

and

$${\mu }_{A_2}=\mathrm{Pr}\left({\mathcal{Y}}_D\right|A_2)=\frac{{\mu }_{A_2{B}_1}{p}_{A_2{B}_1}+{\mu }_{A_2{B}_2}{p}_{A_2{B}_2}}{p_{A_2{B}_1}+p_{A_2{B}_2}}.$$ (2)

Table 1.

Two-Locus Penetrance Values and Population Frequencies of the Haplotypes

Haplotype	P	M
A1B1	$p_{A_1{B}_1}$	${\mu }_{A_1{B}_1}$
A1B2	$p_{A_1{B}_2}$	${\mu }_{A_1{B}_2}$
A2B1	$p_{A_2{B}_1}$	${\mu }_{A_2{B}_1}$
A2B2	$p_{A_2{B}_2}$	${\mu }_{A_2{B}_2}$

The relative risk is

$$RR=\frac{{\mu }_{A_1}}{{\mu }_{A_2}}=\frac{({\mu }_{A_1{B}_1}{p}_{A_1{B}_1}+{\mu }_{A_1{B}_2}{p}_{A_1{B}_2})(p_{A_2{B}_1}+p_{A_2{B}_2})}{({\mu }_{A_2{B}_1}{p}_{A_2{B}_1}+{\mu }_{A_2{B}_2}{p}_{A_2{B}_2})(p_{A_1{B}_1}+p_{A_1{B}_2})}.$$ (3)

The RR remains the same if M is multiplied by a constant. A flip-flop takes place whenever there is a change in sign of ${\mu }_{A_1}-{\mu }_{A_2}$. For a given penetrance configuration, M, a flip-flop point is defined by a combination of haplotype frequencies such that ${\mu }_{A_1}={\mu }_{A_2}$ (or equivalently, RR = 1).

Flip-Flop under a Constant LD

The simplest flip-flop case is the “proxy model,” in which the locus A has no functional significance but is related to the locus B only via LD. The penetrance array for the proxy model has the form M = {x, y, x, y}. In this case, it is necessary that the LD sign should change for a flip-flop to occur, as can be shown by writing the haplotype frequencies in terms of the LD coefficient (D) and solving ${\mu }_{A_1}={\mu }_{A_2}$ for D. This calculation results in D = 0; thus, the proxy model most closely corresponds to the findings of Lin et al.¹ Equations 1 and 2 show that for a given penetrance configuration, allelic effects are functions of haplotype frequencies. Thus, the driving force of flip-flip is a change in haplotype frequencies. There are multiple frequency configurations that can result in the same LD, and a flip-flop is not necessarily accompanied by a change in the LD. As an example, consider a simple noninteractive penetrance model of additive contributions by the two loci, ${\mathcal{\kappa }}_{A_1}=0.2$, ${\mathcal{\kappa }}_{A_2}=0.3$, ${\mathcal{\kappa }}_{B_1}=0.4$, and ${\mathcal{\kappa }}_{B_2}=0.1$, with haplotype effects given by $\mathbf{M}=\{{\mathcal{\kappa }}_{A_1}+{\mathcal{\kappa }}_{B_1},{\mathcal{\kappa }}_{A_1}+{\mathcal{\kappa }}_{B_2},{\mathcal{\kappa }}_{A_2}+{\mathcal{\kappa }}_{B_1},{\mathcal{\kappa }}_{A_2}+{\mathcal{\kappa }}_{B_2}\}$. In this model, a flip-flop is possible without a change in LD. When P = {0.075, 0.01, 0.25, 0.665}, the association is positive; ${\mu }_{A_1}=0.56$ versus ${\mu }_{A_2}=0.48$. A switch of population frequencies to P = {0.075, 0.25, 0.01, 0.665} leads to a flip-flop as follows: ${\mu }_{A_1}=0.37$ versus ${\mu }_{A_2}=0.40$. In both cases, the LD is the same: r_AB = 0.36, D′ = 0.83, D = 0.05, where the correlation r_AB and D′ are the usual LD standardizations.^3,4

Zero LD Flip-Flop

The population haplotype frequencies under LE are given by $\mathbf{P}=\{p_{A_1}{p}_{B_1},p_{A_1}{p}_{B_2},p_{A_2}{p}_{B_1},p_{A_2}{p}_{B_2}\}$, where $p_{A_2}=1-p_{A_1}$ and $p_{B_2}=1-p_{B_1}$. The penetrance values and the relative risk at the observed locus are given by

$${\mu }_{A_1}\stackrel{\mathrm{LD}=0}{=}{\mu }_{A_1{B}_2}+p_{B_1}({\mu }_{A_1{B}_1}-{\mu }_{A_1{B}_2}),$$ (4)

$${\mu }_{A_2}\stackrel{\mathrm{LD}=0}{=}{\mu }_{A_2{B}_2}+p_{B_1}({\mu }_{A_2{B}_1}-{\mu }_{A_2{B}_2}),$$ (5)

and

$$\mathrm{RR}\stackrel{\mathrm{LD}=0}{=}\frac{{\mu }_{A_1{B}_2}+p_{B_1}({\mu }_{A_1{B}_1}-{\mu }_{A_1{B}_2})}{{\mu }_{A_2{B}_2}+p_{B_1}({\mu }_{A_2{B}_1}-{\mu }_{A_2{B}_2})}.$$ (6)

Note that these quantities do not depend on the frequencies of the observed locus, A. Whether any particular M is permitting a flip-flop under LE is determined by the solution of RR = 1 for $p_{B_1}$ (which defines the flip-flop point). This value is given by

$$p_{B_1}^{(\mathrm{RR}=1)}=\frac{1}{1+\frac{{\mu }_{A_2{B}_1}-{\mu }_{A_1{B}_1}}{{\mu }_{A_1{B}_2}-{\mu }_{A_2{B}_2}}}.$$ (7)

For an effect reversal, this value has to be inside the (0, 1) interval. An equivalent condition is $\text{sign}\left({\mu }_{A_2{B}_1}-{\mu }_{A_1{B}_1}\right)=\text{sign}\left({\mu }_{A_1{B}_2}-{\mu }_{A_2{B}_2}\right)$. The condition implies that the effect of A₁ has to be reversed when the background of B is switched from B₁ to B₂. Two examples of such penetrance configurations are shown in Table 2, in which the values (δ₁, δ₂) of the same sign can be considered to be deviations from the “base values” (x, y). The M₂, with some constraints on δ₁, δ₂, is an example of a “yin-yang” model, in which dissimilar haplotypes have similar susceptibilities. This model has been considered in several publications in the context of association mapping.^5–8

Table 2.

Two Examples of Penetrance Configurations

Haplotype	M1	M2
A1B1	x	x
A1B2	y	y
A2B1	x + δ1	y ± δ1
A2B2	y − δ2	x ± δ2

The relations for the binary phenotype discussed above remain the same for the case when $\mathcal{Y}$ is quantitative. For example, the ${\mu }_{A_1},{\mu }_{A_2}$ become the conditional expected values ${\mu }_{A_1}=E\left(\mathcal{Y}\right|A_1)$ and ${\mu }_{A_2}=E\left(\mathcal{Y}\right|A_2)$. These are given by the same formulas as before. The “relative risk” becomes the ratio of the two allelic means. An additional quantity of interest in the case of a quantitative trait is the allele-specific variance:

$$V_{A_1}=\frac{V_{A_1{B}_1}{p}_{A_1{B}_1}+V_{A_1{B}_2}{p}_{A_1{B}_2}}{p_{A_1{B}_1}+p_{A_1{B}_2}}+\frac{p_{A_1{B}_1}{({\mu }_{A_1{B}_1}-{\mu }_{A_1})}^2+p_{A_1{B}_2}{({\mu }_{A_1{B}_2}-{\mu }_{A_1})}^2}{p_{A_1{B}_1}+p_{A_1{B}_2}}$$ (8)

where $V_{A_i{B}_j}$ = Var $\left(\mathcal{Y}\right|A_i{B}_j)$, with a similar expression for A₂. Assuming a common underlying variance, ${\mathit{\sigma }}^2=V_{A_1{B}_1}=V_{A_1{B}_2}=V_{A_2{B}_1}=V_{A_2{B}_2}$, and LE, the allele-specific variances become:

$$\begin{array}{c}{V}_{A_1}\stackrel{LD=0}{=}{\sigma }^2+p_{B_1}(1-p_{B_1}){({\mu }_{A_1{B}_1}-{\mu }_{A_1{B}_2})}^2\\ V_{A_2}\stackrel{LD=0}{=}{\sigma }^2+p_{B_1}(1-p_{B_1}){({\mu }_{A_2{B}_1}-{\mu }_{A_2{B}_2})}^2\end{array}$$

As a function of $p_{B_1}$, the ratio of the variances under LE reaches the maximum or the minimum at $p_{B_1}=0.5$. As a function of the joint effects of A and B, the variances $V_{A_1}$ and $V_{A_2}$ are unequal as long as ${({\mu }_{A_1{B}_1}-{\mu }_{A_1{B}_2})}^2\ne {({\mu }_{A_2{B}_1}-{\mu }_{A_2{B}_2})}^2$. This condition excludes models in which A is a nonfunctional locus. Thus, under LE, $V_{A_1}\ne V_{A_2}$ requires that the A is not merely a proxy for the B but has a functional involvement. This argument assumes that there is no confounding; this is the same assumption that we would make when comparing allelic effects. Under LE, the ratio $V_{A_1}/V_{A_2}$ approaches 1 as $p_{B_1}$ approaches either 0 or 1. Figure 1 illustrates the behavior of the ratio of allelic means and allelic variances at the observed locus, under LE, as a function of the unobserved allele frequency $p_{B_1}$. The variance contrast is strongest around the flip-flop point where the mean effect of A cannot be detected.

Figure 1.

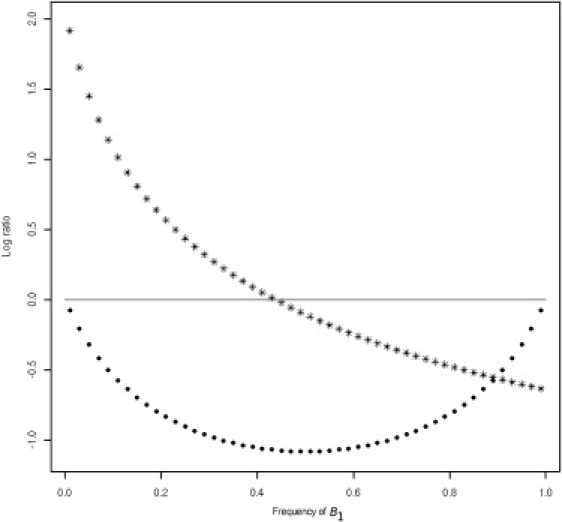
Values for $\ln ({\mu }_{A_1}/{\mu }_{A_2})$ and $\ln (V_{A_1}/V_{A_2})$ for a Zero-LD Model

Values for $\ln ({\mu }_{A_1}/{\mu }_{A_2})$ are indicated by the line of asterisks, and values for $\ln (V_{A_1}/V_{A_2})$ are indicated by the line of filled black dots. (M) = 10 × {0.5, 0.4, 0.95, 0.05} and ${\mathit{\sigma }}^2=10.$

The flip-flop condition under LE between the studied and the unobserved variants has important implications outside of observational studies. Suppose that A₁, A₂ are levels of a factor under investigation, and these levels might be introduced in an interventional study on a random background of an unobserved B. A possible scenario is a study of efficacy of a drug A₁ on a condition in the presence of genetic effects of the locus B. In an interventional study, a possible correlation between A and B is removed via randomization. Suppose an effect of A₁ is claimed by a randomized study. Our analysis shows that in the presence of population heterogeneity with respect to the $p_{B_1}$, there might be an effect reversal in a different study. Some studies could report that there is no effect of A at all, despite the importance of A at specific categories of B.

In the case of a quantitative trait, the allele-specific variances can be compared, in addition to the usual comparison of the means. In both types of comparisons, ${\mu }_{A_1}$ versus ${\mu }_{A_2}$ and $V_{A_1}$ versus $V_{A_2}$, the unknown factor, B, can either be genetic or environmental. According to our analysis, in the absence of correlation between the A and the B, the allelic variances are unequal only in the presence of a functional involvement of the A. In this regard, interpretation of a comparison of the allelic variances is similar to interpretation that follows from the usual comparison of the allelic means. Rejection of the hypothesis $H_0:V_{A_1}=V_{A_2}$ leads to a similar claim as does the rejection of the hypothesis $H_0:{\mu }_{A_1}={\mu }_{A_2}$; yet, the variance contrast might be substantial when the usual mean difference is undetectable. In either case, one can claim that the locus A is either directly associated with the trait or that it is a marker associated via correlation with an unobserved factor, B. When potential confounding due to population stratification is not an issue, the latter case leads to a standard claim that there is a nearby causal locus B correlated with the marker A via LD.

A practical question remains: How do we distinguish a genuine flip-flop from a statistical artifact? Our analysis shows that the underlying mechanism of a flip-flop is a change in the AB haplotype frequencies or, in the case of a zero-LD flip-flop, in the allele frequencies of B between populations. Examples can be constructed where both the allele frequency of the observed variant as well as the population prevalence of the trait (M · P) remain the same across populations, despite the flip-flop. Nevertheless, these are contrived situations that take place only at specific values of the four haplotype frequencies. Thus, a flip-flop is usually accompanied by a change in the population prevalence and in the case of a nonzero LD, by a change in the frequency of the observed variant as well. There would be a higher confidence that the flip-flop is genuine in those cases where studied populations are of distinct ancestry, with evidence of allele-frequency differences at many loci. In addition, we suggest that in the case of a quantitative trait, the allelic-variance contrast can be examined. This contrast can be informative even at the flip-flop point, where no allelic effect can be detected. If normality of the trait can be assumed, the variance contrast provides an independent evidence that the studied variant has a genetic involvement, either as a LD proxy for causal variation or as a part of a functional unit. A significant allelic-variance contrast in both samples that exhibit a flip-flop may serve as an additional evidence for a genuine genetic association. Statistical tests for comparison of allelic and haplotypic variances will be detailed in a subsequent paper.