Down to atomic-scale intracellular water dynamics

Abstract

Water constitutes the intracellular matrix in which biological molecules interact. Understanding its dynamic state is a main scientific challenge, which continues to provoke controversy after more than 50 years of study. We measured water dynamics in vivo in the cytoplasm of Escherichia coli by using neutron scattering and isotope labelling. Experimental timescales covered motions from pure water to interfacial water, on an atomic length scale. In contrast to the widespread opinion that water is ‘tamed' by macromolecular confinement, the measurements established that water diffusion within the bacteria is similar to that of pure water at physiological temperature.

INTRODUCTION

More than 20 years ago, J.S. Clegg described the long-lasting challenge posed by gaining an understanding of water diffusion in the cell (Clegg, 1984). Important progress has been made since then, but many questions remain unanswered. The apparent diffusion coefficient of water in biological tissues and in the brain has been measured by using nuclear magnetic resonance. The measurements showed that diffusion of cell water on a micrometric scale is reduced by a factor of 2–10 when compared with that of pure water in aqueous media; the reduction could be explained partly by tortuosity effects, macromolecular crowding and confinement effects (reviewed by Le Bihan, 2007). This observation led to the emergence of diffusion magnetic resonance imaging to study the brain (Le Bihan, 2003, 2007). By contrast, very little is known at present about the dynamics of cell water on a submicrometric scale. The question can be addressed by using quasi-elastic neutron scattering (QENS) spectroscopy, which monitors the diffusive motions of hydrogen atoms over a few Ångströms, on a pico- to nanosecond timescale. Here, we address the nature of intracellular water dynamics, by using isotope labelling and incoherent neutron scattering, and present a direct measurement of water diffusion in live Escherichia coli at physiological temperature, revealing the intrinsic physical properties of water in the cell interior on an atomic scale.

RESULTS AND DISCUSSION

Neutron scattering spectroscopy relies on incoherent scattering and can be performed on complex macromolecular systems such as living cells (Tehei et al, 2004). Hydrogen ¹H nuclei have an incoherent neutron scattering signal at least 40 times larger than that of deuterium (²H) or any other nucleus or isotope in biological material. We performed QENS experiments on deuterated E. coli containing natural abundance water. Deuterium labelling allowed a strong attenuation of the scattering signal from the deuterated cell components, revealing the water contribution. Intracellular water dominated the scattering signal at more than 93% in the spectra (see Methods). The measurements were carried out on two neutron spectrometers, IN6 and IRIS, with complementary timescales and atomic length scale resolution (see Methods). The combined timescale covered diffusive motions from pure water to interfacial water. The IN6 spectrometer is well suited for the measurement of rotational and translational contributions of pure water (Table 1); the IRIS spectrometer is optimal for the detection of reduced-mobility interfacial water, as well as the translational motions of pure water.

Table 1.

Translational and rotational parameters of water in the pure state, in the cell and in the buffer

Spectrometer (FWHM, μeV)	Origin of water (T, K)	DT( × 10−5 cm2 s−1)	τ0 (ps)	τcor,R (ps)	References
IRIS (17)	E. coli cells (281)	1.53±0.05	2.63±0.11		This work
IN6 (90)	E. coli cells (281)	1.78±0.08	2.95±0.11	1.96±0.07	This work
IRIS (17) and IN6 (90)*	E. coli buffer (281)	1.68±0.04	1.48±0.07	1.89±0.07	This work
IN6 (100)	Pure (285)	1.6	1.66		Teixeira et al (1985)
MIBEMOL (28; 96)	Pure (298)	2.3	1.1	3.3	Bellissent-Funel et al (1995)
IRIS (17)	E. coli cells (301)	2.39±0.05	2.16±0.05		This work
IN6 (90)	E. coli cells (301)	2.94±0.40	2.28±0.27	1.54±0.08	This work
IRIS (17) and IN6 (90)*	E. coli buffer (301)	2.72±0.17	1.04±0.15	1.47±0.08	This work
*E. coli buffer was measured both on IRIS and IN6. The translational parameters were identical on the two spectrometers. The rotational correlation times were extracted from the IN6 data. DT, translational diffusion coefficient; FWHM, full-width at half maximum; T, temperature; τcor, R, rotational correlation times; τo, residence time.

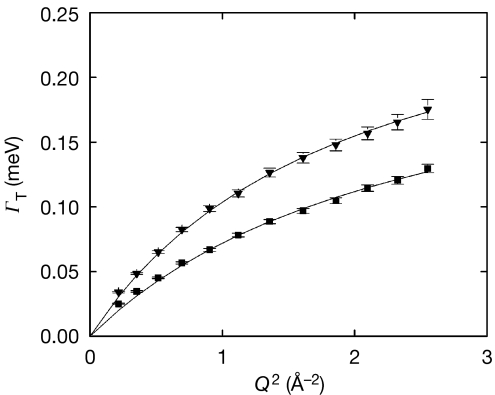
In the case of simple exponential diffusion processes, the QENS spectra can be fitted mathematically by Lorentzian functions, as described in Methods. The dependence of the Lorentzian half-width at half-maximum (HWHM) on the wave-vector transfer modulus Q provides information on the diffusion coefficient and other parameters of the process. Water dynamics parameters of E. coli extracted from IRIS data are shown in Fig 1 and Table 1. The QENS spectra were each fitted with one Lorentzian, which was attributed to translational motions of cell water (see Methods). The HWHM, Γ_T (Fig 1), was extracted and best fitted using a jump diffusion model (Bée, 1988), which describes the diffusion of water protons between sites with a mean residence time τ₀ at each site:

Figure 1.

IRIS data. Half-width at half-maximum of the translational Lorentzian, Γ_T, as a function of Q², at 281 K (filled squares) and 301 K (filled triangles). Γ_T was best fitted (solid lines) using a jump diffusion model (Bée, 1988; equation (1)). We found D_T=(1.53±0.05) × 10⁻⁵ cm²/s, τ₀=2.63±0.11 ps at 281 K and D_T=(2.39±0.05) × 10⁻⁵ cm²/s, τ₀=2.16±0.05 ps at 301 K. D_T, translational diffusion coefficient; τ₀, residence time.

where D_T represents the translational diffusion coefficient. We found translational diffusion coefficients that are very close to those of pure water at corresponding temperatures, with residence times τ₀ about twice as long (Teixeira et al, 1985; Bellissent-Funel et al, 1995; Table 1). Furthermore, the behaviour of Γ_T at low Q values indicated that the water in E. coli cells does not act as if it is being confined (Fig 1). The IRIS results, although obtained on a timescale optimal for the detection of reduced-mobility interfacial water, therefore showed that the translational contribution of E. coli water was neither confined nor significantly slowed down when compared with pure water.

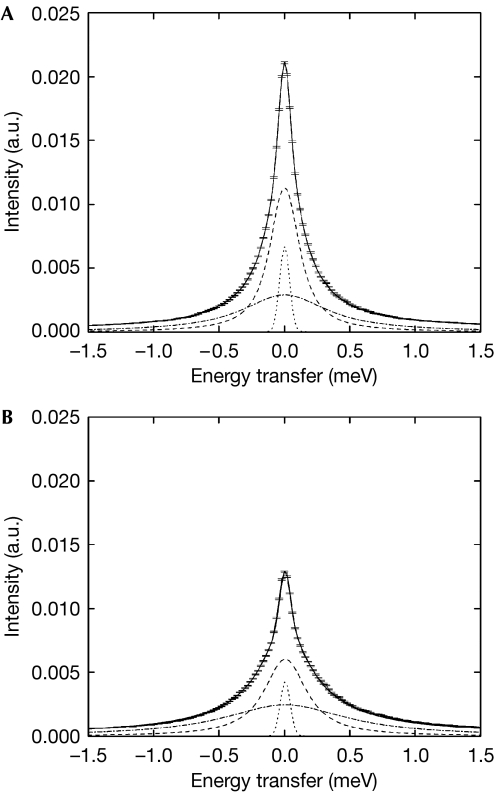
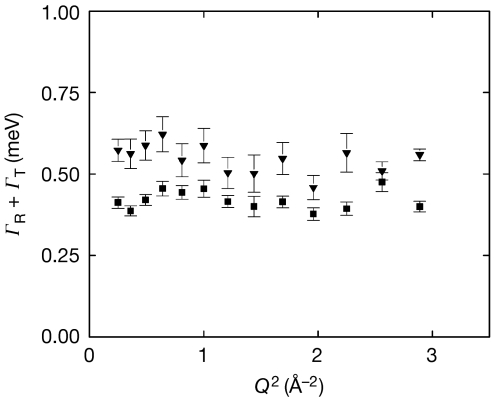
The IN6 QENS spectra were fitted with two Lorentzian functions (see Methods). The translational and rotational motions of cell water were extracted from the narrow and broad Lorentzians, respectively (Fig 2). Parameters for translational diffusion identical to those found on IRIS were extracted from IN6 data (Table 1). In addition, the rotational contribution to the motions emerged (Fig 3). The HWHM of the broad Lorentzian shows a Q-independent profile, as expected for rotational motions (Sears, 1966). Rotational correlation times are close to the values extracted for the buffer under the same conditions and of the same order as the values measured for pure water by QENS (Teixeira et al, 1985) and nuclear magnetic resonance (Sposito, 1981). Rotational relaxation times of protein hydration water are reduced by a factor of 5–10 when compared with pure water (Halle, 2004). Therefore, we concluded that diffusive motions of E. coli water measured over atomic distances are dominated by a cell water component that is similar to pure water at physiological temperature.

Figure 2.

IN6 QENS data and applied fits using equations (4) and (5) for E. coli cell water. Quasi-elastic spectra at Q=1.5 Å⁻¹, at (A) T=281 K and (B) T=301 K. The data are shown with the associated error bars. The solid and dotted lines represent the total fitted curve and the elastic peak, respectively. The narrow Lorentzian (dashed line) was attributed to translational motions and the broad component (dash–dot line) was attributed to rotational motions of cell water, broadened by the translational contribution (see Methods). a.u., arbitary units; Q, wave-vector transfer modulus; QENS, quasi-elastic neutron scattering; T, temperature.

Figure 3.

IN6 data. Half-width at half-maximum of the broad Lorentzian, Γ_R+Γ_T, as a function of Q², at 281 K (filled squares) and 301 K (filled triangles). The rotational correlation times, τ_cor,R=1/Γ_R, were extracted from the broad Lorentzian after correction for the broadening arising from the translational contribution, and were found to be 1.96±0.07 ps at 281 K and 1.54±0.08 ps at 301 K. Q, wave-vector transfer modulus; _R, rotational; _T, translational.

These results are in contrast to the idea that the cell somehow ‘tames' water and renders it different to pure water (Mentré, 2001). In combination with previous studies, this work confirms that the degree of hydration has a crucial role in the dynamic state of water in confined geometries. Studies of water dynamics in deuterated C-phycocyanin found an increase in the mobility of water when hydration coverage reached one layer of water molecules (Bellissent-Funel et al, 1996). Reduced mobility of cellular water on an atomic scale has so far been observed only at cryogenic temperatures (Ford et al, 2004), in low-hydrated Artemia shrimp cysts (Trantham et al, 1984) or in extreme halophiles (Tehei et al, 2007). E. coli contains approximately 2.6 g of cellular water per gram of macromolecule, and the first hydration layer accounts for about 0.5 g of water per gram of macromolecule (Record et al, 1998). On average, cell water would therefore correspond to about five layers of water molecules around macromolecular surfaces. We noted, however, that the residence time was found to be higher by a factor of 2 than that of pure water. This average might reflect the longer time spent by the water molecules in the hydration shells. Once released, however, exchange with external layers would take place with a diffusion rate similar to that of pure water.

The concept derived from indirect experimental observations that the cell interior is a gel- or colloidal-like structure, in which confined water is interfacial with properties that are significantly different to those of pure water, has influenced current opinion in certain sections of the biological community. Pollack et al (2006) state in the preface that “…practically all cell water is interfacial”; however, this claim remains controversial, as reviewed by Ball (2008). Our data are derived from the direct measurement of water properties in situ and in vivo on a wide range of timescales, and refute this concept. By contrast, they show that water forms a network of communication in the crowded cell interior that is as fluid as pure water. Tehei et al (2007) have established that E. coli does not contain a water component that is slower than interfacial hydration water by two orders of magnitude, as was observed in the special case of Dead Sea Archaea (Tehei et al, 2007). The origin of the slow water component in these extreme halophiles is still under investigation; it is unrelated to molecular crowding or the high-salt solution and was interpreted as owing to specific interactions involving macromolecules, water and salt ions, which are yet to be defined.

Our data showed that water dynamics are different on micrometric and atomic scales. Micrometric-scale measurements probe cell water diffusion across the entire length of the cell, along which water can encounter a large number of obstacles (for a review, see Le Bihan, 2007). Water in the extracellular matrix might also contribute appreciably to the micrometric-scale measurements, depending on the sample state and experimental design. Differences could emerge between different types of cell, such as prokaryotic and eukaryotic cells, arising for example, from the presence of the cytoskeleton and the nucleus. The magnitude of the viscosity also depends strongly on the length scale that is probed, as described previously (Lavalette et al, 1999). The results obtained for intracellular water dynamics on an atomic scale suggest that the atomic-scale viscosity in the cell cytoplasm is close to the viscosity of pure water (viscosity is often calculated by using diffusion parameters, according to the Stokes–Einstein relation).

Finally, it is important to emphasize the fundamental biological relevance of these results. It is likely that the remarkable properties of bulk water are essential for cell viability, in particular for functional macromolecular folding, stabilization and activity, transport, membrane formation and protein insertion into membranes. Whenever interfacial water has been obtained in the presence of biological macromolecules, it has always been after these were already synthesized, correctly folded, stabilized and the bulk water subsequently dried or frozen out. Our data show that the water between macromolecules in the in vivo intracellular environment has properties that are essentially the same as those of pure water and can therefore participate as such in all the interactions described above.

To conclude, borrowing from the poetic terms that have been used to describe cell water incorrectly, this study shows that water is not ‘tamed' by the cell environment (Mentré, 2001) nor is ‘life…water dancing to the tune of macromolecules' (Albert Szent-Gyorgyi, cited in Pollack et al, 2006) but vice versa.

METHODS

Samples. Deuterated E. coli (BLE21(DE3) strain) were grown at 37°C to stationary phase, with an optical density of 1.5, in deuterated Enfors minimum growth medium with deuterated glycerol (d8) as the carbon source. Cells were pelleted by centrifugation at 5,000 r.p.m. in a Beckman centrifuge (JLA10500 rotor) for 20 min at 4°C. The supernatant was discarded and the cells were washed twice with 200 ml of H₂O or D₂O buffer solution (150 mM NaCl, 5 mM KCl, 10 mM Tris–HCl (respectively Tris–DCl) pH 6.6). The cells were pelleted by centrifugation for 20 min, transferred to aluminium sample holders (4 cm × 3 cm × 0.02 cm) and sealed with an indium ‘o' ring for the neutron measurements. After the experiments, a small amount of the pellet was resuspended in the buffer and layered on Petri dishes after several dilution steps. The number of colonies was compared with that obtained for cells from the fresh culture and was found to be similar, which indicated that most of the cells remained intact and viable after total beamtime exposure. The rest of the cell pellet was dried in an oven at 80°C for 3 days; the quantity of extracellular water was evaluated taking into account that the proportion of intracellular water would be about 72% of the total cell weight of E. coli (Record et al, 1998). The extracellular water content was found to be less than 7% of the total water.

Neutron measurements. The full-width at half-maximum (FWHM) energy resolution of a neutron spectrometer defines the upper limit of the motions timescale. IN6 (FWHM=90 μeV), at the Institut Laue Langevin (ILL, Grenoble; see www.ill.eu for more information), is suitable for the measurement of motions with characteristic times of τ<15 ps, whereas IRIS (FWHM=17 μeV), at ISIS (Chilton, UK; http://www.isis.rl.ac.uk), can resolve slower motions with τ<75 ps. The scattering was measured over a wave-vector range of 0.5 Å⁻¹<Q<1.7 Å⁻¹, associated with atomic length scale, for each spectrometer. A vanadium sample (a purely incoherent elastic scatterer) was measured to define the instrument resolution and to correct for detector efficiency. IRIS spectra were corrected for detector efficiency, sample container and E. coli macromolecular contribution (see the next paragraph), normalized, grouped and transferred into energy transfer spectra using the IRIS data reduction program Ionian from the MODES package (MODES, 1998–2006). IN6 spectra were corrected in the same way, normalized and the scattering function, S(Q,ω), where ω is the energy transfer, was extracted by using the LAMP data reduction routines (LAMP, 2007). The sample transmissions were greater than 90% on both instruments and multiple scattering was neglected.

Data collection. Cell water dynamics was studied by measuring two samples: deuterated cell pellets resuspended in H₂O buffer; and deuterated cell pellets resuspended in D₂O buffer. A subtraction of the cell spectra measured in D₂O from that measured in H₂O, scaled by the sample mass, provided a good approximation to the scattering signal from the water present in the samples. We found extracellular water content to be less than 7% of the total water. The intracellular water, therefore, dominated the scattering signal by more than 93% in the spectra corrected for macromolecular contribution, as explained above. A sample of H₂O buffer alone was also measured on each spectrometer and used as a reference for interpreting the data.

Data analysis. In the case of translational diffusion and rotational motions of water, the calculated scattering function, S_calc(Q,ω), can be expressed phenomenologically as follows (Bée, 1988):

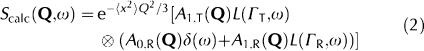Here, 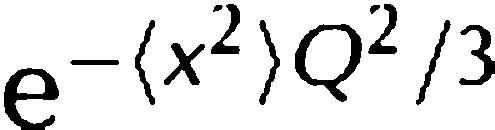is a Debye–Waller (DW) factor, which accounts for vibrational modes; the DW factor is simply a scaling factor in ω-space that does not modify the shape of the quasi-elastic scattering function; the symbol ⊗ denotes convolution. The quasi-elastic component arises from the convolution of the translational and rotational scattering functions, which are described by Lorentzian functions:

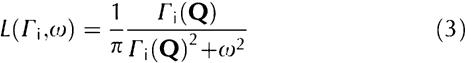where Γ_i is the HWHM of the Lorentzian peak. Equation (2) simplifies as follows:

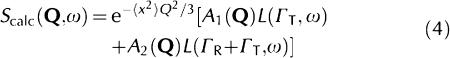The experimental scattering function, S_exp(Q,ω), is obtained by convoluting S_calc(Q,ω) with the energy resolution of the spectrometer, S_res(Q,ω), determined by the vanadium sample:

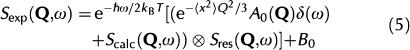where 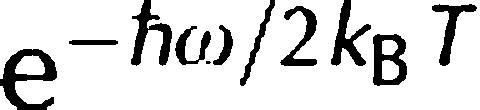is a detailed balance factor, A₀ is the elastic incoherent structure factor arising from the slow motions that are not resolved by the instrumental resolution and B₀ is an inelastic background owing to vibrational modes of lowest energy, which recalls the ‘lattice phonons' in crystals (Bée, 1988).

On IRIS, the rotational motions of cellular water contribute to the scattering signal only as a flat background. The IRIS spectra were fitted well according to equations (4) and (5) by a single Lorentzian, arising from the translational diffusion of cell water. The fits were performed for the energy transfer range −0.2 to +0.5 meV by using the IRIS Bayesian fitting program QL function, from the MODES package (MODES, 1998–2006).

The IN6 spectra were fitted according to equations (4) and (5) by two Lorentzians for the energy transfer range −1.5 to +1.5 meV, by using the QENS_FIT routine present in the LAMP package (LAMP, 2007). The narrow Lorentzian arises from the translational diffusion of cell water. The broad Lorentzian arises mainly from the rotational contribution, which was broadened, however, by the translational contribution as described in equation (4). The rotational correlation times τ_cor,R=1/Γ_R were extracted from the broad Lorentzian after correction for the broadening arising from the translational contribution.