A Unified Model Explaining the Offsets of Overlapping and Near-Overlapping Prokaryotic Genes

Abstract

Overlapping genes are a common phenomenon. Among sequenced prokaryotes, more than 29% of all annotated genes overlap at least 1 of their 2 flanking genes. We present a unified model for the creation and repair of overlaps among adjacent genes where the 3′ ends either overlap or nearly overlap. Our model, derived from a comprehensive analysis of complete prokaryotic genomes in GenBank, explains the nonuniform distribution of the lengths of such overlap regions far more simply than previously proposed models. Specifically, we explain the distribution of overlap lengths based on random extensions of genes to the next occurring downstream stop codon. Our model also provides an explanation for a newly observed (here) pattern in the distribution of the separation distances of closely spaced nonoverlapping genes. We provide evidence that the newly described biased distribution of separation distances is driven by the same phenomenon that creates the uneven distribution of overlap lengths. This suggests a dynamic picture of continual overlap creation and elimination.

Introduction

The genomes of bacteria and archaea contain a high density of genes, sometimes with more than 90% of the DNA sequence coding for proteins. There are thousands of adjacent pairs of genes whose coding regions overlap, a feature that is consistently found across a wide selection of microbes. Multiple reasons have been proposed for the existence of these gene overlaps. It has been suggested that they are maintained as a way to minimize genome size (Sakharkar et al. 2005), that they play a role in regulating the expression of the genes involved (Johnson and Chisholm 2004), and that they constrain the evolution of genes (Keese and Gibbs 1992; Krakauer and Plotkin 2002). Previously, overlapping genes have been studied extensively in viral genomes, where constraints on genome size make them particularly common (e.g., Pavesi 2000; McGirr and Buehuring 2006; Pavesi 2006; Bofkin and Goldman 2007). Here, we explore the dynamic processes associated with this basic feature of genome organization in prokaryotes.

Evidence from previous studies suggests that most overlapping gene pairs are created by the deletion of a stop codon (possibly associated with a larger rearrangement), by a point mutation at a stop codon, or by the introduction of a near-end frameshift (Fukuda et al. 1999, 2003). When a stop codon is removed through any of these mechanisms, the translation machinery will extend the protein sequence until it hits the next in-frame stop codon. If the new stop codon is within the coding region of a neighboring gene, an overlap results. The fraction of genes that overlap is strongly correlated with the number of genes in an organism (Fukuda et al. 2003; Johnson and Chisholm 2004), and Fukuda et al. (2003) take this as evidence that overlapping genes are maintained at a uniform rate across many organisms.

Previously, Rogozin et al. (2002) noted that pairs of overlapping, oppositely oriented genes in bacteria are more likely to be in a particular relative frame, with the wobble bases of each gene base paired with the second-codon bases of the gene on the opposite strand. Because this arrangement maximizes the freedom of each gene to evolve independently (Krakauer 2000), Rogozin et al. (2002) suggest that this freedom is the reason for the preference for oppositely oriented overlapping genes to appear at this relative offset. As do Rogozin et al. (2002), we focus on convergently transcribed (→ ← or tail-to-tail) genes because the annotated locations of stop codons are more accurate than those of start sites.

We develop and present a unified model to explain the relative positioning of both overlapping genes and nearly overlapping (closely spaced) genes. Our explanation for the distribution of overlap lengths is much simpler than that proposed by Rogozin et al. (2002). We find that the bias toward certain overlap lengths can primarily be explained by the expected location of the reverse-complement stop codons within the opposing open reading frame. We show that the observed pattern of overlap lengths likely arises through the loss of stop codons and subsequent extensions of each open reading frame to the next stop codon encountered, followed by selection against longer overlaps. In contrast to Rogozin et al. (2002), our explanation of this broad pattern does not need to appeal to the constraints on sequence coevolution that overlapping genes impose.

We also describe a previously unreported, but striking, bias in the distance between nonoverlapping but closely spaced, convergently transcribed genes and incorporate this effect into our model. The newly observed bias in such near overlaps is the mirror image of the bias observed in overlapping genes. We give computational evidence that this bias also results from selection against longer overlaps.

Thus, we present a single model that explains both the observed distribution of overlap lengths as well as the distribution of the lengths of short intergenic spaces and indicates that overlaps are being created and eliminated often during the evolution of a genome.

Materials and Methods

Sequences and Annotations

Sequence and annotation data for 384 completely sequenced bacterial and archaeal genomes were downloaded from GenBank on 12 October 2006. The annotation in the .ptt file accompanying the sequence was used. Although there undoubtedly are errors in these annotations, in aggregate they are the most comprehensive and reliable data available, and the patterns we discuss are observed across a wide variety of genomes. Only molecules that had at least 250 annotated genes were considered, in order to focus on the main chromosomes of the organisms. Genes that completely contained other genes were discarded as these genes appeared to be misannotations more frequently.

Nonredundant Set of Genomes

To avoid counting near-identical, homologous gene pairs from multiple strains and similar species, we selected a nonredundant subset of 220 dissimilar organisms from all available prokaryotic genomes as described below.

Homologs were identified by performing a Blast search of the amino acid sequence of each gene against databases of the protein sequences of each genome. The Blast search was performed with default parameters except that low-complexity regions were not masked. Two genomes A and B were taken to be “similar” if at least 30% of tail-to-tail pairs in A had good matches (E value ≤ 10⁻⁴⁰) in B for both genes and the matches were a tail-to-tail pair in B. Symmetry of similarity was enforced: if genome A was similar to B, it was assumed that B was similar to A.

We grouped the genomes, placing 2 organisms in the same group if they are similar under this definition. This resulted in 220 groups, 155 of which contain a single genome. The nonredundant set of genomes was created by choosing the genome with the largest number of tail-to-tail pairs in each cluster. An exception to this rule was made to include Escherichia coli O157:H7 rather than E. coli CFT073 as the representative of the Escherichia/Shigella/Salmonella cluster because the annotation of E. coli O157:H7 appears more certain, with fewer genes completely containing other genes and a number of overlaps more typical of genomes in that group. The list of nonredundant genomes is available as Supplementary Material online. All patterns discussed here are similar when the full set of 384 completely sequenced prokaryotic genomes is considered.

Among the 101,735 tail-to-tail pairs of genes within these 220 nonredundant genomes, 13,512 (13.3%) are overlaps and 46,565 (45.8%) are near overlaps (separation <90). Only 1,618 overlapping pairs and 5,940 near-overlapping pairs have 1 or more homologous tail-to-tail pairs also within the nonredundant set. Two tail-to-tail pairs of genes in organisms A and B were considered homologous if both genes of the pair in A matched the genes of the pair in B via Blast hit with E value ≤ 10⁻¹⁵. Hence, at most 12.6% of considered pairs are likely closely related, suggesting that the nonredundant set represents a fairly phylogenetically independent set of tail-to-tail pairs.

Results

Relative Positions of Overlapping and Closely Spaced Tail-to-Tail Genes

Across the 220 nonredundant genomes selected as described above, 15% of adjacent pairs of genes occur in tail-to-tail orientation (→ ←). Among those tail-to-tail pairs, 13% (13,512 instances) have overlapping coding regions at their 3′ ends. Although overlaps also occur between gene pairs in other orientations (21% of codirected (→ →) and 4% of divergent (← →) pairs overlap), the annotated locations of gene start sites are less reliable, and therefore reported overlaps for these other configurations are more likely to be incorrect. Consequently, in this paper we consider only pairs that are in the tail-to-tail arrangement.

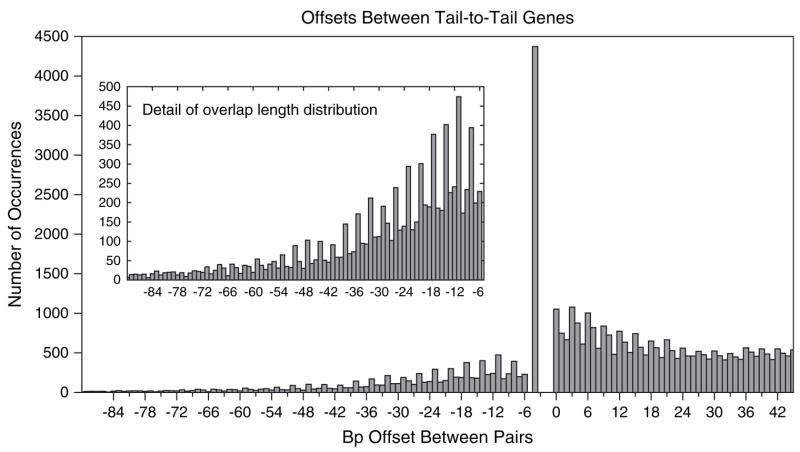
A histogram of relative offsets between adjacent tail-to-tail genes across the 220 nonredundant genomes is shown in figure 1. Negative values indicate overlap lengths, and positive values indicate bases of separation. The absence of overlaps of 1, 2, 3, or 5 bases is caused by the incompatibility of forward stop codons (TAA, TAG, or TGA) with stop codons on the opposite strand (TTA, CTA, or TCA) anywhere except the −4 overlap position. The huge spike at the −4 position (previously noted by Fukuda et al. [1999]) occurs because the stop codons TAA and TAG create a stop codon on the reverse strand at position −4 if the base before the stop codon is either a C or T.

Fig. 1.

Histogram of overlap lengths and separation distances between adjacent pairs of tail-to-tail (convergently transcribed) genes, computed from a nonredundant set of bacterial and archaeal genomes. Only molecules with at least 250 annotated genes were considered. Negative values indicate overlap lengths, whereas positive values indicate bases of separation. Inset shows the detail in the range −90, …, −6.

One of the most striking features of the histogram in figure 1 is the periodicity in both the overlap lengths and separation distances—both distributions have regular spikes every third position. We offer an explanation for these effects below.

Phase Bias in Overlapping Genes

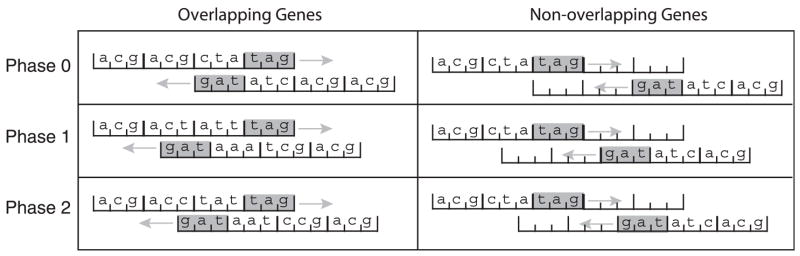
Following others (Rogozin et al. 2002), we use the term “phase” to describe the shift between reading frames of adjacent genes. Specifically, we define the phase of an overlap (x < 0) or separation (x ≥ 0) of size x to be the smallest r ≥ 0 such that r ≡ x (mod 3), so that relative offsets of …, −6, −3, 0, +3, +6, … are phase 0, offsets of …, −5, −2, +1, +4, +7, … are phase 1, and offsets of …, 34, −1, +2, +5, +8, … are phase 2. Figure 2 illustrates the 3 different phases.

Fig. 2.

Schematic of the 3 possible overlap phases, the 3 possible separating distance phases, and their identifiers. Stop codons are shaded and arrows indicate the direction of transcription of the gene. The phase identifier number is equal to the offset between the genes modulo 3.

Overall, 50.7% of overlaps are in phase 2 and, in fact, 32% of all overlaps are exactly length 4. Excluding overlaps of length 4, 46.1% of the remaining overlaps are in phase 1, corresponding to the peaks in the overlap portion of figure 1. (See also the first 2 columns of table 1.) In phase 1, the third, degenerate-codon positions of the forward gene coincide with the second-codon positions of the reverse gene and vice versa. This arrangement maximizes the ability of the overlap regions to evolve independently (Krakauer 2000), and it has been suggested that preserving this freedom is the reason behind the bias toward phase 1 (Rogozin et al. 2002).

Table 1.

Percentage of Gene Pairs Observed in Each Phase, Considering Pairs with Offsets s in Several Ranges

	s < −4 (%)	s <0a (%)	0≤ s<30b (%)	0≤ s<90b (%)	s <90c (%)	s ≥ 90d (%)	All (%)
Phase 0	26.8	18.1	40.8	38.2	33.7	34.0	33.8
Phase 1	46.1	31.2	33.1	33.0	32.6	33.4	32.9
Phase 2	27.1	50.7	26.1	28.8	33.7	32.6	33.3

^aAmong all overlaps (separation s < 0), phase 2 is the most common, followed by phase 1, and then phase 0.

^bThe finite ranges are chosen to be multiples of 3.

^cOnce near overlaps with separations up to 90 bp are added to the overlaps, any bias is nearly erased.

^dThe tail-to-tail pairs separated by ≥90 bp are evenly distributed among the 3 phases.

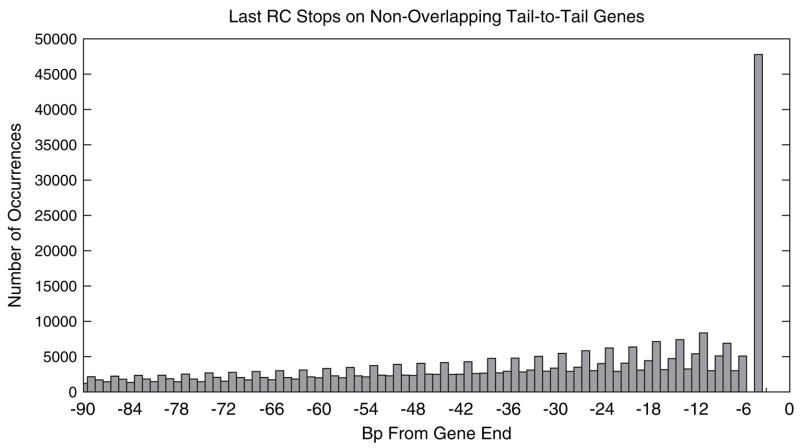
In contrast to this earlier suggestion, we find that this pattern of overlap lengths is consistent with that expected if a gene is extended upon loss of its stop codon to the first stop codon encountered within the region of the opposing gene. In other words, the simple loss of a stop codon will produce a similar 3-periodic pattern of overlapping gene lengths. Due to the nonuniform amino acid composition of proteins and codon bias among synonymous codons, the probability that 3 bases of a coding sequence form a reverse-complement stop codon (TTA, CTA, or TCA, which we abbreviate as “RC stops”) that would arrest an extended, opposing gene varies based on how the complementary strand of the coding sequences is divided into codons. Figure 3 shows a histogram of the positions of the 3′-most RC stops in the last 90 bp of genes that are followed by an oppositely directed gene (excluding genes that are involved in an overlap). It is immediately apparent that this distribution exhibits similar shape to the distribution in figure 1, with the same distinctive 3-periodic pattern. We compare these distributions more carefully below.

Fig. 3.

Histogram of the number of last reverse-complement stop codons (RC stops: TTA, CTA, and TCA) within genes. The x value is the number of bases from the end of the gene to the first base of the RC stop. The counts were computed from the nonredundant set of genomes using genes that are in a tail-to-tail pair but not involved in an overlap.

The most prominent difference between them is that the number of overlaps drops off more quickly with the length of overlap for the observed distribution, almost certainly due to selective pressure against very long overlaps. To adjust for this, we fit a smoothed decay function of the form

$$p_{\text{obs}}(x)=b{\text{e}}^{ax}$$

to the observed distribution of overlap lengths x. We obtain values a = 0.04127 and b = 0.05120 for the parameters by fitting a least-squares regression line to the logarithm of the values in the histogram of observed overlap lengths (fig. 1) over the range x = −96 … −7, after normalizing the values to sum to 1.0. Similarly, we fit a function p_est(x) of the same form to the histogram of last RC stops (fig. 3), with a similar normalization, obtaining a = 0.01397 and b = 0.02054. We use a function of this form because of its simplicity and its close fit to the data in the specified range. Further, an exponential drop-off is expected because the probability of an RC stop is approximately constant across all codons in a given reading frame.

The curves p_obs(x) and p_est(x) are phase-independent estimates of the drop-off of observed and estimated overlap lengths. Their ratio

$$f(x)=p_{\text{obs}}(x)/p_{\text{est}}(x)=2.493{\text{e}}^{0.0273x}$$ (1)

is the factor by which the distribution of observed overlap lengths decays faster than one would expect based solely on the last RC stop distribution. We can correct the expected distribution to account for the selection against longer overlaps by multiplying the values in last RC stop histogram by f(x). Figure 4 plots the observed overlap distribution (fig. 1) side by side with the corrected, expected distribution, after normalizing both to sum to 1. Note that because of this normalization, the b values and their ratio 2.493 become irrelevant.

Fig. 4.

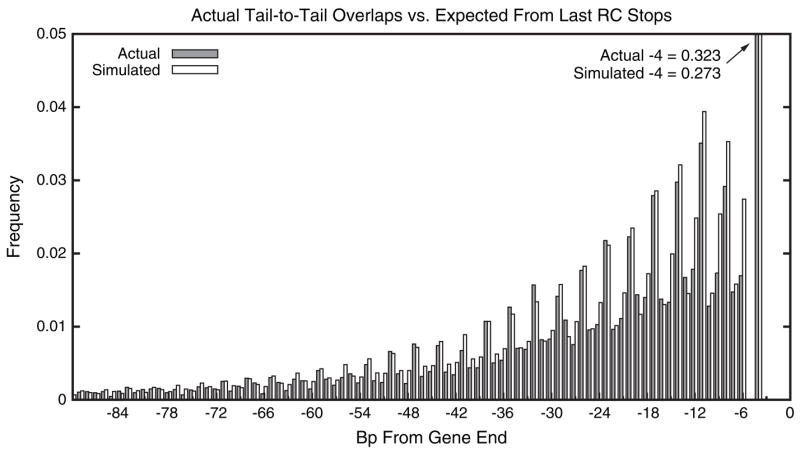
Filled bars show the observed distribution of overlap lengths taken from figure 1 and normalized to sum to 1.0. Empty bars show the expected fraction of overlaps of each length computed as the product of the distribution of the last RC stops (fig. 3) and the fitness function f(x) (eq. 1), again normalized to sum to 1.0. To show the detail in the longer overlaps, the large spike at −4 is truncated, and the values at −4 are given in the figure.

Before correcting with the fitness function f(x), the distribution of last RC stops has equal numbers in each phase by definition, even though they are not uniformly spread over the coding region. For example, the last RC stops in phase 1 and phase 2 are generally closer to the end of genes than those in phase 0. This is evident in the extreme differences in the expected distance from the end of a gene to the last RC stop codon: in phase 0, the expected extension is 287.2, whereas in phase 1 and phase 2 the expected extensions are 83.4 and 87.8, respectively. This nonuniformity means that once simple selection for length has been included, modeled here by multiplying by f(x), there are unequal numbers of predicted overlap instances in each phase. The corrected, expected distribution is remarkably similar to what is observed among actual overlaps (table 2). The ordering of frequencies of phases predicted by the expected model (phase 2 > phase 1 > phase 0) matches that observed among the real overlaps.

Table 2.

Fraction of Overlaps in Each Phase for the Observed and Expected Distributions Shown in Figure 4

	Observed (%)	Expected (%)
Phase 0	18.1	22.8
Phase 1	31.2	32.6
Phase 2	50.7	44.6

The corrected, expected distribution also closely models the periodic spikes in phase 1. Excluding overlaps of length 4, which are a special case due to the presence of the overlapping stop codons, 46.1% of observed overlaps are in phase 1, whereas the expected distribution predicts 44.8% of overlaps would be in this phase. Although it is clear in figure 1 that the height of the simulated bars is not as good a fit for the shortest overlaps (because the simple exponential fitness function is not accurate in this region), the observed pattern of phase bias of overlaps in this region is matched by the simulated values. Thus, the propensity for overlaps of length > 4 to be in phase 1 is almost entirely explained by the distribution of RC stops within coding sequences.

Phase Bias in Closely Spaced Genes

A phase bias is also evident among tail-to-tail genes that are closely spaced but do not overlap (positive x values in fig. 1). The distribution of phases among gene pairs with separations in several ranges is shown in table 1. In fact, 40.8% of very closely spaced pairs (separated by < 30 bp) are in phase 0, whereas only 26.1% are in phase 2. The ordering phase 0 > phase 1 > phase 2 continues to hold even when considering all nonoverlapping gene pairs separated by <90 bp (table 1).

This strict ordering of frequency holds for a large fraction of the genomes. Considering pairs of genes separated by <30 bp, the strict ordering phase 0 > phase 1 > phase 2 exists in 45% of the 165 organisms that have at least 30 occurrences of such gene pairs (P < 6.3 × 10⁻¹⁸; see Supplementary Material online for P value methodology). Note that fewer than 16.7% of genomes are expected to exhibit this ordering by random chance (because there are 6 possible different orderings). The fraction with this strict ordering remains high at 40% even when we include pairs separated by <90 bp from genomes with at least 30 such pairs (P < 5.0 × 10⁻¹⁶). This most frequently observed ordering is the mirror image of the pattern seen in overlapping pairs, which was phase 2 > phase 1 > phase 0.

The preference for phase 0 holds across even more genomes. Considering gene pairs separated by fewer than 90 bases, phase 0 is the most frequently observed phase in 62% of the 212 organisms that have at least 30 such pairs (P < 2.4 × 10⁻¹⁷). The bias toward phase 0 increases as separation distances get shorter: among pairs separated by fewer than 30 bp, phase 0 is the most common in 65% of 165 organisms that have at least 30 such closely separated pairs (P < 3.8 × 10⁻¹⁷). In addition, phase 2 is underrepresented in many genomes. Among pairs separated by fewer than 90 bases, phase 2 is the least common in 56.1% of these genomes (P < 8.4 × 10⁻¹²). When considering only smaller separations (<30 bp), phase 2 is the least common in 57.0% of these genomes (P < 4.2 × 10⁻¹⁰). This indicates that the pattern of phase bias in these near overlaps is caused both by overrepresentation of phase 0 and by underrepresentation of phase 2. Thus, the periodicity and phase bias exhibited in figure 1 is not driven by a small set of organisms.

At first consideration, it is not clear why there should be any bias in the phase of nonoverlapping tail-to-tail genes. Overall, the fraction of tail-to-tail pairs (overlapping or not) in each phase is nearly uniform (33.8%, 32.9%, and 33.3% in phases 0, 1, and 2, respectively; see table 1). Nearly all of the bias among nonoverlapping tail-to-tail pairs comes from closely spaced genes: nonoverlapping genes separated by <90 bp are more likely to be in phase 0 (38.2%) than in phase 1 or 2 (33.0% and 28.8%, respectively). Above a separation of 90 bp, each phase is represented almost equally. This is consistent with the hypothesis that there is no global or long-range mechanism favoring any phase between tail-to-tail pairs.

The bias toward near overlaps in phase 0 is exhibited across many types of organisms. We considered 7 subsets of the nonredundant set of organisms defined based on taxonomy as described in figure 5. The Proteobacteria, Actinobacteria, and Firmicutes groups were chosen because they were the most general subgroups of bacteria that contained at least 10 organisms from our nonredundant set. All 7 groups had at least 33% of their near overlaps (separation at least 0 and at most 44 bases) in phase 0. (See Supplementary Material online for more detail about the phases of overlaps and near overlaps among these groups).

Fig. 5.

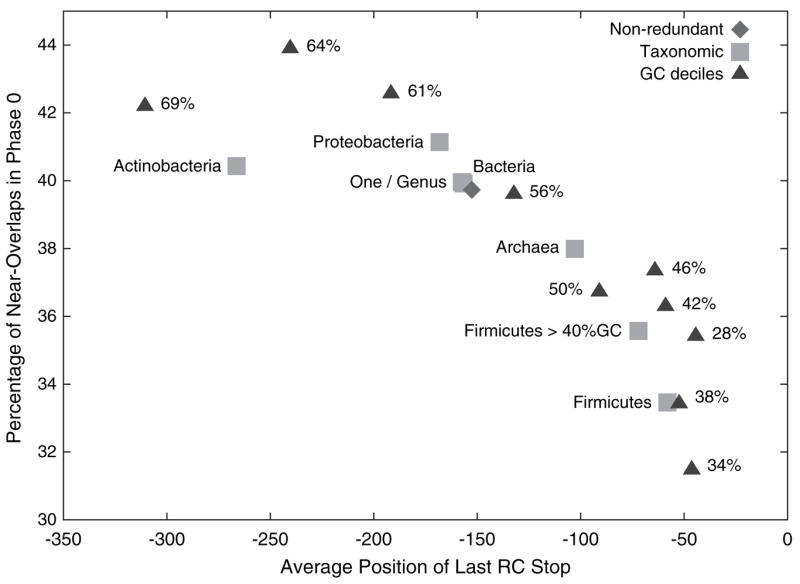
The average position of the last RC stop of the organisms within subgroups of organisms plotted against the phase 0 bias. The more negative the average position of the last RC stop, the longer are the expected overlaps. Each point represents a subset of the nonredundant organisms. The diamond represents the entire nonredundant set of 220 organisms. Triangles define groups based on the deciles of percent GC content, and numbers marking the triangles are the average GC content of the 22 organisms in each group. Taxonomic groups (squares) are subsets of prokaryotes derived from the National Center for Biotechnology Information taxonomy: “Firmicutes >40% GC” are Firmicutes with at least 40% GC content; “One/Genus” is a subset of the nonredundant set obtained by randomly choosing one species from each genus (as inferred from the species name).

Because all 3 stop codons are primarily composed of adenines and thymines, an organism with higher GC content will contain fewer stop codons by chance, and hence, longer overlaps will be expected under our model. To explore the connection between expected overlap length and the near-overlap phase bias, we divide the 220 organisms into 10 equally sized groups based on GC content. Groups for which the last RC stop is, on average, far from the end of a gene exhibit a larger phase 0 bias (fig. 5). The Spearman’s rho rank correlation between the average position of the last RC stop and the percentage of near overlaps in phase 0 among the 10 groups defined by GC content is −0.9151, with 2-sided P value = 4.667 × 10⁻⁴. Among the 7 taxonomically defined groups, rho = 0.9643 with P value = 2.778 × 10⁻³.

Evolutionary Mechanisms Leading to Near-Overlap Bias

Given the correlation observed in figure 5, it is reasonable to conjecture that the bias in near overlaps is also derived from the variation of the expected overlap length by phase. Because of the nonuniform distribution of RC stops discussed above, the propensity for an overlap to be selected against because of its length varies based on the phase of that overlap, with more phase 0 overlaps selected against than phase 1 or 2 and, in turn, more phase 1 overlaps removed than phase 2 (as evidenced by the deviation from 33%, 33%, and 33% in table 2). We next describe 2 evolutionary mechanisms by which this biased selection of overlaps can result in nonuniform distribution of the phases of separation distances of closely spaced genes, depending on whether the near-overlap bias is the result of overlap creation or overlap elimination.

If an overlap is created by a point mutation at the stop codon then the mutant overlapping descendant will compete with the nonoverlapping progenitor within a population of organisms. The shorter the overlap the fitter the overlap mutant will be and the more likely it is that it will outcompete the nonoverlapping genotype. Thus, for phases with long expected extensions, the overlapping mutant is less likely to become fixed in the population, and thus, a larger number of closely spaced genes in these phases will remain near overlaps, rather than becoming overlaps. Conversely, more overlaps between gene pairs in phases that yield short overlaps will become fixed in the population. This will create a pattern of phase frequencies among the closely spaced genes that is the mirror image of that observed among the overlaps, as observed.

In order for the overlap phase bias to match the near-overlap phase bias, the phase of the gene before the stop codon is lost must equal the phase of the created overlap. Such is the case for point mutations that remove a stop codon, whereas other mutations involving indels change the phase and would not yield matching biases. Nonetheless, only a fraction of stop-loss events need to be phase preserving in order to produce the observed phenomenon as long as the other events are collectively phase neutral and do not contribute any compensatory bias.

The biased elimination of overlaps is an alternative process that could lead to an uneven distribution of separation phases of the type observed. If an overlap has become fixed in the population, it can subsequently be repaired by the introduction of an in-frame stop codon. The repair of long overlaps will increase fitness more than the repair of short overlaps, and thus, elimination of overlaps in phases that yield long overlaps will be selected for more often. Because it requires an in-frame introduction of a stop codon in order to yield the observed phase bias, this repair mechanism seems a less probable cause of the observed bias. However, if overlaps are constantly being created, some mechanism to eliminate them must also exist in order to cause the linear correlation between number of genes and number of overlaps observed by Fukuda et al. (2003) and Johnson and Chisholm (2004).

An example of an overlapping gene pair that might have been repaired in a species by the reintroduction of a stop codon is given in figure 6. The illustration shows an alignment between the tail-to-tail overlapping region of genes ECs4695 and ECs4696 in E. coli O157:H7 (top strand) and the corresponding region between genes rbsR and yieO in Shigella dysenteriae. The Shigella genes do not overlap because the highlighted single-base C/T mutation creates a stop codon that terminates gene rbsR before it reaches gene yieO. The matching region in 14 other strains of E. coli, Salmonella, and Shigella in GenBank exhibit the overlapping gene configuration with high fidelity, indicating that the common ancestor contained the overlap, whereas S. dysenteriæ acquired this mutation to remove it.

Fig. 6.

Alignment between the overlapping ends of genes ECs4695 and ECs4696 in Escherichia coli O157:H7 (top strand) and genes rbsR (SDY_3994) and yieO (SDY_3993) in Shigella dysenteriæ. Shading indicates coding regions, arrows indicate direction of gene transcription, and stop codons are underlined. The single-base mutation between the 2 organisms that is the site of a potential overlap-repair event is boxed.

Therefore, although selective fixation of overlaps within particular phases seems the most likely explanation for the majority of the near-overlap phase bias, in-frame repair of long overlaps would also drive a similar bias.

Discussion

We have shown that, to a large extent, the distribution of overlap lengths can be explained by the location of the RC stops within coding regions coupled with a fitness function that models selection against longer overlaps. This explanation is much simpler than the previously proposed mechanism, which postulated selection to arrange genes to maximize their ability to evolve independently.

Further, we have observed a phase bias among closely spaced tail-to-tail genes that is the mirror image to the overlap bias. Because closely spaced pairs are most enriched in the phase that is most selected against due to overlap length and because this bias is most apparent in genomes with longer expected overlaps, we suggest that the uneven distribution of small separation distances also arises from the nonuniform distribution of reverse-complement stop codons.

Given the evolutionary processes underlying our explanations for the observed distribution of overlap lengths and separation distances, it appears that overlapping gene pairs are often transient arrangements that are outcompeted by nonoverlapping variants. The overlapping gene pairs we observe are presumably maintained when the random extension of a gene does little harm to the organism. This is consistent with studies (Fukuda et al. 2003; Johnson and Chisholm 2004) that have observed a linear correlation between number of genes and number of overlaps because such a linear relationship would be expected if each gene had a constant probability of being extended into an overlap.

Although the last RC stop distribution appears to explain much of the length distribution of gene overlaps, it is possible, even likely, that some selection of the type proposed by Rogozin et al. (2002) contributes to this bias as well. The 2 hypotheses are not mutually exclusive. However, as the model presented here relies only on selection against longer overlaps, it can be regarded as the more parsimonious explanation and thus should be favored to the extent it explains the observed offset distributions. Of course, this model does not fit the data perfectly, and thus, there is room for additional processes contributing to the skewed distribution of overlap and near-overlap lengths. For example, considering only conserved overlaps in a smaller data set, Rogozin et al. (2002) found a higher bias toward phase 1 than we observe in our larger set of both conserved and nonconserved overlaps, suggesting that additional factors may play a role among functionally important overlaps.

There are other fine points of the pattern for which we do not yet have clear explanations. For example, our simple model predicts fewer phase 2 overlaps and more phase 0 overlaps than observed among overlaps of more than 4 bases. This is likely due to additional selection against phase 0 overlaps or selection for phase 2 overlaps based on factors other than overlap length, such as amino acid composition. Also intriguing is the local maximum at offset −11 in both the observed overlaps and the distribution of last RC stops. That both distributions share this feature is further evidence that the pattern of overlap lengths is derived from the pattern of last RC stops, but as yet, we do not know what causes the dearth of RC stops at −8, −7, and −6.

An overlap of 4 bases is a special case as only 1 coding nucleotide is constrained in each such overlapping gene and that nucleotide is the wobble base in the last codon of both genes. Under the distribution expected from the last RC stops combined with the fitness function f(x) (eq. 1), we would expect 27.3% of the overlaps to have length 4, whereas in fact 32.3% do. Because it is difficult to quantify the fitness of such configurations, some of this excess may be due to the function f(x) not correctly modeling the fitness of overlaps of length 4. It is also possible that some length 4 overlaps are themselves repaired longer overlaps as typically only a single mutation is necessary to introduce a stop at the −4 position.

Although our explanation of the preference for overlaps in phase 1 is not based on maintaining the ability of both proteins to evolve separately, it may be that the genetic code and codon usage bias in part developed in such a way as to make it more likely that overlapping genes can evolve independently. The choice of a genetic code that is forgiving to the creation of overlaps may have had a particular advantage during the early development of life.

Overlapping genes are a fundamental and prevalent feature of prokaryotic genomes, and understanding them can illuminate the evolution and organization of those genomes. We have given a novel explanation for the distribution of overlap lengths, described a bias in the distribution of closely spaced, tail-to-tail genes, and offered a possible explanation for that bias. As more genomes become available, especially those of closely related organisms, we anticipate finding additional instances of creation and repair of overlapping genes.

Supplementary Material

Species list

Supplementary Material

Supplementary material contains a description of how the P values in the section “Phase bias in closely spaced genes” were derived, tables for the phase distributions of overlaps and near overlaps for various subsets of organisms, and a brief discussion of the distribution of the lengths of overlaps between codirected pairs of genes. In addition, a text file with the list of the accessions and versions of the sequences and annotations used from GenBank is available electronically. Supplementary materials are available at Molecular Biology and Evolution online (http://www.mbe.oxfordjournals.org/).