Co-evolution of strategy and structure in complex networks with dynamical linking

Abstract

In most analytic studies of social networks carried out to date, networks have links which remain unchanged at all times. Hence, individuals have no control over the number, frequency or duration of their interactions with others. Here we introduce a model in which individuals differ in the rate at which they seek new interactions with others, making rational decisions modeled as general symmetric two-player games. Once a link between two individuals has formed, the productivity of this link is evaluated. Links can be broken off at different rates. We provide analytic results for the limiting cases where linking dynamics is much faster than evolutionary dynamics and vice-versa, and show how the individual capacity of forming new links or severing inconvenient ones maps into the problem of strategy evolution in a well-mixed population under a different game. For intermediate ranges, we investigate numerically the detailed interplay determined by these two time-scales and show that the scope of validity of the analytical results extends to a much wider ratio of time scales than expected.

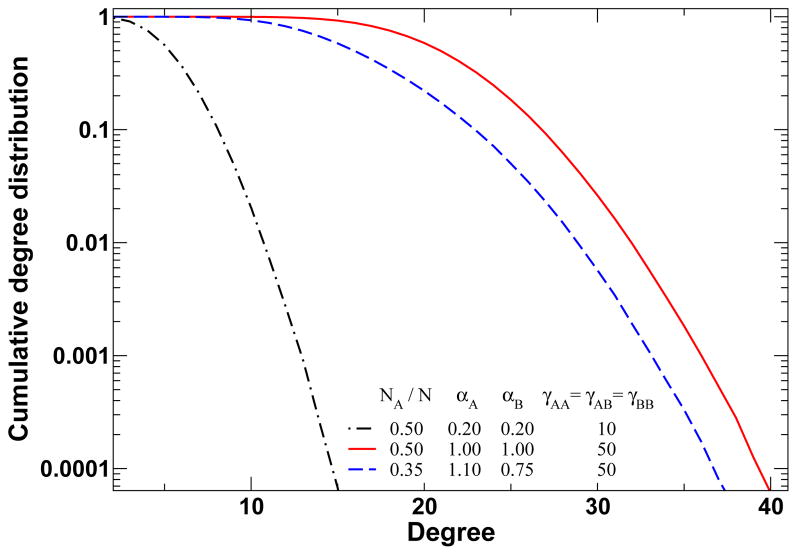
Networks pervade all sciences [1–5]. During recent years, researchers have developed methods to characterize such networks, providing novel insights into the properties accruing to those networked systems and organizations. The classical social network metaphor [6] places individuals at the nodes of a network, the network links representing interactions or connections between those individuals. Citation networks, collaboration networks, co-authorship and movie co-acting networks, as well as the networks of sexual relations, all fall into this metaphoric representation [1–5]. Most analytical studies on this type of networks carried out to date have aimed to explain the emergence of the observed topological properties, as deduced from the empirical data. Networks, however, are dynamical entities, and in this sense the empirical information often only provides a fixed-time snapshot of networks which are continuously evolving. Furthermore, dynamical features of networks have been studied in connection with their growth, modeled in terms of the preferential attachment (or cumulative advantage) mechanism [1, 6, 7], via random addition and removal of nodes [2] or by imposing different forms of connectivity saturation [4, 8–10]. Moreover, individual decisions to establish or remove/rewire a given link have been studied by numerical simulations [4, 8–15]. Here we develop a new model which incorporates decisions of individuals when establishing new links or giving up existing links. Individuals are capable of making rational choices, modeled in terms of a game, associated with well defined strategies. We use evolutionary game theory [16–21] and study the dynamical co-evolution of individual strategies and network structure. We restrict our analysis to symmetric two-player games, although the model can be easily extended to games with an arbitrary number of strategies. We obtain analytical results which are formally valid in the extreme limits when one of the dynamics (strategy or structure) dominates the other, although our numerical simulations show that the range of validity of the analytical results is much wider. The present model leads to single-scale networks as defined in [4], with associated cumulative degree distributions exhibiting fast decaying tails [4], as shown in Fig. 1. Such tails which decay exponentially or faster than exponential, leading to what are known as “broad-scale” and “single-scale” networks, respectively [4], are features which, together with a large variability in the average connectivity [1, 2, 5], characterize most real-world social networks [3, 4]. We start by characterizing the networks emerging from our model. Subsequently, we introduce individuals who adopt definite strategies and make rational decisions by engaging in a game with others, studying how strategy and structure co-evolve. Finally, we strenghten the coupling between strategy and structure by letting individuals evaluate the productivity of links in which they participate.

FIG. 1.

(color online) Cumulative degree distributions for networks generated with the present model, for populations of size N = 10³ and two different types of individuals. The fast decaying tails correlate well with the observed tails of real social networks [1–5]. On the other hand, the dependence of the final network on the frequency of each type of individuals leads to a natural coupling between network dynamics and frequency-dependent strategy evolution.

Let us first consider the structural evolution in a population of two types of individuals (players), A and B, occupying the nodes of a network. The total population size is constant N = N_A + N_B. Links define interactions between individuals, being formed at certain rates and having specific lifetimes. The maximum possible number of AA, AB and BB links is respectively given by N_ij = N_i(N_j − δ_ij)/(1 + δ_ij) (i, j = {A, B}). Suppose A and B players have a propensity to form new links denoted by α_A and α_B, such that ij links are formed at rates α_iα_j. The death rates are given by γ_ij (with associated lifetimes ${\tau }_{ij}={\gamma }_{ij}^{-1}$). With these definitions the mean field equations governing what we call the Active Linking (AL) dynamics of this network are

$${\stackrel{·}{X}}_{ij}={\alpha }_i{\alpha }_j(N_{ij}-X_{ij})-{\gamma }_{ij}{X}_{ij}.$$ (1)

These differential equations lead to an equilibrium distribution of links given by $X_{ij}^{\ast }=N_{ij}{\varphi }_{ij}$, where ϕ_ij = α_iα_j(α_iα_j + γ_ij)⁻¹ denotes the fraction of active links. In Fig. 1 we show how this model leads to stationary regimes of complex networks which can exhibit different degrees of heterogeneity. Note, in particular, the dependence of the stationary networks on the frequency of individuals of a given type will automatically couple network dynamics with the frequency-dependent evolutionary dynamics we introduce in the following.

Let us now introduce a game between A and B leading to frequency-dependent evolution of strategies. The game is given by the payoff-matrix M_ij

$$\begin{array}{l}\begin{array}{c}AB\end{array}\\ \begin{array}{c}A\\ B\end{array}\left(\begin{array}{cc}a& b\\ c& d\end{array}\right).\end{array}$$

In the stationary regime of Active Linking (AL) dynamics, the average fitness of A and B individuals is given by f_i = Σ_j M_ij ϕ_ij (N_j−δ_ij). It is noteworthy that these expressions are equivalent to the average payoffs of N_A and N_B players who play a game specified by the (rescaled) payoff-matrix $M_{ij}^{\prime }=M_{ij}{\varphi }_{ij}$ on a complete graph.

So far we have dealt with AL-dynamics. Let us now study how the frequencies of strategies A and B change under evolutionary game dynamics. We assume that the characteristic time-scale associated with AL-dynamics is T_a, whereas that associated with strategy updating is T_s.

Reproduction can be genetic or cultural. We adopt the pair-wise comparison rule, which provides a convenient framework of game dynamics at all intensities of selection [22]. Two individuals from the population, A and B are randomly chosen for update. The strategy of A will replace that of B with a probability given by the Fermi function $p={[1+e^{-\beta (f_A-f_B)}]}^{-1}$. The reverse will happen with probability 1−p. The quantity β controls the intensity of selection. For β → ∞ the individual with the lower payoff deterministically adopts the strategy of the other individual. For β ≪ 1, we recover the weak selection limit of the frequency dependent Moran process [23].

When T_a ≪ T_s, AL proceeds much faster than strategy update on each node. Hence, the stationary regime of AL-dynamics determines the average payoff and fitness of individuals. This means that strategy evolution proceeds as in a well-mixed population of A and B players (complete graph) engaged in a game specified by the payoff-matrix $M_{ij}^{\prime }=M_{ij}{\varphi }_{ij}$. Since AL-dynamics is fast, the dynamics of the system does not depend on the starting condition, and we can compute analytically the fixation probabilities of strategies A and B. The probability ρ_A(k) that k A-players introduced into a population of B-players will take over the entire population is given by [22]

$${\rho }_A\left(k\right)=\frac{\text{erf}\left[{\xi }_k\right]-\text{erf}\left[{\xi }_0\right]}{\text{erf}\left[{\xi }_N\right]-\text{erf}\left[{\xi }_0\right]},$$ (2)

where erf(x) is the error function and ${\xi }_k=\sqrt{\frac{\beta }{u}}\left(ku+v\right)$. We have 2u = a′ − b′ − c′ + d′ and 2v = −a′ + b′N − c′N + c′. For u = 0, Eq. 2 simplifies to ρ_A(k) = (e^−2βvk − 1)/(e^−2βvN − 1).

On the other hand, in the opposite limit where T_a ≫ T_s, evolution will proceed according to the usual game dynamics [24–37] on a static network reflecting the initial configuration. If we start from a complete graph then Eq. (2) remains valid, except that u and v must be calculated employing the original payoff-matrix M_ij. If we start from another graph topology, analytical and numerical results for static networks apply instead [38–40]. Whenever T_a ∼ T_s, one expects a detailed interplay between these two processes to drive co-evolution. This regime can be explored by computer simulations of AL-dynamics. As an example, we investigate the interaction between cooperators and defectors in the Prisoner's Dilemma (PD). A cooperator, C, pays a cost c for every link, and the partner of this link receives a benefit b > c. Defectors, D, pay no cost and distribute no benefits. The payoff-matrix becomes

$$\begin{array}{l}\begin{array}{cc}C& D\end{array}\\ \begin{array}{c}C\\ D\end{array}\left(\begin{array}{cc}b-c& -c\\ b& 0\end{array}\right).\end{array}$$

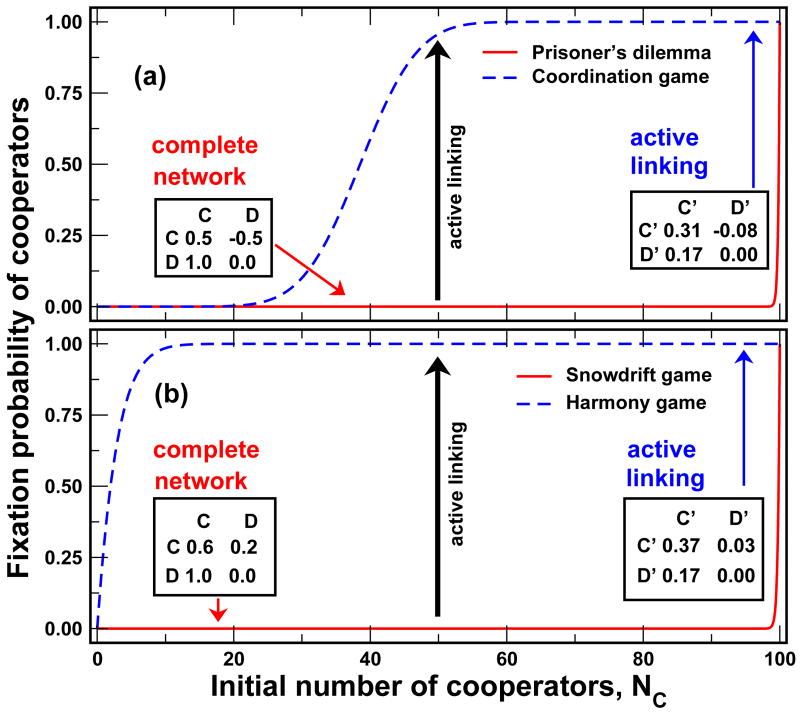
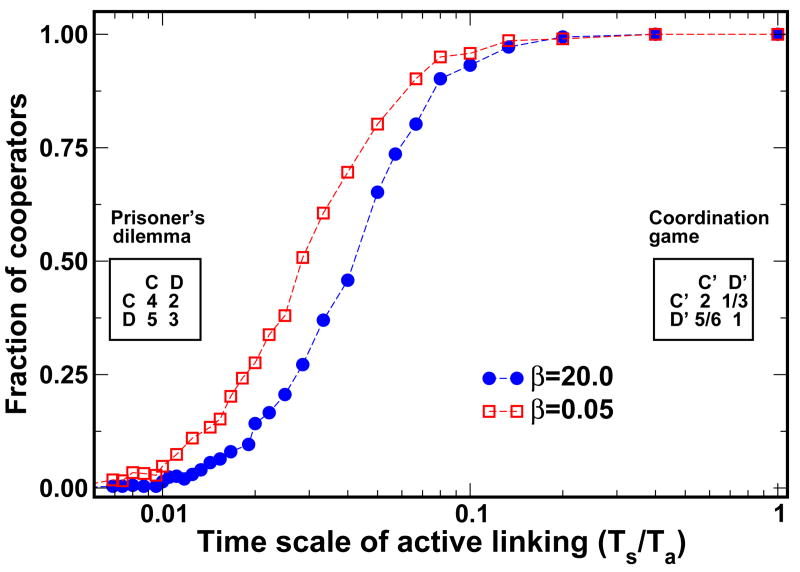
On complete graphs, cooperators are never advantageous compared to defectors. This means if T_a ≫ T_s cooperators are never favored by selection. On the other hand, if T_a ≪ T_s, the effective payoff-matrix is different, and may not correspond anymore to a PD, that is, when AL dominates, the problem becomes equivalent to the evolutionary dynamics of a different game in a complete graph. The advantage of cooperators from AL can be captured by the parameter r = (ϕ_CC − ϕ_CD)/ϕ_CC which provides a measure of the advantage of assortative interactions (CC-links) with respect to disassortative ones (CD-links). In terms of r, the PD is transformed into a coordination game whenever r > c/b, which is formally equivalent to Hamilton's rule of kin selection [41]. In strategy phase space, an unstable interior fixed point develops at a frequency of cooperators given by N_C/N ≈ (1 − r)c/[r(b − c)]. In other words, for T_a ≪ T_s fixation of cooperators is almost certain if the initial fraction of cooperators in the population exceeds this ratio. In Fig. 2 we provide numerical examples of this scenario, whereas in Fig. 3 we investigate the behavior of our co-evolutionary model as T_s/T_a increases. The results of Fig. 3 show how the ratio of time scales affects co-evolution of strategy and structure. In all cases we start from well-mixed populations (complete graphs). Clearly, not only the asymptotic behavior coincides with the analytic prediction but, perhaps more importantly, Fig. 3 shows that only for 0.01 ≤ T_s/T_a ≤ 0.1 does the interplay between the two time scales deviate significantly from the analytic predictions.

FIG. 2.

(color online) Fast active linking (AL) changes the dynamics of the social network and the payoff matrix. a) AL transforms a Prisoner's Dilemma with c = 0.5 and b = 1.0 into a coordination game. While fixation of cooperators is negligible in the Prisoner's Dilemma (solid line), cooperators can take over with AL (dashed line) b) A snowdrift game with c = 0.8 and b = 1.0 in which fixation of defectors is certain is transformed into a harmony game in which cooperators prevail. The vertical arrows show how AL affects the fixation probability when initially 50% cooperators are present: while they have no chances on a complete graph despite their high abundance, AL makes fixation of cooperation almost certain in both systems (β = 0.1, N = 100, α_C = α_D = 0.4, γ_CC = 0.1, γ_CD = 0.8, γ_DD = 0.32).

FIG. 3.

(color online). Co-evolutionary dynamics of strategy and structure. The curves drawn correspond to the results of computer simulations carried out for networks of size N = 100. Parameters and payoff matrices are the same as in Fig. 2. The rescaled payoff-matrix leads to a fixed point at a fraction of cooperators N_C/N ≈ 35%. For each value of the ratio T_s/T_a, we ran 100 simulations, starting from 50% cooperators and a complete graph. The values plotted correspond to the fraction of runs which ended with 100% cooperators. We fix T_s = 1 and vary T_a. In each time step, synchronous updating of strategies is carried out with probability T_a/(T_s + T_a) using Fermi-update, AL beeing carried out otherwise. For the extreme limits we obtain perfect agreement with the analytic predictions. However, the analytic results remain valid for a much larger range of values 0.01 ≤ T_a/T_s ≤ 0.1 than one would expect from pure theoretical considerations. Indeed, only between these two limits a crossover takes place, which depends on the intensity of selection β as illustrated.

Finally, let us further couple the dynamics of links and the dynamics of strategies by introducing payoff dependent AL-dynamics. An interesting coupling arises when we associate the propensity to form new links and the lifetime of different types of links with the productivity of those links assessed in terms of payoffs. Many possibilities can be readily envisaged, which will lead to different context-based justifications for the choices of parameters α_i and γ_ij. Here we explore the case in which cooperators and defectors share the same propensity to form new links α_C = α_D, whereas the lifetimes of ij-links are proportional to the average profit expected from that link. Other linear as well as non-linear alternatives are possible. A simple average relation, based on the expected outcome from different types of interactions leads to τ_ij = κ(M_ij + M_ji)/2 which yields τ_CD = τ_CC/2, whereas τ_DD = 0. More generally, we may assume that τ_CD = τ_CC/p with p > 1, maintaining τ_DD = 0 (this results from the zero-entry in the payoff-matrix). We may now express r in terms of the constant $\theta ={\tau }_{CC}{\alpha }_C^2$, obtaining $r=\frac{p-1}{p+\theta }$, an increasing function of p. The intuition behind this result is clear: The larger the value of p, that is, the smaller the lifetime of CD-links compared to CC-links, the smaller the value of b/c above which cooperation will thrive. Moreover, the larger the value of p the smaller the fraction of cooperators that is necessary to be initially present in the population for cooperation to dominate over defection in the resulting coordination game.

The transformation between a PD and a coordination game is not the only possible one: Inspection of ϕ_ij shows that other transformations are feasible. The Snowdrift Game (SG) has recently attracted a lot of attention, due to its potential biological relevance [31]. In the SG, a cooperator pays a cost c, but two cooperators share this cost. Whenever one player cooperates, both receive a benefit b > c, leading to the payoff matrix

$$\begin{array}{l}\begin{array}{cc}C& D\end{array}\\ \begin{array}{c}C\\ D\end{array}\left(\begin{array}{cc}b-\frac{c}{2}& b-c\\ b& 0\end{array}\right).\end{array}$$

For strong selection on complete graphs, the SG leads to a stable coexistence between cooperators and defectors, corresponding to a stable interior fixed point in strategy phase space at N_C/N ≈ (2b − 2c)/(2b − c), which may become especially small whenever c ≈ b. Nonetheless, for large T_s/T_a the SG is effectively transformed into the Harmony game, for which 1 cooperator is enough to invade the entire population. For the payoff matrix above, the SG is effectively converted into a Harmony game whenever r > c/(2b), where r = (ϕ_CC − ϕ_CD)/ϕ_CC as above. If costs and benefits are the same, the assortment of interactions r has to be only half as high as for the transformation of the PD into a coordination game in order to transform the SG into a Harmony game.

To sum up, by equipping individuals with the capacity to control the number, nature and duration of their interactions with others, we introduce an active linking dynamics which leads to networks exhibiting different degrees of heterogeneity. In the limit when active linking dynamics is much faster than strategy dynamics, we obtain a simple rescaling of the payoff-matrix. Such rescaling can lead to a transformation of the type of game, effectively taking place in a finite, well-mixed population. As the ratio between the time scales associated with linking dynamics and strategy dynamics increases, the interplay between these two dynamical processes leads to a progressive crossover between the analytic results discussed here and the evolutionary dynamics of strategies taking place on static graphs. Unlike previous numerical explorations [11–14], the present model provides a simple analytical pathway towards understanding of how self-interested individuals may actually end up cooperating, showing how selective choice of new links (favouring assortative mixing between cooperators) associated with fast rewiring dynamics may provide the means to achieve long term cooperation.