The one-third law of evolutionary dynamics

Abstract

Evolutionary game dynamics in finite populations provide a new framework for studying selection of traits with frequency-dependent fitness. Recently, a “one-third law” of evolutionary dynamics has been described, which states that strategy A fixates in a B-population with selective advantage if the fitness of A is greater than that of B when A has frequency 1/3. This relationship holds for all evolutionary processes examined so far, from the Moran process to games on graphs. However, the origin of the “number” 1/3 is not understood. In this paper we provide an intuitive explanation by studying the underlying stochastic processes. We find that in one invasion attempt, an individual interacts on average with B-players twice as often as with A-players, which yields the one-third law. We also show that the one-third law implies that the average Malthusian fitness of A is positive.

1 Introduction

Many complex traits of organisms are inherently advantageous, but provide a selective advantage only in terms of interactions between the organisms themselves. The canonical example is the trait of cooperation, whose fitness depends on the proportion of the population (or frequency) which cooperates (Nowak 2006b). Given the importance of such interactive traits, it is of interest to understand how they evolve in a population and when they are advantageous. Evolutionary game theory provides the framework for studying the dynamics of frequency-dependent selection (Von Neumann and Morgenstern 1944, Weibull 1995, Hofbauer & Sigmund 1998, Gintis 2000, Cressman 2003, Nowak & Sigmund 2004, Nowak 2006a).

Unlike in infinite populations, the game dynamics in realistic finite populations are susceptible to demographic stochasticity, hence they are described by stochastic processes rather than by deterministic equations (Maynard Smith 1988, Schaffer 1988, Kandori et al. 1993, Ficici & Pollack 2000, Komarova & Nowak 2003, Nowak et al. 2004, Taylor et al. 2004, Taylor et al. 2006, Wild & Taylor 2004, Imhof et al. 2005, Fudenberg et al. 2006, Nowak 2006a, Ohtsuki & Nowak 2006, Ohtsuki et al. 2006, Traulsen & Nowak 2006, Ohtsuki et al. 2007, Traulsen et al. 2006a, 2007a). In finite-sized populations it is possible that an advantageous mutant goes extinct. It is also possible that a deleterious mutant by chance fixates in the population. Thus, even if traits with frequency-dependent fitness seems advantageous in infinite populations, it is a priori not clear whether they can take over in finite-sized populations, and vice-versa. In Nowak et al. (2004), a natural definition of an advantageous mutation was introduced, which takes into account the stochastic nature of reproduction. The fixation probability of strategy A, denoted by ρ_A, is defined as the probability that the offspring lineage of a single A-mutant invading a population of (N − 1) many B-individuals eventually takes over the whole population. The fixation probability of a neutral mutant is equal to the reciprocal of the population size, 1/N. Therefore, strategy A is deemed advantageous if the fixation probability, ρ_A, is greater than 1/N.

If selection is weak, the likelihood of fixation ρ_A can be computed explicitely. In this case, Nowak et al. (2004) found that strategy A is advantageous if the fitness of an A-player is higher than the fitness of a B-player when the frequency of A is 1/3. This has been dubbed the one-third law. We do not have, however, an intuition of why such a universal law exists, which holds for a variety of update rules and population structure studied so far. In this paper, we provide an intuition of the one-third law.

Let us consider a game with two strategies, A and B. The payoffs of A versus A, A versus B, B versus A, and B versus B, are denoted by a, b, c, and d, respectively. The payoff matrix is thus

$$\begin{array}{c}\begin{array}{cc}A& B\end{array}\\ \begin{array}{c}A\\ B\end{array}\left(\begin{array}{cc}a& b\\ c& d\end{array}\right).\end{array}$$ (1)

The payoffs of players are dependent on the abundance of each strategy in the population. In particular, if there are i many A-players and (N − i) many B-players and random pairwise interactions, then the expected payoffs of A and B are (excluding self-interaction)

$$\begin{array}{c}{F}_i=a\frac{i-1}{N-1}+b\frac{N-i}{N-1},\\ G_i=c\frac{i}{N-1}+d\frac{N-i-1}{N-1}.\end{array}$$ (2)

To account for the contribution of the game’s payoff to the fitness of players, Nowak et al. (2004) introduced a “selection intensity parameter”, 0 ≤ w ≤ 1, such that the fitness of A and B players are respectively given by

$$\begin{array}{c}{f}_i=1-w+w{F}_i,\\ g_i=1-w+w{G}_i.\end{array}$$ (3)

At zero selection intensity, the game has nothing to do with one’s fitness. At the other extreme, w = 1, fitness equals payoff. In the replicator dynamics of infinite populations, the selection intensity cancels out so that it has no effect on the evolutionary outcome. However, it is known that it crucially matters in finite populations (Traulsen et al. 2007b).

To address evolution in this approach, we now consider that reproduction and replacement occur according to some fitness-dependent rule. Nowak et al. (2004) studied the Moran process with frequency-dependent selection (details will be explained in the following sections). In the limit of weak selection, Nw ≪ 1, they found that A is an advantageous mutant (i.e. ρ_A > 1/N) if and only if

$$(N-2)a+(2N-1)b>(N+1)c+(2N-4)d.$$ (4)

For large N, this condition leads to

$$a+2b>c+2d.$$ (5)

Suppose each strategy is the best reply to itself, which means a > c and b < d. Here a single A mutant is initially at a disadvantage. The deterministic replicator equation (Taylor & Jonker 1978, Hofbauer & Sigmund 1998) for infinite populations tells us that a unique unstable equilibrium exists at a frequency of strategy A given by x^* = (d − b)/[(d − b) + (a − c)]. We can now write the one-third law of evolutionary dynamics in the form (Nowak et al. 2004)

$$x\ast <1/3.$$ (6)

Namely, if the basin of attraction of strategy B is less than one-third then an A-mutant overcomes its initial disadvantage and fixates in the population with selective advantage (Fig. 1). Interestingly, the one-third law (6) translates the condition of advantageous mutation in finite populations into a condition on frequency-dependent fitness in infinite populations. The one-third law holds for the Moran process (Nowak et al. 2004), for the Wright-Fisher process (Lessard 2005, Imhof & Nowak 2006), for pairwise comparison updating (Traulsen et al. 2006b), for Cannings exchangeable models that are in the domain of application of Kingman’s coalescent (Lessard & Ladret 2007), and for games on graphs (Ohtsuki et al. 2006, 2007) with modified payoff matrices.

Figure 1.

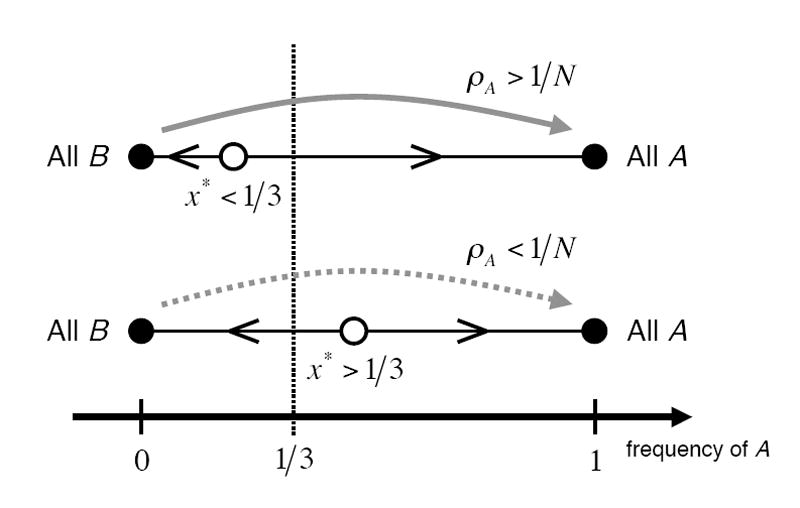
The one-third law. Both A and B are Nash equilibria of the game. Top: If the location of the unstable equilibrium in the replicator equation is x^* < 1/3 then the fixation probability of A is greater than 1/N in finite populations. Bottom: If x^* > 1/3 holds, the fixation probability, ρ_A, is less than 1/N. All these results hold for weak selection such that Nw ≪ 1 is satisfied.

We study the Moran process (main text) and the Wright-Fisher process (Appendix A). We calculate the mean effective sojourn time at each state of the underlying stochastic process. We show that along the path of an invasion attempt, starting with a single A-mutant and ending at either extinction or fixation, an individual on average plays the game with B-players twice as often as with A-players. In other words, the number 1/3 represents the proportion of A-players in all the opponents that one meets. This result leads directly to inequality (5).

This paper is structured as follows. In section 2, we study the dynamics of fixation under neutral drift and show that the neutral mutants play with resident players on average twice as often as with other neutral mutants. In section 3 we generalize the result for non-zero intensity of selection, leading to the one-third rule for frequency-dependent selection. We offer a discussion in section 4.

2 Evolutionary dynamics of neutral drift

The detailed dynamics of evolutionary games depend crucially on the updating rules which relate successive generations. We study the frequency-dependent Moran process introduced by Nowak et al. (2004). In this section, we study the neutral case (w = 0 in eq.(3)), where the fitness of each player is exactly equal to 1.

Consider the game (1) played in a finite population of fixed size, N. At each time step an individual is chosen for reproduction proportional to its fitness. Then he replaces a randomly chosen individual (can be himself) with his clonal offspring. This defines a stochastic process in one random variable i which represents the number of A-players in the population. In the state space {0, …, N} there are two absorbing states, i = 0 (which means A has become extinct) and i = N (which means A has reached fixation).

An invasion of a resident population by a mutant corresponds to a path on the state space. We want to estimate how much time is spent at each state j (1 ≤ j ≤ N − 1) along the path. This time is called the sojourn time of the process in state j. Given all paths which start at state i, let t̄_ij denote the mean sojourn time in state j before absorption into either state 0 or state N. It is easy to see that:

$${\overline{t}}_{ij}=\sum _{k=0}^N{p}_{ik}{\overline{t}}_{kj}+{\delta }_{ij},{\overline{t}}_{0j}={\overline{t}}_{Nj}=0$$ (7)

(see, for example, Ewens 2004). Here p_ij represents the transition probability from state i to state j. To solve this equation, we need to know the transition probabilities in this Moran process of neutral drift. The probability that the number of A-players increases by one factorizes into the probability that an A player is chosen to reproduce and that a B player is chosen to die. Since A is a neutral mutant we have

$$p_{i,i+1}=\frac{N-i}{N}\cdot \frac{i}{N}.$$ (8a)

Similarly, the number of A players decreases by one with probability

$$p_{i,i-1}=\frac{i}{N}\cdot \frac{N-i}{N}.$$ (8b)

It remains unchanged with probability

$$p_{\mathit{ii}}=1-2\frac{i}{N}\frac{N-i}{N}.$$ (8c)

Hence the transition matrix of the Markov chain is tri-diagonal, which is the definition of a “birth-death” process (Karlin & Taylor 1975). From eqs.(7) and (8) we obtain t̄_ij (Ewens 2004). In particular, if we start from a single mutant, i = 1, we obtain

$${\overline{t}}_{1j}=\frac{N}{j}.$$ (9)

Equation (9) means that the stochastic process stays most of the time around the absorbing barrier, state 0. However, notice, for example, that most of the sojourn time at state 1 is spent with events where a B-player is chosen for reproduction and another B player dies, so that the difference in payoffs of A and B players does not matter and the population state is unchanged. These steps are irrelevant for evolution, and therefore they must be excluded from our calculation. More precisely speaking, we observe four different kinds of steps at state j:

• (i)An A-player reproduces and replaces another A-player.
• (ii)An A-player reproduces and replaces a B-player.
• (iii)A B-player reproduces and replaces an A-player.
• (iv)A B-player reproduces and replaces another B-player.

The relevant steps, where an A-player reproduces and replaces a B-player or vice versa ((ii) and (iii) in the list above), actually occur with probability p_j,j+1 + p_j,j−1. Thus, the mean effective sojourn time in state j for paths that start at state i, denoted by τ̄_ij, is given by τ̄_ij = (p_j,j+1 + p_j,j−1)t̄_ij. In particular, from (8) and (9) we obtain

$${\overline{\tau }}_{1j}=\frac{2(N-j)}{N}.$$ (10)

Figure 2 compares the effective sojourn time to the mean sojourn time. We observe that effective sojourn time, which is the mean number of visits to a given state, is proportional to the number of B-players in that state.

Figure 2.

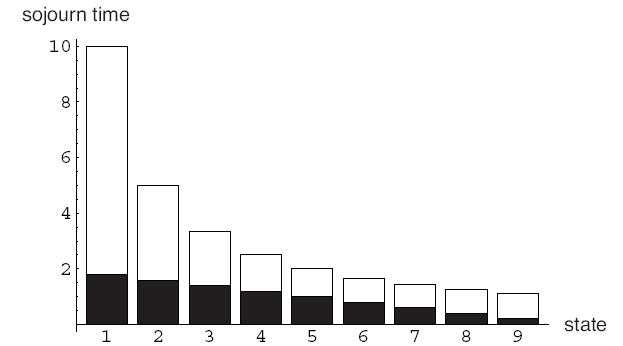
Mean sojourn time (t̄_1j, open bars) and mean effective sojourn time (τ̄_1j, filled bars) in each state, when N = 10.

Knowing the effective sojourn times, we can now count the average number of games played by strategies A and B along a path of invasion. In state j, an A-player meets (j − 1) A-players and (N − j) B-players, while a B-player meets j A-players and (N − j − 1) B-players. We summarize it in a simple form as

$$\left(\begin{array}{cc}A\to A& A\to B\\ B\to A& B\to B\end{array}\right){|}_{\mathrm{state}\hspace{1em}j}=\left(\begin{array}{cc}j-1& N-j\\ j& N-j-1\end{array}\right).$$ (11)

The effective number of encounters is given as the weighted sum of eq.(11) by τ̄_1j. For large N we obtain

$$\begin{array}{c}\sum _{j=1}^{N-1}{\overline{\tau }}_{1j}\left(\begin{array}{cc}A\to A& A\to B\\ B\to A& B\to B\end{array}\right){|}_{\mathrm{state}\hspace{1em}j}=\frac{N-1}{3}\left(\begin{array}{cc}N-2& 2N-1\\ N+1& 2N-4\end{array}\right).\\ \phantom{\sum _{j=1}^{N-1}{\overline{T}}_{1j}\left(\begin{array}{cc}A\to A& A\to B\\ B\to A& B\to B\end{array}\right){|}_{\mathrm{state}\hspace{0.17em}j}}\approx \frac{N^2}{3}\left(\begin{array}{cc}1& 2\\ 1& 2\end{array}\right).\end{array}$$ (12)

Equation (12) suggests that for large N both types of players meet B-players twice as often as A-players. In other words, one-third of the opponents that one meets (in interactions leading to state changes) until either extinction or fixation are A-players and two-thirds are B-players.

3 An intuition behind the one-third law

How are these results changed if the invading mutant is not neutral? Non-neutral mutation affects our calculation via changing the transition probabilities, p_ij. Equation (8) changes to

$$\begin{array}{c}{p}_{i,i+1}=\frac{N-i}{N}\cdot \frac{i{f}_i}{i{f}_i+(N-i)g_i},\\ p_{i,i-1}=\frac{i}{N}\cdot \frac{(N-i)g_i}{i{f}_i+(N-i)g_i},\\ p_{ii}=1-p_{i,i+1}-p_{i,i-1}.\end{array}$$ (13)

However, since under weak selection f_i and g_i remain very close to 1, we can prove that in a first order approximation the effective sojourn times are not affected. Still, the more often state j is visited, the more the fitness difference between A and B in state j is deemed to be important. In the previous section we saw that for large N one meets B-players twice as often as A-players on an average path of invasion. Therefore the average payoffs of A and B players along an invasion-path are (a+2b)/3 and (c+2d)/3, respectively. Surprisingly, the condition (a+2b)/3 > (c + 2d)/3 is exactly the same as eq.(5), thus it leads to ρ_A > 1/N. The mean effective sojourn times elegantly explain the one-third law this way.

More formally, let us compute the average payoffs of strategies A and B along a path of invasion, which are denoted by F̄ and Ḡ, respectively. Since the stochastic process spends τ̄_1j at state j, the relative frequency that the state j is visited is ${\overline{\sigma }}_{1j}={\overline{\tau }}_{1j}/{\sum }_{k=1}^{N-1}{\overline{\tau }}_{1k}=2(N-j)/N(N-1)$. We sum up payoffs over all transient states with each state weighted by the effective sojourn frequency, σ̄_1j. From (2) we obtain

$$\begin{array}{c}\overline{F}=\sum _{j=1}^{N-1}{\overline{\sigma }}_{1j}{F}_j=\frac{(N-2)a+(2N-1)b}{3N-3},\\ \overline{G}=\sum _{j=1}^{N-1}{\overline{\sigma }}_{1j}{G}_j=\frac{(N+1)c+(2N-4)d}{3N-3}.\end{array}$$ (14)

From (4) and (14) we find that

$${\rho }_A>1/N\iff \overline{F}>\overline{G}.$$ (15)

holds for any N. In the limit of large N we have F̄ = (a+2b)/3 and Ḡ = (c+2d)/3. Hence, we reproduce the verbal argument above.

In Appendix A, we study the Wright-Fisher process with frequency-dependent selection by Imhof & Nowak (2006). We show that the mean effective sojourn time explains the one-third law for the Wright-Fisher process, too.

4 Discussion

The one-third law establishes the conditions, in the limit of weak selection and large population size, under which one Nash strategy can be invaded by another. This question is important in biology where different strategies with frequency-dependent fitnesses emerge and compete. The question of equilibrium selection in the presence of multiple Nash equilibria is also central in economics, for instance in the context of competition between incompatible products. In this section we will comment on possible implications of the one-third law to these subjects.

The one third-law provides an easy and universal criterion for advantageousness at weak selection - measuring the fitness of a trait at frequency one-third at such large population size that the dynamics around this frequency become deterministic. In contrast, measuring the fixation probability of a trait would involve repeating evolutionary experiments on numbers of the order of the population size, which is in practice not feasible.

The deterministic population dynamics would describe our game dynamics eq.(1) by the following equations:

$$\begin{array}{c}\dot{x}=x(f_A(x)-\varphi )\\ \phantom{\dot{x}}=x\underset{\begin{array}{c}\left|\right|\\ r(x)\end{array}}{\underbrace{(1-x)(f_A(x)-f_B(x))}}\end{array}$$ (16)

Here x represents the frequency of strategy A, and

$$\begin{array}{c}{f}_A(x)=ax+b(1-x),\\ f_B(x)=cx+d(1-x),\end{array}$$ (17)

represent the average fitnesses of A and B at state x, respectively. The average population fitness at state x is ϕ(x) = xf_A(x) + (1 - x)f_B(x). In eq.(16), the term r(x) represents the Malthusian fitness of strategy A. It is easy to see that the one-third law (5) is equivalent to

$$r(1/3)>0$$ (18)

for large population size. In other words, strategy A is an advantageous mutant if the Malthusian fitness of A is positive when its frequency is 1/3. Again we find an equivalence between selective advantage and average fitness:

$${\rho }_A>1/N\iff r(1/3)>0\iff \langle r(x)\rangle ={\int }_0^{1}r(x)dx>0.$$ (19)

Inequality (19) suggests that A is an advantageous mutant if the average Malthu-sian fitness over the frequency space, [0, 1], is positive. Again, the integral can be estimated experimentally by evaluating the fitness of a trait at different frequencies. The inequality (19) suggests a natural generalization of the one-third law to nonlinear fitness functions, as shown in Appendix B. Non-linear fitness functions are likely to have increasing relevance with the current boom of experimental work on cooperativity in biological systems.

Our present results hold under weak selection limit, Nw ≪ 1. Some evolutionary phenomena in biology, however, happen outside the scope of weak selection Nw ≪ 1. We suggest that the importance of the one-third law in this larger context is that it provides a universal lower bound on the advantageous mutant’s basin of attraction. In fact, by generalizing the arguments of Traulsen et al (2006b) one can prove that in the game where both strategies are strict Nash equilibria (a > c and b < d in (1)), if the unstable coexistence equilibrium is at x^* > 1/3 then the mutant strategy is never advantageous for any Nw (with small w). For each Nw, there is a minimum size of basin of attraction for a mutant strategy to have a selective advantage in fixation. This minimum goes from 2/3 (Nw ≪ 1) to 1 (for large Nw). Therefore, as selection pressure increases, advantageous mutants must have ever larger basins of attraction. At the extreme of Nw → ∞ (with small w), a population of one Nash equilibrium never reaches the other Nash equilibirum, which is in line with the prediction from the replicator equation.

Our results bear on the problem of equilibrium-selection in games in finite populations. Equilibrium-selection out of multiple Nash equilibria is a very important problem in economics (Binmore 1994, Samuelson 1997). Suppose a > c and b < d hold in the payoff matrix (1), which means that both A and B are strict Nash equilbiria of the game. This type of game is called coordination game. An important concept in economics is p-dominance. Strategy A is (strictly) p-dominant over B, if A is the better response than B when one believes his opponent chooses strategy A with probability more than p (Morris et al, 1995; Kajii and Morris, 1997). In this terminology, the one-third law asserts that (strictly) 1/3-dominant strategies have a selective advantage in taking over the population in the weak selection limit. In the general case, where Nw is not necessarily small, the dominance of an invading strategy should be smaller than 1/3.

On the other hand, 1/2-dominance, or equivalently risk-dominance (Harsanyi and Selten 1988), is drawing wide attention in economics. In our game (1), strategy A is risk-dominant if a + b > c + d, that is, if it has a larger basin of attraction than its opponent. Kandori et al. (1993) and Young (1993) studied stochastic evolutionary game dynamics by introducing mutations to best response dynamics, and found that a risk-dominant strategy is chosen most of the time. We observe that risk-dominance is closely related to the ratio of fixation probabilities. In the approximation Nw ≪ 1, Nowak et al. (2004) found that risk dominance is equivalent to ρ_A > ρ_B, which suggests that a risk-dominant strategy dominates the population more often than the other.

Equilibrium selection is also the focus of product economics, where decades of theoretical work are now giving way to empirical studies of the dynamics of product adoption, namely of incompatible technologies (Farrell & Saloner 1985, Lee & Mendelson 2008). It would be interesting to transfer our results to this setting. However, this requires a more detailed study of the evolutionary dynamics of markets (Lee & Mendelson 2008). We leave this for future work.

Appendix A The Wright-Fisher process of stochastic game dynamics

Imhof & Nowak (2006) studied the Wright-Fisher process in finite populations. There, all individuals reproduce synchronously proportional to fitness. Remember that in the Moran process reproduction occurs in an asynchronous fashion among players.

Consider a population of fixed size, N, and let i denote the number of A-players. At each generation, N adult individuals die at the same time, and N individuals are newly born. The number of A-players in the offspring generation follows the binomial distribution, with the transition probability from state i to state j given by

$$p_{ij}=\left(\begin{array}{c}N\\ j\end{array}\right){\left(\frac{i{f}_i}{i{f}_i+(n-i)g_i}\right)}^j{\left(\frac{(N-i)g_i}{i{f}_i+(N-i)g_i}\right)}^{N-j}.$$ (A.1)

The two states, state 0 and state N, are absorbing while the others are transient. Imhof & Nowak (2006) found that in weak selection and for large population size the one-third law (eqs.(5) and (6)) holds for the Wright-Fisher process.

Here we show that the mean effective sojourn time gives an explanation to the one-third law in the Wright-Fisher process. Both Wright (Wright 1931) and Fisher (Fisher 1958) found that the mean sojourn time in state j, given starting from state 1, is approximately

$${\overline{t}}_{1j}\approx \frac{2}{j}\hspace{0.17em}(\mathrm{generations})$$ (A.2)

in neutral selection (see also Ewens (2004)). The equation (A.2) also gives a good approximation to the mean sojourn time in the case of weak selection. We note that the time unit in (A.2) is a generation, during which reproduction occurs N times. For the sake of fair comparison with the Moran process we regard one generation as N separate steps, thus the mean sojourn is

$${\overline{t}}_{1j}\approx \frac{2}{j}\times N=\frac{2N}{j}\hspace{0.17em}(\mathrm{steps}).$$ (A.3)

Because a generation consists of N simultaneous reproductive steps, calculation of the effective mean sojourn time is not so straightforward as in the Moran process. Below, we consider each of N reproductive steps in one generation in state j, separately.

In the first j steps we think that an adult A-player dies. Therefore reproduction is deemed “effective” if a B-player is born, which is the case with probability

$$\frac{(N-j)g_j}{j{f}_j+(N-j)g_j}\approx \frac{N-j}{N}.$$ (A.4)

Here we used the assumption of weak selection. In the last (N − j) steps, on the other hand, we think that an adult B-player dies. Reproduction is deemed “effective” if an A-player is born, which occurs with probability

$$\frac{j{f}_j}{j{f}_j+(N-j)g_j}\approx \frac{j}{N}.$$ (A.5)

Hence the average number of effective steps in one generation is

$$j·\frac{N-j}{N}+(N-j)·\frac{j}{N}=\frac{2j(N-j)}{N}.$$ (A.6)

Thus we obtain the mean effective sojourn time in state j starting from state 1 as follows:

$${\overline{\tau }}_{1j}\approx \frac{2}{j}\times \frac{2j(N-j)}{N}=\frac{4(N-j)}{N}\hspace{0.17em}(\mathrm{steps}).$$ (A.7)

Comparing eq.(A.7) with eq.(10), we see that the mean effective sojourn time in the Wright-Fisher process is the double of that in the Moran process (it is because of the difference in the variance in offspring distribution; see Ewens (2004) pp.121-122). Therefore the same argument as in Sections 2 and 3 holds. We obtain the intuition behind 1/3 in the same manner.

Appendix B Average Malthusian fitness distinguishes between advantageous and non-advantageous mutants for general fitness functions

Consider two strategies, A and B. We study a population of fixed size of N. Let i represent the number of A players in the population. The relative abundance of A-players in the population is given by x = i/N. Suppose that the average payoffs of A and B players depend only on x. These are given by F_A(x) and F_B(x). Under weak selection, w ≪ 1, the average fitness of each type of players is given by f_A(x) = (1−w) + wF_A(x) and f_B(x) = (1−w) + wF_B(x), respectively. As in eq. (16), the Malthusian fitness of strategy A at frequency x is r(x) = (1−x)(f_A(x) − f_B(x)) = w(1 − x)(F_A(x) − F_B(x)).

According to Nowak et al. (2004), the fixation probability of strategy A is given by the following formula:

$${\rho }_A={\left(1+\sum _{k-1}^{N-1}\prod _{i=1}^k\frac{f_B(i/N)}{f_A(i/N)}\right)}^{-1}.$$ (B.1)

Given N ≫ 1, w ≪ 1 and Nw ≪ 1, equation (B.1) is calculated as

$$\begin{array}{c}{\rho }_A\approx {\left(1+\sum _{k=1}^{N-1}\prod _{i=1}^k\left[1+w\{F_B(i/N)-F_A(i/N)\}\right]\right)}^{-1}\\ \phantom{{\rho }_A}\approx {\left(1+\sum _{k=1}^{N-1}\left[1+w\sum _{i=1}^k\{F_B(i/N)-F_A(i/N)\}\right]\right)}^{-1}\\ \phantom{{\rho }_A}\approx {\left(1+(N-1)+w\sum _{k=1}^{N-1}\sum _{i=1}^k\{F_B(i/N)-F_A(i/N)\}\right)}^{-1}\\ \phantom{{\rho }_A}={\left(N+w\sum _{i=1}^{N-1}(N-i)\{F_B(i/N)-F_A(i/N)\}\right)}^{-1}\\ \phantom{{\rho }_A}={\left(N+Nw\sum _{i=1}^N\left(1-\frac{i}{N}\right)\{F_B(i/N)-F_A(i/N)\}\right)}^{-1}\\ \phantom{{\rho }_A}\approx {\left(N-N{\int }_0^{1}w(1-x)\{F_A(x)-F_B(x)\}dx\right)}^{-1}\\ \phantom{{\rho }_A}={\left(N-N{\int }_0^{1}r(x)dx\right)}^{-1}.\end{array}$$ (B.2)

Thus we obtain

$${\rho }_A>\frac{1}{N}\iff {\int }_0^{1}r(x)dx>0.$$ (B.3)

This ends the proof.