Prediction of the Rate of Uptake of Carbon Monoxide From Blood by Extravascular Tissues

Abstract

Uptake of environmental carbon monoxide (CO) via the lungs raises the CO content of blood and of myoglobin (Mb)-containing tissues, but the blood-to-tissue diffusion coefficient for CO (DmCO) and tissue CO content are not easily measurable in humans. We used a multicompartment mathematical model to predict the effects of different values of DmCO on the time courses and magnitudes of CO content of blood and Mb-containing tissues when various published experimental studies were simulated. The model enhances our earlier model by adding mass balance equations for oxygen and by dividing the muscle compartment into 2 subcompartments. We found that several published experimental findings are compatible with either fast or slow rates of blood-tissue transfer of CO, whereas others are only compatible with slow rates of tissue uptake of CO. We conclude that slow uptake is most consistent with all of the experimental data. Slow uptake of CO by tissue is primarily due to the very small blood-to-tissue partial pressure gradients for CO.

1. Introduction

Treatment strategies for victims of carbon monoxide (CO) poisoning are based on two general concepts. The first is the well-established concept that the affinity of hemoglobin (Hb) for CO is two orders of magnitude larger than that for O₂ (Coburn, 1970; Roughton et al., 1957). The second is the presumption that transport of CO between blood and tissue occurs on a time scale similar to that of movement of O₂, and therefore that blood and tissue CO levels equilibrate rapidly. Thus, the usual therapeutic approach is to give the victim a high inspired level of O₂ (either normobaric or hyperbaric) and assume that whole-body CO has been adequately cleared when blood carboxyhemoglobin (%HbCO) falls below some specified small value (e. g., 4%).

The second concept above is based on the similarity of diffusion coefficients in saline of CO and O₂, and on experimental studies of changes in blood CO levels under a variety of transient or steady-state conditions. For example, based on experimental measurements of uptake of radiolabelled CO in blood during rebreathing, Luomanmaki and Coburn (1969) concluded that the half-time for equilibration in the circulatory system, as well as equilibration of tissue and blood partial pressures of CO, is 12.5 min. On the other hand, the measurement of blood volume by CO dilution (Burge and Skinner, 1995; Nomof et al., 1954) assumes that negligible CO leaves the blood within 10 min of the start of the rebreathing procedure; but if the half-time for blood-tissue equilibration were 12.5 min, there would be substantial loss of CO from blood to tissues in 10 min. Furthermore, our earlier report (Bruce and Bruce, 2006) of the biphasic nature of the fall of %HbCO during washout also implies that CO distributes into two compartments at different rates. Direct measurement of tissue CO levels could help to resolve these conflicting observations; however, most tissue CO is bound to myoglobin (Mb), and measurements of carboxymyoglobin (MbCO) are technically challenging and often unreliable in experimental animals because it is difficult either to remove HbCO from the tissue sample with high assurance or to account for it quantitatively. In vivo measurements of MbCO are not currently possible in humans.

Various indirect studies have addressed the movement of CO between blood and tissues. However, given the complex factors which govern the uptake and distribution of CO in the body, many of their conclusions are problematic. For example, the linear increase in %HbCO reported to occur when CO is added to a rebreathing circuit at a constant rate (Luomanmaki and Coburn, 1969) is likely to be compatible with slow equilibration as well as with the authors’ conclusion of rapid blood-tissue equilibration. Furthermore, the experimental findings of Roughton and Root (1946) show that the amount of CO expired during 15-45 minutes after the end of a CO exposure lasting ~4 min is significantly less than the amount lost from the blood, implying that significant blood-to-tissue flux of CO persisted during that period. Additionally, despite the similarity of their diffusion coefficients, the fact that blood-to-tissue partial pressure gradients for O₂ and CO typically differ by two or more orders of magnitude (being smaller for CO) raises the question as to whether CO does move between blood and tissues as rapidly as O₂.

Given the difficulty of obtaining direct experimental data on tissue CO levels in human subjects, computational modeling has been utilized to predict the uptake and distribution of CO in the body. The earliest model, the Coburn-Foster-Kane (CFK) equation (Coburn et al., 1965), cannot be used to address details of CO distribution because it assumes that the body is a single lumped compartment. Smith (1994), using data from Benignus et al., (1994), developed a mathematical model of the circulatory distribution of CO and attempted to explain the arterio-venous (a-v) difference of HbCO in the arm resulting from a brief (5-7 min) exposure to a high inspired CO level (6683 ppm, leading to peak HbCO ~15-20%). To explain this difference, the model required a separate compartment in which vascular mixing was much slower than in the rest of the blood. Our previous modeling study (Bruce and Bruce, 2003) of the hyperoxic rebreathing experiments of Burge and Skinner (1995) considered the effect of the blood-tissue diffusion coefficient of CO on the rate of decrease of HbCO in the period from 10-40 min after the onset of rebreathing. To fit these data, we found that the diffusion coefficient had to be too small to permit rapid blood-tissue equilibration of PCO. Because of this latter property, our model also was able to predict the biphasic nature of the HbCO response during washout of CO after CO exposures (Bruce and Bruce, 2006).

A recent simulation study (Beard and Bassingthwaite, 2000) demonstrates that with a highly diffusible substance the estimate of a diffusion coefficient based on fitting single-compartment models of blood-tissue exchange to washout data can be smaller than expected because simultaneous diffusion of the substance within the tissue is not taken into account. Thus, although our earlier model reproduced CO washin/washout phenomena correctly, the parameter value for CO diffusion out of the circulation may have been underestimated. Furthermore, our single-compartment tissue model did not account for two potentially important phenomena: arteriole to venule shunting of blood gases via short intra-tissue pathways (Pittman, 2005), and diffusion of blood gases into tissues from pre-capillary vessels (e. g., arterioles) (Secomb and Hsu, 1994; Sharan et al., 1998; Ye et al., 1993).

In the present study we have used an improved mathematical model to assess the effects of the blood-tissue diffusion coefficient for CO on the time course of the change in blood CO content when various experimental studies were simulated. We expected that any single experimental result could be compatible with a range of parameter values for the model; therefore, our objective was to fix all parameter values except the CO diffusion coefficient a priori based on physiological considerations, and then to determine the value of the blood-tissue CO diffusion coefficient that provided the most consistent fit to the experimental studies collectively. We expected that this integration of experimental findings via the model would produce more appropriate estimates of the blood-tissue distribution of CO than any individual experiment. Our simulation results indicate that although many published experimental results are compatible with either rapid or slow blood-tissue equilibration of CO (Benignus et al., 1994; Coburn and Mayers, 1971; Luomanmaki and Coburn, 1969), the studies from Burge and Skinner (1995), and from Roughton and Root (1946) are only compatible with slow equilibration. Importantly, the condition of slow equilibration of CO occurs when the diffusion coefficient for CO is of the same order of magnitude as that for O₂. The difference in rates of equilibration of the two gases is due to the much smaller blood-to-tissue partial pressure gradient for CO. These findings imply that current treatments for CO poisoning, particularly those involving treatment with hyperoxia, may result in prolonged elevation of tissue CO levels which might contribute to long-term sequellae.

2. Methods: Description of the model

The current model is a significant enhancement of our previous model (Bruce and Bruce, 2003; Bruce and Bruce, 2006). A major improvement is the addition of mass balance equations for O₂, so that the model directly calculates PO₂ in the various compartments. In addition, metabolic rate of muscle, blood flow to muscle, and resident blood volume in muscle are calculated from physiological data rather than being arbitrarily specified. Also, cardiac output increases in proportion to increases of %HbCO. To reduce the potential parameter estimation error mentioned above, the muscle tissue compartment is represented as two subcompartments (described below), and extravascular diffusion of CO and O₂ between the subcompartments, as well as arterio-venous shunting, are taken into account.

Model structure

The model structure (Figure 1) is a modification of our previously published model (Bruce and Bruce, 2003; Bruce and Bruce, 2006) in which the two major tissue compartments are intended to represent all body tissues that contain (Muscle) or do not contain (NonMuscle) myoglobin. The new structure includes two separate subcompartments for the muscle tissue (Figure 2), and physiological shunting of blood flow in the lungs. The change in the muscle compartment is motivated by the findings of Beard and Bassingthwaite (2000) who compared two different models of exchange of a highly diffusible substance between the microcirculation and tissue. They used a simple Krogh cylinder model to fit washout data generated by a 3-dimensional tissue model having a complex vascular structure and estimated the permeability-surface area product (PS) of the simpler model that yielded the best fit. The estimated PS of the Krogh model best approximated the value actually used in their complex model when, in the Krogh model, the value for diffusivity of the substance within the tissue greatly exceeded (e. g., 10-20 times) measured values in the literature. In that case the exit (venous) concentration profile vs. time of the Krogh model reasonably reproduced the original data from the complex model. Thus, we deemed it necessary to include more than one lumped muscle tissue compartment in our model, and to allow for diffusion of gases within the tissue (i. e., between subcompartments). The specific structure of the muscle tissue compartment (Figure 2) , which also allows for a-v shunting of gas flows through subcompartment 1, is similar to that of Ye, et al., (1993) and Sharan, et al., (1998); however, these latter authors assumed that the multiple vascular subcompartments all communicated with a single tissue compartment having a uniform PO₂

Figure 1.

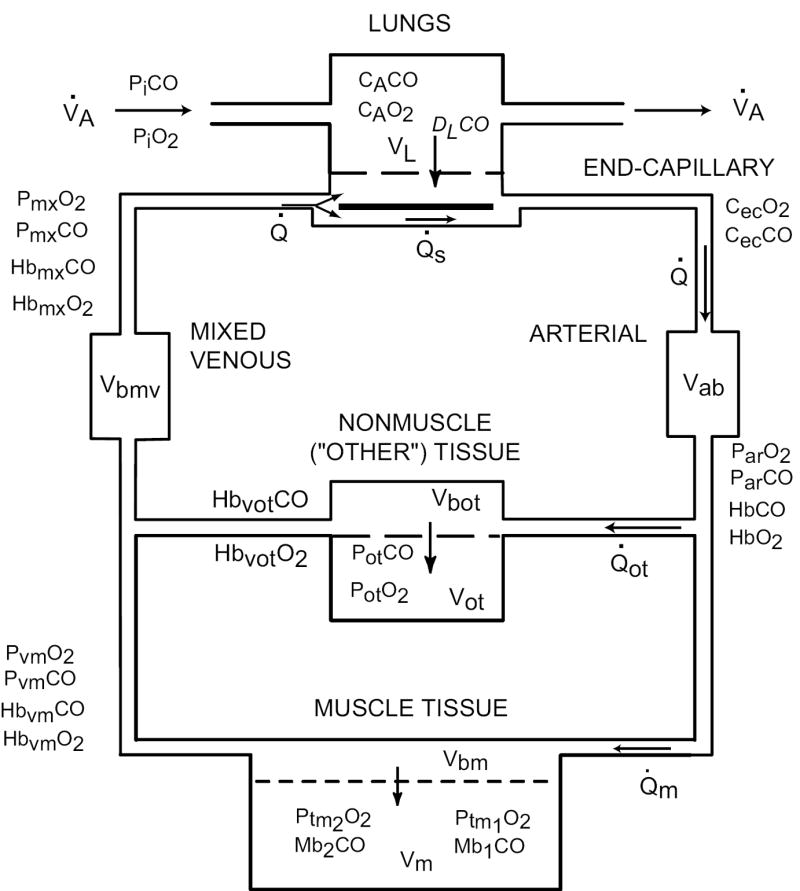
Overall strucure of the model, which expands our previous model (Bruce and Bruce, 2003) by subdividing the MUSCLE TISSUE compartment into two subcompartments. For details, see Figure 2.

Figure 2.

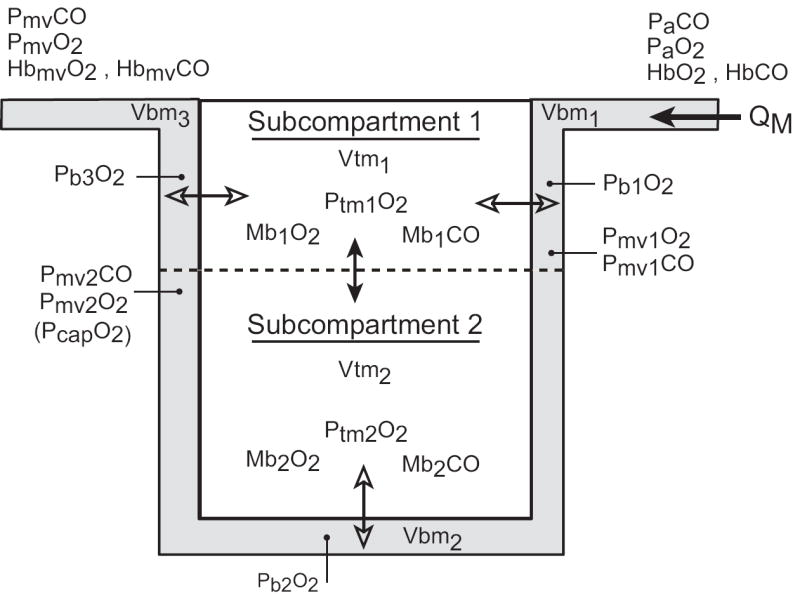
Detailed structure of the MUSCLE TISSUE compartment. The nonvascular tissue is divided into two subcompartments. Subcompartment 1 is considered to be nearer the proximal end of the arterial supply with entering arterioles, capillaries, and exiting venules all existing in this subcompartment. Subcompartment 2 is distal to arterioles and its gas exchange occurs predominantly via capillaries. Arterial blood enters the vascular subcompartment as QM. Open double arrows indicate blood-tissue gaseous fluxes driven by partial pressure gradients. PbjO₂ is the effective pressure in vascular compartment “j” driving this oxygen flux. (See text for details about its calculation.) Closed double arrows represent diffusive gaseous fluxes driven by concentration differences of dissolved gases. In both tissue subcompartments O₂ and CO exist as dissolved gases and combined with Mb.

Equations of the model: CO

The mass balance equations for CO are identical to our previous model (Bruce and Bruce, 2003; Bruce and Bruce, 2006) for the lung, “other” (NonMuscle) tissue, arterial, and mixed venous compartments. Similar mass balance equations for O₂ are applied to these compartments in the standard manner (Modarreszadeh and Bruce, 1994). In the end-capillary compartment, the shunt blood flow is added to the blood flow from the lungs and end-capillary gas concentrations are calculated as flow-weighted averages of the concentrations in the two blood flows. PO₂ in blood from the lungs is assumed to be equilibrated with alveolar gas. PCO in this blood is determined by adding the lung-to-blood CO flux, calculated from DLCO and the alveolar-to-blood CO pressure gradient, to the mixed venous blood entering the lungs. In all simulations reported here, the pulmonary blood flow shunt fraction is set to a “normal” value of 0.05 (Grodins et al., 1967). Pure time delays are ascribed to arterial and mixed venous circulatory transport as described previously (Bruce and Bruce, 2003). Both O₂ and CO can combine with both Hb and Mb. The balance between the O₂ and CO forms of Hb (and separately of Mb) is determined by the corresponding Haldane coefficient and a Hill model of the oxygen dissociation curve whose parameters are functions of %HbCO, as described previously (Bruce and Bruce, 2003). This approach enables us to incorporate both the competition of O₂ and CO for Hb binding sites and the resulting change of shape of the dissociation curve in the presence of CO. It is not assumed that either Hb or Mb is fully saturated. In addition, concentrations of both dissolved and bound O₂ and CO are calculated for each blood and tissue compartment. As in our earlier models, mixing occurs in each vascular compartment; inflowing blood is assumed to be mixed with resident blood according to a first-order differential equation having a time constant equal to the compartmental volume divided by the blood flow through the compartment.

The two muscle subcompartments (Figure 2) have somewhat different volumes because subcompartment 1 (40% of the muscle volume) is viewed as being nearer to arterioles and larger venules while subcompartment 2 (60% of the muscle volume) is envisioned as tissue which is predominantly near capillaries (Pittman, 2005; Segal, 2005). The relative compartment sizes were estimated by comparing predicted subcompartment PO₂ values with experimental data, as discussed below. Within the two subcompartments of muscle tissue the mass balance equations for CO parallel those of the single muscle compartment of the earlier model, with the addition of diffusive flux of CO from one subcompartment to the other; this flux occurs in proportion to the difference in concentrations between the compartments. (See Appendix.) The diffusion coefficients for CO and O₂ are set to 10 times their physically measured values (Salathe and Tseng-Chan, 1980; Whitely et al., 2002). Furthermore, subcompartment 1 communicates with both the arteriolar inflow to the muscle and the venous outflow, and CO (and O₂) can diffuse between this subcompartment and both vascular compartments. Blood-to-tissue movement of CO is linearly proportional to the partial pressure difference; the proportionality constant is the “effective blood to tissue diffusion coefficient” for CO and is given the symbol DmCO in analogy to DLCO. To avoid confusion with gaseous diffusion between subcompartments, we will refer to DmCO as blood to tissue “conductance”, with units of ml CO/min/Torr. Blood to tissue conductance per gram of tissue is equal in the two subcompartments, but blood to tissue conductance itself differs between the 2 subcompartments because of the assumed difference in their volumes. As used here, the symbol “DmCO” will refer to the blood-tissue conductance of CO for muscle subcompartment 2. The equivalent parameter for subcompartment 1 is calculated so that the ratio of the two conductances equals the ratio of the corresponding tissue volumes. For each vascular subcompartment (i. e., Vbm1, Vbm2, Vbm3 of Figure 2), the driving pressure for blood-to-tissue movement of CO is calculated as the difference between the PCO corresponding to the average CO content of the vascular compartment and the tissue PCO.

Equations of the model: O₂

Mass balance equations for O₂ in the muscle tissue subcompartments parallel those for CO, with the addition of a term representing metabolic oxygen consumption. (See Appendix.) Like CO, O₂ also is permitted to diffuse between subcompartments of muscle tissue in proportion to the concentration difference, and to diffuse between subcompartment 1 and venules. Blood-to-tissue O₂ flux is determined by the partial pressure difference and the blood-to-tissue conductance for O₂, DmO₂. The value of blood-to-tissue conductance for O₂ differs between the two subcompartments because of the difference in their volumes. The value of DmO₂ was estimated by comparison of predicted tissue PO₂s with measured values of muscle tissue PO₂s, as discussed below. The partial pressure driving O₂ flux from the vascular subcompartment into the tissue subcompartment was determined as follows: The average O₂ content, CO₂, of blood flowing into and out of the vascular subcompartment was evaluated for each integration time step, then the PO₂ corresponding to this mean CO₂ was calculated via the inverse of the O₂ dissociation curve, using an iterative approach when necessary to achieve accuracy at low PO₂ in the presence of CO. From this O₂ partial pressure, the tissue PO₂, and DmO₂, the current value of blood-to-tissue oxygen flux was determined; O₂ flux was held constant at this value over the subsequent integration step on the assumption that it would change less than the PO₂ values. To support this assumption, a small integration step size (0.01 min) was used.

To account for gaseous fluxes between tissue subcompartment 1 and vascular volume 3 (i. e., Vbm3), we assumed that only a small fraction of the former could actually exchange gases with venules. In all simulations here this fraction was set to 7.5% of the volume of tissue subcompartment 1.

Cardiac output increases in the presence of CO. Via linear regression using human data (Chiodi et al., 1941; Kizakevich et al., 2000), it was determined that the per cent increase in cardiac output was 0.572 times the per cent increase in HbCO. Cardiac output of the model was updated every 0.01 min using this relationship.

Parameter values (Table 2)

Table 2.

Model parameters. Values not given here are available from our earlier models (Bruce and Bruce, 2003, 2006).

Parameter	Value	Source
Specific to subject #120		Benignus, et al., 1994; Smith, et al., 1994
Age (yr)	23.9 (Subject 120)
Height (m)	1.791 (subject 120)
Body weight (Kg)	72.70
Blood volume (ml/kg)	60.94
DLCO, air (ml/min/Torr)	29.00
[Hb] (gm/ml)	0.14
Cardiac output (ml/min)	5800.00
MRO2 (ml/min/gm)		Erupaka, 2007
Whole-body	0.0032
Arm muscles	0.0014
Trunk muscles	0.0020
Leg muscles	0.0020
Blood flow (ml/min)		Erupaka, 2007
Arm muscles	0.0210
Trunk muscles	0.0300
Leg muscles	0.0300
Muscle mass (% of whole body muscle mass)		Erupaka, 2007
Arm muscles	M: 46.63, F: 49.53
Trunk muscles	M: 37.73, F: 36.51
Leg muscles	M: 15.64, F: 13.96
Gaseous volumes (ml)
Lungs	2500.00
Rebreathing circuit	2500.00
Diffusivity of O2	0.00060	Secomb and Hsu, 1994; Li, et al., 1997; Whitely, et al, 2002
Diffusivity of CO	0.00045	Bruce and Bruce, 2003
Solubility of O2 (ml/ml/Torr)	3.00 × 10-5	Beard and Bassingthwaite, 2001
Solubility of CO (ml/ml/Torr)	2.37 × 10-5	Bruce and Bruce, 2003
Mb concentration (gm/ml)	0.0047	Bruce and Bruce, 2003
Net body CO production (ml/min)	0.007	Tobias, et al., 1945; Coburn, 1970

With the exceptions noted below, parameter values for the model were determined as discussed previously (Bruce and Bruce, 2003; Bruce and Bruce, 2006). As indicated in the table, many of the simulations utilized specific parameter values for subject #120 from the study of Benignus, et al., (1994), Smith et al., (1994) and Benignus (personal communication). Typical ventilation for this subject was 5500 ml/min, which (in the model) yielded a baseline arterial PO₂ ~100 Torr when breathing room air. When it is unknown, cardiac output for the model is calculated using a gender-specific regression on weight and height (Bruce and Bruce, 2003). Total muscle mass is also determined for each subject via a gender-specific regression on weight and height (Bruce and Bruce, 2003), with a correction for obesity (i. e., BMI > 30). The relative tissue volumes of the two muscle subcompartments were determined by optimizing the predicted compartmental PO₂s in normoxia and hypoxia, as discussed below.

Total MRO₂ of the muscle compartment is calculated as a sum of the MRO₂s of the arm, trunk, and leg muscles, based on measured resting MRO₂/gm of these muscle groups and the fraction of total muscle mass represented by each group (Erupaka, 2007). Total muscle MRO₂ is divided between the two subcompartments in proportion to their tissue volumes. Blood flow to the muscle compartment is calculated by summing blood flows to the three muscle groups (arms, trunk, legs), which are evaluated by multiplying resting blood flow per gm for each group by its mass (Erupaka, 2007). The volumes of the vascular subcompartments of the muscle and nonmuscle tissue compartments are calculated as 3.5 ml/100 ml of tissue (Raitakari, 1995). Because the sum of these 2 vascular volumes was less than the total blood volume, 75% of the difference was assigned to the mixed venous circulation and 25% to the arterial circulation.

The O₂ dissociation curve was modeled using a modified Hill equation and its parameters (P50 and N) were expressed as functions of HbCO, as previously described (Bruce and Bruce, 2003). P50 and N were re-evaluated every 0.01 min. The corresponding parameters for Mb are the same as in our earlier model (Bruce and Bruce, 2003).

The effective blood-to-tissue conductance for oxygen, DmO₂, depends on the permeability-surface area product (PS). There is controversy concerning the appropriate value for PS. Although PS has been measured for some tissues, its value depends on the tissue and on the model used to fit the experimental data. Beard and Bassingthwaite (2000) have derived a formula for PS based on first principles (their Equation 1) but it too depends heavily on assumptions about the size of capillaries and the “effective” tissue volume served by each capillary. Consequently we have used instead their derived relationship between flux in a 3-dimensional, partial differential equation model and in a simple compartmental model (See Appendix of Beard and Bassingthwaite, 2000). Thus, DmO₂ was calculated as DmO₂ = PS·S_O2 ·V_m/ρ, where SO₂ is the solubility of O₂, V_m is the volume of the tissue, and ρ is the density of the tissue. To determine a value for PS we compared model predictions with measured tissue PO₂ values. The best estimates of tissue PO₂ levels (see below) were obtained using PS = 37.5 ml/min/Torr/gm. Li, et al., (1997) estimated a value of PS for O₂ ~200 ml/min/Torr/gm for myocardium. Since capillary density of myocardium is ~8 times that of resting skeletal muscle, our chosen value seems reasonable. The resulting normalized conductance (i. e., DmO₂ per gm of tissue) equals 0.001082 ml/min/Torr/gm.

The effective blood-to-tissue conductance for CO, DmCO, was specified as a parameter of the model so that the effects of varying this parameter on the simulation results could be studied. Parameter values not discussed above are either given in Table 2 or were the same as in our previous model (Bruce and Bruce, 2003; Bruce and Bruce, 2006).

Numerical solution of the model equations

Simulations were performed in double precision using ACSL™ v. 11.8. Numerical integration was achieved using a Runge-Kutta-Fehlberg, variable-step size algorithm with error flagging; the maximum allowable step size was 0.01 min. Smaller step sizes were tested to ensure accuracy of the simulation. Our earlier model included O₂ partial pressures as fixed parameters, whereas the current model evaluates these partial pressures as a consequence of dynamic variations in O₂ mass balances. Consequently, to determine PO₂, CO₂, and O₂ flux in each blood compartment, it is necessary to satsify three simultaneous algebraic equations: the oxyhemoglobin dissociation curve (which is a function of HbCO), Haldane’s equation, and the blood-to-tissue flux equation for oxygen. These solutions were obtained using a gradient-based search algorithm. The computation most sensitive to step size was this iterative determination of PO₂ and HbO₂ in the presence of HbCO (with simultaneous accounting for dissolved gases). Convergence of the algorithm was accepted when successive iterations yielded solutions for PO₂ within 0.01 Torr.

Each simulation run was initiated with a baseline period of 12 minutes of breathing the gas which would serve as the background inhaled gas for the subsequent CO exposure. The baseline simulation reached a steady state in this period.

3. Results

3.1 Validation of blood and tissue PO₂s calculated by the model

The ability of the model to adequately represent PO₂ values in blood and muscle tissue compartments was evaluated initially in the absence of CO. Our approach was to compare experimentally measured PO₂ values with those predicted by the model under conditions in which arterial PO₂ of the model closely approximated the measured PaO₂, the latter achieved by adjusting ventilation if necessary. Methods for experimental measurement of tissue PO₂ values have significant limitations. When possible, we have emphasized more recent measurements using spectroscopic methods or micro-Clark electrodes which collectively seem to yield somewhat higher values than older measurements using larger Clark-type electrodes.

We identified numerous experimental studies (Table 3) which provided values for PaO₂ and some combination of muscle tissue PO₂, muscle capillary PO₂, muscle venous or mixed venous PO₂, and arteriolar PO₂, in normoxia or hypoxia. (PaO₂ ranged from 26.8 to 122 Torr). Most of these data are from studies on anesthetized animals; however, the available data from human subjects are reasonably consistent with the former, so we have combined the data sets. We simulated each study from Table 3, adjusting ventilation to achieve the reported steady-state PaO₂, and calculated predicted values for muscle tissue PO₂s in the two subcompartments, muscle capillary PO₂, muscle venous PO₂, and mixed venous PO₂. Most of the experimental studies reported either a histogram of tissue PO₂ values or the mean PO₂ and standard deviation. In order to compare these data with our 2-compartment tissue model, we determined the PO₂s corresponding to the reported mean tissue PO₂ plus and minus one standard deviation and compared these 2 values to our model calculations, assuming the higher PO₂ corresponded to muscle subcompartment 1. We also compared our simulation results to those of Secomb and Hsu (1994), who calculated tissue PO₂ values in a finite-element model of muscle tissue.

Table 3.

Experimental data of muscle tissue and vascular PO₂ values.

Source	Preparation	PaO2	PmxO2	PO2 venule	PcapO2	Ptm2O2	Ptm1O2	PO2 arteriole
Guiterrez, et al., 1989	rabbit bic. femor. M.	90.3	48.3		42.8	36.8272	51.736
		69.6	36		26.8	22.0218	33.949
		52.1	29.2		19.1	16.7109	22.674
		38.4	28.8		14.3	11.3989	18.64
		30.5	19.3		5.7	2.45763	10.551
		26.8	15.6		4	2.12284	6.8085
Stein, et al., 1993	hamster retractor m.	73.4	35.8	32.9	24
		62.4	33.4	25.9	22.9
		28.4	19.5	15.9	17.4
Shonat and Johnson, 1997	rat spintrap. m.	91		26	21			33
Zheng, et al., 1996	hamster retractor m.	[30]		10.5	14.1			17.1
Torres Filho, et al., 1996	hamster skinfold	71	27.8	30.8	29	20.859	30.197	35-41
Secomb and Hsu, 1994	model	95*				36	36	50*
Richardson, et al., 2006	human	103				21.762	52.31
		46				10.762	41.31
Marshall and Davies, 1999	rat	80.2	44.8
		40.8	27.7
		32.5	22.6
Shibata, et al., 2006	rat	98				24.485	35.755	46
Wilson, et al., 2006	rat, awake thigh					31.125	55.275	25-52
Sutton, et al., 1988	human	99.3	35.1
		41.1	27
		36.6	24.8
Lund, et al., 1980	human	98.25				12.7095	18.989
		273				11.175	35.325
		429.75				16.4951	40.283
Boekstegers and Weiss, 1990	human	98				28.9785	39.766
Harrison, et al., 1990	dog	122				35.9825	54.498
		30.3	22.1
Kunert, et al., 1996	rat	66				28
		77				35
Behnke, et al., 2003	rat	93				27.45
Richmond, et al., 1999	rat			17.7		14.6
						15
						22.7
Johnson, et al., 2005	rat	98.1		35.1		26.8		52.2
		31.7		11.4		9.6		15.8

^*assumed value

Model predictions were optimized by varying the relative volumes of the two muscle subcompartments, the value of PS for each subcompartment, and the equivalent intercapillary distance for determining diffusive flux between subcompartments. The volume distribution between the two subcompartments significantly influenced tissue PO₂s; based on anatomical renderings of vascularization in muscle (Pittman, 2005; Segal, 2005), we assigned 60% of the muscle volume to subcompartment 2. PS also had a significant effect, and we chose the smallest value that yielded values compatible with the data in hypoxia because any PS value that is satisfactory for hypoxia is also satisfactory for normoxia, but not the converse.

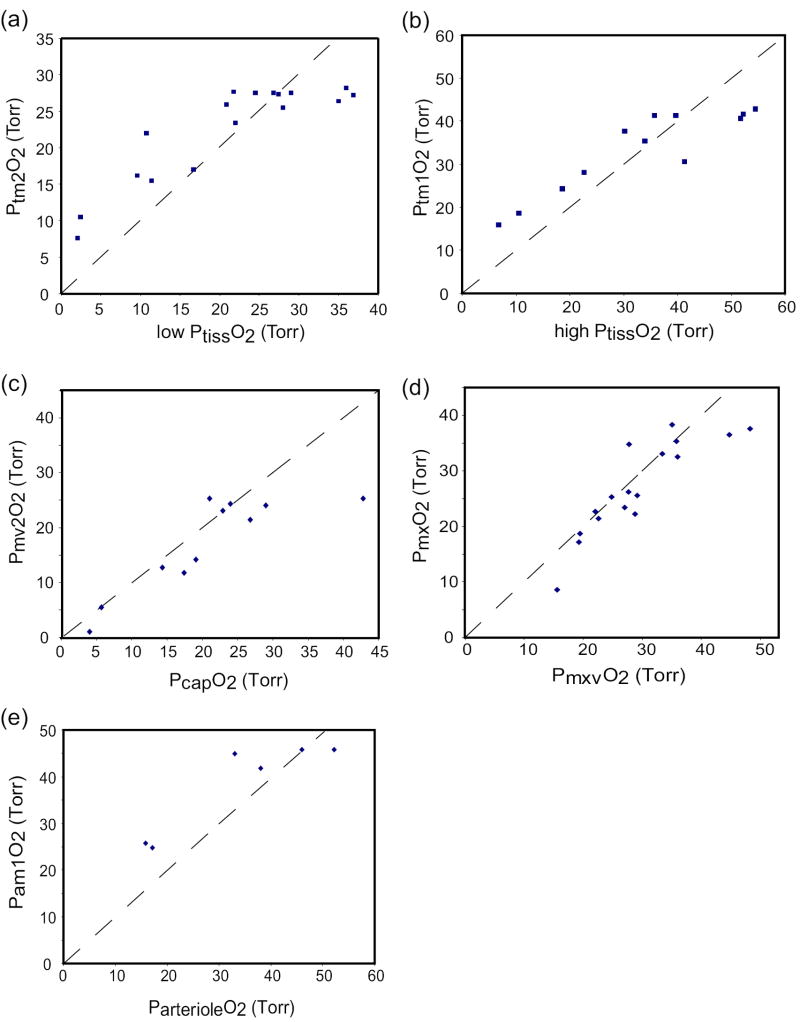
Figure 3 (a-e) compares model predictions to the experimental data for parameter values that qualitatively yielded the best fit to the data - i. e., 60% of muscle volume assigned to subcompartment 2, PS = 0.001082 ml/min/Torr/gm in both subcompartments, intercapillary distance of 0.1 mm. For both tissue subcompartments, the model predictions were reasonably centered within the cluster of data from normoxia but, in both cases, the model overestimated the tissue PO₂s during hypoxia (Figure 3a,b). On the other hand, the simulations were based on estimates of resting O₂ consumption (per unit weight), and even small increases in MRO₂ can reduce tissue PO₂s by several Torr.

Figure 3.

Comparison of model predictions of O₂ partial pressures with experimental data from Table 3. In each case, ventilation and FIO₂ in the model were adjusted to cause PaO₂ to match the experimentally measured PaO₂ when the model was run to a steady state. (a) predicted PO₂ in muscle subcompartment 2 (Ptm2O₂) vs. the “low” tissue PO₂ (determined as mean measured PO₂ minus one standard deviation); (b) predicted PO₂ in muscle subcompartment 1 (Ptm1O₂) vs. the “high” tissue PO₂ (determined as mean measured PO₂ plus one standard deviation); (c) predicted PO₂ in muscle vascular subcompartment 2 (Pmv2O₂) vs. measured capillary PO₂; (d) predicted mixed venous PO₂ (PmxO₂) vs. measured mixed venous PO₂ (PmxvO₂); (e) predicted mean PO₂ in muscle vascular subcompartment 1 (Pam1O₂) vs. measured PO₂ in arterioles. Dashed lines are lines of identity.

Several studies have reported data on tissue capillary PO₂ obtained using micro-O₂ electrodes, and the model predictions of capillary PO₂ agree well with these data (Figure 3c). Similarly, model predictions of mixed venous PO₂ match well with experimental measurements (Figure 3d). Finally, we compared the mean PO₂ in the vascular compartment of muscle subcompartment 1 to microelectrode measurements of arteriolar PO₂. Although the data are scarce, there is reasonable agreement (Figure 3e).

We conclude that the model produces physiologically reasonable estimates of microvascular and tissue PO₂ levels under normoxia and hypoxia, although tissue PO₂s might be somewhat overestimated. Importantly, the model represents the effects of a-v shunting of oxygen flux and of O₂ diffusion within the tissue. (Blocking either of these mechanisms produces changes in predicted PO₂s in normoxia.) In the 3-dimensional muscle tissue model of Secomb and Hsu (1994), diffusive efflux of oxygen from arterioles equals 86% of muscle metabolic O₂ consumption; in our model oxygen diffusion out of blood subcompartment 1 is 86.7% of muscle O₂ consumption. In the former model excess O₂ is delivered to distant tissue (and, by implication, to venules) via both diffusion and re-uptake by capillaries; in our model this delivery occurs via within-tissue diffusion (in parallel with capillaries) with some of the excess O₂ flux flowing into venules.

Other tests of the model were conducted. Kunert et al. (1996) reported that infusion of 200 mg/kg of 100 mM RSR-13 increased P50 of rat blood from 37 to 51 Torr and reduced %HbO₂ from 88 to 70. Changing P50 in the model from 25.0 to 37.4 also reduced %HbO₂, from 90 to 77.4. Findley et al. (1983) observed that a 30-sec apnea at FRC caused %HbO₂ to fall from ~97 to ~91.5 in sitting or supine humans. The model predicts a similar response -- %HbO₂ decreases from 96.5 to 92 during a 30-sec apnea. Similarly, one can compare the decreases in arterial and mixed venous %HbO₂ reported by Fletcher et al. (1989) in a male subject during an obstructive apnea of one minute duration. When ventilation and cardiac output of the model were adjusted to match the pre-apnea arterial %HbO₂ of this subject, the model closely predicts the 30% fall in arterial %HbO₂ during the apnea and the 17% fall in mixed venous %HbO₂. A further test of transient behavior is the response to suddenly switching FIO₂ to a value below normal. The model response to changing FIO₂ from 0.208 to 0.09 (with constant ventilation) is shown in Figure 4. Compared to the ventilated dog (Reinhart,et al., 1989), the predicted response of mixed venous %HbO₂ is about half as rapid. Similar open-loop data from the human are difficult to find, but the half-time of the predicted response is compatible with closed-loop responses of humans to hypoxia (acknowledging that the latter are complicated by an overshoot in ventilation). Note also that even though PO₂ levels in rat cremaster muscle respond much more rapidly to a similar stimulus (Johnson et al., 2005), the relative responses are qualitatively the same, especially the decrease of muscle venous PO₂ so that it approximately equals the tissue PO₂ near capillaries.

Figure 4.

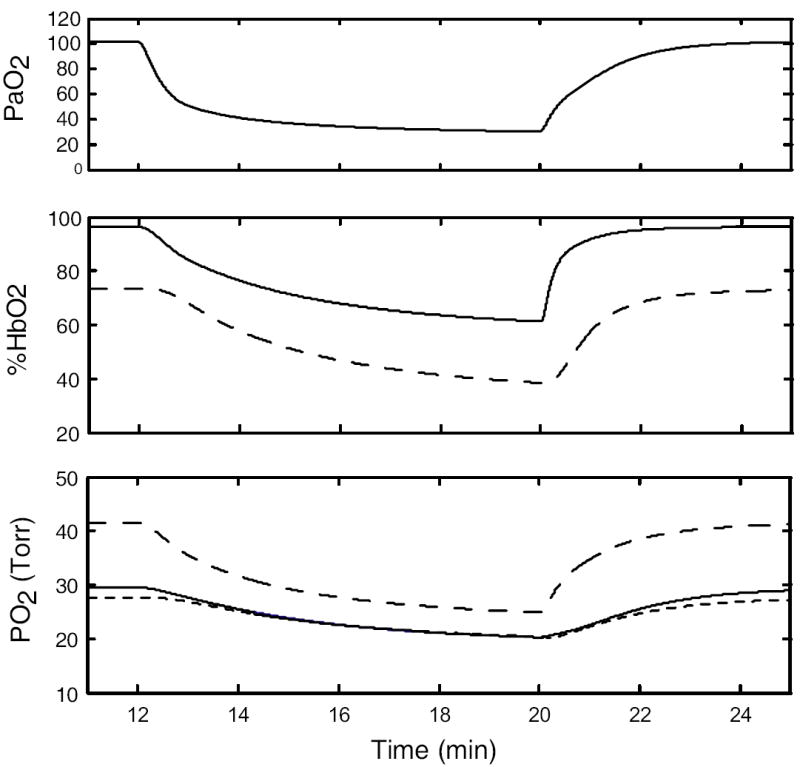
Model responses to sudden lowering of FIO₂ from 0.208 to 0.09 (at t = 12 min). Top: arterial PO₂. Middle: arterial (solid) and mixed venous (dashed) %HbO₂. Bottom: PO₂ in muscle subcompartments 1 (long dash) and 2 (short dash) and in muscle venous blood (solid).

3.2 Validation of CO mass balance calculations

In addition to comparing experimentally measured and calculated HbCO values (see Results), a further check was obtained by calculating, by 2 different approaches, the total CO content of blood compartments and of tissue compartments every 0.01 min and comparing the 2 calculations. Thus, CO content was evaluated both by integrating the fluxes between compartments and by multiplying concentrations by volumes of compartments. During simulated transient CO exposures followed by washout, the two methods agreed within ~1.5% at every point in time. In addition, the total body burden of CO was calculated by integrating the lung to blood flux of CO and comparing this result to the sum of total blood and tissue CO levels. Again the two calculations agreed to within ~1.5% at all simulation times. The former result is a check for errors in implementing the mass balance equations, as well as a check for errors due to the integration step size, whereas the latter is sensitive to errors in accounting for bound and dissolved CO in blood which might occur due to the iterative solution of the oxygen dissociation equation in the presence of CO.

3.3 Re-evaluation of our previous simulation results

Simulation of 5-min CO exposure

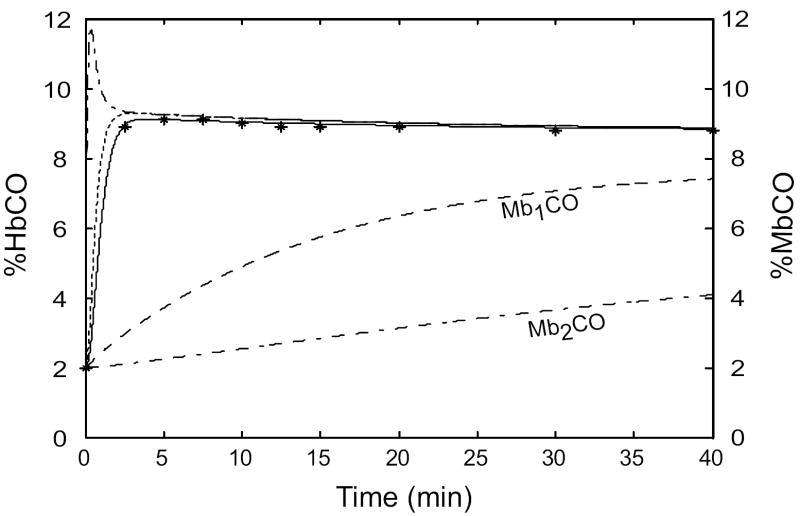
To assess the ability of the improved model to reproduce experimental data from transient CO exposures, we fit it to data from the studies of Benignus, et al. (1994). The authors have previously supplied us with subject-specific parameter values (Bruce and Bruce, 2003; Bruce and Bruce, 2006). The Benignus study involved brief exposures to 6683 ppm CO during room air breathing, followed by washout on air for ~4.3 hours. Previously we adjusted values for blood volume in muscle, and for blood flow to muscle, to obtain a good fit to the a-v difference of HbCO for each subject, whereas the current model replaces these ad hoc values with physiologically-based estimates. The fit of the current model to these data (Figure 5) was similar to that published previously (Bruce and Bruce, 2006). This experimental design is not very sensitive to the value of DmCO except in the time range of 5-15 min. The data could be fit using DmCO in the range 1.5 - 15.0 (albeit with changes to other parameters such as ventilation). For DmCO > 25, the simulation could not reproduce the decline in %HbCO from 5-15 min and the predicted a-v difference of %HbCO before 5 min was too small. Thus, the improved model fits these data similarly to the earlier model but the experimental data do not allow us to specify an optimal value for DmCO.

Figure 5.

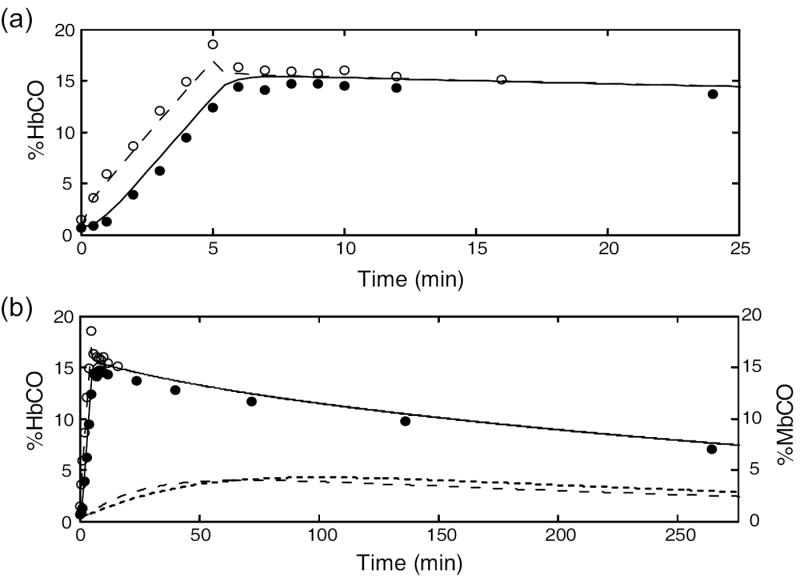
Simulation of the 5-min CO exposure and subsequent washout from the study of Benignus, et al. (1994) (subject #120). The simulation results and experimental data are shown on two different time scales. Filled circles: measured %HbCO, decubitus vein. Open circles: measured arterial %HbCO. Outputs from model: muscle venous %HbCO (solid line); arterial %HbCO (long dashes); %MbCO in subcompartment 1 (short dashes); %MbCO in subcompartment 2 (dotted line). DmCO = 7.0.

Simulation of hyperoxic rebreathing

Burge and Skinner (1995) measured HbCO in 3 human subjects during 40 min of hyperoxic rebreathing after injecting 60-70 ml of CO into the rebreathing circuit. When we simulated these studies with the enhanced model, the predicted HbCO levels depended on the value used for total blood volume. Because the authors calculated total blood volume based on CO uptake after 10 min of rebreathing, and because these calculations assumed that whole-body average hematocrit equals that in a peripheral vein, their calculated blood volumes most likely underestimate true blood volumes by as much as 10%. The results using data from their subject #2 (Figure 6) illustrates the fit of the improved model. Using the reported blood volume value (66.24 ml/kg), the HbCO data points are best fitted visually when DmCO = 4.5 ml/min/Torr. For smaller values of DmCO, HbCO did not fall enough from its early peak to match the data. For larger values of DmCO, HbCO fell quickly from its early peak but then changed too little during the last 30 min of rebreathing, often overshooting the final data point. As blood volume is increased, DmCO for the best fit decreases - e. g., when blood volume is 68.89 ml/kg (i. e., 4% larger), the best fit occurs when DmCO = 3.75. Furthermore, the fit is sensitive to the value of DmCO. For all three subjects, the best fits to the data depended on the value assumed for blood volume (between 100 - 110% of the reported value) but were always in the range for DmCO of 2.5 - 5.0.

Figure 6.

Simulation of the hyperoxic rebreathing study of Burge and Skinner (1995) (subject #2). * measured venous %HbCO. Outputs from model: muscle venous %HbCO (solid line); arterial %HbCO (dash-dot line); mixed venous %HbCO (dotted line); %MbCO in subcompartment 1 (long dashes); %MbCO in subcompartment 2 (dash-dash-dot line). DmCO = 2.5. Total blood volume is 4% larger than the value reported by Burge and Skinner. (See text.)

3.4 Comparisons to other experimental studies

Roughton and Root (1946) exposed human subjects briefly (~4 min) to a high inspired CO level, then collected expired gases during the ensuing washout of CO from the body. They compared the change in amount of CO in the blood during a given time period (calculated as the change in HbCO multiplied by total blood volume) with the amount collected from the expired air, and found that the former was greater than the latter. We simulated these experiments using parameters for subject 120 of Benignus, et al. (1994). It was, however, necessary to estimate values for ventilation and the inspired CO level. A ventilation of 5500 ml/min yielded PaO₂ ~100 Torr on room air, whereas an inspired CO level of 6000 ppm yielded a peak %HbCO ~9% (i. e., within the reported range of 5-10%). We first simulated their experimental study conducted on a background of room air, in which expired CO was collected over the period 10-40 min post-exposure. Figure 7(a) shows the simulation results for various values of DmCO. The predicted ratio of the amount of CO expired to the net change in amount of CO in blood reproduces the data (0.72-0.78) for DmCO in the range 2.5-8.0. The data from the model in Figure 7(b) explain this finding. For DmCO below 2.5, there is little movement of CO from blood to muscle, so the ratio is close to one. For DmCO > 8.0, the muscle tissue takes up CO during exposure and loses some of it back to the blood during 10-40 min post-exposure. At very high DmCO (i. e., > 35), there is more CO expired than the net change in the blood because there is rapid uptake by tissues followed by flux of CO from tissues back into blood.

Figure 7.

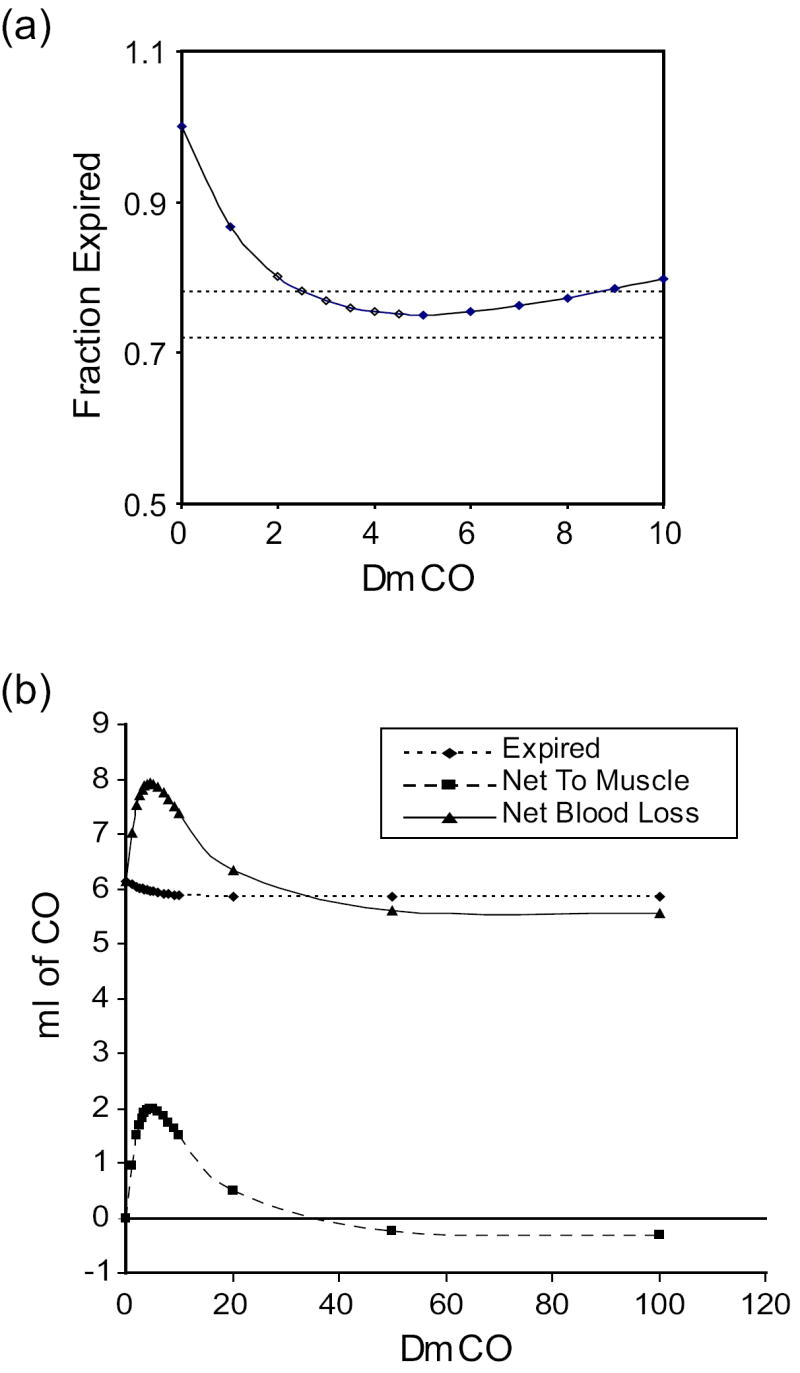
Simulation of the study of Roughton and Root (1946) in which the change in amount of CO in the blood from 10 to 40 min after a short, high-level CO exposure was compared to the amount of CO exhaled during this time. Parameters for subject #120 of the Benignus, et al., (1994) study were used for the simulation. (a) Amount of CO expired as a fraction of the amount lost from blood for various values of DmCO. Dotted lines mark the values reported for the 2 subjects who were studied (Roughton and Root, 1946). (b) Comparison of the net amount of CO lost from blood (solid line) with the amount expired (dotted line) and the net change in amount of CO in muscle tissues (dashed line). Note that for DmCO > ~ 35, more CO is expired than the net loss from the blood.

We also simulated the reported study in hyperoxia in which CO collection ensued for 4 hours post-exposure. The authors found an average ratio of CO expired to net change in blood of 0.956, whereas the simulation yielded a ratio of 1.00 for DmCO = 3.0. Finally, the authors also reported data based on measurements in hyperoxia taken for 15 minutes, starting 15 minutes after hyperoxic CO exposure ended. Although the average ratio reported for 3 experiments was 0.60, the lowest value determined through simulations was 0.85 at DmCO = 3.0.

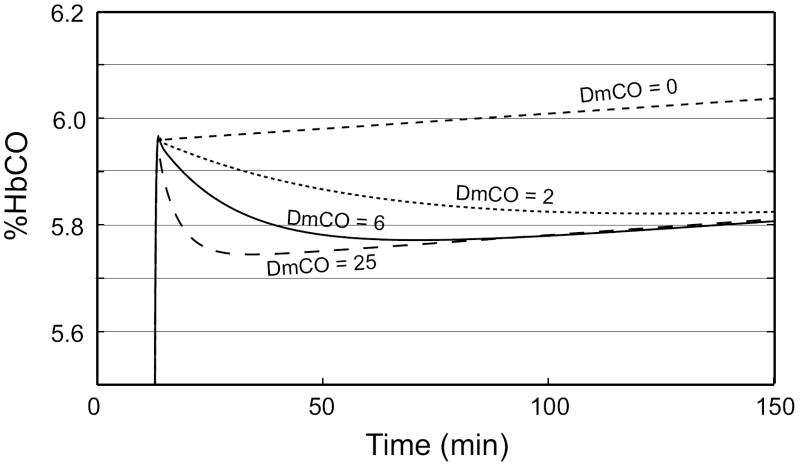
Several experimental studies of the uptake and distribution of CO have measured the rate of loss of CO from blood while the subject rebreathes from a closed circuit for 2 hrs or longer (Luomanmaki and Coburn, 1969; Coburn and Mayers, 1971). To aid in interpreting these studies, we did simulations to determine the effects of DmCO on the change of %HbCO during such an extended period of rebreathing. Figure 8(a) shows the simulation results for four values of DmCO when the subject rebreathes from a bag initially containing air plus CO (starting at t = 12 min), with continuous replacement of oxygen lost from the circuit (see, for example, Luomanmaki and Coburn, 1969). When DmCO = 0, there is no loss of CO from blood and %HbCO increases linearly with time, reflecting the net rate of addition of CO due to production of CO, primarily from degradation of heme, less metabolism of CO to CO₂. For intermediate values (DmCO = 2 or 6), loss of CO to tissues predominates for several tens of minutes, causing a progressive decrease in %HbCO; eventually, however, blood-tissue equilibration is achieved and thereafter the net production of CO causes %HbCO to rise slowly, as observed here for DmCO = 6. When DmCO = 25, blood-tissue equilibration occurs rapidly and thereafter %HbCO rises with time at nearly the same rate as it does when DmCO = 0. Consequently, the dependence on DmCO of the net change in %HbCO during the last 2 hrs of the simulation period is complex. For very low values of DmCO near zero, the net change is positive, but it becomes negative when DmCO increases (e. g., DmCO = 2). For DmCO = 6, the net change is still negative, but it becomes positive again when DmCO is large enough that blood-tissue equilibration is achieved within ~15 min (e. g., DmCO = 25). The exact quantitative relationship to DmCO will depend on the specific time interval over which the %HbCO measurement is made.

Figure 8.

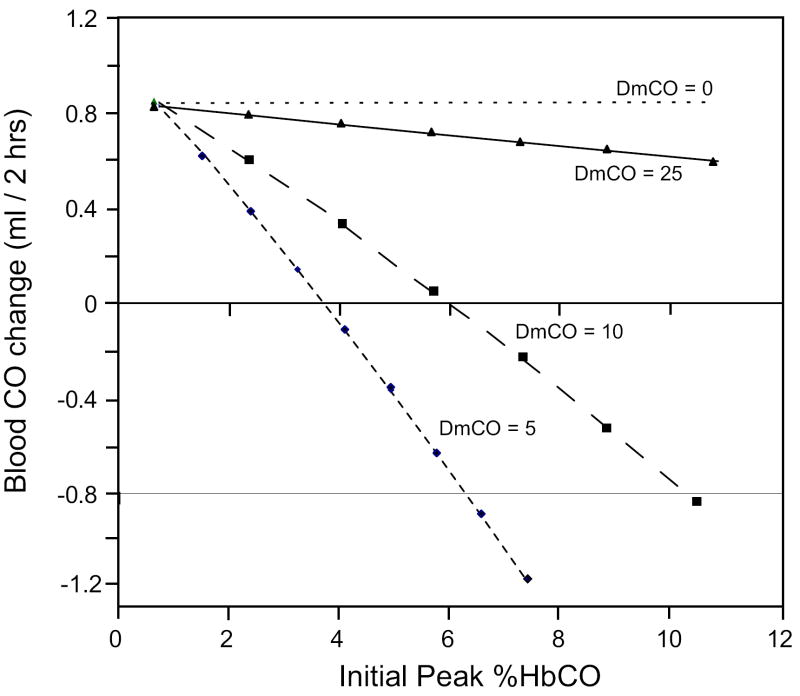
(a) Predicted time course of muscle venous %HbCO during a 2-1/2 hr rebreathing experiment in which the O₂ lost from the rebreathing circuit to metabolism is exactly replaced by an inflowing O₂ gas stream and CO₂ is scrubbed. Rebreathing from a 2.5 L. bag initially containing air and ~60 ml of CO begins at t = 12 min. The net change in %HbCO over the final 2 hr of rebreathing is dependent on the value of DmCO. (b) The net change in the total amount of CO in all vascular compartments during the final 2 hr of rebreathing as a function of the height of the initial peak of %HbCO. Solid line: DmCO = 25; long dashes: DmCO = 10; short dashes: DmCO = 5; dotted line: DmCO = 0.

A further complication to understanding experimental studies of this sort is that the net change of %HbCO also depends on its absolute level. Figure 8(b) graphs the change in the total amount of CO in all vascular compartments from 15 to 135 min after the start of rebreathing (on a background of air) as a function of the initial peak value of %HbCO for 4 different DmCO values. At any fixed %HbCO, the dependence on DmCO reflects the behavior discussed above (although for low %HbCO the net change of CO never becomes negative). Furthermore, for any constant value of DmCO, the net change varies nearly linearly with the peak %HbCO. For any combination of peak %HbCO and DmCO, the net change of CO in blood in 2 hrs represents a balance between CO lost due to blood-tissue equilibration and CO gained due to net production. These simulation results clearly demonstrate the difficulty of interpreting experimental data regarding the net change of CO in blood during extended rebreathing periods. In particular, any conclusions about the rate of blood-tissue equilibration must be qualified by the degree to which the %HbCO was shown to be similar in different studies, as well as the degree to which the measurements were made over the same time intervals. To our knowledge, these issues were not considered by previous investigators.

Another strategy to address the distibution of CO between blood and tissues is to determine the effects of hyperoxia and hypoxia on the concentration of previously administered C¹⁴O in the blood. It has been observed in anesthetized dogs connected to a rebreathing circuit that a change from arterial hyperoxia to moderate arterial hypoxia was not associated with any change in blood C¹⁴O content; in contrast, after a transition from moderate to severe hypoxia, blood C¹⁴O content decreased by an average of ~20% over a period of 30-60 min (Coburn and Mayers, 1965; Luomanmaki and Coburn, 1969). The former response can be explained by the observations that venous PO₂ (and, likely, tissue PO₂) and arterial %HbCO changed only slightly. Muscle blood flow also would increase only slightly, if at all, with moderate hypoxia. Furthermore, because of the reduced competition from oxygen, Hb would take up more CO and reduce PaCO. Thus, there is no mechanism to drive significant amounts of CO from blood into the tissues in moderate hypoxia (and one might expect a small shift in the opposite direction).

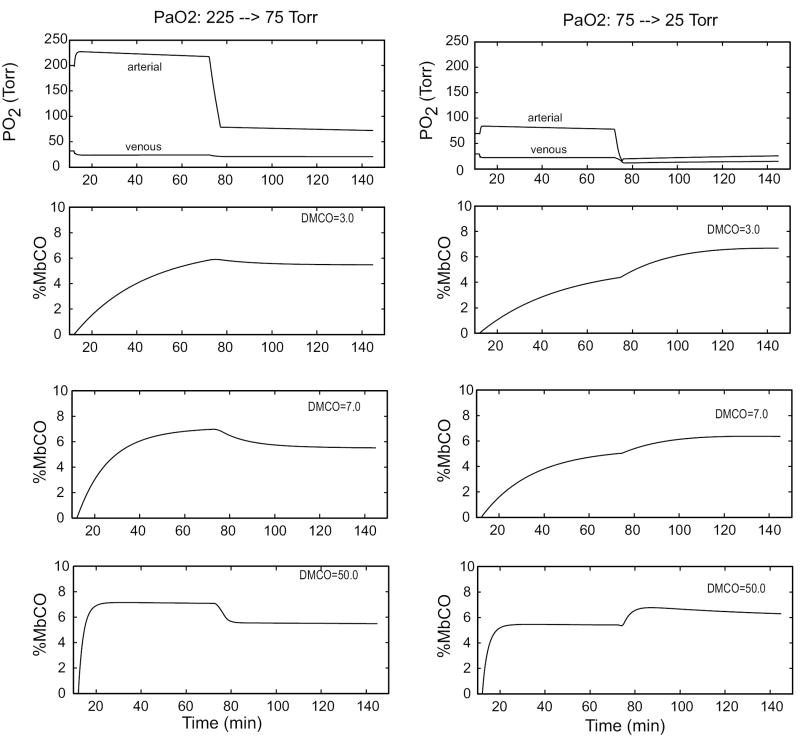
The shift of CO into tissues during severe hypoxia is predicted by the model if two reasonable assumptions are incorporated: (i) muscle blood flow increases in severe hypoxia (Chalmers et al., 1966; Hepple et al., 2000); (ii) the increase in muscle blood flow is partly due to capillary recruitment, and therefore PS (and the effective DmCO and DmO₂) also increases (Caldwell et al., 1994). Figure 9 presents results from simulation studies in which a human subject was connected at t = 12 min to a rebreathing circuit initially containing 200 ml of CO in 2.5 L. A slow inflow of O₂ to the circuit replaced oxygen lost to metabolism. After one hour, the oxygen supply to the circuit was interrupted for 3 - 4 min until the desired PaO₂ was achieved, and then rebreathing with replacement of metabolically consumed O₂ continued for another hour. In the figure, the response of muscle %MbCO is shown for 3 values of DmCO. Note that the transition from hyperoxia to mild hypoxia causes a slight shift of CO out of muscle tissue, whereas a transition from mild to severe hypoxia causes a large shift of CO into muscle. These qualitative effects are independent of the value of DmCO; however, the model predictions are most consistent with published data (i. e., no measurable change for the hyperoxic to mild hypoxia transition and a large shift out of blood for the mild to severe hypoxia transition) for DmCO in the range 3.0 - 7.0.

Figure 9.

Predicted responses of MbCO when PaO₂ is sudenly decreased from 225 to 75 Torr (left panels) or from 75 to 25 Torr (right panels) for 3 values of DmCO. In these simulations the subject rebreathes as in Figure 7(a) and, at t = 72 min, the O₂ inflow is stopped until PaO₂ falls to the desired level. The change from hyperoxia to mild hypoxia (left) results in an insignificant or small decrease in CO content of muscles (%MbCO = average of %MbCO of the two muscle subcompartments), whereas the change from to severe mild hypoxia (right) causes a significant shift of CO into muscle.

In another experimental study, when CO was added at a constant rate to the rebreathing system for ~4 hours, %HbCO of an anesthetized dog increased “linearly” until it exceeded ~50% (Luomanmaki and Coburn, 1969). This result was interpreted as indicating rapid equilibration of CO between blood and tissues. Our simulation of this experiment (Figure 10) demonstrates that %HbCO responds similarly for all values of DmCO between 2 and 100, and that the small differences in the responses are unlikely to be resolvable from noisy experimental data. Therefore, the published experimental findings are inconclusive with respect to the speed of equilibration of CO between blood and tissues.

Figure 10.

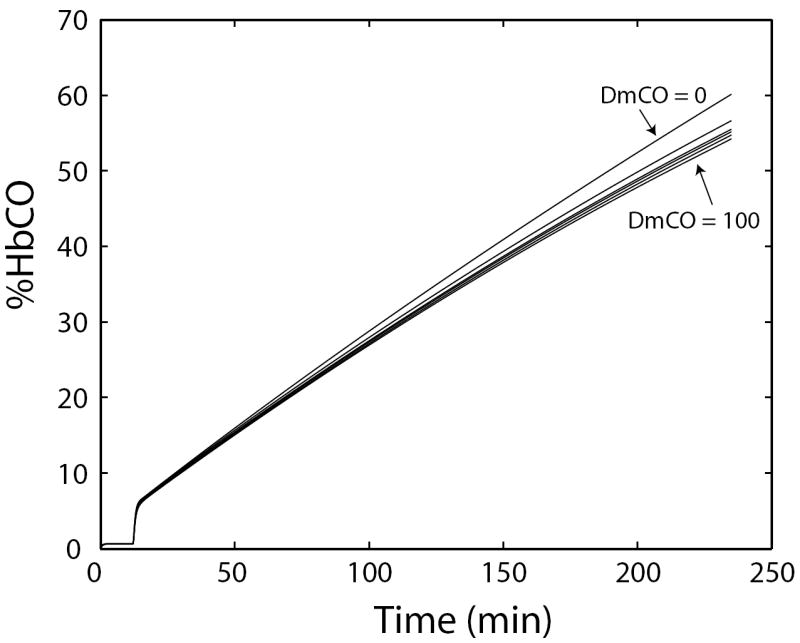
Simulation of a rebreathing experiment in which CO is added to the rebreathing circuit at a constant rate. Venous %HbCO increases nearly linearly with time for any DmCO between 0 and 100. (Larger values were not tested.) The simulation results imply that the experimental outcome would be essentially insensitive to the value of DmCO.

3.5 Predictions of carboxymyoglobin levels during CO exposure and hyperoxic therapy

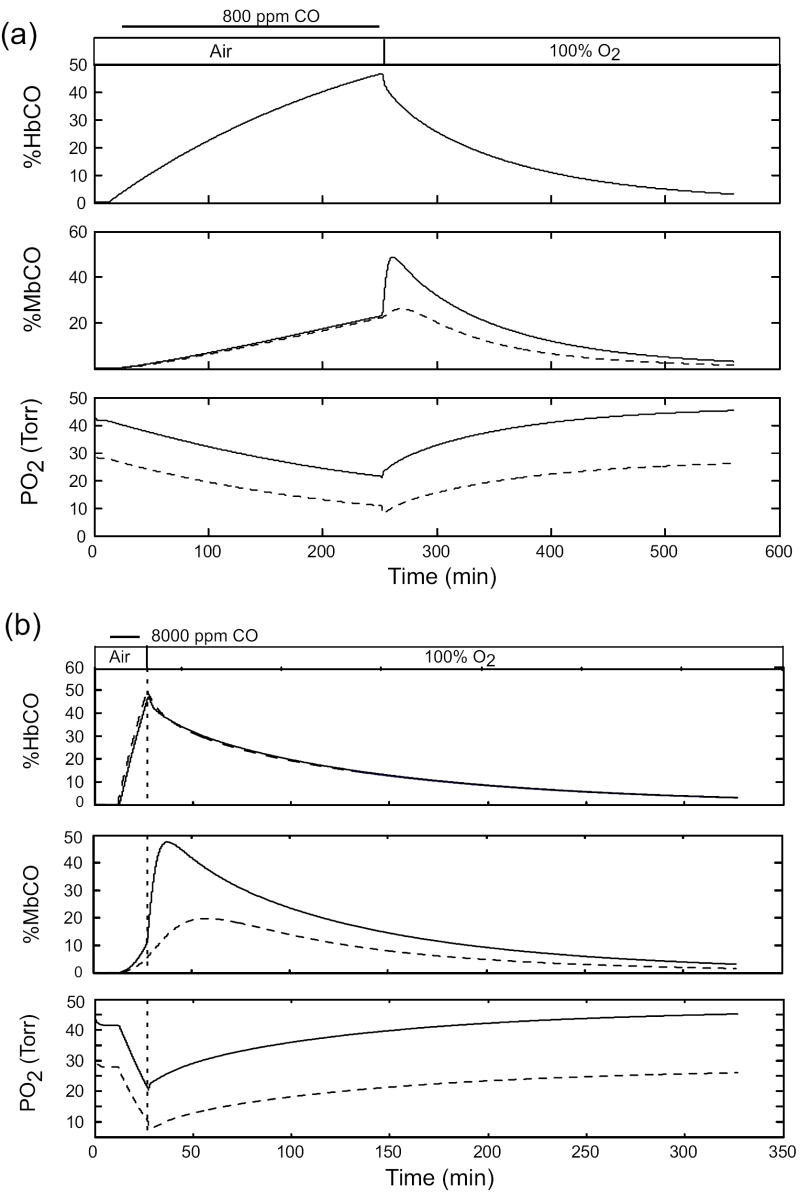
Our previous simulation studies (Bruce and Bruce, 2006) predicted that MbCO levels would increase progressively during CO exposure on a background of air breathing and continue to increase, at an even faster rate, during the initial part of hyperoxic therapy. This response during therapy was most significant following short exposures to high CO levels (Bruce and Bruce, 2006). This behavior occurs because arterial PCO continues to be greater than muscle PCO early in hyperoxic therapy, and this pressure difference drives CO from blood into muscle tissues. When %HbCO is sufficiently reduced to reverse this pressure gradient, then CO flows out of the muscle tissues. We determined whether this behavior would be predicted by the new model, using a value for DmCO (i. e., 7.0) that is consistent with the results discussed above. Figure 11 presents simulation results for exposure to 800 ppm CO for 4 hours (Figure 11(a)) and exposure to 8000 ppm CO for 15 min (Figure 11(b)). The initial rise of %MbCO during washout on 100% O₂ is also predicted by the new model, which demonstrates that %MbCO increases much more in muscle subcompartment 1 than in subcompartment 2. Apparently the nonlinearity of the content vs. pressure relationship for CO of blood (primarily the O₂ dissociation curve) results in a smaller increase of vascular PCO in subcompartment 2 than in subcompartment 1. Also, despite the increases in %MbCO, the tissue PO₂’s increase progressively during hyperoxic therapy.

Figure 11.

Predicted MbCO and PO₂ levels in muscle tissues during long and short CO exposures on air which cause peak %HbCO to be ~40-50%, followed by washout on 100% O₂. Exposure to 600 ppm CO for 4 hrs. (b) Exposure to 8000 ppm CO for 15 min. For both the %MbCO graphs and the PO₂ graphs, solid curves represent subcompartment 1 and dashed curves represent subcompartment 2.

4. Discussion

Our objective in this simulation study was to integrate a large body of indirect experimental findings on the uptake and distribution of CO in (primarily) human subjects by developing a mathematical model that is consistent with, and therefore could concisely represent, these findings. Our approach assumes that this quantitative, integrative, model provides a sounder basis for inferences about the partitioning of CO between vascular and extravascular (tissue) compartments than has been achieved previously on the basis of qualitative analyses of these studies. A modeling approach is advantageous because it is currently impossible to measure directly the CO content of muscle tissues noninvasively in human subjects. Starting with our earlier model of whole-body CO uptake and distribution (Bruce and Bruce, 2003; Bruce and Bruce, 2006), we enhanced this model by adding mass balance equations for oxygen and by separating the muscle compartment into two subcompartments. Thus, in the improved model not only are the time-varying effects of PO₂ on CO stores and fluxes explicitly calculated by the model, but also the mechanistic basis of CO (and O₂) fluxes in the muscle compartment is arguably more physiologically appropriate than in other models of whole-body CO uptake and distribution. The enhanced model was validated against a large body of literature (Table 3) on tissue PO₂ levels in normoxia, mild hyperoxia, and hypoxia. The model also was shown to reproduce well the studies of transient CO exposure and washout, and of hyperoxic rebreathing of CO, that were used to validate our original model.

Subsequently we used the enhanced model to simulate several additional experimental studies of (i) vascular uptake and loss of CO during rebreathing, (ii) short and long-term CO exposure and washout, (iii) transient severe hypoxia, and (iv) continuous administration of CO during rebreathing. These experimental studies comprise the core observations upon which the qualitative conclusion has been drawn that CO equilibrates rapidly between blood and tissue compartments. In each case we examined the effect of varying the blood-tissue conductance for CO, DmCO, on the predicted response and found that DmCO values in the range 3 - 8 ml/min/Torr yielded the most consistent fits to the body of experimental data. For these values the uptake of CO by muscle tissues is much slower than the distribution and mixing of CO in the vascular system, which occurs within 6 - 30 min, depending on the experimental protocol (Luomanmaki and Coburn, 1969; Prommer and Schmidt, 2007). Thus, we conclude that the equilibration of CO between vascular and extravascular tissues during CO exposure, as well as the removal of extravascular CO during therapy, occurs over a much longer time scale than do the major changes in vascular CO content as represented by %HbCO. These results have implications for designing therapies for victims of CO poisoning.

4.1 Limitations of the model

Our model represents physiological details at a level appropriate for analyzing whole-body uptake and distribution of CO. Thus, it does not include details of cellular metabolism or Mb diffusion. It combines many tissue beds into each compartment and assumes a degree of uniformity that is not physiologically realistic. This approach is justifiable, however, because the available experimental data include measurements of vascular CO levels and not tissue CO levels. We recognize that model predictions of CO contents of tissue compartments are idealized estimates of “average” values across many tissue beds, for which validation is technically difficult at the current time. On the other hand, our objective is to predict the quantity of CO that leaves the blood per minute and enters extravascular spaces. Mb concentration and muscle tissue volume can be measured experimentally, and to the extent that the values used in the model are physiologically appropriate, the predicted MbCO level should be a reasonable estimate of the average MbCO in muscle tissue. For each individual muscle, its MbCO may vary from this average value due to differences in blood flow, capillary density (and therefore PS), Mb concentration, and oxygen consumption. For example, it is likely that MbCO and tissue PO₂ levels may differ substantially between muscles containing mainly fast glycolytic or slow oxidative fibers. In contrast, predicted tissue oxygen levels were validated against actual experimental measurements of tissue PO₂ levels. In this case also model predictions are “averages” across multiple muscle tissue beds and the factors that cause MbCO to vary would cause MbO₂, and PtO₂, to vary; however, we would argue that the predicted PO₂ values probably represent at least the central part of the range of PO₂s found in many muscle tissues.

An important question is whether a compartmental modeling approach is appropriate for the issues we have addressed. Many researchers have recognized the limitations of compartmental models, but these models comprise the predominant approach to predicting whole-body uptake and distribution of respiratory gases, usually in relation to ventilatory control mechanisms. Investigators studying gas exchange in microscopic tissue samples (e. g., Beard and Bassingthwaighte, 2000; Beard and Bassingthwaighte, 2001; Secomb and Hsu, 1994) apply finite element methods; however, it is unclear how to extrapolate these microscopic anatomies to a whole muscle. Furthermore, these approaches often do not account for the fall in PO₂ between arteries and small arterioles. An intermediate approach (Ye, et al., 1993; Sharan, et al., 1998) separates the vascular system into several serial, lumped, subcompartments (similar to our approach). Recently Zhou, et al. (2007), extended this approach by representing the vascular pathway using 21 subcompartments having a 2-dimensional spatial distribution. In these latter cases, however, the investigators assumed that a single, well-mixed, tissue compartment communicated with all (or a subset) of the vascular compartments. Although these approaches can represent arteriolar-venular shunting of gases and excess flux of oxygen from the arteriolar end of the vascular system, they cannot account for within-tissue diffusion of gases,.

We separated the tissue compartment into 2 subcompartments, each of which communicates with a subset of the vascular subcompartments. By doing so, we can represent physiological phenomena that may be important in determining O₂ (and CO) exchange between the vascular system and tissues (from a whole-body perspective) but that have typically not been represented in whole-body models of respiratory gas uptake and distribution. In this regard, the model closely predicts a variety of steady-state PO₂ data as well as changes in arterial and mixed venous Hb saturation during apneas, and also the predicted responses to sudden lowering of FIO₂ are reasonable. Therefore, from the perspective of whole-body fluxes of respiratory gases, we believe that the model represents these fluxes quantitatively. One would need to be more circumspect in interpreting predicted changes in within-tissue mechanisms, such as the amount of oxygen flux between the tissue subcompartments, because our model greatly simplifies within-tissue spatial variability.

We subdivided the muscle compartment into 2 subcompartments in part because of concerns that blood-to-tissue CO flux might be underestimated if extravascular, longitudinal diffusion of CO within the tissue were ignored. Beard and Bassingthwaite (2000) showed that the blood-tissue diffusion coefficient (our “conductance”) of a highly diffusible substance was underestimated when a 2-dimensional Krogh cylinder model was fit to vascular concentration data from a 3-dimensional tissue model having complex vascularity. This result occurred because diffusion within the 3-dimensional tissue raised the tissue level of the substance near the distal end of the vascular bed. This error from the 2-dimensional model could be avoided by using, in that model, a value for tissue diffusivity that was 10 - 20 times that actually measured in physiological medium. By utilizing two homogeneous subcompartments, we represented within-tissue diffusion of CO and O₂ without requiring the solution of partial differential equations, which would greatly increase the numerical complexity of the whole-body model. We observed that Pt2O₂ did increase in the presence of within-tissue diffusion of O₂, and we chose an effective diffusion distance of 0.1 mm so that in normoxia about 10-20% of oxygen metabolism in subcompartment 2 was supplied via this pathway. Because the predicted PO₂ in this compartment typically overestimated the experimental data (Figure 3), this level of diffusive flux might be somewhat too high.

We also allowed a small amount of gas exchange between subcompartment 1 and “venules” coming from subcompartment 2. This concept is consistent with anatomical descriptions of muscle vascular beds (Pittman, 2005; Segal, 2005) and was included in the tissue models of Ye et al. (1993) and Sharan et al. (1998). With the chosen parameters, there is a small O₂ flux from subcompartment 1 into the venous vasculature in normoxia, causing muscle venous PO₂ to be a few Torr higher than in the vascular bed of subcompartment 2 (assumed to be capillaries). This result is consistent with experimental measurements (Table 3). Thus, an advantage of our approach is that it was no longer necessary to invoke the common assumption of whole-body models of respiratory gases that tissue and venous PO₂s are equal.

Our model utilizes anthropometric regression relationships to estimate muscle mass (and cardiac output when it is not known). It also estimates both muscle and whole-body metabolic rates based on average resting values per Kg of body weight. Thus, it attempts to account for some inter-subject variability that is expected to affect CO uptake and distribution, as we did when studying the biphasic nature of CO washout (Bruce and Bruce. 2006). On the other hand, the regression relationships themselves only model average effects. Nonetheless, the new model accounts for much of the inter-subject variability of the arterio-venous difference of HbCO in the Benignus, et al., (1994) study (data not shown).

4.2 Determining DmCO

An important result from this study is the demonstration that some experimental protocols are much less sensitive to the value of blood-tissue conductance for CO than others. The most striking example is the protocol of slowly injecting CO into the rebreathing system (Figure 10), whose outcome is nearly independent of DmCO. In other cases the published data were compatible with 2 or more values for DmCO or with a range of values (Figures 5, 8, 9). In some cases, however, the acceptable range for DmCO could be narrowed considerably by examining the detailed time course of the data (Figures 6, 7). Such results are difficult to anticipate without quantitative modeling and the failure to appreciate these effects has, almost certainly, biased previous interpretations of experimental studies of CO uptake and distribution.

The experiments for which the modeling predictions were most sensitive to the value chosen for DmCO are the rebreathing studies of Burge and Skinner (1995) and the washout studies of Roughton and Root (1946). Despite uncertainty about the precise value of blood volume in the former study, the DmCO values that produced the best fit to the data were typically in the range 2.5 - 5.0 ml/min/Torr. In these data, the net change in %HbCO during the last 30 min of rebreathing was a decrease on the order of 0.3%, corresponding to an average flux of 0.113 ml/min (i. e., 0.3% × 0.002 ml/ml/% × 5646 ml / 30 = 3.38 ml/30 min). A recent study (Prommer and Schmidt, 2007) estimated the flux of CO from blood to tissues after loading the blood with CO via a 2-min rebreathing procedure. The authors measured the amount of CO exhaled and subtracted it from that lost from the blood during air breathing 4 -11 min after the rebreathing ended. For 10 male human subjects the estimated blood-to-tissue flux of CO was 0.24 +/- 0.13 ml/min. This value is expected to be higher than that estimated from the data of Burge and Skinner (1995) because the rate of fall in %HbCO decreases during the 4 - 11 min period both in the data and in the simulation results. Thus, this new study is compatible with the range of DmCO values we determined from the Burge and Skinner data.

Like the recent study of Prommer and Schmidt (2007), the washout studies of Roughton and Root (1946) also provide evidence that all of the CO lost from the blood during air or oxygen breathing after CO exposure does not appear in the exhaled gas. Their calculated values of CO lost from blood depend on the value used for total blood volume, which had been measured previously in their subjects using the method of CO dilution (Nomof, et el., 1954; Burge and Skinner, 1995). Assuming this method to be accurate within 10% and that slight overestimation of blood volume (due to loss of CO to tissues) is likely, the reported ratios of “CO exhaled” to “CO lost from blood” may be too low by ~10%. This underestimation would not substantially affect our conclusion that DmCO values in the range of 2.5 - 8.0, rather than much higher DmCO values consistent with rapid blood-tissue equilibration, provide the best fit of the model to their data. For the only case in which there was a significant difference between model prediction and experimental data, underestimation of blood volume could explain about half of the difference between the ratio measured during 15 min of hyperoxic washout (0.60) and the model prediction (0.85). In addition, the calculations of exhaled CO and change in blood CO content for 15 min are more susceptible to errors in measurement, given the small reported changes in %HbCO. An important finding from modeling is that the ratio of exhaled CO to net loss of CO from blood becomes greater than one for DmCO values that are large enough to produce blood-tissue equilibration within a few minutes, reinforcing our conclusion that DmCO must be sufficiently small that blood-tissue equilibration of PCO occurs more slowly than vascular mixing.

The slow loss of CO from blood during long rebreathing procedures has been measured in numerous experimental studies (Luomanmaki and Coburn, 1969; Coburn and Mayers, 1971). The proper interpretation of this finding depends on the rates of production and metabolism of CO in the body. When measured separately using radiolabelling, net production is found to exceed net metabolism (Tobias, et al., 1945; Coburn, 1970; Delivoria-Papadopoulos, et al., 1974) by ~0.007 ml/min. If either or both of these factors are affected by the average CO content of blood, then it is difficult to separate their effects from slow diffusion of CO into tissues. On the other hand, the net loss of CO from blood during rebreathing is significantly greater than reported values for rates of CO metabolism and production. Therefore, our conclusions about the quantitative value of DmCO based on rebreathing studies are unlikely to be altered significantly by changes in CO production or metabolism. Furthermore, the model predictions in Figure 8, which indicate that the rate of change of blood CO content depends on a nonlinear interaction between %HbCO and DmCO, cast doubt on any conclusion that changes in CO production or metabolism can be evaluated from changes in the rate of CO loss from blood as %HbCO is altered.

The loss of radiolabelled CO from blood when an anesthetized dog on a rebreathing circuit is made severely hypoxic has been said to support the belief that CO equilibrates rapidly between blood and tissues (Luomanmaki and Coburn, 1969; Coburn and Mayers, 1971). The model predicts this behavior if it is assumed that blood flow to muscle increases in severe hypoxia and that PS also increases because of recruitment and/or dilation of blood vessels (Chalmers, et al, 1966; Caldwell, et al., 1994; Hepple, et al., 2000). Thus, movement of CO from blood into muscle tissues will occur whenever the level of hypoxia is sufficient to cause muscle blood flow and PS to increase, independent of the value of DmCO. It is difficult to assess the time course of the change in radiolabelled CO in blood in published data because of the sparseness of data points, but in some examples a new steady state was not achieved after one hour of hypoxia. Model predictions with a DmCO in the range of 3.0 - 7.0 exhibit similar behavior.

It was reported that injection of labeled CO into the rebreathing system produced a rapid increase in label in right atrial blood of an anesthetized dog, followed by a prominent decrease with a half-time of 12.5 min (Luomanmaki and Coburn, 1969). Subsequently the concentration of labeled CO continued to decrease, but at a much slower rate. The authors assumed that the initial, faster decrease represented both vascular mixing and blood-tissue equilibration of CO. Our simulation results (e. g., Figure 6) imply that this initial decline is due predominantly to vascular mixing and the later slow decline is due predominantly to CO flux out of the blood.

The slow rate of exchange of CO between blood and muscle tissues, compared to that of O₂, results from both the blood-tissue conductance for CO and the pressure difference driving this flow. PCO in both blood and tissue typically remains in the range of a few tenths of a Torr; therefore, the pressure gradient for CO is 2 orders of magnitude smaller than that driving O₂ flux in normoxia. In the model, the blood-tissue conductance for O₂ in muscle tissue is 1.08 × 10^-3 ml/min/Torr/gm, whereas that for CO is 0.357 × 10^-3 ml/min/Torr/gm when DmCO = 7.0. On the basis of their relative diffusivities, one might expect CO conductance to be about 75% of that for O₂ -- i. e., DmCO ~10-12. On the other hand, tissue PO₂s in the model systematically overestimated the experimental data, suggesting that the O₂ conductance in the model may be too high. Reducing the latter might actually increase CO flux for a given DmCO (because tissue PO₂s would be lower). In any case, the estimated value for DmCO that provides the best fit to a wide range of experimental data is within a factor of 2 of that expected based on relative diffusivities and the blood-tissue conductance for O₂ in muscle.

4.3 Clinical implications

Since a typical volume for muscle subcompartment 2 used in the model is 18,864 ml., a DmCO of 7.0 corresponds to an average blood-to-tissue diffusion coefficient of 0.357 × 10^-3 ml/min/Torr/gm. Even such small CO flux to extravascular tissues is potentially important in long CO exposures or short intense exposures that are washed out slowly, as the simulations of the Benignus, et al., (1994) study (Figure 5) and the graphs in Figure 11 demonstrate. Although MbCO levels increase slowly during CO exposure, they can eventually reach high levels. Note also from Figure 11 that MbCO levels fall more slowly during washout than does %HbCO. This figure also suggests that tissue PO₂ levels are correlated more with %HbCO than with %MbCO, probably due to the impairment of O₂ delivery to tissues when %HbCO is elevated. Although our model does not include exercise, it has been suggested that Mb provides a storage site for O₂ which is mobilized to support increased metabolism at the onset of exercise until O₂ delivery via the blood is increased sufficiently (Deussen and Bassingthwaite, 1996; Whitely, et al., 2002). In the presence of elevated MbCO, this store of O₂ is diminished and muscle tissue might be susceptible to any additional hypoxia even when %HbCO has fallen significantly from its peak level. This effect may be particularly important if it occurs in the myocardium. The model has not been tested for situations involving exercise; however, the potential lethality of CO exposure is elevated by concomitant exercise, and extending the model to this situation should be fruitful.

Figure 11 also shows that if the CO exposure occurs during air breathing, then during washout on 100% O₂ MbCO increases sharply because the subject is not able to rapidly exhale all of the CO that has been dislodged from Hb by hyperoxia. This response may exacerbate the impairment of O₂ availability in exercising muscle (e. g., the heart) or in resting muscles in severe CO poisoning. Extension of the model to predict the consequences of therapy using hyperbaric oxygen will provide additional insights regarding the optimal treatment protocol for CO poisoning. One could also expand the model by adding mass balance equations for CO₂ in order to predict the quantitative benefits of adding various levels of CO₂ to the inspired gas during therapy (Fisher, et al., 1999).

4.4 Conclusions

We developed an improved model of whole-body uptake and distribution of carbon monoxide, and used this model to determine the value for the blood to muscle tissue conductance of CO that provides the most consistent fit to data from several different experimental studies. The best fits to the data occurred with DmCO in the range 3.0 - 8.0 ml/min/Torr. This value is physiologically reasonable since it is on the order of half of that expected based on the corresponding conductance for O₂ in the model. Furthermore, the pressure gradients driving CO flux between blood and tissue compartments are two orders of magnitude smaller than those driving O₂ flux. Consequently, CO uptake from blood by muscle is much slower than O₂ uptake. During long CO exposures, and during short intense CO exposures which produce high PaCO, muscle uptake in the form of MbCO can be significant, leading to high levels of Mb saturation by CO. Washout of CO after CO exposure by either air or O₂ breathing will cause %HbCO to fall more rapidly than %MbCO; therefore, victims of CO poisoning may be susceptible to deleterious effects of high MbCO for several tens of minutes after %HbCO falls significantly from its peak. Previous conclusions that CO equilibrates rapidly between blood and tissues cannot be substantiated when interpretations of experimental findings are based on the rigorous quantitative relationships implemented in the model.

5. Appendix: Equations of the Model

Mass balance equations for CO are the same as those in our original model (Bruce and Bruce, 2003) except for the muscle compartment which is described below.

Mass balance equations for O₂ parallel those for CO. (See Figures 1 and 2 and Table 1 for definitions of symbols.) Thus, in the alveolar compartment,

Table 1.

Definitions of symbols.

Variables	Subscripts	Definition
C		Concentration, ml/ml
P		Partial pressure, Torr
Q		Blood flow, ml/min
D		Blood to tissue conductance, ml/min/Torr
V		Volume, ml
HbO2		Oxyhemoglobin concentration, ml/ml
HbCO		Carboxyhemoglobin concentration, ml/ml
MbCO		Oxymyoglobin concentation,ml/ml
MbO2		Carboxymyoglobin concentration, ml/ml
	A	alveolar compartment
	m (m1, m2)	muscle (muscle subcompartments 1 and 2)
	ot	other tissue compartment
	ar	arterial blood compartment
	ec	end-capillary blood compartment
	t (tm1, tm2)	muscle tissue compartment (subcompartments 1 and 2)
	bm (bm1, bm2, bm3)	muscle blood compartment (subcompartments 1, 2, and 3)
	bot	other tissue blood compartment
	bmv	mixed venous blood compartment
	s	pulmonary shunt compartment
	vm	muscle venous blood compartment
	i	inspired
	mxv	mixed venous

$$V_L\frac{d{C}_A{O}_2\left(t\right)}{dt}=\left[P_i{O}_2\left(t\right)-P_A{O}_2\left(t\right)\right]{\dot{V}}_A/P_B-\dot{Q}\left(1-\mathit{SF}\right)\left[C_{\mathit{ep}}{O}_2\left(t\right)-C_{\mathit{mx}}{O}_2\left(t\right)\right]$$

In vascular compartments O₂ exists in dissolved and combined forms so that in compartment “i”, the total O₂ concentration is C_iO₂ = HbO₂ + S_o2 ·P_iO₂. Blood flowing into a vascular compartment mixes with resident blood according to a time constant which equals compartmental volume divided by blood flow; the resulting mixing of O₂ is described by equations of the form

$$T\frac{d{C}_{O_2}}{dt}=-C_{O_2}+C_{O_2,\mathit{in}}\dot{Q}/V_b$$

where C, T, and Vb are the concentration, time constant, and volume of the blood compartment, and CO₂,in is the O₂ concentration of blood entering the compartment. The CO content of the vascular compartments is modified by mixing in a similar manner.

Equations describing mass balances in the two muscle subcompartments all have the same structure. In each subcompartment, CO and O₂ mass balances are represented by an equation of the form

$$\frac{d{C}_{mk,g}\left(t\right)}{dt}={\mathit{Flux}}_{mk,g}\left(t\right)/V_{mk}+D_{mk,g}\left(C_{mk,g}\left(t\right)-C_{m{k}^{\prime },g}\left(t\right)\right)/Dx$$

where

$${\mathit{Flux}}_{mk,g}\left(t\right)=\left[D_{\mathit{bmk},g}\left(P_{\mathit{tck},g}\left(t\right)-P_{mk,g}\left(t\right)\right)\right]-M{R}_{mk,g}$$

and “g” refers to either O₂ or CO, “k” represents subcompartment k (1 or 2), Vmk is the volume of that subcompartment, Cmk,g and P_mk,g are the concentration and partial pressure of gas g in subcompartment k, Dmk,g is the intra-tissue diffusion coefficient for gas g, Dbmk,g is the blood-tissue conductance for gas g, Cmk,g is the dissolved gas concentration, and MRmk,g is the metabolic rate of gas g in subcompartment k. In both cases, MRmk,CO = 0.

P_tck,g is the effective partial pressure of gas g in the vascular compartment of subcompartment k driving the flux of g from the blood to the tissue. For CO, this pressure is the average of the inlet and outlet partial pressures (e. g., for subcompartment 1, PaCO and Pmv1CO in Figure 2). For O₂, this effective pressure is found by first determining the average HbO₂ concentration in the vascular compartment, then evaluating the corresponding pressure from the oxygen dissociation curve using an iterative method. The within-tissue diffusion coefficient for O₂ is set to 10 times the standard diffusivity (Table 2). The corresponding coefficient for CO was set to 75% of that for O₂. Dbmk,O₂ is the product of PSm, solubility, and tissue mass for both compartments (Beard and Bassingthwaite, 2000). PSm is the permeability-surface area for muscle, which was set to 37.5. Dbm2,CO equals DmCO, whereas Dbm1,CO is scaled from DmCO by the ratio of Vm1 to Vm2. For exchange of O₂ and CO between subcompartment 1 and the venular blood compartment (Figure 2), all blood-tissue conductances were set to 7.5% of their values for subcompartment 1.