Polarizable Atomic Multipole Solutes in a Poisson-Boltzmann Continuum

Abstract

Modeling the change in the electrostatics of organic molecules upon moving from vacuum into solvent, due to polarization, has long been an interesting problem. In vacuum, experimental values for the dipole moments and polarizabilities of small, rigid molecules are known to high accuracy; however, it has generally been difficult to determine these quantities for a polar molecule in water. A theoretical approach introduced by Onsager used vacuum properties of small molecules, including polarizability, dipole moment and size, to predict experimentally known permittivities of neat liquids via the Poisson equation. Since this important advance in understanding the condensed phase, a large number of computational methods have been developed to study solutes embedded in a continuum via numerical solutions to the Poisson-Boltzmann equation (PBE). Only recently have the classical force fields used for studying biomolecules begun to include explicit polarization in their functional forms. Here we describe the theory underlying a newly developed Polarizable Multipole Poisson-Boltzmann (PMPB) continuum electrostatics model, which builds on the Atomic Multipole Optimized Energetics for Biomolecular Applications (AMOEBA) force field. As an application of the PMPB methodology, results are presented for several small folded proteins studied by molecular dynamics in explicit water as well as embedded in the PMPB continuum. The dipole moment of each protein increased on average by a factor of 1.27 in explicit water and 1.26 in continuum solvent. The essentially identical electrostatic response in both models suggests that PMPB electrostatics offers an efficient alternative to sampling explicit solvent molecules for a variety of interesting applications, including binding energies, conformational analysis, and pK_a prediction. Introduction of 150 mM salt lowered the electrostatic solvation energy between 2–13 kcal/mole, depending on the formal charge of the protein, but had only a small influence on dipole moments.

I. INTRODUCTION

Modeling the change in the electrostatic moments of organic molecules upon moving from vacuum to solvent has a long history, with an important initial contribution from Onsager, who in 1936 identified the difference between the cavity field and reaction field.¹ The approach used was to treat the solvent as a high dielectric continuum surrounding a spherical, low dielectric solute with a dipole moment, which was considered to be a sum of permanent and induced contributions. Using the vacuum dipole moment, molecular polarizability, and an estimate of molecular size, a prediction of the experimentally observable liquid permittivity was achieved for a range of molecules. Through the use of computers, this approach has been extended in order to treat solutes with arbitrary geometry and charge distributions by numerically solving the Poisson-Boltzmann equation using finite-difference, finite element and boundary element methods.² An advantage of using a continuum solvent over explicit representation of solvent molecules is alleviation of the need to sample over water degrees of freedom in order to determine the mean solvent response. Applications that have benefited from using continuum solvent approaches include predictions of pK_as, redox potentials, binding energies, molecular design, and conformational preferences.

An accurate implicit solvation model does not necessitate any loss of solute thermodynamic information.³ For most implicit solvent models, the total solvation energy Δ W_solvation as a function of solute conformation is separated into contributions due to nonpolar Δ W_np and electrostatic Δ W_elec effects

$$\mathrm{\Delta }{\text{W}}_{\text{solvation}}=\mathrm{\Delta }{\text{W}}_{\text{np}}+\mathrm{\Delta }{\text{W}}_{\text{elec}}.$$ (1)

Here we concentrate on the electrostatic contribution, motivated by recent work on improving the accuracy of force field electrostatic models through the incorporation of polarizable multipoles.^4–7 This requires revisiting the theory underlying the electrostatic component of implicit solvent models, including those based on solving the linearized Poisson-Boltzmann equation (LPBE)

$$\nabla •[\epsilon (\mathbf{r})\nabla \mathrm{\Phi }(\mathbf{r})]-{\overline{\kappa }}^2(\mathbf{r})\mathrm{\Phi }(\mathbf{r})=-4\pi \rho (\mathbf{r}),$$ (2)

where the coefficients are a function of position r, Φ(r) is the potential, ε(r) the permittivity, κ̄²(r) the modified Debye-Hückel screening factor and ρ(r) is the solute charge density. For an introduction to Poisson-Boltzmann based methodology and applications, see the review of Honig and Nichols⁸ or those of Baker.^2,9

In spite of the fact that the dipole moment of a polar solute can increase by 30% or more during transfer from gas to aqueous phase, empirical potentials have typically neglected explicit treatment of polarization for reasons of computational efficiency. However, ab initio implicit solvent models, including the Polarizable Continuum Model (PCM) introduced in 1981 by Miertus, Scrocco and Tomasi^10,11, the Conductor-Like Screening Model (COSMO) of Klamt¹², the distributed multipole approach of Rinaldi et al.¹³ and the SMx series of models introduced in the early 90s by Cramer and Truhlar¹⁴ have long incorporated self-consistent reaction fields (SCRF).^10,15 These models allow the solute, described using a range of ab initio or semi-empirical levels of theory, and continuum solvent to relax self-consistently based on their mutual interaction. The principle advantage of the present PMPB model over these existing formulations is computational savings resulting from a purely classical representation of the solute Hamiltonian, which facilitates the study of large systems. However, each of these models demonstrates that there continues to be broad interest in coupling highly accurate solute potentials with a continuum treatment of the environment.

For example, there is growing evidence that current goals of computational protein design, including incorporation of catalytic activity and protein-protein recognition, may require a more accurate description of electrostatics than has been achieved by fixed partial charge force fields used in conjunction with implicit solvents.¹⁶ For example, it has been shown that both Poisson-Boltzmann and generalized Born models used with the CHARMM22¹⁷ potential tend to favor burial of polar residues over non-polar ones.¹⁸ It is important to note that this behavior may not be directly due to the treatment of solvation electrostatics, but could result from inaccuracies in the underlying protein force field or the nonpolar component of the solvation model. However, the fixed charge nature of traditional protein potentials may also contribute to such discrepancies. Polar residues elicit a solvent field that increases their dipole moment via polarization relative to a nonpolar environment, which has a favorable energetic consequence that cannot be captured by a fixed charge force field even when using explicit water.

Along with the AMOEBA force field, other efforts toward developing polarizable force fields for biomolecular modeling are also under way, for example see the review of Ponder and Case.⁷ Here we comment more thoroughly on the Polarizable Force Field (PFF) of Maple and coworkers,¹⁹ since it has recently been incorporated into a continuum environment. Specifically, there are a number of salient differences between AMOEBA and PFF, including facets of the underlying polarization model and the use of permanent quadrupoles in AMOEBA. Significantly, AMOEBA allows mutual polarization between atoms with 1–2, 1–3 and 1–4 bonding arrangements, which is crucial for reproducing molecular polarizabilities.

The current work addresses a number of issues raised in the description of the PFF solvation model. First, discretization procedures previously reported for mapping partial charges onto a source grid are inadequate for higher order moments. Instead, we present a multipole discretization procedure using B-splines that leads to essentially exact energy gradients. Furthermore, we provide a rigorous demonstration of the numerical precision of our approach, similar in spirit to the work of Im et al. with respect to partial charge models.²⁰ We also show that divergence of the polarization energy is not possible due to use in AMOEBA of Thole-style damping at short range.²¹

Formulation of consistent energies and gradients based on the LPBE has been reported previously for partial charge force fields.^20,22–24 Gilson et al. pointed out limitations in previous approaches using variational differentiation of an electrostatic free energy density functional.²³ Later Im et al. showed that it is possible to begin the derivation based upon the underlying finite-difference calculation used to solve the LPBE.²⁰ This approach leads to a formulation with optimal numerical consistency and will be adopted here.

II. BACKGROUND

In order to describe the total electrostatic energy of the PMPB model, specifically of an AMOEBA solute in a LPBE continuum solvent, it is first necessary to present the energy in vacuum using a convenient notation. We will also summarize the previously developed procedure for determining robust energies and gradients for fixed charge force fields in a LPBE continuum.^20,23 Given this background, the theoretical infrastructure required to implement the PMPB model is motivated and presented in a self-contained fashion.

A. AMOEBA vacuum electrostatic energy

Following Ren and Ponder⁵, each permanent atomic multipole site can be considered as a vector of coefficients including charge, dipole and quadrupole components

$${\mathbf{M}}_i={[q_i,d_{i,x},d_{i,y},d_{i,z},{\mathrm{\Theta }}_{i,xx},{\mathrm{\Theta }}_{i,xy},{\mathrm{\Theta }}_{i,xz},\dots ,{\mathrm{\Theta }}_{i,zz}]}^t,$$ (3)

where the superscript t denotes the transpose. The interaction energy between two sites i and j separated by distance s_ij can then be represented in tensor notation as

$$\begin{array}{l}\text{U}({\mathbf{s}}_{ij})={\mathbf{M}}_i^t{\mathbf{T}}_{ij}{\mathbf{M}}_j\\ ={\left[\begin{array}{c}{q}_i\\ d_{i,x}\\ d_{i,y}\\ d_{i,z}\\ {\mathrm{\Theta }}_{i,xx}\\ ⋮\end{array}\right]}^t\left[\begin{array}{ccccc}1& \frac{\partial }{\partial x_j}& \frac{\partial }{\partial y_j}& \frac{\partial }{\partial z_j}& \cdots \\ \frac{\partial }{\partial x_i}& \frac{{\partial }^2}{\partial x_i\partial x_j}& \frac{{\partial }^2}{\partial x_i\partial y_j}& \frac{{\partial }^2}{\partial x_i\partial z_j}& \cdots \\ \frac{\partial }{\partial y_i}& \frac{{\partial }^2}{\partial y_i\partial x_j}& \frac{{\partial }^2}{\partial y_i\partial y_j}& \frac{{\partial }^2}{\partial y_i\partial z_j}& \cdots \\ \frac{\partial }{\partial z_i}& \frac{{\partial }^2}{\partial z_i\partial x_j}& \frac{{\partial }^2}{\partial z_i\partial y_j}& \frac{{\partial }^2}{\partial z_i\partial z_j}& \cdots \\ ⋮& ⋮& ⋮& ⋮& \ddots \end{array}\right]\frac{1}{s_{ij}}\left[\begin{array}{c}{q}_j\\ d_{j,x}\\ d_{j,y}\\ d_{j,z}\\ {\mathrm{\Theta }}_{j,xx}\\ ⋮\end{array}\right].\end{array}$$ (4)

Each site may also be polarizable, such that an induced dipole μ_i proportional to the strength of the local field is present

$$\begin{array}{l}{\mathit{\mu }}_i={\alpha }_i{\mathbf{E}}_i\\ ={\alpha }_i\left(\sum _{j\ne i}{\mathbf{T}}_{\text{d},ij}^{(1)}{\mathbf{M}}_j+\sum _{k\ne i}{\mathbf{T}}_{ik}^{(1)}{\mathit{\mu }}_k\right).\end{array}$$ (5)

Here α_i is an isotropic atomic polarizability and E_i is the total field, which can be decomposed into contributions from permanent multipole sites and induced dipoles, and the summations are over N_s multipole sites. Later, this expression will be modified to include the solvent reaction field. The interaction tensors ${\mathbf{T}}_{\text{d},ij}^{(1)}$ and ${\mathbf{T}}_{ik}^{(11)}$ are, respectively,

$${\mathbf{T}}_{\text{d},ij}^{(1)}=\left[\begin{array}{ccccc}\frac{\partial }{\partial x_j}& \frac{{\partial }^2}{\partial x_i\partial x_j}& \frac{{\partial }^2}{\partial x_i\partial y_j}& \frac{{\partial }^2}{\partial x_i\partial z_j}& \cdots \\ \frac{\partial }{\partial y_i}& \frac{{\partial }^2}{\partial y_i\partial x_j}& \frac{{\partial }^2}{\partial y_i\partial y_j}& \frac{{\partial }^2}{\partial y_i\partial z_j}& \cdots \\ \frac{\partial }{\partial z_i}& \frac{{\partial }^2}{\partial z_i\partial x_j}& \frac{{\partial }^2}{\partial z_i\partial y_j}& \frac{{\partial }^2}{\partial z_i\partial z_j}& \cdots \end{array}\right]\frac{1}{s_{ij}},$$ (6)

and

$${\mathbf{T}}_{ik}^{(11)}=\left[\begin{array}{ccc}\frac{{\partial }^2}{\partial x_i\partial x_k}& \frac{{\partial }^2}{\partial x_i\partial y_k}& \frac{{\partial }^2}{\partial x_i\partial z_k}\\ \frac{{\partial }^2}{\partial y_i\partial x_k}& \frac{{\partial }^2}{\partial y_i\partial y_k}& \frac{{\partial }^2}{\partial y_i\partial z_k}\\ \frac{{\partial }^2}{\partial z_i\partial x_k}& \frac{{\partial }^2}{\partial z_i\partial y_k}& \frac{{\partial }^2}{\partial z_i\partial z_k}\end{array}\right]\frac{1}{s_{ik}}.$$ (7)

where the subscript d in ${\mathbf{T}}_{\text{d},ij}^{(1)}$ indicates that masking rules for the AMOEBA group-based polarization model are applied.^4–7 This linear system of equations can be solved via a number of approaches, including direct matrix inversion or iterative schemes such as successive over-relaxation (SOR). Note at short range the field is damped via the Thole model, which is not included above for clarity and is discussed elsewhere.⁵ The total vacuum electrostatic energy ${\text{U}}_{\text{elec}}^{\text{v}}$ includes pairwise permanent multipole interactions and many-body polarization

$${\text{U}}_{\text{elec}}^{\text{v}}=\frac{1}{2}[{\mathbf{M}}^t\mathbf{T}-{({\mathit{\mu }}^{\text{v}})}^t{\mathbf{T}}_{\text{p}}^{(1)}]\mathbf{M},$$ (8)

where the factor of one-half avoids double-counting of permanent multipole interactions in the first term and accounts for the cost of polarizing the system in the second term. Furthermore, M is a column vector of 13N_s multipole components

$$\mathbf{M}=\left[\begin{array}{c}{\mathbf{M}}_1\\ {\mathbf{M}}_2\\ ⋮\\ {\mathbf{M}}_{{\text{N}}_{\text{s}}}\end{array}\right],$$ (9)

T is a N_s × N_s supermatrix with T_ij as the off-diagonal elements

$$\mathbf{T}=\left[\begin{array}{cccc}0& {\mathbf{T}}_{12}& {\mathbf{T}}_{13}& \cdots \\ {\mathbf{T}}_{21}& 0& {\mathbf{T}}_{23}& \cdots \\ {\mathbf{T}}_{31}& {\mathbf{T}}_{32}& 0& \cdots \\ ⋮& ⋮& ⋮& \ddots \end{array}\right],$$ (10)

μ^v is a 3N_s column vector of converged induced dipole components in vacuum

$${\mathit{\mu }}^{\text{v}}=\left[\begin{array}{c}{\mu }_{1,x}\\ {\mu }_{1,y}\\ {\mu }_{1,z}\\ ⋮\\ {\mu }_{N_s,z}\end{array}\right],$$ (11)

and ${\mathbf{T}}_{\text{p}}^{(1)}$ is a 3N_s × 13N_s supermatrix with ${\mathbf{T}}_{\text{p},ij}^{(1)}$ as off-diagonal elements

$${\mathbf{T}}_{\text{p}}^{(1)}=\left[\begin{array}{cccc}0& {\mathbf{T}}_{\text{p},12}^{(1)}& {\mathbf{T}}_{\text{p},13}^{(1)}& \cdots \\ {\mathbf{T}}_{\text{p},21}^{(1)}& 0& {\mathbf{T}}_{\text{p},23}^{(1)}& \cdots \\ {\mathbf{T}}_{\text{p},31}^{(1)}& {\mathbf{T}}_{\text{p},32}^{(1)}& 0& \cdots \\ ⋮& ⋮& ⋮& \ddots \end{array}\right].$$ (12)

The subscript p denotes a tensor matrix that operates on the permanent multipoles to produce the electric field in which the polarization energy is evaluated, while the subscript d was used above to specify an analogous tensor matrix that produces the field that induces dipoles. The differences between the two are masking rules that scale short-range through-bond interactions in the former case and use the AMOEBA group-based polarization scheme for the later.⁴

B. LPBE energies and gradients for fixed partial charge force fields

LPBE solvation energies and gradients have been determined previously by a number of groups for fixed partial charge force fields.^22,23 We will briefly restate the results of Im et al. to introduce the approach extended here for use with the PMPB model.²⁰ The solvation free energy Δ G of a permanent charge distribution is

$$\mathrm{\Delta }{\text{G}}_{\text{elec}}=\frac{1}{2}({\mathit{\Phi }}_{\text{s}}^t-{\mathit{\Phi }}_{\text{v}}^t)\mathit{q},$$ (13)

where q is a column vector of fractional charges, ${\mathit{\Phi }}_{\text{s}}^t$ is the transpose of a column vector containing the electrostatic potential of the solvated system and ${\mathit{\Phi }}_{\text{v}}^t$ is the corresponding vacuum potential. The number of components in each vector is equal to the number of grid points used to represent the system. In the present work the grid will always be cubic, and as discussed in the section on multipole discretization must use equal grid spacing in each dimension, although the number of grid points along each axis can vary. The potential can be determined numerically using a finite-difference representation of the LPBE^20,25,26, which can be formally defined as a linear system of equations

$$\mathbf{A}\mathit{\Phi }=-4\pi \mathit{q},$$ (14)

where A is a symmetric matrix that represents the linear operator (differential and linear term). An equivalent, but more cumbersome representation that makes clear the underlying finite-difference formalism is given in the Appendix. Solving Eq. (14) for the potential

$$\mathit{\Phi }=-4\pi {\mathbf{A}}^{-1}\mathit{q},$$ (15)

highlights that A⁻¹ is the Green’s function with dimensions N_r × N_r, where N_r is the number of grid points. By defining the Green’s function for the solvated ${\mathbf{A}}_{\text{s}}^{-1}$ and ${\mathbf{A}}_{\text{v}}^{-1}$ homogeneous cases, the electrostatic hydration free energy is

$$\mathrm{\Delta }{\text{G}}_{\text{elec}}=\frac{1}{2}(-4\pi {\mathit{q}}^t)({\mathbf{A}}_{\text{s}}^{-1}-{\mathbf{A}}_{\text{v}}^{-1})\mathit{q}$$ (16)

The derivative with respect to movement of the γ coordinate of atom j is

$$\frac{\partial \mathrm{\Delta }{\text{G}}_{\text{elec}}}{\partial s_{j,\gamma }}=-2\pi \left[\frac{\partial {\mathit{q}}^t}{\partial s_{j,\gamma }}({\mathbf{A}}_{\text{s}}^{-1}-{\mathbf{A}}_{\text{v}}^{-1})\mathit{q}+{\mathit{q}}^t\frac{\partial ({\mathbf{A}}_{\text{s}}^{-1}-{\mathbf{A}}_{\text{v}}^{-1})}{\partial s_{j,\gamma }}\mathit{q}+{\mathit{q}}^t({\mathbf{A}}_{\text{s}}^{-1}-{\mathbf{A}}_{\text{v}}^{-1})\frac{\partial \mathit{q}}{\partial s_{j,\gamma }}\right].$$ (17)

This expression can be simplified by noting that the derivative of the homogeneous Green’s function is zero everywhere

$$\frac{\partial {\mathbf{A}}_{\text{v}}^{-1}}{\partial s_{j,\gamma }}=0,$$ (18)

and the derivative of the solvated Green’s function can be substituted for using a standard relationship of matrix algebra.

$$\begin{array}{l}{\mathbf{A}}_{\text{s}}^{-1}{\mathbf{A}}_{\text{s}}=\mathbf{I}\\ \frac{\partial {\mathbf{A}}_{\text{s}}^{-1}}{\partial {\text{s}}_{j,\gamma }}{\mathbf{A}}_{\text{s}}+{\mathbf{A}}_{\text{s}}^{-1}\frac{\partial {\mathbf{A}}_{\text{s}}}{\partial {\text{s}}_{j,\gamma }}=0\\ \frac{\partial {\mathbf{A}}_{\text{s}}^{-1}}{\partial {\text{s}}_{j,\gamma }}={\mathbf{A}}_{\text{s}}^{-1}\frac{\partial {\mathbf{A}}_{\text{s}}}{\partial {\text{s}}_{j,\gamma }}{\mathbf{A}}_{\text{s}}^{-1}\end{array}$$ (19)

Finally, due to the symmetry of the Green’s function, the first and third terms of Eq. (17) are equivalent

$$\frac{\partial {\mathit{q}}^t}{\partial s_{j,\gamma }}({\mathbf{A}}_{\text{s}}^{-1}-{\mathbf{A}}_{\text{v}}^{-1})\mathit{q}={\mathit{q}}^t({\mathbf{A}}_{\text{s}}^{-1}-{\mathbf{A}}_{\text{v}}^{-1})\frac{\partial \mathit{q}}{\partial s_{j,\gamma }}.$$ (20)

Using the relationships in Eqs. (18 – 20), Eq. (17) becomes

$$\frac{\partial \mathrm{\Delta }{\text{G}}_{\text{elec}}}{\partial s_{j,\gamma }}=-4\pi {\mathit{q}}^t({\mathbf{A}}_{\text{s}}^{-1}-{\mathbf{A}}_{\text{v}}^{-1})\frac{\partial \mathit{q}}{\partial s_{j,\gamma }}+\frac{1}{8\pi }(4\pi {\mathit{q}}^t{\mathbf{A}}_{\text{s}}^{-1})\frac{\partial {\mathbf{A}}_2}{\partial s_{j,\gamma }}(4\pi {\mathbf{A}}_{\text{s}}^{-1}\mathit{q}).$$ (21)

Finally, the two products of Green’s functions with source charges in the second term on the right-hand side can be replaced by the resulting potentials using Eq. (15) to give

$$\frac{\partial \mathrm{\Delta }{\text{G}}_{\text{elec}}}{\partial s_{j,\gamma }}={({\mathit{\Phi }}_{\text{s}}-{\mathit{\Phi }}_{\text{v}})}^t\frac{\partial \mathit{q}}{\partial s_{j,\gamma }}+\frac{1}{8\pi }{\mathit{\Phi }}_{\text{s}}^t\frac{\partial {\mathbf{A}}_s}{\partial s_{j,\gamma }}{\mathit{\Phi }}_{\text{s}}.$$ (22)

In the limit of infinitesimal grid spacing and infinite grid size, it was shown that this solution is equivalent to the forces derived by Gilson et al.^20,23 To generalize this result for permanent atomic multipoles, the derivative ∂q/∂s_j,γ remains to be defined and is discussed below. Additionally, all moments except the monopole are subject to torques, which are equivalent to forces on the local multipole frame defining sites.

III. METHODOLOGICAL DEVELOPMENTS

Based on the AMOEBA electrostatic energy in vacuum and previous work in obtaining the energy and gradients for a solute represented by a fixed partial charge force field described above²⁰, we now derive the formulation needed to describe the electrostatic solvation energy within the PMPB model. First, we consider the steps necessary to express the LPBE on a grid, including discretization of the source multipoles or induced dipoles, assignment of the permittivity, assignment of the modified Debye-Hückel screening factor and estimation of the potential at the grid boundary. A variety of techniques are available to solve the algebraic system of equations that result, although this work uses an efficient multigrid approach implemented in PMG²⁶ and used via the APBS software package.²⁷ Second, given the electrostatic potential solution to the LPBE, we describe how to determine the electrostatic solvation energy and its gradient. In fact, at least four LPBE solutions are required to determine the PMPB electrostatic solvation energy, and at least six to determine energy gradients. For comparison, fixed charged models typically require at most two LPBE solutions, the vacuum and solvated states, as outlined in the previous background section, although formulations that eliminate the self-energy exist.²⁸ The reasons and implications for the increased number of solutions of the LPBE required for the PMPB model will be discussed below.

A. Atomic multipoles as the source charge density

An important first step to expressing the LPBE in finite-difference form is discretization of an ideal point multipole onto the source charge grid. We begin by recalling that an ideal multipole arises from a Taylor series expansion of the potential in vacuum at a location R due to n charges near the origin, each with a magnitude and position denoted by c_i and r_i, respectively.²⁹

$$\text{V}(\mathbf{R})=\sum _{i=1}^n\frac{c_i}{\mid \mathbf{R}-{\mathbf{r}}_i\mid }$$ (23)

In performing the expansion, the convention for repeated summation over subscripts is utilized and we truncate after second order

$$\text{V}(\mathbf{R})=\sum _{i=1}^n{c}_i\left[\frac{1}{R}-r_{i,\alpha }{\nabla }_{\alpha }\frac{1}{R}+\frac{1}{2}{r}_{i,\alpha }{r}_{i,\beta }{\nabla }_{\alpha }{\nabla }_{\beta }\frac{1}{R}\right],$$ (24)

where the α and β subscripts each denote an x-, y- or z-component of a position vector or differentiation with respect to that coordinate. Based on this expansion, the monopole q, dipole d, and traceless quadrupole Θ moments are defined as

$$\begin{array}{c}q=\sum _{i=1}^n{c}_i\\ d_{\alpha }=\sum _{i=1}^n{r}_{i,\alpha }{c}_i\\ {\mathrm{\Theta }}_{\alpha \beta }=\sum _{i=1}^n\frac{3}{2}{r}_{i,\alpha }{r}_{i,\beta }{c}_i-\frac{1}{2}{r}_i^2{\delta }_{\alpha \beta }\end{array}.$$ (25)

There are various ways to define the quadrupole moment because only five quadrupole components are independent. This particular formulation ensures that the diagonal components are traceless, which simplifies many formulae because summations over the trace vanish.²⁹ Substitution into the potential gives

$$\text{V}(\mathbf{R})=q\left(\frac{1}{R}\right)-d_{\alpha }{\nabla }_{\alpha }\left(\frac{1}{R}\right)+\frac{1}{3}{\mathrm{\Theta }}_{\alpha \beta }{\nabla }_{\alpha }{\nabla }_{\beta }\left(\frac{1}{R}\right).$$ (26)

The reverse operation, representation of an ideal multipole by partial charges at grid sites (or charge density over finite volumes), is degenerate. However, some necessary properties reduce the space of practical solutions. These include local support (region of non-zero values on the grid) and smooth derivatives for the change in charge magnitude due to movement of a multipole site with respect to the grid. For fixed partial charges a normalized cubic basis spline, or B-spline, has been used successfully for discretizing monopole charge distributions (delta functions) on finite difference grids. For quadrupole moments at least 4^th order continuity is required such that a normalized 5^th order B-spline N₅ (x), which is a piecewise polynomial (Fig. 1), is appropriate.³⁰

Figure 1.

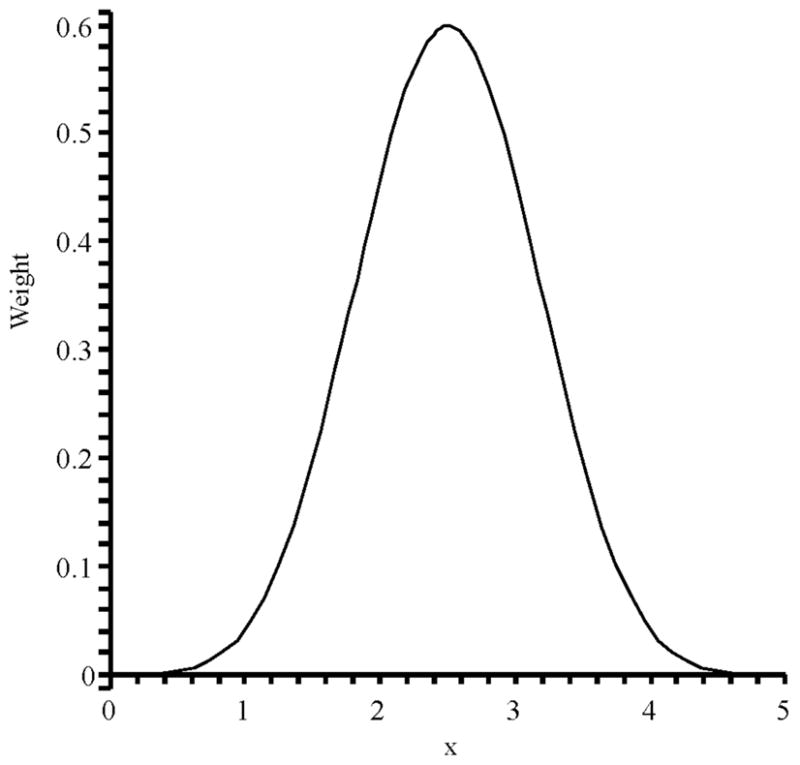
Normalized 5th order B-spline on the interval [0, 5].

$${\text{N}}_5(x)=\{\begin{array}{cc}\frac{1}{24}{x}^4,& 0\le x\le 1\\ -\frac{1}{8}+\frac{1}{6}x+\frac{1}{4}{(x-1)}^2+\frac{1}{6}{(x-1)}^3-\frac{1}{6}{(x-1)}^4,& 1\le x\le 2\\ -\frac{13}{24}+\frac{1}{2}x-\frac{1}{4}{(x-2)}^2-\frac{1}{2}{(x-2)}^3-\frac{1}{4}{(x-2)}^4,& 2\le x\le 3\\ -\frac{47}{24}-\frac{1}{2}x-\frac{1}{4}{(x-3)}^2-\frac{1}{2}{(x-3)}^3-\frac{1}{6}{(x-3)}^4& 3\le x\le 4\\ \frac{17}{24}-\frac{1}{6}x-\frac{1}{4}{(x-4)}^2-\frac{1}{6}{(x-4)}^3+\frac{1}{24}{(x-4)}^4,& 4\le x\le 5\\ 0,& \text{otherwise}\end{array}$$ (27)

The sum of this function evaluated at any five evenly spaced points between 0 and 5 is unity. The second part of the Appendix gives a rigorous demonstration that B-splines satisfy the properties of the delta functional and therefore can be used to implement a gradient operator.

To illustrate this approach, the fraction of charge that a grid point with coordinates r_i will receive from a charge site with coordinates s_j will now be described. We use r to denote an N_r × 3 matrix containing all grid coordinates, while s is an N_s × 3 matrix containing the coordinates of multipole sites. Elements of both matrices will be specified using two subscripts, the first is an index and the second is a dimension. We first consider the x-dimension, which requires the relative distance of nearby y-z planes from the charge site in dimensionless grid units (r_i,x − s_j,x)/h, where h is the grid spacing. The B-spline domain is centered over the charge site by shifting its domain from [0,5] to [−2.5,2.5] by adding 2.5 to its argument. Therefore, the weights of the 5 closest y-z planes to the charge site will be nonzero and sum to 1, where each weight is given by

$$\text{W}(r_{i,x},s_{j,x})={\text{N}}_5\left(\frac{r_{i,x}-s_{j,x}}{h}+2.5\right).$$ (28)

If the charge site is located on a y-z grid plane, then the maximum of the B-spline will be assigned to that plane. Repeated partitioning in the y- and z-dimensions leads to a tensor product description of the charge density

$$\text{B}({\mathbf{r}}_i,{\mathbf{s}}_j)=\text{W}(r_{i,x},s_{j,x})\text{W}(r_{i,y},s_{j,y})\text{W}(r_{i,z},s_{j,z}).$$ (29)

A further useful property of nth order B-splines is that their derivative can be formulated as a linear combination of n-1 order B-splines.³⁰

$$\frac{\partial {\text{N}}_n(x)}{\partial x}={\text{N}}_{n-1}(x)-{\text{N}}_{n-1}(x-1)$$ (30)

For example, the first derivative of the normalized 5^th order B-spline can be constructed from two of 4^th order, suggesting a dipole basis (or gradient stencil) for determining the electric field from the potential grid as shown in Fig. 2.

Figure 2.

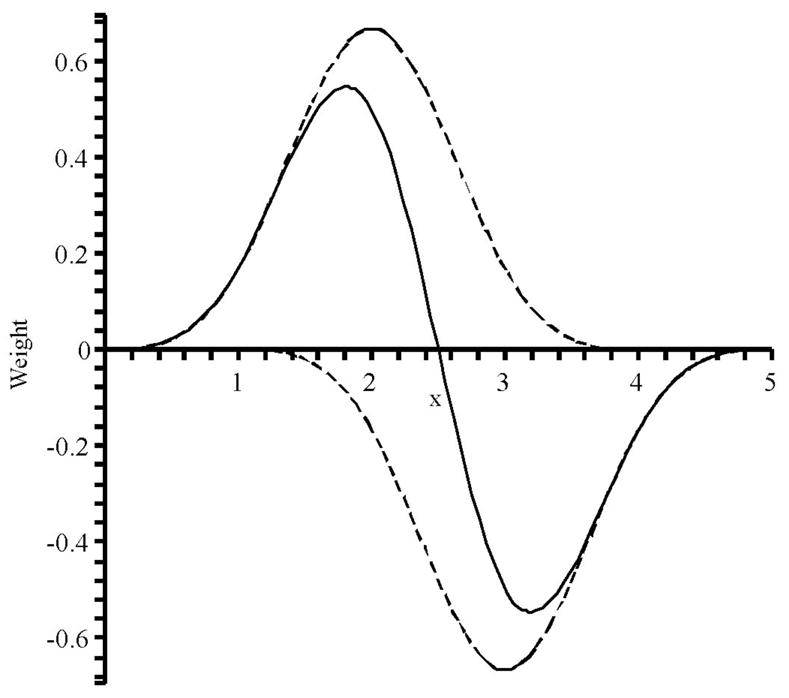
The sum of two 4^th order B-splines (dashed) equal the first derivative of a normalized 5th order B-spline (solid).

$$\frac{\partial {\text{N}}_5(x)}{\partial x}={\text{N}}_4(x)-{\text{N}}_4(x-1)$$ (31)

Similarly, the 2^nd derivative can be constructed from a linear combination of 3^rd order B-splines, suggesting an axial quadrupole basis as well as an axial 2^nd potential gradient stencil as in Fig. 3.

Figure 3.

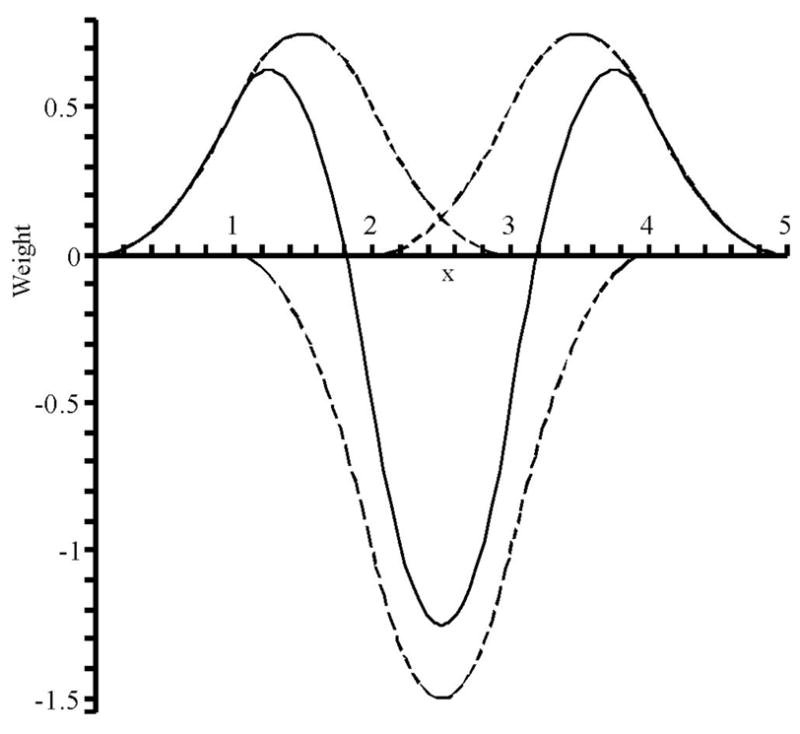
The sum of three 3^rd order B-splines (dashed) equal the second derivative of a normalized 5th order B-spline (solid).

$$\frac{{\partial }^2{\text{N}}_5(x)}{\partial x^2}={\text{N}}_3(x)-2{\text{N}}_3(x-1)+{\text{N}}_3(x-2)$$ (32)

For notational convenience we define a matrix B with dimension N_r × N_s which is used to convert a collection of N_s permanent atomic multipole sites into grid charge density over the N_r grid points

$$\mathbf{B}=\left[\begin{array}{ccc}\text{B}({\mathbf{r}}_1,{\mathbf{s}}_1)& \cdots & \text{B}({\mathbf{r}}_1,{\mathbf{s}}_{{\text{N}}_{\text{s}}})\\ ⋮& \ddots & ⋮\\ \text{B}({\mathbf{r}}_{{\text{N}}_{\text{r}}},{\mathbf{s}}_1)& \cdots & \text{B}({\mathbf{r}}_{{\text{N}}_{\text{r}}},{\mathbf{s}}_{{\text{N}}_{\text{s}}})\end{array}\right].$$ (33)

Only 125 entries per column will have non-zero coefficients, due to each multipole being partitioned locally among 5³ grid points.

Given the matrix B, the charge density at all grid points due to the permanent multipoles of an AMOEBA solute is

$${\mathit{q}}_{\text{M}}=\mathbf{B}\mathit{q}-\frac{1}{h}{\nabla }_{\alpha }{\mathbf{B}\mathit{d}}_{\alpha }+\frac{1}{3h^2}{\nabla }_{\alpha }{\nabla }_{\beta }\mathbf{B}{\mathit{\Theta }}_{\alpha \beta },$$ (34)

where q, d_x, d_y, d_z, Θ_xx, Θ_xy, Θ_xz, …, Θ_zz are column vectors and h normalizes for grid size. This is, in effect, the inverse operation to the original Taylor expansion by which the multipole moments were defined from a collection of point charges. All atomic multipole moments are exactly conserved to numerical precision as long as equal grid spacing is used in each dimension. While most finite difference methods can be generalized to non-uniform Cartesian meshes²⁶, the nature of traceless multipoles requires uniform Cartesian mesh discretizations. If unequal grid spacing is used, then the trace will be nonzero due to inconsistent coupling between the axial quadrupole components.

The gradient of the charge density at grid sites with respect to an atomic coordinate can be written

$$\frac{\partial {\mathit{q}}_{\text{M}}}{\partial s_{j,\gamma }}=\frac{\partial \mathbf{B}}{\partial s_{j,\gamma }}\mathit{q}-\frac{1}{h}{\nabla }_{\alpha }\frac{\partial \mathbf{B}}{\partial s_{j,\gamma }}{\mathit{d}}_{\alpha }+\frac{1}{3h^2}{\nabla }_{\alpha }{\nabla }_{\beta }\frac{\partial \mathbf{B}}{\partial s_{j,\gamma }}{\mathit{\Theta }}_{\alpha \beta }.$$ (35)

A more compact notation is needed for derivations presented below, and can be achieved by defining a matrix T_B of size N_r × 13N_s

$${\mathbf{T}}_{\text{B}}=\left[\begin{array}{cccccc}\text{B}({\mathbf{r}}_1,{\mathbf{s}}_1)& -\frac{1}{h}\frac{\partial \text{B}({\mathbf{r}}_1,{\mathbf{s}}_1)}{\partial s_{1,x}}& \cdots & -\frac{1}{3h^2}\frac{{\partial }^2\text{B}({\mathbf{r}}_1,{\mathbf{s}}_1)}{\partial s_{1,z}^2}& \cdots & -\frac{1}{3h^2}\frac{{\partial }^2\text{B}({\mathbf{r}}_1,{\mathbf{s}}_{{\text{N}}_{\text{s}}})}{\partial s_{{\text{N}}_{\text{s}},z}^2}\\ ⋮& ⋮& \ddots & ⋮& \ddots & ⋮\\ \text{B}({\mathbf{r}}_{{\text{N}}_{\text{r}}},{\mathbf{s}}_1)& -\frac{1}{h}\frac{\partial \text{B}({\mathbf{r}}_{{\text{N}}_{\text{r}}},{\mathbf{s}}_1)}{\partial s_{1,x}}& \cdots & \frac{1}{3h^2}\frac{{\partial }^2\text{B}({\mathbf{r}}_{{\text{N}}_{\text{r}}},{\mathbf{s}}_1)}{\partial s_{1,z}^2}& \cdots & \frac{1}{3h^2}\frac{{\partial }^2\text{B}({\mathbf{r}}_{{\text{N}}_{\text{r}}},{\mathbf{s}}_{{\text{N}}_{\text{s}}})}{\partial s_{{\text{N}}_{\text{s}},z}^2}\end{array}\right].$$ (36)

The matrix product Φ^t T_B, where Θ is a column vector of length N_r containing the potential from a numerical solution to the LPBE, produces the same tensor components (i.e., the potential, field and field gradient) as M^t T in Eq. (8) for the AMOEBA vacuum electrostatic energy. Using this notation allows manipulation of reaction potentials and intramolecular potentials to be handled on equal footing. The same approach is appropriate for induced dipoles.

There is a trade-off between higher order B-splines and the goal of maintaining the smallest possible support for the multipoles. As the support grow s, the charge density is less representative of the ideal multipole limit. Additionally, placement of solute charge density outside the low-dielectric cavity should be avoided. This restriction of charge density to the solute interior places an upper bound on acceptable grid spacings for use with finite difference discretizations of higher-order B-splines. If, for example, the solute cavity for a hydrogen atom ends approximately 1.2 Å from its center, then the maximum recommended grid spacing when using 5^th order B-splines is 0.48 Å (1.2/2.5), whereas for third order B-splines a value of 0.80 Å is reasonable (1.2/1.5). Therefore, the use of quintic B-splines requires a smaller upper bound on grid spacing than cubic B-splines.

B. Permittivity and modified Debye-Hückel screening factor

The permittivity ε(r) and modified Debye-Hückel screening factor κ̄²(r) functions are defined through a characteristic function H(r_i,s), where r_i represents the coordinates of a grid point and s the coordinates of all multipole sites. Inside the solute cavity the characteristic function is 0, while in the solvent it is 1. For the homogeneous calculation the permittivity is set to unity over all space, while for the solvated state it takes the value 1 inside the solute, ε_s in solvent, and intermediate values over a transition region

$$\epsilon ({\mathbf{r}}_i)=1+({\epsilon }_s-1)\text{H}({\mathbf{r}}_i,\mathbf{s}).$$ (37)

The modified Debye-Hückel screening factor is zero everywhere for the vacuum calculation and for the solvated calculation is defined by

$${\overline{\kappa }}^2({\mathbf{r}}_i)={\overline{\kappa }}_b^2\text{H}({\mathbf{r}}_i,\mathbf{s}),$$ (38)

where ${\overline{\kappa }}_b^2={\epsilon }_s{\kappa }_b^2$ is the modified bulk screening factor and is related to the ionic strength and $I=\frac{1}{2}{\displaystyle \sum _i}{q}_i^2{c}_i\text{ via }{\kappa }_b^2=8\pi I/{\epsilon }_s{k}_{B}T$. Here q_i c_i are the charge and number concentration of mobile ion species i, respectively, k_B is the Boltzmann constant and T the absolute temperature. The characteristic function itself can be formulated as the product of a radially symmetric function applied to each solute atom

$$\text{H}({\mathbf{r}}_i,\mathbf{s})=\prod _{j=1,N_s}{H}_j(\mid {\mathbf{r}}_i-{\mathbf{s}}_j\mid )$$ (39)

where H_j(r) must allow for a smooth transition across the solute-solvent boundary to achieve stable Cartesian energy gradients.^20,31 This is a result of terms that depend on the gradient of the characteristic function with respect to an atomic displacement. A successful approach to defining a differentiable boundary is the use of a polynomial switch S_n(r) of order n, although other definitions have been suggested based on atom centered Gaussians.³² For any atom j, H_j(r) takes the form

$$H_j(r)=\{\begin{array}{ll}0,\hfill & r\le b\hfill \\ S_n(r,b,e)\hfill & b<r<e\hfill \\ 1,\hfill & e\le r\hfill \end{array},$$ (40)

where b is the beginning of the transition between solute and solvent and e the end of the transition. For the permittivity, the switch begins and ends at

$$\begin{array}{c}b={\sigma }_j-w\\ e={\sigma }_j-w\end{array},$$ (41)

where σ_j is the radius of atom j and w indicates how far the smoothing window extends radially inward and outward. For the modified Debye-Hückel screening factor the radius of the largest ionic species σ_ion is also taken into account

$$\begin{array}{c}b={\sigma }_j+{\sigma }_{\mathit{ion}}-w\\ e={\sigma }_j+{\sigma }_{\mathit{ion}}-w\end{array}.$$ (42)

For fixed partial charge force fields, a cubic switch S₃ has been used with success. However, a characteristic function with higher order continuity has been found to improve energy conservation at a given grid spacing. Table V reports representative examples of this effect. By using a 7^th order polynomial switch S₇,

TABLE V.

The norm of the gradient sum over all atoms (kcal/mole/Å) for three different solutes is shown for cubic, quintic and heptic characteristic functions at two grid spacings. A norm of zero, indicating perfect conservation of energy, is nearly achieved for acetamide and ethanol at 0.11 Å grid spacing using a heptic characteristic function. Conservation of energy is improved by reducing grid spacing and also by increasing the continuity of the solute-solvent boundary via the characteristic function.

	Acetamide		Ethanol		CRN
Grid Spacing	0.21	0.11	0.22	0.11	0.32	0.18
Cubic	2.48	0.46	0.77	0.29	18.82	2.58
Quintic	1.93	0.23	0.32	0.15	9.38	2.42
Heptic	0.88	0.06	0.21	0.06	6.27	1.26

$$\begin{array}{l}{S}_7(r,b,e)=\frac{(c_7{r}^7+c_6{r}^6+c_5{r}^5+c_4{r}^4+c_3{r}^3+c_2{r}^2+c_{1}r+c_0)}{-b^7+7b^{6}e-21b^5{e}^2+35b^4{e}^3-35b^3{e}^4+21b^2{e}^5-7b{e}^6+e^7},\\ c_0=b^4(-b^3+7b^{2}e-21b{e}^2+35e^3),\\ c_1=-140b^3{e}^3,\\ c_2=210b^2{e}^2(b+e),\\ c_3=-140be(b^2+3be+e^2),\\ c_4=35(b^3+9b^2+9b{e}^2+e^3),\\ c_5=-84(b^2+3be+e^2),\\ c_6=70(b+e),\\ c_7=-20\end{array}$$ (43)

the first three derivatives of the characteristic function can be constrained to zero at the beginning and end of the switching region. The cubic, quintic and heptic volume exclusions functions are shown in Fig. 4.

Figure 4.

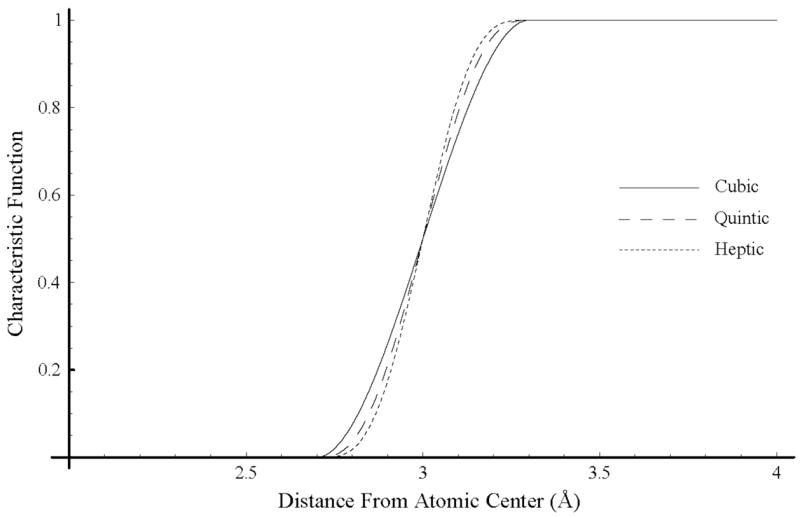
Comparison of cubic, quintic and heptic characteristic functions for an atom with radius 3 Å using a total window width of 0.6 Å.

C. Boundary conditions

Single Debye-Hückel (SDH) and multiple Debye-Hückel (MDH) boundary conditions for a solute are two common approximations to the true potential used to specify Dirichlet boundary conditions for non-spherical solutes described by a collection of atomic multipoles.² SDH assumes that all atomic multipole sites are collected into a single multipole at the center of the solute, which is approximated by a sphere. MDH assumes the superposition of the contribution of each atomic multipole considered in the absence of all other sites that displace solvent. Therefore, to construct the Dirichlet problem for a solute described by an arbitrary number of atomic multipole sites, the potential outside a solvated multipole located at the center of a sphere is required.

For solvent described by the LPBE

$${\nabla }^2\mathit{\Phi }(\mathbf{r})={\kappa }_b^2\mathit{\Phi }(\mathbf{r}),$$ (44)

a solution was first formulated by Kirkwood.³³ This form of the LPBE is simplified relative to Eq. (2) since there is no fixed charge distribution and no spatial variation in either the permittivity or Debye-Hückel screening factor. Inside the cavity, the Poisson equation is obeyed

$${\nabla }^2\mathit{\Phi }(\mathbf{r})=-\frac{4\pi \rho (\mathbf{r})}{\epsilon },$$ (45)

where the charge density ρ(r) may contain moments of arbitrary order. The boundary conditions are enforced by requiring the potential and dielectric displacement to be continuous across the interface between the solute and solvent via

$$\mathit{\Phi }{(\mathbf{r})}_{\text{in}}=\mathit{\Phi }{(\mathbf{r})}_{\text{out}},\text{ and}$$ (46)

$$\epsilon \frac{{\partial \mathit{\Phi }(\mathbf{r})}_{\text{in}}}{\partial r}={\epsilon }_{\text{out}}\frac{\partial \mathit{\Phi }{(\mathbf{r})}_{\text{out}}}{\partial r},$$ (47)

respectively. Additional requirements on the solution are that it be bounded at the origin and approach an arbitrary constant at infinity, usually chosen to be zero.

In presenting the solution, it is convenient for our purposes to continue using Cartesian multipoles, rather than switching to spherical harmonics, although there is a well-known equivalence between the two approaches.³⁴ The potential at r due to a symmetric, traceless multipole in a homogeneous dielectric ε is

$${\mathit{\Phi }}_{\epsilon }({\mathbf{r}}_{ij})={({\mathbf{T}}_{\epsilon })}^t{\mathbf{M}}_j={\left(\left[\begin{array}{c}1\\ -\frac{\partial }{\partial x}\\ -\frac{\partial }{\partial y}\\ -\frac{\partial }{\partial z}\\ \frac{1}{3}-\frac{{\partial }^2}{\partial x\partial x}\\ ⋮\end{array}\right]\left(\frac{1}{\epsilon r_{ij}}\right)\right)}^t\left[\begin{array}{c}{q}_j\\ {\mu }_{x,j}\\ {\mu }_{y,j}\\ {\mu }_{z,j}\\ {\mathrm{\Theta }}_{xx,j}\\ ⋮\end{array}\right],$$ (48)

where r_ij = r_i − s_j might be the difference between a grid location and a multipole site. The potential inside the spherical cavity is the superposition of the homogeneous potential and the reaction potential

$${\mathit{\Phi }}_{\text{in}}({\mathbf{r}}_{\text{ij}})={[(\mathbf{I}+{\mathbf{R}}_{\text{in}}){\mathbf{T}}_{\epsilon }]}^t{\mathbf{M}}_j,$$ (49)

where I is the identity matrix and R_in is a diagonal matrix with diagonal elements

$$[c_{\text{in}}(0),c_{\text{in}}(1),c_{\text{in}}(1),c_{\text{in}}(1),c_{\text{in}}(2),\cdots ]$$ (50)

that are based on coefficients for multipoles of order n to be determined by the boundary conditions

$$c_{\text{in}}(n)={\beta }_n{\left(\frac{r_{ij}}{a}\right)}^{2n+1}.$$ (51)

Similarly, the potential outside the cavity is

$${\mathit{\Phi }}_{\text{out}}({\mathbf{r}}_{\text{ij}})={({\mathbf{R}}_{\text{out}}{\mathbf{T}}_{\epsilon })}^t{\text{M}}_j,$$ (52)

where R_out is a diagonal matrix with diagonal elements

$$[c_{\text{out}}(0),c_{\text{out}}(1),c_{\text{out}}(1),c_{\text{out}}(1),c_{\text{out}}(2),\cdots ]$$ (53)

based on a second set of coefficients for multipoles of order n also determined by the boundary conditions

$$c_{\text{out}}(n)=\frac{\epsilon }{{\epsilon }_{\text{out}}}\kappa r_{ij}{\alpha }_n{k}_n(\kappa r_{ij}){\left(\frac{r_{ij}}{a}\right)}^n.$$ (54)

where k_n(x) is the modified spherical Bessel function of the third kind

$$k_n(x)=\frac{\pi {\text{e}}^{-\text{x}}}{2x}\sum _{i=0}^n\frac{(n+i)!}{i!(n-i)!{(2x)}^i}.$$ (55)

Kirkwood first solved Eqs. (44) and (45) subject to the boundary conditions in Eqs. (46) and (47) to determine α_n and β_n as

$${\alpha }_n=\frac{(2n+1)/\kappa a}{n{k}_n(\kappa a)/\widehat{\epsilon }-\kappa a{k}_n^{\prime }(\kappa a)}$$ (56)

and

$${\beta }_n=\frac{(n+1)k_n(\kappa a)/\widehat{\epsilon }+\kappa a{k}_n^{\prime }(\kappa a)}{k_n(\kappa a)/\widehat{\epsilon }-\kappa a{k}_n^{\prime }(\kappa a)},$$ (57)

where $k_n^{\prime }(x)$ is the derivative of k_n(x) and ε̂ is the ratio of the permittivity in solvent to that inside the sphere ε_out/ε.³³ We only require the potential outside the cavity to construct SDH and MDH boundary conditions and therefore we provide specific values of α_n and k_n through quadrupole order as shown in Table I. As the ionic strength goes to zero, the Laplace equation is obeyed in solvent. For multipoles through quadrupole order, the difference between the LPBE and Laplace potentials outside the cavity are summarized in Table II.

TABLE I.

Explicit values for the functions α_n(x)and k_n(x) up to quadrupole order.

n	${\alpha }_n(x)/\left(\frac{2exp(x)}{\pi }\right)$	$k_n(x)/\left(\frac{\pi }{2exp(x)}\right)$
0	$\frac{1}{(1+x)}$	$\frac{1}{x}$
1	$\frac{3\widehat{\epsilon }x}{1+x+\widehat{\epsilon }(2+2x+x^2)}$	$\frac{1+x}{x^2}$
2	$\frac{5\widehat{\epsilon }{x}^2}{2(3+3x+x^2)+\widehat{\epsilon }(9+9x+4x^2+x^3)}$	$\frac{(3+3x+x^2)}{x^3}$

TABLE II.

Explicit values of the coefficients used to calculate the potential at the grid boundary of LPBE and PE calculations, respectively, under the SDH or MDH approximation. The LPBE coefficients reduce to the PE coefficients as salt concentration goes to zero.

n	$\kappa r{\alpha }_n(\kappa a)k_n(\kappa r){\left(\frac{r}{a}\right)}^n$	$\underset{\kappa \to 0}{lim}\left[\kappa r{\alpha }_n(\kappa a)k_n(\kappa r){\left(\frac{r}{a}\right)}^n\right]$
0	$\frac{exp(\kappa (a-r))}{1+\kappa a}$	1
1	$\frac{3\widehat{\epsilon }exp(\kappa (a-r))(1+\kappa r)}{1+\kappa a+\widehat{\epsilon }(2+2\kappa \alpha +{(\kappa a)}^2)}$	$\frac{3\widehat{\epsilon }}{1+2\widehat{\epsilon }}$
2	$\frac{5\widehat{\epsilon }exp(\kappa (a-r))(3+3\kappa r+{(\kappa r)}^2)}{2(3+3\kappa a+{(\kappa a)}^2)+\widehat{\epsilon }(9+9\kappa a+4{(\kappa a)}^2+{(\kappa a)}^3)}$	$\frac{5\widehat{\epsilon }}{2+3\widehat{\epsilon }}$

D. Permanent atomic multipole solvation energy and gradient

The PMPB permanent atomic multipole (PAM) solvation energy and gradient are very similar to those for fixed partial charge force fields. Based on Eqs. (15) and (34) the PAM vacuum, solvated and reaction potentials are, respectively,

$$\begin{array}{c}{\mathit{\Phi }}_{\text{v}}^{\text{M}}=-4\pi {\mathbf{A}}_{\text{v}}^{-1}{\mathit{q}}_{\text{M}}\\ {\mathit{\Phi }}_{\text{s}}^{\text{M}}=-4\pi {\mathbf{A}}_{\text{s}}^{-1}{\mathit{q}}_{\text{M}}\\ {\mathit{\Phi }}^{\text{M}}={\mathit{\Phi }}_{\text{s}}^{\text{M}}-{\mathit{\Phi }}_{\text{v}}^{\text{M}}\end{array}.$$ (58)

The expression for the permanent electrostatic solvation energy is then identical to that for a fixed partial charge force field given in Eqs. (13) and (16), except the source charge density is based on PAM via q_M

$$\begin{array}{c}\mathrm{\Delta }{\text{G}}_{\text{M}}=\frac{1}{2}{({\mathit{\Phi }}^{\text{M}})}^t{\mathit{q}}_{\text{M}}\\ =\frac{1}{2}{(-4\pi {\mathit{q}}_{\text{M}})}^t({\mathbf{A}}_{\text{s}}^{-1}-{\mathbf{A}}_{\text{v}}^{-1}){\mathit{q}}_{\text{M}}\end{array}.$$ (59)

Derivation of the energy gradient is identical to Eqs. (17–22) and yields

$$\frac{\partial \mathrm{\Delta }{\text{G}}_{\text{M}}}{\partial s_{j,\gamma }}={({\mathit{\Phi }}^{\text{M}})}^t\frac{\partial {\mathit{q}}_{\text{M}}}{\partial s_{j,\gamma }}+\frac{1}{8\pi }({\mathit{\Phi }}_{\text{s}}^{\text{M}})\frac{\partial {\mathbf{A}}_s}{\partial s_{j,\gamma }}{\mathit{\Phi }}_{\text{s}}^{\text{M}}.$$ (60)

There are, however, some important differences between achieving smooth gradients for a fixed partial charge force field and one based on PAM. First, as discussed in the section on multipole discretization, quadrupoles require at least 5^th order B-splines to guarantee continuous derivatives of the source charge density with respect to movement of a multipole site

$$\frac{\partial {\mathit{q}}_{\text{M}}}{\partial s_{j,\gamma }}=\frac{\partial {\mathbf{T}}_{\text{B}}}{\partial s_{j,\gamma }}\mathbf{M}.$$ (61)

Second, we have found that if a third order polynomial is used to define the transition between solute and solvent for purposes of assigning the permittivity and the modified Debye-Hückel screening factor, energy conservation is achieved only for very fine grid spacing. As discussed earlier, use of a 7^th order polynomial improves energy conservation for coarser grids. Details of the numerical realization of Eq. (60), including torques, are presented in part 3 of the Appendix.

E. Self-consistent reaction field

An SCRF protocol is used to achieve numerical convergence of the coupling between a polarizable solute and continuum solvent. The starting point of the iterative convergence is the total “direct” field E_d at each polarizable site. This is defined by the sum of the PAM intramolecular field

$${\mathbf{E}}_{\text{d}}={\mathbf{T}}_{\text{d}}^{(1)}\mathbf{M},$$ (62)

where T_d⁽¹⁾ is analogous to the tensor matrix used in deriving the AMOEBA vacuum energy in Eq. (12), and the PAM reaction field

$${\mathbf{E}}_{\text{RF}}^{\text{M}}=-{\mathbf{D}}_{\text{B}}^t{\mathit{\Phi }}^{\text{M}},$$ (63)

where D_B is a matrix of B-spline derivatives of size N_r by 3N_s

$${\mathbf{D}}_{\text{B}}=-\frac{1}{h}\left[\begin{array}{ccccc}\frac{\partial \text{B}({\mathbf{r}}_1,{\mathbf{s}}_1)}{\partial s_{1,x}}& \frac{\partial \text{B}({\mathbf{r}}_1,{\mathbf{s}}_1)}{\partial s_{1,y}}& \frac{\partial \text{B}({\mathbf{r}}_1,{\mathbf{s}}_1)}{\partial s_{1,z}}& \cdots & \frac{\partial \text{B}({\mathbf{r}}_1,{\mathbf{s}}_{{\text{N}}_{\text{s}}})}{\partial s_{{\text{N}}_{\text{s}},z}}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ \frac{\partial \text{B}({\mathbf{r}}_{{\text{N}}_{\text{r}}},{\mathbf{s}}_1)}{\partial s_{1,x}}& \frac{\partial \text{B}({\mathbf{r}}_{{\text{N}}_{\text{r}}},{\mathbf{s}}_1)}{\partial s_{1,y}}& \frac{\partial \text{B}({\mathbf{r}}_{{\text{N}}_{\text{r}}},{\mathbf{s}}_1)}{\partial s_{1,z}}& \cdots & \frac{\partial \text{B}({\mathbf{r}}_{{\text{N}}_{\text{r}}},{\mathbf{s}}_{{\text{N}}_{\text{s}}})}{\partial s_{{\text{N}}_{\text{s}},z}}\end{array}\right],$$ (64)

that produces the reaction field at induced dipoles sites given a potential grid. The induced dipoles are determined as the product of the direct field E_d with a vector of isotropic atomic polarizabilities α:

$$\begin{array}{c}{\mathit{\mu }}_{\text{d}}=\mathit{\alpha }{\mathbf{E}}_{\text{d}}\\ =\mathit{\alpha }({\mathbf{T}}_{\text{d}}^{(1)}\mathbf{M}-{\mathbf{D}}_{\text{B}}^t{\mathit{\Phi }}^{\text{M}})\end{array}.$$ (65)

We define the direct model of polarization to consist of induced dipoles not acted upon by each other or their own reaction field. Although this is a nontrivial approximation, the direct model requires little more work to compute energies than a fixed partial charge force field since the limiting factor in both cases is two numerical LPBE solutions. Energy gradients under the direct model require three pairs of LPBE solutions and are therefore a factor of 3 more expensive than for a fixed charge solute. The direct model is expected to be quite useful for many applications. For example, a geometry optimization might utilize the direct polarization model initially, then switch to the more expensive mutual polarization model described below as the minimum is approached.

In contrast to the direct model, the total solvated field E has two additional contributions due to the induced dipoles and their reaction field,

$$E={\mathbf{T}}_{\text{d}}^{(1)}\mathbf{M}+{\mathbf{T}}^{(11)}\mathit{\mu }-{\mathbf{D}}_{\text{B}}^t({\mathit{\Phi }}^{\text{M}}+{\mathit{\Phi }}^{\mu }),$$ (66)

for a sum of 4 contributions. The procedure for determining the vacuum, solvated and reaction potential, respectively, due to the induced dipoles is identical to that of the PAM

$$\begin{array}{c}{\mathit{\Phi }}_{\text{v}}^{\mu }=-4\pi {\mathbf{A}}_{\text{v}}^{-1}{\mathit{q}}_{\mu }\\ {\mathit{\Phi }}_{\text{s}}^{\mu }=-4\pi {\mathbf{A}}_{\text{s}}^{-1}{\mathit{q}}_{\mu }\\ {\mathit{\Phi }}^{\mu }={\mathit{\Phi }}_{\text{s}}^{\mu }-{\mathit{\Phi }}_{\text{v}}^{\mu }\end{array},$$ (67)

except the source charge density is

$${\mathit{q}}_{\mu }={\mathbf{D}}_{\text{B}}\mathit{\mu }.$$ (68)

The induced dipoles

$$\mathit{\mu }=\mathit{\alpha }[{\mathbf{T}}_{\text{d}}^{(1)}\mathbf{M}+{\mathbf{T}}^{(11)}\mathit{\mu }-{\mathbf{D}}_{\text{B}}^t({\mathit{\Phi }}^{\text{M}}+{\mathit{\Phi }}^{\mu })],$$ (69)

can be determined in an iterative fashion using successive over-relaxation (SOR) to accelerate convergence.³⁵ The SCRF is usually deemed to have converged when the change in the induced dipoles is less than 10⁻² RMS debye between steps. This generally requires 4–5 cycles and therefore the mutual polarization model necessitates 8–10 additional numerical solutions of the LPBE to determine the PMPB solvation energy. Although calculation of the direct polarization energy is no more expensive than that for fixed multipoles, mutual polarization energies that depend on SCRF convergence are approximately a factor of 5 more costly.

F. PMPB electrostatic solvation energy

Having described the PAM solvation energy and gradients and our approach for determining the induced dipoles, it is now possible to discuss the total solvated electrostatic energy for the PMPB model,

$${\text{U}}_{\text{elec}}=\frac{1}{2}[{\mathbf{M}}^t\mathbf{T}-{\mathit{\mu }}^t{\mathbf{T}}_{\text{p}}^{(1)}+{\mathit{\Phi }}^t{\mathbf{T}}_B]\mathbf{M},$$ (70)

where Φ is the LPBE reaction potential for the converged solute charge distribution

$$\mathit{\Phi }={\mathit{\Phi }}^M+{\mathit{\Phi }}^{\mu }.$$ (71)

The total electrostatic energy in solvent is similar to the vacuum electrostatic energy of Eq. (8), with an important difference. The vacuum induced dipoles μ^v change in the presence of a continuum solvent by an amount represented by μ^Δ, such that the SCRF induced moments μ can be decomposed into a sum

$$\mathit{\mu }={\mathit{\mu }}^{\text{v}}+{\mathit{\mu }}^{\mathrm{\Delta }}.$$ (72)

The change in the potential, field, etc. within the solute is not only a result of the solvent response, but also due to changes in intramolecular polarization. By definition, the electrostatic solvation energy ΔG_elec is the change in total electrostatic energy due to moving from vacuum to solvent

$$\begin{array}{c}\mathrm{\Delta }{\text{G}}_{\text{elec}}={\text{U}}_{\text{elec}}-{\text{U}}_{\text{elec}}^{\text{v}}\\ =\frac{1}{2}[-{({\mathit{\mu }}^{\mathrm{\Delta }})}^t{\mathbf{T}}_{\text{p}}^{(1)}+{\mathit{\mu }}^t{\mathbf{T}}_{\text{B}}]\mathbf{M}\end{array}.$$ (73)

In practice, it is convenient to compute the total solvated electrostatic energy U_elec and vacuum electrostatic energy ${\text{U}}_{\text{elec}}^{\text{v}}$ using the SCRF μ and vacuum μ^v induced dipole moments, respectively. The electrostatic solvation energy ΔG_elec is then determined as the difference.

G. Polarization energy and gradient

As described previously, the induced dipoles are determined using an iterative SOR procedure until a predetermined convergence criterion is achieved. Since this is a linear system, it is possible to solve for the induced dipoles directly, which facilitates derivation of the polarization energy gradient with respect to atomic displacements. Substitution of the reaction potential due to the induced dipoles μ^ν from Eq. (67) into the expression for the induced dipoles in Eq. (69) makes clear all dependencies on μ.

$$\mathit{\mu }=\mathit{\alpha }[{\mathbf{T}}_{\text{d}}^{(1)}\mathbf{M}-{\mathbf{D}}_{\text{B}}^t{\mathit{\Phi }}^{\text{M}}+{\mathbf{T}}^{(11)}\mathit{\mu }-4\pi {\mathbf{D}}_{\text{B}}^t({\mathbf{A}}_{\text{s}}^{-1}-{\mathbf{A}}_{\text{v}}^{-1}){\mathbf{D}}_{\text{B}}].$$ (74)

Collecting all terms containing the induced dipoles on the left hand side gives

$$[{\mathit{\alpha }}^{-1}-{\mathbf{T}}^{(11)}+4\pi {\mathbf{D}}_{\text{B}}^t({\mathbf{A}}_{\text{s}}^{-1}-{\mathbf{A}}_{\text{v}}^{-1}){\mathbf{D}}_{\text{B}}]\mathit{\mu }={\mathbf{T}}_{\text{d}}^{(1)}\mathbf{M}-{\mathbf{D}}_{\text{B}}^t{\mathit{\Phi }}^{\text{M}}.$$ (75)

For convenience, a matrix C is defined as

$$\mathbf{C}=[{\mathit{\alpha }}^{-1}-{\mathbf{T}}^{(11)}+4\pi {\mathbf{D}}_{\text{B}}^t({\mathbf{A}}_{\text{s}}^{-1}-{\mathbf{A}}_{\text{v}}^{-1}){\mathbf{D}}_{\text{B}}],$$ (76)

which is substituted into Eq. (75) to show the induced dipoles are a linear function of the PAM M

$$\begin{array}{c}\mathit{\mu }={\mathbf{C}}^{-1}({\mathbf{T}}_{\text{d}}^{(1)}\mathbf{M}-{\mathbf{D}}_{\text{B}}^t{\mathit{\Phi }}^{\text{M}})\\ ={\mathbf{C}}^{-1}({\mathbf{E}}_{\text{d}}+{\mathbf{E}}_{\text{RF}}^{\text{M}})\end{array}.$$ (77)

The first term results from the intramolecular interaction tensor ${\mathbf{T}}_{\text{d}}^{(1)}$ that implicitly contains the AMOEBA group based polarization scheme, and the second term is the permanent reaction field.

The polarization energy can now be described in terms of the permanent reaction field and permanent intramolecular solute field E_p

$${\text{U}}_{\mu }=-\frac{1}{2}{({\mathbf{E}}_{\text{p}}+{\mathbf{E}}_{\text{RF}}^{\text{M}})}^t\mathit{\mu }.$$ (78)

To find the polarization energy gradient, we wish to avoid terms that rely on the change in induced dipoles with respect to atomic displacement. Therefore, the induced dipoles in Eq. (78) are replaced using Eq. (77) to yield

$${\text{U}}_{\mu }=-\frac{1}{2}{({\mathbf{E}}_{\text{p}}+{\mathbf{E}}_{\text{RF}}^{\text{M}})}^t{\mathbf{C}}^{-1}({\mathbf{E}}_{\text{d}}+{\mathbf{E}}_{\text{RF}}^{\text{M}}).$$ (79)

By the chain rule, the polarization energy gradient is

$$\begin{array}{l}\frac{\partial U_{\mu }}{\partial s_{j,\gamma }}=-\frac{1}{2}[{\left(\frac{\partial {\mathbf{E}}_{\text{p}}}{\partial s_{j,\gamma }}+\frac{\partial {\mathbf{E}}_{\text{RF}}^{\text{M}}}{\partial s_{j,\gamma }}\right)}^t{\mathbf{C}}^{-1}({\mathbf{E}}_{\text{d}}+{\mathbf{E}}_{\text{RF}}^{\text{M}})+{({\mathbf{E}}_{\text{p}}+{\mathbf{E}}_{\text{RF}}^{\text{M}})}^t\frac{\partial {\mathbf{C}}^{-1}}{\partial s_{j,\gamma }}({\mathbf{E}}_{\text{d}}+{\mathbf{E}}_{\text{RF}}^{\text{M}})\\ +{({\mathbf{E}}_{\text{p}}+{\mathbf{E}}_{\text{RF}}^{\text{M}})}^t{\mathbf{C}}^{-1}\left(\frac{\partial {\mathbf{E}}_{\text{d}}}{\partial s_{j,\gamma }}+\frac{\partial {\mathbf{E}}_{\text{RF}}^{\text{M}}}{\partial s_{j,\gamma }}\right)]\end{array}$$ (80)

For convenience a mathematical quantity _ is defined as

$$\mathit{\nu }=({\mathbf{E}}_{\text{p}}+{\mathbf{E}}_{\text{RF}}^{\text{M}}){\mathbf{C}}^{-1},$$ (81)

which is similar to μ. We can now greatly simplify Eq. (80) using Eqs. (77) and (81) along with the identity $\frac{\partial {\mathbf{C}}^{-1}}{\partial s_{j,\gamma }}=-{\mathbf{C}}^{-1}\frac{\partial {\mathbf{C}}^{-1}}{\partial s_{j,\gamma }}{\mathbf{C}}^{-1}$ to give

$$\frac{\partial {\text{U}}_{\mu }}{\partial s_{j,\gamma }}=-\frac{1}{2}\left[{\left(\frac{\partial {\mathbf{E}}_{\text{p}}}{\partial s_{j,\gamma }}\right)}^t\mathit{\mu }+{\mathit{\nu }}^t\frac{\partial {\mathbf{E}}_{\text{d}}}{\partial s_{j,\gamma }}+\left(\frac{\partial {\mathbf{E}}_{\text{RF}}^{\text{M}}}{\partial s_{j,\gamma }}\right)\mathit{\mu }+{\mathit{\nu }}^t\frac{\partial {\mathbf{E}}_{\text{RF}}^{\text{M}}}{\partial s_{j,\gamma }}-{\mathit{\nu }}^t\frac{\partial \mathbf{C}}{\partial s_{j,\gamma }}\mathit{\mu }\right].$$ (82)

G II. Direct polarization gradient

Under the direct polarization model, C is an identity matrix whose derivative is zero, and therefore Eq. (82) simplifies to

$$\frac{\partial {\text{U}}_{{\mu }_{\text{d}}}}{\partial s_{j,\gamma }}=-\frac{1}{2}\left[{\left(\frac{\partial {\mathbf{E}}_{\text{p}}}{\partial s_{j,\gamma }}\right)}^t\mathit{\mu }+{\mathit{\nu }}^t\frac{\partial {\mathbf{E}}_{\text{d}}}{\partial s_{j,\gamma }}+\left(\frac{\partial {\mathbf{E}}_{\text{RF}}^{\text{M}}}{\partial s_{j,\gamma }}\right)\mathit{\mu }+{\mathit{\nu }}^t\frac{\partial {\mathbf{E}}_{\text{RF}}^{\text{M}}}{\partial s_{j,\gamma }}\right].$$ (83)

The first two terms on the RHS appear in the polarization energy gradient even in the absence of a continuum reaction field and are described elsewhere.⁴ The third and fourth terms are specific to LPBE calculations and will now be discussed. The derivative of the LPBE reaction field due to permanent multipoles with respect to movement of any atom has a similar form to the analogous derivative of the potential. Substitution for the field using Eq. (63) into the third term of Eq. (83) gives

$${\left(\frac{\partial {\mathbf{E}}_{\text{RF}}^{\text{M}}}{\partial s_{j,\gamma }}\right)}^t\mathit{\mu }=-\frac{\partial {\mathbf{D}}_{\text{B}}^t{\mathit{\Phi }}^{\text{M}}}{\partial s_{j,\gamma }}\mathit{\mu }.$$ (84)

Substitution of the permanent multipole potential from Eq. (58) into Eq. (84) yields

$${\left(\frac{\partial {\mathbf{E}}_{\text{RF}}^{\text{M}}}{\partial s_{j,\gamma }}\right)}^t\mathit{\mu }=4\pi \frac{\partial }{\partial s_{j,\gamma }}[{\mathbf{D}}_{\text{B}}^t({\mathbf{A}}_{\text{s}}^{-1}-{\mathbf{A}}_{\text{v}}^{-1}){\mathbf{T}}_{\text{B}}\mathbf{M}]\mathit{\mu },$$ (85)

which is differentiated by applying the chain rule

$${\left(\frac{\partial {\mathbf{E}}_{\text{RF}}^{\text{M}}}{\partial s_{j,\gamma }}\right)}^t\mathit{\mu }=4\pi \left[\frac{\partial {\mathbf{D}}_{\text{B}}^t}{\partial s_{j,\gamma }}({\mathbf{A}}_{\text{s}}^{-1}-{\mathbf{A}}_{\text{v}}^{-1}){\mathbf{T}}_{\text{B}}\mathbf{M}+{\mathbf{D}}_{\text{B}}^t\frac{\partial {\mathbf{A}}_{\text{s}}^{-1}}{\partial s_{j,\gamma }}{\mathbf{T}}_{\text{B}}\mathbf{M}+{\mathbf{D}}_{\text{B}}^t({\mathbf{A}}_{\text{s}}^{-1}-{\mathbf{A}}_{\text{v}}^{-1})\frac{\partial {\mathbf{T}}_{\text{B}}}{\partial s_{j,\gamma }}\mathbf{M}\right]\mathit{\mu }.$$ (86)

The same simplifications described in Eqs. (18-22) are applied to Eq. (86), except that in this case the first and third terms are not equivalent and cannot be combined

$${\left(\frac{\partial {\mathbf{E}}_{\text{RF}}^{\text{M}}}{\partial s_{j,\gamma }}\right)}^t\mathit{\mu }=-{({\mathit{\Phi }}^{\mu })}^t\frac{\partial {\mathbf{T}}_{\text{B}}}{\partial s_{j,\gamma }}\mathbf{M}-\frac{1}{4\pi }({\mathit{\Phi }}_{\text{s}}^{\mu })\frac{\partial {\mathbf{A}}_{\text{s}}}{\partial s_{j,\gamma }}{\mathit{\Phi }}_{\text{s}}^{\text{M}}-{\mathit{\mu }}^{\text{t}}\frac{\partial {\mathbf{D}}_{\text{B}}^t}{\partial s_{j,\gamma }}{\mathit{\Phi }}^{\text{M}}.$$ (87)

The fourth term on the RHS of Eq. (83) leads to a result analogous to Eq. (87) using similar arguments

$${\mathit{\nu }}^t\frac{\partial {\mathbf{E}}_{\text{RF}}^{\text{M}}}{\partial s_{j,\gamma }}=-{({\mathit{\Phi }}^{\nu })}^t\frac{\partial {\mathbf{T}}_{\text{B}}}{\partial s_{j,\gamma }}\mathbf{M}-\frac{1}{4\pi }({\mathit{\Phi }}_{\text{s}}^{\mu })\frac{\partial {\mathbf{A}}_{\text{s}}}{\partial s_{j,\gamma }}{\mathit{\Phi }}_{\text{s}}^{\text{M}}-{\mathit{\nu }}^{\text{t}}\frac{\partial {\mathbf{D}}_{\text{B}}^t}{\partial s_{j,\gamma }}{\mathit{\Phi }}^{\text{M}}.$$ (88)

G III. Mutual polarization gradient

In addition to the implicit difference due to the induced dipoles being converged self-consistently, the full mutual polarization gradient includes an additional contribution beyond the direct polarization gradient. Specifically, the derivative of the matrix C leads to four terms

$$\begin{array}{l}{\mathit{\nu }}^t\frac{\partial \mathbf{C}}{\partial s_{j,\gamma }}\mathit{\mu }={\mathit{\nu }}^t[\frac{\partial {\mathbf{T}}^{(11)}}{\partial s_{j,\gamma }}+4\pi \frac{\partial {\mathbf{D}}_{\text{B}}^t}{\partial s_{j,\gamma }}({\mathbf{A}}_{\text{s}}^{-1}-{\mathbf{A}}_{\text{v}}^{-1}){\mathbf{D}}_{\text{B}}+4\pi {\mathbf{D}}_{\text{B}}^t\frac{\partial {\mathbf{A}}_{\text{s}}^{-1}}{\partial s_{j,\gamma }}{\mathbf{D}}_{\text{B}}\\ +4\pi {\mathbf{D}}_{\text{B}}^t({\mathbf{A}}_{\text{s}}^{-1}-{\mathbf{A}}_{\text{v}}^{-1})\frac{\partial {\mathbf{D}}_{\text{B}}}{\partial s_{j,\gamma }}]\mathit{\mu }\end{array}.$$ (89)

The first term on the RHS occurs in vacuum and is described elsewhere⁴, while the final three terms are specific to LPBE calculations. Using the simplifications described in Eqs. (18–22) results in

$${\mathit{\nu }}^t\frac{\partial \mathbf{C}}{\partial s_{j,\gamma }}\mathit{\mu }={\mathit{\nu }}^t\frac{\partial {\mathbf{T}}^{(11)}}{\partial s_{j,\gamma }}\mathit{\mu }-{\mathit{\nu }}^t\frac{\partial {\mathbf{D}}_{\text{B}}^t}{\partial s_{j,\gamma }}{\mathit{\Phi }}^{\mu }-\frac{1}{4\pi }{({\mathit{\Phi }}_s^{\nu })}^t\frac{\partial {\mathbf{A}}_{\text{s}}}{\partial s_{j,\gamma }}{\mathit{\Phi }}_{\text{s}}^{\mu }-{({\mathit{\Phi }}^{\nu })}^t\frac{\partial {\mathbf{D}}_{\text{B}}}{\partial s_{j,\gamma }}\mathit{\mu }.$$ (90)

Substitution of Eqs. (87), (88) and (90) into Eq. (82) gives the total mutual polarization energy gradient for an AMOEBA solute interacting self-consistently with the PMPB continuum.

$$\begin{array}{l}\frac{\partial {\text{U}}_{\mu }}{\partial s_{j,\gamma }}=-\frac{1}{2}\left[{\left(\frac{\partial {\mathbf{E}}_{\text{p}}}{\partial s_{j,\gamma }}\right)}^t\mathit{\mu }+{\mathit{\nu }}^t\frac{\partial {\mathbf{E}}_{\text{d}}}{\partial s_{j,\gamma }}\right]-\frac{1}{2}{\mathit{\nu }}^t\frac{\partial {\mathbf{T}}^{(11)}}{\partial s_{j,\gamma }}\mathit{\mu }\\ +\frac{1}{2}\left[{({\mathit{\Phi }}^{\mu })}^t\frac{\partial {\mathbf{T}}_{\text{B}}}{\partial s_{j,\gamma }}\mathbf{M}+{\mathit{\mu }}^t\frac{\partial {\mathbf{D}}_{\text{B}}^t}{\partial s_{j,\gamma }}{\mathit{\Phi }}^{\text{M}}\right]+\frac{1}{8\pi }{({\mathit{\Phi }}_{\text{s}}^{\mu })}^t\frac{\partial {\mathbf{A}}_{\text{s}}}{\partial {\text{s}}_{j,\gamma }}{\mathit{\Phi }}_{\text{s}}^{\text{M}}\\ +\frac{1}{2}\left[{({\mathit{\Phi }}^{\nu })}^t\frac{\partial {\mathbf{T}}_{\text{B}}}{\partial s_{j,\gamma }}\mathbf{M}+{\mathit{\nu }}^t\frac{\partial {\mathbf{D}}_{\text{B}}^t}{\partial s_{j,\gamma }}{\mathit{\Phi }}^{\text{M}}\right]+\frac{1}{8\pi }{({\mathit{\Phi }}_{\text{s}}^{\nu })}^t\frac{\partial {\mathbf{A}}_s}{\partial s_{j,\gamma }}{\mathit{\Phi }}_{\text{s}}^{\text{M}}\\ +\frac{1}{2}\left[{({\mathit{\Phi }}^{\nu })}^t\frac{\partial {\mathbf{D}}_{\text{B}}}{\partial s_{j,\gamma }}\mathit{\mu }+{\mathit{\nu }}^t\frac{\partial {\mathbf{D}}_{\text{B}}^t}{\partial s_{j,\gamma }}{\mathit{\Phi }}^{\mu }\right]+\frac{1}{8\pi }{({\mathit{\Phi }}_{\text{s}}^{\nu })}^t\frac{\partial {\mathbf{A}}_{\text{s}}}{\partial s_{j,\gamma }}{\mathit{\Phi }}_{\text{s}}^{\mu }\end{array}$$ (91)

The first two terms (where each set of square brackets will be considered a single term) are evaluated even in the absence of continuum solvent, although in this case μ and ν have been converged in a self-consistent field that includes continuum contributions. The remaining terms are analogous to those found in Poisson-Boltzmann calculations involving only permanent electrostatics. The number of LPBE calculations required for evaluation of the energy gradient includes two for the permanent multipoles and two each for μ and ν at each SOR convergence step. Further details on the numerical implementation of Eq. (91) can be found in the third section of the Appendix.

IV. VALIDATION AND APPLICATION

This section presents useful benchmarks for demonstrating the expected numerical precision of the present work. Our first goal is to compare against analytical results for a source charge distribution described by a single charge, dipole, polarizable dipole or quadrupole located at the center of a low dielectric sphere in high dielectric solvent. The transition between solute and solvent is initially specified using a step function, and then subsequently using a smooth transition described by a heptic polynomial. We then compare analytic gradients to those determined using finite-differences of the energy for a variety of two sphere systems to isolate the reaction field, dielectric boundary and ionic boundary gradients for the permanent multipole solvation energy, the direct polarization model and the mutual polarization model. Finally, the method is applied to a series of proteins and comparisons are made to corresponding simulations in explicit water.

A. Energy

The numerical accuracy of the multipole discretization procedure was studied by comparison to analytical solutions of the Poisson equation for a monopole, dipole, polarizable dipole and quadrupole located within a spherical cavity of radius 3.0 Å. The monopole case, or Born ion³⁶, has a well-known analytical solution

$${\text{U}}_q=\frac{1}{2}\left(\frac{1}{\epsilon }-1\right)\frac{q^2}{a}$$ (92)

where q is the charge magnitude, a the cavity radius and ε is the solvent dielectric. For a permanent dipole, the analogous solution was first determined by Onsager¹,

$${\text{U}}_d=-\frac{1}{2}\left(\frac{2(\epsilon -1)}{1+2\epsilon }\right)\frac{\mathit{d}\cdot \mathit{d}}{a^3},$$ (93)

where d is the dipole vector. For a polarizable dipole, the energy is the sum of two contributions, the cost of polarization and the energy of the total dipole in the total reaction field³⁷

$${\text{U}}_{\alpha ,d}=-\frac{1}{2}\frac{f\mathit{d}\cdot \mathit{d}}{1-f\alpha },$$ (94)

where α is the polarizability, d is the permanent dipole and f is the reaction field factor

$$f=\frac{1}{a^3}\left[\frac{2(\epsilon -1)}{1+2\epsilon }\right].$$ (95)

The analytic solution for the self-energy of a traceless Cartesian quadrupole can be derived beginning from the energy of a quadrupole in an electric field gradient

$${\text{U}}_{{\mathrm{\Theta }}_{\gamma \delta }}\frac{{\mathrm{\Theta }}_{\gamma \delta }}{3}{\nabla }_{\delta }{\nabla }_{\gamma }\mathit{\Phi },$$ (96)

where we are summing over the subscripts γ and δ, and the factor of 1/3 is due to use of traceless quadrupoles.²⁹ To determine the needed reaction field gradient, which for the moment will be assumed to come from any quadrupole component and not necessarily be a self-interaction, we begin from the reaction potential inside the cavity

$${\mathit{\Phi }}_{{\mathrm{\Theta }}_{\alpha \beta }}=-\frac{{\mathrm{\Theta }}_{\alpha \beta }}{3}\left[\frac{3(\epsilon -1)}{2+3\epsilon }\right]\frac{3\alpha \beta }{a^5}$$ (97)

and take the first derivative

$${\nabla }_{\gamma }{\mathrm{\Phi }}_{{\mathrm{\Theta }}_{\alpha \beta }}=-\frac{{\mathrm{\Theta }}_{\alpha \beta }}{3}\left[\frac{3(\epsilon -1)}{2+3\epsilon }\right]\frac{3(\beta {\delta }_{\alpha \gamma }+\alpha {\delta }_{\beta \gamma })}{a^5},$$ (98)

followed by a second differentiation to achieve the reaction field gradient

$${\nabla }_{\delta }{\nabla }_{\gamma }{\mathit{\Phi }}_{{\mathrm{\Theta }}_{\alpha \beta }}=-\frac{{\mathrm{\Theta }}_{\alpha \beta }}{3}\left[\frac{3(\epsilon -1)}{2+3\epsilon }\right]\frac{3({\delta }_{\alpha \gamma }{\delta }_{\beta \delta }+{\delta }_{\beta \gamma }{\delta }_{\alpha \delta })}{a^5}.$$ (99)

Substituting Eq. (98) into Eq. (95) and taking into account that half the energy is lost due to polarizing the continuum gives the self-energy of a traceless quadrupole in its own reaction field gradient

$${\text{U}}_{{\mathrm{\Theta }}_{\alpha \beta },{\mathrm{\Theta }}_{\gamma \delta }}=-\frac{1}{2}\left[\frac{3(\epsilon -1)}{2+3\epsilon }\right]\frac{{\mathrm{\Theta }}_{\alpha \beta }({\delta }_{\alpha \gamma }{\delta }_{\beta \delta }+{\delta }_{\beta \gamma }{\delta }_{\alpha \delta }){\mathrm{\Theta }}_{\gamma \delta }}{3a^5}.$$ (100)

From Eq. (100), it is seen that all non-self interactions, for example Θ_xx with Θ_yy, are zero, and the quadrupole self-energy is simply the sum of nine terms,

$${\text{U}}_{{\mathrm{\Theta }}_{\alpha \beta }}=-\frac{1}{2}\left[\frac{3(\epsilon -1)}{2+3\epsilon }\right]\frac{2{\mathrm{\Theta }}_{\alpha \beta }^2}{3a^5}.$$ (101)

The first series of numerical tests used a step function at the dielectric boundary rather than the smooth transition that is required for continuous energy gradients described previously. This simplification is necessary in order to compare the known analytic results directly with the numerical solver. In each case, the solution domain was a 10.0 Å cube with the low-dielectric sphere located at the center. In Table III it is shown that each test case converges toward the analytic result as grid spacing is decreased.

TABLE III.

As grid spacing decreases, the numerical solution to the PE approaches the analytic solution for four canonical test cases including a charge, dipole, polarizable dipole and quadrupole. Each test case involved a 3 Å sphere of dielectric 1 and solvent dielectric of 78.3 with a step-function transition between solute and solvent (kcal/mole).

Grid Points	Grid Spacing	Charge	Dipole	Polarizable Dipole	Quadrupole
33 × 33 × 33	0.313	−55.6514	−5.3556	−5.8011	−1.8487
65 × 65 × 65	0.156	−54.9150	−5.1450	−5.5548	−1.7211
129 × 129 × 129	0.078	−54.8024	−5.1134	−5.5180	−1.7038
225 × 225 × 225	0.045	−54.7236	−5.0915	−5.4925	−1.6912
Analytic	-	−54.6355	−5.0675	−5.4645	−1.6783

Our next goal was to determine the energy change due to introduction of a smooth dielectric boundary with a window width of 0.6 Å. Using a grid spacing slightly less than 0.1 Å, it can be seen in Table IV that the smooth dielectric boundary increases the solvation energy over the analogous step function boundary. By increasing the radius of the low dielectric cavity by approximately 0.2 Å, the energy of the charge, dipole, polarizable dipole and quadrupole can be adjusted to simultaneously mimic the known analytic results.

TABLE IV.

The tests from Table III are repeated using 129 grid points (0.078 Å spacing), however, the transition between solute and solvent is defined by a 7^th order polynomial, which acts over a total window width of 0.6 Å. Increasing the radius of the low dielectric sphere by approximately 0.2 Å raises the energies to mimic the step function transition results (kcal/mole).

Radius Increase	Charge	Dipole	Polarizable Dipole	Quadrupole
0.0	−58.4926	−6.2126	−6.8202	−2.3555
0.1	−56.4762	−5.5922	−6.0798	−1.9767
0.2	−54.5941	−5.0518	−5.4463	−1.6687
Step Function	−54.8024	−5.1134	−5.5180	−1.7038

B. Energy gradient

Our first goal is to show that the energy gradient is continuous for higher order moments as a result of using 5^th order B-splines. This is seen in Figs. (5) through (7) for a charge, dipole and quadrupole interacting with a neutral cavity, respectively. It is also clear that the sum of the forces between the neutral and charged site (and a third reference site that defines the local multipole frame in the cases of the dipole and quadrupole) is zero, indicating conservation of energy. Similarly, the reaction field and dielectric boundary gradients of the polarization energy for both the direct and mutual models are smooth and demonstrate conservation of energy, as shown in Figs. (8) and (9), respectively. Finally, it is clear that polarization catastrophes are avoided even when a charged site is moved toward superimposition with a polarizable site, due to use of a modified Thole model that damps mutual polarization at short range.²¹

C. The electrostatic response of solvated proteins

As described in the introduction, a motivation for the current work is study of polar macromolecules by an improved electrostatic model within an empirical molecular mechanics framework. From explicit water simulations it is possible to measure the total dipole moment of a solvated protein in a fixed folded conformation by sampling over the water degrees of freedom. The resulting ensemble average electrostatic response can then be directly compared to the PMPB model.

Simulations of five proteins taken from the Protein Databank³⁸ (1CRN³⁹, 1ENH⁴⁰, 1FSV⁴¹, 1PGB⁴² and 1VII⁴³) were equilibrated under NPT conditions (1 atm, 298 K) using a standard protocol. Formal charge and system size are given in Table VI. A single snapshot for each protein system was taken from equilibrated molecular dynamics simulations using the AMOEBA force field. The protein coordinates were frozen, and sampling of the solvent degrees of freedom continued for 150 ps under the same NPT conditions, with the first 50 ps discarded prior to analysis. For all simulations the Berendsen weak coupling thermostat and barostat were employed with time constants of 0.1 and 2.0 ps, respectively.⁴⁴ Long range electrostatics were treated using particle mesh Ewald (PME) summation with a cutoff for real space interactions of 7.0 Å and an Ewald coefficient of 0.54 Å^−1.45 The PME methodology used tinfoil boundary conditions, a 54 × 54 × 54 charge grid and 6^th order B-spline interpolation. van der Waals interactions were smoothly truncated to zero at 12.0 Å using a switching window of width 1.2 Å. Simulations were run using TINKER version 4.2.⁴⁶

TABLE VI.

Synopsis of the protein systems studied in explicit and continuum solvent.

		Number of Atoms
Protein	Formal Charge	Protein	Protein +Water
CRN	0	642	4980
ENH	+7	947	5039
FSV	+5	504	6435
PGB	−4	855	6143
VII	+2	596	4271

The same conformation of each protein studied in explicit water was examined using the LPBE methodology developed in this work at a range of grid spacings using the direct and mutual polarization models. In addition, 150 mM electrolyte was used in conjunction with the mutual polarization model to determine the relative effect of salt on the electrostatic response. The results are summarized in Table VII. Similar to the analytic test cases, as grid spacing is reduced the total electrostatic energy rises monotonically toward the converged solution. The total dipole moments are less sensitive to grid spacing than are the energies, with little change observed in moving from 0.3 Å to 0.2 Å. Adding 150 mM salt lowers the electrostatic energy by 1.7–12.5 kcal/mole at the smallest grid spacing studied, with CRN (neutral) and ENH (+7) showing the smallest and largest response, respectively. The magnitude of the energetic change indicates that salt concentration plays an important role in protein energetics, especially for highly charged species. For these calculations we have chosen an ionic radius of 2.0 Å, however smaller or larger values increase or decrease the energetic response, respectively.

TABLE VII.

The energy (kcal/mole) and dipole moment (debye) of each protein system was studied using a range of grid spacings under the direct polarization model, mutual polarization model, and mutual polarization model with 150 mM salt. The cavity was defined using AMOEBA R_min values for each atom and smooth dielectric and ionic boundaries via a total window width of 0.6 Å.

		Direct Polarization		Mutual Polarization		150 mM Salt
Protein	Grid Spacing	Energy	μ	Energy	μ	Energy	μ
CRN	0.61	−597.4	83.9	−679.1	81.0	−680.9	81.6
	0.31	−563.3	83.4	−641.3	80.6	−643.0	81.1
	0.18	−554.7	83.4	−632.1	80.6	−633.8	81.1
ENH	0.63	−1892.6	265.2	−2055.1	265.1	−2067.5	266.8
	0.32	−1851.1	265.8	−2008.8	265.8	−2021.2	267.4
	0.18	−1834.9	265.7	−1991.1	265.7	−2003.6	267.3
FSV	0.66	−1207.0	208.1	−1293.8	215.7	−1301.0	216.3
	0.33	−1184.3	208.4	−1269.3	216.0	−1276.5	216.6
	0.19	−1173.1	208.4	−1257.1	215.9	−1264.3	216.5
PGB	0.71	−1327.7	128.4	−1453.5	132.7	−1458.9	133.4
	0.36	−1275.7	127.8	−1400.5	132.0	−1405.9	132.6
	0.20	−1259.3	127.7	−1380.3	131.9	−1385.7	132.5
VII	0.62	−902.4	194.2	−1009.8	197.1	−1014.3	198.1
	0.31	−866.0	194.4	−970.6	197.3	−975.0	198.3
	0.18	−858.3	194.3	−962.0	197.2	−966.5	198.2

Finally, we compare the increase in dipole moment between the explicit water simulations and the continuum LPBE environment for each protein. As shown in Table VIII, both the direct and mutual models lead to total moments that are in good agreement with those found by molecular dynamics sampling of explicit water degrees of freedom. On average, the dipole moment increased by a factor of 1.27 in explicit water and 1.26 using the mutual polarization model. This result, which was achieved without detailed parameterization of atomic radii (AMOEBA Buffered-14-7 R_min values were used), indicates that at the length scale of whole proteins the continuum assumption is justified. Timings and memory requirements for the LPBE calculations as a function of grid size are shown in Table IX.

TABLE VIII.

The dipole moment (debye) of each protein in vacuum m_v, under the direct and mutual polarization models interacting with a continuum of permittivity 78.3, and in explicit water. Ensemble averages were taken over 100 psec trajectories and each has a std. err. of less than ± 0.3. The ratio of the solvated to vacuum dipole moment is given in each case. The cavity was defined using AMOEBA R_min values for each atom and smooth dielectric and ionic boundaries via a total window width of 0.6 Å.

	Vacuum	Direct Polarization		Mutual Polarization		Explicit Water
Protein	μv	μ	μ/μv	μ	μ/μv	< μ >	< μ>/μv
CRN	62.1	83.4	1.34	80.6	1.30	81.8	1.32
ENH	208.3	265.7	1.28	265.7	1.28	267.0	1.28
FSV	184.7	208.4	1.13	215.9	1.17	213.5	1.16
PGB	101.4	127.7	1.26	131.9	1.30	134.3	1.32
VII	158.3	194.4	1.23	197.3	1.25	197.7	1.25
Average	143.0	175.9	1.25	178.3	1.26	178.9	1.27

TABLE IX.

Memory requirements and wall clock timings for each protein system are shown. All calculations were run on a 2.4 Ghz Opteron.

Protein	Cubic Box Size	Grid Points	Memory (MB)	Direct (s)	Mutual (s)
CRN	39.31	65	84	6.9	50.2
		129	487	34.5	276.8
		225	2027	189.3	1414.7
ENH	40.50	65	81	9.2	80.3
		129	491	45.5	414.7
		225	1983	253.0	2457.3
FSV	42.35	65	73	5.7	42.7
		129	487	31.9	234.6
		225	2040	188.1	1463.8
PGB	45.48	65	80	8.2	60.7
		129	375	30.6	230.9
		225	1880	156.9	1176.5
VII	39.47	65	73	6.4	65.2
		129	487	37.2	360.6
		225	2040	194.8	2062.8

V. CONCLUSION

We have presented methodology required to determine the energy and gradient for the AMOEBA force field in conjunction with numerical solutions to the LPBE, which captures the electrostatic response of solvent by treating it as a dielectric continuum. The PMPB model was then applied to a series of proteins that were also studied using explicit water simulations. The resulting increases in dipole moment found using each approach were in excellent agreement. This indicates that the continuum assumption is a reasonable approximation at the length scale of the systems studied here.

Future work will include detailed parameterization of the solute cavity to reproduce small molecule electrostatic solvation energies. All of the methodology described in this paper is implemented in the TINKER molecular modeling package. This will facilitate use of the PMPB model using a variety of algorithms including molecular dynamics, Monte Carlo and a range of optimization methods. Additionally, parallelization of the LPBE calculations using existing approaches in APBS, which have been applied to fixed partial charge models, would be an important improvement in terms of speed and increasing the size of systems that can be routinely studied.

The methodology presented here is also expected to be useful for the development of continuum electrostatics models for coarse grain potentials. For example, Golubkov and Ren have recently described a generalized coarse grain model based on point multipoles and Gay-Berne potentials, which saves several orders of magnitude over all atom models.⁴⁷ We have also begun to use the PMPB model as a standard of accuracy in the testing of a polarizable analytic approximation similar in spirit to the generalized Born model, which was recently reviewed by Feig and Brooks.⁴⁸

Figure 5.

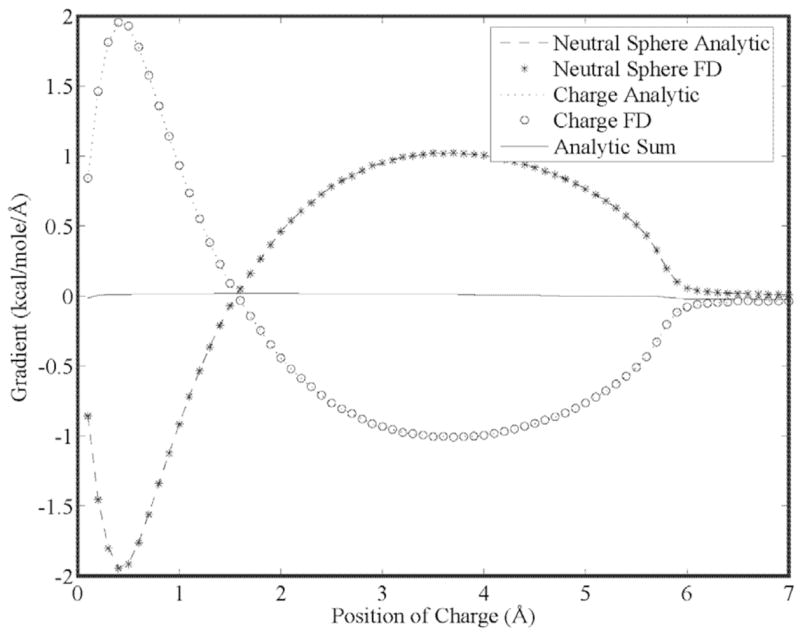
Analytic and finite-difference gradients for a neutral cavity fixed at the origin and a sphere with unit positive charge vs. separation. Both spheres have a radius of 3.0 Å and the solvent dielectric is 78.3. The gradient of the neutral cavity is due entirely to the dielectric boundary force and cancels exactly the force on the charged sphere.

Figure 6.

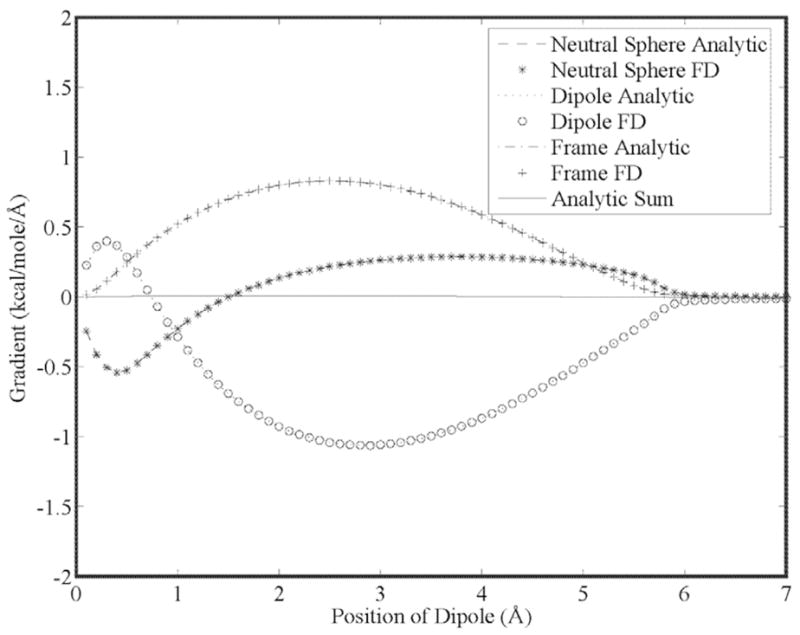
Analytic and finite-difference gradients for a neutral cavity fixed at the origin and a sphere with dipole moment components of (2.54, 2.54, 2.54) debye vs. separation. Both spheres have a radius of 3.0 Å and movement of the dipole is along the x-axis. The gradient of the neutral cavity is due entirely to the dielectric boundary force and cancels exactly the sum of the forces on the dipole and a third site (that has no charge density or dielectric properties) that defines the local coordinate system of the dipole.

Figure 7.

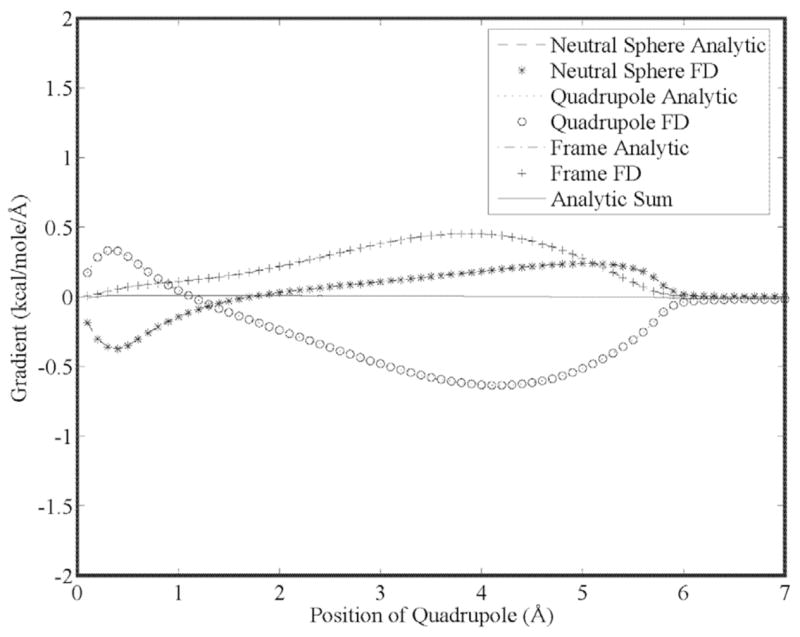
Analytic and finite-difference gradients for a neutral cavity fixed at the origin and a sphere with quadrupole moment components of (5.38, 2.69, 2.69, 2.69, −2.69, 2.69, 2.69, 2.69, −2.69) Buckinghams vs. separation. Both spheres have a radius of 3.0 Å and movement of the quadrupole is along the x-axis. The gradient of the neutral cavity cancels exactly the sum of the forces on the quadrupole and a third site (that has no charge density or dielectric properties) that defines the local coordinate system of the quadrupole.

Figure 8.

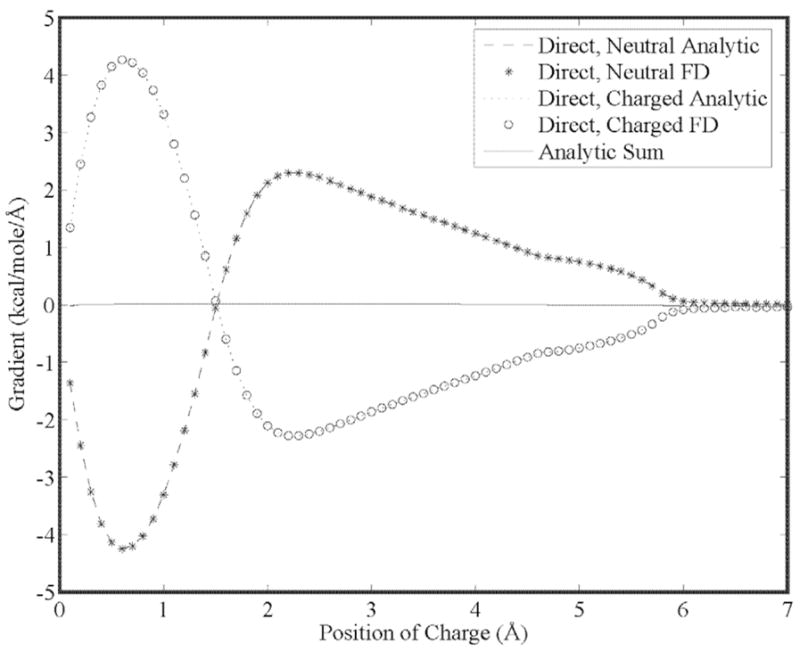
Analytic and finite-difference gradients for a neutral, polarizable cavity fixed at the origin and a sphere with unit positive charge vs. separation using the direct polarization model. Both spheres have a radius of 3.0 Å. The gradient can be seen to approach zero at a number of points, notably when the spheres are separated by approximately 1.5 Å leading to a maximum in the reaction field produced by the charge at the polarizable site, and again when the spheres are superimposed and the reaction field is zero at the polarizable site.

Figure 9.

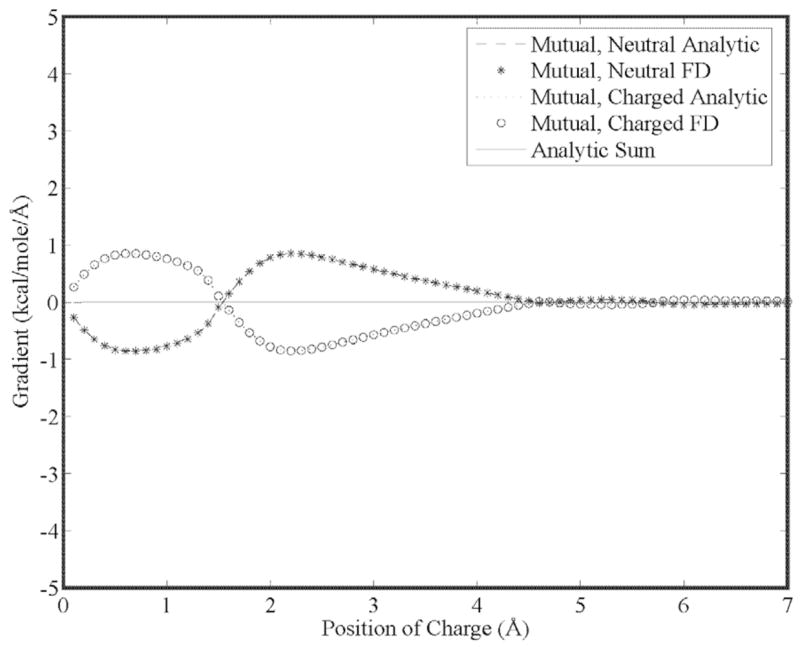
Analytic and finite-difference gradients for a neutral, polarizable cavity fixed at the origin and a polarizable sphere with unit positive charge vs. separation using the mutual polarization model. Both spheres have a radius of 3.0 Å and a polarizability of 1.0 Å ⁻³. Note that the mutual polarization gradients are smaller than those of Figure 8 for the otherwise equivalent direct polarization model.

Figure 10.

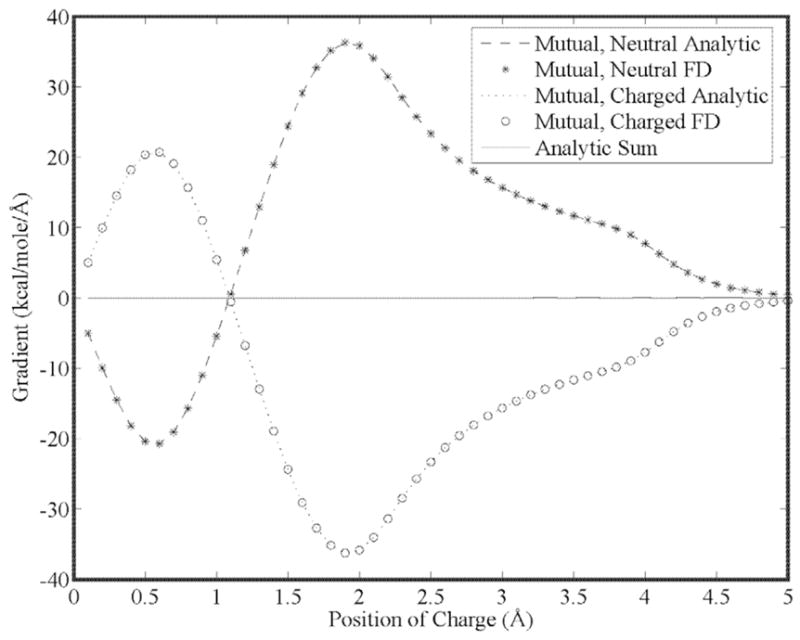
The dielectric of the solvent and test spheres are both set to 1 in this case, while a salt concentration of 150 mM is used to isolate the ionic boundary gradients. Analytic and finite-difference gradients for a neutral, polarizable cavity fixed at the origin (3.0 Å radius) and a polarizable sphere with a unit positive charge (1.0 Å radius) vs. separation using the mutual polarization model. Both spheres have a polarizability of 1.0 Å ⁻³, and the ionic radius is set to zero Å.

APPENDIX A: FINITE-DIFFERENCE REPRESENTATION OF THE LPBE

The finite-difference representation of the LPBE for uniform grid spacing is ²⁰,²⁵,²⁶

$$\begin{array}{l}{\epsilon }_x(i,j,k)[\Phi (i+1,j,k)-\Phi (i,j,k)]+{\epsilon }_x(i-1,j,k)[\Phi (i-1,j,k)-\Phi (i,j,k)]\\ +{\epsilon }_y(i,j,k)[\Phi (i,j+1,k)-\Phi (i,j,k)]+{\epsilon }_y(i,j-1,k)[\Phi (i,j-1,k)-\Phi (i,j,k)]\\ +{\epsilon }_z(i,j,k)[\Phi (i,j,k+1)-\Phi (i,j,k)]+{\epsilon }_z(i,j,k-1)[\Phi (i,j,k-1)-\Phi (i,j,k)],\\ +{\overline{\kappa }}^2(i,j,k)\Phi (i,j,k)h^2=-4\pi \frac{q(i,j,k)}{h}\end{array}$$ (A1)

where h is the grid spacing, Φ (i, j, k) is the electrostatic potential, κ̄² (i, j, k) is the modified Debye-Hückel screening factor and q (i, j, k) is the fractional charge. The permittivity is specified by three separate arrays, ε_x, ε_y and ε_z, where each is shifted along its respective grid branch such that ε_x(i, j, k) represents the location (x_i + h/2, y_i, z_i) for the grid point ( x_i, y_i, z_i). Eq. (A1) is the basis for formulating the LPBE as a linear system of equations, which are represented compactly by Eq. (14).

APPENDIX B: DEFINITION OF THE DELTA FUNCTIONAL USING B-SPLINES

The delta functional δ is defined by

$$\underset{-\infty }{\overset{\infty }{\int }}\delta (x-a)dx=1$$ (A2)

and δ(x − a) = 0 for x ≠ a. An approximate discrete 1-dimensional realization of this definition (approximate because the width is not infinitesimally small) is

$$\sum _{i=1}^5\text{W}(x_i,a)=1,$$ (A3)

where the function W has been defined in Eq. (28) via 5^th order B-splines and {x₁,…,x₅} are the 5 closest grid points to a. In the limit of infinitesimal grid spacing, the properties of the Delta functional are met exactly by expressing Eq. (A3) above as a continuous integral

$$\underset{-\epsilon }{\overset{\epsilon }{\int }}\text{W}(x,a)dx=1,$$ (A4)

where ε > 0. The value at a of any function known to be defined over the grid can then be determined as

$$\underset{-\epsilon }{\overset{\epsilon }{\int }}\text{W}(x,a)f(x)dx=f(a),$$ (A5)

and the negative of its gradient as

$$\begin{array}{c}\underset{-\epsilon }{\overset{\epsilon }{\int }}(\nabla \text{W}(x,a))f(x)dx=\text{W}(x,a)f(x){\mid }_{-\epsilon }^{\epsilon }-\underset{-\epsilon }{\overset{\epsilon }{\int }}\text{W}(x,a)\nabla f(x)dx\\ =-\nabla f(a)\end{array}.$$ (A6)

Further differentiations can be found in an analogous fashion, limited only by the continuity of the B-spline.

APPENDIX C: IMPLEMENTATION OF THE PERMANENT, DIRECT POLARIZATION AND MUTUAL POLARIZATION FORCES

After solving the linear system, the permanent electrostatic solvation forces are determined via Eq. (60), which in the limit of infinitesimal grid spacing becomes ²⁰

$${\text{F}}_{i,\gamma }=-\frac{\partial \mathrm{\Delta }{\text{G}}_{\text{M}}}{\partial s_{i,\gamma }}=-\underset{V}{\int }\left[{\Phi }^{\text{M}}\frac{\partial {\rho }_{\text{M}}}{\partial s_{I,\gamma }}+\frac{1}{8\pi }{\Phi }_{\text{s}}^{\text{M}}\nabla \left(\frac{\partial {\epsilon }_s}{\partial s_{i,\gamma }}\nabla {\Phi }_{\text{s}}^{\text{M}}\right)-\frac{1}{8\pi }{({\Phi }_{\text{s}}^{\text{M}})}^2\frac{\partial {\overline{\kappa }}^2}{\partial s_{i,\gamma }}\right]d^3\mathbf{r},$$ (A7)

where γ represents differentiation with respect to either the x-, y- or z-coordinate of atom i. The three terms on the RHS of Eq. (A7) are usually referred to as the reaction field force, dielectric boundary force and ionic boundary force, respectively. We briefly review the implementation of these forces, in order to develop the foundation necessary to discuss additional details of realizing the polarization forces.

C I. Permanent reaction field force and torque

The γ -component of the “Permanent Reaction Field Force” ${\mathbf{F}}_i^{\text{Perm RF}}$ for atom i is

$${\text{F}}_{i,\gamma }^{\text{Perm RF}}=-\frac{\partial }{\partial s_{i,\gamma }}\left[q_i{\mathbf{B}}_i-d_{i,\alpha }{\nabla }_{\alpha }{\mathbf{B}}_i+\frac{{\mathrm{\Theta }}_{i,\alpha \beta }}{3}{\nabla }_{\alpha }{\nabla }_{\beta }{\mathbf{B}}_i\right]{\mathit{\Phi }}^{\text{M}},$$ (A8)

where B_i is a single column of the B-spline matrix in Eq. (33), d_i,α is the α -component of the permanent dipole, Φ_i,αβ is the αβ component of the quadrupole and the convention for summation over the α and β subscripts is implied. There is also an associated “Permanent Reaction Field Torque” ${\mathbf{\tau }}_i^{\text{Perm RF}}$, whose x-component is

$${\mathit{\tau }}_{i,x}^{\text{Perm q-Phi}}=d_{i,y}{\text{E}}_{\text{RF},i,z}^{\text{M}}-d_{i,z}{\text{E}}_{\text{RF},i,y}^{\text{M}}-\frac{2}{3}[{\mathrm{\Theta }}_{i,y\alpha }{\nabla }_{\alpha }{\text{E}}_{\text{RF},i,z}^{\text{M}}-{\mathrm{\Theta }}_{i,z\alpha }{\nabla }_{\alpha }{\text{E}}_{\text{RF},i,y}^{\text{M}}],$$ (A9)

where ${\text{E}}_{\text{RF},i,\alpha }^{\text{M}}$ is the α -component of the permanent multipole reaction field. The y- and z- components are analogous, and we note that all torques are equivalent to forces on neighboring atoms that define the local frame of the multipole.

C II. Direct polarization reaction field force and torque

Similarly, the third term of the polarization gradient given in Eq. (91) results in a “Direct Polarization Reaction Field Force”

$${\text{F}}_{i,\gamma }^{\text{Direct RF}}=\frac{1}{2}\frac{\partial }{\partial s_{i,\gamma }}\left[(-{\mu }_{i,\alpha }{\nabla }_{\alpha }{\mathbf{B}}_i){\mathbf{\Phi }}^{\text{M}}+\left(q_i{\mathbf{B}}_i-d_{i,\alpha }{\nabla }_{\alpha }{\mathbf{B}}_i+\frac{{\mathrm{\Theta }}_{i,\alpha \beta }}{3}{\nabla }_{\alpha }{\nabla }_{\beta }{\mathbf{B}}_i\right){\mathit{\Phi }}^{\mu }\right],$$ (A10)

while the fifth term we label the “Non-Local Direct Polarization Reaction Field Force”

$${\text{F}}_{i,\gamma }^{\text{NL}-\text{Direct RF}}=\frac{1}{2}\frac{\partial }{\partial s_{i,\gamma }}\left[(-{\nu }_{i,\alpha }{\nabla }_{\alpha }{\mathbf{B}}_i){\mathit{\Phi }}^{\text{M}}+\left(q_i{\mathbf{B}}_i-d_{i,\alpha }{\nabla }_{\alpha }{\mathbf{B}}_i+\frac{{\mathrm{\Theta }}_{i,\alpha \beta }}{3}{\nabla }_{\alpha }{\nabla }_{\beta }{\mathbf{B}}_i\right){\mathit{\Phi }}^{\nu }\right],$$ (A11)

respectively. The label “non-local” is used to denote that the term σ results from omitting or scaling the contribution to the intramolecular field of permanent multipoles that are in a 1-5 connected or closer, as opposed to the induced dipoles μ that result from the AMOEBA group based polarization scheme. Additionally, the x-component of the torques, ${\mathit{\tau }}_i^{\text{Direct RF}}$ and ${\mathit{\tau }}_i^{\text{NL-Direct RF}}$, on the permanent moments due to the continuum reaction field of μ and ν are, respectively,

$${\mathit{\tau }}_{i,x}^{\text{Direct RF}}=\frac{1}{2}[d_{i,y}{\text{E}}_{\text{RF},i,z}^{\mu }-d_{\sigma ,z}{\text{E}}_{\text{RF},i,y}^{\mu }-\frac{2}{3}({\mathrm{\Theta }}_{i,y\alpha }{\nabla }_{\alpha }{\text{E}}_{\text{RF},i,z}^{\mu }-{\mathrm{\Theta }}_{i,z\alpha }{\nabla }_{\alpha }{\text{E}}_{\text{RF},i,y}^{\mu })],$$ (A12)

and

$${\mathbf{\tau }}_{i,x}^{\text{NL}-\text{Direct RF}}=\frac{1}{2}[d_{i,y}{\text{E}}_{\text{RF},i,z}^{\nu }-d_{\sigma ,z}{\text{E}}_{\text{RF},i,y}^{\nu }-\frac{2}{3}({\mathrm{\Theta }}_{i,y\alpha }{\nabla }_{\alpha }{\text{E}}_{\text{RF},i,z}^{\nu }-{\mathrm{\Theta }}_{i,z\alpha }{\nabla }_{\alpha }{\text{E}}_{\text{RF},i,y}^{\nu })].$$ (A13)

C III. Mutual polarization reaction field force

The last reaction field force results from the seventh term of Eq. (91) and is due to mutual polarization

$${\text{F}}_{i,\gamma }^{\text{Mutual RF}}=\frac{1}{2}\frac{\partial }{\partial s_{i,\gamma }}({\mu }_{i,\alpha }{\nabla }_{\alpha }{\mathbf{B}}_i{\mathit{\Phi }}^{\nu }+{\nu }_{i,\alpha }{\nabla }_{\alpha }{\mathbf{B}}_i{\mathit{\Phi }}^{\mu }).$$ (A14)

C IV. Permanent dielectric boundary force

The second term in Eq. (A7), the “Permanent Dielectric Boundary Force”, is determined from Eq. (A1) as

$$\begin{array}{c}{\text{F}}_{i,\gamma }^{\text{Perm DB}}=-\frac{h}{8}\sum _{i,j,k}{\Phi }_{\text{s}}^{\text{M}}(i,j,k)\\ \{\frac{\partial {\epsilon }_x(i,j,k)}{\partial r_{i,\gamma }}[{\Phi }_{\text{s}}^{\text{M}}(i+1,j,k)-{\Phi }_{\text{s}}^{\text{M}}(i,j,k)]\\ +\frac{\partial {\epsilon }_x(i-1,j,k)}{\partial r_{i,\gamma }}[{\Phi }_{\text{s}}^{\text{M}}(i-1,j,k)-{\Phi }_{\text{s}}^{\text{M}}(i,j,k)]\\ +\frac{\partial {\epsilon }_y(i,j,k)}{\partial r_{i,\gamma }}[{\Phi }_{\text{s}}^{\text{M}}(i,j+1,k)-{\Phi }_{\text{s}}^{\text{M}}(i,j,k)]\\ +\frac{\partial {\epsilon }_y(i,j-1,k)}{\partial r_{i,\gamma }}[{\Phi }_{\text{s}}^{\text{M}}(i,j-1,k)-{\Phi }_{\text{s}}^{\text{M}}(i,j,k)]\\ +\frac{\partial {\epsilon }_z(i,j,k)}{\partial r_{i,\gamma }}[{\Phi }_{\text{s}}^{\text{M}}(i,j,k+1)-{\Phi }_{\text{s}}^{\text{M}}(i,j,k)]\\ +\frac{\partial {\epsilon }_z(i,j,k-1)}{\partial r_{i,\gamma }}[{\Phi }_{\text{s}}^{\text{M}}(i,j,k-1)-{\Phi }_{\text{s}}^{\text{M}}(i,j,k)]\}\end{array},$$ (A15)

where the partial derivatives of the permittivity depend on Eqs. (37), (39) and the heptic characteristic function presented in Eqs. (40–43).

$$\begin{array}{c}\frac{\partial {\epsilon }_x(i,j,k)}{\partial r_{i,\gamma }}=(1-{\epsilon }_s)\frac{{\text{H}}_x(i,j,k)}{{\text{H}}_{xi}(i,j,k)}\frac{\partial {\text{H}}_x(i,j,k)}{\partial r_{i,\gamma }}\\ =[{\epsilon }_x(i,j,k)-1]\frac{{\text{H}}_{xi}^{\prime }(i,j,k)}{{\text{H}}_{xi}(i,j,k)}\frac{-r_{i,\gamma }}{r_i}\end{array},$$ (A16)

where H_x and H_xi are the characteristic function of the solute and atom i for the x-branch of the cubic grid at (x_i + h/2, y_j, z_k), respectively, and the vector r_i is the distance from the atomic center to the grid point.

C V. Direct and mutual polarization dielectric boundary forces

The fourth, sixth and eighth terms in Eq. (91) result in dielectric boundary force components. For example, the “Direct Polarization Dielectric Boundary Force” is

$$\begin{array}{l}{\text{F}}_{i,\gamma }^{\text{Direct DB}}=-\frac{h}{8}\sum _{i,j,k}{\Phi }_{\text{s}}^{\mu }(i,j,k)\\ \{\frac{\partial {\epsilon }_x(i,j,k)}{\partial {\text{r}}_{i,\gamma }}[{\Phi }_{\text{s}}^{\text{M}}(i+1,j,k)-{\Phi }_{\text{s}}^{\text{M}}(i,j,k)]\\ +\frac{\partial {\epsilon }_x(i-1,j,k)}{\partial {\text{r}}_{i,\gamma }}[{\Phi }_{\text{s}}^{\text{M}}(i-1,j,k)-{\Phi }_{\text{s}}^{\text{M}}(i,j,k)]\\ +\frac{\partial {\epsilon }_y(i,j,k)}{\partial {\text{r}}_{i,\gamma }}[{\Phi }_{\text{s}}^{\text{M}}(i,j+1,k)-{\Phi }_{\text{s}}^{\text{M}}(i,j,k)]\\ +\frac{\partial {\epsilon }_y(i,j-1,k)}{\partial {\text{r}}_{i,\gamma }}[{\Phi }_{\text{s}}^{\text{M}}(i,j-1,k)-{\Phi }_{\text{s}}^{\text{M}}(i,j,k)]\\ +\frac{\partial {\epsilon }_z(i,j,k)}{\partial {\text{r}}_{i,\gamma }}[{\Phi }_{\text{s}}^{\text{M}}(i,j,k+1)-{\Phi }_{\text{s}}^{\text{M}}(i,j,k)]\\ +\frac{\partial {\epsilon }_z(i,j,k-1)}{\partial {\text{r}}_{i,\gamma }}[{\Phi }_{\text{s}}^{\text{M}}(i,j,k-1)-{\Phi }_{\text{s}}^{\text{M}}(i,j,k)]\}\end{array}$$ (A17)

or

$$\begin{array}{l}{\text{F}}_{i,\gamma }^{\text{Direct DB}}=-\frac{h}{8}\sum _{i,j,k}{\Phi }_{\text{s}}^{\text{M}}(i,j,k)\\ \{\frac{\partial {\epsilon }_x(i,j,k)}{\partial {\text{r}}_{i,\gamma }}[{\Phi }_{\text{s}}^{\mu }(i+1,j,k)-{\Phi }_{\text{s}}^{\mu }(i,j,k)]\\ +\frac{\partial {\epsilon }_x(i-1,j,k)}{\partial {\text{r}}_{i,\gamma }}[{\Phi }_{\text{s}}^{\mu }(i-1,j,k)-{\Phi }_{\text{s}}^{\mu }(i,j,k)]\\ +\frac{\partial {\epsilon }_y(i,j,k)}{\partial {\text{r}}_{i,\gamma }}[{\Phi }_{\text{s}}^{\mu }(i,j+1,k)-{\Phi }_{\text{s}}^{\mu }(i,j,k)]\\ +\frac{\partial {\epsilon }_y(i,j-1,k)}{\partial {\text{r}}_{i,\gamma }}[{\Phi }_{\text{s}}^{\mu }(i,j-1,k)-{\Phi }_{\text{s}}^{\mu }(i,j,k)]\\ +\frac{\partial {\epsilon }_z(i,j,k)}{\partial {\text{r}}_{i,\gamma }}[{\Phi }_{\text{s}}^{\mu }(i,j,k+1)-{\Phi }_{\text{s}}^{\mu }(i,j,k)]\\ +\frac{\partial {\epsilon }_z(i,j,k-1)}{\partial {\text{r}}_{i,\gamma }}[{\Phi }_{\text{s}}^{\mu }(i,j,k-1)-{\Phi }_{\text{s}}^{\mu }(i,j,k)]\}\end{array}$$ (A18)

where the superscript on the solvated potentials have been exchanged between Eq. (A17) and Eq. (A18). In other words, both Eqs. (A17) and (A18) are equivalent to numerical precision and either may be implemented. Analogous expressions for the sixth and eighth terms in Eq. (91) are referred to as the “Non-Local Direct Polarization Dielectric Boundary Force” and the “Mutual Polarization Dielectric Boundary Force”, respectively.

C VI. Permanent ionic boundary force

The last term in Eq. (A7), the “Permanent Ionic Boundary Force”, is determined from Eq. (A1) as

$${\text{F}}_{i,\gamma }^{\text{Perm IB}}=-\frac{h^3}{8\pi }\sum _{i,j,k}{\mathit{\Phi }}_{\text{s}}^{\text{M}}{(i,j,k)}^2\frac{\partial {\overline{\kappa }}^2(i,j,k)}{\partial r_{i,\gamma }}$$ (A19)

using

$$\begin{array}{l}\frac{\partial {\overline{\kappa }}^2(i,j,k)}{\partial r_{i,\gamma }}={\overline{\kappa }}_b^2\frac{\text{H}(i,j,k)}{{\text{H}}_i(i,j,k)}\frac{\partial {\text{H}}_i(i,j,k)}{\partial r_{i,\gamma }}\\ ={\overline{\kappa }}^2(i,j,k)\frac{{\text{H}}_i^{\prime }(i,j,k)}{{\text{H}}_i(i,j,k)}\frac{-r_{i,\gamma }}{r_i}\end{array}$$ (A20)

where H and H_i are the characteristic function of the solute and atom i, respectively, and the vector r_i is the distance from the atomic center to the grid point.

C VII. Direct and mutual polarization ionic boundary force

The fourth, sixth and eighth terms in Eq. (91) result in ionic boundary force components. For example, the “Direct Polarization Ionic Boundary Force” is

$${\text{F}}_{i,\gamma }^{\text{Direct IB}}=\frac{h^3}{8\pi }\sum _{i,j,k}{\mathit{\Phi }}_{\text{s}}^{\text{M}}(i,j,k){\mathit{\Phi }}_{\text{s}}^{\mu }(i,j,k)\frac{\partial {\overline{\kappa }}^2(i,j,k)}{\partial r_{i,\gamma }}$$ (A21)

Analogous expressions for the sixth and eighth terms in Eq. (91) are termed the “Non-Local Direct Polarization Ionic Boundary Force” and the “Mutual Polarization Ionic Boundary Force”, respectively. Note the difference between Eqs. (A19) and (A21); specifically the potential is squared in Eq. (A19), but is asymmetric in Eq. (A21).