A hierarchical neuronal network for planning behavior

Abstract

Planning a goal-directed sequence of behavior is a higher function of the human brain that relies on the integrity of prefrontal cortical areas. In the Tower of London test, a puzzle in which beads sliding on pegs must be moved to match a designated goal configuration, patients with lesioned prefrontal cortex show deficits in planning a goal-directed sequence of moves. We propose a neuronal network model of sequence planning that passes this test and, when lesioned, fails in a way that mimics prefrontal patients’ behavior. Our model comprises a descending planning system with hierarchically organized plan, operation, and gesture levels, and an ascending evaluative system that analyzes the problem and computes internal reward signals that index the correct/erroneous status of the plan. Multiple parallel pathways connecting the evaluative and planning systems amend the plan and adapt it to the current problem. The model illustrates how specialized hierarchically organized neuronal assemblies may collectively emulate central executive or supervisory functions of the human brain.

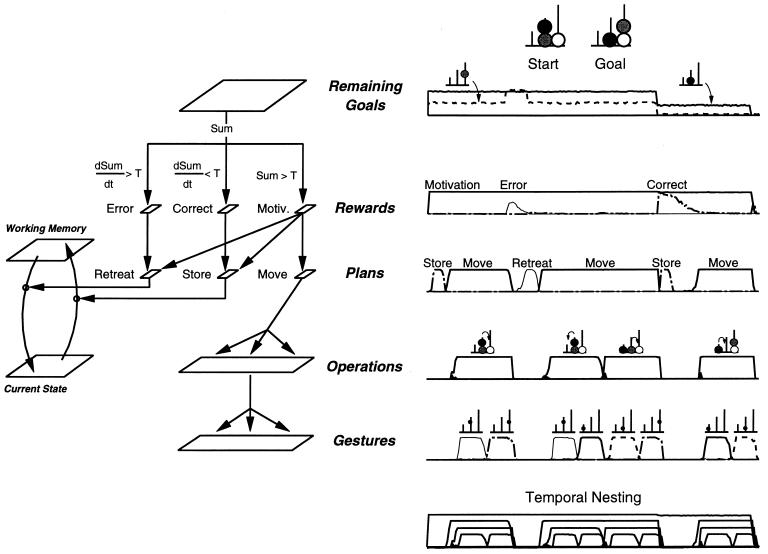
The Tower of London test (1) consists of moving three colored beads, mounted on vertical rods of unequal length, from an initial position to a prespecified goal (Fig. 1). To solve this task, various levels of motor programming are needed (Fig. 2). At the first and lowest level, here called the “gesture” level, sensory–motor coordination is needed to point to the location of the beads. At a second level, called the “operation” level, a sequence of two elementary gestures (an operation) must be programmed to move a bead from its initial to its final destination. The operation level suffices to solve the simplest Tower of London problems, where each bead can be brought directly to its desired final destination. More difficult problems, however, call for the planning of nondirect, provisory moves and their evaluation by trial and error. These problems pose specific difficulty to human patients with anterior lesions: they experience little or no difficulty executing individual moves but have trouble organizing them into a goal-directed sequence (1–3). We suggest that a third level of programming, the “plan” level, is needed to solve such problems. At this level, sequences of operations (plans) must be selected, executed, evaluated, and accepted or withdrawn depending on their ability to bring the problem to a solution. Our model implements these functions.

Figure 1.

State space for the Tower of London test. A problem is defined by the joint selection of an initial state and a goal. Legal moves (lines) consist in moving the top bead of any given peg to an empty, supported location on another peg.

Figure 2.

Architecture of the model. Squares represent sets of functionally related units (neuronal assemblies), and arrows depict connection pathways. The model is divided into ascending evaluative and descending planning pathways with multiple horizontal interconnections at each of three hierarchical levels (gestures, operations, and plans). At the top level, plan units receive inputs from reward units. At the intermediate level, operation units receive inputs from “current state,” “movable beads,” and “reachable goals” units. Finally, at the lowest level, gestures units receive direct inputs from “current state” units, enabling the fine details of the motor plan to be adapted to the current configuration of the beads. Within each assembly, units pool the activation or inhibition they receive and compete for the control of behavior through self-excitation and nonlinear shunting lateral inhibition, resulting in the selection, at any given time, of a single, active unit at each level, the one that is best adapted to the constraints received from other assemblies.

Biological Premises

Our modeling approach (4–9) views the brain not as a passive input–output system, but as an active, projective device that spontaneously generates “hypotheses” and tests their adequacy (4). Neuronal circuits are modeled as hierarchically organized assemblies of neuronal clusters linked in multiple parallel pathways by bundles of synapses (5). In the prefrontal cortex, neurons within each cluster are connected by excitatory collaterals and thus can maintain a long-lasting, self-sustained level of activation implementing an elementary form of working memory (6, 7, 10). In the absence of specific inputs, prefrontal clusters activate with a fringe of variability, implementing a “generator of diversity” whose circuitry and hypothetical molecular mechanisms have been outlined (6, 7). The spontaneous activity patterns thus generated are selected (stabilized) or eliminated (destabilized) by a simple Hebbian rule modulated by positive or negative reward signals received from diffuse projection systems (7, 11). Rewards may be received from an external teacher, or they may be internally generated by the organism itself using autoevaluation circuits (7, 11). Here, we show how the spontaneous generation of diversity at multiple hierarchical levels, followed by selection by internally generated evaluation signals, provides a plausible neuronal model for complex problem solving by trial and error.

Implementation of the model

Gesture Level.

To operate on Tower of London problems, the organism must be able to point to the beads on the pegs. In our model, such simple sensory–motor coordination is implemented by a direct projection between input and output units. The input location of the beads on the pegs is coded by 18 “current state” units, 1 for each combination of 6 locations on the pegs and 3 colors for the beads. On the output side, six “gesture” units code for the six possible locations on the pegs. Direct input–output connections allow the network to program a pointing gesture toward one of the beads, and lateral shunting inhibition among gesture units ensures the activation of a single gesture. Thus, the gesture level, by itself, is capable only of pointing to beads.

Operation Level.

Moving a bead calls for two pointing gestures, first toward the bead and then toward its desired destination (3, 12). In our simulation, the execution of this sequence is controlled by a hierarchically higher “operation” network comprising operation and transition units. Operation units code for each combination of an initial and a destination peg, whereas gesture-transition and operation-transition units code for all possible succession relations between gesture units and between operation units (13). The projections from and to operation units incorporate knowledge of the rules of the test (see legend of Fig. 1). At both the gesture and the operation levels, termination and exhaustion units control the state of execution of the sequence (Fig. 2). Whenever an operation unit activates, there follows the successive activation of a first-gesture unit (pointing to a bead), then the gesture-termination unit (suppressing the currently active gesture unit), a second-gesture unit (pointing to an empty location), the gesture-exhaustion unit (signaling the exhaustion of all gestures for that operation), and finally, the operation-termination unit (suppressing the currently active operation unit).

At any given time, any of the six operation units may activate, so a mechanism is needed by which the move most appropriate for reaching the desired goal can be selected. In our simulation, the goal configuration is coded by 18 “goal state” units using a color × location code isomorphic to that used for “current state” unit. Eighteen units compare the goal with the current state and signal which beads in the goal configuration have not yet been brought into place (“remaining goals” units). Another set of 18 units compute which of the beads are movable and are not yet in place (“movable beads” units). Finally, another 18 units compute which of the goal beads, if any, are reachable, which means that they are movable, not yet in place, and that their desired destination is empty and attainable (“reachable goals” units). “Reachable goals” and “movable beads” units project to operation units and therefore are used to constrain the choice of which operation is most appropriate to the current problem.

Behaviorally, the network, when equipped with these representations, can only execute moves that place beads directly at their goal location: a “reachable goal” unit activates and the corresponding sequence of gestures systematically is executed first. Thus, the network with both gesture and operation levels, but no plan level, is capable of executing stimulus-driven motor sequences but is not able to program nondirect intermediate moves that call for temporarily placing a ball at a provisory location.

Plan Level.

Planning, which we define here as the goal-directed, trial-and-error exploration of a tree of alternative moves, requires additional computations. When no direct move is available, a move must be self-generated, tried out, and accepted or rejected depending on its ability to bring the problem closer to a solution. This production/selection process (4, 14), which is considered to be an important function of prefrontal areas (6, 7), is implemented here at the plan level by three major neural systems (Fig. 2): working-memory units capable of maintaining a self-sustained activity and hence a memory of a previous problem state while a plan is tested; plan units that cause novel activation patterns among lower-level operation units, thus generating a novel plan; and reward units that evaluate the correct/incorrect status of the plan and may alter plan unit activity accordingly. Three plan units encode whether a new operation should be attempted (“move” unit), whether the operation just performed should be withdrawn and the current state reverted to the memorized state (“retreat” unit), or whether the current state should be memorized to permit subsequent backtracking (“store” unit). When the “move” plan unit is activated, it provides excitation to all hierarchically lower operations, thus enabling them to activate, with an intrinsic variability, even in the absence of any directly reachable goal. The corresponding operation is then executed, and the ensuing change in problem state is evaluated. The sum of activity over “remaining goals” units is used as an approximate measure of distance to the goal, d, which provides input to three reward units. The “motivation” unit activates whenever the problem is as yet unsolved (d > 0) and projects to all plan units, thus maintaining the generation of novel plans until the problem is solved. The “correct” unit activates when d decreases, indicating that a move just made is likely to be correct, and projects to the “store” plan unit, which will ensure storage of the new problem state. The “error” unit activates when d increases, suggesting an incorrect move, and projects to the “retreat” plan unit, which will restore the problem state from memory as it was before the attempted move.

Fig. 2 summarizes the main features of the full model. There is a descending planning system, with hierarchically organized plan, operation, and gestures levels and their corresponding transition, termination, and exhaustion units, an ascending evaluative system that analyzes the current state and the goal state and culminates into an internal reward, and multiple horizontal pathways that connect the two systems and ensure the adaptation of the plan to the problem at hand. The outcome of this architecture is a hierarchical network that, given the static input of a Tower of London problem (an initial state and a goal state), selects a sequence of moves that solves the problem.

Simulation Details

Details of the connections and a complete listing of the program are available from the first author. Briefly, at each time step, the unit activities x_i are updated in parallel according to Eq. 1:

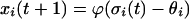1

where θ_i is a threshold, ϕ is the sigmoid function ϕ(x) = 1/1 + e^−x, and the net input to unit i, σ_i (t), is computed according to Eq. 2:

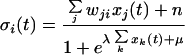2

where w_ji is the positive or negative connection weight from unit j to unit i, n is a noise term, and λ and μ are parameters. In this expression, the top sum is computed over all units j that belong to a different neuronal assembly than unit i, and the lower sum is computed only over units k that belong to the same neuronal assembly as unit i and implements nonlinear inhibition within each assembly. Combined with a large self-connection (typically w_ii = 13), this construction ensures that regardless of input strength, only one or a few units of each assembly can activate at any given time. Typical values for the parameters are m = 1.5, λ = 2.3, μ = 2, and θ_i = 5. A lesion is simulated by letting θ_i = 40 for plan units only, thus preventing them from activating. For reward units, the time derivative of “remaining goal” units activity, dx_i(t)/dt, was used instead of σ_i (t) in Eq. 2, as in other models of reward systems (11), so that reward units were activated by increases or decreases in the distance to the goal.

The connection weights w_ji were not subjected to a learning rule. However, the afferents to plan, operation, and gesture units obeyed the following desensitization/recovery rule (6, 7):

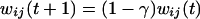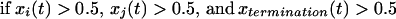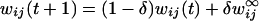3

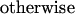where γ and δ are respectively desensitization and recovery parameters (typically γ = 0.07 and δ = 0.02). Eq. 3 implements an exponential desensitization of active connection weights to plan, operation, and gesture units that are active whenever the termination unit of the corresponding level is activated, and a recovery to their initial value w_ij otherwise. Desensitization ensured the termination of unit activity once the corresponding lower-level sequence was executed.

Behavior and Predictions of the Normal Model

The normal behavior of the model was evaluated by submitting it to a large number of Tower of London problems of varying complexity and recording its success rate, solution time, and trajectory in state space (Fig. 3). Like a normal human subject (1–3), the model shows an increase in error rate and solution time as the number of moves required to solve the problem increases (Fig. 3 C and D). Nevertheless, even problems of intermediate difficulty requiring three, four, or five moves, including nonobvious intermediate moves, are solved accurately and with a direct trajectory (Fig. 3A and Fig. 4). Only the most difficult problems that require six, seven, or eight moves, almost never used in neuropsychological testing because of their difficulty, are rarely solved by the model after 1,000 iterations. Given more time, even these problems are eventually solved because noise and habituation of excitatory connections ensure that moves with a very low initial probability of being selected are eventually tried out. Hence, the normal network exhibits flexibility and is rarely stuck in an impasse.

Figure 3.

Simulations of normal and impaired performance in the Tower of London test. (A and B) Sample resolution attempts, plotted as trajectories on the state space of Fig. 1. Starting from various positions (stars), the normal network (A) detects and withdraws inappropriate moves (dotted lines) and quickly converges to the goal. The network with lesioned plan units (B) never withdraws the moves it selects and is often stuck in impasses (solid disks). (C) Average time to reach a given goal, starting from various initial states, for networks with intact (white) and lesioned (black) plan units. Disk diameter is proportional to solution time. A time limit of 1,000 update cycles, corresponding to about 20 attempted moves, was imposed. Initial states are grouped by “iso-distance” lines according to their distance to the goal, a measure of problem complexity. Both networks quickly solve problems within two moves of the goal, where beads can be moved directly to their final location. The lesioned network performs abnormally slowly on complex problems that require intermediate moves. (D) Percent problems solved by the intact and lesioned networks as a function of problem complexity. The dotted lines are taken from Shallice’s groups of normal controls and left anterior patients (1). (E–G) Predicted dissociations in performance in normal subjects. Problems requiring the disassembling of a “tower” of beads (E, dotted arrow) and problems in which a direct move is incorrect and must be inhibited (F, dotted arrow) are predicted to yield more errors (G) than the converse, superficially similar problems (E and F, continuous arrows).

Figure 4.

Functional architecture (Left) and single-unit activity (Right) during the resolution of a problem of intermediate difficulty. Following the presentation of initial and goal states, the network compares them and activates one “remaining goal” unit for each misplaced bead (Top). The total activity of “remaining goals” units being positive, the “motivation” unit activates, followed by the “store” plan unit, resulting in the storage of the initial state in “working memory” units. The “move” plan unit then activates, triggering a cascade of activation through which an operation is selected and the corresponding sequence of two gestures is executed. The first operation thus selected happens to be inadequate, because the resulting state is even farther from the goal (the black bead occupies the desired location of the gray bead). Hence, the total activity of “remaining goals” units increases, which results in the activation of the “error” unit and the “retreat” plan unit, causing the withdrawal of the previous move and the restoration of the initial state from working memory. A second operation is then performed, immediately followed by a third operation that places the gray ball at its desired final location. The current state is now judged closer to the goal, as signaled by the activation of the “correct” unit. The “store” unit therefore is activated, again storing the current state in working memory. Finally, the final direct move is performed, making the current state identical to the goal. Because of this match, the “motivation” unit switches off and activity ceases in all layers. In the lower graph, single-unit activity curves were scaled by an arbitrary factor and superimposed to show the temporal nesting of lower-level units by successively higher levels.

Although Shallice (1) originally used the total number of moves as a measure of problem difficulty, empirical research with normal subjects (15) has shown that a better predictor of normal performance is the number of indirect moves (moves that do not place a disc in its final position). Our network performs similarly. Multiple regression on a simulated data set of 2,081 problems indicated that both the solution time and the error rate were better predicted by separate variables for the number of direct and indirect moves required than by a single variable for the total number of moves. Each additional indirect move added about 110 simulation cycles to the solution time, whereas each additional direct move required only 45 additional cycles. These results are directly analogous to empirical findings (15), except that human subjects also learn to represent whole series of moves as a single chunk in working memory (15), a feat beyond the reach of the present model.

On the basis of a detailed analysis of normal subjects’ behavior in a similar test, Ward and Allport (15) suggested that humans solve Tower of London problems using a heuristic of look-ahead, evaluation, and backtracking similar to the one used by our model. To directly compare normal subjects’ evaluation function with the one used by our network, we computed, after each tentative move, the difference in the activation level of the positive and negative reward units in our network (evaluation index; positive values indicate positive evaluation). Moves that placed a bead to its final location (direct moves) were rated “best” in Ward and Allport’s (15) empirical study and had an average evaluation index of +0.697 in our simulation. Likewise, moves that cleared the top of a current goal bead or cleared a current goal location were rated “good” (+0.438), those that blocked these locations were “bad” (−0.611), and those that moved a disc away from its goal location were “worst” (−0.838). All other moves were rated by our network as “neutral” on average (+0.028). Thus, the internal evaluations computed by our network matched those of normal subjects.

At least two behavioral predictions follow from this evaluation function. First, for a fixed number of direct and indirect moves, problems requiring the assembling of a tower of beads all onto one peg should be easier than converse problems requiring the disassembling of a tower (Fig. 3E). This is because assembling a tower provides an unambiguous ordering of goals (15). This prediction was verified by Ward and Allport in normal subjects (15), and is also valid for our network (Fig. 3G). Second, problems in which a direct move is actually incorrect and must be inhibited should be much harder to solve than problems in which the same direct move is correct (Fig. 2F). This prediction was verified in our network (0% correct under a 1,000-cycle time limit for “direct move incorrect” problems; 100% correct, average solution time 243 cycles for “direct move correct” problems) but remains to be tested empirically.

Simulation of Prefrontal Lesions

When the network is lesioned by removing the plan units, accuracy drops and solution time increases considerably for problems of intermediate difficulty (Fig. 3 C and D), paralleling the performance of patients with frontal lesions (1–3). Depending on the problem, different behaviors are observed (Fig. 3B). Either moves are selected and executed at random, leading to a purposeless trajectory in state space, or the network reaches a dead end where it is incapable of generating further moves because operation units, being deprived of inputs from plan units, now fail to reach their activation threshold. However, there is a relative preservation of simple problems that can be solved by direct, stimulus-driven placement of beads at their final location (Fig. 3 B–D). In fact, direct moves are often executed faster by the lesioned network than by the intact network, and in more complex problems the lesioned network can no longer inhibit a direct move even when it leads away from the goal. This behavior is analogous to the impulsivity (16, 17) and utilization behavior (18, 19) attributed to patients with frontal lesions.

According to our simulation, the lesioning of plan units effectively disconnects the operation network from the reward network. Hence, the planning deficit can be attributed to an inability to guide the selection of motor operations by an internal evaluation of their relevance to reaching the goal (10, 20). There is an adherence to the immediately apprehensible sensory characteristic of the problems (18) but no consideration of the global objective of solving them. Note that plan-unit lesions leave the reward system fully functional but unable to affect the selection of moves. Thus, a testable prediction is that some patients with frontal lesions, although unable to generate a goal-directed sequence of moves, might remain able to evaluate its correctness when performed by a third party. The predicted dissociation between preserved internal evaluation and incorrect generation of plans is analogous to the observation that in the Wisconsin Card Sorting Test, some patients with frontal lesions may verbally criticize their errors, all the while failing to correct them (21, 22).

Functional brain imaging experiments show that when normal subjects engage in the Tower of London task, an extended network of areas activates, including parietal, prestriate, insular/opercular, premotor, and prefrontal cortices (12, 23, 24). Because parietal, prestriate, premotor, and insular/opercular areas are active even for simple problems, they may contribute to the operation level, with occipitoparietal areas contributing to identifying movable beads and reachable goals, and premotor and insular cortex involved in mentally selecting and executing direct moves. During the resolution of more complex Tower of London problems, increased activity is detected in this network as well as in dorsolateral, rostrolateral, and medial prefrontal areas and in the basal ganglia (12, 23, 24). This set of areas thus may contribute to the anatomical substrates of working memory, plan, and reward units that together form the plan level of the model. Within dorsolateral prefrontal cortex in monkeys, neurons exhibiting long-lasting firing during delayed-response tasks (10) may correspond to the working-memory units. Sequential dependencies in neuronal firing, including selective firing to a sequence of motor actions, have been observed in prefrontal cortex (25) and in supplementary motor area (26) and may correspond to the transition units. Finally, some neurons in dorsolateral prefrontal cortex (27) and in subcortical mesencephalic dopamine nuclei (11, 28) fire when an animal expects to receive a reward. Hence, dopaminergic input to prefrontal cortex may contribute to reward information necessary to modify the plan according to its success or failure. Lesions of dopaminergic neurons may be simulated in the model by removing the reward units, whereas alterations of dopamine action on its receptors and/or related signal transduction mechanisms (29) may be mimicked by altering the parameters determining the impact of reward units on plan units. In both cases, a severe planning deficit similar to that caused by plan-unit lesions is observed, in good agreement with the deficits of Parkinsonian patients in the Tower of London test (30–32).

Inasmuch as motor, parietal-premotor, and mesolimbic-prefrontal circuits correspond to the gesture, operation, and plan levels, the model predicts a specific temporal organization of their activation during problem solving. A given plan unit may remain active while multiple operation units are sequentially tested, each in turn calling for a sequence of gesture-unit activity. This “temporal nesting” of activity (Fig. 4) remains to be tested empirically.

Conclusion

We have described a neural architecture comprising multiple hierarchical levels and capable of solving complex problems that, in humans, require frontal lobe integrity. Our model uses heuristics similar to those of normal subjects and mimics the performance of normal subjects and of frontal patients in considerable detail. Future work should address some of its obvious limitations. The “chunking” of series of moves (15) and the spatial interference effects (2, 33) that have been observed in normal and lesioned subjects may require only small modifications to the coding scheme of input and operation units. Most important, learning mechanisms should be added to allow the model to adapt to different problem types and domains. Currently, the exact values of the model’s connections are specific to the Tower of London test. However, we believe that its architecture with interconnected ascending and descending hierarchical streams for evaluation and planning may be generalized to other tasks and provides a general framework for understanding planning behavior.

Cognitive models of prefrontal cortex function during problem solving have emphasized its role as a supervisory structure, capable of selecting and controlling lower-level automated behaviors (19, 34, 35). Our neuronal implementation of this influential view suggests that “supervision” and “planning” cannot be related to a single brain region. Rather, they rely on multiple neural circuits coding for specialized subprocesses such as working memory, plan generation, or internal reward.