The tactile integration of local motion cues is analogous to its visual counterpart

Abstract

The visual and somatosensory systems have been shown to process spatial information similarly. Here we investigate tactile motion processing using stimuli whose perceptual properties have been well established in vision research, namely superimposed gratings (plaids), barber poles, and bar fields. In both modalities, information about stimulus motion (speed and direction) conveyed by neurons at low levels of sensory processing is ambiguous, a conundrum known as the aperture problem. Our results suggest that the tactile perception of motion, analogous to its visual counterpart, operates in multiple stages: first, the perceived direction of motion is determined by a majority vote from local motion detectors, which are subject to the aperture problem. As in vision, the conflict between the cues from terminators and other local motion cues is gradually resolved over time so that the perceived direction approaches the veridical direction of motion.

Both vision and touch share the common problem of inferring stimulus form, texture, and motion from a spatiotemporal pattern of activation across a two-dimensional sensory sheet (i.e., the retina and skin). The two systems have been found to process information about two-dimensional spatial form in a similar fashion (1–3). In both systems, information about motion can be acquired by analyzing how stimulus contours change over time. Both the visual and somatosensory systems may therefore have evolved analogous mechanisms to process motion information as well. Then again, the analogy between the two systems is not absolute: for instance, depth ordering and transparency are problems that have no obvious analogue in the cutaneous sense (although palpation through gloves may involve a tactile equivalent of transparency). Furthermore, shear forces, which have no direct visual analogue, may contribute to the tactile perception of motion (4, 5). These differences between vision and touch may lead to differences in the way the two systems process motion.

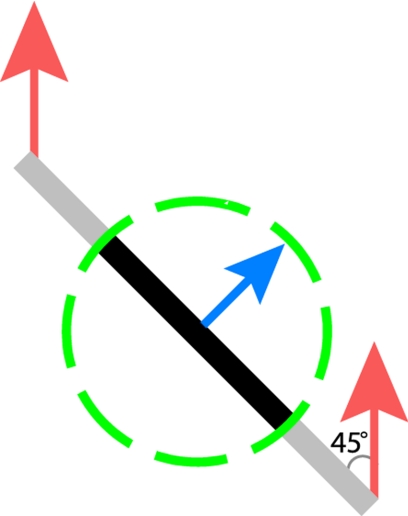
The study of motion processing provides an opportunity to address an important question in sensory neuroscience, namely: how is the environment represented at each stage of perceptual processing? Indeed, the speed and direction of motion of individual (one-dimensional) edges is ambiguous because information about the motion component parallel to their orientation is not available, a predicament known as the aperture problem (6) (Fig. 1). To acquire a veridical percept of an object's direction of motion, then, it is often necessary to integrate motion information across multiple stimulus contours that differ in orientation (7, 8) or to rely on so-called terminators—such as end points, corners, and intersections—whose direction of motion is unambiguous (9, 10).

Fig. 1.

The geometry of the aperture problem. The red arrows show the actual motion of the bar; the blue arrow shows the motion of the bar as observed through the circular aperture (dashed circle). When an edge is observed through a circular aperture, the only available information about its direction of motion is along the axis perpendicular to its orientation. In other words, no time-varying information is conveyed along the parallel axis. In the example, a bar oriented at 45° and moving upwards at speed s seems to be moving up and to the right with speed s × sin(45°). Only the terminators (i.e., its corners) convey information about the bar's veridical direction of motion.

The aperture problem is inherent to individual neurons at low levels of processing because these neurons have spatially restricted receptive fields and only “see” local contours of the stimulus. From the standpoint of these neurons, then, the direction of motion is always orthogonal to the orientation of the contour that impinges on their receptive fields. This ambiguity is resolved at higher processing levels as evidenced by the fact that the veridical direction of motion of objects comprising multiple contours can be readily perceived. The objective of the present study is to determine whether local motion signals, conveyed by local motion detectors, which lie at the early stages of somatosensory processing (11–14), are integrated to form a global motion percept. To that end, we present the tactile equivalent of stimuli whose perceptual properties are well established in vision, including superimposed gratings (plaids), barber poles, and moving bar fields. The stimuli are delivered using a 400-probe stimulator (15), the tactile analogue of a visual monitor.

Results and Discussion

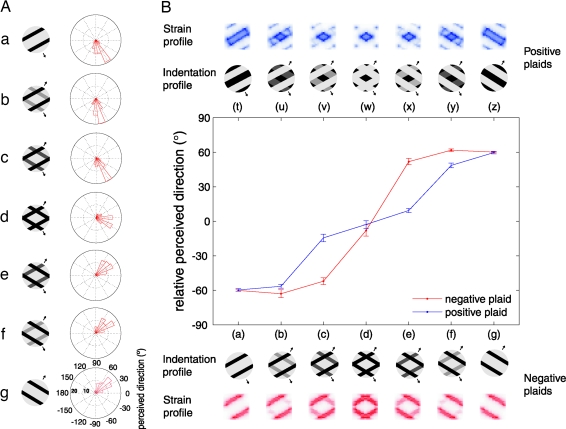
In the plaid paradigm (16–18), two gratings, moving in directions separated by 120°, are superimposed and the relative intensity of the two gratings is varied. When one component is dominant, the perceived direction of the stimulus is determined by the direction of that component. When the amplitudes of the two gratings are similar, the stimulus is perceived to move in the direction that bisects the two components' directions of motion; i.e., pattern motion is perceived. In the present study, when single square-wave gratings were presented through a circular aperture, subjects perceived the direction of motion to be orthogonal to the orientation of the gratings (Fig. 2). When the pattern was gradually morphed from a simple square-wave grating to a plaid pattern, the perceived direction of motion dramatically shifted to the bisector of the two directions of motion (see Fig. 2B, d, for results obtained with a negative plaid). That is, the perceived direction when one component was dominant was consistently that of the dominant grating; the mean perceived directions for stimuli a, b, and c were equal, as were the perceived directions for stimuli e, f, and g (main effect analysis, P > 0.05). In contrast, the perceived direction reflected the direction of the pattern motion when both gratings were equal in amplitude. The ambiguity of the stimulus motion was thus resolved in a way analogous to that observed when comparable stimuli are presented visually. A similar effect was observed when the polarity of the gratings was reversed (i.e., with positive plaids). Differences in the motion percepts evoked by the two plaid patterns are likely due to skin mechanics (see below). One possibility is that the motion percept evoked by plaids was bistable or tristable but that the mean perceived direction across trials was that of pattern motion. According to this scenario, judgments of perceived direction would be distributed multimodally, which was not the case (Fig. S3A). Another possibility is that subjects simultaneously perceived multiple directions of motion when presented with the plaids but selected the bisector of the velocities of the two components as a compromise. In a control experiment, we allowed subjects to select several directions of motion after the presentation of each plaid. On very few trials (<2% on average), subjects reported perceiving more than one direction of motion (see Fig. S4A). The discrete nature of the behavioral response to a continuous morph from grating to plaid suggests a winner-takes-all mechanism in the formation of a global percept of motion direction.

Fig. 2.

The perceived direction in plaid paradigms. (A) Distribution of perceived directions for one subject in the negative plaid paradigm. Dark patches indicate indentations into the skin, and the light gray indicates baseline position of the array. In A, from a to d: a set of patterns gradually morphed from a simple grating into a plaid pattern. The perceived direction was initially orthogonal to the orientation of the grating; it then shifted abruptly to the direction that bisects the directions orthogonal to the gratings' orientations. g to d illustrates the same phenomenon when the other component grating morphed into the plaid. In addition, a systematic clockwise shift from the veridical direction of motion was observed, which was corrected for later analysis [see supporting information (SI) Fig. S1]. (B) Perceived direction—averaged across subjects—of two crossed moving gratings that formed a negative plaid (red line) and positive plaid (blue line) (error bars denote mean ± SEM). The images show the indentation and strain profiles of the plaids. The strain profiles at the approximate depth of the receptor sheet (500 μm under the surface of the skin) were estimated by using a continuum mechanical model (33). When one component was dominant, the perceived direction of the stimulus was determined by the direction of that component; when the intensities of the two gratings were similar, the stimulus was perceived as a plaid moving in the direction that bisected the two components' directions. The perceived direction could be predicted from the strain profiles but not the indentation profiles (see Fig. S2).

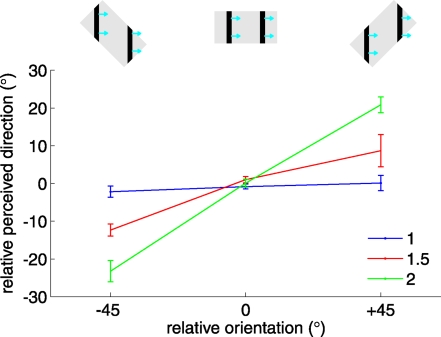
In the barber pole paradigm, a moving grating is presented through a rectangular aperture. The perceived direction of motion of the so-called barber pole is biased toward the long axis of the aperture, suggesting that the terminators, intersections between the grating and aperture, are used to solve the aperture problem (6, 9, 19). Perceived direction is biased toward the long axis because terminators signal motion parallel to the edge of the aperture and the long axis of the aperture comprises more terminators than does the short one. In the present study, we varied both the aspect ratio of the aperture and its orientation relative to that of the grating. The relative orientation of the aperture had a strong effect on the perceived direction of motion of the grating (Fig. 3), and the effect grew stronger as the aspect ratio increased [repeated-measures ANOVA, relative orientation × aspect ratio interaction: F(4,40) = 21.2, P < 0.001]. In the control condition, when the aperture ratio was 1, the perceived direction was always perpendicular to the orientation of the grating regardless of the aperture's orientation (blue trace in Fig. 3). For stimuli with aspect ratios of 1.5 and 2, the mean angular deviations were 10.5° and 22°, close to the 11.3° and 18.4° deviations predicted by the terminator-average model (see Experimental Procedures) (20). In other words, the perceived direction was entirely determined by the motion of the terminators. These results closely parallel what has been observed in visual studies of the barber pole phenomenon (6, 21). Unlike their visual counterparts (22), however, the tactile barber poles yielded stable percepts (Figs. S4B and S5).

Fig. 3.

The effect of aspect ratio on the barber pole effect. The relative orientation is the angular difference between the aperture's orientation and the direction orthogonal to the grating's orientation (as shown in the Insets for barber poles with aspect ratios of 2). Data obtained in matching conditions (i.e., with stimuli of matching relative orientation) were pooled across absolute orientations. The perceived direction is plotted relative to the direction orthogonal to the grating's orientation. The strength of the barber pole effect, i.e., the degree to which the perceived direction was biased toward the aperture's orientation, grew stronger when the aspect ratio increased.

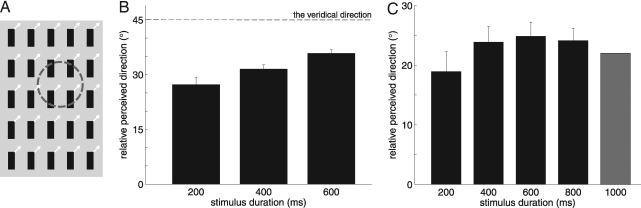
In a third paradigm, fields of bars, moving in directions oblique relative to their orientation, are presented for varying durations. In vision, the perceived direction is initially biased toward the direction orthogonal to the bars' orientation, suggesting that cues from local contours are dominant in the early stages of motion processing. In the present study, the bar fields drifted in a direction that was perpendicular (0°) to the bars' orientation or at ±45° with respect to it (Fig. 4A); the duration of the stimuli was 200, 400, or 600 ms. The strength of the aperture effect was quantified by the degree to which the perceived direction was biased toward the direction orthogonal to the bars' orientation. The aperture effect was most prominent for the shortest stimuli (200 ms) and diminished with time (Fig. 4B) [repeated-measures ANOVA: F(2,20) = 11.8, P < 0.001]; note that the bias had not disappeared at longer stimulus durations (400 or 600 ms). In fact, even after 2 s, the bias remained (Fig. S6). Why the bias does not disappear at long stimulus durations is unclear. The persistence of the bias suggests that both edges and terminators determine the perceived direction of bar fields, in contrast to barber poles, the perceived direction of which seems to be solely determined by terminators. Interestingly, the responses of neurons in the middle temporal (MT) area to visual bar fields seem to exhibit a similar although lesser bias even after having reached steady state (23). Similar dynamics were observed when we tested the time course of the barber pole effect: When barber pole stimuli (aspect ratio = 2) were presented for 200 ms, the barber pole effect was substantially diminished (Fig. 4C) [main effect of stimulus duration, F(3,18) = 3.8, P < 0.05], suggesting that the grating contours determine the perceived direction during the initial stages of motion perception. For longer durations (400 and 600 ms), the barber pole effect was almost back to full strength, so the motion of the terminators again determined the perceived direction. Similar dynamics of motion integration have been observed for visual barber poles (24). Note that the shortest duration (200 ms) and travel length for both the bar fields (8 mm) and the barber poles (6 mm) were long enough for subjects to acquire information about the direction of motion (25). Furthermore, if subjects had failed to adequately perceive the stimulus at these short durations, judgments would be uniformly distributed. Instead, their distribution was significantly shifted toward the direction perpendicular to the orientation of the bars.

Fig. 4.

Temporal dynamics of motion perception. (A) A field of moving bars, moving ±45° relative to the their orientation or perpendicular to it, was displayed within a circular aperture, represented by a dashed circle (only probes within the aperture were active). (B) The perceived direction of the bars changed with time; the dashed line represents their veridical direction of movement. The perceived direction is represented as the angular difference between the perceived direction and the direction orthogonal to the bars' orientation. The bias was most prominent for the short duration stimuli but was still present after 600 ms of stimulation. (C) The perceived direction of the barber pole (aspect ratio = 2) changed with time. The gray bar shows the perceived direction when the stimulus duration was 1 s (same data as shown in Fig. 3). The perceived direction is expressed relative to the direction orthogonal to the grating's orientation. The aperture effect was weaker for short-duration stimuli and plateaued after ≈400 ms. Note that different subjects participated in the main barber pole experiment (the results of which are shown in Fig. 3 and as the 1,000-ms bar in C here) and in the experiment investigating the temporal dynamics of the barber pole effect (the results of which are shown as the black bars in C), which may explain why the steady-state bias is slightly smaller in the former than in the latter.

These results suggest that the tactile perception of motion, analogous to its visual counterpart, operates in multiple stages: first, the perceived direction of motion is determined by a majority vote from local motion detectors, which are subject to the aperture problem. The conflict between the cues from terminators and other local motion cues is gradually resolved over time so that the perceived direction approaches the veridical direction of motion. Note that the system has not stabilized even after 600 ms, at least for bar fields. This behavior is identical to that observed in analogous visual psychophysical experiments (26). Furthermore, the steady-state bias observed at long stimulus durations is similar to that observed in the responses of neurons in the MT area (23).

The similarity in visual and tactile motion perception may be interpreted as evidence that the two are mediated by similar neural mechanisms. The consensus in vision research is that motion perception relies on motion-sensitive neurons in the primary visual cortex (V1) (27, 28) that project onto neurons in MT, where most neurons are selective for motion direction (17, 29). Neurons in V1 tend to be subject to the aperture problem, whereas MT neurons integrate information across populations of V1 neurons to compute the veridical direction of motion. Neurons that detect local motion have been identified in the primary somatosensory cortex (SI) (11–14), but these neurons have yet to be systematically probed with stimuli whose local motion cues are ambiguous.

Nevertheless, there are fundamental differences between tactile and visual motion perception. First, the perceived direction of visual barber poles is multistable (22) whereas that of their tactile counterparts is not (see Figs. S4B and S5), suggesting that visual and tactile motion processing are not identical.

Second, depth ordering (9, 30), which is critical when inferring three-dimensional structure from a pair of two-dimensional retinal images, does not present a problem when analyzing tactile stimuli presented to a single finger pad. This fundamental difference between the two systems can be investigated by using, for example, the depth–context effect in the barber pole paradigm: if a moving visual grating is placed behind an aperture frame, the grating is perceived as sliding behind the frame and the perceived direction is orthogonal to the grating's orientation. Whereas depth–context information can abolish the barber pole phenomenon visually (9, 30, 31), it does not tactually (see Fig. S7). The absence of a tactile depth–context effect is not surprising given that occlusion on a single finger pad does not occur naturally and so is likely not interpreted as such.

Third, skin mechanics enhance some features while making others intangible in a manner that has no direct analogue in vision (32, 33). The perceived direction of the plaids could be predicted from their strain profiles (but not their indentation profiles): The strain profiles—computed at each time step—of patterns that evoked pattern motion were almost completely plaid-like whereas the strain profiles of patterns that evoked component motion fell within the continuum between plaid and grating (Fig. 2B; see Fig. S2). Because afferent responses have been found to be linearly related to local strain (33), the strain profile of a stimulus can be used as a proxy for its peripheral neural representation.

Finally, the results of the present study were obtained in the absence of shear forces. In natural tactile experience, shear forces exerted on the skin likely provide additional information about direction of motion (4). The objective of the present study is to understand how information about direction of motion is conveyed without shear force signals, when tactile motion perception must thus rely on changes in stimulus contour over time, analogous to its visual counterpart. The dense tactile array (15), which is capable of delivering arbitrary spatial-temporal stimuli without exerting shear forces, affords us a unique opportunity to do so.

Experimental Procedures

Subjects.

Twenty-four healthy subjects (11 males and 13 females, 18–30 years old) participated in these experiments: nine (four males and five females) in the negative plaid experiment, 14 (six males and eight females) in the positive plaid experiment, 11 (six males and five females) in the barber pole experiment, and 11 (four males and seven females) in the bar field experiment. All subjects reported that they had normal tactile sensations and did not have any history of peripheral neurological disease. We excluded from the study three subjects whose data were more variable than those of other subjects. Specifically, the standard deviation of their judgments of direction fell 1.5 times the interquartile range above the third or below the first quartile (34). All testing procedures were performed in compliance with the policies and procedures of the Institutional Review Board for Human Use of the Johns Hopkins University. Subjects were paid for their participation.

Apparatus.

The tactile stimuli were generated and delivered using a dense tactile array consisting of 400 independently controlled probes arrayed in a 20 × 20 matrix (15). The tips of the probes, spaced at 0.5 mm, center to center, covered a 10-mm × 10-mm area. The depth of indentation of each probe could be specified every millisecond. To simulate motion, adjacent probes were indented in succession at a rate that was determined by the nominal speed of the stimulus (as it is in visual displays). The indentation of one probe overlapped in time with the retraction of the other to create a smooth percept of motion (see ref. 15 for details). The subject's finger, volar side up, was pressed against the array with a force of 100 g by using a counterweight mounted on a vertical stage (LOT Oriel). This assembly allowed for accurate and repeatable finger positioning on the probe array. The density of the probes is greater than the innervation density on the fingertip, which leads to a smooth motion percept despite the inherent pixilation of the array.

In all protocols, the phases (i.e., initial positions) of the patterns were randomized across trials. Furthermore, the depth of indentation of the stimulus increased gradually to its maximum level over its outermost 1-mm edge to avoid onset transients and paradoxical motion: Indeed, in the absence of these linear ramps, subjects sometimes perceived the stimulus moving in the direction opposite to the veridical direction, likely reflecting a failure to solve the correspondence problem.

Procedure.

On each trial, a moving tactile pattern, lasting 1 s unless otherwise specified, was presented to the subject's left distal index finger pad. In all protocols except the barber pole, only probes within 5 mm of the center of the array were active; all other pins were retracted by 500 μm so that they did not contact the skin. The inactive pins were withdrawn at the onset of the stimulus and remained withdrawn until its offset. The subject's task was to indicate the direction of motion by selecting by mouse click using his free hand one of a set of arrows presented on the computer screen. The arrows ranged in direction from 0° to 345° in 15° steps. There was a 500-ms interval between the subject's response and the subsequent stimulus. Each stimulus was repeated five times in pseudorandom order. Each protocol was split into five blocks to allow the subject a break. The stimuli for individual protocols are described in detail below.

In all of the experiments, subjects' responses exhibited a systematic clockwise shift relative to the veridical direction of motion; that is, the perceived direction of motion was identified as being shifted clockwise from the veridical direction of motion; the shift varied across subjects (mean ± SD: −28.6 ± 9.3°). When subjects' right index finger pad was stimulated, the shift was counterclockwise and of the same magnitude. This bias has also been observed in tactile judgments of stimulus orientation (3). Subjects' identification judgments were corrected for this systematic shift (see Fig. S1). Specifically, we subtracted from each response the mean discrepancy between the perceived direction and veridical directions. Note that this correction resulted in a uniform rotation of all of the data obtained from each subject. Because our conclusions were based on the relative perceived direction of motion in different conditions (i.e., gratings with different aperture orientations or a plaid vs. its component gratings), the rotation had no impact on our conclusions. The correction was applied to the data obtained in all of the protocols. Fig. 2A shows the uncorrected responses whereas subsequent figures show the corrected responses.

Negative Plaids.

On each trial, the subject was presented with a stimulus consisting of two superimposed square-wave gratings moving in directions separated by 120°. We used a separation of 120° because it elicits robust percepts of pattern motion (when both components are of comparable amplitude) and the difference in perceived direction between component and pattern motion is easily resolved experimentally (the two are separated by 60°). The direction of motion of the components varied from 0° to 330° in steps of 30° (Fig. 2). The wavelength of the component gratings was 5 mm, their speed was 40 mm/s, and their duty cycle was 30% (3/10). The relative amplitudes of the two component gratings were manipulated to yield a set of patterns that gradually morphed from a simple square-wave grating into a standard plaid pattern (Fig. 2B, a–e). Specifically, the amplitude of one component grating was 500 μm whereas the amplitude of the other was 0, 167, or 334 μm. The plaid pattern consisted of diamond-shaped grooves bounded by an indented grid. If I₁(x, y) and I₂(x, y) are the displacements of components 1 and 2, respectively, at position (x, y), the displacement, I(x, y), of the pattern was the greater of I₁(x, y) and I₂(x, y):

The minimum and maximum displacements of the pattern at any location were therefore 0 and 500 μm, respectively.

Positive Plaids.

In vision, white bars moving over a black background and black bars moving over a white background yield similar motion percepts. In this condition, we tested whether reversing the polarity of the plaids affects the way in which tactile motion information is processed (Fig. 2B, t–z). The wavelength of the component gratings was 6 mm, and their duty cycle was 42% (5/12) to ensure that the plaids were tangible; indeed, given the constraints imposed by skin mechanics and tactile spatial acuity, positive plaids with the same spatial parameters as those used to generate the negative plaids were not clearly palpable (as determined in preliminary experiments). The speed of the component gratings was 40 mm/s, as was the case with the negative plaids. For the positive plaids, the displacement at location (x, y), I(x, y), was 500 μm minus the maximum of the component displacements, I₁(x, y) and I₂(x, y):

Barber Pole.

A drifting grating was presented through a rectangular aperture; only probes within the aperture were active (Fig. 3). On each trial, the aspect ratio and orientation of the aperture varied, as did the direction of movement of the grating relative to the orientation of the aperture. The aspect ratios were 1, 1.5, and 2, the orientations of the rectangular apertures varied from 0° to 315° in 45° steps, and the directions of movements were −45°, 0°, and +45° relative to the orientation of the aperture. The total area of stimulation was approximately constant at 40 mm² across all conditions: the sides of the square apertures (aspect ratio = 1) were 6.5 mm in length; for apertures of aspect ratio 1.5, the short and long axes were 5 and 7.5 mm in length; to obtain an aspect ratio of 2, the long and short axes were 4.5 and 9 mm in length, respectively. The wavelength of the gratings was 5 mm, their velocity was 30 mm/s, their amplitude was 500 μm, and their duty cycle was 20% (1/5). We used this wavelength and duty cycle because it was the shortest wavelength that yielded clear percepts of direction (as determined in preliminary experiments). The strength of the barber pole illusion was characterized by the degree to which the perceived direction was biased toward the long axis of the aperture.

We derived predictions for the perceived direction of motion based on the assumption that the global percept is determined entirely by motion information stemming from terminators (20). The predicted perceived direction, d̂, was given by the weighted average of unit vectors along the long and short axes of the aperture:

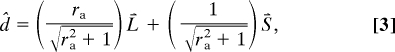where r_a is the aspect ratio of the aperture and L⃑ and S⃑ are unit vectors along its long axis and short axis, respectively.

The predicted angular deviation (Δφ) is the angular difference between d̂ and the unit vector orthogonal to the grating:

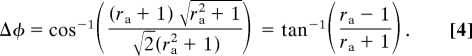Depth–Context Effect in the Barber Pole Phenomenon.

In vision, if a moving grating is placed behind an aperture frame, the grating is perceived as sliding behind the aperture frame and its direction is perceived to be orthogonal to its orientation. We tested whether this effect was also observed in touch. The basic barber pole protocol was modified by manipulating the depth of the drifting grating relative to that of the aperture (Fig. S7). Each drifting grating was framed by a static rectangular aperture (aspect ratio = 2). On each trial, the aperture frame was indented at 300 μm for 1 s before the onset of the drifting grating and remained static throughout the stimulus interval. The wavelength of the gratings was 5 mm, their velocity was 30 mm/s, and their duty cycle was 20% (1/5). The amplitude of the grating was 200, 300, 400, or 800 μm. Thus, the ridges of the 200-μm grating were depressed relative to the aperture by 100 μm, the ridges of the 300-μm grating were flush with the aperture, and the 400- and 800-μm gratings protruded beyond the aperture by 100 and 500 μm, respectively. The orientations of the rectangular apertures varied from 0° to 315° in 45° steps, and the drifting direction of the gratings relative to the orientation of the aperture was −45°, 0°, or 45°. The strength of the barber pole phenomenon was characterized by the degree to which the perceived direction was biased toward the orientation of the aperture.

Temporal Dynamics of the Aperture Problem.

Each stimulus consisted of a field of identically oriented bars moving in the same direction. The size of each bar was 4 × 1.5 mm, and the distance between bars was 3 mm. The velocity of the bars was 40 mm/s, and their amplitude was 350 μm. The use of multiple bars ensured that the subject did not identify the direction of motion by tracking the position of a single bar. The direction of motion was either orthogonal to the orientation of the bar (0°) or at ±45° with respect to the orthogonal direction; the stimulus moved in one of eight directions from (0° to 315° in steps of 45°) for 200, 400, or 600 ms. The aperture effect was quantified by the degree to which the perceived direction was biased toward the direction orthogonal to the bars' orientation.

Temporal Dynamics of the Barber Pole Phenomenon.

The paradigm was almost identical to the barber pole paradigm described above. The only difference was that the aspect ratio was always 2 and the duration of the stimulus was 200, 400, 600, or 800 ms.