A Robust Method for Estimating Regional Pulmonary Parameters in Presence of Noise

Abstract

Rationale and Objectives

Estimation of regional lung function parameters from hyperpolarized gas magnetic resonance images can be very sensitive to presence of noise. Clustering pixels and averaging over the resulting groups is an effective method for reducing the effects of noise in these images, commonly performed by grouping proximal pixels together, thus creating large groups called bins. This method has several drawbacks, primarily that it can group dissimilar pixels together, and it degrades spatial resolution. This study presents an improved approach to simplifying data via principal component analysis (PCA) when noise level prohibits a pixel-by-pixel treatment of data, by clustering them based on similarity to one another rather than spatial proximity. The application to this technique is demonstrated in measurements of regional lung oxygen tension using hyperpolarized ³He MRI.

Materials and Methods

A synthetic data set was generated from an experimental set of oxygen tension measurements by treating the experimentally-derived parameters as “true” values, and then solving backwards to generate “noiseless” images. Artificial noise was added to the synthetic data, and both traditional binning and PCA-based clustering were performed. For both methods, the RMS error between each pixel’s “estimated” and “true” parameters was computed and the resulting effects were compared.

Results

At high signal-to-noise ratios, clustering does not enhance accuracy. Clustering does however improve parameter estimations for moderate SNR values (below 100). For SNR values between 100 and 20, the PCA-based K-means clustering analysis yields greater accuracy than Cartesian binning. In extreme cases (SNR < 5). Cartesian binning can be more accurate.

Conclusions

The reliability of parameters estimation in imaging-based regional functional measurements can be improved in presence of noise by utilizing principal component analysis-based clustering without sacrificing spatial resoltuin as compared to Cartesian binning. Results suggest that this approach has a great potential for robust grouping of pixels in hyperpolarized ³He MRI maps of lung oxygen tension.

Introduction

Pulmonary disorders such as emphysema, asthma, and acute respiratory distress syndrome are among the most common illnesses in the world; asthma alone is estimated to afflict 150 million people globally and costs the Untied States over $6 billion each year [1]. Emphysema may impact over 3% of the United States population, which is more than 9 million people [2]. Because the lung is a large and heterogeneous organ, these conditions can be difficult to diagnose clinically. It is thus important to develop sensitive radiological techniques for regional measurement of lung function to assist physicians in diagnosing such diseases.

Functional lung imaging using hyperpolarized gas magnetic resonance imaging (HP gas MRI) allows various pulmonary parameters to be assessed regionally [3]. This method is safe and does not deliver ionizing radiation to patients. Patients inhale hyperpolarized helium-3 (³He) or xenon-129 (¹²⁹Xe), and images of the airspaces are subsequently acquired. Signal intensity in each region of the lungs is directly related to the degree of polarization of the gas and the amount of gas that is present in that region. The images can be post-processed to reveal physiologic information. HP gas MRI allows researchers to rigorously assess a wide range of pulmonary parameters, such as regional ventilation [4], the regional alveolar partial pressure of oxygen (P_AO₂) [5], and the apparent diffusion coefficient (ADC) of gasses, which is linked to the size of the alveoli and structure of small airway [6], turning them into powerful tools for diagnosing and studying lung diseases.

Functional parameters such as alveolar oxygen tension, P_AO₂, and oxygen depletion rate, ODR, are altered by lung pathologies that affect regional ventilation (such as emphysema and asthma) or perfusion (such as pulmonary embolism). Regional oxygen measurements can help physicians detect early changes in lung function and structure associated with pulmonary disorders, quantitatively follow the progression of disease, and assess response to therapy [7]. Oxygen causes hyperpolarized ³He to depolarize at a time constant proportional to the regional oxygen concentration. The regional O₂ concentration and its variation, can therefore be estimated by fitting a model to the regional ³He signal decay kinetics [8]. In this approach data points with inherent uncertainty due to a low signal-to-noise ratio (SNR) can yield unreliable results. Thus the radio frequency (RF) noise in HP gas MRI datasets can make it challenging to accurately estimate regional oxygen parameters.

One way to reduce the effects of noise in estimating regional O₂ tension parameters is to cluster pixels together and average them. This increases SNR by a factor roughly proportional to the square root of the number of pixels included in a cluster. A common method of clustering is to combine adjacent pixels into larger groups, known as Cartesian binning [3, 7]. The most obvious drawback to this method is that it degrades spatial resolution. Additionally, because there is no guarantee that adjacent pixels are necessarily similar to one another, differently behaving pixels may be grouped together. It is also possible for bins to include low-signal points that ordinarily fall outside of an image mask, such as points on the edge of the lung. These inherent weaknesses can cause less accurate estimations of physiological parameters. Fischer et al. used this binning method to estimate regional oxygen parameters in a rabbit lung [8] on 8×8 grids, but they acknowledged several drawbacks to their approach. Predictably, their study suffers from degraded spatial resolution and loss of perimeter information caused by Cartesian binning. Improving the accuracy of the estimated parameters and improving spatial resolution would represent key advances in the technique. Both of these improvements were attempted in the work presented here.

A different approach in grouping pixels is reducing the dimensionality of a data space via principal component analysis (PCA), clustering data points within the reduced data space, and then transposing to the image domain, thereby making it possible to control noise without sacrificing image resolution. PCA has found applications in virtually any case of statistical pattern detection in large datasets, including optics, genetics, and geometrical modeling [9, 10]. After simplifying the data with PCA, it is possible to average similarly behaving pixels together by clustering within the data space. After performing a principal component analysis, numerous ways to decompose the data can be utilized, such as an eigenvector decomposition (EVD). This decomposition technique with an EVD and the subsequent grouping of resembling data points is referred to as PCA-based clustering, and has many useful applications in medical imaging [11–16].

Much of the existing literature on PCA/EVD data processing in lung imaging is applied to positron emission tomography (PET). Like MRI, PET scans are subject to random noise that can be controlled by averaging pixels together. Kimura et al. proposed a clustering method for PET images that increases SNR without degrading spatial resolution. They presented a two-parameter model describing a tracer entering and leaving a target compartment [14]. In a 2002 paper, they extended their work to a three-parameter model and used PCA to cluster pixels with similar kinetics by dividing the principal component space into equally populated subregions, each of which defined a cluster [15]. They then limited noise propagation in images by averaging over these groups of pixels. Layfield and Venegas modified Kimura’s method by introducing a synthetic set of principal components (PCs) and weighted PCA [16]. Instead of calculating the PCs of the experimental PET data set, a synthetic image is generated by removing pixels with physically implausible values and replacing them with values interpolated from neighboring pixels. They weighted the synthetic data by the inverse of the standard deviation of the noise (w_i = 1/ṣ_i), and found that this weighting method identified the directions that maximize SNR in the data set.

A key advantage to PCA-based clustering is that it groups pixels based on their similarity in kinetics, not their proximity in the spatial parameter map. The applicability of this approach to HP gas MRI of the lungs has not been investigated. This paper applies this method to HP ³He MRI data and demonstrates that it yields more robust results than Cartesian binning with better resolution. Both PCA-based clustering and spatial clustering are used to analyze P_AO₂ and ODR in a synthetic dataset derived from actual HP ³He MR images of rabbit lungs and the performance is demonstrated on an additional in vivo dataset. The deviation between the value assigned to each pixel by the clustering algorithm and the “true” value is assessed. This work aims to establish PCA-based clustering as a rigorous method for increasing SNR without degrading spatial resolution in post-processing of HP gas MRI data of the lungs.

Theory

Measurement of Regional Oxygen Tension

P_AO₂ and ODR can be estimated by analyzing the regional signal decay of HP ³He in a series of MR images of lung after inhaling a mixture of ³He and O₂ gases. Multiple images with specific interscan delay times (in the order of a few seconds) are acquired from a given slice of lung during a single breath hold using a low-flip-angle gradient-echo pulse sequence [8]. The time delay between images results in a signal intensity drop in each successive image as a function of the time-varying regional O₂ tension. This decay occurs for two main reasons. First, the polarization decreases due to the unrecoverable effect of applying radio frequency (RF) pulses in the imaging sequence. For a given flip angle α the polarization decay during one image acquisition is given by the factor cos^N (α), where N is the number of phase encoding lines per image. Second, ³He depolarizes in the presence of oxygen due to dipolar interactions between the two molecules. The depolarization time constant for this process is given by [17]:

$${\mathrm{\Gamma }}_{O_2}=\frac{P_A{O}_2}{\xi },$$ (1)

where ξ = 2.6 bar·s at body temperature. Signal decay is evident throughout the lung as time progresses. The decay rate, however, is different for each region, and is a function of local P_AO₂ and ODR. Theoretically, this relation is given by the following equation for the n-th image in the sequence [7]:

$$S(n)=S(0)·\text{exp}\lfloor N·n·\text{ln}(\text{cos}(\alpha ))-\frac{1}{\xi }\left(P_A{O}_2·t(n)-\frac{1}{2}\text{ODR}·t^2(n)\right)\rfloor ,$$ (2)

where S(0) indicates the original signal intensity in each region. In general the interscan time delay t(n) can be an arbitrary function of the image number n. In the case of equally spaced images, t(n) = T·n, where T is time interval between each pair of images. The form of Equation 2 follows from the common approximation that uptake of oxygen into the blood stream can be expressed as a linear function:

$${\mathrm{P}}_{\mathrm{A}}{\mathrm{O}}_2(t)={\mathrm{P}}_{\mathrm{A}}{\mathrm{O}}_2(0)-\text{ODR}·t$$ (3)

where P_AO₂(0) denotes oxygen partial pressure at the beginning of the breath hold (t=0). If two images are obtained with no – or negligible with respect to Γ_O2 – interscan time delay in each slice at the beginning of the image series, they can be used to fairly accurately calculate the flip angle in each region of the lung by analyzing the signal decay induced by RF pulse. Subsequent images are obtained at longer time intervals, and are used to calculate signal decay caused by oxygen. The time evolution of P_AO₂(t) and ODR(t) values at acquisition times, can therefore be obtained in this manner from a single series of images acquired during one single breath-hold [8].

Formation of the Data Space

Depending on the available ³He polarization, allowable breath-hold time and desired accuracy, N > 2 images (typically 6~8) are acquired to perform oxygen tension measurements as described in the previous section. Therefore each pixel in the lung with a specific P_AO₂ and ODR value can be expressed as a point in an N-dimensional data space. In other words each pixel is assigned a position along N linearly independent vectors, each of which representing signal intensity in one of the images. Each point in this data space describes a mathematically plausible series of signal intensities that a pixel may experience. As a result, points that are near one another in this space are considered to behave similarly over time, but there is no guarantee that they are near one another in the image.

Principal Component Analysis

In data sets with several variables, multiple factors often vary together because several variables can proxy for the same governing principle of a system. PCA is a quantitatively rigorous method for identifying the directions of maximum variance in the data. Performing EVD on the PCs allows us to identify contribution of each component independent from the rest. By definition, the full set of PCs is as large as the dimensionality of the original dataset. But it is common for the sum of the variances of the first few PCs to contain the majority of the variance in the original data [18]. Applying EVD to the covariance matrix of the dataset allows us to identify which principal components contribute the most information, and eliminate those that carry much less information and therefore are more susceptible to be affected by noise. It is important to note that EVD is a distinct process from PCA. Other decomposition methods can be implemented [16], but EVD is used here because it allows easy identification of the most significant PCs [19].

When using this approach, the data set is transformed to a new coordinate system in which the basis vectors are defined and ordered by their contributions to the total variance of the data. This way, the PCs of the data vectors will be uncorrelated with each other, and it is possible to eliminate those components that contribute the least to the variation. The first basis vector points in the data’s direction of maximum variance. The second basis vector is defined perpendicular to the first one, again in the direction of maximum variance available to it. Subsequent basis vectors are defined orthogonal to those already created, and always point in the direction of maximum variance available to them, in that order. An N-dimensional dataset will have N such basis vectors. These basis vectors are called the principal components of the data. These PCs tag the N dimensions in order of decreasing significance because they are ordered according to the amount of variance in the data [16].

The method of identifying the principal components using Eigenvalue Decomposition, EVD, is briefly described as follows. A data matrix X composed of A vectors of length B is created. In the framework of this manuscript, the data matrix is obtained by transforming the pixel signals to the N-dimensional data space. Each column represents a unique pixel, and the rows represent the successive images in the series. First, the mean of each row is calculated, giving an A × 1 mean vector, u. Second, matrix B is formed by subtracting the vector u from each column of the data matrix X,

$$B=X-u·h$$ (4)

where h is a 1 × N vector of all ones. Next, the covariance matrix C is computed and its unit eigenvectors V_n (1 ≤ n ≤ A) are determined, as are their corresponding eigenvalues l_n. C is given by:

$$C=\frac{1}{A-1}B·B^{*},$$ (5)

where * represents the conjugate transpose operation. The eigenvectors are sorted in decreasing order of eigenvalues l. By theorem, these unit eigenvectors are orthogonal to one another, and they define a space identical to the data space [19]. The eigenvector corresponding to the highest eigenvalue is the first principal component, and the following eigenvectors represent the remaining principal components in decreasing order of eigenvalues. Also, the eigenvalue of the n-th principal component tells us what proportion P of the variation in the data it describes, as given by the identity:

$$P=\frac{{\lambda }_n}{{\lambda }_1+\cdots +{\lambda }_N}.$$ (6)

We assume that projecting all our data points into the two-dimensional space defined by the first two principal components effectively eliminates variation in the data due to insignificant variables, although this property cannot be universally assumed. The desired result is a lower dimension data space in which noise effects has been reduced. Clustering points in this reduced data space can theoretically allow parameters estimations to be performed with less uncertainty in presence of noise.

Data Clustering – Cartesian Binning and K-means

As discussed in the Introduction, several approaches can be adopted for grouping data points in order to increase SNR. The most straightforward method is to reduce the resolution of images by combining adjacent pixels into larger bins, often done by converting an n × n image to an m × m image, where m = n/k for some positive integer k, the bin size, and averaging over all pixels within each bin. The SNR is typically higher for larger bins because the average of the uncorrelated noise in adjacent pixels is usually small. However, this method sacrifices anatomical detail and may average together pixels with different signal kinetics. There is also a tendency to eliminate significant information at the edges of an image, where a bin may contain so many background pixels that its SNR drops below a predetermined threshold, causing any information within it to be discarded, or the bin may be discarded due to an imposed homogeneity criterion. These flaws limit the usefulness of functional parameters derived via this method.

It is also possible to group the pixels within the data space. This places pixels in clusters based on their similar signal history, not their proximity within the image. One way to achieve this is to apply the Cartesian binning approach to the data space by creating a uniformly-spaced grid and averaging points that fall within common boundaries. A potential drawback with this approach is that bins may contain very different number of data points than others – especially on the outskirts of the data space – and therefore this option is not considered. Another available algorithm is K-means, which is a dynamic technique and commonly used for data clustering [20]. It finds a partition for the data in which pixels within each cluster are as close to each other in the data space as possible, and as far as possible from pixels in other clusters. Each cluster is defined by its member objects and its centroid. An iterative approach is used to minimize the objective function:

$$v={\displaystyle \sum _{i=1}^k{\displaystyle \sum _{x_j\in S_i}{|x_j-{\mu }_i|}^2,}}$$ (7)

where each S_i is a cluster with the centroid µ_i. Objects are moved between clusters until v is minimized. The theoretical result is a set of clusters that are as compact and separated as possible.

The K-means technique suffers from two drawbacks. First, a sub-optimal result may occur if the algorithm becomes trapped at a local minimum. Secondly, the number of clusters must be determined exogenously. The number of clusters should generally be decreased as noise in the image sequence rises, but the algorithm cannot make this assessment. Therefore a priori knowledge of the dataset SNR should be available so that a decision on the number of clusters can be made.

Materials and Methods

Helium-3 Polarization

Hyperpolarized (HP) ³He gas was produced in a commercial polarizer (GE Healthcare, Durham, NC) using spin-exchange collisions with optically pumped rubidium atoms. After about 14~16 hours of optical pumping, polarization levels of 30–35% were achieved. The hyperpolarized ³He was mixed with oxygen in a 4:1 ³He:O₂ ratio before being delivered to the subject. Helium thus replaced the nitrogen portion of normal breathing air.

Animal Preparation

All animal experiments were conducted using an Institutional Animal Care and Use Committee-approved protocol. The rabbit was sedated with Ketamine via an intravenous injection and intubated with a 3-mm ID endotracheal tube. Anesthesia was maintained with hourly injections. The animal was placed supine in a solenoid coil inside a 1.5-T MR scanner (Magnetom Sonata; Siemens Medical Systems, Erlangen, Germany). A tidal volume of 60 mL consisting of helium and oxygen in the ratio described in the previous section was administered to the rabbit. At the time of imaging, the HP ³He:O₂ mixture was delivered to the rabbit via the endotracheal tube directly following end-expiration and images were acquired during a 30-s breath hold. Upon completion of the study, the general anesthesia was increased, and the animal was euthanized with an intracardiac injection of potassium chloride.

Oxygen Tension Measurement Experiment

Datasets for estimating P_AO₂ and ODR were obtained by a single-acquisition technique as described by Fischer et al. [8]. This approach entails rapidly acquiring two initial images in the beginning of breath hold with minimum interscan delay time, Δτ, in order to determine the regional flip angle information, followed by eight more images at regular time intervals, τ. Signal evolution in the latter images allows solving for the two unknowns: alveolar partial pressure of oxygen, P_AO₂ and oxygen depletion rate, ODR.

Imaging Protocol

A multi-slice 2D gradient echo sequence was used to acquire images with the following imaging parameters: field-of-view = 16 × 16 cm₂, slice thickness = 7 mm, repetition time = 6.2 ms, echo time = 2.8 ms, matrix size = 64 × 64, flip angle = 3 ° and a scan delay time Δτ/τ = 0.4/6 s. Six slices were obtained at each time point during the 30-s breath hold.

Data Analysis

Initially an estimate of the local flip angle value will be obtained using the first two images, during which the oxygen-induced polarization decay is considered negligible. Next, the N-point signal history for each pixel – or equivalently for each cluster – will be fitted to Equation 2 by solving for P_AO₂ and ODR values that minimize the RMS error.

Synthetic Data

To properly assess the validity of PCA-based clustering methods, a noiseless synthetic data set was generated. This artificial data set was created by estimating P_AO₂ and ODR values from the experimental animal dataset as described above, and then solving backwards for the signal intensity of every pixel in an imaginary series of images. The result is that the signal decay in each pixel perfectly matches the estimated best-fit curve. In other words, this procedure creates an artificial, noiseless decay sequence. The background-subtracted SNR of each pixel is calculated as:

$$\text{SNR}=\frac{1}{N}\sqrt{S^2-N^2},$$ (8)

where S is the signal intensity of the pixel, and N is the normalized noise level in the image:

$$N=\sqrt{\frac{2}{\pi }}·\hat{N}.$$ (9)

The unbalanced noise N^, is estimated by averaging the intensity of a group of pixels in an area of the image that no MR signal is presenet, away from the actual lung tissue. Pixels not exceeding an SNR of 3 in the first image of the series were excluded in the synthetic data set. The synthetic data was only generated for a single slice near the middle of the lung that contained the trachea.

Principal Component Analysis

PCA was used in the manner described in Theory section to simplify the image dataset. Calculations for this analysis were conducted using Matlab software (Mathworks, Natick, MA). All data points were projected into the two dimensional system defined by the first two principal components.

Data Clustering

Pixels were clustered within the reduced 2-dimension data space using a K-means algorithm, as described in the Theory section. Clustering was performed six times, with 192, 58, 17, 6, 4, and 1 clusters, respectively. These are the number of clusters obtained when the images were spatially binned at resolutions of 64 × 64, 32 × 32, 16 × 16, 8 × 8, 4 × 4, and 2 × 2, respectively. For comparison purposes, unfiltered images – that is, images that had not been simplified by either traditional binning or PCA-based clustering – were also binned six times with a Cartesian gird, each with an identical number of clusters as the corresponding K-means result.

Noise Simulations

Artificial noise was added to the synthetic images to simulate noisy experimental conditions. The noise added to each pixel was drawn from a Rician distribution [20]. Noise was added so that the image SNR ranged from 1000:1 to 3:1.

Comparison of Clustering Techniques

To assess the accuracy of the PCA-based clustering method, the root mean square (RMS) error between the derived P_AO₂ and ODR values assigned to each pixel in the noisy synthetic image and the “true” value of each pixel was computed. The value of the original fit to the experimental data was the “true” value in this analysis. To distinguish lung tissue from the image background, spatial bins with SNR below 3 were excluded from the analysis. A ‘sliding-scale’ mask was used as follows: images were first masked to exclude those pixels with SNR < 1.5. Each image was then re-masked to exclude those with an SNR of less than 10/(n+1)², where n is the number of unmasked pixels immediately bordering the pixel being re-masked. Re-masking is repeated until a stable state is achieved. This heuristic masking algorithm was intended to lower the acceptance threshold in regions of relatively weak signal, and it correctly selects the lung pixels even in the presence of significant noise. Nonetheless, because all techniques can assign values to pixels that fall outside the lungs, or exclude pixels that actually are part of the lung, statistics were only collected on pixels that had a non-zero signal intensity in the noise-free image (i.e., points that were actually in the lung) and that were not masked during the analysis in the calculation of RMS error.

Results

Experimental Data and Synthetic Images

Figure 1 displays a typical MR image sequence of a rabbit lung taken during a single breath-hold, with the timing pattern described in the Methods section. The decay of signal intensity in successive image acquisitions due to oxygen interactions and RF excitations is apparent. Using these calculated values a synthetic dataset was generated as described in Methods, and noise was added systematically. Figure 2 displays four typical synthetic images with varying amounts of noise added corresponding to a mean SNR of infinity, 100, 10 and 3 respectively.

Figure 1.

A time-series of ³He lung images acquired in a healthy rabbit during a breath-hold. The signal decay, largely caused by collisions with oxygen molecules, is analyzed to yield the concentration (P_AO₂) and uptake rate (ODR) of oxygen into the bloodstream.

Figure 2.

The last in a series of eight images used to test the relative merits of principal-component analysis and clustering. Figure 2.a shows the synthetic ‘noise-free’ image derived from experimental data. Figure 2.b–d show the same image with Rician noise added to achieve an SNR of 100:1 (b), 10:1 (c) and 3:1 (d), respectively.

Principal Component Analysis

Figure 3 shows the proportion of total variance of the synthetic data that is contained in the 8 principal components, in decreasing order of magnitude. It is evident that over 99.8% of the variance in the unfiltered data is described by the first two principal components. The remaining eight PC’s contribute little to the variance of the data and therefore we dropped in the analysis that follows.

Figure 3.

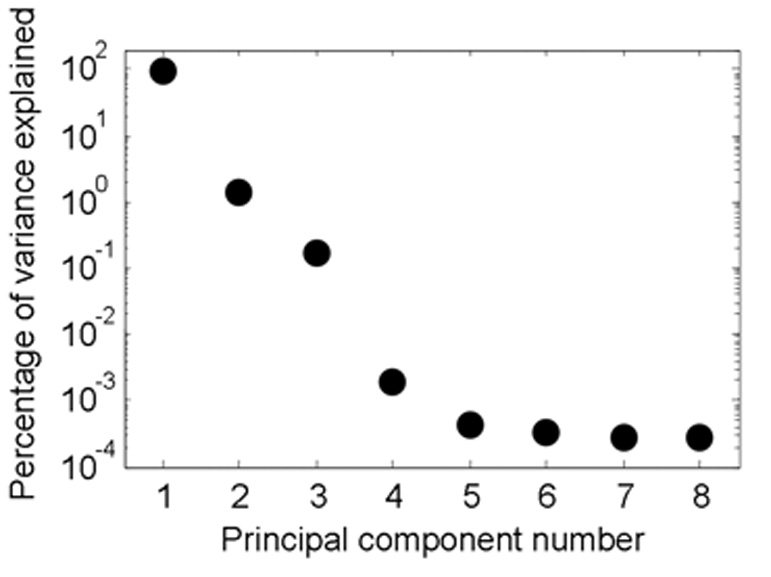
Relative magnitudes of the information (variance) explained by each of the eight principal components in the data space. Note that the first two PCs contain virtually all of the information in the data set analyzed in this study, allowing significant simplification of the data space by omitting the other six components.

Oxygen Parameter Estimation in the Synthetic Dataset

The results of oxygen tension analysis of the synthetic dataset are presented in Figure 4. In addition to the original “true” P_AO₂ and ODR values (Figures 4.a and 4.e respectively, corresponding to an SNR = ∞,), analysis results for the case of SNR = 20:1 are shown. Qualitatively, PCA/EVD analysis of P_AO₂ and ODR (Figures 4.d and 4.h respectively) using 192 K-means clusters retains much of the original spatial structure of the noise-free image, which is compromised by either uncorrected noise (Figures 4.b and 4.f) or spatially binning groups of 2 × 2 pixels (Figure 4.c and 4.g). Figure 5 represents a more extreme example of P_AO₂ analysis with larger spatial bins (on a 16 × 16 grid), leaving only six unmasked bins for analysis. For comparison, a PCA/EVD-simplified dataset is shown using the same number of clusters. Comparing to Figure 4, in both cases, significant physiologically relevant information is lost through the simplification, but anatomical detail is largely preserved in PCA-based analysis.

Figure 4.

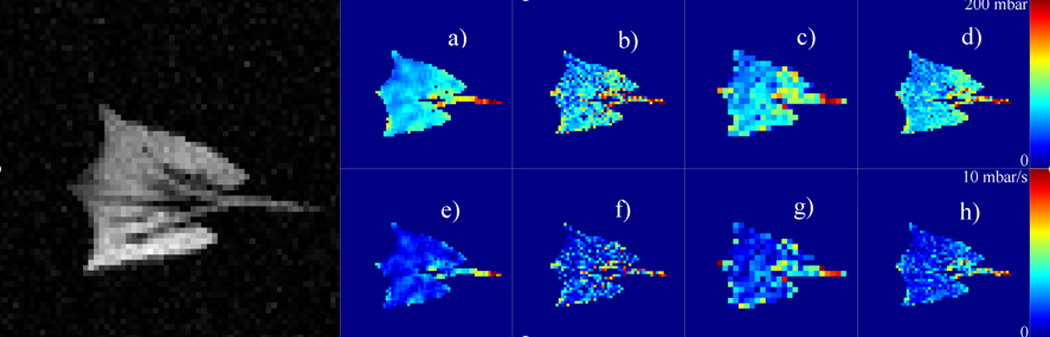
P_AO₂ values for the "true" noiseless case derived from the synthetic data set (4.a), and three estimations at an SNR of 20:1 (4.b–d). Frame (4.b) displays the estimation in an unfiltered and unclustered case on a pixel-by-pixel basis, frame (4.c) displays the results when forming 2 × 2 spatial bins, and frame (4.d) displays the results of K-means clustering in a PCA/EVD-simplified data space with 192 clusters. A visual inspection shows that the PCA-based method is most similar to the true case. Loss of spatial information increases as the bin size increases beyond the minimal binning shown here. The remaining frames (4.e–h) depict the corresponding effect of filtering schemes on the derived oxygen uptake rate (ODR). The unlabeled, black and white image to the left depicts the first image in the series with its simulated noise.

Figure 5.

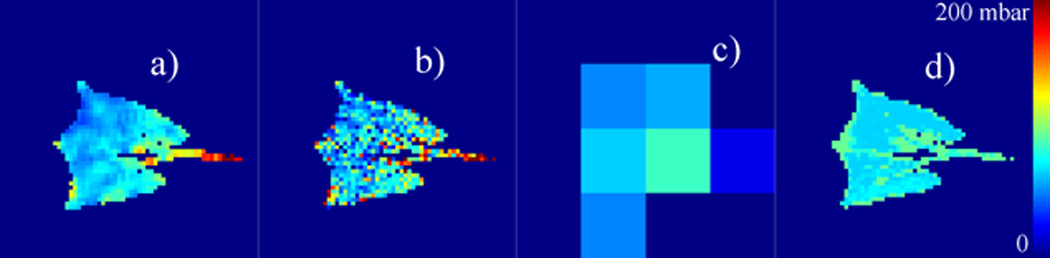
P_AO₂ values derived as shown in Figure 4, but with 16 × 16 Cartesian binning. This results in six unmasked bins. For comparison, a PCA/EVD-simplified dataset is shown using the same number of clusters. In both cases, significant physiologically relevant information is lost through the simplification, but anatomical detail remains in the latter case. Image 5.a depicts fit to the ‘noise-free’ dataset, and 5.b–d are unfiltered, spatially binned, and PCA/EVD-simplified images, respectively.

The quantitative comparison of the PCA-based and conventional binning methods was further examined by performing the oxygen tension analysis on a wide range of SNR values ranging from 20 to 10⁴ (practically infinity). This goal was achieved by adding the desired noise level to the synthetic images. Each random noise level was simulated 50 times in order to assure a normal distribution of Rician noise in the images, and the average result was reported for that specific noise level. Figure 6 summarizes the total pixel-by-pixel accuracy of the derived P_AO₂ maps for these conditions. The analysis was conducted six times, using 192, 58, 17, 6, 4, and 1 bins, respectively. In each case the results of PCA-based and conventional binning methods were compared to the “true” and noise-added pixel-by-pixel datasets (i.e. number of clusters approaching infinity). In general for SNR > 100, the unfiltered pixel-by-pixel analysis generally yields better accuracy in parameter estimates. Under these conditions the PCA-based clustering approach performs better than Cartesian binning especially for larger number of clusters (17 and above in this study). As the number of clusters get smaller (6 and below), the performance of Cartesian and PCA-based clustering methods become more and more similar. On the other hand for SNR values typically encountered in experimental data (100 > SNR > 20) the PCA-based clustering approach almost always yields results that are closer to the “true” value than any other approach, whereas results form Cartesian binning method fall between PCA-based and pixel-by-pixel approaches. In extremely low SNR conditions (SNR < 5), Cartesian binning starts to deliver more accurate results. However such low SNR conditions are rarely of any practical use. Finally Figure 7 shows the corresponding results for ODR estimation under the same conditions described for P_AO₂ analysis. In a similar fashion the PCA-based approach delivers highest accuracy in parameter estimation for 100 > SNR > 20, whereas the unfiltered pixel-by-pixel analysis shows the best performance in extreme conditions of SNR > 100.

Figure 6.

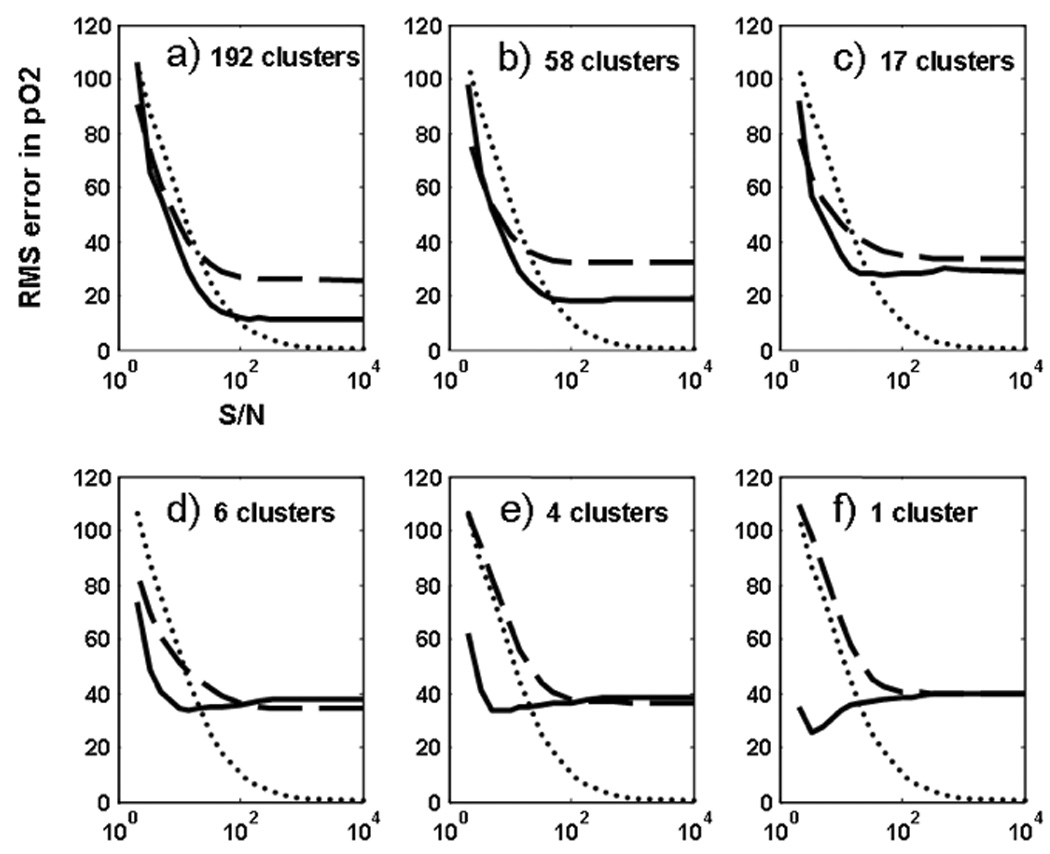
Evolution of RMS error between “true” P_AO₂ values and estimated values of the entire oxygen map in the lung, generated from 50 random noise level simulations in each case. Shown is the RMS error evolution for the unfiltered case (dotted), Cartesian binning (dashed) and PCA-based K-means clustering (solid). Frames (a)–(f) are for estimations performed with 192, 58, 17, 6, 4, and 1 clusters, respectively. Error bars were too small to aid visual analysis. Units on the y-axis are in mbar.

Figure 7.

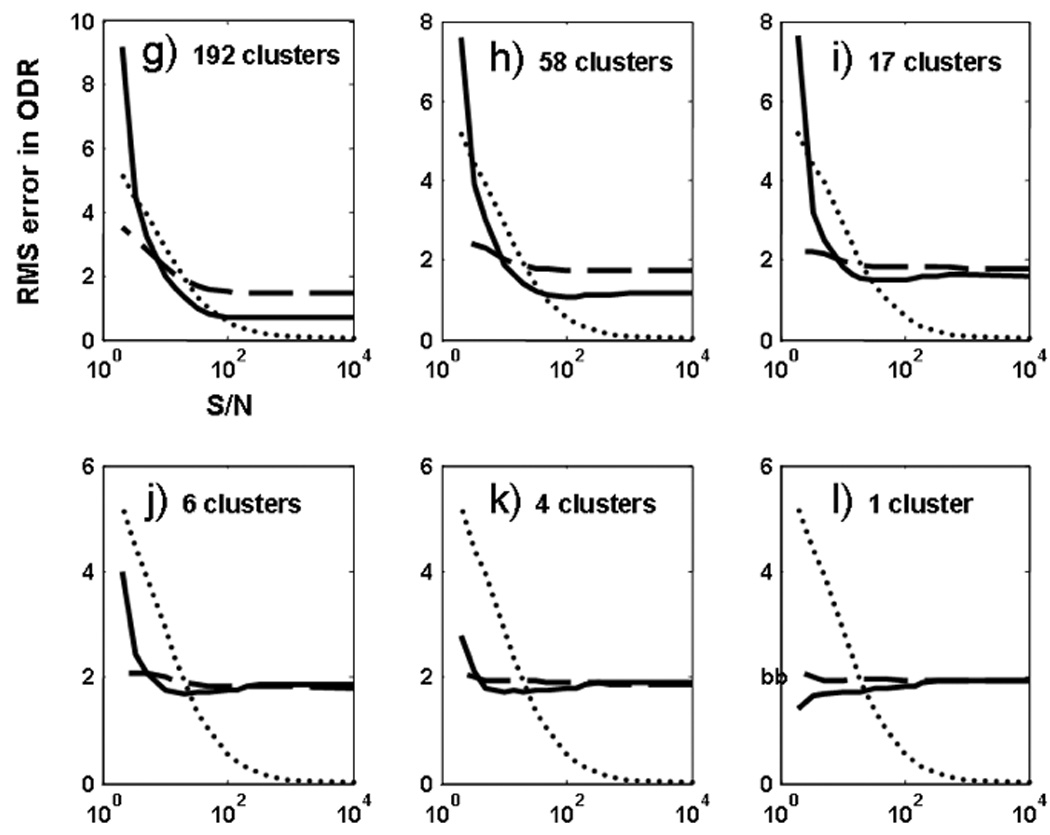
Evolution of RMS error between “true” ODR values and estimated values of the entire oxygen map in the lung, generated from 50 random noise level simulations in each case. Shown is the RMS error evolution for the unfiltered case (dotted), Cartesian binning (dashed) and PCA-based K-means clustering (solid). Frames (a)–(f) are for estimations performed with 192, 58, 17, 6, 4, and 1 clusters, respectively. Error bars were too small to aid visual analysis. Units on the y-axis are in mbar/s.

Discussion

Principal Component Analysis

Since over 99% of the variance in the data was contained in the first two PCs, it seems reasonable to eliminate the information contained along the remaining six PC vectors. However, this also suggests that reducing the dimensionality of the data does not control a significant amount of noise. With the dataset analyzed in this paper, data clustering algorithms must be used to control noise. In noisy real-world data sets, this result may not hold, and simplifying via PCA may yield significant benefits. Additionally, other datasets might contain less information in the first few principal components. In such a case, eliminating all but the first two PCs may remove valuable information from the analysis. Care should be taken to ensure that PCs are not eliminated if they are contributing significantly to the variance of the data. The EVD method that is used here can serve as a guide for this decision, since it quantifies how much information is contained in each PC (Equation 6).

Oxygen Parameter Estimation

It is clear that spatial information is sacrificed when the image is binned, although the necessity of increasing SNR has justified this method in previous works. The analysis of the noise-added synthetic dataset shows that when working with a dataset with 100 > SNR > 20, the PCA-based clustering method generally gives an estimated functional parameter map that is closer to the “true” map, and which retains more spatial information compared to Cartesian binning with the same number of clusters. The unfiltered (pixel-by-pixel) analysis method provides a more accurate result than any clustering algorithm when SNR is exceptionally high (i.e. 100 or higher). These results, in conjunction with the data in Figure 6 and Figure 7, suggest that – under general conditions – at high SNR the best approach is to perform a straight-forward fit, which in many case is considered an intuitive decision. Since all clustering techniques sacrifice some information in order to control noise, it is intuitive that clustering data points is detrimental if SNR is very high. The apparent rise in the accuracy of parameter estimations when using Cartesian binning at very low SNR values is attributed to masking bins with high intravoxel variation, and limiting the analysis to a more homogeneous set of bins in the comparison. The apparent increased accuracy therefore arises from a biased comparison. However, at intermediate SNR values, which are of signifiance in most practical situations, the PCA-based method appears to yield the most accurate results.

Number of Clusters

The number of clusters can have a substantial effect on the RMS error depending on the method of choice. Theoretically, when a very large number of clusters are used, both Cartesian binning and PCA-based clustering methods approach the unfiltered pixel-by-pixel analysis, corresponding to number of clusters approaching infinity. When a using a moderately large number of clusters (58 and 192 in this case), PCA-based clustering appears to outperform the unfiltered pixel-by-pixel method for SNR < 100. However, using a larger number of clusters limits the ability of the clustering algorithms to control noise at lower SNR values, as depicted by an increasing RMS error in Figure 6 and Figure 7. The advantage of a pixel-by-pixel analysis at higher SNRs is even more pronounced when fewer clusters are used. Note that with only one cluster or one spatial bin and high SNR, the two techniques are practically equivalent.

The results of the demonstrated analysis implies that for moderate SNR values (100 > SNR > 10) PCA-based clustering approach with an intermediate number of clusters (10~30) can provide a good balance between robustness to noise and maintaining the special features of the lung. It is however very difficult to generalize these results and declare an “optimum” number of clusters to achieve this balance, primarily because the optimality criterion can be tightly linked to the purpose of study and specific features of interest that the investigator is studying. In an extreme case of a highly uniform oxygen distribution, a lower number of clusters, or even Cartesian binning with relatively large bins may be desirable in low SNR conditions, since a higher number of clusters only undermines the certainty of parameter estimation without delivering any new spatial information. However in the hypothetical example of an extremely inhomogeneous lung in which every single pixel exhibits a very different value compared to its adjacent pixels, a PCA-based approach with a large number of K-means clusters can be very effective. In practice however the functional distribution of oxygen tension in lung falls well between these two extremes, with the possibility of a more heterogonous distribution in a diseased lung, e.g. an emphysematous. The final decision on the number of clusters therefore has to be made as a function of the desired spatial differentiation of features, the available SNR and in regards to the pixel-by-pixel analysis baseline, and remains the subject for future studies.

Potential Clinical Applications

The PCA-based approach for post-processing of functional MR images has obvious potentials for clinical use. Because the lung is a large, heterogeneous organ, defects that occur in restricted regions may not be detected by global function tests. That is, the relatively large regions of healthy tissue surrounding the diseased areas may mask their impact. Recent research indicating that fairly small, localized defects are precursors to acute pulmonary disease highlights the insufficiency of pulmonary function measures with low spatial resolution [22]. This makes radiological techniques that allow physicians to regionally assess lung function very useful, particularly if these methods preserve the spatial resolution of raw images. HP ³He MRI has demonstrated sensitivity to small lung defects [23], giving it great clinical promise. However, a central problem will be maximizing SNR so that local pathologies can be confidently distinguished, especially in presence of degraded ventilation in diseased lungs. The presented methods for simplifying and clustering image data may allow reliable estimates of regional pulmonary parameters in the presence of noise without sacrificing anatomical detail. Although this work focuses on measuring regional oxygen parameters with HP ³He MRI, there is no fundamental factor limiting the applicability of these methods to other functional or structural pulmonary parameters of interest (such as regional ventilation and apparent diffusion coefficient of gas in alveolar spaces) or other imaging modalities (such as computed tomography).

Study Limitations

The presented approach in post-processing of functional MR images of the lung bears several limitations. The greatest theoretical problem with the described technique is that it is only useful if distal regions of the lung behave similarly to one another, and if real physiologic effects and not random noise cause that behavior. In fact, the PCA-based clustering method may be detrimental if distal parts of an image that are actually quite different appear similar due to noise effects, because it will then combine dissimilar pixels that seem to be behaving in the same way. This problem was avoided in the presented analysis since the “true” value of each pixel in the noiseless, synthetic data was known. This permitted meaningful calculations of the error induced by both clustering algorithms. However, for a real-world dataset this a priori knowledge of absolute truth-value is missing and therefore it is not possible to calculate the RMS error for a given condition explicitly.

One possible alternative to this approach when applied to real experimental data is to solve for oxygen parameters on a pixel-by-pixel basis as a starting point and reconstruct the noise-free images as described earlier. The original noise level can then be calculated from the raw dataset and added to this synthetic dataset. Finally a variation of clustering parameters (such as number of clusters) can be applied to this dataset and find the optimum set of parameters that minimizes the RMS error between the original dataset and the noise-added synthetic images.

Several other limitations should be noted. Because this paper only assessed the robustness of PCA-based clustering when measuring P_AO₂ and ODR, we cannot be certain that our results are generalizable to studies of other functional parameters. This work only examines HP ³He MRI data, so firm generalizations to proton MRI and other imaging modalities are not possible. However, there is no theoretical reason that PCA-based clustering cannot be utilized in when mapping functional parameters of other heterogeneous organs, or when using other imaging modalities.

There is clearly room for future work in this area. Assessing the robustness of other clustering algorithms would be very useful. Although PCA-based clustering is expected to be useful for the regional estimation of other functional lung parameters, specific work validating this assumption is required. Further research assessing PCA-based clustering with data from other imaging modalities would also be useful.

Conclusion

Simplifying data sets by PCA and dynamically clustering in the data space before transposing to the image space was shown to preserve anatomical information and group similarly behaving pixels together in hyperpolarized ³He MR images of the lungs. PCA was also found to be an efficient way to identify the elements of the data space that contribute the most information. The drawbacks to established Cartesian binning methods are apparent, and a more robust method for estimating physiologic parameters in the presence of noise is clearly needed. This work advocates PCA-based clustering as a useful method for post-processing and analyzing hyperpolarized ³He MR images of airspaces at moderate to low signal-to-noise ratios. The theory underlying this technique was presented, and its utility was demonstrated by analyzing a synthetic dataset derived from actual experimental data. Even though an identical approach is not implementable on a real dataset – due to absence of the actual truth-value – the presented analysis provides a general understanding of the error behavior in different clustering methods and therefore better parameter estimation. There is clearly room for future research in this area, specifically assessing the performance of other dynamic clustering methods in a reduced data space and developing quantitative performance indices for different applications.