Flexible Fitting of Atomic Structures into Electron Microscopy Maps Using Molecular Dynamics

Abstract

A novel method to flexibly fit atomic structures into electron microscopy (EM) maps using molecular dynamics simulations is presented. The simulations incorporate the EM data as an external potential added to the molecular dynamics force field, allowing all internal features present in the EM map to be used in the fitting process, while the model remains fully flexible and stereochemically correct. The molecular dynamics flexible fitting (MDFF) method is validated for available crystal structures of protein and RNA in different conformations; measures to assess and monitor the fitting process are introduced. The MDFF method is then used to obtain high-resolution structures of the E. coli ribosome in different functional states imaged by cryo-EM.

Introduction

A key to understanding how biological systems work is to look at their structures captured in their various functional states. Experimental techniques reveal different levels of macromolecular structure: high-resolution techniques such as X-ray crystallography furnish atomic detail, but structures obtained are often in functionally undefined states; techniques such as cryo-electron microscopy (cryo-EM) image systems captured in different functional states, albeit at lower resolution (Saibil, 2000). Computational techniques can help bridge the resolution gap by adapting high-resolution crystallographic structures to EM maps, thus providing atomic detail of the system in different functional states. These techniques can also be used to analyze the physical and dynamical properties of the resulting structures, revealing astonishing views of cellular processes.

Until a few years ago, typical resolutions for EM maps of biomolecules were 15-30 Å, and high-resolution crystal structures were often available only for domains of a biomolecular complex (Frank, 2002; Rossmann, 2000). This led to the development of so-called rigid-body docking techniques, that fit atomic structures into density maps keeping the high-resolution structure rigid, usually by performing an exhaustive search over all rotational and translational degrees of freedom in real or reciprocal space, guided by some choice of similarity measure. Rigid-body docking has reached maturity, permitting today the independent docking of parts of the assembly into a map, thus producing a jigsaw structure of the macromolecular complex as a whole. The main limitation of this class of methods is that neither the interaction between the docked subunits nor the difference in conformation between the structures of the domains in crystal form and in the complex can be determined. A comprehensive review of the available rigid-body docking methods can be found in Wriggers and Chacón (2001).

Recent improvements in the resolution of cryo-EM structures motivated the development of methods to flexibly fit atomic structures into density maps. In these methods, many degrees of freedom are considered in the fit, allowing the atomic structures to undergo conformational changes that improve their correspondence to the EM map. Various approaches to flexible fitting have recently been employed, and have provided insight into the structural mechanisms of a number of biomolecular processes. One of the first attempts to introduce flexibility in the fitting process, still in use today, consists in dividing a macromolecule studied into “rigid bodies” and fitting them independently (e.g., Volkmann et al., 2000). Refinement techniques can then be applied to the resulting structure, such as the real-space refinement originally developed for X-ray crystallography (Chapman, 1995; Chen et al., 2001). Other approaches include the use of so-called vector quantization, where a reduced representation is derived from both the atomic structure and the EM map and used as constraints in a molecular mechanics refinement (Wriggers et al., 2000; Wriggers and Birmanns, 2001); the use of a linear combination of low-frequency normal modes to deform the atomic structure, applying minimization techniques to maximize the correlation coefficient between atomic structure and EM map (Tama et al., 2004; Suhre et al., 2006); the combination of comparative modeling, based on alternative alignments and loop conformations, and structure refinement (Topf et al., 2006); the generation of deformed structures based on the variability exhibited by the protein domains of a superfamily and subsequent selection of the best fit based on the cross-correlation coefficient (Velazquez-Muriel et al., 2006); the use of a combination of restraints imposed by the EM map and a deformable elastic network (Schröder et al., 2007); the use of Monte Carlo simulations with constraints derived from a rigidity analysis (Jolley et al., 2008); and a hierarchical approach consisting of docking the structure as one or more rigid bodies with a Monte Carlo search, followed by two refinement steps based on minimization of a scoring function and simulated annealing (Topf et al., 2008). Li and Frank (2007) recently correlated an ensemble of conformations from equilibrium molecular dynamics (MD) simulations with cryo-EM data, suggesting that a cryo-EM map can be interpreted as a conformational average, and that using MD to flexibly fit structures into EM maps should yield structures representative of the conformational ensemble represented by the EM map, particularly when combined with an enhanced sampling technique.

We suggest here a novel method to perform MD simulations to flexibly fit atomic structures into EM maps, the MD simulation incorporating EM data through an external potential. Forces proportional to the density gradient of the EM map are added in the MD simulation of the atomic structure, effectively biasing the system toward the region of conformational space of interest, i.e., one that is consistent with the density distribution of the EM map. Since large forces are applied and simulations presently are performed in vacuo, harmonic restraints must be applied to keep secondary structure elements intact, thus preventing structural distortions and “overfitting”. The molecular dynamics flexible fitting (MDFF) method presented brings together several of the most desirable features of existing methods. First, MDFF takes into account all information contained in the map by avoiding the use of reduced representations or global measures of similarity to drive the fitting. Since the external potential is applied locally, it is possible to fit some components of a macromolecular assembly even when the structure of the remaining components is not available. Moreover, the degree of success of the MDFF method is independent of system size, which is an advantage over the use of optimization or Monte Carlo-based approaches where an increase in system size decreases the likelihood of successful transitions.

The two methods that MDFF is based on, namely, conventional MD simulation and 3-D cryo-EM single particle reconstruction, are introduced in Supplemental Data S1 and S2 for the non-expert reader. In the following, we describe how the MDFF method incorporates EM data into MD simulations, and how it applies restraints to preserve the integrity of structural elements. We demonstrate MDFF by fittings into noise-free, simulated maps created from atomic structures. Finally, as an example application of MDFF, we fit atomic structures into cryo-EM maps of the E. coli ribosome at different resolutions.

MD simulation with an EM-derived external potential

In the MDFF method, an external potential derived from the EM map is introduced into an MD simulation to steer the atoms into high-density regions. The stereochemical quality of the structure is preserved by the MD force field, and also through harmonic restraints applied to enforce the integrity of secondary structure. The method, therefore, adds two extra terms to the potential energy function of an MD simulation

$$U_{\text{total}}=U_{MD}+U_{EM}+U_{SS}$$ (1)

where U_MD is the conventional MD potential energy function (see Supplemental Data S1), U_EM corresponds to a potential derived from the EM data, and U_SS is a potential that aims to preserve the secondary structure of protein and nucleic acids. We now describe the latter two terms.

The data provided by cryo-EM reconstructions represent the Coulomb potential of the macromolecule (see Supplemental Data S2); the dependence of this potential on the atomic number of the composing atoms makes it roughly proportional to the mass density of the macromolecule. It is then sensible to define a potential so that when the atomic structure is placed in it, the atoms are driven through application of forces into high-density areas and away from low-density areas. This potential can be defined on a grid, thus preserving all the information contained in the EM density map. The potential energy function corresponding to this map is

$$U_{EM}\left(\mathbf{R}\right)=\sum _j{w}_j{V}_{EM}\left({\mathbf{r}}_j\right),$$ (2)

where

$$V_{EM}\left(\mathbf{r}\right)=\{\begin{array}{cc}\xi \left[\frac{\Phi \left(\mathbf{r}\right)-{\Phi }_{\mathit{thr}}}{{\Phi }_{\max -{\Phi }_{\mathit{thr}}}}\right]\hfill & \text{if}\Phi \left(\mathbf{r}\right)\ge {\Phi }_{\mathit{thr}},\hfill \\ \xi \hfill & \text{if}\Phi \left(\mathbf{r}\right)<{\Phi }_{\mathit{thr}}.\hfill \end{array}\phantom{\}}$$ (3)

Here Φ(r) is the Coulomb potential revealed by cryo-EM, Φ_max is the maximum value of all voxels in the EM map, ζ is an arbitrary scaling factor (ζ<0) discussed below, Φ_thr is a threshold value used to disregard data not corresponding to the biomolecule, i.e., solvent density, w_i is a weight that can be varied according to the type of atom placed in this potential, typically set to the atomic mass, and r_j is the position of atom j. The global minimum of U_EM alone corresponds to all atoms collapsed on the density maximum; however, the other two terms in Eq. (1) counterbalance this effect, preserving physically sound structures.

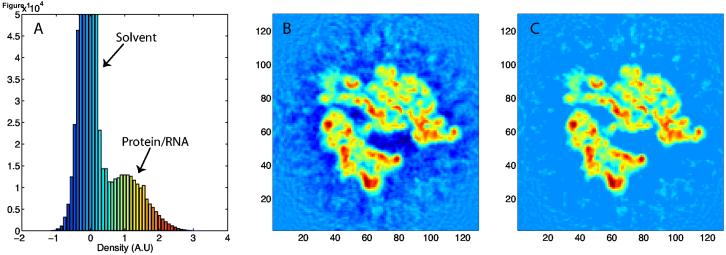
The threshold value Φ_thr is selected in accordance with the density histogram of the EM map, which reveals two peaks of different density (Frank, 2006); an example is shown in Fig. 1A. The first and higher peak corresponds to solvent density, whereas the second, broader peak corresponds to protein and nucleic acid density. The density histogram thus suggests a natural threshold value at the minimum between the two density peaks; clamping all values below this threshold removes the solvent contribution and yields a flat potential in the solvent regions. For cases where the solvent and biomolecule peaks are not well resolved, the average, which generally lies at the solvent peak, is chosen as the threshold, thus removing much of the undesired density while conservatively avoiding loss of macromolecular density information, as portrayed in Fig. 1C.

Figure 1.

Reconstruction of the E. coli ribosome from cryo-EM data at ∼12.8 Å resolution (K.M., L.G.T., E.V., A. Zavialov, M. Ehrenberg, K.S., and J.F., in preparation). (A) A density histogram shows two distinct peaks pertaining to the solvent and macromolecule; (B) 2-D slice of the density; (C) 2-D slice of the density after clamping values below the average, thus homogenizing the density corresponding to the solvent surrounding the macromolecule and the bulk solvent.

The force applied to an atom inside the potential defined by Eq. (3) is

$${\mathbf{f}}_i^{EM}=-\frac{\partial }{\partial {\mathbf{r}}_i}{U}_{EM}\left(\mathbf{R}\right)=-w_i\frac{\partial }{\partial {\mathbf{r}}_i}{V}_{EM}\left({\mathbf{r}}_i\right)$$ (4)

where U_EM is the potential energy function introduced in Eqs. (2, 3). ${\mathbf{f}}_i^{EM}$ can thus be tuned via the scaling factor ζ, which is the same for all atoms, and the weight w_i, which can be defined on a per-atom basis. The external forces ${\mathbf{f}}_i^{EM}$ are applied in MDFF using grid-steered molecular dynamics, an extension of the SMD method (Isralewitz et al., 2001; Sotomayor and Schulten, 2007) that allows an arbitrary steering potential to be defined on a grid (Wells et al., 2007). The force applied to each atom i depends only on the gradient of the potential derived from the EM density map at position r_i; and thus, the fitting in MDFF is performed locally.

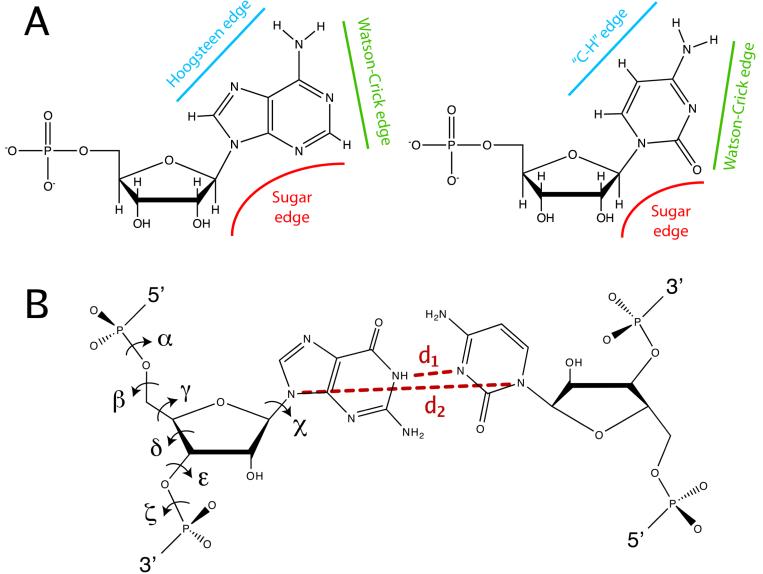
In order to preserve the stereochemical quality of the structure and prevent overfitting in MDFF, harmonic restraints are applied to a set of internal coordinates relevant to the secondary structure of the macromolecule in its initial conformation - in many cases, the crystal structure. For protein structures, harmonic restraints are applied to ϕ and ψ dihedral angles of amino-acid residues in helices and β strands. For nucleic acids, the software package RNAView (Yang et al., 2003) is used to identify and classify base pairs. The following base pair types, that were observed to preserve the secondary structure of RNA in simulation when restrained, are selected: W/W, W/H, W/S, H/H, H/S, and stacked (W = Watson-Crick edge, H = Hoogsteen edge, S = sugar edge; see Fig. 2A). For these base pairs, harmonic restraints are applied to the seven dihedral angles (α, β, γ, δ, ε, ζ and χ) and two interatomic distances (d₁ and d₂) depicted in Fig. 2B, the latter to preserve the planarity of the base pair. Thus, an extra term introducing secondary structure harmonic restraints is added to the potential energy function, namely

$$U_{SS}=\sum _{\mu }{k}_{\mu }{(X_{\mu }-X_{\mu }^0)}^2,$$ (5)

where the restraints X_μ stand for protein dihedral angles ϕand ψ, RNA dihedral angles α, β, γ, δ, ε, ζ, and χ, and RNA distances d₁ and d₂. The equilibrium values $X_{\mu }^0$ are generally taken from the initial atomic structure, but can also be set to ideal values. Additional restraints can be added, such as codon-anticodon interactions in the ribosome, as discussed below.

Figure 2.

Harmonic restraints applied to base-paired RNA residues. (A) RNA interaction edges for both purines (adenine is shown of the left) and pyrimidines (cytosine is shown on the right), according to Leontis and Westhof (1998); (B) dihedral angles, and the two interatomic distances (dashed lines) to which harmonic restraints are applied.

The MDFF simulations are performed using NAMD (Phillips et al., 2005), with the CHARMM27 force field (MacKerell et al., 1998; Foloppe and MacKerrell Jr., 2000) in vacuo, using a dielectric constant of 80. A multiple time-stepping integration scheme is used, calculating bonded interactions every 1 fs and nonbonded interactions every 2 fs; a cutoff distance of 10 Å is used for the nonbonded interactions. Temperature is maintained at 300 K using a Langevin thermostat (Brünger et al., 1984) coupled to all heavy atoms with a damping coefficient of 5ps^-1. Rigid-body docking performed as the initial step of a fitting protocol in all examples presented was executed using Situs (Wriggers et al., 1999).

Flexible-fitting protocol

Obtaining an optimal fit in MDFF relies on a balance among the three terms in Eq. (1). For the first term, U_MD, parameters are given by the choice of standard force field and are here not subject to alteration; the other two terms, U_EM and U_SS, contain parameters that can be tuned and represent a trade-off: higher forces derived from the EM map (U_EM) and lower restraints to secondary structure (U_SS) can yield a better fit, but can also lead to distortions of the macromolecular structure, a natural concern in flexible fitting methods generally referred to as “overfitting” (Tama et al., 2004). For U_EM, parameters that can be varied are the scaling factor ζ and atomic weights w_i (Eqs. 2, 3). The latter are typically set to the atomic masses while ζ determines the range in magnitude of forces applied to the atoms and is usually set to values around 0.3 kcal/mol, resulting in forces typically on the order of 10-15 pN (piconewton) per atom (for a carbon atom). The gradient of the potential derived from the EM density map can be calculated before the fitting to pick a value of ζ: high values can result in high accelerations of atoms rendering the simulation unstable. The term U_SS requires the selection of spring constants k_μ in Eq. (5). Typical values used in MDFF are k_μ = 200 kcalmol^-1 rad^-2, or 200kcalmol^-1Å^-2 in the case of RNA distances; (300 kcal mol^-1 Å^-2 is a typical spring constant value for a carbon-carbon bond in the CHARMM27 force field). The choice of these values renders the restrained secondary structure elements relatively stiff, thus preserving their structure throughout the simulation.

MDFF can also be performed in multiple steps, varying parameters at every step, such that the atomic structure gradually converges into the EM map. Generally, a step is considered “finished” when the MD simulation has converged as evaluated by a goodness measure, e.g., by stabilization of the root mean square deviation (RMSD, given by 〈(r_i-〈r_i〉)²〉^1/2, where r_i is the position of each atom i); one can also track the correlation between the trajectory and the EM map, as described later. Naturally, in a last step of MDFF one can switch U_EM and U_SS off and equilibrate the system subject only to the intrinsic potential U_MD.

In this multi-step protocol of MDFF, several parameters can be varied besides those mentioned above: (i) Temperature can be adjusted to allow the system to overcome energy barriers, exploring a larger portion of the conformational space in less time, often done in simulated annealing simulations (Frenkel and Smit, 2002); (ii) low-pass filtering the map in a first step can be used to avoid getting trapped in local minima, followed by use of the original map; this approach first induces overall domain motions and refines the structure subsequently on the local scale using the high-resolution information in the original map; (iii) along the same line, one can initially apply strong harmonic restraints to the secondary structure and in a subsequent step weaken the restraints to refine the structure; (iv) at any given time, any portion of the structure may be fixed or restrained to its current position (positional restraints); this is useful, e.g., when factors or low-occupancy ligands are introduced for fitting, and the rest of the previously fitted structure can be fixed or restrained while the ligands are fitted; (v) one can also delete the density corresponding to parts of the structure, which is useful, e.g., for fitting protein-RNA complexes, as discussed below; the deletion is done by assuming the current fit is perfect, creating a simulated map from the fitted structure as described in the next section, and using it as a mask to selectively delete a portion of the original EM map. The new map Φ’ defining U_EM as in Eq. (3) is given by

$${\Phi }^{\prime }=\left(1-\frac{{\Phi }_{\mathit{sim}}}{\max \left({\Phi }_{\mathit{sim}}\right)}\right)\Phi$$ (6)

where Φ is the original EM map, and Φ_sim is the simulated map, with a maximum voxel value of max(Φ_sim). Equation 6 results in potentials with smoother gradients than those obtained from difference maps.

An important advantage of a multi-step protocol in MDFF is evident when fitting protein-RNA complexes into EM maps. The atomic number of the atoms composing RNA is on average higher than those composing protein, which may lead to incorrect fitting of proteins due to lower energy minima attracting them into RNA density. To avoid this problem, the RNA can be fitted first, followed by deleting the RNA contribution from the EM map once it is well fitted and proceed with the fitting of the proteins, or by positionally restraining the RNA structure to prevent the protein from being drawn into the density the RNA occupies.

Fitting atomic structures into simulated maps

In the following sections, we demonstrate application of MDFF to noise-free, simulated EM maps as a means of validation of the method. We briefly describe how simulated maps are generated from atomic structures and how we calculate correlation coefficients between a fitted structure and the EM map. Using examples where X-ray crystal structures are available in two different conformations of the same molecule, we apply the method to fit one conformation into simulated maps generated from the other.

Simulated EM maps from atomic structures

Noise-free simulated EM maps can be created from atomic structures using the approach described in Stewart et al. (1993), which assumes that the EM map represents the electrostatic potential of the nuclei. The atomic number of each atom is interpolated onto a grid, and the resulting 3-D density map is subsequently low-pass filtered to the desired resolution. Simulated maps can be generated from a single structure or from a set of structures obtained from an MD simulation by averaging maps created from each frame of the trajectory (see Li and Frank, 2007). In the present work, simulated maps are used for three different purposes: (i) calculate correlation coefficients between EM maps and atomic structures; (ii) delete selected regions from the experimental EM map based on a fitted atomic structure; and (iii) provide noise-free maps for validation purposes.

Cross-correlation coefficients

To quantify the goodness of the fit, a simulated map can be generated from the fitted atomic structure with the same target resolution as the EM map. The Pearson’s correlation coefficient (usually referred to in the EM literature as the cross-correlation coefficient) between these two data sets, i.e., the simulated (S) and the experimental (E) 3-D maps, can be used as a measure of similarity between them, and is given by

$${\rho }_{SE}=\frac{\langle (S-\langle S\rangle )(E-\langle E\rangle )\rangle }{{\sigma }_S{\sigma }_E},$$ (7)

where 〈S〉 and 〈E〉 correspond to the average voxel values of the simulated and experimental maps, respectively, and σ_S and σ_E correspond to their standard deviation (Frank, 2006). Note that the cross-correlation coefficient is normalized, i.e., ρ_SE ∈[-1,1]. All cross-correlation coefficients reported were computed both considering all voxel values in the density maps (“global correlation”) and considering only voxels inside the molecular envelope of the simulated map (“local correlation”) (Roseman, 2000), using a threshold that we report as the number of standard deviations (σ) above the mean of the simulated map. The global correlation, commonly quoted in the literature, depends sensitively on the box size arbitrarily selected by the electron microscopist. Larger boxes result in artificially higher correlation values, leading to overestimation of the quality of the fit; thus, local correlations should be preferred.

Validation using atomic structures in two conformations

In order to validate the method and estimate the accuracy of the fitted structures, we use X-ray structures of molecules available in two conformations as test cases. One of the structures is fitted into noise-free simulated maps of the other at 5, 10, and 15-Å resolutions, after an initial phase of rigid-body docking. Here we present two examples, acetyl-coenzyme A synthase/carbon monoxide dehydrogenase (ACS/CODH) (Darnault et al., 2003) and a 16S rRNA (Schuwirth et al., 2005). Several other examples are presented in Supplemental Data S3.

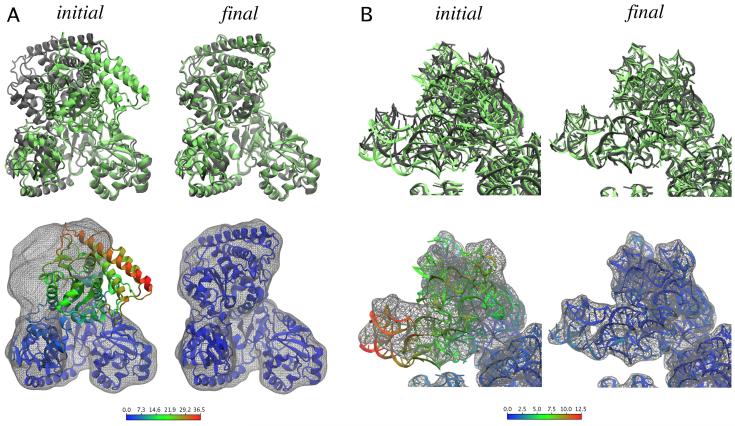
All simulations used ζ=0.3kcal/mol and k_μ =200kcalmol^-1 rad^-2 (or 200kcalmol^-1 Å^-2) for the harmonic restraints (see Eq. 5 and Fig. 2B), except for 16S rRNA dihedral restraints that were enforced using k_μ = 50 kcalmol^-1 rad^-2. The simulations converged in less than 200ps of simulation, but they were run for 500 ps to improve statistics. Table 1 lists the correlation coefficients and mean backbone RMSD between the fitted and target structures, calculated from the last 200 ps of trajectories (a plot of the RMSD through the entire trajectories for ACS/CODH can be found in Supplemental Data S3). One can see that the RMSD decreases with higher resolution. It is important to note that the simulations result in a representative set of structures that fit the map. Since fitting atomic structures into low-resolution data is an indeterminate problem, a representative set of conformers should be considered when interpreting the data. The structures presented in this paper serve as an illustration of one such representative structure for each of the problems considered. Figure 3 shows the initial and target conformation for each of the systems, as well as representative structures from MDFF into 10-Å resolution simulated maps.

Table 1.

Effect of resolution and grid spacing on flexible fitting into noise-free simulated maps using MDFF. For each system, maps were created computationally from a given crystal structure of conformation I and a crystal structure available in an alternative conformation, II, was fitted into the computed map. The initial backbone RMSD and cross-correlation coefficients correspond to rigid-body docked structures into computed maps with grid spacing of 2.0 Å using Situs with default options. The final mean backbone RMSD values were calculated from the last 200ps of 500-ps trajectories. The final mean cross-correlation coefficients were calculated using computed maps generated from the average of the trajectories. Corresponding local cross-correlation coefficients that consider only the molecular envelope are also shown in parenthesis (a threshold of 0.2σ was used in these examples)

System (PDB codes)	Resolution (Å)	Initial RMSD (Å)	Initial (local) correlation	Grid spacing (Å)	Final mean RMSD (Å)	Final mean (local) correlation
ACS/CODH (1OAO)	5.0	14.82	0.677 (0.282)	1.0 2.0	0.75 1.04	0.988 (0.934) 0.986 (0.917)
	10.0	14.33	0.778 (0.478)	1.0 2.0	2.01 2.07	0.995 (0.980) 0.995 (0.980)
	15.0	13.92	0.817 (0.582)	1.0 2.0	2.01 2.07	0.995 (0.980) 0.995 (0.980)
16S rRNA (2AW7, 2AVY)	5.0	3.60	0.873 (0.611)	1.0 2.0	0.65 0.84	0.992 (0.961) 0.988 (0.939)
	10.0	3.57	0.947 (0.812)	1.0 2.0	1.04 1.21	0.996 (0.984) 0.995 (0.976)
	15.0	3.56	0.973 (0.901)	1.0 2.0	2.06 2.21	0.992 (0.972) 0.991 (0.965)

Figure 3.

Validation of the MDFF method using X-ray structures in two conformations. (A) Acethyl-CoA synthase; (B) 16S rRNA (only the head is shown for clarity, since it is the only region where the two conformations differ significantly). The target structures and simulated maps are shown in gray, whereas the initial and final fitted structures are shown in green (top) and colored by backbone RMSD per residue with respect to the target structures (bottom; color scales in Å). The final structures correspond to fittings into 10-Å simulated maps generated from the target structures. Movies of the fittings are included in Supplemental Data S4.

The final structures closely match the target structures used to generate the simulated maps; as expected, the match is less precise for lower resolutions or larger grid spacings. As an example, at 10-Å resolution, which represents a typical resolution for EM maps today, the final mean backbone RMSD is 1.25Å for ACS/CODH and 1.04 Å for the 16S rRNA. The additional test cases presented in Supplemental Data S3 also show that the accuracy obtained by applying MDFF is comparable to other methods (Jolley et al., 2008; Topf et al., 2008) and that MDFF can describe a large range of conformational changes, such as movements around a hinge and domain shearing. The fact that smaller grid spacings yield better results suggests that higher-order interpolation schemes in the grid-based force calculation can improve the fitting; indeed, the use of cubic interpolation in the current implementation of grid-steered molecular dynamics in NAMD (used in the calculations presented) yielded slightly better results when compared to linear interpolation (data not shown). The simulated maps presented in this section differ significantly from EM maps in that they do not contain noise emerging from the imaging process and numerical errors due to image processing and reconstruction, and in that they represent a single structure instead of an ensemble average as captured by cryo-EM. An attempt to address the latter is presented in Supplemental Data S5, where a protein structure is fitted into maps created from an ensemble of structures obtained from equilibrium MD simulations. For these tests, the fluctuation of atomic positions observed in MDFF reproduce reasonably well the fluctuations on the target map, especially for resolutions in the range of 10-15Å.

Example application: The E. coli ribosome

The ribosome, a complex macromolecular machine responsible for protein synthesis in all cells, is one of the biological systems for which cryo-EM has provided much insight to date (Frank, 2003). The ribosome undergoes several conformational changes and binds a number of co-factors throughout the process of protein synthesis. Different functional states have been extensively imaged by cryo-EM at ever-increasing resolution (Frank and Spahn, 2006). The ribosome has driven the development of methods to obtain quasi-atomic structures by combining X-ray crystallographic structures with cryo-EM maps (e.g., Wriggers et al., 2000; Gao et al., 2003; Tama et al., 2004; Mitra et al., 2005; Mitra et al., 2006; for a review, see Mitra and Frank, 2006).

We present the ribosome as an application of MDFF, using EM maps corresponding to two functional states, namely, the E. coli ribosome in complex with the ternary complex EF-Tu·aminoacyl-tRNA·GDP stalled by the antibiotic kirromycin (70S-fMet-tRNA^fMet-Phe-tRNA^Phe·EF-Tu·GDP·kir) at resolutions of 9 Å (Valle et al., 2003) and 6.7 Å (J. LeBaron, R. A. Grassucci, T. Shaikh, W. Baxter, J. Sengupta, and J.F., in preparation), and a ribosome with an accommodated A-site tRNA at 9-Å resolution (Valle et al., 2003). The first functional state corresponds to the initial selection of the ternary complex (TC) in the elongation cycle, after which EF-Tu leaves the ribosome and, subsequently, the peptide bond is transferred, resulting in the second functional state, with a deacylated tRNA occupying the P site, and an accommodated fMet-Phe-tRNA^Phe in the A site (70S-tRNA^Phe-MF-tRNA^Phe). The atomic model of the ribosome used in this section is described in Supplemental Data S6.

The flexible fitting was performed following a multi-step protocol: (i) After rigid-body docking, the 30S and 50S subunits were flexibly fitted, using ζ=0.3 kcal/mol, k_μ,RNA = 200 kcal mol^-1 rad^-2 or 200 kcal mol^-1 Å^-2 for angles and distances, respectively, and k_μ,protein = 400 kcal mol^-1 rad^-2. In addition to the secondary structure restraints, the ϕ and ψ angles of the rest of the amino acid residues were restrained with k_{μ, protein} = 200 kcal mol^-1 rad^-2. (ii) The potential corresponding to the 5S, 16S, and 23S rRNAs was deleted, and the atoms in these chains were restrained to their current positions (positional restraints) with a relatively stiff force constant of 10kcal mol^-1 Å^-2, effectively fixing them. This allowed the fitting of ribosomal proteins to improve, since the potential energy minima corresponding to the ribosomal RNA were removed from the simulation. (iii) The harmonic restraints applied to the ribosomal proteins were relaxed to 200 kcal mol^-1 rad^-2, restraining only residues in helices and β sheets. (iv) The remaining ligands, namely EF-Tu, tRNAs, and mRNA were introduced using rigid-body docking. For this step, the original EM potential (before RNA deletion) was used, all ribosomal proteins were positionally restrained, and the positional restraints on the rRNAs were lifted. The same secondary structure restraints to proteins and RNAs used in the previous step were preserved, and also applied to the recently introduced ligands. In addition, equivalent RNA restraints were imposed to enforce codon-anticodon interactions between the A-site mRNA codon and the tRNA. During this last step, force scaling was increased to ζ=1.0 kcal/mol. Convergence times and cross-correlation coefficients for each step are presented for all maps in Supplemental Data S7. A movie of the fitting into the 6.7-Å map illustrating the multi-step protocol can be found in Supplemental Data S9.

The MDFF method applied to different ribosome cryo-EM maps yielded quasi-atomic models that closely fit the EM densities; indeed, the cross-correlation coefficients between the maps and the fitted structures are significantly higher than those obtained from rigid-body docking (local correlations with a threshold of 0.2 σ are given in parenthesis): 0.913 (0.764) versus 0.858 (0.632) (TC-bound ribosome at 6.7 Å); 0.919 (0.739) versus 0.835 (0.503) (TC-bound ribosome at 9.0 Å); and 0.878 (0.735) versus 0.756 (0.513) (ribosome with accommodated A-site tRNA at 9.0 Å). Selected regions for which conformational changes have been previously characterized are presented in Fig. 4. It can be seen that distinct structural elements such as RNA and protein helices fit well into their corresponding densities, despite internal restraints imposed to avoid structural distortions. Local cross-correlation coefficients of different elements are presented in Supplemental Data S8.

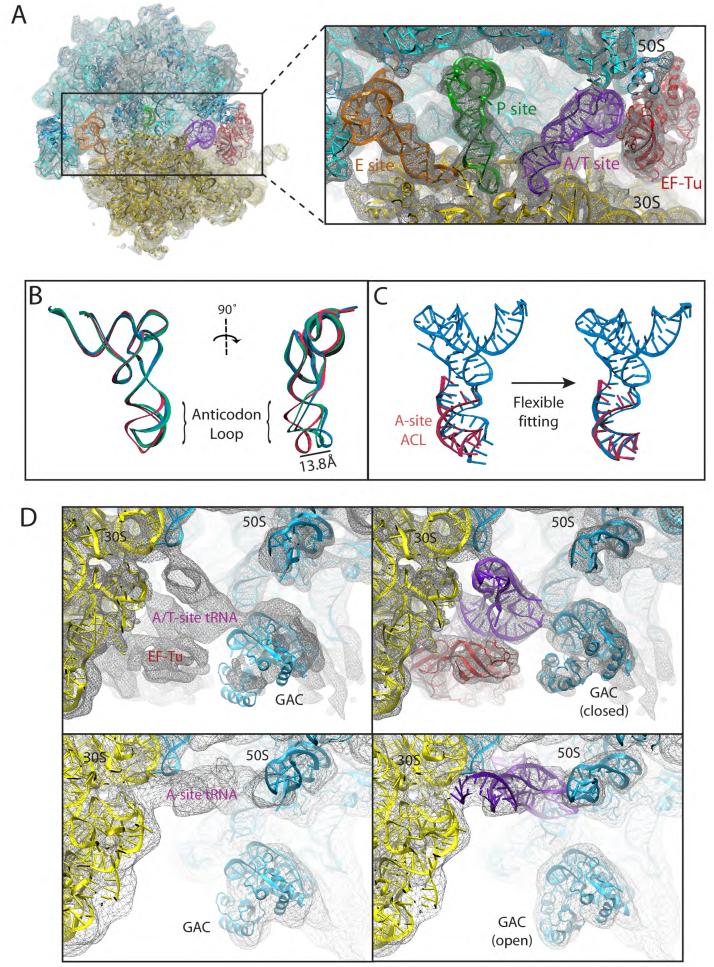
Figure 4.

Fitting into the TC-bound ribosome cryo-EM map at 6.7-Å resolution by means of MDFF. (A) Overview of the all-atom ribosome structure fitted into the 6.7-Å map, with a close view into the decoding center (inset). (B) Conformation of tRNA in the A/T site. The crystal structure from the free TC used as a starting point for the fitting (PDB 1OB2, unpublished data) is shown in red; the A/T tRNA model obtained by applying the MDFF method to the 6.7-Å map is shown in blue; the A/T tRNA model previously obtained using a 9.0-Å map constructed by interpolating two manual fittings of tRNA (PDB 1OB2) is shown in green (Valle et al., 2003). (C) Conformation of tRNA in the A/T site (blue) compared to a partial crystal structure of the A-site tRNA (Selmer et al., 2006) (red). The crystal structure from the free TC used as a starting point for the fitting (PDB 1OB2, unpublished data) is shown on the left; the A/T tRNA model obtained by applying the MDFF method to the 6.7-Å map is shown on the right. (D) Conformational dynamics of the GTPase-associated center. Shown are differences in the conformation of the GTPase-associated center between the TC-bound ribosome (EM map at 6.7-Å resolution, top), and the accommodated ribosome (EM map at 9-Å resolution, bottom). Rigid-body docked structures into the corresponding maps, used as initial coordinates for flexible fitting, are shown on the left; flexibly fitted structures are shown on the right.

An overview of the fitting into the 6.7-Å map of the TC-bound ribosome is depicted in Fig. 4A, along with a detailed view of the decoding center. Figure 4B shows the X-ray structure of tRNA (crystallized in complex with EF-Tu), a fitted structure, and the same crystal structure fitted manually in a previous study (Valle et al., 2003). It can be seen that the conformation of the anticodon loop (ACL) of the A/T-site tRNA is significantly different from the one adopted in the free TC. Interestingly, our fitted structure is very similar to the previously proposed one; however, the previous work assumed that the ACL of the A/T-site tRNA adopts the same conformation as that of the free ternary complex, and thus a model of the structure was built by interpolating coordinates between two manual fittings of the same crystal structure (Valle et al., 2003). With the MDFF method we obtained the conformational change that the ACL undergoes when the TC binds to the ribosome without any assumptions, the fitting being driven only by the EM data. The structure of the ACL of the A/T-site tRNA obtained from our fitting has the same conformation as the ACL of the A-site tRNA observed by Selmer et al. (2006), as shown in Fig. 4C. A comparison between the fittings into cryo-EM maps of the TC-bound ribosome at different resolutions (6.7Å and 9.0Å) is presented in Supplemental Data S7.

Binding of the TC to the ribosome induces a conformational change in the GTPase-associated center (GAC) (Valle et al., 2003). Figure 4D presents a comparison of the GAC conformation in the TC-bound ribosome and the ribosome in complex with an accommodated A-site tRNA. In the first conformation (closed), the GAC approaches the 50S to interact with the TC; when EF-Tu leaves the ribosome, the second conformation (open) arises in which the GAC lobe moves back to its original position. One can see that rigid-body docking of the crystal structure to the ribosomal cryo-EM map with an accommodated A-site tRNA shows a good fit for the GAC, revealing that the crystal structure captures this conformation. Flexible fitting obtains a closer match to the EM map for this state, and reveals the closed conformation of the GAC and TC in the TC-bound ribosome. The details of the atomic structures obtained from the 6.7-Å map will be discussed elsewhere (J. Sengupta, E.V., L.G.T., J. LeBaron, W. T. Baxter, T. Shaikh, R. A. Grassucci, P. Nissen, M. Ehrenberg, K.S., and J.F, in preparation).

Even at subnanometer resolution that permits the identification of secondary structure elements, some regions are not well defined in an EM map. For example, the switch regions of EF-Tu in the 6.7-Å TC-bound ribosomal EM map are not resolved, presumably due to their high flexibility. Though information about their structure is not directly available in the EM map, MD simulations can be performed in the presence of the EM potential to assess the feasibility of different conformations of the switches: an unfeasible conformation will either change during simulation, or alter the quality of the fit of neighboring domains. The conformational dynamics of the interaction of EF-Tu with the ribosome can be deduced from the computational studies, even though a crystal structure of a ribosome-bound EF-Tu is not yet available, and density for some key elements governing the interaction is missing in the EM map (J. Sengupta, E.V., L.G.T., J. LeBaron, W. T. Baxter, T. Shaikh, R. A. Grassucci, P. Nissen, M. Ehrenberg, K.S., and J.F, in preparation).

Discussion

We have developed a novel method, MDFF, for combining atomic structures and EM maps to reveal atomic details of macromolecular complexes in functional states. High-resolution structures of complexes imaged by cryo-EM permit a better interpretation of the data, e.g., by characterizing the flexibility of the complex, identifying key interactions between its composing elements, or locating bound co-factors. The MDFF method takes advantage of the impressive advances both in X-ray crystallography and cryo-EM, by using MD simulations that incorporate EM data through a potential driving an atomic structure into a conformation corresponding to an EM map. The method has several characteristics that bring together the best features of previously developed methods: (i) MDFF avoids the use of reduced representations which necessarily discard some of the information contained in the crystal structure or the EM map. (ii) MDFF considers information contained in the map through a potential, such that the fitting is performed locally, i.e., independently of other regions of a molecule. (iii) MDFF uses global measures of the fit only to assess convergence, and not to drive the fit. Methods that rely on global measures to obtain a good fit become less efficient as the size of the system increases. (iv) MDFF can be used to fit both protein and nucleic acids, as well as systems composed of both. (v) MDFF can fit parts of the complex independently when complete atomic structures are not available. (vi) MDFF does not require user input to divide a molecule into pieces to flexibly fit them into the map; rather, the flexibility is indigenous to the molecular structure, with additional restraints dictated by the secondary structure. (vii) MDFF follows multi-step protocols that permit adjusting the method to face various challenges, e.g., in case of systems composed of protein and nucleic acids, fitting can be performed on nucleic acids first and the protein component second. (viii) MDFF ensures stereochemical correctness during the fitting process, obviating the need for post-fitting refinement, which often results in deviations from the EM map. In fact, the structures obtained by MDFF can be used as initial coordinates for further simulation studies; in particular, for an equilibration testing the stability of the model arrived at. (ix) MDFF uses restraints to preserve secondary structure elements and other structural features in order to prevent overfitting; in this respect it bears some similarity to real-space refinement (Chapman, 1995), but MDFF is more automated and more adaptive; (x) MDFF can represent the structural variability present in the experimental map by providing a representative set of fitted structures instead of a single one; (xi) MDFF can be extended to take advantage of other enhanced-sampling techniques such as the use of elastic network models (Tama et al., 2004; Schröder et al., 2007).

A natural concern about flexible fitting methods is overfitting. We have shown that the harmonic restraints proposed are enough to prevent overfitting into noise-free maps. However, the degree of overfitting into experimental EM maps prevented by applying the restraints presented here cannot be evaluated at this time, and thus users are discouraged from softening the tight restraints suggested in this paper. The choice of restraints in MDFF might be improved further, e.g., through incorporation of restraints based on rigidity analysis (Jacobs et al., 2001; Jolley et al., 2008). A limitation intrinsic to our method is that rotation of structural elements are difficult to capture; this may be addressed, e.g., by enhancing the lowest-frequency normal modes in the simulation (Zhang et al., 2003), or by refining with MDFF models generated with a flexible fitting method based on normal modes (Tama et al., 2004; Suhre et al., 2006). Naturally, with the current restraints it is not possible to capture conformational changes that involve unfolding of secondary structure elements. Even though the fitting in MDFF is performed locally, proteins that interact with nucleic acids should not be fitted in the absence of the latter, since they might be attracted to the higher nucleic acid density. An interesting alternative involves the use of local, but not global, cross-correlation maps to define U_EM.

Naturally, MDFF results cannot be better than the EM data used permit. Any artifact in the molecular density reported in the EM map can be propagated to the fitted structure. The quantitative use of the density map requires high-quality data collection and efficient 3-D reconstruction algorithms, as extensively discussed in Frank (2006). The fitting and the interpretation of the resulting structures must be done taking into account factors that prevent the 3-D reconstruction from accurately representing the molecular density. An additional concern that the MDFF technique might raise is computational cost. Indeed, the necessary calculations are extensive, akin to other available flexible-fitting methods (Schröder et al., 2007; Wriggers and Birmanns, 2001). However, with the prospect of automated cryo-EM data eventually being able to match the speed of throughput achieved by other structural methods (Zhu et al., 2001), the advantages of not requiring ad hoc user input and of incorporating as much of information from the original data as possible, together with expected increases in computer power, will make MDFF a feasible and attractive tool for obtaining atomic structures from the wealth of EM data. Moreover, by using NAMD, the computational cost of the MDFF method scales linearly with system size, permitting the application of MDFF to large macromolecular complexes.

The success of the MDFF method is evident from the quality of the high-resolution structures obtained for cryo-EM maps of ribosomal complexes. The ribosome represents one of the greatest challenges to fitting methods due to its sheer size, its lack of symmetry, and its mixed composition of protein and RNA. We have recently fitted atomic structures to several ribosomal cryo-EM maps to study the conformational changes that take place during the decoding process (K.M., L.G.T., E.V., A. Zavialov, M. Ehrenberg, K.S., and J.F., in preparation; J. Sengupta, E.V., L.G.T., J. LeBaron, W. T. Baxter, T. Shaikh, R. A. Grassucci, P. Nissen, M. Ehrenberg, K.S., and J.F., in preparation). Typical cross-correlation coefficients obtained improve from ∼0.8 after rigid-body docking, to ∼0.9 after completion of the flexible fitting.

In recent years, it has become evident that cellular functions are carried out by assemblies of interacting macromolecules (Alberts, 1998), many of them existing only transiently in the cell. In order to provide a comprehensive description of such complexes, spanning the atomic and the system-level, data obtained from various structural techniques must be combined into high-resolution structures with the aid of theoretical approaches (Sali et al., 2003; Alber et al., 2007). MD is a method of choice, being increasingly used to refine macromolecular structures, and an established tool for studying structural dynamics of large biomolecules. The conceptual grounds of the methodology presented here can easily be extended to other sources of structural data by including them in MD simulations of atomic or coarse-grained structures (Shih et al., 2007; Arkhipov et al., 2006) as external potentials that merge several levels of description into high-resolution structures.

As structural methods become more prolific, automated software capable of interpreting intermediate-resolution structures at the atomic level is becoming crucial; indeed, it seems likely that in years to come this type of approach will yield the main, and perhaps only, source of atomic structures for large macromolecular complexes in functional conformations. The software should be widely available and should not require very detailed technical expertise or ad hoc input, but rather should be easy to use and general. These requirements are met by the MDFF method. The method is currently implemented in the molecular dynamics software package NAMD (Phillips et al., 2005), and the automated setup and analysis of the simulations is done through the molecular visualization software package VMD (Humphrey et al., 1996).