Translating network models to parallel hardware in NEURON

Abstract

The increasing complexity of network models poses a growing computational burden. At the same time, computational neuroscientists are finding it easier to access parallel hardware, such as multiprocessor personal computers, workstation clusters, and massively parallel supercomputers. The practical question is how to move a working network model from a single processor to parallel hardware. Here we show how to make this transition for models implemented with NEURON, in such a way that the final result will run and produce numerically identical results on either serial or parallel hardware. This allows users to develop and debug models on readily available local resources, then run their code without modification on a parallel supercomputer.

1. Introduction

Over the past decade, network modeling has become a widely practiced research activity in computational neuroscience. Investigators often find that they need to study larger and more complex networks, but storage and run time limitations may prevent them from reaching their goals. At the same time, the computer industry has been shifting to parallel computing architectures, beginning with supercomputers in the early 1990s; by 2002 all but 7% of the “TOP500” list of high-performance computers were parallel machines (Kirkpatrick, 2003). This shift is so pervasive that many academic institutions now have at least one parallel supercomputer, and with device physics limitations nearly halting advances in processor speed in recent years (Sutter, 2005), inexpensive multiprocessor desktop and laptop computers have become commonly available consumer goods.

The obvious solution to the challenge posed by large network models is to move to parallel simulations, in order to take advantage of hardware with multiple processors and large amounts of total memory. Several studies have shown that distributing network models over multiple processors can achieve significant speedups. For example, Migliore et al. (2006) introduced the framework employed in NEURON for parallel simulations, and used published models to test its performance scaling. They obtained large gains, with a linear speedup of simulation speed as the number of processors increased, until each processor had so little work to do (~100 equations) that communication became rate limiting.

NEURON offers users the ability to parallelize network models while maintaining, as much as possible, a separation between the specification of the network, i.e. all of the cells and all of the connections between them, and how the cells are distributed among all the host CPUs. It is thus possible to write code that executes properly, without modification, in any serial or parallel hardware environment, and produces quantitatively identical results regardless of the number of CPUs or which CPU handles which cell. This means that users can develop and debug their models locally--on serial hardware, an ad hoc cluster of two or more PCs linked by ethernet, or a multiprocessor PC--and then switch to production runs on parallel hardware without having to make further program modifications.

Here we illustrate how this is done by parallelizing two network models that have different architectures: a ring, and a net with random connectivity. This paper is written from the perspective of UNIX/Linux, but the basic concepts that are involved, and all NEURON programming issues, are independent of the operating system. Source code for the models described in this paper is available from ModelDB (http://modeldb.yale.edu\) via accession number 96444.

2. Materials and Methods

The literature on parallel processing is full of “terms of art,” such as CPUs, cores, processors, processing units, nodes, and hosts, but unfortunately these are not used synonymously by everyone. In this paper we define the number of processing units in a computer to be the number of programs that can be executed simultaneously. For the sake of convenience, we refer to each processing unit as a processor, so what is commonly called a “dual core, dual processor” PC has four processing units, or four processors. When a processor is part of a parallel computing architecture, it is called a host. Note that the latter differs from the usage of host in discussions of computer networking, where it refers to an individual server or workstation.

2.1 Installation and configuration of software

2.1.1 Installing and testing MPI

For parallel simulations, installation of NEURON requires a pre-existing installation of MPI-1.1 (Message Passing Interface) standard or greater. MPI almost certainly exists on any parallel hardware that accepts remote login clients. The easiest way to find out if MPI has already been installed is to ask the system administrator. Otherwise, with a UNIX command line, these statements

which mpicc

which mpic++ # or mpicxx, mpiCC, …

will at least tell if it is in one’s PATH.

Individuals who have multiprocessor workstations, or who wish to configure their own private workstation cluster, have a variety of choices of open source implementation of the MPI standard. For example one can obtain MPICH2 from http://www-unix.mcs.anl.gov/mpi/mpich2\.

Unfortunately, the syntax for launching a program is different for every implementation of MPI, and also depends on the nature of the parallel hardware, i.e. supercomputer, workstation cluster, or standalone multiprocessor personal computer. Furthermore, the launch process itself is often encapsulated in batch queue control programs, e.g. LoadLeveler, PBS, etc.. Regardless of the details, the underlying principles are the same, but for the sake of illustration it is helpful to have a concrete example, so we will assume the simplest case: MPICH2 on a standalone multiprocessor personal computer.

With the proviso that versions and README instructions may change, this sequence of commands will download and install MPICH2

curl http://www-unix.mcs.anl.gov/mpi/mpich2/downloads/

/mpich2-1.0.5p4.tar.gz > mpich2-1.0.5p4.tar.gz

tar xzf mpich2-1.0.5p4.tar.gz

cd mpich2-1.0.5p4

./configure --prefix=$HOME/mpich2 --with-device=ch3:nemesis

make

make install

export PATH=$HOME/mpich2/bin:$PATH

(the nemesis device specified in the configure line provides very much faster communication for shared memory multiprocessors than does the default socket device). Setting up a cluster that has several hosts will also probably involve creating a file that lists those hosts. Also, before testing on a workstation cluster that has a shared file system, make sure that it is possible to login to any node using ssh without a password, e.g. ssh ‘hostname’. If not,

ssh-keygen -t rsa

cd $HOME/.ssh; cat id_rsa.pub >> authorized_keys

It may also be necessary to explicitly set permissions on the authorized_keys file

chmod 600.ssh/authorized_keys

Of course, proper functioning of the installed software should be verified. It must be possible to start, query, and stop the MPI daemon

$ mpdboot

$ mpdtrace

localhost

$ mpdallexit

(listings that combine user entries and computer responses use $ to denote the system prompt, display user entries in bold monospace, and show computer responses as plain monospace). In addition, it is a good idea to build and run one or more of the test programs that are distributed with MPICH2, such as cpi_anim.

$ cd $HOME/mpich2/share/examples_graphics

$ make

$ mpiexec -np 4 cpi_anim

Process 0 on localhost.localdomain

Process 2 on localhost.localdomain

Process 3 on localhost.localdomain

Process 1 on localhost.localdomain

pi is approximately 3.1416009869231249, Error is 0.0000083333333318

wall clock time = 0.041665

Observe that the −np 4 argument caused four processes to be launched. Ordinarily, the chosen number of processes will match the number of processing units. However, to check that things are working properly, it is very useful to test with a single process ( −np 1). If the processes have a very wide range of run times, it may be useful to launch many more processes than there are processing units, thereby letting the operating system balance the problem.

2.1.2 Building and testing NEURON

This sequence of commands will download and install NEURON 5.9 and InterViews 17:

mkdir $HOME/neuron

cd $HOME/neuron

# download and install InterViews

# unnecessary if you will only run in batch mode

curl http://www.neuron.yale.edu/ftp/neuron/versions\/v5.9/iv-17.tar.gz | tar xzf

cd iv-17

./configure --prefix=‘pwd’

make

make install

cd ..

# download and install NEURON

curl http://www.neuron.yale.edu/ftp/neuron/versions\

//v5.9/nrn-5.9.tar.gz |tar xzf

cd nrn-5.9

# if InterViews is not installed, replace “--with-iv…” with

# --without-x

./configure --prefix=‘pwd’ --with-iv=$HOME/neuron/iv-17 \--with-paranrn

make

make install

export CPU=i686 # or perhaps x86_64--to decide which you have, # list the directory, or run ./config.guess

export PATH=$HOME/neuron/iv-17/$CPU/bin:$HOME/neuron\

/nrn-5.9/$CPU/bin:$PATH

NEURON is distributed with several test programs that are located in nrn-x.x/src/parallel, where x.x is the version number. The simplest is test0.hoc

objref pc

pc = new ParallelContext ( )

strdef s

{

system (“hostname”, s)

printf (“There are %d processes. My rank is %d and I am on %s\n” \pc.nhost, pc.id, s)

}

{pc.runworker ( )

{pc.done ( )

quit ( )

pc.nhost is a synonym for the number of processes, i.e. the value of the -np argument. pc.id is a synonym for the MPI rank of a process, and ranges from 0 to pc.nhost-1. Running test0.hoc under MPI with −np 4

$ cd src/parallel

$ mpiexec −np 4 $HOME/neuron/nrn-5.9/$CPU/bin/nrniv −mpi test0.hoc

should generate this output on a “dual core, dual processor” PC

There are 4 processes. My rank is 0 and I am on localhost.localdomain

There are 4 processes. My rank is 1 and I am on localhost.localdomain

There are 4 processes. My rank is 2 and I am on localhost.localdomain

There are 4 processes. My rank is 3 and I am on localhost.localdomain

Note the −mpi switch in the command line, which tells NEURON that it is running in parallel mode, so that each process is assigned a different rank. Trying again but omitting -mpi

$ mpiexec −np 4 $HOME/neuron/nrn-5.9/$CPU/bin/nrniv test0.hoc

makes NEURON run in serial mode, so the four processes will execute with no communication between them, and NEURON sets pc.id to 0 and pc.nhost to 1

There are 1 processes. My rank is 0 and I am on localhost.localdomain

There are 1 processes. My rank is 0 and I am on localhost.localdomain

There are 1 processes. My rank is 0 and I am on localhost.localdomain

There are 1 processes. My rank is 0 and I am on localhost.localdomain

One small but very practical issue deserves mention: NEURON has many commonly used procedures and methods that return a numerical result which is printed to standard output when they are executed at the top level of the interpreter, e.g. load_file ( ), system ( ), pc.runworker ( ). This may be helpful for development and debugging, but can be a big nuisance when a program runs in parallel mode on more than a few processors. Printing of dozens (or thousands) of lines of 0s and 1s can be suppressed by surrounding offending statements with pairs of curly brackets, as in

{pc.runworker ( )}

2.2 Important concepts

NEURON uses an event delivery system to implement spike-triggered synaptic transmission between cells ((Hines and Carnevale, 2004), chapter 10 in (Carnevale and Hines, 2006)). In the simplest case on serial hardware, the connection between a spike source (presynaptic cell) and its target is made by executing a statement of the form

nc = new NetCon (source, target)

This creates an object of the NetCon (Network Connection) class, which monitors a source (presynaptic cell) for spikes. Detection of a spike launches an event which, after an appropriate delay, will be delivered to the NetCon’s target. The target is either an artificial spiking cell or a synaptic mechanism attached to a biophysical model cell (Fig. 2.2.1; also see Fig. 3.2). In either case, delivery of the event causes some change in the postsynaptic cell.

Figure 2.2.1.

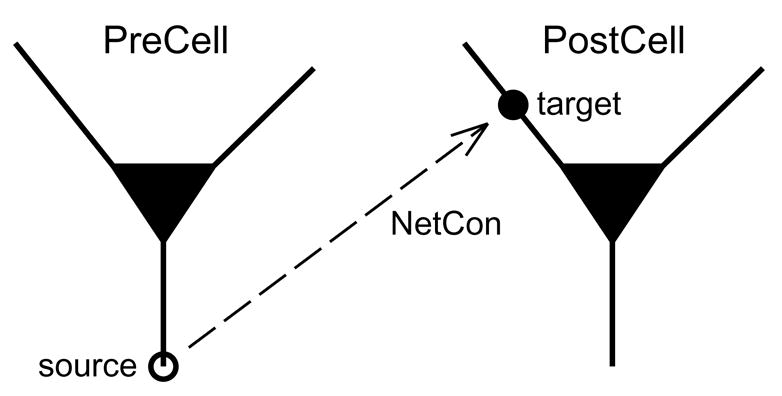
A NetCon attached to the presynaptic neuron PreCell detects spikes at the location labeled source, and delivers events to the synapse target which is attached to the postsynaptic neuron PostCell.

Fig. 3.2.

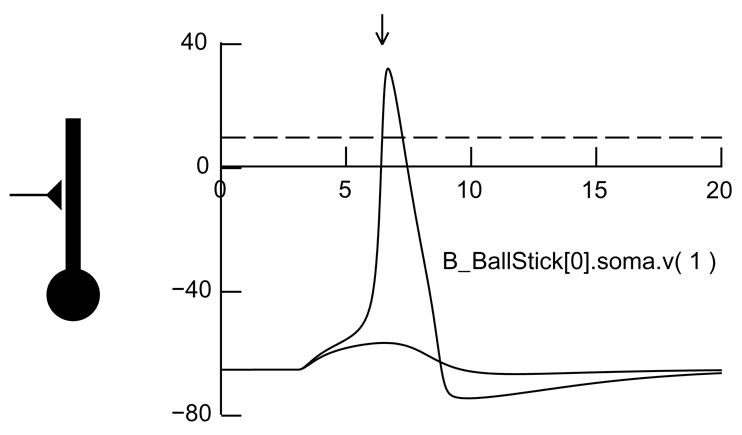
Left: A ball and stick model cell driven by an excitatory synapse at the middle of its dendrite. Right: Effects of weak and strong synaptic inputs on membrane potential v observed at the junction of the dendrite and soma, where a NetCon is attached whose threshold is 10 mV (dashed line). The strong input elicits a spike, making v cross the NetCon’s threshold in a positive-going direction (arrow) so that an event will be sent to the NetCon’s target.

The basic problem that has to be overcome in a parallel simulation environment is that the source cell and its target usually do not exist on the same host. The solution is to give each cell (spike source) its own global identifier (gid) that can be referred to by every host. Then, if a presynaptic cell on one host generates a spike, a message that notes the gid and time of the spike will be passed to all other hosts. NetCons on those hosts that have this gid as their source will then deliver events to PreCell’s targets with appropriate delays and weights (Fig. 2.2.2).

Figure 2.2.2.

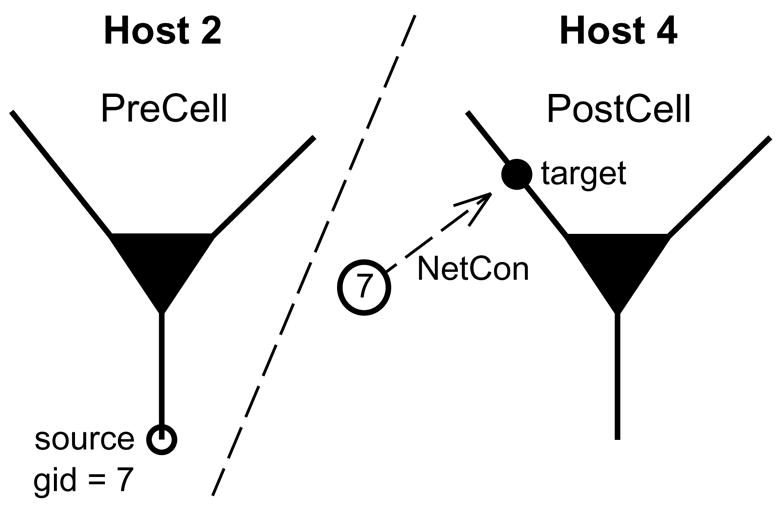
A presynaptic spike source PreCell with gid = 7 is on host 2, but its target is a synapse attached to PostCell on host 4. If PreCell spikes, a message is passed to all hosts so that NetCons that have gid 7 as their source will deliver events to their targets.

Synapses usually far outnumber spike sources, but fortunately synapse identifiers are unnecessary because we use a target-centric strategy to set up network connections. That is, each host is asked to execute the following conceptual task

• for each cell c on this host {

• for each spike source gid s that targets c {

• set up a connection between spike source s and the proper target synapse on c

• }

• }

3. First example: a ring network

A good strategy for developing parallel network models is to first create a scalable serial implementation, and then transform the implementation into a parallel form. The basic steps in constructing any network model are to define the cell types, create instances of the cells, and finally to connect them together. For our first example of how to do this with NEURON, we imagine 20 cells connected in a ring where cell i projects to cell i+1, and the last cell (cell 19) projects to the first cell (cell 0) (Fig. 3.1). For didactic purposes we give each cell some structure consisting of a soma and a dendrite, as in the classical ball and stick model (Fig. 3.2). The soma has Hodgkin-Huxley channels so that it can generate spikes. The dendrite is passive, with an excitatory synapse attached to it. Activating the synapse produces a large enough depolarization to trigger a somatic spike.

Fig. 3.1.

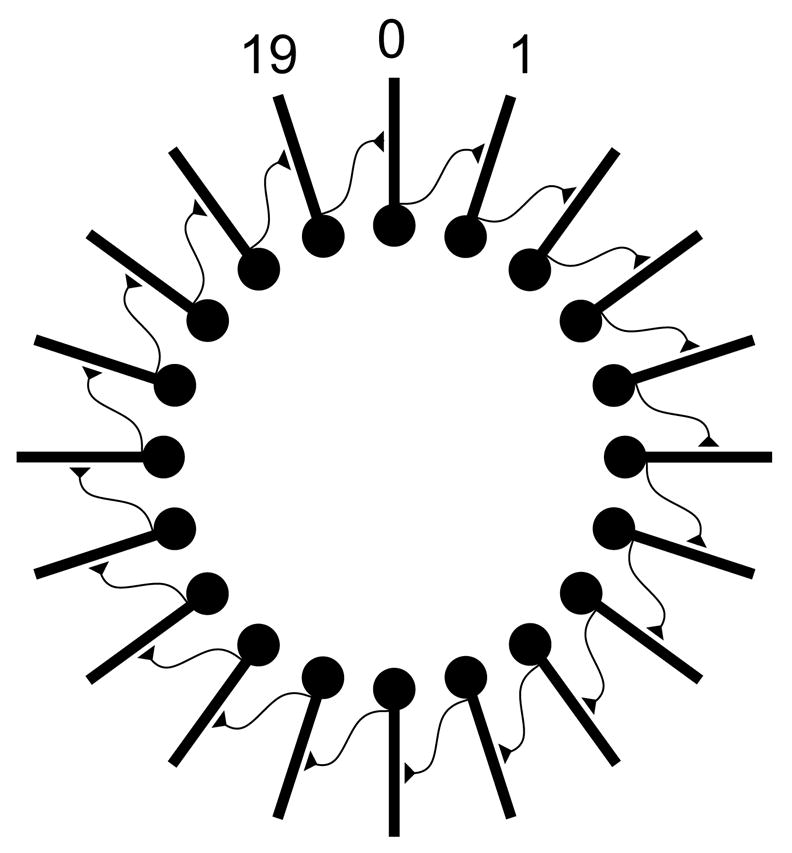
Fig. 3.1. A network of 20 ball and stick cells arranged in a ring. Each cell i makes an excitatory synaptic connection to the middle of the dendrite of cell i+1, except for cell 19 which projects back to cell 0.

3.1 Define the cell type

To define a cell type, one would either write hoc code, or use the Network GUI tools as described in the tutorial at http://www.neuron.yale.edu/neuron/docs/netbuild/main.html, then export a hoc file and extract the cell type definition from it as described in chapter 11 of The NEURON Book (Carnevale and Hines, 2006). In either case, the essential elements of a cell type are its morphology and distributed membrane properties. It is also generally convenient to specify the location of the spike trigger zone, and the threshold for spike detection (see Fig. 3.2), which are almost always the same for all cells of a given type. This makes it easier to implement a source.connect2target procedure for connecting cells with simple syntax.

Synapses are a different matter. The question is whether, apart from toy networks, it is possible to construct all synapses with proper locations and types when a cell is created, without regard to what the connections are going to be. If synapse properties depend in any way upon the source cell type and location, it will be simpler to create the synapse at the same time as the NetCon. In any event, it is useful for each cell instance to have a list that holds the synaptic instances.

For this example we can just extract the template that defines the B_BallStick cell type from the tutorial example at http://www.neuron.yale.edu/course/net2/net2run_.hoc . Reading through the template (Listing 1), we find that it follows our recommendations with regard to specifying the spike trigger zone and detection threshold; obfunc connect2target ( ) contains the statements

soma nc = new NetCon (&v (1), $o1)

nc.threshold = 10

which specify the variable and location that is monitored for occurrence of a spike (membrane potential v at the 1 end of soma, which also happens to be where the dendrite is attached), and the threshold at which the spike triggers an event (v rising above 10 millivolts). A bit farther into the listing, we discover that proc synapses ( ) has this statement

/* E0 */ dend syn_ = new ExpSyn (0.8) synlist.append (syn_)

where synlist is a public list that contains all synapses that are attached to a B_BallStick cell. In passing, we should mention that:

1. The reversal potential e of this ExpSyn is left unchanged from its default value of 0 mV, so we know that ExpSyn is excitatory.

2. geom_nseg ( ) sets dend.nseg to 7 before synapses ( ) is called (see proc init ( ) for the execution sequence when a new B_Ballstick is created), so the ExpSyn is actually located at 0.78571429 instead of 0.8.

3. If we were developing de novo, it would be essential to verify that the anatomical and biophysical properties are correct and that the cell generates a spike when driven when the excitatory synapse is activated. However, from the tutorial example, we already know that the B_Ballstick cell type works.

3.2 Serial implementation of the network

Listing 2 is a program that implements and exercises the network model in a manner that is suitable for execution on serial hardware. For ease of development and debugging, the program has a modular structure with a sequence of procedures, each of which has a particular purpose, and it makes extensive use of lists so that collections of objects can be treated as sets (see chapter 11 in (Carnevale and Hines, 2006).

In broad outline, it starts by following the natural sequence of defining the cell types that are involved, creating the instances of the cells, and then setting up the connections between them. The rest of the program is devoted to instrumentation (stimulating the network and recording the times at which cells fire), simulation control (launching a simulation for a specified time), and reporting simulation results (printing out which cell fired when).

We already discussed the definition of the cell type in the previous section. Since all cells are to exist on a single host, the remaining tasks are quite straightforward.

3.2.1 Creating and connecting the cells

A simple for loop in proc mkcells ( ) is sufficient to create all instances of cells that will be part of the ring, and append them to a list called cells.

proc mkcells ( ){local i localobj cell

cells = new List ( )

for i=0, $1-1 {

cell = new B_BallStick ( )

cells.append (cell)

}

}

Another for loop in proc connectcells ( ) iterates over the contents of this list to set up the network connections by creating a NetCon for each cell i that will drive the excitatory synapse on cell i+1, and wraps around so that the last cell in the ring drives the synapse on the first cell. These NetCons are appended to another list called nclist.

proc connectcells ( ) {local i localobj src, target, syn, nc

nclist = new List ( )

for i=0, cells.count−1 {// iterating over sources

src = cells.object (i)

target = cells.object ((i+1)%cells.count)

syn = target.synlist.object (0) // the first object in synlist

// is an ExpSyn with e = 0, therefore an excitatory synapse

nc = src.connect2target (syn)

nclist.append (nc)

nc.delay = 1

nc.weight = 0.01

}

}

Note that the iteration in connectcells ( ) is source-centric, i.e. each new i is treated as the index of a source cell, so that the index of its target is i+1 modulo NCELL. We could just as easily have used a target-centric strategy by treating i as the index of a target, and found the index of the source as i−1 modulo NCELL. In either case, the computational effort would have been the same. However, in a parallel environment the choice of source-centric vs. target-centric iteration has a bearing on setup efficiency; we will return to this later.

3.2.2 Instrumentation and simulation control

Stimulation is achieved by proc mkstim ( ), which creates a NetStim that will generate a single spike event source and attaches it via a NetCon to the excitatory synapse on cell 0. Recording of spike times is set up by proc spikerecord ( ), which uses the NetCon class’s record ( ) method to capture spike times to a Vector. Simulation control makes use of the run ( ) procedure which is part of NEURON’s standard run system, and proc spikeout ( ) handles printout of spike times.

3.3 Transforming the implementation from serial to parallel

A parallel implementation of the ring network is presented in Listing 3. Creating an instance of the ParallelContext class gives us access to the methods that support the ideas discussed in 2.2 Important concepts. We will discuss these methods as they come up in the revised implementation of our model network.

Note the use of curly brackets around load_file ( ) to suppress printing of superfluous 0s and 1s to standard output, as mentioned at the end of 2.1.2 Building and testing NEURON. This has also been done to several ParallelContext method calls near the end of the listing.

3.3.1 Creating the cell instances

For the sake of illustration, the parallel implementation of mkcells ( ) is excerpted here with a bold monospace typeface that marks changes from the serial implementation.

proc mkcells ( ) {local i localobj cell, nc, nil

cells = new List ( )

// each host gets every nhost’th cell,

// starting from the id of the host

// and continuing until all cells have been dealt out

or (i=pc.id; i < $1; i += pc.nhost) {

cell = new B_BallStick ( )

cells.append (cell)

pc.set_gid2node (i, pc.id) // associate gid i with this host

nc = cell.connect2target (nil) // attach spike detector to cell

pc.cell (i, nc) // associate gid i with spike detector

}

}

The for loop no longer iterates over all cells in the net; instead, on each host the for statement iterates i over just those gid values that belong on that host. In essence, this “deals out” the cells to the hosts, one at a time., so that the cells are distributed more or less evenly over the hosts. In the end, each host will have its own cells list, which will be about 1/N as long as the cells list in the serial implementation.

The for loop also associates each gid with a spike source on a particular host. In principle this could be done with a single primitive method, but for the sake of flexibility the process has been divided into three steps. First, we call set_gid2node ( ) on the host that “owns” the cell to associate the cell’s gid with the id of the host. Second, we create a temporary NetCon that specifies the location of the spike detector on the cell; this NetCon does not need to have a real target. Third, we use pc.cell ( ) to associate the spike detector location with the gid. Note that the gid of a cell’s spike detector will have the same value as the index of that cell in the cells list of the original serial implementation, and since there is only one spike detector per cell, we can use the gids to refer to individual cells. If the number of hosts is N, the mapping of cells to hosts will be as shown in Table 1.

Table 1.

The mapping of cells to hosts in this example. There are N hosts whose ids range from 0 to N − 1, and the gids are the global identifiers of the cells.

host id	gid
0	0, N, 2N …
1	1, 1 + N, 1 + 2N…
.	.
.	.
.	.
N − 1	N − 1, 2N − 1, 3N − 1 …

3.3.2 Setting up the network connections

In the serial program, when we made connections between cells i and i+1, we were able to exploit the cells list as a map between index integers and the corresponding cell objects. This is not possible in the parallel implementation because the indices of cells no longer have that meaning; as noted above, each host has its own cells list, which contains just those cells that belong to that host.

Parallelizing this model requires several changes to connectcells ( ), all of which are direct consequences of the need to refer to cells by their gids instead of cells list indices (revisions indicated by bold monospace typeface).

proc connectcells ( ) {local i, targid localobj src, target, syn, nc

nclist = new List ( )

for i=0, NCELL - 1 {// iterating over source gids

targid = (i+1)%NCELL

if (!pc.gid_exists (targid)) { continue }

target = pc.gid2cell (targid)

syn = target.synlist.object (0) // the first object in synlist

// is an ExpSyn with e = 0, therefore an excitatory synapse

nc = pc.gid_connect (i, syn)

nclist.append (nc)

nc.delay = 1

nc.weight = 0.01

}

}

The first significant change is that the for statement, which iterates over all spike source gids, must use NCELL (the total number of cells in the net) instead of cells.count to specify the number of iterations.

The simple rule that defined the architecture of the ring network must now be expressed in terms of gids, hence targid = (i+1)%NCELL where i is the gid of a source and targid is the gid of the corresponding target. Also, before trying to set up a synaptic connection on any host, we verify that targid belongs to a cell that actually exists on that host by executing

if (!pc.gid_exists (targid)) { continue }

If the target cell does not exist, the remaining statements inside the for loop will be skipped. Otherwise, gid2cell ( ) gets an objref for the cell, which is used to get an objref for the synapse that is to receive events from the spike source. The last change in connectcells ( ) is to use gid_connect ( ), which creates a NetCon that conveys events from spike source gid i to target synapse syn.

Earlier we noted that the computational effort required to set up a serial implementation of this network was the same regardless of whether the for loop iterated over sources or targets. On parallel hardware, however, it is less efficient to iterate over sources. In this particular example, each host must iterate over all source gids in order to find the gids of the targets that exist. The penalty is small because it doesn’t take that much time to increment i from 0 to NCELL−1, generate the target’s gid, and check to see if that gid exists, but as a rule it is better for each host to iterate over the targets that exist on itself. Later in this paper we will present a strategy for doing this.

3.3.3 Instrumentation

As in the serial implementation, stimulation is accomplished by a NetStim that sends a single event to the excitatory synapse on the first cell in the net, i.e. the cell whose gid is 0. This NetStim, and the NetCon that delivers its event, need to exist only on the host that has the first cell, so we have inserted

if (!pc.gid_exists (0)) { return }

at the start of proc mkstim ( ) so that nothing is done on the hosts that do not have this cell. We also changed the statement that creates the NetStim so that it uses gid 0 to retrieve the cell’s objref

ncstim = new NetCon (stim, pc.gid2cell (0).synlist.object (0))

Also as in the serial implementation, the NetCon class’s record method is used to capture the spiking of the ring network’s cells into a pair of Vectors. However, each host can only record the spike times of the cells that exist on itself, so each host must have its own tvec and idvec to hold the spike times and corresponding cell gids. Furthermore, the for loop must iterate over all cells on any particular host, which is the same as all items in that host’s cells list. Finally, we must remember to record the cell’s gid, which is unique to each cell, not its index i into the cells list. Consequently the record ( ) statement must be changed to

nc.record (tvec, idvec, nc.srcgid)

where the NetCon class’s srcgid method is used to retrieve the gid of the spike source to which a NetCon is attached.

3.3.4 Simulation control

With the serial implementation, it is only necessary to specify the duration tstop of a simulation, and then call the standard run system’s run ( ). In turn, run ( ) calls stdinit ( ) which initializes the model, and continuerun (tstop) which carries out the simulation per se.

Simulations of distributed network models require replacing run ( ) by three statements. The first is pc.set_maxstep ( ), which examines all connections between cells on different hosts (i.e. the delays of all NetCons that were created by calling gid_connect ( )) to find the minimum delay, then sets the maximum integration step size on every host to that value (but not greater than the value of its second argument). The second statement is just stdinit ( ) which initializes the model, and the third is pc.psolve (tstop) which has an effect similar to cvode.solve (tstop), i.e. integrates until its step passes tstop, then interpolates the values of the states at exactly tstop and calls the functions necessary to update the assigned variables.

3.3.5 Reporting simulation results

Simulations on parallel hardware are generally done in batch mode with no graphical user interface, and typically produce a large volume of data that must be stored for later analysis. For this toy example, we will just dump the spike times and cell gids to the terminal.

The serial version collects all spike times and cell ids in a pair of Vectors called tvec and idvec, in the sequence in which the spikes occurred. The spikeout ( ) procedure prints a header, then uses a for loop to print out all contents of these Vectors, e.g.

time	cell
2.05	0
5.1	1
8.15	2
11.2	3
…
93.55	10
96.6	11
99.65	12

However, in the parallel version each host has its own tvec and dvec, which can only capture the spike times and gids of the cells that exist on that host. Printing out these results requires a nested pair of for loops: the outermost iterates over the hosts, and the inner one iterates over the contents of the individual host’s tvec and idvec. Special care must be taken or else each host will compete to print its own tvec and idvec, scrambling the printout because there is no guarantee as to which host starts printing first, nor is there any protection against one host’s output stream being interrupted at any arbitrary point by the output stream from another host.

We can prevent this by forcing the parallel computer to emulate a serial computer while outputting simulation results. This is done with the ParallelContext class’s barrier ( ) method, which makes hosts that are racing ahead wait until all other hosts have caught up before proceeding further. The first pc.barrier ( ) statement in spikeout ( ) ensures completion of all printing that must be finished before the header is printed. The second one is the last statement in the outermost for loop, so that each host has sufficient time to finish printing its spike times. These changes are shown below in bold monospace typeface.

proc spikeout ( ) { local i, rank

pc.barrier ( ) // wait for all hosts to get to this point

if (pc.id==0) printf (“\ntime\t cell\n”) // print header just once

for rank=0, pc.nhost-1 { // host 0 first, then 1, 2, etc.

if (rank==pc.id) {

for i=0, tvec.size−1 {

printf (“%g\t %d\n”, tvec.x[i], idvec.x[i])

}

}

pc.barrier ( ) // wait for all hosts to get to this point

}

}

The parallel version’s printout will be grouped according to which cells are on which hosts, as in this run with four hosts

time	cell
2.05	0
14.25	4
26.45	8
38.65	12
…
72.2	3
84.4	7
96.6	11

But all the spike times and cells are the same as in the serial implementation, as we can verify by capturing the outputs of the two programs to files, sorting the parallel output, and comparing

$ sort -g parout.txt > sorted_parout.txt

$ cmp serout.txt sorted_parout.txt

$

Further tests (results not shown) confirm that this program generates identical firing patterns regardless of the number of hosts. It also produces the same firing patterns when run on a single processor PC without MPICH2.

4. Second example: a network with random connectivity

A recurring theme in computational modeling is randomness, which may be manifested in the model specification (anatomical and biophysical attributes of cells, locations and properties of synapses, network topology and latencies of connections between cells) or as stochastic perturbations of variables in the course of a simulation (noisy voltage or current sources, fluctuation of model parameters such as ionic conductances, stochastic transmitter release or channel gating, spatiotemporally varying patterns of afferent spike trains). It is essential to achieve statistical independence of such parameters, while at the same time ensuring reproducibility--i.e. the ability to recreate any particular model specification and simulation--no matter how many hosts there are, or how the cells are distributed over them. Being able to generate quantitatively identical results on parallel or serial hardware is particularly important for debugging.

The key to achieving this goal is for each cell to have its own independent random number generator. This is the one thing that will be the same regardless of the number of hosts and the distribution of cells. To see how this is done with NEURON, let us consider a network with 20 cells in which each cell receives excitatory inputs from three other cells, chosen at random. The network is perturbed by an excitatory input to the “first” cell at t = 0. The cells and synapses are identical to those used in the first example (Fig. 3.2), so we can omit any discussion of cell types and focus on how to set up the network.

4.1 Serial implementation of the network

The problem of achieving reproducible, statistically-independent randomness can be solved by assigning each cell its own pseudorandom sequence generator, which is seeded with a unique integer so that the sequences will be independent. For this model, the sequences will be used to select the presynaptic sources that target each cell.

The final implementation of a program to create this network on serial hardware is presented in Listing 4. The general outline of this program is very similar to the serial implementation of the ring network, and many the details are identical (especially simulation control and reporting results). There are some cosmetic differences, e.g. the renaming of the mkring ( ) procedure, which is now called mknet ( ) and new parameter declarations, e.g. C_E which defines the number of excitatory inputs per cell, and connect_random_low_start_ which is the lower 32 bit seed for the pseudorandom sequence generators that determine network connectivity. The most substantive changes, however, are those that we have focused on in the preceding paragraphs, which fall into two categories. The first category is code that introduces randomness into the network architecture. The second category, which is necessitated by the first, is code that analyzes and reports the network architecture. The following discussion examines these changes and the rationale behind them.

4.1.1 Planning ahead: verification of network architecture

Verification of network architecture is a critical test of reproducibility. The ring network was simple enough that we could write a program whose correctness could be determined almost by inspection. For a random net it is not enough to write code that purports to set up connections according to our plan; we must also make sure that the resulting network really does meet our design specifications. This can be done by exploiting the same NetCons that are used to set up the network connections. In the serial implementation, they are all contained in a single nclist, so we can iterate over the elements of this list and use the NetCon class’s precell ( ) and syn ( ) methods to discover the identities of each spike source - target pair. What we really want, however, are the identities of the presynaptic cell, the synaptic mechanism that receives input events, and the postsynaptic cell to which that mechanism is attached. We can get these if we add “synapse id” and “cell id” variables to the synaptic mechanisms, and initialize the contents of these variables when each cell instance is created. With slight modification, this same strategy will work for the parallel implementation.

The original ball and stick model cell used the ExpSyn synaptic mechanism, so we make a local copy of nrn-6.0/src/nrnoc/expsyn.mod (c:\nrn60\src\nrnoc\expsyn.mod under MSWin), and change its NEURON block to

NEURON {

: POINT_PROCESS ExpSyn

POINT_PROCESS ExpSid

RANGE tau, e, i, sid, cid

NONSPECIFIC_CURRENT i

}

and change its PARAMETER block to

PARAMETER {

tau = 0.1 (ms)<1e-9,1e9>

e = 0 (mV)

sid = −1 (1) : synapse id, from cell template

cid = −1 (1) : id of cell to which this synapse is attached

}

(changes indicated in bold monospace). We also copy cell.hoc to a new file called cellid.hoc, then edit cellid.hoc to change each appearance of ExpSyn to ExpSid in the template that defines the B_BallStick class. Below in 4.1.4 Verifying network architecture we will see how to use these changes to discover the architecture of a network after it has been set up.

4.1.2 Creating the cell instances

A first draft of the mkcells ( ) procedure is very similar to what we used for the ring network, with two new statements that associate each cell with a pseudorandom sequence generator.

proc mkcells ( ) {local i localobj cell

cells = new List ( )

ranlist = new List ( )

for i=0, $1-1 {

cell = new B_BallStick ( )

cells.append (cell)

ranlist.append (new RandomStream (i))

}

}

Every time a new cell is created and appended to the cells list, a corresponding object of the RandomStream class is also created and appended to a list called ranlist by the statement ranlist.append (new RandomStream (i)). The file ranstream.hoc, which is loaded near the beginning of the program, defines the RandomStream class plus an integer called random_stream_offset_ as shown here:

random_stream_offset_ = 1000

begintemplate RandomStream

public r, repick, start, stream

external random_stream_offset_

objref r

proc init ( ) {

stream = $1

r = new Random ( )

start ( )

}

func start ( ) {

return r.MCellRan4(stream*random_stream_offset_ + 1)

}

func repick ( ) {

return r.repick ( )

}

endtemplate RandomStream

From this we see that the for i=0, $1-1 { } loop in mkcells ( ) creates a set of RandomStream objects whose MCellRan4 generators have highindex values which differ by unique integer multiples of 1000. To quote from the entry on MCellRan4 in NEURON’s online Programmer’s Reference, “each stream should be statistically independent as long as the highindex values differ by more than the eventual length of the stream”. A difference of 1000 is more than enough for our purpose, because it is only necessary to draw a few samples from each cell’s random stream in order to determine the three cells that drive its excitatory synapse. Note that the argument to r.MCellRan4 is 1 + stream*random_stream_offset_, which is always > 0. This is necessary because an argument of 0 would result in the system automatically choosing a highindex value that depends on the number of instances of the random generator that have been created--an undesirable outcome that would defeat the reproducibility that we are trying to achieve.

Of course we must also initialize the sid and cid variables that belong to the synaptic mechanisms, as discussed in the previous section. This is done by inserting this for loop

for j=0, cell.synlist.count-1 {

cell.synlist.o (j).sid = j

cell.synlist.o (j).cid = i

}

after the cells.append (cell) statement in mkcells ( ). This inner loop iterates over all synapses in a new cell’s synlist to assign the appropriate values to their sids and cids.

4.1.3 Setting up the network connections

The algorithm for setting up this network’s connections can be expressed in pseudocode as

for each cell c in the network {

repeat {

pick a cell s at random

if s is not the same as c {

if s does not already send spikes to the excitatory synapse syn on c {

set up a connection between s and syn

}

}

} until 3 different cells drive syn

}

Note that the network architecture lends itself naturally to a target-centric approach, so the outer loop iterates over target cells. This algorithm is implemented in connectcells ( ), which is excerpted here. Substantive differences from the ring network’s connectcells ( ) are in bold monospace.

proc connectcells ( )

{local i, nsyn, r localobj src, syn, nc, rs, u

// initialize the pseudorandom number generator

mcell_ran4_init (connect_random_low_start_)

u = new Vector (NCELL) // for sampling withoutreplacement

nclist = new List ( )

for i=0, cells.count−1 {

// target synapse is synlist.object (0) on cells.object (i)

syn = cells.object (i).synlist.object (0)

rs = ranlist.object (i) // the corresponding RandomStream

rs.start ( )

rs.r.discunif (0, NCELL−1) // return integer in range 0..NCELL−1

u.fill (0) // u.x[i]==1 means spike source i has already been chosen

nsyn = 0

while (nsyn < C_E) {

r = rs.repick ( ) // no self-connection, & only one connection from any source

if (r != i) if (u.x[r] == 0) {

// set up connection from source to target

src = cells.object (r)

nc = src.connect2target (syn)

nclist.append (nc)

nc.delay = 1

nc.weight = 0.01

u.x[r] = 1

nsyn += 1

}

}

}

}

The outer loop is a for loop that marches through the list of cells, one cell at a time. On each pass, the local object reference syn is made to point to the excitatory synapse of the current target cell, and the u Vector’s elements and the “connection tally” nsyn are all set to 0. The inner loop is a while loop that repeatedly

• picks a new random integer r from the range [0, cells.count − 1] until it finds an r that {is not the index of the current target cell} and {is not the index of a cell that has already been connected to syn}

• creates a new NetCon nc that connects cell r’s spike source to syn, and appends nc to nclist

• sets the corresponding element of the u Vector to 1 and increases the synapse count nsyn by 1

until nsyn equals the desired number of connections C_E.

4.1.4 Verifying network architecture

The network architecture is analyzed by tracenet ( ). This procedure iterates over each NetCon in nclist to retrieve and report the source cell id, target cell id, and target synapse id information for every network connection, using information that was stored in the network’s cells and synaptic mechanisms at the time they were created.

proc tracenet ( ) { local i localobj src, tgt

printf (“source\ttarget\tsynapse\n”)

for i = 0, nclist.count−1 {

src = nclist.o (i).precell

tgt = nclist.o (i).syn

printf (“%d\t%d\t%d\n”, src.synlist.o (0).cid, tgt.cid, tgt.sid)

}

}

For our random net, the output of tracenet ( ) is

source	target	synapse
12	0	0
16	0	0
17	0	0
9	1	0
16	1	0
…
10	18	0
5	19	0
15	19	0
13	19	0

which immediately confirms that

• each target cell receives only three streams of spike events

• all events are delivered to the excitatory synapse

• there is no obvious regularity to the pattern of connectivity

4.1.5 Instrumentation, simulation control, and reporting simulation results

Here the only difference from the code used for the ring network is in the spikerecord ( ) procedure. With the ring network, it was acceptable to let the for loop run from 0 to nclist.count−1 because nclist.count was identical to cells.count. However, the random network has more connections than cells, so this loop must stop at cells.count−1.

4.2 A parallel implementation with reproducible randomness

As with the parallelized ring network model, the code starts by creating an instance of the ParallelContext class and uses curly brackets to suppress printing of unwanted results.

4.2.1 Creating the cell instances

The parallelized mkcells ( ) procedure for the random net is excerpted here, with differences from the serial implementation indicated by bold monospace.

proc mkcells ( ) {local i localobj cell, nc, nil

cells = new List ( )

ranlist = new List ( )

gidvec = new Vector ( )

for (i=pc.id; i < $1; i += pc.nhost) {

cell = new B_BallStick ( )

cells.append (cell)

for j=0, cell.synlist.count−1 {

cell.synlist.o (j).sid = j

cell.synlist.o (j).cid = i

}

pc.set_gid2node (i, pc.id) // associate gid i with this host

nc = cell.connect2target (nil) // attach spike detector to cell

pc.cell (i, nc) // associate gid i with spike detector

ranlist.append (new RandomStream (i)) // ranlist.o (i)corresponds to

// cell associated with gid i

gidvec.append (i)

}

report_gidvecs ( )

}

Most of these differences are similar to what we did with the ring network: a for loop deals out the cells across the hosts, so that each host gets every nhost’th cell, starting from the id of the host and continuing until no more cells are left. Each host has its own cells list to hold the cells that belong to it, plus a ranlist to hold the corresponding RandomStream objects. Two statements have been added so that each host also has a Vector called gidvec. The elements of gidvec are the gids that correspond to the cells in the cells list; in the next section we will see that this simplifies the task of setting up the network connections. Creating a cell involves appending it to the cells list, initializing the sids and cids that belong to its synapses, attaching a spike detector ( NetCon) to it, associating a unique gid with the spike detector and with the host to which the cell belongs, creating a new RandomStream object and appending it to ranlist, and appending the gid to gidvec.

For the sake of debugging and development, we have added a purely diagnostic report_gidvecs ( ) that is called at the end of mkcells ( ):

proc report_gidvecs ( ) { local i, rank

pc.barrier ( ) // wait for all hosts to get to this point

if (pc.id==0) printf (“\ngidvecs on the various hosts\n”)

for rank=0, pc.nhost−1 { // host 0 first, then 1, 2, etc.

if (rank==pc.id) {

print “host “, pc.id

gidvec.printf ( )

}

pc.barrier ( ) // wait for all hosts to get to this point

}

}

This procedure prints out the gids of the cells that are on each host, one host at a time. With four hosts, the distribution of gids is

host 0
0	4	8	12	16
host 1
1	5	9	13	17
host 2
2	6	10	14	18
host 3
3	7	11	15	19

4.2.2 Setting up the network connections

We assembled cells, ranlist, and gidvec in tandem so that the nth element in each of these data structures corresponds to the nth elements in the other two. Consequently we can use the same index i to iterate over each cell on a host plus its associated RandomStream object and gid. This reduces the task of parallelizing connectcells ( ) to making just two changes:

1. The test for “no self-connection and only one connection from any source” changes from

   if (r != i) if (u.x[r] == 0) { }

   to

   if (r != gidvec.x[i]) if (u.x[r] == 0) { }

2. Setting up a connection from source to target changes from

   src = cells.object (r)

   nc = src.connect2target (syn)

   to

   nc = pc.gid_connect (r,syn)

4.2.3 Verifying network architecture

Most of the necessary revisions to tracenet ( ) are required for the sake of orderly execution, and are similar to those that were necessary to parallelize the ring network’s spikeout ( ) procedure: in essence, using ParallelContext barrier ( ) statements and iteration over hosts to reduce a parallel computer to a serial machine. The other change, which is needed because source cells may not be on the same host as their targets, consists of referring to the source cell by its gid, and affects two statements in tracenet ( ) (indicated in bold monospace):

proc tracenet ( ) { local i, rank, srcid localobj tgt

pc.barrier ( ) // wait for all hosts to get to this point

if (pc.id==0) printf (“source\ttarget\tsynapse\n”) // print header once

for rank=0, pc.nhost−1 { // host 0 first, then 1, 2, etc.

if (rank==pc.id) {

for i = 0, nclist.count−1 {

srcid = nclist.o (i).srcgid ( )

tgt = nclist.o (i).syn

printf (“%d\t%d\t%d\n”, srcid, tgt.cid, tgt.sid)

}

}

pc.barrier ( ) // wait for all hosts to get to this point

}

}

On parallel hardware, the revised tracenet ( ) prints out the connectivity information in a different sequence than it does on serial hardware, but sorting reveals that connectivity is identical regardless of the architecture of the computer on which it is run, and also identical to the connectivity produced by the serial implementation of this model.

source	target	synapse
12	0	0
16	0	0
17	0	0
1	4	0
0	4	0
2	4	0
10	8	0
0	8	0
…
12	15	0
5	19	0
15	19	0
13	19	0

4.2.4 Instrumentation, simulation control, and reporting simulation results

These are identical to the parallel implementation of the ring network. The serial implementation’s spike times are reported in a monotonically increasing sequence

time	cell
2.05	0
5.1	16
5.1	8
…
34.1	14
36.675	11

but, as with connectivity, the parallel implementation’s output is grouped according to which cells are on which hosts

time	cell
2.05	0
5.1	4
5.1	8
…
31.4	7
36.675	11

After capturing the spike times of the serial and parallel implementations to files and sorting them, comparison finds no difference in simulation results between the output of the serial or parallel implementations

• $ sort -g serout.txt > sorted_serout.txt

• $ sort -g parout.txt > sorted_parout.txt

• $ cmp sorted_serout.txt sorted_parout.txt

• $

regardless of whether the parallel code is run on serial hardware with or without MPICH2, or on parallel hardware under MPICH2 with any number of hosts.

5. Discussion

This paper shows how to parallelize network models implemented with NEURON in such a way that the resulting code will run and produce identical results on computers with serial or parallel architectures. The strategy we presented uses global identifiers (gids) for two purposes: distributing cells over hosts to achieve load balance, and specifying connections between cells that may exist on different hosts. A single gid was sufficient for both purposes because the example networks had a one-to-one correspondence between each cell and its spike detector. Certain other network architectures (e.g. nets with dendrodendritic synapses) require some cells to have multiple spike detectors. For such cases it may be convenient to use one set of gids strictly for the purpose of assigning cells to hosts, and another set of gids for setting up connections.

We should note that network modeling on parallel hardware raises a whole host of issues. Before ending this discussion, we will briefly address testing and debugging, and performance optimization. There are many others that we must skip entirely, e.g. checkpointing (saving and restoring the state of a model) and how to how to deal with networks that involve gap junctions; for those, interested readers are referred to the Programmer’s Reference at http://www.neuron.yale.edu/neuron/docs/docs.html .

5.1 Testing and debugging

It is essential to verify a model before spending a great deal of time generating and analyzing simulation results. For the simple, small models in this paper, it was sufficient to print out the complete network connectivity, but this becomes impractical with more complex network architectures.

A necessary--perhaps approaching sufficient--requirement for parallel simulation correctness is that the network spiking pattern be independent of the number of processors and the distribution of cells over the processors. Fortunately, quantitative comparison of spiking patterns sorted by time and gid is easy, even for large networks.

The reason for any discrepancy between patterns must be determined. A difference that emerges in the first few hundred milliseconds is almost certainly due to a bug. Differences that arise after a second or more, beginning as shifts of a single time step in the same cell, may be caused by accumulation of roundoff error resulting from multiple spikes being handled at the same time step at the same synapse, but in a different order. Roundoff errors can accumulate more rapidly when individual cells are distributed over several processors.

A good way to diagnose the cause of spiking pattern discrepancies is to start by identifying of the earliest difference, and the gid of the “error cell” in which it appears. The the time t_err question then becomes whether the problem lies in the error cell and/or in the synaptic mechanisms attached to it, or if instead there is something wrong with the network architecture.

In order to distinguish between these alternatives, it is necessary to monitor the stream of events that target the synapses attached to the error cell. This can be done by adding some diagnostic code so that each input event to the error cell triggers printing of the time, weight, source and target gid, and the id of the synapse itself. The diagnostic code includes modifications to the PARAMETER and NET_RECEIVE blocks of synaptic mechanisms, which would look something like this (additions indicated by bold monospace):

PARAMETER {

…

tgtid = −1

synid = −1

xid = −2

}

tgtid and synid are to be filled in with the corresponding gid and synlist index values after each cell and its synapses have been constructed. xid is a GLOBAL variable that must be set to the gid of the error cell, so that only information about the inputs to this particular cell will be printed.

NET_RECEIVE (w, srcgid) {

…

if (tgtid == xid) {

printf (“%g %g %d %d %d\n”, t, w, srcgid, tgtid, synid)

}

}

The value of srcgid would have to be initialized at the hoc level by a statement of the form

NetCon.weight[1] = gid_of_spike_source

after the connection has been set up. However, srcgid can often be omitted because differences in t, w, tgtid, and synid are frequently sufficient to diagnose network connection problems.

With these changes, executing a simulation will generate a printout of all event streams that target the synapses of the error cell. As a practical note, we should mention that there is no need for such diagnostic simulations to continue past t_err.

If the input streams to the error cell depend on the number of processors, then something is wrong with the network architecture or NetCon parameters. If the input streams are identical, the problem is with the error cell’s parameters or state initializations, and it will be necessary to print out and analyze the state variable trajectories leading up to t_err.

5.2 Performance

5.2.1 Basic improvement with parallelization

Using NEURON 5.8, Migliore et al. (2006) found that the speedup from parallelizing large network models was nearly proportional to the number of processors np. That is, as long as each processor had at least ~100 equations to integrate, run time trun (np) ≈ trun (1)/np where trun (1) is the run time with a single processor. While their findings were based primarily on simulations on workstation clusters or parallel supercomputers, they obtained similar results with a PowerMac G5 that had two 2 GHz processors, each with 512 KB L2 cache (see their Figure 4).

To see what kind of speedup an “ordinary user” might experience with a single multicore PC running a more recent version of NEURON, we downloaded their source code from ModelDB (accession number 64229) and ran some tests using NEURON 6.1 on a PC with four processing units (a 3.2GHz x86_64 “dual core dual processor” with 2 MB L2 cache). We found that increasing the number of processors (cores) from 1 to 4 sped up simulations by a factor of 3.8 to 4.8 depending on the particular model (see Table 2).

Table 2.

Speedup with four processors ranged from 3.8 to 4.8. These tests were performed on three of the models used by Migliore et al. (2006): parbulbNet (olfactory bulb (Davison et al., 2003)), pardentategyrus (dentate gyrus of hippocampus (Santhakumar et al., 2005)), and parscalebush (scalable model of layer V of neocortex based on (Bush et al., 1999)), with 500 cells). See text for other details.

	trun for np =
Model	1	4	speedup
parbulbNet	466	108	4.3
pardentategyrus	198	52.4	3.8
parscalebush	145	30.0	4.8

Superlinear speedup as the number of processors increases is a cache effect. While details of cache usage on this particular PC have not been investigated, two likely explanations come to mind for the superlinear speedup seen in these tests. First, it may simply be that each core pair has its own cache, so that running with all four cores makes twice as much cache available. Alternatively, separation of the model into four equal cell groups, which communicate only by spike exchange and therefore can be independently integrated over the minimum delay interval, increases the efficiency of cache usage because each group’s memory is used for many time steps. This motivates us to seek further enhancement of NEURON by implementing the notion of “cell groups,” each of which fits into cache and can be integrated independently.

5.2.2 Performance optimization

In the course of implementing network models on parallel hardware, one must sooner or later address the question of performance optimization. NEURON has several functions that can be used to measure simulation performance, in order to obtain clues for improvements that might be made. Two particularly helpful measures are the processors’ computation times, and the time that is spent on interprocessor communication.

A wide range of computation times suggests load imbalance, with some processors wasting time waiting for others to catch up before the data exchange can occur that is necessary for the solution to advance to the next integration interval. Frequently a very effective way to improve load balance is to use NEURON’s multisplit feature to break one or more cells into subtrees that are distributed over multiple processors.

Another clue is the ratio of communication time to computation time. Communication time becomes significant compared to computation time if a simulation run involves an excessive number of interprocessor data exchanges. This may occur if each processor has only a few equations to integrate, or if the maximum integration interval is very short. The former can be corrected simply by reducing the number of processors that have been allocated for the simulation; this frees up computer resources for other jobs. The latter may be susceptible to techniques for decreasing the overhead associated with spike exchange, e.g. spike exchange compression, which reduces amount of data that must be transferred between processors, and bin queuing, which can be used in fixed time step simulations to handle spike events much more quickly than the default splay tree queue does.

Listings

Listing 1. Definition of the ball and stick model cell class

begintemplate B_BallStick

public is_art

public init, topol, basic_shape, subsets, geom, biophys, geom_nseg, \

biophys_inhomo

public synlist, x, y, z, position, connect2target

public soma, dend

public all

objref synlist

proc init ( ) {

topol ( )

subsets ( )

geom ( )

biophys ( )

geom_nseg ( )

synlist = new List ( )

synapses ( )

x = y = z = 0 // only change via position

}

create soma, dend

proc topol ( ) { local i

connect dend (0), soma (1)

basic_shape ( )

}

proc basic_shape ( ) {

soma {pt3dclear ( ) pt3dadd (0, 0, 0, 1) pt3dadd (15, 0, 0, 1)}

dend {pt3dclear ( ) pt3dadd (15, 0, 0, 1) pt3dadd (105, 0, 0, 1)}

}

objref all

proc subsets ( ) { local i

objref all

all = new SectionList ( )

soma all.append ( )

dend all.append ( )

}

proc geom ( ) {

forsec all { }

soma { /*area = 500 */ L = diam = 12.6157 }

dend { L = 200 diam = 1 }

}

external lambda_f

proc geom_nseg ( ) {

forsec all { nseg = int ((L/(0.1*lambda_f (100))+.9)/2)*2 + 1 }

}

proc biophys ( ) {

forsec all {

Ra = 100

cm = 1

}

soma {

insert hh

gnabar_hh = 0.12

gkbar_hh = 0.036

gl_hh = 0.0003

el_hh = −54.3

}

dend {

insert pas

g_pas = 0.001

e_pas = −65

}

}

proc biophys_inhomo ( ){}

proc position ( ) { local i

soma for i = 0, n3d ( )−1 {

pt3dchange (i, $1−x+x3d (i), $2−y+y3d (i), $3−z+z3d (i), diam3d (i))

}

x = $1 y = $2 z = $3

}

obfunc connect2target ( ) { localobj nc //$o1 target point process, \

optional $o2 returned NetCon

soma nc = new NetCon (&v (1), $o1)

nc.threshold = 10

if (numarg ( ) == 2) { $o2 = nc } // for backward compatibility

return nc

}

objref syn_

proc synapses ( ) {

/* E0 */ dend syn_ = new ExpSyn (0.8) synlist.append (syn_)

syn_.tau = 2

/* I1 */ dend syn_ = new ExpSyn (0.1) synlist.append (syn_)

syn_.tau = 5

syn_.e = −80

}

func is_art ( ) { return 0 }

endtemplate B_BallStick

Listing 2. Serial implementation of the ring network

load_file (“nrngui.hoc”) // load the GUI and standard run libraries

//////////////////////////////////

// Step 1: Define the cell classes

//////////////////////////////////

load_file (“cell.hoc”)

//////////////////////////////////////////////////////////////

// Steps 2 and 3 are to create the cells and connect the cells

//////////////////////////////////////////////////////////////

NCELL = 20 // total number of cells in the ring network

objref cells, nclist // will be Lists that hold all network cell

// and NetCon instances, respectively

proc mkring ( ) {

mkcells ($1) // create the cells

connectcells ( ) // connect them together

}

// creates the cells and appends them to a List called cells

// argument is the number of cells to be created

proc mkcells ( ) {local i localobj cell

cells = new List ( )

for i=0, $1-1 {

cell = new B_BallStick ( )

cells.append (cell)

}

}

// connects the cells

// appends the NetCons to a List called nclist

proc connectcells ( ) {local i localobj src, target, syn, nc

nclist = new List ( )

for i=0, cells.count−1 { // iterating over sources

src = cells.object (i)

target = cells.object ((i+1)%cells.count)

syn = target.synlist.object (0) // the first object in synlist

// is an ExpSyn with e = 0, therefore an excitatory synapse

nc = src.connect2target (syn)

nclist.append (nc)

nc.delay = 1

nc.weight = 0.01

}

}

mkring (NCELL) // go ahead and create the net!

//////////////////////////////////////////////////

// Instrumentation, i.e. stimulation and recording

//////////////////////////////////////////////////

// stim will be an artificial spiking cell that generates a “spike” event

// that is delivered to the first cell in the net by ncstim

// in order to initiate network spiking.

// We won’t bother including this “external stimulus source” or its NetCon

// in the network’s lists of cells or NetCons.

objref stim, ncstim

proc mkstim ( ) {

stim = new NetStim ( )

stim.number = 1

stim.start = 0

ncstim = new NetCon (stim, cells.object (0).synlist.object (0))

ncstim.delay = 0

ncstim.weight = 0.01

}

mkstim ( )

objref tvec, idvec // will be Vectors that record all spike times (tvec)

// and the corresponding id numbers of the cells that spiked (idvec)

proc spikerecord ( ) {local i localobj nc, nil

tvec = new Vector ( )

idvec = new Vector ( )

for i=0, nclist.count−1 {

nc = cells.object (i).connect2target (nil)

nc.record (tvec, idvec, i)

// the Vector will continue to record spike times

// even after the NetCon has been destroyed

}

}

spikerecord ( )

/////////////////////

// Simulation control

/////////////////////

tstop = 100

run ( )

////////////////////////////

// Report simulation results

////////////////////////////

proc spikeout ( ) { local i

printf (“\ntime\t cell\n”)

for i=0, tvec.size−1 {

printf (“%g\t %d\n”, tvec.x[i], idvec.x[i])

}

}

spikeout ( )

quit ( )

Listing 3. Parallel implementation of the ring network

{load_file (“nrngui.hoc”)} // load the GUI and standard run libraries

objref pc pc = new ParallelContext ( )

//////////////////////////////////

// Step 1: Define the cell classes

//////////////////////////////////

{load_file (“cell.hoc”)}

//////////////////////////////////////////////////////////////

// Steps 2 and 3 are to create the cells and connect the cells

//////////////////////////////////////////////////////////////

NCELL = 20 // total number of cells in the ring network

// identical to total number of cells on all machines

objref cells, nclist // cells will be a List that holds

// all instances of network cells that exist on this host

// nclist will hold all NetCon instances that exist on this host

// and connect network spike sources to targets on this host (nclist)

proc mkring ( ) {

mkcells ($1) // create the cells

connectcells ( ) // connect them together

}

// creates the cells and appends them to a List called cells

// argument is the number of cells to be created

proc mkcells ( ) {local i localobj cell, nc, nil

cells = new List ( )

// each host gets every nhost’th cell,

// starting from the id of the host

// and continuing until all cells have been dealt out

for (i=pc.id; i < $1; i += pc.nhost) {

cell = new B_BallStick ( )

cells.append (cell)

pc.set_gid2node (i, pc.id) // associate gid i with this host

nc = cell.connect2target (nil) // attach spike detector to cell

pc.cell (i, nc) // associate gid i with spike detector

}

}

// connects the cells

// appends the NetCons to a List called nclist

proc connectcells ( ) {local i, targid localobj src, target, syn, nc

nclist = new List ( )

for i=0, NCELL − 1 { // iterating over source gids

targid = (i+1)%NCELL

if (!pc.gid_exists (targid)) { continue }

target = pc.gid2cell (targid)

syn = target.synlist.object (0) // the first object in synlist

// is an ExpSyn with e = 0, therefore an excitatory synapse

nc = pc.gid_connect (i, syn)

nclist.append (nc)

nc.delay = 1

nc.weight = 0.01

}

}

mkring (NCELL) // go ahead and create the net!

//////////////////////////////////////////////////

// Instrumentation, i.e. stimulation and recording

//////////////////////////////////////////////////

// stim will be an artificial spiking cell that generates a “spike” event

// that is delivered to the first cell in the net by ncstim

// in order to initiate network spiking.

// We won’t bother including this “external stimulus source” or its NetCon

// in the network’s lists of cells or NetCons.

objref stim, ncstim

proc mkstim ( ) {

// exit if the first cell in the net does not exist on this host

if (!pc.gid_exists (0)) { return }

stim = new NetStim ( )

stim.number = 1

stim.start = 0

ncstim = new NetCon (stim, pc.gid2cell (0).synlist.object (0))

ncstim.delay = 0

ncstim.weight = 0.01

}

mkstim ( )

objref tvec, idvec // will be Vectors that record all spike times (tvec)

// and the corresponding id numbers of the cells that spiked (idvec)

proc spikerecord ( ) {local i localobj nc, nil

tvec = new Vector ( )

idvec = new Vector ( )

for i=0, cells.count−1 {

nc = cells.object (i).connect2target (nil)

nc.record (tvec, idvec, nc.srcgid)

// the Vector will continue to record spike times

// even after the NetCon has been destroyed

}

}

spikerecord ( )

/////////////////////

//Simulation control

/////////////////////

tstop = 100

{pc.set_maxstep (10)}

stdinit ( )

{pc.psolve (tstop)}

////////////////////////////

// Report simulation results

////////////////////////////

proc spikeout ( ) { local i, rank

pc.barrier ( ) // wait for all hosts to get to this point

if (pc.id==0) printf (“\ntime\t cell\n”) // print header once

for rank=0, pc.nhost−1 { // host 0 first, then 1, 2, etc.

if (rank==pc.id) {

for i=0, tvec.size−1 {

printf (“%g\t %d\n”, tvec.x[i], idvec.x[i])

}

}

pc.barrier ( ) // wait for all hosts to get to this point

}

}

spikeout ( )

{pc.runworker ( )}

{pc.done ( )}

quit ( )

Listing 4. Serial implementation of the network with random connectivity

{load_file (“nrngui.hoc”)} // load the GUI and standard run libraries

//////////////////////////////////

// Step 1: Define the cell classes

//////////////////////////////////

{load_file (“cellid.hoc”)}

{load_file (“ranstream.hoc”)} // to give each cell its own sequence generator

//////////////////////////////////////////////////////////////

// Steps 2 and 3 are to create the cells and connect the cells

//////////////////////////////////////////////////////////////

NCELL = 20 // total number of cells in the ring network

C_E = 3 // # of excitatory connections received by each cell

// 2 gives more sustained activity!

connect_random_low_start_ = 1 // low seed for mcell_ran4_init ( )

objref cells, nclist // will be Lists that hold all network cell

// and NetCon instances, respectively

objref ranlist // for RandomStreams, one per cell

proc mknet ( ) {

mkcells ($1) // create the cells

connectcells ( ) // connect them together

}

// creates the cells and appends them to a List called cells

// argument is the number of cells to be created

proc mkcells ( ) {local i,j localobj cell

cells = new List ( )

ranlist = new List ( )

for i=0, $1-1 {

cell = new B_BallStick ( )

for j=0, cell.synlist.count−1 {

cell.synlist.o (j).cid = i

cell.synlist.o (j).sid = j

}

cells.append (cell)

ranlist.append (new RandomStream (i))

}

}

// connects the cells

// appends the NetCons to a List called nclist

// each target will receive exactly C_E unique non-self random connections

proc connectcells ( ) {local i, nsyn, r localobj src, syn, nc, rs, u

// initialize the pseudorandom number generator

mcell_ran4_init (connect_random_low_start_)

u = new Vector (NCELL) // for sampling without replacement

nclist = new List ( )

for i=0, cells.count−1 {

// target synapse is synlist.object (0) on cells.object (i)

syn = cells.object (i).synlist.object (0)

rs = ranlist.object (i) // the corresponding RandomStream

rs.start ( )

rs.r.discunif (0, NCELL−1) // return integer in range 0..NCELL−1

u.fill (0) // u.x[i]==1 means spike source i has already been chosen

nsyn = 0

while (nsyn < C_E) {

r = rs.repick ( )

// no self-connection, & only one connection from any source

if (r != i) if (u.x[r] == 0) {

// set up connection from source to target

src = cells.object (r)

nc = src.connect2target (syn)

nclist.append (nc)

nc.delay = 1

nc.weight = 0.01

u.x[r] = 1

nsyn += 1

}

}

}

}

mknet (NCELL) // go ahead and create the net!

//////////////////////////

// Report net architecture

//////////////////////////

proc tracenet ( ) { local i localobj src, tgt

printf (“source\ttarget\tsynapse\n”)

for i = 0, nclist.count−1 {

src = nclist.o (i).precell

tgt = nclist.o (i).syn

printf (“%d\t%d\t%d\n”, src.synlist.o (0).cid, tgt.cid, tgt.sid)

}

}

tracenet ( )

//////////////////////////////////////////////////

// Instrumentation, i.e. stimulation and recording

//////////////////////////////////////////////////

// stim will be an artificial spiking cell that generates a “spike” event

// that is delivered to the first cell in the net by ncstim

// in order to initiate network spiking.

// We won’t bother including this “external stimulus source” or its NetCon

// in the network’s lists of cells or NetCons.

objref stim, ncstim

proc mkstim ( ) {

stim = new NetStim ( )

stim.number = 1

stim.start = 0

ncstim = new NetCon (stim, cells.object (0).synlist.object (0))

ncstim.delay = 0 ncstim.weight = 0.01

}

mkstim ( )

objref tvec, idvec // will be Vectors that record all spike times (tvec)

// and the corresponding id numbers of the cells that spiked (idvec)

proc spikerecord ( ) {local i localobj nc, nil

tvec = new Vector ( )

idvec = new Vector ( )

// the next line causes problems if there are more NetCons than cells

// for i=0, nclist.count−1 {

for i=0, cells.count−1 {

nc = cells.object (i).connect2target (nil)

nc.record (tvec, idvec, i)

// the Vector will continue to record spike times

// even after the NetCon has been destroyed

}

}

spikerecord ( )

/////////////////////

// Simulation control

/////////////////////

tstop = 100

run ( )

////////////////////////////

// Report simulation results

////////////////////////////

proc spikeout ( ) { local i

printf (“\ntime\t cell\n”)

for i=0, tvec.size−1 {

printf (“%g\t %d\n”, tvec.x[i], idvec.x[i])

}

}

spikeout ( )

quit ( )

Listing 5. Parallel implementation of the network with random connnectivity

{load_file (“nrngui.hoc”)} // load the GUI and standard run libraries

objref pc pc = new ParallelContext ( )

//////////////////////////////////

// Step 1: Define the cell classes

//////////////////////////////////

{load_file (“cellid.hoc”)}

load_file (“ranstream.hoc”) // to give each cell its own sequence generator

//////////////////////////////////////////////////////////////

// Steps 2 and 3 are to create the cells and connect the cells

//////////////////////////////////////////////////////////////

NCELL = 20 // total number of cells in the ring network

// identical to total number of cells on all machines

C_E = 3 // # of excitatory connections received by each cell

// 2 gives more sustained activity!

connect_random_low_start_ = 1 // low seed for mcell_ran4_init ( )

objref cells, nclist // cells will be a List that holds

// all instances of network cells that exist on this host

// nclist will hold all NetCon instances that exist on this host

// and connect network spike sources to targets on this host (nclist) objref ranlist // for RandomStreams on this host

proc mknet ( ) {

mkcells ($1) // create the cells

connectcells ( ) // connect them together

}

objref gidvec // to associate gid and position in cells List

// useful for setting up connections and reporting connectivity

// creates the cells and appends them to a List called cells

// argument is the number of cells to be created

proc mkcells ( ) {local i localobj cell, nc, nil

cells = new List ( )

ranlist = new List ( )

gidvec = new Vector ( )

// each host gets every nhost’th cell,

// starting from the id of the host

// and continuing until no more cells are left

for (i=pc.id; i < $1; i += pc.nhost) {

cell = new B_BallStick ( )

for j=0, cell.synlist.count−1 {

cell.synlist.o (j).cid = i

cell.synlist.o (j).sid = j

}

cells.append (cell)

pc.set_gid2node (i, pc.id) // associate gid i with this host

nc = cell.connect2target (nil) // attach spike detector to cell

pc.cell (i, nc) // associate gid i with spike detector

ranlist.append (new RandomStream (i)) // ranlist.o (i) corresponds to

// cell associated with gid i

gidvec.append (i)

}

report_gidvecs ( )

}

// reports distribution of cells across hosts

proc report_gidvecs ( ) { local i, rank

pc.barrier ( ) // wait for all hosts to get to this point

if (pc.id==0) printf (“\ngidvecs on the various hosts\n”)

for rank=0, pc.nhost−1 { // host 0 first, then 1, 2, etc.

if (rank==pc.id) {

print “host “, pc.id

gidvec.printf ( )

}

pc.barrier ( ) // wait for all hosts to get to this point

}

}

// connects the cells

// appends the NetCons to a List called nclist

proc connectcells ( ) {local i, nsyn, r localobj syn, nc, rs, u

// initialize the pseudorandom number generator

mcell_ran4_init (connect_random_low_start_)

u = new Vector (NCELL) // for sampling without replacement

nclist = new List ( )

for i=0, cells.count−1 {

// target synapse is synlist.object (0) on cells.object (i)

syn = cells.object (i).synlist.object (0)

rs = ranlist.object (i) // the RandomStream that corresponds to

// cells.object (i)

rs.start ( )

rs.r.discunif (0, NCELL−1) // return integer in range 0..NCELL−1

u.fill (0) // u.x[i]==1 means spike source i has already been chosen

nsyn = 0

while (nsyn < C_E) {

r = rs.repick ( )

// no self-connection, & only one connection from any source

if (r != gidvec.x[i]) if (u.x[r] == 0) {

// set up connection from source to target

nc = pc.gid_connect (r, syn)

nclist.append (nc)

nc.delay = 1

nc.weight = 0.01

u.x[r] = 1

nsyn += 1

}

}

}

}

mknet (NCELL) // go ahead and create the net!

//////////////////////////

// Report net architecture

//////////////////////////

proc tracenet ( ) { local i, srcid localobj src, tgt, nil

pc.barrier ( ) // wait for all hosts to get to this point

if (pc.id==0) printf (“source\ttarget\tsynapse\n”) // print header once

for rank=0, pc.nhost−1 { // host 0 first, then 1, 2, etc.

if (rank==pc.id) {

for i = 0, nclist.count−1 {

srcid = nclist.o (i).srcgid ( )

tgt = nclist.o (i).syn

printf (“%d\t%d\t%d\n”, srcid, tgt.cid, tgt.sid)

}

}

pc.barrier ( ) // wait for all hosts to get to this point

}

}

tracenet ( )

//////////////////////////////////////////////////

// Instrumentation, i.e. stimulation and recording

//////////////////////////////////////////////////

// stim will be an artificial spiking cell that generates a “spike” event

// that is delivered to the first cell in the net by ncstim

// in order to initiate network spiking.

// We won’t bother including this “external stimulus source” or its NetCon

// in the network’s lists of cells or NetCons.

objref stim, ncstim

proc mkstim ( ) {

// exit if the first cell in the net does not exist on this host

if (!pc.gid_exists (0)) { return }

stim = new NetStim ( )

stim.number = 1

stim.start = 0

ncstim = new NetCon (stim, pc.gid2cell (0).synlist.object (0))

ncstim.delay = 0

ncstim.weight = 0.01

}

mkstim ( )

objref tvec, idvec // will be Vectors that record all spike times (tvec)

// and the corresponding id numbers of the cells that spiked (idvec)

proc spikerecord ( ) {local i localobj nc, nil

tvec = new Vector ( )

idvec = new Vector ( )

for i=0, cells.count−1 {

nc = cells.object (i).connect2target (nil)

nc.record (tvec, idvec, nc.srcgid)

// the Vector will continue to record spike times

// even after the NetCon has been destroyed

}

}

spikerecord ( )

/////////////////////

// Simulation control

/////////////////////

tstop = 100

{pc.set_maxstep (10)}

stdinit ( )

{pc.psolve (tstop)}

////////////////////////////

// Report simulation results

////////////////////////////

proc spikeout ( ) { local i, rank

pc.barrier ( ) // wait for all hosts to get to this point

if (pc.id==0) printf (“\ntime\t cell\n”) // print header once

for rank=0, pc.nhost−1 { // host 0 first, then 1, 2, etc.

if (rank==pc.id) {

for i=0, tvec.size−1 {

printf (“%g\t %d\n”, tvec.x[i], idvec.x[i])

}

}

pc.barrier ( ) // wait for all hosts to get to this point

}

}

spikeout ( )

{pc.runworker ( )}

{pc.done ( )}

quit ( )