A transient expansion of the native state precedes aggregation of recombinant human interferon-γ

Abstract

Aggregation of proteins, even under conditions favoring the native state, is a ubiquitous problem in biotechnology and biomedical engineering. Providing a mechanistic basis for the pathways that lead to aggregation should allow development of rational approaches for its prevention. We have chosen recombinant human interferon-γ (rhIFN-γ) as a model protein for a mechanistic study of aggregation. In the presence of 0.9 M guanidinium hydrochloride, rhIFN-γ aggregates with first order kinetics, a process that is inhibited by addition of sucrose. We describe a pathway that accounts for both the observed first-order aggregation of rhIFN-γ and the effect of sucrose. In this pathway, aggregation proceeds through a transient expansion of the native state. Sucrose shifts the equilibrium within the ensemble of rhIFN-γ native conformations to favor the most compact native species over more expanded ones, thus stabilizing rhIFN-γ against aggregation. This phenomenon is attributed to the preferential exclusion of sucrose from the protein surface. In addition, kinetic analysis combined with solution thermodynamics shows that only a small (9%) expansion surface area is needed to form the transient native state that precedes aggregation. The approaches used here link thermodynamics and aggregation kinetics to provide a powerful tool for understanding both the pathway of protein aggregation and the rational use of excipients to inhibit the process.

Formation of biologically inactive proteins by aggregation is a problem of considerable importance in many disciplines (1–3). For example, protein aggregates can be formed in vivo and in vitro during folding of nascent polypeptide chains, eliminating or reducing the protein’s biological function (4, 5). Misfolded protein aggregates often can be observed as inclusion bodies (6, 7) and are implicated in amyloid deposition in vivo (8). In the biotechnology industry, protein aggregation is encountered routinely during purification, refolding, sterilization, shipping, and storage processes because of the presence of chemical, physical, and thermal stresses (9).

In addition to significant losses in protein activity, clinical dangers result from parenteral administration of aggregated material (10). Even aggregation levels as low as 1% over a 2-year shelf life can render a product clinically unacceptable. Thus, proteins must be protected against even relatively mild stresses by the addition of proper excipients. Rational choice of these excipients requires insight into the mechanism of aggregation.

The detailed mechanism of protein aggregation is still unclear. Usually, the aggregation pathway is modeled as shown in Scheme 1 by using the Lumry–Erying framework (11, 12). The model involves a first-order reversible unfolding of the protein and subsequent aggregation of nonnative species in a higher order process (2, 11–13):

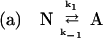Scheme 1

In this scheme, N refers to native protein, and A refers to an intermediate conformational state preceding aggregation. A_m refers to an aggregated form composed of m protein molecules, which is thought to form because of association between hydrophobic residues exposed in A. The rate constants for each reaction, i, are represented by k_i.

This model has been applied to a number of aggregating systems (11, 12, 14). If the first step is in equilibrium, the model predicts that aggregation should follow second- or higher-order kinetics. However, we have observed that mild guanidine hydrochloride (GdnHCl) stress [e.g., 1 M, a concentration at which, at low protein concentration, native protein can be recovered during refolding from a denatured state at 4M GdnHCl (15)] induces aggregation of recombinant human interferon-gamma (rhIFN-γ), which follows first-order kinetics (16). The aggregates formed under these conditions contain a substantial fraction of nonnative intermolecular β-sheet, but retain ≈1/3 of the original native α-helix content. Aggregates with similar secondary structure were formed under other, mildly stressful conditions, such as in pH 2.0 buffer and in the presence of 0.3 M sodium thiocyanate (15). In contrast, precipitates formed by salting out of the protein in 25 wt/vol% poly(ethylene glycol) retain full native secondary structure (16).

In the current study, we show that GdnHCl-induced aggregation of rhIFN-γ is inhibited in the presence of sucrose. Thus, one purpose of the current study is to develop a model to account for these observations. Furthermore, the nature of the intermediate state preceding aggregation has been the subject of much investigation. A number of intermediate conformations have been hypothesized, ranging from transiently expanded species within the native-state ensemble to a molten-globule structure to a fully unfolded molecule (2, 3, 12, 17–19). Ultimately, the nature of the intermediate state is key to understanding the aggregation pathway. Such insight is fundamentally important, and, in practical terms, the aggregation mechanism must be understood to provide a rational basis for protein stabilization. Thus, a second purpose of the current study is to quantify the magnitude of any conformational changes within the native state ensemble that lead to aggregation. These goals are accomplished by taking advantage of the well known thermodynamic effect of sucrose on protein state equilibria. We apply the preferential exclusion mechanism elucidated by Timasheff and colleagues (20) to understand how sucrose slows the rate of rhIFN-γ aggregation.

EXPERIMENTAL PROTOCOL

Protein and Reagents.

Recombinant DNA derived rhIFN-γ was purified from Escherichia coli extracts at Genentech, and buffer was exchanged into 5 mM sodium succinate (pH 5.0) and was stored at 4°C until use. Purity was checked by size exclusion chromatography on a Tosohaas (Montgomeryville, PA) TSK-GEL G2000SW_XL column before all experiments and was >99%. Chemicals were purchased from Sigma and were of reagent grade or higher quality. High purity sucrose was purchased from Pfanstiehl Chemicals.

Aggregation Reaction.

Equal volumes of 50 mg/ml protein in 5 mM sodium succinate (pH 5.0) and stock solutions of GdnHCl/sucrose, preequilibrated at 25°C, were pipetted into a 1-ml polypropylene Eppendorf tube and were vortexed gently to initiate the aggregation reaction at the desired GdnHCl/sucrose final concentration. The reaction was quenched at various time points by removing 8-μl aliquots from the reaction container and pipetting into 192 μl of ice-cold 5 mM sodium succinate (pH 5.0) followed by gentle vortexing. Aggregated protein was removed by centrifugation, and the supernatant was assayed by size exclusion chromatography.

Size Exclusion Chromatography.

Loss of native rhIFN-γ was determined at various time points during the aggregation reactions. Size exclusion chromatography was performed by injecting 20 μl of the above-mentioned supernatant onto a Tosohaas TSK-GEL G2000SW_XL column. The mobile phase was 1.2 M KCl delivered at a rate of 0.8 ml/min. The column eluate was monitored at 214 nm. Peak heights were taken as a measure of native protein concentration, based on our unpublished results.

Dynamic Light Scattering.

The hydrodynamic radius of rhIFN-γ was measured by dynamic light scattering on a DynaPro-801 (Protein Solutions, Charlottesville, VA) molecular size detector, with appropriate viscosity and refractive index corrections (21).

Surface Area Calculations.

The solvent accessible surfaces were calculated by using programs areaimol and resarea of the CCP4 package, using a 1.4-A probe (22). Lack of a high resolution structure of the recombinant human isoform necessitated use of the bovine isoform of IFN-γ in the accessible surface area calculations.

RESULTS AND DISCUSSION

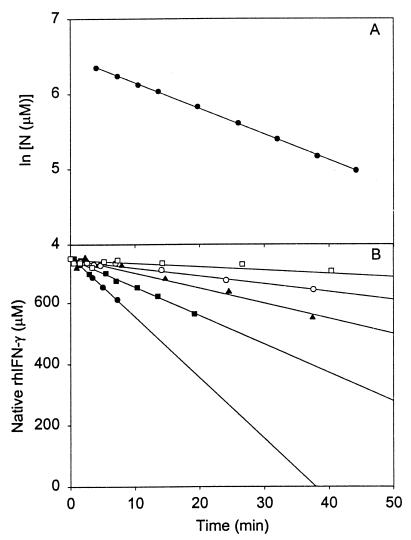
rhIFN-γ was chosen as a model for studying protein aggregation because of its propensity to aggregate quickly (16) under mildly stressful conditions. For example, in the presence of 0.9 M GdnHCl, aggregation of 25 mg/ml rhIFN-γ proceeds rapidly. Surprisingly, the aggregation process follows first-order kinetics (16) even at high conversions (up to 85% of the protein aggregated), based on the linearity of a plot of ln(N) vs. time (Fig. 1A). This unexpected result for a bimolecular reaction shows that the process is rate-limited not by protein–protein collisions but, rather, by a preceding unimolecular step.

Figure 1.

Rate of loss of native rhIFN-γ because of aggregation in 0.9 M GdnHCl. (A) ln [N] vs. time in the absence of sucrose. (B) •, no sucrose; ■, 0.25 M sucrose; ▴, 0.5 M sucrose; ○, 0.75 M sucrose; □, 1 M sucrose. Lines indicate linear regression at each sucrose concentration, and the values of the slopes are given in Table 1 for initial rates.

Sucrose causes the initial rate of loss of N to decrease from 20.9 to 1.13 μM/min in 0 and 1 M sucrose, respectively, a factor of 18 reduction in aggregation rate (Fig. 1B; Table 1). To gain insight into the mechanism of sucrose inhibition of aggregation, we first consider the thermodynamic nature of sucrose–protein interactions, as explained by the Timasheff mechanism of preferential exclusion of sucrose from the protein surface (20). Lee and Timasheff found that sucrose is excluded preferentially from the surface of proteins, which increases protein chemical potential (23). The degree of preferential exclusion and the increase in chemical potential are directly proportional to the surface area of protein exposed to solvent. By the LeChatelier Principle, the system will minimize the thermodynamically unfavorable effect of preferential sucrose exclusion by favoring the state with the smallest surface area. This corresponding shift in the equilibrium toward compact species can be explained by the Wyman relationship between ligand binding and state equilibria (24).

Table 1.

Effect of sucrose on the aggregation rate of rhIFN-γ

Sucrose, M	v, μM/min	Surface tension, mN/m*
0.00	20.9	71.24
0.25	9.31	72.05
0.50	4.84	72.82
0.75	2.42	73.60
1.00	1.13	74.30

^*Values obtained from ref. 39. 

Experimentally, it has been shown that sucrose is excluded from the surface of all proteins studied to date (20, 23, 25, 26). Formally, the extent of exclusion of sucrose from a protein can be described by the Gibbs adsorption isotherm (23, 27, 28):

1

In this relation, (∂m₃/∂m₂)_T, is the preferential interaction parameter. A positive value indicates an excess of the solute around the protein (binding) whereas a negative value indicates a deficiency (exclusion) relative to the bulk solution. Interaction parameters measured to date for sucrose with proteins are all negative, indicative of preferential exclusion of sucrose from the protein’s surface. The notation follows that of Scatchard (29) and Stockmayer (30) in which component 1 indicates water, component 2 indicates protein, and component 3 indicates the solute, sucrose. m_i is the molal concentration of component i. On the right hand side of Eq. 1, s is the protein surface area, and a₃ is the activity (approximated by concentration) of the solute. σ is the surface tension of the protein–water interface. By the equality in Eq. 1, preferential interactions of solutes with protein surfaces necessarily result in surface tension increments at protein surfaces. In the particular case of sucrose–protein interactions, σ can be approximated by the surface tension of the air–water interface of a given sucrose solution in the absence of protein (23). By using these approximations, preferential interaction parameters for a number of sucrose–protein systems calculated from Eq. 1 are in agreement with experimentally measured values (23, 25).

Eq. 1 can be applied to the native state ensemble, in which the most compact species, N, is in equilibrium with another native conformation, N*, which has a larger surface area, through the Wyman linkage relation (24):

2

Δv₃ is the difference in binding (or exclusion) of a solute between N and N*, which exist in equilibrium (20):

According to Eq. 1, increasing the protein surface area, s, increases the degree of preferential exclusion of sucrose. Thus, by Eq. 2, in the presence of sucrose, the ensemble equilibrium is shifted to favor the species with the smallest surface area (N). This has been shown to hold not only for the equilibrium between N and the fully unfolded state (23) but also for that between N and expanded states (e.g., N*) arising from protein conformational fluctuations within the native state ensemble (25, 31).

The shifting of equilibria by preferential exclusion of sucrose can be combined with kinetic analysis to explain how sucrose inhibits the first-order aggregation process of rhIFN-γ observed in this study. To do so, it is necessary to modify Scheme 1 as follows:

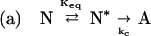Scheme 2

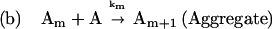In this scheme, N* is a transiently expanded conformational species within the native ensemble, which is in equilibrium with N. K_eq is an equilibrium constant for the reaction N to N*. N^* is irreversibly transformed to an aggregation-competent state A. State A undergoes further reaction to form insoluble aggregates A_m composed of m monomer units. The irreversible, unimolecular isomerization reaction of N^* to A is the rate-limiting step in the formation of aggregates and has a rate constant denoted as k_c. For unimolecular isomerizations, k_c is not expected to depend on solvent viscosity. Furthermore, because the N* to A reaction is irreversible, k_c is not expected to be affected by sucrose-induced changes in ΔG_N*−A.

Modification of the Lumry–Eyring model (Scheme 1) to include the transiently expanded conformation, N*, in the reaction pathway is consistent with several observations regarding the aggregation of rhIFN-γ. First, the aggregation kinetics are irreversible and first-order, even to 85% aggregation (Fig. 1A). In contrast, by Scheme 1, higher order aggregation processes would be expected. In addition, intermediates are so transient as to be undetectable by our methods, consistent with the assumption that the formation of aggregates from A is not rate limiting. Of importance, the inhibition of aggregation by sucrose (Fig. 1B) is explained by the shifting of the first equilibrium step in the presence of sucrose to favor N over N*.

Based on the known thermodynamic interaction of sucrose with protein surfaces, we can take our mechanistic insight a step further by quantifying the partial molar volume difference between N and N*. Following Scheme 2, the significant rate processes for formation of A are (32)

3a

or, alternatively,

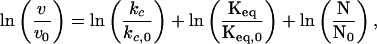3b

where the terms in the numerators indicate values in the presence sucrose, and the terms in the denominators are taken in the absence of sucrose, indicated by the subscript 0. At low conversions (i.e., initial rates) and identical initial concentrations of N, and assuming k_c is independent of solvent viscosity and ΔG_N*−A as described above, Eq. 3b reduces to

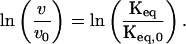4

This relationship provides the critical link between the irreversible loss of N and the equilibrium between N and N*. In turn, thermodynamic theory can be applied to calculate the surface area change between N and N* as follows. First, addition of sucrose increases surface tension. Surface tension affects the equilibrium constant (23):

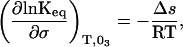5

and then, by incorporation of Eq. 4, Eq. 5 becomes

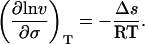6

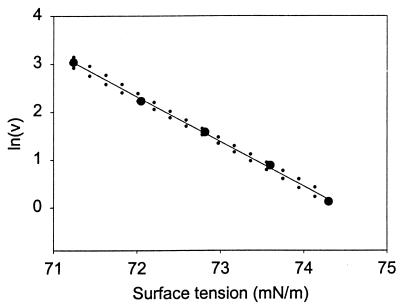
Thus, the slope of ln v vs. σ gives the change in surface area (−Δs/RT) for a protein going from N to N*, when this transition precedes an irreversible first-order process, N* → A. Plotting the results listed in Table 1 in this fashion (Fig. 2) gives a constant negative slope equal to 935 ± 67 m/N (95% confidence interval). This is equivalent to a surface area increase of 3.85 ± 0.28 nm²/molecule at 25°C. Estimating the hydrodynamic radius of rhIFN-γ to be 1.85 nm (based on dynamic light scattering measurements), this surface area increase corresponds to an increase in hydrodynamic diameter from 3.70 to 3.86 nm, a 4% increase in diameter, a 9% increase in surface area, or, equivalently, a 14% increase in volume.

Figure 2.

Effect of surface tension on the rate of rhIFN-γ aggregation. The slope is equivalent to −Δs/RT, which is 935 ± 67 m/N (95% confidence interval). Confidence intervals (95%) on the slope are indicated by dotted lines.

The magnitude of the expansion can be compared readily with that calculated from an independent model developed by Winzor and colleagues (14, 33). Winzor and colleagues modeled sucrose effects on equilibrium processes by using a statistical thermodynamic approach, which can be described as follows. In Scheme 2, an equilibrium constant is defined in terms of thermodynamic activities rather than in concentration terms: K_eq^sm = a_N*/a_N, where sm refers to the statistical mechanical model. Activities vary directly with sucrose concentration based on a solid sphere model for volumes occupied by sucrose and the protein (a truncated form of the statistical mechanical definition of activity) (14, 34–36). This results in the following:

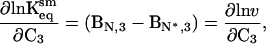7

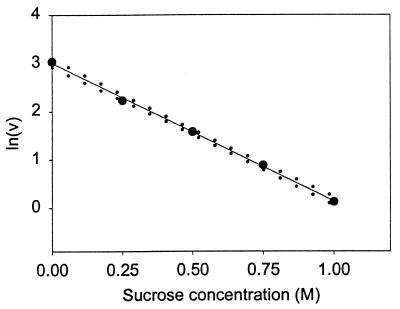
which is an alternative form of Eq. 6 in which B_i,3 is the second virial coefficient, or the covolume occupied by component i (N or N*) and component 3, and C₃ is the molar concentration of sucrose. The slope of a plot of ln v vs. C₃ will give the difference in covolumes (sucrose + protein) between N and N*. The results of this treatment for the aggregation of rhIFN-γ are presented in Fig. 3 and give a covolume expansion of 2.87 ± 0.17 liters/mol (95% confidence interval). The volume occupied by sucrose can be accounted for in the expression (37)

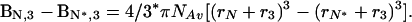8

Substituting r₃ = 0.34 nm [effective thermodynamic radius of sucrose (37)], r_N = 1.85 nm (hydrodynamic radius from dynamic light scattering measurements), and Avagadro’s number, N_Av, into Eq. 8 gives a diameter increase from 3.70 nm (2r_N) to an expanded diameter of 3.85 nm. This is in remarkable agreement with the surface tension treatment, which predicted an expansion to a diameter of 3.86 nm.

Figure 3.

Effect of sucrose concentration on the rate of rhIFN-γ aggregation. The slope is equivalent to the difference in covolumes of N-sucrose, and N*-sucrose, which is 2.87 ± 0.17 liters/mol (95% confidence interval). Confidence intervals (95%) on the slope are indicated by dotted lines.

Because native rhIFN-γ exists as a dimer (K_d is <50 nM) (38), it might be expected that the surface area increase preceding aggregation may involve a dimer–monomer transition. However, based on the large apparent surface area of the dimer interface (35 to 40% of the total surface area of the dimer), it appears that the dimeric nature of the protein remains intact before aggregation.

CONCLUSIONS

Sucrose stabilizes rhIFN-γ against GdnHCl-induced aggregation by shifting the equilibrium within the native state ensemble toward the most compact species, N, over a transiently expanded native species, N*. This phenomenon can be attributed to the preferential exclusion of sucrose from the protein surface, which creates a system that favors the most compact conformation of the protein. Furthermore, the model developed here (Scheme 2) accounts for the observed first-order aggregation kinetics for rhIFN-γ. In addition, thermodynamic analysis applied to our model documents that only a relatively small (9%) expansion of the native state surface area is needed to form the intermediate state preceding aggregation. Finally, in addition to first-order protein aggregation processes, this thermodynamic analysis should be applicable to other first-order protein degradation processes that are accompanied by a volume change. An example is the oxidation of interior methionine residues that require protein conformational change for reaction.

ABBREVIATIONS

GdnHCl

guanidine hydrochloride

rhIFN-γ

recombinant human interferon-γ