Quantitative insight into proliferation and differentiation of oligodendrocyte type 2 astrocyte progenitor cells in vitro

Abstract

As part of our attempts at understanding fundamental principles that underlie the generation of nondividing terminally differentiated progeny from dividing precursor cells, we have developed approaches to a quantitative analysis of proliferation and differentiation of oligodendrocyte type 2 astrocyte (O-2A) progenitor cells at the clonal level. Owing to extensive previous studies of clonal differentiation in this lineage, O-2A progenitor cells represent an excellent system for such an analysis. Previous studies have resulted in two competing hypotheses; one of them suggests that progenitor cell differentiation is symmetric, the other hypothesis introduces an asymmetric process of differentiation. We propose a general model that incorporates both such extreme hypotheses as special cases. Our analysis of experimental data has shown, however, that neither of these extreme cases completely explains the observed kinetics of O-2A progenitor cell proliferation and oligodendrocyte generation in vitro. Instead, our results indicate that O-2A progenitor cells become competent for differentiation after they complete a certain number of critical mitotic cycles that represent a period of symmetric development. This number varies from clone to clone and may be thought of as a random variable; its probability distribution was estimated from experimental data. Those O-2A cells that have undergone the critical divisions then may differentiate into an oligodendrocyte in each of the subsequent mitotic cycles with a certain probability, thereby exhibiting the asymmetric type of differentiation.

Developing a quantitative analysis of the process(s) through which precursor cells generate appropriate numbers of differentiated progeny represents a major challenge in theoretical biology. This challenge has multiple components and includes both cellular biological and mathematical elements. Although the narrative description of biological events is required to generate hypotheses, the tools of quantitative analysis are indispensable for testing alternative descriptive hypotheses. Mathematical analyses have proven of great benefit to our understanding of such diverse topics as prey–predator interactions, population genetics, DNA sequence analysis, and kinetics of cell proliferation in normal and neoplastic tissues. Although there have been several attempts to analyze temporally regulated differentiation of cells, there remains a lack of models that have been tested quantitatively against experimental data. Moreover, there are relatively few cellular systems for which the analysis of differentiation has been carried out in such a detailed manner as to support extensive efforts to develop quantitative insights into the underlying processes.

One of the problems in developing a quantitative analysis of differentiation is that although most analyses of this process are carried out at the level of populations, actual differentiation events occur at the level of individual cells that frequently share a clonal relationship with each other. The importance of clones in generating particular cell types is seen in many instances, from the formation of crypts in the colon and intestine, and differentiation of clonally related cells in the development of a functioning immune system to the lineage segregation observed at the clonal level in development of the central nervous system. Obtaining reliable data at the clonal level has been a difficult task, however, and such data is available for only a small number of instances. Thus, a quantitative analysis that satisfactorily describes the behavior of individual cells, or of clones of related cells, has not yet been achieved.

One of the differentiation processes that has been studied extensively at the clonal level is that of the generation of oligodendrocytes, the myelin-forming cells of the central nervous system (CNS), from dividing oligodendrocyte type 2 astrocyte (O-2A) progenitor cells. These bipotential precursor cells can be purified from optic nerves and other regions of the embryonic, postnatal, and adult rat CNS. Conditions that promote their division and differentiation in vitro are well understood and have been applied to analysis of the behavior of individual clones of cells (1–4). For example, a number of studies have examined clonal differentiation of O-2A progenitor cells growing on the surfaces of, or in medium conditioned by, type 1 astrocytes (a distinct glial cell population derived from a separate lineage), or in chemically defined medium supplemented with platelet-derived growth factor (the major O-2A progenitor cell mitogen secreted by type 1 astrocytes).

The outcomes of the analyses of differentiation of O-2A progenitor cells at the clonal level have been interpreted as supporting two competing hypotheses. In initial studies, it was observed that clonally related O-2A progenitor cells tended to undergo synchronous and symmetric differentiation after a limited number of cell divisions when induced to divide in the presence of type 1 astrocytes or platelet-derived growth factor (1, 2). (In the language of the present paper, symmetric differentiation refers to a situation where progenitor cells produce two further progenitor cells for a certain number of cycles and then in the next cycle each cell undergoes differentiation with probability 1, being subsequently nonproliferative.) Observations from these initial studies were interpreted to suggest that the timing of oligodendrocyte generation was modulated by a cell-intrinsic biological clock, which, in some unknown manner, promoted symmetric division and differentiation within clonal families (1, 2). This concept has been referred to as a biological clock model for controlling temporally regulated differentiation.

More recently (4), it was found that clonal differentiation is considerably more complex than originally envisaged and has at least three distinct components. The first component causes oligodendrocytes to first appear within clonal families at a developmentally appropriate time. This component has both deterministic and stochastic features, in that while the time of first oligodendrocyte appearance is highly predictable, the percentage of cells becoming oligodendrocytes within any individual clone can range from <1% up to 80% (in clones of >15 cells) and even up to 100% (in clones of <15 cells). According to these results, a process that allows for a substantial degree of asymmetric differentiation within clones of cells regulates the initial generation of oligodendrocytes. (Asymmetric differentiation refers to situations in which a progenitor cell can, with a certain probability, either produce two further progenitor cells or differentiate, the probabilistic situation continuing as long as there are any progenitor cells in the clone.) The second component is associated with the continued self-renewal of dividing progenitor cells with a probability that is modulated by environmental signals, with some signals promoting differentiation and other factors promoting self-renewal. The third component is associated with eventual differentiation of all cells within a clone, mostly into oligodendrocytes but occasionally into adult O-2A progenitor cells with markedly different biological properties (3). This last component can be overridden by appropriate combinations of growth factors (5) or by certain classes of oncogenes (6).

It can be seen from the above that the development of a quantitative model of differentiation even within this well-studied biological system faces significant challenges. First, depending on environmental factors, the pattern of differentiation observed in families of dividing O-2A progenitor cells in vitro may appear to be more or less clonal, thus making quantitative inferences about the development of O-2A progenitor cells particularly challenging. In addition, one of the important complex features of both patterns of differentiation is that the probability of progenitor cell self-renewal clearly changes dramatically after a particular time point. To illustrate this point, suppose that every progenitor cell either gives rise to two progenitor cells with probability P, or it differentiates into one oligodendrocyte with probability 1 − P. In the symmetric model, P would go from 1 to 0 for all clonally related cells just before the occurrence of differentiation, whereas in a more general model P would decrease from 1 to a value less than or equal to 0.5 (to allow asymmetric division in association with eventual clonal extinction). Based on observations of clonal behavior of O-2A progenitor cells in vitro, it would appear that the number of mitotic cycles for which P = 1 (which we term the critical cycles) varies randomly from clone to clone, probably depending on the history of the founder cell of the clone. The actual number of critical mitotic cycles, however, cannot be observed directly; it should be thought of as a random variable that varies from zero to some unknown value. Nonetheless, as we demonstrate in the present paper, it is possible to estimate this quantity through the use of appropriate quantitative analysis.

In an earlier paper (7), we suggested representing the process of oligodendrocyte generation in vitro as a multitype Bellman-Harris branching stochastic process. When applied to experimental data on clonal growth and differentiation of purified O-2A progenitor cells from optic nerves of 7-day-old rats, the model provides a good fit to the mean number of progenitors and oligodendrocytes per clone at various points in time (7, 8). However, this model was inadequate in other key respects, including prediction of the variance values between clones and description of the underlying distribution of the number of critical mitotic cycles (8). Thus, our previous work did not provide a comprehensive mathematical model of differentiation of clonal families of O-2A progenitor cells into oligodendrocytes.

In the present paper, by relaxing constraints on our previous model so as to allow for an arbitrary distribution of the number of critical cycles, we have been able to provide a realistic quantitative theory for proliferation and differentiation of O-2A progenitor cells. This approach enables reliable estimation of the maximum number of critical cycles, the probability of progenitor cell renewal in the subsequent mitotic cycles, and the basic numerical characteristics (mean and variance) of the mitotic cycle duration.

Materials and Methods

All clonal data used in this analysis have been reported in detail (4). Data were obtained by analyzing (on days 3–6 after plating) the composition of clones of purified O-2A progenitor cells derived from optic nerves of 7-day-old rats. Only clones consisting of a single cell at day 1 after plating were analyzed. Cells were grown in chemically defined medium, supplemented with platelet-derived growth factor, in the presence or absence of thyroid hormone (T3, which promotes oligodendrocyte generation). Cell types were identified visually by the bipolar morphology of O-2A progenitor cells and the multipolar morphology of oligodendrocytes. The accuracy of this categorization is supported by historical data and also was confirmed at the end of each of these experiments by immunofluorescent analysis with cell-type specific antibodies. The number of clones examined at each time after plating varied from 106 to 131.

Theoretical Basis for the Proposed Model

Any theory requires that certain underlying assumptions be made. The following observationally based assumptions are incorporated into the present analysis:

The process begins with a single progenitor cell cultured at time t = 0. At the end of the mitotic cycle, every progenitor cell either gives rise to two progenitor cells with probability P, or it differentiates into one oligodendrocyte with probability 1 − P. We have seen that the founder cell and its immediate descendants appear to have a very high survival rate, and thus the model assumes that these particular cells do not die during the time of the experiment.

As we have observed that in the conditions of our experiments oligodendrocytes do not divide and their survival is virtually complete for the first week after plating, we assume that oligodendrocytes neither divide nor die during the time of the experiment.

The founding progenitor cell acquires the competence for differentiation only after it undergoes a certain number, N, of critical mitotic divisions. In other words, it is assumed that P = 1 for the first N mitotic cycles. As most clones tend to eventual differentiation of all members under the conditions analyzed in these experiments, we further assume that P = P_s ≤ 0.5 for those cycles occurring once the critical cycles have been completed. The parameter N is treated as a non-negative random variable, and its distribution is to be estimated from experimental data.

The lengths of the mitotic cycle of the founder cell and its descendants of the same type are independent and identically distributed non-negative random variables with a common cumulative distribution function F(t) such that F(0) = 0.

Because of the manner in which the experiments are conducted, the progenitor cells, the only migratory cells in the population, do not migrate out of the field of observation.

In addition to the above, the usual independence assumptions regarding the evolution of age-dependent branching processes (9) are adopted.

Mathematical Formulation of the Proposed Model

The model specified above is a special case of the Bellman-Harris age-dependent branching process with N+2 types of cells; its properties for N = 0 were studied in detail by Jagers (10, 11). Let Z₁(t) be the number of progenitor cells and Z₂(t) the number of oligodendrocytes in a clone at time t. By using general methods of the theory of branching processes it is possible to obtain integral equations for the expected values, M_i(t) = E{Z_i(t)}, of the stochastic processes Z_i(t), i = 1, 2 (see ref. 8 for details). Given N, these equations can be solved analytically to give

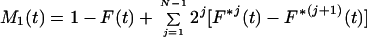1

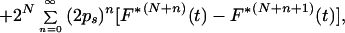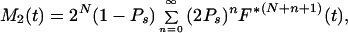2

where F*^k is the k-fold convolution of the interdivision time distribution F with itself. A solution for the corresponding variances can be obtained (8) along similar lines, but the resultant formulas are quite cumbersome and for this reason are not displayed here. If P_s = 0, then all clonally related cells would differentiate in the (N + 1)th mitotic cycle. Mathematically, this special case is the equivalent of the original model of synchronous and symmetric differentiation by entire clones of cells.

We allow for an arbitrary distribution of N:

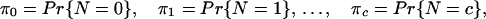with a finite discrete support {0, 1, … , c}, where c is the maximum number of critical mitotic cycles. This compounding distribution is to be used for randomizing the parameter N in formulas 1 and 2, as well as in expressions for the variances. The parameters π₀, … , π_c and c are included in an estimation procedure (see below); this formulation makes our inference regarding the number of critical cycles essentially nonparametric.

Results of Data Analysis

To ensure computationally convenient formulas for the mean values and variances, the function F(t) was specified as the Erlang distribution with shape parameter α and scale parameter β. This distribution is the most popular choice in cell kinetics studies (12), because the gamma family is quite flexible and reflects a multistage structure of the cell cycle. Furthermore, in this case the functions M₁(t) and M₂(t), given by formulas 1 and 2, can be found in an explicit form. We estimated numerical parameters by fitting the model through data on the sample mean number of both types of cells per colony at different time intervals from the start of experiment. The weighted least-squares method was used to find the best fit.

Our preliminary studies (7, 8) indicated that thyroid hormone, T3, does not exert any significant effect on the number of critical mitotic divisions (see also Discussion). On this basis we required the estimates of π₀, … , π_c and c to be equal for experiments with and without thyroid hormone, thereby reducing the number of unknown parameters; we found c = 2 for our present data. Because the model describing the development of O-2A progenitor cells in vitro contains three extra parameters (α, β, and P) for each of the two experimental settings (with and without thyroid hormone), we ended up with nine adjustable parameters to simultaneously fit four (two curves for each setting) sets of experimental data. The variances for both types of cells, computed with the estimated parameter values, then were compared with their sample counterparts. This test is a stringent one for the model adequacy.

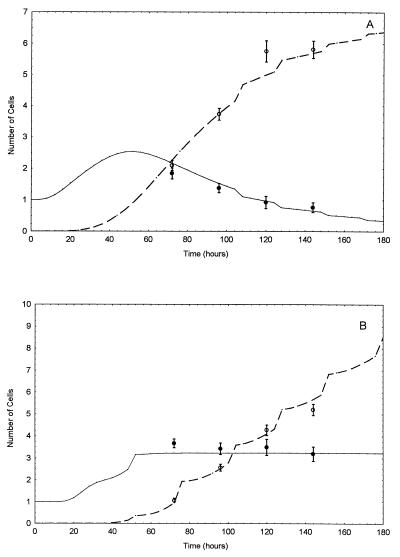
The model we propose provides a very good description not only of the mean values (Fig. 1) but also of the variances (Tables 1 and 2) in this specific predictive setting.

Figure 1.

Fitting data on cell cultures growing with (A) and without (B) thyroid hormone in the culture medium. Solid line represents the expected number of O-2A cells as a function of time; dashed line represents the expected number of oligodendrocytes; closed and open circles are the corresponding sample mean values. Bars represent one square root error of the sample mean at each time point.

Table 1.

Parametric versus sample estimates for the variance of the number of progenitor cells and oligodendrocytes: Experiments without thyroid  hormone

Time, hours	Progenitor cells		Oligodendrocytes
	Model SD	Sample SD	Model SD	Sample SD
72	1.65	2.10	1.01	1.24
96	2.40	2.71	1.32	1.67
120	3.13	3.81	1.63	2.46
144	3.47	3.74	2.47	2.88

Table 2.

Parametric versus sample estimates for the variance of the number of progenitor cells and oligodendrocytes: Experiments with thyroid  hormone

Time, hours	Progenitor cells		Oligodendrocytes
	Model SD	Sample SD	Model SD	Sample SD
72	1.85	1.81	1.23	1.35
96	1.90	1.54	1.52	2.02
120	1.80	1.99	1.77	3.49
144	1.52	1.78	2.75	3.23

The estimated value of c is ĉ = 2, because the estimate of π_i reduces abruptly to zero at i = 3 so that π̂_i = 0 for i ≥ 3. The estimates of the common parameters π₀, π₁, and π₂ are as follows: π̂₀ = 0, π̂₁ = 0.39, and π̂₂ = 0.61.

For the process of oligodendrocyte generation in the absence of thyroid hormone, we obtained the following estimates: P̂_s = 0.50, α̂ = 20.0, and β̂ = 0.79. Thus, the mean, τ = α/β, and the SD, σ = 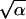/β, of the mitotic cycle duration are estimated as τ̂ = 25.3 h and σ̂ = 5.7 h, respectively. That small value of σ̂ is responsible for the partial synchrony in the development of progenitor cells that is clearly seen in Fig. 1; this synchrony is theoretically predicted, not inferred directly from observations. When precursor cells isolated from optic nerves of P7 animals were studied by time-lapse video recording while growing in the absence of thyroid hormone (13), the sample mean time between mitoses was 27 h (with the square root error of 1 h) and the corresponding SD was 7.7 h. These values are in excellent agreement with the above values obtained by our estimation procedure. As to the process of oligodendrocyte generation in the presence of thyroid hormone, the analysis resulted in the following estimates: P̂_s = 0.35, α̂ = 5.0, and β̂ = 0.23, when we have τ̂ = 21.3 h and σ̂ = 9.5 h. Our model thus suggests that the effect of thyroid hormone is 2-fold. As proposed earlier (4), thyroid hormone decreases the probability for an O-2A progenitor cell to undergo self-renewal, thereby increasing the probability of oligodendrocyte generation. The estimated values of model parameters also suggest that the mean duration of the mitotic cycle for O-2A progenitor cells tends to be shorter in the presence of thyroid hormone.

Discussion

We have developed a mathematical model of clonal differentiation of O-2A progenitor cells into oligodendrocytes that provides a good description of our data, yielding estimated values of such biologically meaningful parameters as the probability of differentiation, cell cycle parameters, and the distribution of the number of critical cycles undergone before a progenitor cell becomes competent to differentiate.

The outcome of our analyses is highly surprising in respect to our hopes of rigorously distinguishing between the competing hypotheses of symmetric vs. asymmetric generation of oligodendrocytes from dividing O-2A progenitor cells, as discussed in the Introduction. These hypotheses represent special cases of our more general model, and acceptation of either hypothesis was a possible outcome of data analysis. What we have seen, however, is that the data do not drive the model to either of these extreme cases. Instead, our quantitative analysis reveals the need for both types of processes to quantitatively describe experimental observations. Specifically, we found that O-2A progenitor cells undergo a period of symmetric development up to a certain point (i.e., up to completion of the critical cycles), after which point an asymmetric differentiation process manifests itself. The concept of critical divisions that emerges from our analyses cannot be directly discerned through the narrative analytical method traditionally used in biological studies. The implication of this aspect of the generalized clock model presented in this paper is that every progenitor cell, isolated from optic nerves of postnatal rats and grown in the conditions of our experiments, divides not more than twice (c = 2) before it becomes competent for differentiation into an oligodendrocyte under in vitro conditions. Experimental data reported by Gao and colleagues (13) provide indirect support for the concept of a distinctive role of the initial mitotic cycles in the development of O-2A progenitor cells in vitro. The authors demonstrated that the mean clonal size in cultures of O-2A progenitor cells isolated from embryonic day 18 optic nerves differs from the mean clonal size in their counterparts isolated from postnatal rats, with the mean number of cells per clone tending to be smaller for progenitor cells isolated from postnatal animals. The observed difference is fairly small after 3 days of in vitro growth, but is quite substantial at subsequent time points. Furthermore, those authors have reinforced our previous analyses (4, 8), suggesting that progenitor cells may become more sensitive to thyroid hormone after going through a requisite set of initial cell cycles.

A critical concern in interpreting a quantitative value of the number of critical cycles is likely to be the prehistory of the progenitor cells studied. Thus, we would suggest that O-2A progenitor cells that differentiate into oligodendrocytes in the absence of division in our experiments represent cells that already have undergone their critical divisions in vivo before their isolation and growth in vitro. At this stage of research, it is not inconceivable that the value of c may be larger for embryonic cells and it may vary with the age of prenatal animals. In a recent paper, Gao et al. (14) reported data on generation of oligodendrocytes by precursor cells purified from embryonic day 18 rat optic nerves. When these cells were cultured at clonal density in the absence of thyroid hormone, no oligodendrocytes developed during the first 6 days. This finding may be interpreted in favor of the hypothesis that embryonic precursor cells undergo a longer sequence of critical cycles before the commencement of oligodendrocyte generation than do their postnatal counterparts. The alternative explanation is that the probability of differentiation P is smaller in embryonic tissues. The latter possibility seems to be quite plausible in view of the fact that oligodendrocytes tend to appear much earlier if embryonic cells are grown in the presence of thyroid hormone. Further quantitative analyses, similar to those given in the present paper, are necessary to conclusively evaluate the role of each factor.

Some doubts may be cast on the estimate π̂₀ = 0. Indeed, the proportion of clones represented by a single oligodendrocyte is 3.3% in experiments with hormone (3.2% without hormone), and even this value underestimates the actual π₀. This result indicates that our estimation procedure is not sensitive enough to detect small values of π₀. To make estimation of the distribution of N more efficient, one needs to invoke distributional information on the number of progenitor cells and oligodendrocytes, but explicit analytic expressions necessary for this purpose do not seem feasible within the framework of our stochastic model. However, our computer simulations, conducted with the use of gpss/h (Wolverine Software, Annandale, VA) have shown that the least-squares estimation procedure yields accurate estimates of the parameters c, P and the mean mitotic cycle duration that are robust to moderate perturbations in values of the parameters π₀, … , π_c (data not shown).

Given a realistic quantitative description of clonal differentiation, a number of important biological questions become approachable. For example, only a quantitative analysis can rigorously distinguish between the various models of O-2A progenitor differentiation that have been suggested by narrative biological analyses (1, 4, 14). Thus, it will be important to know whether the model we propose is consistent with clonal data on the development of O-2A progenitor cells isolated from prenatal animals of different ages, or grown in different conditions, and thus provides a truly general model. In other words, do the specific values of the probability of differentiation, cell cycle parameters, etc., change without leading to a change in the model structure itself? On a deeper level, the derivation of a quantitative model should allow determination of whether the specific inferences obtained from the analysis of O-2A progenitor cells provide general principles that apply more broadly to other cellular lineages.

An alternative to the concept of critical cycles is that the division probability P gradually decreases with cycle number. No previous information on this dependency is available in the existing experimental data, so finding a pertinent form is the main challenge in developing the corresponding mathematical model.

ABBREVIATION

O-2A

oligodendrocyte type 2 astrocyte