Abstract
Ion nanocalorimetry is used to measure the effects of electron kinetic energy in electron capture dissociation (ECD). With ion nanocalorimetry, the internal energy deposited into a hydrated cluster upon activation can be determined from the number of water molecules that evaporate. Varying the heated cathode potential from −1.3 to −2.0 V during ECD has no effect on the average number of water molecules lost from the reduced clusters of either [Ca(H2O)15]2+ or [Ca(H2O)32]2+ even when these data are extrapolated to a cathode potential of zero volts. These results indicate that the initial electron kinetic energy does not go into internal energy in these ions upon ECD. No effects of ion heating from inelastic ion-electron collisions are observed for electron irradiation times up to 200 ms, although some heating occurs for [Ca(H2O)17]2+ at longer irradiation times. In contrast, this effect is negligible for [Ca(H2O)32]2+, a cluster size typically used in nanocalorimetry experiments, indicating that energy transfer from inelastic ion-electron collisions is negligible compared to effects of radiative absorption and emission for these larger clusters. These results have significance towards establishing the accuracy with which electrochemical red-ox potentials, measured on an absolute basis in the gas phase using ion nanocalorimetry, can be related to relative potentials measured in solution.
Introduction
Capture of an electron by a multiply charged protein can result in extensive backbone fragmentation from which information about the sequence,1–3 sites of posttranslational modifications3–7 and even tertiary structure can be obtained.2,8,9 Since the introduction of this electron capture dissociation (ECD) method by Zubarev, Kelleher and McLafferty1 who combined thermally generated electrons with trapped ions in a Fourier-transform ion cyclotron resonance (FT/ICR) mass spectrometer, others have demonstrated that similar fragmentation pathways can be obtained when the electron is captured from an atom10,11 or from molecular anions.12,13 These methods provide a new route to obtain structural information from intact proteins and large peptides, making applications, such as “top-down” proteomics,7 feasible.
Ion-electron recombination or electron capture (EC) is exothermic by a value corresponding to the recombination energy (RE).14,15 This energy can partition into internal modes of the precursor ion and into translational, rotational, and vibrational modes of the dissociation products. The extent of internal energy deposition upon ion activation can be measured using “chemical thermometers,” which are ions that have fragmentation pathways with known activation energies and entropies. For example, Cooks and coworkers used Fe(CO)5+• to compare the energy deposition of collision induced dissociation and surface induced dissociation.16 The appearance energies for fragments of Fe(CO)5+• are known, and their formation occurs with similar entropies so that the internal energy deposition is directly reflected by the fragment ion abundances. A measure of the internal energy deposition into molecular ions of n-butylbenzene molecules can be obtained from the relative abundance of fragment ions at m/z 91 and 92.17–19 The appearance potential of the former is higher, but so is the entropy, making it the favored process when more internal energy is deposited into the molecular ion. Rate constants can be measured using thermal activation methods, such as blackbody infrared radiative dissociation (BIRD),20–23 and these values can be used to establish “effective” temperatures of ions activated by other methods.20
Recently, we demonstrated that hydrated cluster ions are ideal “nanocalorimeters” that can be used to measure accurately the internal energy deposited into these ions upon activation.24–27 This nanocalorimetry method has been used to measure the internal energy deposited by EC with thermally generated electrons as a function of cluster size and cation identity.24–27 For sufficiently large hydrated clusters containing divalent or trivalent ions, EC results in loss of multiple water molecules from the reduced precursor. For example, EC by [Ru(NH3)6(H2O)55]3+ results in formation of [Ru(NH3)6(H2O)n]2+, n = 36, 37 and 38, corresponding to the loss of 17 – 19 water molecules from the reduced precursor ion.26 For these large clusters, all the available recombination energy is deposited into internal modes of the ion and the dissociation is statistical. In contrast, dissociation of much smaller clusters in which loss of a hydrogen atom and water molecules occurs can be nonstatistical.25
For large clusters where the dissociation is statistical, the RE can be obtained from the average number of water molecules lost from the reduced precursor. To obtain the RE, the threshold dissociation energy for the loss of each water molecule from the reduced precursor must be known. Values for clusters of the size typically investigated have not been measured, but these values can be obtained from the Thomson liquid drop model.28,29 Various implementations of this model have been recently evaluated by comparison to experimental data for both monovalent and divalent ions.29 A recently introduced discrete implementation of the Thomson model that takes into account ion size appears to fit most experimental and quantum chemical data accurately.29 Energy can also partition into translational, rotational, and vibrational modes of each water molecule that is lost and can be accounted for using a simple statistical model. A more detailed description about how RE values can be accurately obtained from the number of water molecules lost, including effect of energy partitioning, is presented elsewhere.27
Unlike some methods, such as photoionization spectroscopy, which can be used to obtain vertical ionization energies, the RE values obtained from this experiment are adiabatic values and correspond to the adiabatic ionization energy of the reduced precursor.26,27 Although the initial electron capture may be a vertical process, solvent reorganization is fast (few picoseconds) compared to the time scale of these nanocalorimetry experiments (10’s to 100’s of milliseconds). Energy released upon solvent reorganization will appear as internal energy in these clusters and is reflected by the number of water molecules that evaporate from the reduced clusters.
An emerging application of this nanocalorimetry method is measuring physical properties of ions in bulk solution that are difficult to obtain by other methods. For example, reduction potentials of red-ox active species in bulk solution are measured on a relative basis where the potential of one half-cell is measured relative to that of another. Such measurements result in a ladder of thermochemical values that is anchored to that of the standard hydrogen electrode, which is arbitrarily assigned a value of exactly zero V. We have recently reported the use of our ion nanocalorimetry method to obtain absolute solution-phase reduction potentials.26,27 By comparing these values to relative values measured in solution, an absolute value for the standard hydrogen potential of 4.2 ± 0.4 V is obtained.27
Many factors contribute to the ultimate accuracy of the nanocalorimetry method. Two important factors are the roles of the electron kinetic energy and ion-electron inelastic collisions on values of the RE obtained by ion nanocalorimetry. Here, we demonstrate that the internal energy deposited into hydrated clusters does not depend on the cathode voltage, which can be used to vary the electron kinetic energy, over the range of values typically used in an ECD experiment. In addition, we show that inelastic ion-electron collisions occur, but that these collisions do not significantly affect the internal energy deposition reported in these nanocalorimetry experiments under typical experimental conditions.
Experimental
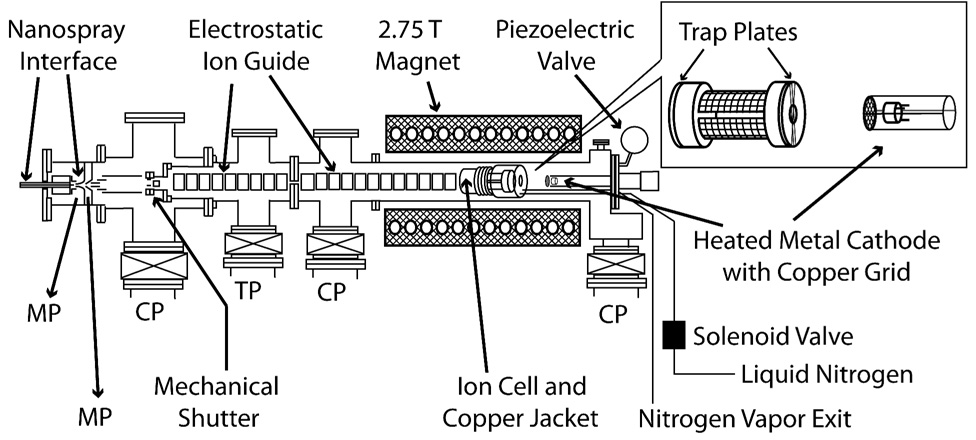
Experiments were performed in a 2.75 Tesla FT/ICR mass spectrometer, equipped with a nanoelectrospray ion source,30 a temperature controlled ion cell,31 and a heated metal cathode25 (Figure 1). The cylindrical ion cell is 10 cm in length and 7 cm in diameter and consists of four copper mesh excite/detect plates separated from two beryllium-copper trapping plates by macor rings. The trapping plates are solid except for a central 1.0 cm hole and are wound with thin copper wire to ensure a uniform electric field across the hole. An oxygen-free copper jacket surrounds the cell and a controlled flow of liquid nitrogen is introduced into the copper jacket by means of a solenoid regulated by a temperature controller (Model No. CN 76000, Omega Engineering, Inc., Stamford, CT). The cell is allowed to equilibrate to a temperature of −140.0 °C for at least 8 hours prior to conducting these experiments.
Figure 1.
Schematic of the 2.75 T FT/ICR mass spectrometer used in these experiments. The inset shows details of the ion cell and heated metal cathode with copper grid. The heated metal cathode is mounted on the central axis of the vacuum chamber and is positioned 20 cm from the center of the ion cell. MP, CP and TP indicate mechanical pump, cryopump and turbopump, respectively.
The nanoelectrospray ion source, with which extensively hydrated ion clusters are generated, is described in detail elsewhere.30 Briefly, borosilicate capillaries with tips pulled to an inner diameter of ~1 µm are filled with 4 mM aqueous solution of calcium chloride (Fisher Scientific, Fair Lawn, NJ). A platinum wire is placed in direct contact with the solution and held at a potential of ~450 V relative to the ~90 °C heated metal capillary entrance to the mass spectrometer. Ions are guided through five stages of differential pumping and trapped in the ion cell. A 7 s pulse of nitrogen gas, which raises the cell pressure to ~5×10−7 Torr, is used to assist in trapping and thermalizing the ions. A mechanical shutter is closed at all other times to prevent additional ions from entering the cell. The trapped ions are allowed to reach a steady state internal energy distribution by exchange of photons with the blackbody radiation field inside the cell21–23 over a period of 8 s, during which time the cell pressure returns to <10−8 Torr. Except where noted, the trapping plate potentials were held at 8.5 V (source side) and 9.5 V (far side) during ion accumulation, stepped down gradually during the 8 s delay to 2.0 V, and held at this potential for the remainder of the experimental sequence.
Clusters of interest are isolated using stored waveform inverse Fourier transforms (SWIFTs), followed by a 50 ms delay. This is followed by either electron irradiation or BIRD. Electrons are thermally generated using a 1.0 cm diameter barium scandate-impregnated cathode (HeatWave Laboratories, Watsonville, CA) mounted axially 20 cm away from the cell center. A direct current of 3 A is used to heat the cathode to a temperature of ~950 °C. To introduce electrons into the cell, the potential of the cathode housing is pulsed from +10.0 V to values between 0.0 and −10.0 V. A value of −1.5 V for the cathode potential during electron irradiation resulted in maximum ECD efficiency, and this setting was used in all experiments where cathode potential was not a variable. Electrons that pass through the cell should be reflected back through the cell due to the ion injection optics that are maintained at high negative potentials.22 For BIRD experiments, the heated cathode potential was kept at +10.0 V to prevent electrons from entering the cell. In all experiments, a potential of +9 V was applied to a copper wire mesh mounted 0.5 cm in front of the cathode. All potentials are referenced to instrumental ground.
A MIDAS data system32 was used to acquire 32 K data point transients. Ion abundances were obtained by subtracting the average noise in a ~30 m/z signal-free region near the precursor. For ECD experiments, the average number of water molecules lost from a cluster upon reduction was calculated as the weighted average of reduced product cluster abundances and corrected for background dissociation from BIRD by subtracting the water loss due to BIRD as measured with no electrons present in the cell. Experimental error was propagated assuming a distribution of noise that is uniform and uncorrelated with respect to m/z in the mass spectral regions investigated, and normal with respect to intensity. The standard deviation in noise intensity over the aforementioned signal-free region was propagated through all calculations to estimate error.
Results and Discussion
Electron Kinetic Energy
In these ECD experiments, the electron kinetic energy is poorly defined and depends on a number of experiment parameters, including position inside the ion cell; trapping plate potentials; cell geometry; cathode voltage, temperature and location; electron current; etc. Electrons produced from the heated cathode should have an initial velocity spread given by a Maxwell-Boltzmann distribution at the cathode temperature. At 950 °C, the temperature of the heated cathode in these experiments, the average electron velocity is 1.9 × 105 m/s corresponding to a kinetic energy of 0.1 eV. In addition to the thermal distribution, electron-electron repulsion at the high electron currents typically used in these experiments will result in an even broader distribution of electron kinetic energies.
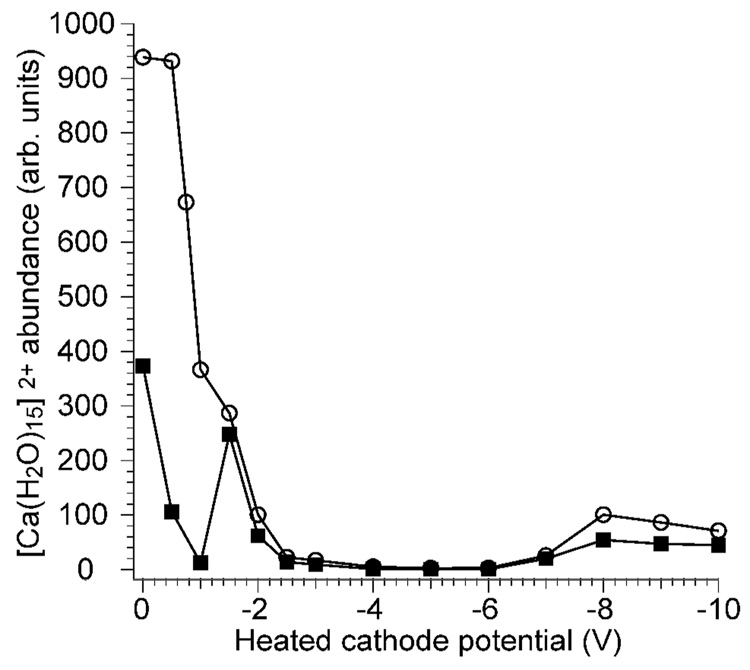
To study possible effects of electron kinetic energy on the internal energy deposition into ions upon EC, the potential of the cathode can be varied while keeping all other parameters constant. However, there is a limited range over which the cathode potential can be varied (about −1.2 to −2.0 V in these experiments) and ECD products observed. To investigate the origin of this effect, [Ca(H2O)15]2+ was isolated in the cell and the precursor abundance was measured as a function of cathode potential with electron irradiation times of 120 ms (Figure 2). With symmetric trapping potentials of 2.0 V during ECD and ion detection, rapid loss of the precursor is observed when the cathode potential is varied from 0 to −1.0 V (Figure 2; solid black squares). A local maximum in precursor intensity occurs at about −1.5 V and the precursor intensity rapidly decreases at cathode potentials more negative than −2.0 V. Another local maximum in precursor intensity is observed at −8.0 V. To investigate effects of trapping plate potentials on this phenomenon, asymmetric trapping potentials of 8.3 and 9.2 V were used during ECD (2.0 V during ion detection). With these higher trap potentials, precursor ion loss is significantly reduced at low cathode potentials, but otherwise the trapping potentials during ECD have little effect (Figure 2; open circles). Similar results to the higher trapping plate data have been reported by Lioe and O’Hair, who irradiated singly charged ions with electrons and concluded that the loss of signal was due to neutralization.33 However, no singly charged ions are observed in our experiments with cathode potentials between −3.0 and −7.0 V, indicating that ion-electron recombination is not the origin of precursor loss. Marshall and coworkers demonstrated that manipulation of the trapping potentials during and immediately after the ECD event or the use of single pass vs. reflected electron configurations can shift the peak in ECD efficiency as a function of cathode potential.34 High electron currents can reduce the effective potential inside the cell which could result in loss of positively charged ions, consistent with retention of ion signal with high trap potentials when the cathode potential is low. However, the maximum observed at −1.5 V with 2.0 V trap potentials suggests that other effects, such as inelastic or elastic collisions with electrons which could “push” the ions out of the cell, may occur.
Figure 2.
[Ca(H2O)15]2+ precursor abundance after 120 ms of electron irradiation as a function of heated cathode potential, measured with two different trapping plate potential conditions: a symmetric 2.0 V trap potential during electron irradiation and ion detection (solid squares); and asymmetrical 8.3/9.2 V source-side/far-side trap potentials during electron irradiation, 2.0 V during ion detection (open circles).
Effects of Cathode Potential on ECD Spectra
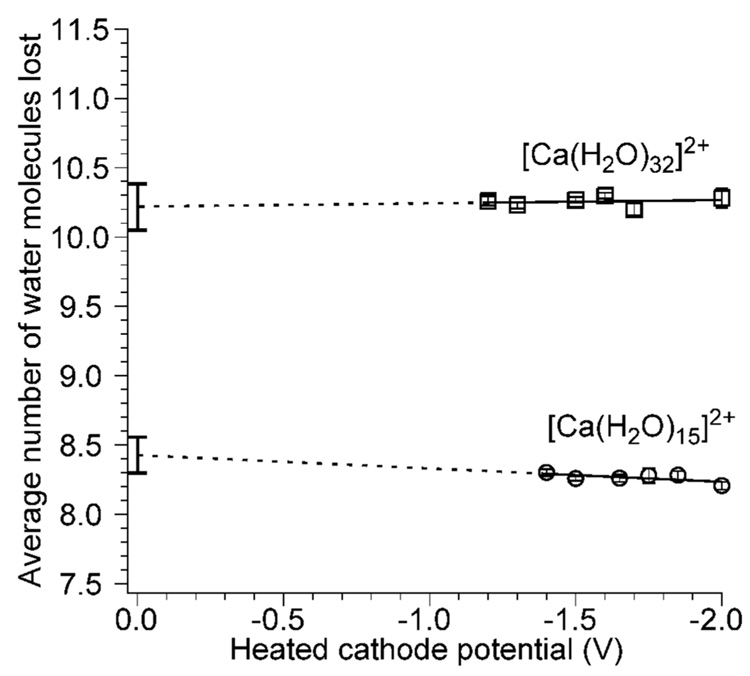
To determine how the electron kinetic energy affects the internal energy deposition upon EC, ECD spectra of [Ca(H2O)32]2+ and [Ca(H2O)15]2+ were measured as a function of cathode potential. ECD of the former results in exclusively loss of either 10 or 11 water molecules from the reduced precursor, whereas ECD of the later results in loss of an H atom and 8 or 9 water molecules, resulting in formation of hydrated calcium hydroxide with a single charge. For [Ca(H2O)32]2+, there is no discernable trend in the average number of water molecules lost from the reduced precursor for cathode potentials ranging from −1.2 to −2.0 V (Figure 3). The average number of water molecules lost over this range is 10.26 ± 0.04. Extrapolation of these data to a cathode housing potential of 0.0 V results in a value of 10.2 ± 0.2 water molecules. If the electron kinetic energy were deposited into internal modes of the ion, the ECD spectra should reflect a 0.80 eV (18.4 kcal/mol) change in internal energy deposition over this 0.80 V range of cathode potentials. Because ~0.4 eV (~9 kcal/mol) is required to evaporate a water molecule from a monovalent cluster of this size,29 if the entire electron kinetic energy had been deposited into the ion, the average number of water molecules that evaporate from these clusters should have changed by approximately 0.80/0.4 = 2.0 water molecules over the 0.80 V range in cathode potentials. The insensitivity of the ECD spectra to cathode voltage clearly indicates that the internal energy deposited into these hydrated clusters is not a function of the electron kinetic energy over the range of cathode potentials typically used in ECD experiments.
Figure 3.
Average number of water molecules lost upon reduction of [Ca(H2O)15]2+ and [Ca(H2O)32]2+ as a function of heated cathode potential. Dashed lines indicate extrapolated least squares fits of the data, and the error bars at 0.0 V indicate the propagated error in the intercept.
Similar results are obtained for [Ca(H2O)15]2+ where there is again no discernable trend in the average number of water molecules lost as a function of the cathode housing potential over a range of −1.4 to −2.0 V with an average value of 8.26 ± 0.04 (Figure 3). Extrapolation of these data to a cathode potential of 0.0 V results in a value of 8.4 ± 0.1. As was the case for [Ca(H2O)32]2+, the cathode potential and hence electron kinetic energy have no effect on the internal energy deposited into this ion. Zubarev et al. reported that the fragmentation patterns in ECD spectra of 11+ ubiquitin ions did not change over a 0.0 to −0.4 V range of cathode potentials and concluded that the electron kinetic energy was minor compared to the energy released upon EC.35 Our results show that changing cathode potentials does not affect ECD energy deposition in the low electron energy regime. However, different fragment ions have been observed in “hot” ECD experiments where the electron kinetic energy is >5 eV.36,37
Trapping plate potentials during ECD also influence the electron kinetic energy inside the ion cell. To investigate the effects of trap potentials in these experiments, an ECD spectrum of [Ca(H2O)32]2+ was measured using asymmetric trap potentials of 8.3 and 9.2 V (source-side and far-side, respectively) during ECD. An average of 10.25 ± 0.01 water molecules is lost from the reduced precursor, essentially the same number observed when the spectrum was acquired with a symmetric trapping potential of 2.0 V. These results indicate that the trapping potentials do not influence the internal energy deposited into ions upon ECD over the range of values typically used in these experiments.
Although these results may seem counterintuitive, it is important to consider that the capture of an electron is most efficient when the relative velocity between an ion and an electron is zero. The relative velocities of positive ions and electrons can be carefully controlled by merging the corresponding ion beams in ion storage rings.38–41 From such experiments, accurate recombination cross sections as a function of relative ion-electron velocity can be obtained. The cross section for dissociative recombination when a protonated water molecule captures an electron increases by about 5 orders of magnitude as the center-of-mass kinetic energy decreases from 30 eV to 0.001 eV.40 The EC cross section for D+(D2O)2 increases by about three orders of magnitude when the ion-electron center-of-mass kinetic energy decreases from 0.01 to 0.001 eV.41
In the ECD experiments described here, the spread of electron velocities is very broad. Contributing further to the broadening is electron-electron repulsion which is significant at the high electron currents used in these experiments. In addition, inelastic ion-electron collisions that do not result in electron capture can result in lower electron kinetic energies. All of these factors could result in a small fraction of electrons with near-zero kinetic energies inside the ion cell, and these electrons should be the most efficiently captured by the slow moving positive ions in our experiment.
Effects of Inelastic Ion-Electron Collisions on ECD Spectra
Inelastic ion-electron collisions can deposit energy into either the intact precursor or the fragment ions resulting in ion heating that could contribute to the extent of dissociation observed. A method to fragment organic ions based on this phenomenon has been implemented previously in FT/ICR mass spectrometers by Freiser and Beauchamp42 and has been affectionately called electron impact excitation of ions from organics or EIEIO.43 This method has been used to dissociate singly charged peptides.33,44
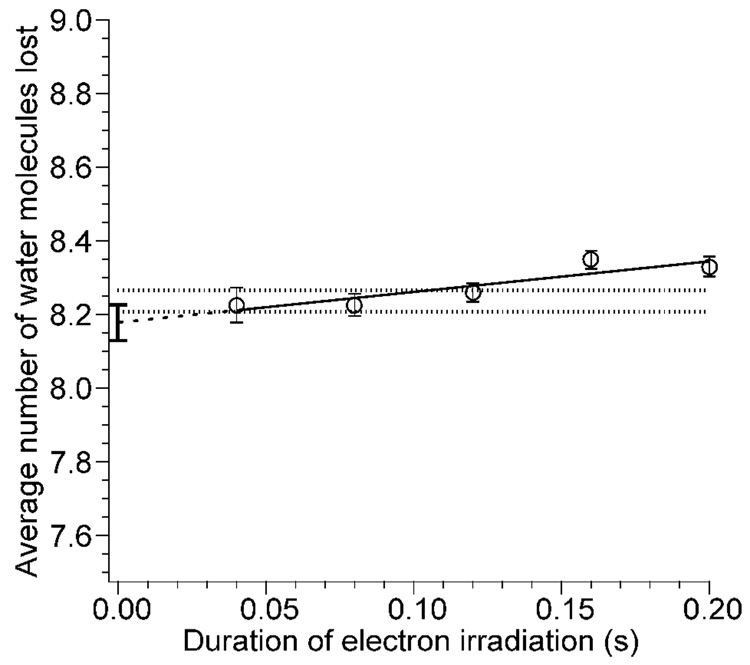
To investigate the extent to which inelastic ion-electron collisions occur and influence the internal energy deposition in these experiments, [Ca(H2O)15]2+ was isolated, and ECD experiments were performed as a function of electron irradiation time from 40 to 200 ms with a cathode potential of −1.5 V. These data are corrected for contributions to ion heating by BIRD originating from the heated cathode and the cooled cell and surroundings. The average number of water molecules lost from the reduced precursor as a function of electron irradiation time is shown in Figure 4. There is a slight trend in the average number of water molecules lost as a function of electron irradiation time. The average numbers of water molecules lost at 40, 80, and 120 ms irradiation time are indistinguishable within experimental error; the average of these three values is 8.24 ± 0.03. Values at 160 and 200 ms are slightly higher and outside experimental error indicating that inelastic ion-electron collisions do play a minor role in ion heating at these longer irradiation times. Extrapolation of these data to zero irradiation time should give the number of water molecules lost solely due to EC in the absence of any heating from inelastic ion-electron collisions. This value is 8.18 ± 0.05. From these results, we conclude that although inelastic ion-electron collisions occur, they contribute negligibly to the internal energy of the ions when the electron irradiation is less than 120 ms. At longer irradiation times, this effect can be measured but continues to be negligible at least up to 200 ms.
Figure 4.
Average number of water molecules lost from reduced [Ca(H2O)15]2+ due to EC as a function of electron irradiation time. The dashed line indicates the extrapolated least squares fit to the data, and the error bars at 0.0 s indicate the propagated error in the intercept. The dotted lines represent one standard deviation above and below the average value of the data at 40, 80, and 120 ms.
Effects of Inelastic Ion-Electron Collisions on Precursor Heating
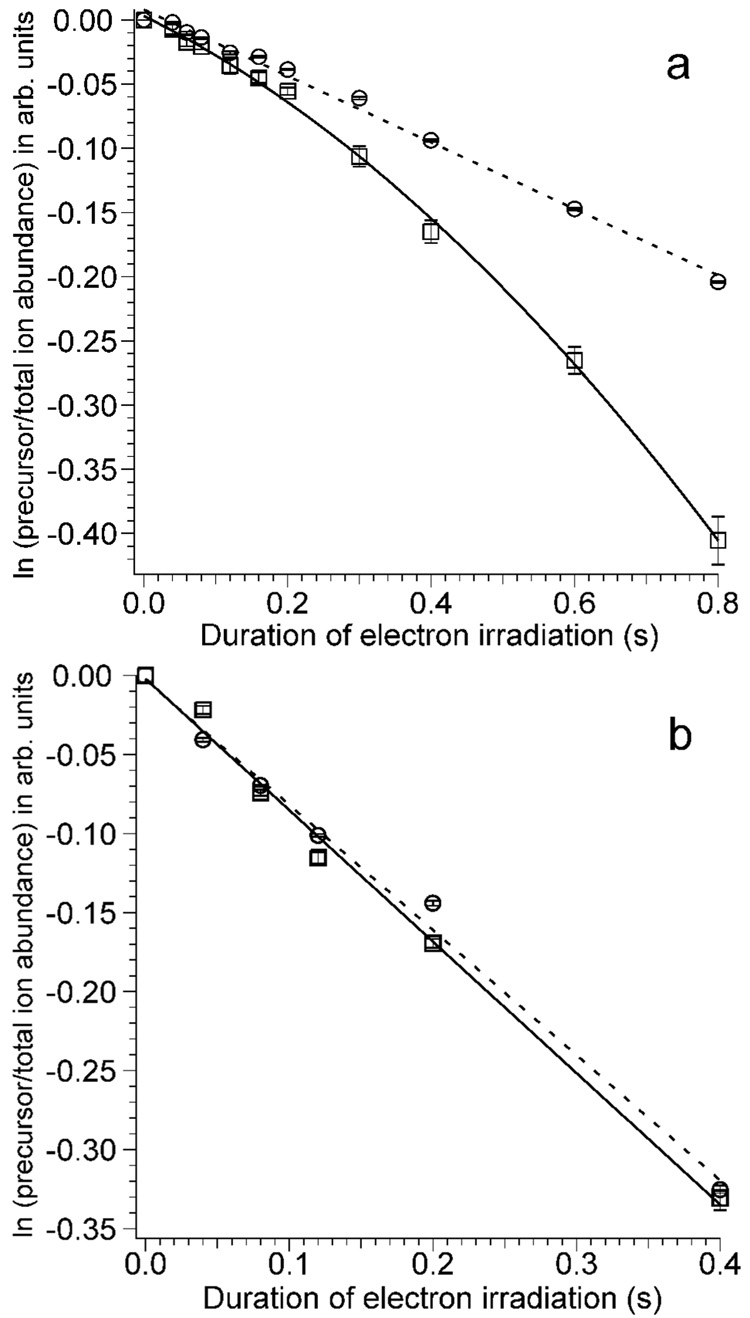
In separate experiments, effects of precursor heating due to inelastic ion-electron collisions were obtained for both [Ca(H2O)17]2+ and for [Ca(H2O)32]2+ by measuring the extent of water loss from the precursor ions as a function of electron irradiation time. For both ions, loss of one or two water molecules from the precursor are the only products observed in addition to singly charged product ions due to ECD. In these experiments, blackbody infrared radiative dissociation occurs21–23 that can be directly attributed to the heated cathode that is located 20 cm away from the cell center.25 Effects of precursor ion heating due to inelastic ion-electron collisions can be obtained from differences in the extent of water loss with and without electrons introduced into the cell. To do this, the cathode remains at ~950 °C in both experiments, but for the blackbody comparison, the cathode potential is +10 V at all times so that no electrons enter the cell. Differences in the water loss from the precursor ion measured in these two experiments can be directly attributed to inelastic electron-ion collisions. The water loss from the precursor ions, corrected for loss of the precursor due to ECD, as a function of electron irradiation time is shown in Figure 5. For [Ca(H2O)17]2+, there is no significant difference in the fragmentation rate with or without electron irradiation up to 200 ms, but at longer times, more fragmentation occurs when electrons are introduced into the ion cell (Figure 5a). This result indicates that inelastic ion-electron collisions result in heating of the precursor ion over this longer time frame. The induction period at times below about 200 ms indicates that the precursor ions require some initial heating to a steady state temperature before pseudo first-order kinetics are observed, analogous to preheating in laser dissociation kinetic studies.45
Figure 5.
Dissociation kinetics of (a) [Ca(H2O)17]2+ and (b) [Ca(H2O)32]2+ with (squares, cathode potential −1.5 V) and without (circles, cathode potential +10.0 V) electron irradiation as a function of electron irradiation time. The dashed lines are least squares fits to the data obtained with the heated cathode potential at +10.0 V, and the solid lines are a parabolic ([Ca(H2O)17]2+) and least squares fit ([Ca(H2O)32]2+) to the data with a heated cathode potential of −1.5 V.
In contrast, there is no observable effect of inelastic ion-electron collisions for [Ca(H2O)32]2+ (Figure 5b) for times up to 400 ms. In these experiments, the initial internal energy of this larger cluster is approximately twice that of the smaller cluster as are the rates of radiative absorption and emission. However, the threshold dissociation energies for loss of a water molecule from these two different size clusters are nearly the same. These experiments indicate that the rate of ion heating due to inelastic ion-electron collisions is negligible compared to that from radiative absorption (and emission) at this cluster size. Thus, for the cluster sizes typically used in nanocalorimetry experiments, heating of the ions due to inelastic ion-electron collisions is negligible under typical experimental conditions.
Conclusions
Ion nanocalorimetry is an accurate and highly sensitive method for measuring how much internal energy is deposited into ions upon activation.24–27 This method has been recently applied to measuring absolute reduction potentials of red-ox couples in bulk solution.26,27 In order to improve the accuracy with which these values can be obtained, effects of electron kinetic energy and inelastic ion-electron collisions on the internal energy deposition in ECD must be known. In typical ECD experiments done in FT/ICR mass spectrometry, the relative kinetic energies of the electrons generated by heated metal cathodes and the trapped ions vary over a relatively wide range and are poorly defined. The kinetic energy of electrons in these ECD experiments can be precisely varied by changing the heated cathode potential. Under typical experimental conditions, varying the cathode potential has no measurable effect on the internal energy deposited into ions that capture electrons. These results are consistent with the presence of some small fraction of electrons with near zero kinetic energy inside the cell. Such low energy electrons can be produced by effects of electron-electron repulsion in the high-density electron beam and/or by inelastic ion-electron collisions that occur inside the ion cell. Capture cross sections for EC are significantly higher when the relative ion-electron velocity approaches zero, and it is capture of this small population of low-energy electrons that results in the observed ECD. These results may explain in part the poor absolute cross section for ion-electron recombination in these experiments.
With electron irradiation times up to 200 ms, no discernable effects of inelastic ion-electron collisions are observed. At longer irradiation times, some ion heating due to inelastic ion-electron collisions is measurable for small nanoclusters but this effect is negligible for the larger size clusters typically used in nanocalorimetry experiments. These results indicate that the cathode potential, trapping plate potential, and inelastic ion-electron collisions do not play a significant role in the internal energy deposition in ECD under typical experimental conditions.
Acknowledgements
The authors thank Professor Roman A. Zubarev for his pioneering contributions to the field of electron capture dissociation. We also acknowledge Matthew F. Bush, William A. Donald, and Ryan D. Leib for helpful discussions. This work was supported by the National Science Foundation (CHE-0718790), the National Institutes of Health (RO1 GM064712) and the European Project ITS-LEIF (RII 3/02 6016; support for A.I.S.H.).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Zubarev RA, Kelleher NL, McLafferty FW. Electron capture dissociation of multiply charged protein cations. A nonergodic process. J. Am. Chem. Soc. 1998;120:3265–3266. [Google Scholar]
- 2.Breuker K, Oh HB, Horn DM, Cerda BA, McLafferty FW. Detailed unfolding and folding of gaseous ubiquitin ions characterized by electron capture dissociation. J. Am. Chem. Soc. 2002;124:6407–6420. doi: 10.1021/ja012267j. [DOI] [PubMed] [Google Scholar]
- 3.Stensballe A, Jensen ON, Olsen JV, Haselmann KF, Zubarev RA. Electron capture dissociation of singly and multiply phosphorylated peptides. Rapid Commun. Mass Spectrom. 2000;14:1793–1800. doi: 10.1002/1097-0231(20001015)14:19<1793::AID-RCM95>3.0.CO;2-Q. [DOI] [PubMed] [Google Scholar]
- 4.Mirgorodskaya E, Roepstorff P, Zubarev RA. Localization of O-Glycosylation Sites in Peptides by Electron Capture Dissociation in a Fourier Transform Mass Spectrometer. Anal. Chem. 1999;71:4431–4436. doi: 10.1021/ac990578v. [DOI] [PubMed] [Google Scholar]
- 5.Sze SK, Ge Y, Oh HB, McLafferty FW. Top-down mass spectrometry of a 29-kDa protein for characterization of any posttranslational modification to within one residue. Proc. Natl. Acad. Sci. U. S. A. 2002;99:1774–1779. doi: 10.1073/pnas.251691898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Kelleher NL, Zubarev RA, Bush K, Furie B, Furie BC, McLafferty FW, Walsh CT. Localization of labile posttranslational modifications by electron capture dissociation: The case of gamma-carboxyglutamic acid. Anal. Chem. 1999;71:4250–4253. doi: 10.1021/ac990684x. [DOI] [PubMed] [Google Scholar]
- 7.Ge Y, Lawhorn BG, ElNaggar M, Strauss E, Park JH, Begley TP, McLafferty FW. Top down characterization of larger proteins (45 kDa) by electron capture dissociation mass spectrometry. J. Am. Chem. Soc. 2002;124:672–678. doi: 10.1021/ja011335z. [DOI] [PubMed] [Google Scholar]
- 8.Robinson EW, Leib RD, Williams ER. The role of conformation on electron capture dissociation of ubiquitin. J. Am. Soc. Mass Spectrom. 2006;17:1469–1479. doi: 10.1016/j.jasms.2006.06.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Breuker K, Oh HB, Lin C, Carpenter BK, McLafferty FW. Nonergodic and conformational control of the electron capture dissociation of protein cations. Proc. Natl. Acad. Sci. U. S. A. 2004;101:14011–14016. doi: 10.1073/pnas.0406095101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Hvelplund P, Liu B, Nielsen SB, Tomita S. Electron capture induced dissociation of peptide dications. Int. J. Mass Spectrom. 2003;225:83–87. [Google Scholar]
- 11.Hvelplund P, Liu B, Nielsen SB, Tomita S, Cederquist H, Jensen J, Schmidt HT, Zettergren H. Electron capture and loss by protonated peptides and proteins in collisions with C60 and Na. Eur. Phys. J. D. 2003;22:75–79. [Google Scholar]
- 12.Coon JJ, Shabanowitz J, Hunt DF, Syka JEP. Electron transfer dissociation of peptide anions. J. Am. Soc. Mass Spectrom. 2005;16:880–882. doi: 10.1016/j.jasms.2005.01.015. [DOI] [PubMed] [Google Scholar]
- 13.Syka JEP, Coon JJ, Schroeder MJ, Shabanowitz J, Hunt DF. Peptide and protein sequence analysis by electron transfer dissociation mass spectrometry. Proc. Natl. Acad. Sci. U. S. A. 2004;101:9528–9533. doi: 10.1073/pnas.0402700101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Iavarone AT, Paech K, Williams ER. Effects of charge state and cationizing agent on the electron capture dissociation of a peptide. Anal. Chem. 2004;76:2231–2238. doi: 10.1021/ac035431p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Zubarev RA. Reactions of polypeptide ions with electrons in the gas phase. Mass Spectrom. Rev. 2003;22:57–77. doi: 10.1002/mas.10042. [DOI] [PubMed] [Google Scholar]
- 16.Dekrey MJ, Kenttämaa HI, Wysocki VH, Cooks RG. Energy deposition in Fe(Co)5+• upon collision with a metal-surface. Org. Mass Spectrom. 1986;21:193–195. [Google Scholar]
- 17.Griffiths IW, Harris FM, Mukhtar ES, Beynon JH. Calculation of the abundance ratio [91+/92+] from n-butylbenzene molecular-ions as a function of internal energy. Int. J. Mass Spectrom. Ion Processes. 1981;41:83–88. [Google Scholar]
- 18.Baer T, Dutuit O, Mestdagh H, Rolando C. Dissociation dynamics of n-butylbenzene ions - the competitive production of m/z 91-fragment and 92-fragment ions. J. Phys. Chem. 1988;92:5674–5679. [Google Scholar]
- 19.Chen JH, Hays JD, Dunbar RC. Competitive 2-channel photodissociation of n-butylbenzene ions in the Fourier-transform ion-cyclotron resonance mass-spectrometer. J. Phys. Chem. 1984;88:4759–4764. [Google Scholar]
- 20.Schnier PD, Jurchen JC, Williams ER. The effective temperature of peptide ions dissociated by sustained off-resonance irradiation collisional activation in Fourier transform mass spectrometry. J. Phys. Chem. B. 1999;103:737–745. doi: 10.1021/jp9833193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Price WD, Schnier PD, Jockusch RA, Strittmatter EF, Williams ER. Unimolecular reaction kinetics in the high-pressure limit without collisions. J. Am. Chem. Soc. 1996;118:10640–10644. doi: 10.1021/ja961812r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Price WD, Schnier PD, Williams ER. Tandem mass spectrometry of large biomolecule ions by blackbody infrared radiative dissociation. Anal. Chem. 1996;68:859–866. doi: 10.1021/ac951038a. [DOI] [PubMed] [Google Scholar]
- 23.Price WD, Williams ER. Activation of peptide ions by blackbody radiation: Factors that lead to dissociation kinetics in the rapid energy exchange limit. J. Phys. Chem. A. 1997;101:8844–8852. doi: 10.1021/jp9722418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Leib RD, Donald WA, O'Brien JT, Bush MF, Williams ER. Internal energy deposition in electron capture dissociation measured using hydrated divalent metal ions as nanocalorimeters. J. Am. Chem. Soc. 2007;129:4894–4895. doi: 10.1021/ja0666607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Leib RD, Donald WA, Bush MF, O'Brien JT, Williams ER. Nonergodicity in electron capture dissociation investigated using hydrated ion nanocalorimetry. J. Am. Soc. Mass Spectrom. 2007;18:1217–1231. doi: 10.1016/j.jasms.2007.03.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Leib RD, Donald WA, O'Brien JT, Bush MF, Williams ER. Reduction energy of 1 M aqueous ruthenium(III) hexaammine in the gas phase: A route toward establishing an absolute electrochemical scale. J. Am. Chem. Soc. 2007;129:7716–7717. doi: 10.1021/ja067794n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Donald WA, Leib RD, O'Brien JT, Bush MF, Williams ER. The absolute standard hydrogen electrode potential measured by reduction of aqueous nanodrops in the gas phase. J. Am. Chem. Soc. 2008 doi: 10.1021/ja073946i. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Holland PM, Castleman AW. Thomson equation revisited in light of ion-clustering experiments. J. Phys. Chem. 1982;86:4181–4188. [Google Scholar]
- 29.Donald WA, Williams ER. Evaluation of different implementations of the Thomson liquid drop model: Comparison to monovalent and divalent cluster ion experimental data. J. Phys. Chem. A. 2008 doi: 10.1021/jp711012b. accepted. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Bush MF, Saykally RJ, Williams ER. Formation of hydrated triply charged metal ions from aqueous solutions using nanodrop mass spectrometry. Int. J. Mass Spectrom. 2006;253:256–262. doi: 10.1016/j.ijms.2006.04.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Wong RL, Paech K, Williams ER. Blackbody infrared radiative dissociation at low temperature: hydration of X2+(H2O)n, for X = Mg, Ca. Int. J. Mass Spectrom. 2004;232:59–66. [Google Scholar]
- 32.Senko MW, Canterbury JD, Guan SH, Marshall AG. A high-performance modular data system for Fourier transform ion cyclotron resonance mass spectrometry. Rapid Commun. Mass Spectrom. 1996;10:1839–1844. doi: 10.1002/(SICI)1097-0231(199611)10:14<1839::AID-RCM718>3.0.CO;2-V. [DOI] [PubMed] [Google Scholar]
- 33.Lioe H, O'Hair RAJ. Comparison of collision-induced dissociation and electron-induced dissociation of singly protonated aromatic amino acids, cystine and related simple peptides using a hybrid linear ion trap-FT-ICR mass spectrometer. Anal. Bioanal. Chem. 2007;389:1429–1437. doi: 10.1007/s00216-007-1535-1. [DOI] [PubMed] [Google Scholar]
- 34.McFarland MA, Chalmers MJ, Quinn JP, Hendrickson CL, Marshall AG. Evaluation and optimization of electron capture dissociation efficiency in Fourier transform ion cyclotron resonance mass spectrometry. J. Am. Soc. Mass Spectrom. 2005;16:1060–1066. doi: 10.1016/j.jasms.2005.03.020. [DOI] [PubMed] [Google Scholar]
- 35.Zubarev RA, Horn DM, Fridriksson EK, Kelleher NL, Kruger NA, Lewis MA, Carpenter BK, McLafferty FW. Electron capture dissociation for structural characterization of multiply charged protein cations. Anal. Chem. 2000;72:563–573. doi: 10.1021/ac990811p. [DOI] [PubMed] [Google Scholar]
- 36.Chan TWD, Ip WHH. Optimization of experimental parameters for electron capture dissociation of peptides in a Fourier transform mass spectrometer. J. Am. Soc. Mass Spectrom. 2002;13:1396–1406. doi: 10.1016/S1044-0305(02)00703-1. [DOI] [PubMed] [Google Scholar]
- 37.Kjeldsen F, Haselmann KF, Budnik BA, Jensen F, Zubarev RA. Dissociative capture of hot (3–13 eV) electrons by polypeptide polycations: an efficient process accompanied by secondary fragmentation. Chem. Phys. Lett. 2002;356:201–206. [Google Scholar]
- 38.Adams NG, Poterya V, Babcock LM. Electron molecular ion recombination: Product excitation and fragmentation. Mass Spectrom. Rev. 2006;25:798–828. doi: 10.1002/mas.20084. [DOI] [PubMed] [Google Scholar]
- 39.Al Khalili A, Thomas R, Ehlerding A, Hellberg F, Geppert WD, Zhaunerchyk V, af Ugglas M, Larsson M, Uggerud E, Vedde J, Adlhart C, Semaniak J, Kamińska M, Zubarev RA, Kjeldsen F, Andersson PU, Österdahl F, Bednarska VA, Paal A. Dissociative recombination cross section and branching ratios of protonated dimethyl disulfide and N-methylacetamide. J. Chem. Phys. 2004;121:5700–5708. doi: 10.1063/1.1782772. [DOI] [PubMed] [Google Scholar]
- 40.Neau A, Al Khalili A, Rosen S, Le Padellec A, Derkatch AM, Shi W, Vikor L, Larsson M, Semaniak J, Thomas R, Någård MB, Andersson K, Danared H, af Ugglas M. Dissociative recombination of D3O+ and H3O+: Absolute cross sections and branching ratios. J. Chem. Phys. 2000;113:1762–1770. [Google Scholar]
- 41.Någård MB, Pettersson JBC, Derkatch AM, Al Khalili A, Neau A, Rosen S, Larsson M, Semaniak J, Danared H, Kallberg A, Österdahl F, af Ugglas M. Dissociative recombination of D+(D2O)2 water cluster ions with free electrons. J. Chem. Phys. 2002;117:5264–5270. [Google Scholar]
- 42.Freiser BS, Beauchamp JL. Electron-impact dissociation of cyanobenzene radical cations by ion-cyclotron resonance spectroscopy. Chem. Phys. Lett. 1976;42:380–382. [Google Scholar]
- 43.Cody RB, Freiser BS. Electron-impact excitation of ions from organics - An alternative to collision-induced dissociation. Anal. Chem. 1979;51:547–551. [Google Scholar]
- 44.Wang BH, McLafferty FW. Electron-impact excitation of ions from larger organic molecules. Org. Mass Spectrom. 1990;25:554–556. [Google Scholar]
- 45.Jockusch RA, Paech K, Williams ER. Energetics from slow infrared multiphoton dissociation of biomolecules. J. Phys. Chem. A. 2000;104:3188–3196. doi: 10.1021/jp993147p. [DOI] [PMC free article] [PubMed] [Google Scholar]