Dynamics of Microtubule Instabilities

Abstract

We investigate an idealized model of microtubule dynamics that involves: (i) attachment of guanosine triphosphate (GTP) at rate λ, (ii) conversion of GTP to guanosine diphosphate (GDP) at rate 1, and (iii) detachment of GDP at rate μ. As a function of these rates, a microtubule can grow steadily or its length can fluctuate wildly. For μ = 0, we find the exact tubule and GTP cap length distributions, and power-law length distributions of GTP and GDP islands. For μ = ∞, we argue that the time between catastrophes, where the microtubule shrinks to zero length, scales as e^λ. We also discuss the nature of the phase boundary between a growing and shrinking microtubule.

Microtubules are linear polymers of the protein tubulin that perform major organizational tasks in living cells [1, 2]. They provide transport tracks for molecular machines [3, 4], and move cellular structures during cellular processes such as reproduction [2, 5]. A surprising feature of microtubules is that they remain out of equilibrium under fixed external conditions and can undergo alternating periods of growth and rapid shrinking (Fig. 1).

FIG. 1.

Schematic illustration of the growth and catastrophic shrinkage of a microtubule as a function of time (adapted from [1]).

These sudden polymerization changes are driven by the interplay between growth by the attachment of guanosine triphosphate tubulin complexes (GTP) at the free end [1, 3, 6, 7], irreversible hydrolysis of GTP into guanosine diphosphate (GDP) anywhere in the tubule, and subsequent GDP detachment from the free end of the tubule. One avenue of theoretical work on this dynamical instability is based on detailed models of mechanical stability [8, 9]. For example, a detailed stochastic model of a microtubule that includes all the thirteen constituent protofilaments has been investigated in Ref. [9]. By using model parameters that were inferred from equilibrium statistical physics, VanBuren et al. [9] found characteristics of the tip evolution of a microtubule that agreed with experimental data [10].

Another approach for modeling the dynamics of microtubules is based on effective two-state models that describe the dynamics in terms of a switching between a growing and a shrinking state [7, 11–16]. The essence of many of these models is that a microtubule exists either in a growing phase (where a GTP cap exists at the end of the microtubule) or a shrinking phase (without a GTP cap), and that there are stochastic transitions between these two states. By tuning parameters appropriately, it is possible to reproduce the phase changes between the growing and shrinking phases of microtubules that have been observed experimentally [3]. In another important contribution, Flyvbjerg et al. [17] constructed an effective continuous theory to describe the dynamics of the cap length.

What is missing in these models is a clear connection between microscopic parameters and the evolution of the spatial structure of the microtubule. Most of the models discussed thus far are too complicated to permit a complete solution. Thus the present work is motivated by the goal of formulating and solving a minimal and idealized coarse-grained model of microtubule dynamics that incorporates the main features of growth and shrinking. We view this idealized model as an Ising-like description that captures the most interesting features of microtubule dynamics even though the connection between model parameters and experimental variables is indirect. One of the main advantages of the model is its simplicity so that many of its geometrical and dynamical features can determined analytically. These solutions reveal many rich geometrical and time-dependent features that should help our understanding of real microtubule dynamics.

The model studied in this paper [18] treats a microtubule as a linear polymer that consists of GTP or GDP monomers that we denote as + and −, respectively. To emphasize this connection between chemistry and the model, we write the former as GTP⁺ and the latter as GDP⁻. The state of a microtubule evolves by the following steps:

1. Attachment of GTP⁺ at the end of a microtubule:

   $$\begin{array}{cc}|\cdots \rangle \Rightarrow |\cdots +\rangle & \text{rate}\lambda \end{array}$$
2. Independent conversion of each GTP⁺ to GDP⁻:

   $$\begin{array}{cc}|\cdots +\cdots \rangle \Rightarrow |\cdots -\cdots \rangle & \text{rate}1.\end{array}$$
3. Detachment of a GDP⁻ from the microtubule end:

   $$\begin{array}{cc}|\cdots -\rangle \Rightarrow |\cdots \rangle & \text{rate}\mu .\end{array}$$

Here the symbols | and 〉 denote the terminal and the free end of the microtubule. It is worth mentioning that these steps are similar to those in a recently-introduced model of DNA sequence evolution [19], and that some of the results about the structure of DNA sequences seem to be related to our results about island size distributions in microtubules.

With the above steps for the evolution of a microtubule, we find that the (λ, μ) phase plane separates into a region where the microtubule grows, on average, and a phase where the microtubule length is finite. On the boundary between these two regions, the microtubule length fluctuates wildly. To understand these different phases, we first focus on the extreme cases of no detachment μ = 0 and infinite detachment rate μ = ∞, where we can analytically solve the microtubule structure.

No Detachment

Here GTP⁺ monomers attach at rate λ and convert to GDP⁻ at rate 1. The probability Π_N(t) that the microtubule consists of N GTP⁺ monomers at time t evolves according to

$$\frac{d{\Pi }_N}{dt}=-\left(N+\lambda \right){\Pi }_N+\lambda {\Pi }_{N-1}+\left(N+1\right){\Pi }_{N+1}.$$ (1)

The loss term (N + λ)Π_N accounts for the attachment of a GTP⁺ at the end of the microtubule of length N with rate λ and the conversion events GTP⁺ → GDP⁻ that occur with total rate N. The gain terms can be explained similarly. This equation can be solved by the generating function method and the final result is

$${\Pi }_N\left(t\right)=\frac{[\lambda \left(1-e^{-t}\right){]}^N}{N!}{e}^{-\lambda \left(1-e^{-t}\right)}.$$ (2)

From this Poisson distribution, the mean number of GTP⁺ monomers and its variance are

$$\langle N\rangle =\langle N^2\rangle -{\langle N\rangle }^2=\lambda \left(1-e^{-t}\right).$$ (3)

Similarly, the length distribution P(L, t) of the microtubule evolves according to the master equation

$$\frac{dP\left(L,t\right)}{dt}=\lambda \left[P\left(L-1,t\right)-P\left(L,t\right)\right]$$ (4)

For the initial condition P(L, 0) = δ_L,0, the solution is again the Poisson distribution

$$P\left(L,t\right)=\frac{{\left(\lambda t\right)}^L}{L!}{e}^{-\lambda t}$$ (5)

from which the growth rate of the microtubule and the diffusion coefficient of the tip are V = λ and D = λ/2.

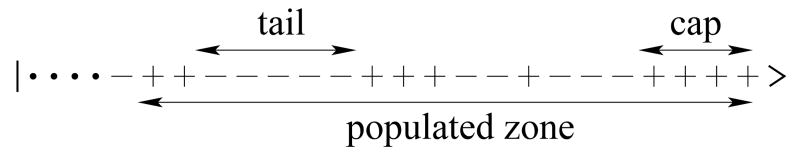
Because of the conversion of GTP⁺ to GDP⁻, the tip of the microtubule is comprised predominantly of GTP⁺, while the end exclusively consists of GDP⁻. The region from the tip until the first GDP⁻ is known as the cap (Fig. 2) and it plays a fundamental role in microtubule function. We use a master equation approach to determine the cap length distribution [20].

FIG. 2.

Representative configuration of a microtubule, with a cap of length 4, three GTP⁺ islands of lengths 1, 3, and 2, and three GDP⁻ islands of lengths 3, 2, and a “tail” of length 5. The rest of the microtubule consists of GDP⁻.

Consider a cap of length k. Its length increases by 1 due to the attachment of a GTP⁺ at rate λ. The conversion of any GTP⁺ into a GDP⁻ at rate 1 reduces the cap length from k to an arbitrary value s < k. These processes lead to the following master equation for the probability n_k that the cap length equals k:

$${\stackrel{·}{n}}_k=\lambda \left(n_{k-1}-n_k\right)-k{n}_k+\sum _{s\ge k+1}{n}_s.$$ (6)

Equation (6) remains valid for k = 0 if we set n₋₁ ≡ 0. We solve for the stationary distribution by summing the first k − 1 of Eqs. (6) with ${\stackrel{·}{n}}_k$ set to zero to obtain

$$n_{k-1}=\frac{k}{\lambda }\sum _{s\ge k}{n}_s.$$ (7)

The cumulative distribution, N_k = Σ_s≥k n_s, thus satisfies the recursion N_k = λN_k−1/(k + λ). Using the normalization N₀ = 1 and iterating, we obtain the solution in terms of the Gamma function [21]:

$$N_k=\frac{{\lambda }^k\Gamma \left(1+\lambda \right)}{\Gamma \left(k+1+\lambda \right)}.$$ (8)

Hence the cap length distribution is

$$n_k=\frac{\Gamma (1+\lambda \text{)}}{\Gamma \left(k+2+\lambda \right)}\left(k+1\right){\lambda }^k$$ (9)

From this distribution, we find that in the realistic limit of λ ≫ 1 the average cap length is given by

$$\begin{array}{ccc}\langle k\rangle \to \sqrt{\frac{\pi \lambda }{2}}& \text{as}& \lambda \to \infty \end{array}$$ (10)

Thus even though the average number of GTP⁺ monomers equals λ, only $\sqrt{\lambda }$ of them organize themselves into the microtubule cap.

At a finer level of resolution, we determine the distribution of island sizes in the GTP⁺-populated zone of a microtubule (Fig. 2). When λ → ∞, both the length of the cap and the length of the region that contains GTP⁺ become large and a continuum description is appropriate. Since the residence time of each monomer increases linearly with distance from the tip and the conversion GTP⁺ → GDP⁻ occurs independently, the probability that a monomer remains a GTP⁺ decays exponentially with distance from the tip. This fact alone is sufficient to derive all the island distributions.

Consider first the length ℓ of the populated zone (Fig. 2). For a monomer at a distance x from the tip, its residence time is τ = x/λ for large λ. Thus the probability that this monomer remains a GTP⁺ is e^−τ = e^−x/λ. We thus estimate ℓ from the extremal criterion [22]

$$1=\sum _{x\ge \ell }{e}^{-x/\lambda }=(1-e^{-1/\lambda }{)}^{-1}{e}^{-\ell /\lambda },$$ (11)

that merely states that there is of the order of a single GTP⁺ further than a distance ℓ from the tip. When λ is large, (1 − e^−1/λ)⁻¹ → λ, and the length of the active region scales as

$$\ell =\lambda \text{ln}\lambda$$ (12)

The probability that the cap has length k is given by

$$(1-e^{-\left(k+1\right)/\lambda })\prod _{j=1}^k{e}^{-j/\lambda }.$$

The product ensures that all monomers between the tip and a distance k from the tip are GTP⁺, while the prefactor gives the probability that a monomer a distance k + 1 from the tip is a GDP⁻. Expanding the prefactor for large λ and rewriting the product as the sum in the exponent, we obtain

$$n_k\sim \frac{k+1}{\lambda }{e}^{-k(k+1)/2\lambda },$$ (13)

a result that agrees with the large-λ limit of the exact result for n_k in Eq. (9).

Similarly, the probability to find a positive GTP⁺ island of length k that occupies sites x + 1, x + 2, …, x + k is

$$(1-e^{-x/\lambda })(1-e^{-\left(x+k+1\right)/\lambda })\prod _{j=1}^k{e}^{-\left(x+j\right)/\lambda }.$$ (14)

The two prefactors ensure that sites x and x + k + 1 are GDP⁻, while the product ensures that all sites between x + 1 and x + k are GTP⁺.

Most islands are far from the tip and they are short, k ≪ x, so that (14) simplifies to (1 − e^−x/λ)²e^−kx/λ. The total number of GTP⁺ islands of length k is obtained by summing this island density over all x. Since λ ≫ 1, we replace the summation by integration and obtain

$$I_k={\int }_0^{\infty }dx(1-e^{-x/\lambda }{)}^2{e}^{-kx/\lambda }=\frac{2\lambda }{k\left(k+1\right)\left(k+2\right)}.$$ (15)

By similar reasoning, we find that the density of negative GDP⁻ islands of length k ≪ x with one end at x is given by e^−2x/λ(1 − e^−x/λ)^k. The total number of negative islands of length k is therefore

$$J_k={\int }_0^{\infty }dx{e}^{-2x/\lambda }(1-e^{-x/\lambda }{)}^k=\frac{\lambda }{\left(k+1\right)\left(k+2\right)}.$$ (16)

Again, we find a power-law tail for the GDP⁻ island size distribution, but one that is much broader than the corresponding GTP⁺ distribution. Strikingly, these two distributions are of the same form as those found for the degree distribution of growing networks [23, 24]. The total number of GDP⁻ monomers within the populated zone is Σ_k≥1 kJ_k. While this sum formally diverges, we invoke the upper size cutoff, k_* ∼ λ that again follows from an extremal criterion [22] to obtain Σ_k≥1 kJ_k ≃ λ ln λ. Since the length of the populated zone ℓ ∼ λ ln λ, we thus see that this zone predominantly consists of GDP⁻ islands.

In analogy with the cap, consider now the “tail”—the last island of GDP⁻ within the populated zone (Fig. 2). The probability m_k that it has length k is

$$m_k=e^{-\ell /\lambda }(1-e^{-\ell /\lambda }{)}^k.$$ (17)

Hence, by summing the geometric series and using ℓ = λ ln λ from (12), the average length of the tail is

$$\langle k\rangle \equiv \sum _{k\ge 1}k{m}_k=e^{\ell /\lambda }-1\to \lambda .$$ (18)

Thus the tail is (on average) much longer than the cap. In summary, the microtubule consists of GTP⁺ islands that systematically get shorter away from the tip and vice versa for GDP⁻ islands (Fig. 3).

FIG. 3.

Cartoon of a microtubule. The GTP⁺ regions (dark) get shorter further from the tip that advances as λt, while the GDP⁻ regions (light) get longer.

Instantaneous Detachment

For μ > 0, a microtubule can recede if the monomer(s) at its tip are GDP⁻. If there are many such GDP⁻ end monomers the microtubule length can fluctuate wildly under steady conditions. Here we focus on the limiting case of instantaneous detachment, μ = ∞. As soon as the monomer at the tip changes from a GTP⁺ to a GDP⁻, this monomer and any contiguous GDP⁻ monomers detach immediately. We term such an event an avalanche of size k. If the avalanche encompasses the entire microtubule, we have a global catastrophe. The probability for such a catastrophe to occur is

$$\mathcal{C}\left(\lambda \right)=\frac{1}{1+\lambda }\prod _{n=1}^{\infty }(1-e^{-n/\lambda }).$$ (19)

The factor (1 + λ)⁻¹ gives the probability that the monomer at the tip converts to a GDP⁻ before the next attachment event, while the product gives the probability that all other monomers in the microtubule are GDP⁻. In principle, the upper limit in the product is set by the microtubule length. However, for n > λ, each factor in the product is close to 1 and the error made in extending the product to infinity is small.

The asymptotic behavior of the infinite product in Eq. (19) is found by first expressing it in terms of the Dedekind η function [25]

$$\eta \left(z\right)=e^{i\pi z/12}\prod _{n=1}^{\infty }(1-e^{2\pi \text{i}nz}),$$ (20)

and then recalling a remarkable identity satisfied by this function, $\eta \left(-1/z\right)=\sqrt{-iz}\eta \left(z\right)$. Using these facts, the probability of a catastrophe is given by

$$\begin{array}{l}\mathcal{C}\left(\lambda \right)=\frac{\sqrt{2\pi \lambda }}{1+\lambda }{e}^{-{\pi }^2\lambda /6}{e}^{1/24\lambda }\prod _{n\ge 1}(1-e^{-4{\pi }^2\lambda n})\\ \backsim \sqrt{\frac{2\pi }{\lambda }}{e}^{-{\pi }^2\lambda /6}.\end{array}$$ (21)

Since the time between catastrophes scales as the inverse of the occurrence probability, this inter-event time becomes astronomically long for large λ.

Similar arguments can be used to calculate the size distribution of finite avalanches. We first notice that the configuration $|+\underset{k-1}{\underbrace{-\cdots -}}+\rangle$ occurs with probability

$$\prod _{n=1}^{k-1}(1-e^{-n/\lambda }).$$

Then multiplying by the probability that the monomer at the tip converts before the next attachment event gives the probability for an avalanche of size k:

$$A_k={\left(1+\lambda \right)}^{-1}\prod _{n=1}^{k-1}(1-e^{-n/\lambda })$$ (22)

Using 1 − e^−n/λ ≈ n/λ − n²/(2λ²), Eq. (22) becomes

$$A_k={\lambda }^{-k}\Gamma \left(k\right)\prod _{n=1}^{k-1}\left(1-\frac{n}{2\lambda }\right)\sim {\lambda }^{-k}\Gamma \left(k\right)e^{-k^2/4\lambda }.$$

General Growth Conditions

For arbitrary attachment and detachment rates λ and μ, we can approximately map out the boundary between different phases of microtubule dynamics in the λ, μ parameter space. For λ, μ ≪ 1, the unit conversion rate GTP⁺ → GDP⁻ is much faster than the rates λ, μ of the other dynamical microtubule processes. Hence we assume that conversion is instantaneous. Consequently, a microtubule consists of a string of GDP⁻ monomers | ⋯ − − − 〉 in which the tip advances at rate λ and retreats at rate μ. Thus the tip performs a biased random walk, and its velocity is V (λ, μ) = λ − μ when λ > μ. The boundary between the growing phase, where the average tubule length grows as V t, and the compact phase, where the average tubule length is finite, is found by setting V = 0. This condition gives μ_* = λ when λ ≪ 1. On this phase boundary, the average tubule length grows as $\sqrt{t}$.

For the phase boundary for large μ, consider first μ = ∞. Since the leading behavior for the probability of a catastrophe scales as $e^{-{\pi }^2\lambda /6}$, the typical time between catastrophes is $e^{{\pi }^2\lambda /6}$. Since V ≈ λ for large λ, the typical length of a microtubule just before a catastrophe is again (ignoring all power-law factors) $e^{{\pi }^2\lambda /6}$. Suppose now the detachment rate μ is very large but finite. The microtubule is compact if the time to shrink a microtubule of length $e^{{\pi }^2\lambda /6}/\mu$ is smaller than the time λ⁻¹ required to generate a GTP⁺ by | ⋯ − 〉 ⇒ | ⋯ − + 〉 and thereby stop the shrinking. We estimate the location of the phase boundary by equating these two times to give ${\mu }_{\ast }\sim e^{{\pi }^2\lambda /6}$ when λ ≫ 1 (Fig. 4).

FIG. 4.

Schematic phase diagram for a microtubule in the λ-μ parameter space.

To summarize, our model predicts rich microtubule dynamics as a function of GTP⁺ attachment and GDP⁻ detachment. In the growing phase, GTP⁺ and GPD⁻ organize into alternating domains, with gradually longer GTP⁺ domains and gradually shorter GDP⁻ domains toward the tip of the microtubule. The size distributions of these two species are exact power laws with respective exponents of 3 and 2. Between the limiting cases of a finite-length and a growing microtubule, its length can fluctuate wildly under steady external conditions. This unusual behavior emerges naturally in our model. From a simple probabilistic approach and in the limit instantaneous detachment of GDP⁻ (μ = ∞), we found that the time between catastrophes, where the microtubule shrinks to zero length, scales exponentially with the attachment rate λ. Thus for large λ, the microtubule will grow essentially freely for a very long time before undergoing a catastrophe.