Complexities in the genetic structure of Anopheles gambiae populations in west Africa as revealed by microsatellite DNA analysis

Abstract

Chromosomal forms of Anopheles gambiae, given the informal designations Bamako, Mopti, and Savannah, have been recognized by the presence or absence of four paracentric inversions on chromosome 2. Studies of karyotype frequencies at sites where the forms occur in sympatry have led to the suggestion that these forms represent species. We conducted a study of the genetic structure of populations of An. gambiae from two villages in Mali, west Africa. Populations at each site were composed of the Bamako and Mopti forms and the sibling species, Anopheles arabiensis. Karyotypes were determined for each individual mosquito and genotypes at 21 microsatellite loci determined. A number of the microsatellites have been physically mapped to polytene chromosomes, making it possible to select loci based on their position relative to the inversions used to define forms. We found that the chromosomal forms differ at all loci on chromosome 2, but there were few differences for loci on other chromosomes. Geographic variation was small. Gene flow appears to vary among different regions within the genome, being lowest on chromosome 2, probably due to hitchhiking with the inversions. We conclude that the majority of observed genetic divergence between chromosomal forms can be explained by forces that need not involve reproductive isolation, although reproductive isolation is not ruled out. We found low levels of gene flow between the sibling species Anopheles gambiae and Anopheles arabiensis, similar to estimates based on observed frequencies of hybrid karyotypes in natural populations.

An. gambiae is extremely versatile regarding tolerance to a wide variety of micro- and macro-environmental conditions, as evidenced by its broad geographic distribution. In this species, ecological and behavioral plasticity is associated with polymorphisms in the form of paracentric chromosome inversions. The spatial distribution of certain gene arrangements show strong association with specific regional habitats, and their frequencies change seasonally, in places with seasonal fluctuations in the weather, especially rainfall (1–4). For this reason, chromosomally distinct subpopulations of An. gambiae have been recognized and referred to as chromosomal forms. The names Bamako, Mopti, and Savannah have been applied to chromosomal forms in west Africa. Studies of karyotype frequencies at sites where the three forms occur in sympatry have revealed significant departures from the Hardy–Weinberg (H-W) equilibrium (1–5). Specifically, heterokaryotypes representing hybrids between the Savannah form and the other two were under-represented, and Bamako-Mopti hybrids were never observed. This was inferred to result from partial reproductive isolation between Savannah and the other forms and complete isolation between the Bamako and Mopti forms. However, hybridization experiments involving crosses between the Bamako and Mopti forms typically result in viable offspring, indicating a lack of postmating reproductive barriers between them, at least in the laboratory (3, 6, 7). Estimates of genetic distance (based on allozyme frequencies) between the Bamako and Mopti forms are low, 0.015 (8), a value not higher than that typically found between local populations of a single anopheline species (9). We further observed that genotypic frequencies at 15 enzyme encoding loci in a population composed of three chromosomal forms in Mali did not depart from H-W expectations, suggesting that this population represents a single gene pool and that deficiencies in the frequencies of certain karyotypes may not be the result of reproductive isolation (G.L., unpublished data). For example, deficiencies of certain karyotypes might result from selection at these karyotypes alone and not representative of the genome as a whole. It should be emphasized that although these studies do not support reproductive isolation among chromosomal forms, they do not disprove it. For example, premating isolating mechanisms may act as a barrier between subpopulations, even if postmating mechanisms have not evolved, and isolation may be recent, so that insufficient time has passed for the accumulation of substantial allozyme divergence between forms. Recently Favia et al. (10, 11) have found random amplified polymorphic DNA and ribosomal RNA encoding gene regions which they report as being diagnostic for the Bamako and Mopti forms, leading them to suggest that these two represent species.

Difficulties in resolving the genetic structure of An. gambiae populations may be due, in part, to limitations in the approaches thus far applied to the problem. Karyotype frequencies themselves are poor markers for gene flow because their frequencies are apparently strongly effected by natural selection. The presence of inversion polymorphisms may pose a problem in estimating gene flow even when markers assumed to be neutral are used. Reduced recombination and selection can influence loci within or near inversions resulting in gene flow being lower relative to loci elsewhere in the genome.

Microsatellite DNA polymorphisms may be the best tool currently available for a study of the population genetics of An. gambiae (12). Approximately 130 microsatellite loci have been isolated and some of these cytogenetically mapped within the An. gambiae genome (13, 14). Studies using microsatellites may shed light on a number of basic problems in evolutionary genetics, which deal with the effects of chromosomal rearrangements on the distribution of genetic variation within the genome and their long-term impact on the genetic structure of populations.

MATERIALS AND METHODS

Collection Sites.

Samples of adult An. gambiae and An. arabiensis were obtained by using mouth aspirators from the walls of huts in Banambani and Selenkenyi, two villages near Bamako, Mali in west Africa. Banambani has been described by Touré (5, 15). It is located at 12° 48 min N and 8° 3 min W, approximately 20 km from Bamako. There are ≈700 inhabitants, most of who are Bambara. Located in the Sudan–Savannah region of Mali, Banambani is largely agricultural with sorghum, maize, and millet as the dominant crops. The An. gambiae population at Banambani is highly seasonal, corresponding to the availability of breeding sites created by rain during the wet season. The wet season typically extends from May to October, alternating with the dry season from November to April. During 1993, the year of our collection, the precipitation was 740 mm on 73 days.

Selenkenyi is a much larger village, with ≈700,000 inhabitants, most of who are Malinke and Bozo. It is located 140 km from Bamako, 11° 42 min N and 8° 17 min W, on the bank of the Sankarani river, in the Sikasso region. In this area, an important ecological change is underway, due to the existence of a hydroelectric dam (built in 1980). The dam has created an artificial lake (40 km long and 7 km wide), which provides water for rice cultivation (two harvests a year). The availability of permanent water provides breeding opportunities for mosquitoes, and An. gambiae adults are present throughout the year. Collections were made from Banambani on July 1–15, 1993 and from Selenkenyi a few weeks later, on August 4–7.

Cytological Examination of Polytene Chromosomes.

Chromosome preparations were made by extracting ovaries from the abdomen of each sample, following established protocols (16, 17). Species identification and karyotype scoring was done by using a phase-contrast microscope with the aid of the polytene chromosome map for the An. gambiae complex developed by Coluzzi, et al. (18). The chromosomal forms of An. gambiae were distinguished by scoring paracentric inversions on the right arm of chromosome 2 (3). The species/form composition was different between localities: (Banambani: 216 An. arabiensis, 57 Mopti, 17 Bamako, 8 Savannah, 5 Mopti-Savannah hybrids, and 2 Bamako-Savannah hybrids; Selenkenyi: 2 An. arabiensis, 170 Mopti, 46 Bamako, 8 Savannah, 10 Mopti-Savannah hybrids, and 5 Bamako-Savannah hybrids). Samples for microsatellite DNA analysis were taken from females whose karyotype had been determined.

Microsatellite Analysis.

Genotypes were determined at 21 microsatellite loci selected from 131 included in the genomic map of An. gambiae described by Zheng et al. (14). A total of 159 individuals of An. gambiae were analyzed: 62 Bamako form and 97 Mopti form and 61 An. arabiensis. Markers were chosen to achieve a representative sample of the entire genome (2n = 6), as follows: AGXH38, AGXH25, AGXH8, AGXH7, and AGXH293 on the X chromosome; AG2H175, AG2H156, AG2H79, AG2H26, AG2H125, AG2H95, AG2H135, AG2H637, AG2H603, and AG2H143 on chromosome 2; and AG3H128, AG3H119, AG3H83, AG3H158, AG3H88, and AG3H577 on chromosome 3 (14). Procedures for PCR amplification, gel separation, band visualization, and allele designation were as described in Lanzaro et al. (12). Autoradiographs were optically scanned and analyzed by using the Scanalytics (Billerica, ME) one-d scan software to determine fragment sizes. New primers were developed to test for the presence of null alleles at the AG3H158 and AG3H88 loci. For the AG3H158 locus, a primer was developed from flanking sequence 3′ of the repeat. The sequence for this primer was 5′-CGTTCATGTTCAAGACGATGGTGT-3′. For the AG3H88 locus, new primers were made both 5′ and 3′ of the repeat; these had the following sequence: 5′-AGCCCGGTCCATACTCATCCTA-3′ for the forward primer and 5′-CGCGCCGACAATACAAC-3′ for the reverse primer.

Statistical Analyses.

Data were analyzed by using the arlequin software package (available at http://anthropologie.unige.ch/arlequin/), developed by Excoffier and coworkers (19). Each locus was tested separately for significant departure from H-W equilibrium. These tests were done by using a Markov-chain algorithm (20), which is analogous to Fisher’s exact test. Pairwise linkage disequilibrium was tested for significance by a likelihood-ratio test. This statistic was calculated by the ratio of the likelihood of the data assuming linkage equilibrium and the likelihood not assuming linkage equilibrium obtained by using the Expectation–Maximization algorithm. The distribution of the likelihood ratio statistic was approximated under the null hypothesis of linkage equilibrium by a permutation procedure because of the large number of alleles per locus. Measures of genetic structure (R_ST and F_ST) were estimated by using the analysis of molecular variance (AMOVA) procedure (21). The AMOVA procedure is an analysis of variance framework with the significance of the variance components tested by permutation. Both F_ST and R_ST were tested for statistical significance by permuting individual genotypes among populations. The estimates of F_ST and R_ST differ in the way genetic differences were calculated. In the case of F_ST, the absolute frequencies of different alleles were used, and in the case of R_ST, the sum of squared number of repeat differences was used (22).

RESULTS AND DISCUSSION

Allele Frequencies.

In general, differences among alleles correspond to repeats of equal size but that was not observed in all cases. Distinguishing among “canonical” and “noncanonical” alleles seems somewhat arbitrary, so we followed the convention of Excoffier and coworkers (19) and recognized all alleles that differed in size to be distinct alleles. In nearly all of the cases, alleles could be inferred to be dinucleotide repeats. The few exceptions were assumed to be indels and were assigned to neighboring repeat classes (23).

Allele frequency distributions were analyzed by χ² tests to determine both the effects of collection site and chromosomal form in explaining differences among populations (Table 1). Because of low cell counts, adjacent size classes were, in some cases, pooled. In comparing populations at the two sites with chromosomal forms pooled at each site (Table 1, “combined”), only a single locus, AG3H88, was significantly different at the 0.01 level and none were significant at the 0.001 level. The aberrant behavior of AG3H88 probably resulted from a high frequency of null alleles, as discussed below. Although there were few differences between locations, there were many differences between forms. Ten of 21 loci were different at the 0.001 level between the Mopti and Bamako forms (collection sites pooled). A striking pattern is evident when these loci are studied on the basis of their chromosome linkage association. Nine of the 10 loci that differ at the 0.001 level are on chromosome 2, the chromosome on which inversions used to define these forms are located. The pattern is similar for other levels of significance. That is to say, there were few differences between locations, and chromosome forms differ consistently for the microsatellite alleles linked to the gene arrangements that define them but only sporadically for genes elsewhere in the genome.

Table 1.

Contigency χ² data for homogeneity of allele frequencies among four An. gambiae populations

Locus	d.f.	Effect of site			Effect of form
		Bamako	Mopti	Combined	Banambani	Selinkenyi	Combined
2R
AG2H26	4	1.83 (3 d.f.)	3.46	2.55	43.11‡	86.78‡	129.08‡
AG2H79	3	4.51	12.04†	3.52	27.45‡	40.80‡	53.43‡
AG2H95	2	3.02	4.33	0.08	21.04‡	48.84‡	64.92‡
AG2H125	3	0.86	1.75	0.15	6.03	13.91†	17.16‡
AG2H135	3	1.40	2.52	5.24	29.78‡	58.15‡	88.03‡
AG2H156	3	1.89	2.04	2.20	12.34†	29.75‡	39.62‡
AG2H175	3	14.09†	4.68	2.36	13.54†	39.37‡	38.78‡
2L
AG2H143	4	7.67	8.76	9.16	13.30†	10.02*	15.41†
AG2H603	4	0.54	2.74	4.90	7.24	18.23†	26.76‡
AG2H637	2	2.53	4.13	8.57*	35.67‡	35.02‡	70.29‡
3L
AG3H577	4	1.26	2.06	4.84	5.08	8.89	15.51†
3R
AG3H83	3	0.48	1.08	2.19	11.60†	11.83†	23.92‡
AG3H88	4	4.62	16.02†	17.14†	8.83	9.84*	15.60†
AG3H119	4	3.29	2.98	4.89	4.37	1.32	4.27
AG3H128	4	2.41	2.46	3.34	3.60	2.01	4.29
AG3H158	3	2.03	4.60	1.76	4.56	3.89	3.74
X
AGXH7	4	2.47	10.17*	6.18	5.28	6.81	5.54
AGXH8	2	4.17	3.91	5.69	3.26	1.82	2.75
AGXH25	3	10.98*	4.71	3.65	8.00*	8.50*	4.50
AGXH38	2	1.82	1.32	0.63	2.75	1.12	1.74
AGXH293	4	9.60*	5.98	7.79	6.38	4.51	3.50

Data were analysed to estimate the effects of collection site and chromosomal form. Loci are grouped by their chromosome location (2R, right arm of chromosome 2, 2L, left arm of chromosome 2, etc.); d.f., degrees of freedom. 

^*P < 0.05;  

^†P < 0.01;  

^‡P < 0.001. 

Genotype Frequencies.

Genotype frequencies were compared with H-W expectations by using a repeated sampling protocol (19). The results are shown in Table 2. In the pooled An. gambiae populations, 11 of 21 loci (52%) were away from the H-W equilibrium at the 0.01 level. When each of the four form and location subpopulations is tested individually, 12 of 84 tests (14%) are still significant at this level. It is apparent that the combined populations show more evidence of departure from H-W, consistent with a Wahlund effect from pooling subpopulations with unequal allele frequencies. But there are still substantial departures between local populations as well. Some of this is possibly the result of null alleles. For example, both AG3H88 and AG3H158 are on chromosome 3. Even casual inspection reveals an apparent excess of homozygotes at these loci. The possibility of null alleles occurring at these loci was examined by designing new PCR primers for these loci from sequence flanking the repeat. Five of 7 and 17 of 18 samples that failed to yield PCR product with the original primers, for the AG3H88 and AG3H158 locus, respectively, did yield product with the new primer, indicating that nonamplification was due to nucleotide substitutions in the primer-annealing sites. The departures from H-W are examined in more detail in the discussion of R_ST and F_ST below.

Table 2.

Statistical significance of deviations from Hardy–Weinberg expectations for 21 loci in populations of An. gambiae in Mali, west Africa

		An. gambiae spp.		Banambani-Bamako		Banambani-Mopti		Selinkenyi-Bamako		Selinkenyi-Mopti		An. arabiensis
	LOCUS	Exact P	Conf.	Exact P	Conf.	Exact P	Conf.	Exact P	Conf.	Exact P	Conf.	Exact P	Conf.
2	AG2H26	0.00000	0.00000	0.00117	0.00013	0.01096	0.00022	0.00000	0.00000	0.20168	0.00102	0.00000	0.00000
	AG2H79	0.00615	0.00013	0.47235	0.00136	0.33538	0.00131	0.00409	0.00017	0.01311	0.00040	0.10807	0.00078
	AG2H95	0.00000	0.00000	0.80151	0.00125	0.03206	0.00061	0.01603	0.00037	0.80716	0.00103	0.98913	0.00027
	AG2H125	0.03705	0.00047	0.99185	0.00028	0.04884	0.00053	0.41270	0.00147	0.17165	0.00057	0.00002	0.00001
	AG2H135	0.00000	0.00000	0.08418	0.00060	0.00933	0.00014	0.21567	0.00092	0.51357	0.00065	0.27399	0.00117
	AG2H143	0.27439	0.00066	0.28902	0.00146	0.66844	0.00134	0.02859	0.00051	0.94255	0.00058	0.38128	0.00094
	AG2H156	0.11272	0.00066	0.12599	0.00104	0.42440	0.00125	0.77045	0.00111	0.46289	0.00127	0.04490	0.00062
	AG2H175	0.00000	0.00000	0.29816	0.00148	0.02353	0.00028	0.02523	0.00045	0.06253	0.00070	0.03196	0.00054
	AG2H603	0.02495	0.00035	0.81586	0.00063	0.70251	0.00036	0.04988	0.00037	0.12744	0.00035	0.01968	0.00027
	AG2H637	0.00000	0.00000	0.00308	0.00010	0.10076	0.00084	0.00000	0.00000	0.01345	0.00026	0.00347	0.00018
X	AGXH7	0.00448	0.00017	0.14779	0.00095	0.12469	0.00084	0.02407	0.00036	0.21789	0.00122	0.41260	0.00100
	AGXH8	0.15217	0.00092	1.00000	0.00000	0.01308	0.00032	0.79528	0.00102	0.72936	0.00102	N/A	N/A
	AGXH25	0.22930	0.00102	0.95383	0.00067	0.38715	0.00103	0.01609	0.00037	0.52651	0.00120	1.00000	0.00000
	AGXH38	0.31433	0.00105	0.29679	0.00139	0.37330	0.00149	0.69395	0.00110	0.31004	0.00105	0.71683	0.00095
	AGXH293	0.00000	0.00000	0.12524	0.00056	0.00594	0.00013	0.00045	0.00006	0.03165	0.00021	N/A	N/A
3	AG3H83	0.00667	0.00022	0.07456	0.00071	0.10308	0.00086	0.32397	0.00120	0.33327	0.00162	0.00756	0.00027
	AG3H88	0.00000	0.00000	0.56645	0.00092	0.00000	0.00000	0.48575	0.00152	0.00029	0.00005	0.10824	0.00092
	AG3H119	0.93063	0.00045	0.84166	0.00072	0.76455	0.00080	0.31783	0.00057	0.36782	0.00104	0.73339	0.00058
	AG3H128	0.74218	0.00038	1.00000	0.00000	0.55412	0.00069	0.95465	0.00031	0.16586	0.00038	0.40356	0.00061
	AG3H158	0.00000	0.00000	0.71960	0.00052	0.00013	0.00004	0.00057	0.00007	0.08037	0.00049	0.00000	0.00000
	AG3H577	0.56293	0.00069	0.96560	0.00047	0.23865	0.00075	0.92098	0.00061	0.37422	0.00074	0.54111	0.00071

“Conf” refers to the standard error of the probability of a deviation as large or larger than that observed, “Exact P”. See ref. 19 for details of the calculations. Underlined areas refer to P < 0.01. Loci are grouped by chromosome location. 

Gametic Phase Disequilibrium.

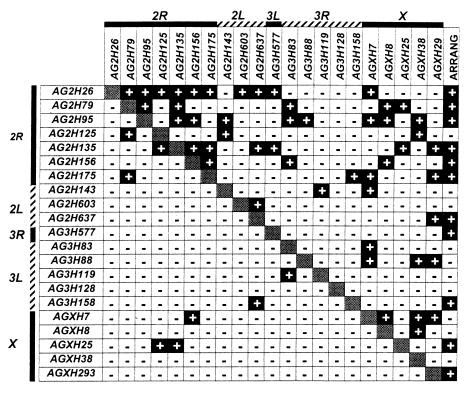
All pairwise coefficients of gametic phase disequilibrium were calculated for the pooled An. gambiae populations. Those significant at the 0.01 level are shown in Fig. 1, above the diagonal. Coefficients of disequilibrium also were calculated for An. arabiensis (Fig. 1, below diagonal). For each species, there are 210 more-or-less independent comparisons, so we would expect 2–3 of them to be significant at the 0.01 level by chance alone. For An. gambiae there were 49 values that were statistically significant at the 0.01 level, so we must infer that gametic phase disequilibrium was widespread for this species. There was far less linkage disequilibrium in An. arabiensis, only eight values were statistically significant, but also in slight excess of what should be expected by chance alone.

Figure 1.

Pairwise gametic phase disequilibria for 21 microsatellite loci for pooled An. gambiae populations (above diagonal) and An. arabiensis (below diagonal). Black boxes with + sign indicate significant (0.01 level) linkage disequilibrium; white boxes with a − sign indicate lack of significant (0.01 level). Loci are grouped by linkage association, indicated at top and far left. 2R, right arm of chromosome 2; 2L, left arm of chromosome 2, etc.; ARRANG., chromosome 2R gene arrangements, treated as alleles for purposes of calculating gametic phase disequilibria.

The numbers of statistically significant–nonsignificant interactions involving chromosome 2 in An. gambiae were 60:40; for loci on chromosome 3 the numbers were 13:107; and for those on the X chromosome the numbers were 25:75. The values for chromosome 2 are significantly different from the others, G = 17.2; 2 degrees of freedom; P < 0.001. The two most likely explanations for this disequilibrium would seem to be association with inversions on chromosome 2 and structuring of the population. Included in Fig. 1, in the far right column, are linkage disequilibria for gene arrangements with the microsatellite loci. For these comparisons, the various gene arrangements are regarded as alleles. It is apparent that all three chromosomes contributed to the disequilibrium; hence it would seem that the populations were structured. That loci on chromosome 2 showed the greatest amount of disequilibrium suggests, but does not prove, that the gene arrangements themselves also were involved.

We investigated this further by looking at gametic phase disequilibrium within each population separately. The overall occurrence of linkage disequilibrium within each population was less than that observed in the pooled population; in the pooled sample, 23% of the pairwise comparisons were statistically significant at the 0.01 level, whereas a comparable average 4.9% of the comparisons were significant in the unpooled populations. This latter figure is somewhat more than the 1% expected to be significant by chance alone. It is likely that some of the difference between the pooled and unpooled populations are the result of differences in sample size, but the possibility remains that some disequilibrium resulted from differences in allele frequencies among populations large enough to cause a Wahlund effect (24).

Population Structure.

Differences in allele frequencies between locations and forms were studied by using two measures—F_ST and R_ST. These measures differ in their assumptions about the mode of mutation; viz. F_ST is the appropriate measure of differentiation if mutations occur equally to all alleles (infinite allele model), whereas R_ST is theoretically better if mutations occur more commonly to alleles with similar numbers of repeats, especially if mutations occur only to alleles a single repeat unit away (step-wise mutation model). Simulations by Slatkin (22) showed that, over the range of N_em values observed here and where there was imperfect adherence to the single step mutation model, F_ST and R_ST gave approximately equal values, although F_ST had consistently smaller standard errors. In practice, the best measure to use is far from clear (25, 26), so we present both F_ST and R_ST in Table 3. Unlike some reports (26), the two measures calculated here are similar, in accordance with Slatkin (22). Rank-order correlations for F_ST and R_ST values in this table were high, ranging from 0.61 on chromosome 3 (where most differences in allele frequencies were not statistically significant, and thus largely the result of chance) to 0.89 on chromosome 2 (where many differences were significant). In view of the theoretical advantage to stepwise mutation measures (27), for brevity our discussion will emphasize R_ST.

Table 3.

R_ST (above diagonal) and F_ST (below diagonal), two measures of population structure among subpopulations of An. gambiae spp. in Mali, west Africa

	BnB	SeB	BnM	SeM	BnR
All Loci
BnB	—	−0.01690  (0.915)	0.02433  (0.057)	0.02303  (0.073)	0.18186  (0.000)
SeB	0.00217  (0.394)	—	0.02617  (0.003)	0.02312  (0.011)	0.17365  (0.000)
BnM	0.04225  (0.000)	0.02553  (0.000)	—	−0.00022  (0.461)	0.17260  (0.000)
SeM	0.04758  (0.000)	0.04111  (0.000)	0.00566  (0.028)	—	0.18089  (0.000)
BnR	0.16618  (0.000)	0.15078  (0.000)	0.16124  (0.000)	0.17105  (0.000)	—
2R Loci
BnB	—	−0.00908  (0.600)	0.06207  (0.011)	0.08294  (0.003)	0.12113  (0.001)
SeB	0.01441  (0.047)	—	0.07287  (0.000)	0.07829  (0.000)	0.12881  (0.000)
BnM	0.06653  (0.000)	0.04180  (0.000)	—	−0.00401  (0.666)	0.15169  (0.000)
SeM	0.08899  (0.000)	0.07335  (0.000)	0.00718  (0.031)	—	0.18575  (0.000)
BnR	0.16643  (0.000)	0.13954  (0.000)	0.12795  (0.000)	0.14175  (0.000)	—
X Loci
BnB	—	0.03529  (0.059)	0.08703  (0.019)	0.03645  (0.081)	0.59629  (0.000)
SeB	−0.01980  (0.998)	—	0.00056  (0.335)	−0.01358  (0.993)	0.64714  (0.000)
BnM	−0.00825  (0.685)	−0.00372  (0.706)	—	0.00958  (0.165)	0.63941  (0.000)
SeM	−0.01380  (0.920)	0.00303  (0.329)	0.00585  (0.194)	—	0.66666  (0.000)
BnR	0.25568  (0.000)	0.25200  (0.000)	0.25430  (0.000)	0.26945  (0.000)	—
3R Loci
BnB	—	−0.02169  (0.933)	0.00118  (0.391)	−0.01198  (0.739)	0.14396  (0.000)
SeB	−0.00654  (0.890)	—	0.00297  (0.257)	−0.00438  (0.591)	0.12788  (0.000)
BnM	0.02387  (0.005)	0.01278  (0.003)	—	0.00159  (0.363)	0.12066  (0.000)
SeM	0.00711  (0.168)	0.00814  (0.031)	0.00346  (0.208)	—	0.10961  (0.000)
BnR	0.12513  (0.000)	0.12150  (0.000)	0.16615  (0.000)	0.16807  (0.000)	—

Statistical significance is shown in parentheses. These were calculated using the arlequin statistical package (19) by using a repeated sampling procedure. 

The product of effective population size, N_e, and migration rate, m, is a useful and commonly used measure of gene flow. Values of N_em, estimated from R_ST and F_ST calculated separately by chromosome according to Slatkin (22), are presented in Table 4. Such estimates between the Bamako and Mopti forms show a marked difference in the level of gene exchange at loci on the several chromosomes. Estimates of gene flow for loci on both the X chromosome and chromosome 3 are quite high (N_êm = 20 to ∞) whereas comparable values for loci on chromosome 2 are much lower (N_êm = 3.3–3.4), but still greater than expected if the forms were reproductively isolated. Between species gene flow was low as expected, ranging between 0.19 and 1.8.

Table 4.

Estimated N_em for An. gambiae spp. chromosomal forms and An. arabiensis

	Estimates from RST
	X chromosome	Chromosome 2	Chromosome 3	All
Bamako vs. Mopti	∞	3.4	∞	10.3
Bamako vs. arabiensis	0.23	1.8	1.5	1.1
Mopti vs. arabiensis	0.19	1.4	1.8	1.2
	Estimates from FST
	X chromosome	Chromosome 2	Chromosome 3	All
Bamako vs. Mopti	∞	3.3	20.3	5.8
Bamako vs. arabiensis	0.97	1.2	1.7	1.2
Mopti vs. arabiensis	0.98	1.7	1.3	1.3

Results are presented for loci grouped by chromosome and averaged over all loci. The values shown for “Bamako vs. Mopti” are the mean of that value over the Selinkenyi and Banambani subpopulations. For gene flow with An. arabiensis only values from the Banambani subpopulation could be calculated. Values of N_em for the X chromosome are predicated on the assumption that N_e of the X chromosome is two-thirds that for the autosomes. 

Locations.

In no instance were there statistically significant differences between the two locations within a single chromosomal form (Table 3). This is in accord with observations by Lehmann and coworkers for gene flow across areas within the Savannah chromosomal form (23, 28), though they speculate that some barriers to gene flow have been observed in east Africa (29).

Species.

An. gambiae differs significantly from An. arabiensis in all instances shown in Table 3. Gene flow between these two clearly established species is much less than between chromosomal forms.

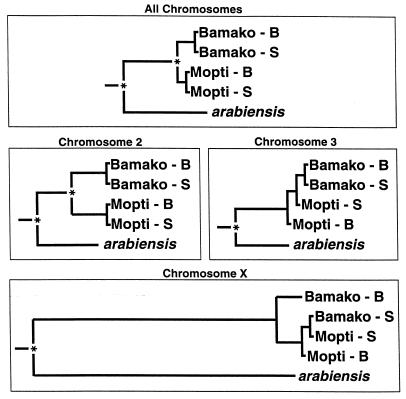
It is possible to compare estimates of N_em derived from microsatellite DNA variation to similar values calculated from chromosome studies and direct observations of hybridization frequency. Effective population sizes have been estimated from mark-release-recapture experiments (15) and from fluctuations in gene arrangement frequencies (30). Both studies gave an estimate of N_e to be 2,000–6,000, approximately. At the same time, Touré et al. (4) observed three An. gambiae-An. arabiensis hybrids in their survey of 17,705 polytene chromosome preparations from throughout Mali, the remainder clearly belonging to one species or the other. Combining these values, we get an estimate of N_em observed from chromosome data to be 0.34–1.02, quite in accord with the comparable estimates of 0.19–1.80 calculated here from microsatellite DNA data. This agreement lends credence to the values of N_em estimated for gene flow between the Bamako and Mopti chromosomal forms. That value (10.3) is thought to be much too high for populations which are reproductively isolated (31, 32). The estimates of N_em between An. gambiae and An. arabiensis were lower on the X compared with the autosomes. This observation may be the result of forces opposing introgression of the X chromosome, as described by della Torre et al. (33). A phenogram based on R_ST values for each chromosome separately and for the pooled ensemble is presented in Fig. 2. These were prepared with an unweighted pair-group method with arithmetic averaging of R_ST values, calculated with the phylip software package (34). Notations at the nodes of trees indicate statistically significant values of R_ST (obtained from arlequin). The phenograms for chromosome 2 and for the ensemble are similar and agree with the prevailing taxonomy of Coluzzi et al. (3). That is to say, chromosomal forms cluster together regardless of location. The chromosome 2 loci provide a pattern that was most similar to the pooled loci, possibly because 10/21 of the loci were on this chromosome, and possibly because they are associated with the gene arrangements that define and characterize the chromosomal forms. The X chromosome showed very sharp differences between species but did not show much differentiation among the chromosomal forms. The chromosome 3 loci likewise did not show much differentiation among forms, although species differences were clearly observed. It would appear that classification based on chromosome 2 is not characteristic for the genome as a whole.

Figure 2.

Phenograms based on Unweighted pair-group method with arithmetic averaging of R_ST values to illustrate relationships among the An. gambiae chromosomal forms and An. arabiensis. Separate phenograms illustrate results for loci on all chromosomes and for loci on each chromosome separately. Bamako-B, Bamako form from the village of Banambani; Mopti-S, Mopti form from the village of Selenkenyi; etc. An “∗” indicates that two or more members of the joining operational taxonomic units differ statistically at the 0.01 level by an analysis of molecular variance (AMOVA) test for the loci on that chromosome combined. See text for further explanation.

CONCLUSIONS

An. gambiae is the nominal species in a complex composed of six sibling species. Within the taxon An. gambiae, several subspecific chromosomal forms have been described, which may or may not represent additional species. The major objective of this study was to describe the genetic structure of An. gambiae populations as a means of determining to what extent these chromosomal forms are genetically distinct. The primary basis for identifying chromosomal forms lies with the deficiency of heterozygotes for gene arrangements among forms. The most likely explanations for this heterozygote deficiency are: (i) reproductive isolation between forms; or (ii) natural selection against certain of the heterozygotes, so that adult females (karyotypes are only obtained from females) would not be observed. Was reproductive isolation the explanation, then we would expect, all else being equal, to find that the forms differ throughout their genomes. This was not observed. Rather, gene flow was moderately low between forms for loci on the second chromosome (N_em ∼ 3–4) but quite high for loci on the other chromosomes (N_em ∼ 20-∞). This seems to favor the hypothesis that gene flow was restricted by selection against loci on the second chromosome, and not by reproductive isolation.

It must be recognized, however, that these estimates of gene flow are predicated on the assumption of equilibrium conditions, and those equilibria may take a very long time to become established. Transportation, agriculture, irrigation, and human modification of the environment have changed dramatically in the past few decades in this area. So while the estimates of gene flow between An. gambiae and An. arabiensis obtained from microsatellite DNA variation do seem consistent with those obtained from direct observation, this need not be the case for gene flow among chromosomal forms. Although the observations made here do suggest that the majority of observed microsatellite divergence between the two chromosomal forms is not the result of reproductive isolation, the alternative explanation of reproductive isolation cannot be ruled out absolutely.

ABBREVIATION

H-W

Hardy–Weinberg equilibrium