High-pressure synthesis of the cubic perovskite BaRuO₃ and evolution of ferromagnetism in ARuO₃ (A = Ca, Sr, Ba) ruthenates

Abstract

The cubic perovskite BaRuO₃ has been synthesized under 18 GPa at 1,000°C. Rietveld refinement indicates that the new compound has a stretched Ru–O bond. The cubic perovskite BaRuO₃ remains metallic to 4 K and exhibits a ferromagnetic transition at T_c = 60 K, which is significantly lower than the T_c ≈ 160 K for SrRuO₃. The availability of cubic perovskite BaRuO₃ not only makes it possible to map out the evolution of magnetism in the whole series of ARuO₃ (A = Ca, Sr, Ba) as a function of the ionic size of the A-site r_A, but also completes the polytypes of BaRuO₃. Extension of the plot of T_c versus r_A in perovskites ARuO₃ (A = Ca, Sr, Ba) shows that T_c does not increase as the cubic structure is approached, but has a maximum for orthorhombic SrRuO₃. Suppressing T_c by Ca and Ba doping in SrRuO₃ is distinguished by sharply different magnetic susceptibilities χ(T) of the paramagnetic phase. This distinction has been interpreted in the context of a Griffiths' phase on the (Ca Sr)RuO₃ side and bandwidth broadening on the (Sr,Ba)RuO₃ side.

Transition-metal oxides with perovskite (1) and perovskite-related compounds have been extensively studied in recent years; for example, high-T_c superconductivity in copper oxides, the colossal magnetoresistance effect in manganese oxides, and more recently multiferroic phenomena. Because perovskite has a densely packed crystal structure (2), high-pressure synthesis, which is widely used in the field of geoscience for studying the lower mantle, is very effective and critical, in some cases, to synthesize compounds with the perovskite structure (3). Application of the high-pressure technique enables us to explore new perovskites that are not formed under ambient pressure and have unknown physical properties.

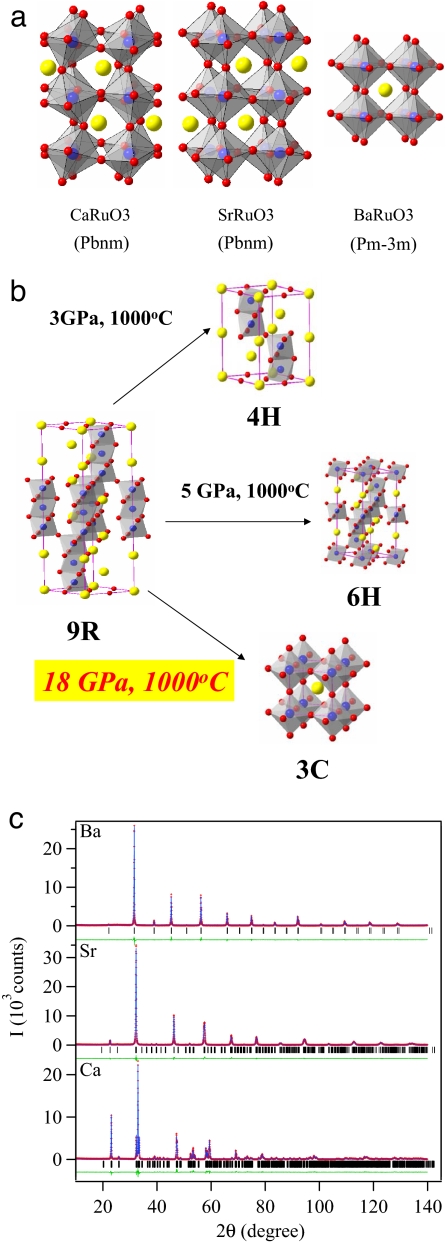
The ruthenium oxides with perovskite-related structure have received growing attention because they exhibit physical properties such as a superconductivity in Sr₂RuO₄ (4), the meta magnetic metallic behavior of Sr₃Ru₂O₇ (5), and quantum phase transitions in BaRu₆O₁₂ (6). The perovskites ARuO₃ (A = Sr, Ca) are technically important materials as a conducting buffer layer in electronic devices. Moreover, the cause of the unusual disappearance of ferromagnetism in the Sr_1−xCa_xRuO₃ is currently under hot debate. In the orthorhombic perovskite with Pbnm space group shown in Fig. 1a, the magnetic coupling in these ARuO₃ (A = Ca and Sr) perovskites is determined by the Ru–O–Ru bond angle and Ru–O covalent bonding. CaRuO₃ remains paramagnetic to the lowest temperature (7, 8), but it is near the verge of ferromagnetic order (9, 10). However, SrRuO₃ is an itinerant-electron ferromagnet with a T_c ≈ 164 K (11–16). As a representation of currently popular models about the ferromagnetism in SrRuO₃, Mazin and Singh (17) have calculated the band structure of Sr_1−xCa_xRuO₃ by taking into account the cooperative RuO₆ site rotation that bends the Ru–O–Ru bond angle from 163° in SrRuO₃ to148° in CaRuO₃; they found that the increased bending of the Ru–O–Ru bond angle reduces the band degeneracy and, therefore, the density of electronic states at the Fermi energy ρ(ε_F), perhaps to where the Stoner criterion ρ(ε_F)U ≈ 1, where ρ(ε_F) is the electron at the Fermi energy and U is the electron correlation energy, is no longer valid in CaRuO₃. This model predicts that the maximum T_c will be achieved as the high-symmetry cubic structure is approached because a higher ρ(ε_F) is created at high-symmetry points in the Brillouin zone. The striking difference of the magnetic properties between SrRuO₃ and CaRuO₃ makes cubic perovskite BaRuO₃ an interesting candidate since an ideal cubic perovskite is expected because of the larger A-site ionic radius. Mapping out the evolution of the magnetism for the whole perovskite series of ARuO₃ from A = Ca across Sr to Ba will shed a new light on the mysterious itinerant-electron ferromagnetism in these ruthenates. However, a literature search shows that BaRuO₃ has polytype structures (18–20) depending on how it is synthesized, i.e., the nine-layered rhombohedral (9L), the four-layered hexagonal (4H), and the six-layered hexagonal (6H) as shown in Fig. 1b. All of these polytype structures can be described by different stacking sequences of RuO₆ octahedra along the c axis. High-pressure synthesis of an AMO₃ compound as a cubic perovskite is necessary where the mismatch between the equilibrium (A–O) and (M–O) bond lengths gives a tolerance factor $t\equiv (A-O)/\sqrt{(M-O)}>1$ > 1. The perovskite structure can accommodate a t <1 by a cooperative rotation of the corner-shared MO₆ octahedra, which bends the M–O–M bond angle from 180° to (180° − φ) and lowers the symmetry from cubic, but it accommodates to a t > 1 by forming hexagonal polytypes (3). Tabulated ionic radii (21) give room-temperature BaRuO₃ a t = 1.0625, and it crystallizes as a 9R polytype with close-packed BaO₃ layers stacked cubic-hexagonal-hexagonal-cubic…along the c axis. Because the (M–O) bond is less compressible than the (A–O) bond for most A²⁺M⁴⁺O₃ compounds (3), pressure reduces t. Therefore, sintering under high pressure results in the structure sequence in BaRuO₃ from 9R to 4H and to 6H polytypes as reported in the literature. The end member in this family, the perovskite structure (3C), could not be synthesized under the highest pressure available in early days. Here, we report that the perovskite BaRuO₃ can be obtained under 18 GPa at 1,000°C, nearly the same pressure found at the boundary of the Earth's Upper and Lower mantle. The new compound has the cubic perovskite structure with space group Pm-3m.

Fig. 1.

The crystallography of ARuO₃. (a) Schematic drawing of the three perovskites CaRuO₃, SrRuO₃, and BaRuO₃ where red balls stand for O, blue balls for Ru, and yellow balls for alkaline earth Ca, Sr, and Ba. (b) The crystal structures of the BaRuO₃ polytypes. Blocks of the face-shared and corner-shared RuO₆ octahedra are stacked alternately along the c axis. (c) X-ray powder diffraction spectra of the perovskites CaRuO₃, SrRuO₃, and BaRuO₃ and their best fit with the Rietveld analysis at room temperature.

Results and Discussion

Fig. 1c shows that all x-ray diffraction peaks of the high-pressure product under 18 GPa of BaRuO₃ can be indexed with cubic perovskite structure of space group Pm-3m. Results of Rietveld analysis of the x-ray diffraction for perovskite ruthenates ARuO₃ (A = Ca, Sr, Ba) are given in Table 1, which illustrates a systematical structural change from CaRuO₃ to SrRuO₃ and to BaRuO₃. The significant structural changes as a function of r_A include (i) the bending of the (180° − φ) Ru–O–Ru bonds decreases from 148.6° in CaRuO₃ to 162.6 ° in SrRuO₃ and finally to 180° in cubic BaRuO₃; (ii) the (Ru–O) bond length d = 2.003 Å in cubic BaRuO₃ is slightly stretched in comparison with the average Ru–O bond length d = 1.986 Å in SrRuO₃ and d = 1.996 Å in CaRuO₃; (iii) the octahedral-site distortion as measured by the difference between three Ru–O bond lengths becomes more obvious in CaRuO₃, but it remains within the level of intrinsic structural distortion generally found in the orthorhombic perovskite structure with Pbnm space group. The cubic BaRuO₃ is stable down to 10 K as checked by x-ray diffraction.

Table 1.

Results of the Rietveld refinement of the x-ray diffraction of Fig. 1c

	CaRuO3(Orthorhombic)	SrRuO3 (Orthorhombic)	BaRuO3(Cubic)
Space group	Pnma(62)	Pnma(62)	Pm-3m(221)
a, Å	5.35744(3)	5.57108(4)	4.0059(2)
b, Å	5.53298(3)	5.53543(4)
c, Å	7.66333(4)	7.85040(7)
Ru-O1 (Å) ×2	1.9909(4)	1.9842(7)	2.0029
Ru-O2 (Å) ×2	2.000(3)	1.986(7)
Ru-O2 (Å) ×2	1.997(2)	1.988(6)
Ru-O1-Ru, °	148.60(2)	163.08(3)	180
Ru-O2-Ru, °	148.7(1)	162.4(3)
Rp, %	8.19	5.9	7.6
χ 2	3.1	2.3	2.5

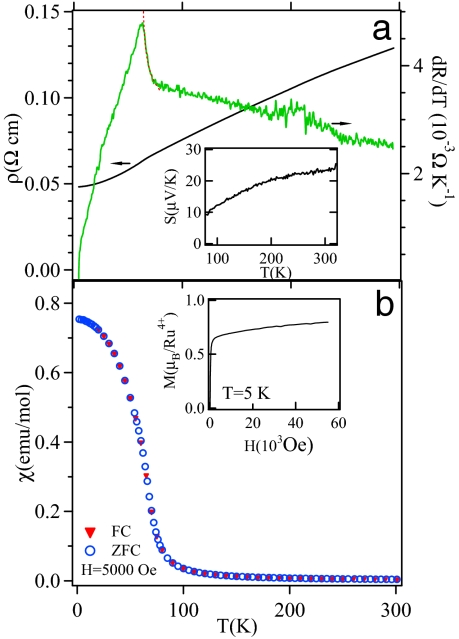
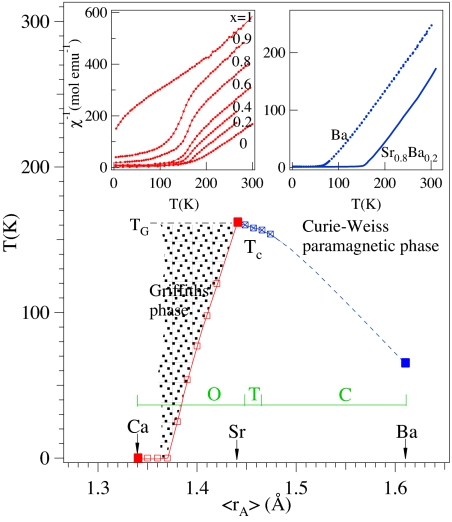
The transport properties of Fig. 2 show that cubic BaRuO₃ remains metallic down to 4.2 K. However, the ferromagnetic transition temperature T_c is 60 K, ≈100 K lower than that of SrRuO₃, and the saturation magnetization at 5 K in a magnetic field of 5 Tesla remains near 0.8 μ_B/Ru, far <2.0 μ_B/Ru expected for a localized electron-spin-only moment for low-spin Ru(IV):t⁴e⁰ and significantly lower than the 1.4 μ_B/Ru in SrRuO₃. A small substitution of Ba for Sr in Sr_1−yBa_yRuO₃ does not change the magnetization at 5 K; it remains ≈1.4 μ_B/Ru. However, the effective magnetic moment μ_eff ≈ 2.6 μ_B/Ru calculated from the paramagnetic phase, which is close to the spin-only 2.8 μ_B/Ru for S = 1, is similar for all of the Ba doped Sr_1−yBa_yRuO₃ perovskites in this study. The thermoelectric power S(T) (Fig. 2 Inset) of the perovskite BaRuO₃ is nearly identical to that of CaRuO₃ (22) and it is ≈5 μV/K smaller than that of SrRuO₃ at room temperature (15). We have fit dρ/dT of BaRuO₃ in the vicinity of T_c with the scaling law |(T − T_c)/T_c|^−α. The fitting for T → T_c from above gives an α = 0.11, which matches well theoretical prediction for itinerant-electron ferromagnetism (23). However, the law fails to describe dρ/dT as T → T_c from below. Beyond the critical spin-fluctuation range near T_c, however, ρ(T) of BaRuO₃ shows a temperature dependence similar to that of SrRuO₃ below and above T_c. As T approaches 4.2 K, ρ(T) is described by the power law ρ(T) − ρ(0) ∼ T², indicating a Fermi-liquid character. The availability of Sr_1−yBa_yRuO₃ with perovskite structure and the literature data for well studied Ca_1−xSr_xRuO₃ allows us to map out completely T_c versus 〈r_A〉 for the whole family of ARuO₃ perovskites as shown in Fig. 3. Interestingly, T_c peaks out at 〈r_A〉 ≈ r_Sr where it remains within the orthorhombic phase. A preliminary result shows that the transition to a cubic phase occurs at y ≈ 0.15 in Sr_1−yBa_yRuO₃. For the compositions with Ba doping y >0.15, the Ru–O bond is stretched from its equilibrium value. One should keep in mind that the size variance (i.e., the composition combination) induced by Ca or Ba doping will also reduce the magnetic transition temperature T_c as has been demonstrated (24). This effect, however, has little to do with a complete suppression of the ferromagnetic transition in CaRuO₃ and a dramatic reduction of T_c in cubic BaRuO₃. The symmetry argument as mentioned in the introduction also does not work because T_c is reduced in cubic BaRuO₃. To identify the mechanism of T_c suppression beyond the size variance induced by the Ca and Ba doping on both sides of SrRuO₃, we made a comparison between two compositions of Sr_1−xCa_xRuO₃ and Sr_1−yBa_yRuO₃ with approximately the same σ² = (〈r_A²〉 − 〈r_A〉²) (a measure to define size variance) (24). As a matter of fact, all compositions of Sr_1−yBa_yRuO_3, including y = 0, show typical Curie–Weiss (CW) behavior at T > T_c and Gaussian or critical fluctuations in the vicinity of T_c, whereas compositions of Sr_1−xCa_xRuO₃ show an unusual χ⁻¹(T) as T_c is approached in the paramagnetic phase, as is shown in Fig. 3 Inset. It is clear that the T_c reductions in Sr_1−xCa_xRuO₃ and Sr_1−yBa_yRuO₃ appear to be caused by different mechanisms.

Fig. 2.

The primary electric and magnetic properties of BaRuO₃ cubic perovskite. (a) Temperature dependence of the resistivity ρ and its derivative dρ/dT of cubic BaRuO₃; dashed line on the curve dρ/dT vs. T is a curve fitting to the formula |(T − T_c)/T_c|^−α, α = 0.11. (Inset) Shown is the temperature dependence of thermoelectric power. (b) Temperature dependence of the molar magnetic susceptibility of perovskite BaRuO₃. (Inset) Shown is the magnetization at 5 K.

Fig. 3.

Phase diagram of the magnetic transition temperatures versus the tabulated average A-site ionic radius 〈r_A〉 for Sr_1−yBa_yRuO₃ and Sr_1−xCa_xRuO₃. Three members in the phase diagram CaRuO₃, SrRuO₃, and BaRuO₃, in which the A-site size variance is zero, are distinguished by the solid symbols. The shaded area in the phase diagram represents the phase having the characteristic χ⁻¹(T) of the Griffiths' phase. Letters inside the diagram stand for the crystal structure as determined by x-ray diffraction at room temperature, O for orthorhombic, T for tetragonal, and C for cubic. (Inset) Temperature dependence of inverse magnetic susceptibility of Sr_1−xCa_xRuO₃ measured with a magnetic field H = 1 T (data are from ref. 28) and of Sr_1−yBa_yRuO₃ measured with a magnetic field H = 0.5 T in this work.

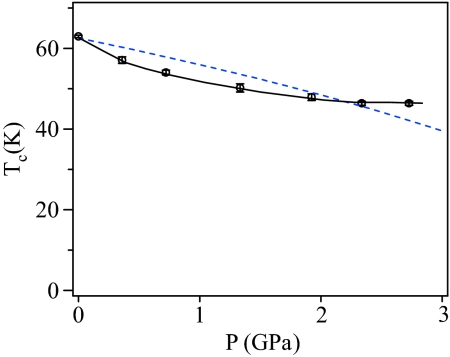
On the Sr_1−yBa_yRuO₃ (y ≥0) side, T_c reduction is likely caused by band broadening in a uniform ferromagnetic system because a well defined CW paramagnetism is found at T > T_c (25). Ba doping could change the bandwidth through two opposite effects. Because the A–O interaction in a perovskite ARuO₃ competes with the Ru⁴⁺ ions for the O-2p_π electrons, the stronger ionic character of the Ba²⁺, which makes it less competitive for the O-2p orbitals, enhances the covalent admixture of O:2p_π character into the π* bands of primarily 4d-electron character, therefore broadening the bandwidth W associated with the Ru–O bond. However, the Ba doping for y >0.15 in the cubic perovskite phase stretches the Ru–O bond length as obtained from the Rietveld refinement of this work, which reduces the bandwidth. To distinguish which effect plays the dominant role in controlling the bandwidth, we have carried out a structure study and measurement of T_c under pressure on the cubic BaRuO_3, as shown in Fig. 4. Pressure does not alter the fact that Ba²⁺ has strong ionic character, but it does change the Ru–O bond length. The cubic phase is stable up to 100 kbar, the maximum pressure used in this study, and the Ru–O bond length shortens continuously under pressure. T_c drops at a rate dT_c/dP ≈ 0.7 K/kbar at low pressures, which is similar to that of SrRuO₃ (26) and then gradually approaches a saturated T_c ≈ 50 K at P > 20 kbar. The saturation T_c at high pressures in the cubic BaRuO₃ is lower than that of thin-film SrRuO₃ found for P > 130 kbar (27). This observation indicates unambiguously that the strong ionic character of Ba²⁺ broadens W; the broadening is offset slightly by a stretched Ru–O bond length in cubic BaRuO₃. High pressure decreases T_c by reducing the Ru–O bond length. It requires a much higher pressure in SrRuO₃ than that in the BaRuO₃ to lower T_c to a saturation value. The saturation of T_c vs. P curve in both SrRuO₃ and the cubic BaRuO₃ suggests there is a critical W above which there may be a first-order transition to a Pauli paramagnetic phase. The bandwidth broadening by Ba doping reduces the density of states ρ(ε_F) near the Fermi energy and, therefore, T_c according to the Stoner model.

Fig. 4.

Pressure dependence of the ferromagnetic transition temperature T_c in cubic BaRuO₃. The dashed line is from the prediction of an itinerant-electron ferromagnetism model (34). T_c ≈ (P_c − P)^1/2, where P_c (P_c = 5 GPa is used in the plotting) is the critical pressure where T_c vanishes.

In sharp contrast, χ⁻¹(T) for all Sr_1−xCa_xRuO₃ (x > 0) deviates from the CW law at a T ≈ T_c of SrRuO₃ with a curvature that is opposite to that caused by critical fluctuations shown in the vicinity of T_c for Sr_1−yBa_yRuO₃. T_c reduction and the final vanishing in Sr_1−xCa_xRuO₃ appears to be correlated to the anomalous paramagnetic susceptibility. The peculiar χ⁻¹(T) for all Sr_1−xCa_xRuO₃ (x > 0) (28) is characteristic of a diluted ferromagnetic system (29) in which Griffiths (30) has predicted a nonanalytic χ⁻¹(T) below a T_G = T_c of the undiluted parent phase. Moreover, the phase diagram of T_c vs. x on the side of Sr_1−xCa_xRuO₃ matches stunningly well to the prediction based on the model for a diluted Heisenberg ferromagnet (31). The implication of these observations is straightforward: suppression of T_c in Sr_1−xCa_xRuO₃ has little to do with either reducing the ρ(ε_F) or a competition between ferromagnetic and antiferromagnetic interactions, but is caused by the dilution of ferromagnetic spin–spin coupling across Ru–O–Ru bonds. A thorough study of the magnetic property of the BaRuO₃ from the whole series of hexagonal polytypes to the 3C phases helps us to clarify this long-standing puzzle.

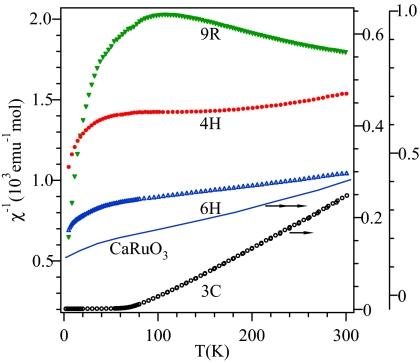
The systematic change in the magnetic susceptibility of the polytype phases of BaRuO₃ is shown in Fig. 5. The change of χ(T) can be easily correlated with the characteristics of the polytype structures, which consist of face shared (F) and corner shared (C) RuO₆ octahedra. These shared interfaces repeat as CFFCFFCFF, CFCF, FCCFCC, and CCC along the c axis from the 9R, 4H, 6H, to 3C phases. On crossing these interfaces, two Ru–Ru bonds can be defined, i.e., a θ = 180° Ru–[C]–Ru bond of ≈3.9 Å and a θ ≈ 135° Ru–[F]–Ru bond of ≈2.55 Å. The metallic 9R phase shows no magnetic ordering and exhibits neither a CW law nor Pauli paramagnetic susceptibility. Changing the balance of Ru–[F]–Ru bonds vs. Ru–[C]–Ru bonds from the 9R, 4H, 6H, and finally to the 3C phase makes the χ⁻¹(T) evolve from a wiggled curve to the CW law. The relationship between the structural features and a systematic change of χ⁻¹(T) suggests that the Ru–[C]–Ru bond is dominated by the spin–spin interaction, whereas the Ru–[F]–Ru bond has a much reduced magnetic character at low temperatures. In a qualitative discussion, the rhombohedral symmetry of the shared faces splits the threefold-degenerate t orbitals into an a₁ and twofold-degenerate e_± orbitals carrying an orbital angular momentum. The a₁ orbital will be half-filled, forming a Ru–Ru homopolar bond, which leaves a localized hole in the e_±³ manifold to give a large orbital angular momentum. A strong spin-orbit λL·S coupling, which is commonly found in the 4d transition-metal compounds (32), would lead at lowest temperature to a state with J = 0 of the Ru⁴⁺ ions of a Ru–[F]–Ru pair. The unusual χ(T) of the 9R phase of BaRuO_3, where the Ru–[F]–Ru bonds dominate, can indeed be accounted for quantitatively by taking into account the spin–orbit coupling and spin–spin exchange interaction (32). As for the 6H phase in which 2 of 3 blocks consist of the Ru–[C]–Ru bonds, 3D ferromagnetic coupling is not established and spins are not ordered to the lowest temperatures. It is important to note that an approximately linear fitting of χ⁻¹(T) within 90 K < T < 240 K for the 6H phase in Fig. 5 may mean a strong antiferromagnetic coupling, as predicted by a Curie–Weiss law, only at higher temperatures, but a suppression by spin–orbit coupling at lower temperatures of the magnetic moment on the Ru⁴⁺ ions of the Ru–[F]–Ru bonds destroys any long-range magnetic order. More interestingly, χ⁻¹(T) of 6H phase of BaRuO₃ can be seen in Fig. 5 to resemble the essential feature of the χ⁻¹(T) curve of CaRuO₃. This observation suggests that the unusual χ⁻¹(T) found for CaRuO₃ and its lack of long-range magnetic order is related to a spin–orbit coupling on the Ru⁴⁺ ions that suppresses the ferromagnetic spin–spin coupling across the Ru–O–Ru bonds. Narrowing of the π* band of SrRuO₃ by the introduction of the more acidic Ca²⁺ ion and by reducing the Ru–O–Ru bond angle allows removal of the band degeneracy, which enhances the intraatomic spin–orbit coupling λL·S to where it competes with the interatomic spin-spin interaction across the Ru–O–Ru bonds having a bond angle much reduced from 180°. In the Sr_1−xCa_xRuO₃ system, the reduced bond angle suppresses these Ru–O–Ru interactions to dilute the ferromagnetic interactions so as to give a χ⁻¹(T) behavior typical of a Griffiths' phase.

Fig. 5.

Temperature dependences of the inverse magnetic susceptibility of the 9R, 4H, 6H, and 3C phases of BaRuO₃. The χ⁻¹(T) data of the perovskite CaRuO₃ are superimposed for comparison.

In conclusion, we have synthesized the new perovskite BaRuO₃ under high pressure, which enables us to map out the evolution of magnetic properties for the perovskite ruthenates. The maximum ferromagnetic Curie temperature T_c = 164 K is found for SrRuO₃. Substitution of the more ionic and larger Ba²⁺ ion for Sr²⁺ straightens the Ru–O–Ru bond angle and broadens the π* bandwidth W even where the Ru–O bond is stretched in BaRuO₃. The ferromagnetism of the Sr_1−yBa_yRuO₃ system can be well described by the Stoner–Wohlfarth model of band ferromagnetism. Substitution of the more acidic and smaller Ca²⁺ ion for Sr²⁺ lowers the Ru–O–Ru bond angles as well as the strength of the interatomic Ru–O–Ru interaction to where the intraatomic spin–orbit λL·S coupling competes with the interatomic spin–spin interactions. As a consequence, the ferromagnetic Ru–O–Ru interactions of SrRuO₃ become diluted, and the Sr_1−xCa_xRuO₃ phase behaves as a Griffiths' phase.

Methods

Synthesis.

The starting materials for high-pressure synthesis were prepared by solid-state chemical reaction. The starting materials of BaCO₃ (3N), SrCO₃ (3N), CaCO₃ (3N), and RuO₂ (3N) powders were weighed according to the metal-ion ratio and then thoroughly mixed before sintering at ambient pressure to form single-phase precursors. The single phase of orthorhombic SrRuO₃ and CaRuO₃ were obtained through solid-state reaction at ambient pressure. The well prepared precursors of BaRuO₃ and Sr_1−yBa_yRuO₃, which have the 9R polytype structure and a mixture of perovskite and the 9R phase, respectively, were further sintered under high pressure and high temperature. The cubic perovskite BaRuO₃ was obtained at 18 GPa at 1,100°C with a KAWAI-type multianvil high-pressure apparatus. The Ba-doped perovskites Sr_1−yBa_yRuO₃ y ≤ 0.2 were made with a cubic high-pressure apparatus under 6 GPa and 1,000°C. The same apparatus has also been used to synthesize the hexagonal polytypes phase of BaRuO₃, i.e., the 4H phase BaRuO₃ at 1,000°C under 3 GPa, and the 6H phase of BaRuO₃ at 1,000°C under 5 GPa. During high-pressure synthesis the samples were held at the targeting pressure and temperature for 30 min before quenching to room temperature followed by release of the pressure.

Crystal Structure Determination.

Products of the high-pressure synthesis were characterized by x-ray powder diffraction with a Philips X'pert diffractometer. Diffraction data were collected with 0.02° and 15 s per step. Rietveld analysis has been performed by using the program FullPROF software package.

Measurements of Physical Properties.

The magnetic properties of the samples were measured with a superconducting quantum interference device (SQUID) (Quantum Design). The electrical conductivity and thermoelectric power were measured with home-made setups (33). Transport properties under pressure were measured in a piston cylinder high-pressure cell with silicon oil as the pressure medium.