Double-quantum resonances and exciton-scattering in coherent 2D spectroscopy of photosynthetic complexes

Abstract

A simulation study demonstrates how the nonlinear optical response of the Fenna–Matthews–Olson photosynthetic light-harvesting complex may be explored by a sequence of laser pulses specifically designed to probe the correlated dynamics of double excitations. Cross peaks in the 2D correlation plots of the spectra reveal projections of the double-exciton wavefunctions onto a basis of direct products of single excitons. An alternative physical interpretation of these signals in terms of quasiparticle scattering is developed.

The photosynthetic apparatus depends on light-harvesting complexes, which absorb photons and funnel their energy to reaction centers where it is converted and stored as chemical energy (1, 2). The Fenna–Matthews–Olson (FMO) complex is the prototype photosynthetic antenna (3, 4). The complex (Fig. 1) is a trimer of identical units, each containing seven chlorophyll a chromophores embedded in the protein matrix. The structure and properties of the complex have been studied extensively over the past decade (3–7).

Fig. 1.

●●●. (Left) Monomer of the FMO complex and its absorption. The eigenstate level scheme is shown in Inset: g is the ground state, whereas e and f are the single- and the double-exciton manifolds, respectively. Absorption was simulated as described in ref. 11. Narrow peaks indicate state positions and oscillator strengths. (Right) The four-wave-mixing experiment: three pulses (k₁, k₂, and k₃) interact with the system and generate nonlinear polarization, which is probed by using the fourth (signal) pulse (k₄). For ultrashort nonoverlapping pulses, the delay times between pulses t₁, t₂, and t₃ coincide with the delay times between interactions. The two Feynman diagrams that contribute to the signal in the phase-matching direction (k_III ≡ k₄ = k₁ + k₂ − k₃) in the RWA are shown at the bottom.

Electronically excited FMO complexes prepared by the absorption of a single photon are well understood, and their properties are described by the Frenkel exciton model (2, 8, 9). The elaborate exciton-relaxation pattern can be monitored by using multidimensional coherent optical spectroscopy (10–12): peak redistribution on the picosecond time scale reflects excited-state population relaxation (7), whereas femtosecond oscillations indicate electronic coherences (13). Excited-state lifetimes, intraband exciton-relaxation pathways (7, 14), and long-lived electronic quantum coherences (13) have been reported, and the Hamiltonian parameters were refined to simulate these measurements.

In the native environment, under the intense flux of sunlight, photosynthetic complexes have multiple electronic excitations, the interactions of which cause dissipation of the excess energy (1, 2, 9, 15, 16). Biological complexes have developed various protective mechanisms for excess energy discharge to avoid overheating and damage (17, 18). Understanding the coherent many-exciton dynamics, which precedes the incoherent relaxation, is necessary for revealing the initial steps in excitation dynamics. Information about the two-exciton manifold is also important for the applications of the coherent control of excited-state dynamics of photosynthetic complexes (19). Double-exciton resonances are much more complicated and less studied than the single excitations. Exciton annihilation, which depends on incoherent multiexciton dynamical properties, often complicates the analysis of nonlinear optical measurements.

In this article we present simulations of an impulsive third-order 2D coherent spectroscopic (2DCS) technique aimed at directly probing double-exciton features in an FMO complex. In most commonly used four-wave-mixing techniques, such as pump-probe, three-pulse peak shift and photon echo, double-exciton information is convoluted with single-exciton resonances, which complicates the analysis (15, 16, 20–23). The present technique (20, 24), analogous to double-quantum coherence techniques in multidimensional NMR (25), has shown high sensitivity to coupling patterns and high spectral resolution in vibrational excitons (11, 26–28).

When the excitons form a set of independent quasiparticles, the double-exciton wavefunctions are given by simple products of pairs of single excitons. Because of exciton interactions, the actual wavefunctions should be represented as superpositions of such products. We show that the trails of peaks in the 2DCS spectra reflect the form of the double-exciton wavefunction and are sensitive to its delocalized projections into the space of single-exciton products.

In the following sections we initially describe the properties of single- and double-exciton states in the FMO complex. The 2DCS pulse sequence designed for probing double-exciton resonances and dynamics in chromophore aggregates is introduced next. We then present the simulated signals for the FMO complex. Finally, these signals are analyzed by using an alternative (quasiparticle-scattering) description of double-exciton dynamics.

Single- and Double-Exciton Manifolds of the FMO Complex

We shall describe the electronic excitations of the FMO complex by using the Frenkel exciton Hamiltonian representing N two-level chromophores:

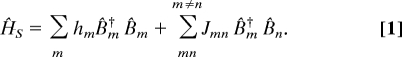Here, h_m is the excitation energy of the mth chromophore, J_mn is the excitonic coupling between chromophores m and n, and B̂_m^† (B̂_m) is the creation (annihilation) operator for an exciton on the mth chromophore. These operators satisfy the Pauli commutation relations [B̂_m, B̂_n^†] = δ_mn(1 − 2B̂_n^†B̂_n). The dipole interaction between the complex and the optical electric field E is given by

where P̂ = Σ_mμ_m(B̂_m^† + B̂_m), μ_m is the transition dipole of chromophore m.

This Hamiltonian is commonly used for describing the optical responses of coupled chromophores in aggregates (1, 2, 9, 22, 29). The eigenstates of this Hamiltonian form independent manifolds that can be classified by the number of excitations. Each manifold is obtained by diagonalizing a given block of the Hamiltonian. Third-order 2DCS signals only depend on the single- and double-exciton states. These states will be the focus of our study.

We denote the state where chromophore m is excited by ∣m〉 ≡ B̂_m^†∣0〉. The N single-exciton eigenstates ∣e〉 are related to ∣m〉 by the transformation matrix φ_me:

The eigenstate creation operator is similarly given by ê^† = Σ_mφ_meB̂_m^† and its energy is ε_e = Σ_mn J_nmφ_neφ_me (we use J_mm ≡ h_m).

The double-exciton states ∣f〉 will be described by using a basis set of direct product of real-space excitations (PRSE) ∣mn〉 with m ≥ n. This set has M = N(N + 1)/2 elements. We then have

where ν≡ mn with m ≥ n. Thus, Φ is a (M × M) transformation matrix. The eigen energies are ε_f = Σ_νν′J_νν′⁽²⁾Φ_ν,fΦ_ν′,f, where J_νν′⁽²⁾ ≡ J_mn,m′n′⁽²⁾ = δ_mm′J_nn′+δ_nn′J_mm′ + δ_mn′J_nm′ + δ_m′nJ_mn′. Note that for our model of hard core bosons two excitations cannot reside on the same chromophore, so the states ∣mm〉 = 2^−1/2B̂_m^†2∣0〉 should be excluded. To simplify the notation we include it in the basis set but require that Φ_mm,f ≡ 0. The Φ matrix is obtained by diagonalizing the double-exciton block of the Hamiltonian.

Double-exciton states may be alternatively expressed in the basis of products of single-exciton eigenstate space excitations (PESE). To that end, we introduce the boson operators [ê,ê′^†] = δ_ee′. The double-exciton basis is ∣ee′〉 = ζ_ee′ê^†ê′^†∣0〉, where ζ_ee′ = 1 + δ_ee′(2^−1/2 − 1) (we note that for bosons ê^†∣e〉 = $\sqrt{2}$∣ee〉). We further define bosonic single-exciton operators in real-space B̂_m^† = Σ_eφ_meê^†: [B̂_n,B̂_m^†] = δ_mn. For the double-exciton space using ∣mn〉 = ζ_mnB̂_m^†B̂_n^†∣0〉, we get

where

is the unitary M × M transformation matrix (m ≥ n and e ≥ e′). The double-exciton states may then be expanded in the PESE basis as

and the wavefunctions are

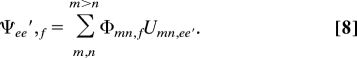A useful measure for exciton delocalization is provided by the participation ratio κ. For a singly excited state e, it is defined as κ(e) = [Σ_nφ_n,e⁴]⁻¹. κ then varies between 1 (localized state) and N (state delocalized over the entire aggregate). Similarly, we define a measure of double-exciton delocalization among the pairs of product states in PRSE space, χ_R(f) = [Σ_mn^m>nΦ_mn,f⁴]⁻¹, and in PESE space, χ_E(f) = [Σ_ee′^e≥e′Ψ_(ee′),f⁴⁰]⁻¹. These show how many pairs of molecules (in PRSE) or single excitons (in PESE) participate in a double-exciton state f. χ varies between 1 and N × (N ± 1)/2 (“+” for PESE and “−” for PRSE).

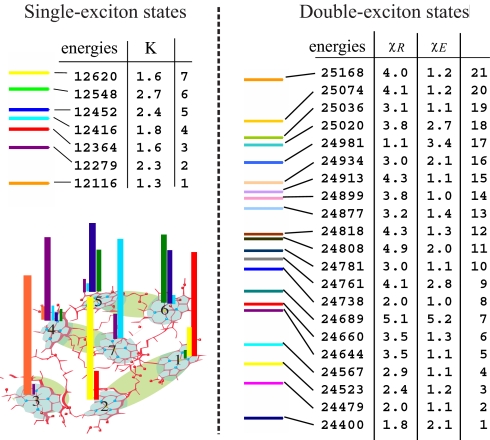
The FMO complex has n = 7 single-exciton states and M = 21 double-exciton states. The Hamiltonian parameters were acquired from previous simulations (7, 8, 30). In a recent study we examined single-exciton properties and their coherent versus incoherent dynamics (30). Here we focus on double-exciton coherent dynamics and show how nonlinear signals can be designed to resolve double-exciton wavefunction, localization, and scattering. The single-exciton state energies are shown in Fig. 2. The participation ratios vary between 1 and 3, indicating that the single excitons are essentially localized. The entire set of double-exciton states is given in Fig. 2 as well. Their participation ratios indicate that fewer double-exciton states are delocalized in the PESE than in the PRSE basis, which implies that the PESE basis is better suited for describing double excitons.

Fig. 2.

Analysis of exciton states. (Left) Single-exciton energies and their participation ratios κ in the FMO complex; the wavefunction, ∣ψ_me∣², is shown on the bottom by color bars (the bar color corresponds to the eigenstate color). (Right) Double-exciton state energies and participation ratios in real-space χ_R and in the space of single-exciton eigenstate products χ_E.

Coherent Double-Quantum Spectroscopy of Excitons

The proposed 2DCS technique is performed with four temporally well-separated laser pulses (Fig. 1). The optical electric field is given by

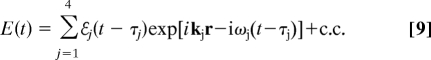The first three pulses generate a nonlinear polarization in the complex, which is heterodyne-detected with the fourth pulse. We shall focus on the signal generated along the phase-matching direction k_III ≡ +k₁ + k₂ − k₃ (see ref. 31 for this notation). The signal recorded versus the three delay times between pulses t₁, t₂, and t₃ will be denoted S(t₃, t₂, t₁). As is common in resonant spectroscopies, we shall invoke the rotating wave approximation (RWA) and only retain the dominant contributions to S, where all interactions are resonant. For our exciton model, there are only two contributions to the k_III signal. These are represented by the Feynman diagrams shown in Fig. 1. The two diagrams represent the same evolution during the first two time intervals: during t₁ the density matrix oscillates with frequency ω_eg = ε_e − ε_g, and during t₂ the density matrix oscillates with frequency ω_fg = ε_f − ε_g. During t₃ the diagrams are different: the oscillation frequency is either ω_fe′ (Fig. 1 Right, diagram B) or ω_e′g (Fig. 1 Right, diagram A). S(t₃, t₂, t₁) constitutes a 3D signal. It can be represented conveniently in the frequency domain by a triple Fourier transform with respect to the delay times:

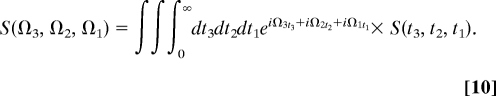This signal is given by (32):

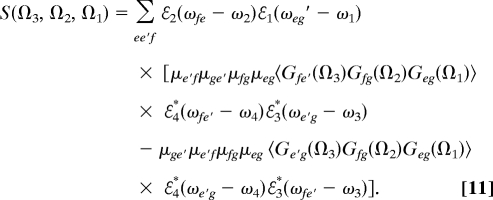The two terms correspond to Fig. 1 Right, diagrams B and A, respectively. Here G_ab(Ω) = (Ω − ω_ab + iγ_ab)⁻¹ is the frequency domain Green's function for density matrix coherence ∣a〉〈b∣, and γ_ab is the dephasing rate. In the time domain we have G_ab(t) = θ(t)exp(−iω_abt − γ_abt); angular brackets denote averaging over fluctuations caused by other degrees of freedom (e.g., phonons, solvent). ω_j are the carrier frequencies and ℰ_j(ω) are the pulse envelopes centered at ω = 0. Note that ω₄ = ω₁ + ω₂ − ω₃ is required by phase matching. We shall display some 2D sections of the complete 3D signal. This can be done either in the time or frequency domain or in a mixed representation where we replace any of the Green's function G(Ω_j) by its Fourier transform G(t_j). We shall focus on two signals. The first is S₂₁ ≡ S(t₃; Ω₂,Ω₁) displayed in (Ω₂,Ω₁) space for various values of t₃. This signal vanishes for t₃ = 0. The second choice will be S₃₂ ≡ S(Ω₃,Ω₂; t₁). This signal will be displayed in (Ω₃,Ω₂) space. The delay time t₁ in S₃₂ induces phase rotation and does not change the peak amplitudes. Thus, we set t₁ = 0.

Double-Exciton Resonances of the FMO Complex: 2D Signals

The signals (Eq. 11) were calculated by using the cumulant expansion for Gaussian fluctuations as implemented in the SPECTRON package, which incorporates correlated bath fluctuations (33–36). Each chromophore is coupled to its own, statistically independent bath; the fluctuation statistics of all chromophore frequencies is identical and described by the overdamped Brownian oscillator spectral density. By transforming the bath fluctuation parameters to the eigenstate basis we obtain the correlated statistical properties of fluctuations of eigenstates. All parameters are the same as those described in ref. 30 except one: numerical averaging over static disorder with 20 cm⁻¹ variance (inhomogeneous linewidth) made no noticeable difference on the signal and was eliminated. The calculated homogeneous linewidth is approximately 70 cm⁻¹.

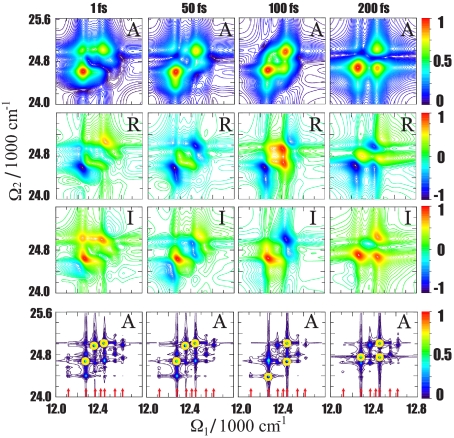
S₂₁ is displayed in Fig. 3 for several values of t₃. Only single-exciton resonances appear along Ω₁, and double-exciton states show up along Ω₂. The signal vanishes for t₃ = 0 and quickly grows until t₃ ≈ 50 fs. The subsequent variation of the signal with t₃ reflects the evolution in the double-exciton manifold. We present the absolute value of the signal (A) as well as its real (R) and imaginary (I) parts. The I (absorptive) part clearly shows oscillations of peaks with t₃, whereas A helps to identify the peaks and relate them with the exciton states. R is shown for completeness. To reveal how each double-exciton resonance is connected to a specific set of single-exciton states, we present on the bottom row in Fig. 3 the same signal at which all linewidths were reduced by a factor of 20. Each Ω₂ selects a given double-exciton state, and the corresponding peaks along Ω₁ show its projection onto the various single-exciton states, the resonant frequencies of which are marked by red arrows. The peak positions along Ω₁ agree with the single-exciton resonances. By using the states listed in Fig. 2, we find that the spectrum is dominated by three double-exciton states: 1, 7, and 18. Three other states (9, 16, and 17) make a weaker contribution. The participation ratios of these states (see Fig. 2) indicate that these are the most delocalized states in the PESE basis.

Fig. 3.

The S₂₁ signal. Its amplitude (A, first row), real part (R, second row), and imaginary part (I, third row) are shown for different delay times t₃. Shown in the fourth row is the amplitude of the S₂₁ signal calculated with a narrow spectral linewidth. The strongest peaks are circled in yellow, and red arrows indicate single-exciton resonances. Color codes of the A, R, and I signals are indicated on the right-most bars.

The contributions of various single-exciton states to each double-exciton state can be rationalized by examining the transformation matrix φ. Ψ_ee′,f² is the probability that the system in the double-exciton state f be found in the pair of states ee′. These probabilities for states 1, 7, and 18 are displayed in Fig. 4[the probability distributions for all 21 states are shown in Supporting Information (SI) Figs. S1 and S2]. As suggested by the participation ratios of states 1, 7, and 18 given in Fig. 2, these states are delocalized in the PESE representation, indicating that 2D signals are sensitive to exciton delocalization. We further note that the single-exciton states contributing to the specific double-exciton state directly correspond to the series of peaks along Ω₁ for a fixed Ω₂. Thus, the S₂₁ signal directly reflects the double-exciton wavefunction in the PESE space, and the peaks for each Ω₂ resonance reflect its projections onto the single-exciton basis.

Fig. 4.

Two-exciton states showing strong contributions in 2D signals. Double-exciton wavefunctions of states 1, 7, and 18 in PESE (A) and PRSE (B). (C) The single-exciton wavefunctions in real space, which contribute to the double-exciton states. Color codes: B, a pair of bars with the same color indicates a pair of real-space excitations; C, the same as that described in the legend for Fig. 2 Left.

The S₃₂ signals are depicted in Fig. 5A. The amplitude spectrum clearly shows a contribution from three double-exciton states. On the Ω₃ axis there are now two types of resonances: ω_fe′ and ω_e′g. This spectrum, therefore, carries more details than S₂₁ (Fig. 3), which only has ω_eg resonances along Ω₁; however, interference between the ω_fe′ and ω_e′g peaks complicates the peak assignment. We also present the same signal at which the linewidth was reduced by a factor of 20. Each peak can now be assigned to a specific set of eigenstates. We find that the double-exciton states 1, 9, and 18 with the largest PESE participation ratios (Fig. 2) are dominant.

Fig. 5.

Comparison of full and MFA simulations. (A) S₃₂ signal for t₁ = 0. This signal with broad and narrow linewidth is shown. Color codes of the A and I signals are the same as those described in the Fig. 3 legend. (B) S₃₂ for t₁ = 0 and S₂₁ 2DCS signals calculated by using the MFA.

Quasiparticle-Scattering Picture of Double Excitations and the Mean-Field Approximation

So far, our analysis was based on the properties of single- and double-exciton wavefunctions. Single excitons carry information on the couplings between chromophores and their interaction with the environment. The double-exciton states reflect the many-body properties: exciton–exciton interactions.

An alternative physical picture for excitons in aggregates is provided by the quasiparticle approach. Rather than computing double-exciton wavefunctions, we view the excitons as interacting quasiparticles. All relevant properties can then be viewed in terms of their scattering. The exciton-scattering matrix, rather than two-exciton wavefunction, then plays a central role in the analysis. The quasiparticle approach provides a highly intuitive physical picture of exciton dynamics. Powerful approximation schemes, stemming from the short-range nature of exciton–exciton interactions, make the calculations much easier compared with the eigenstate calculations and provide deep insights into the nature of multiexciton dynamics.

In the quasiparticle approach, the optical signals are calculated by solving equations of motion for relevant exciton variables 〈B̂〉 and 〈B̂B̂〉. These are known as the nonlinear exciton equations (10, 12, 33, 37–39). In the single-exciton eigenstate representation of quasiparticle scattering, the response function for k_III technique is (12, 39, 40):

where I_e(ω) = i(ω − ε_e + iγ)⁻¹ and 𝒢_ee′(ω) = i(ω − ε_e − ε_e′ + 2iγ)⁻¹ are the single-exciton and noninteracting double-exciton Green's functions, and γ is the dephasing rate.

Γ(ω) is the exciton-scattering matrix:

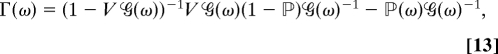where V and ℙ are the tetradic matrices. In real space for two-level chromophores V_mn,kl = 2J_ml(δ_nkδ_kl − δ_mnδ_nk) and ℙ_mn,kl = δ_mnδ_nkδ_kl; 1_mnkl ≡ δ_mkδ_nl (39). This is equivalent to sum-over-eigenstates (SOS) expression (11). The two approaches only differ by the dephasing model.

A mean-field approximation (MFA) is often used to simplify the exciton-scattering picture (41, 42). It assumes 〈B̂_mB̂_n〉 = 〈B̂_m〉〈B̂_n〉. The MFA response is also given by Eq. 12, but the scattering matrix is much simpler:

This approximation ignores the effects of exciton statistics in doubly excited resonances. Therefore, doubly excited-state energies are simply given by sums of single-exciton excitation energies. Fewer peaks will survive the interference of the two Feynman diagrams in this case (38). Exciton scattering takes place during the intervals t₂ and t₃ where the particles interact. The MFA neglects pairwise interactions of excitons but includes the perturbation of an exciton pair by a third exciton.

The MFA S₂₁ and S₃₂ signals are displayed in Fig. 5B. As expected, they contain fewer peaks compared with complete SOS calculations (for S₂₁, see Fig. 3). The peak positions are different in the MFA and SOS; however, the double-exciton resonances still appear between 24,500 and 25,000 cm⁻¹. Thus, the fine structure of double-exciton states of the FMO complex in MFA is distorted, whereas the average resonance energy is the same. The peak positions along Ω₁ can be associated with the single-exciton states, because the MFA does not affect the single-exciton dynamics. The peaks along Ω₂ are related to combinations ε_e + ε_e′. Compared with the full calculation (Eq. 13), the MFA (Eq. 14), thus, does not miss frequency shifts caused by exciton–exciton interactions.

By expanding Eq. 13 to first order in V we get Γ(ω) ≈ V[1 − 𝒢(ω)ℙ𝒢(ω)⁻¹] − ℙ𝒢(ω)⁻¹. This result is similar but not identical to the MFA. Only when the particle statistics is a weak perturbation, such that 𝒢ℙ𝒢⁻¹ ℙ, do we recover the MFA. The two are identical for bosons, where ℙ = 0 and the scattering matrix is Γ_(b)^(MFA) = V. The MFA, therefore, is an approximation in terms of coupling strength and nonbosonic nature of excitons, whereas the weak coupling limit still retains nonbosonic nature.

Finally, we note that a different strategy for treating exciton scattering based on bosonization may be used, as well. With bosonization, particle statistics is greatly simplified, and its effects are incorporated in a modified exciton Hamiltonian. Paulion operators can be exactly mapped into a boson representation (43). An approximate empirical bosonization has also been used (20, 37, 44) for calculation of multidimensional signals in the UV region of polypeptides (44, 45).

Conclusions

The various levels of description of 2DCS signals employed here provide insights into the excited state dynamics of photosynthetic complexes. Weak coupling/weak scattering limits can then be described by comparing the signals obtained by using eigenstate expressions (11), the exciton-scattering picture (Eq. 12), the MFA, and the weak coupling limits. Comparison of Figs. 3 and 5A shows that double-exciton dynamics in the FMO complex can be approximately described by the MFA: the couplings and nonbosonic nature of excitons are strong, and a full calculation of the scattering matrix is preferred.

The localized double-exciton states in PESE affect the 2D signal only weakly, which can be rationalized by the quasiparticle-scattering picture. The localized double-exciton states ∣f〉 = ∣ee′〉 can be isolated; by energy conservation their energy must be ε_f = ε_e + ε_e′, which implies that scattering of excitons does not occur and such states do not contribute to the nonlinear signal. This argument does not hold in the real-space representation, because real-space single excitons are coupled by excitonic interactions at the single-excitation level. Accordingly, the PESE basis better connects with the experiment rather than the real-space basis. The double-exciton state delocalization, χ_E, is a good indicator for the strength of the double-exciton features in the 2D spectrum: double-exciton states with χ_E = 1 do not contribute to the signal. These contributions increase with χ_E. The requirement Φ_mm,f ≡ 0 reflects Pauli statistics and, therefore, is responsible for exciton scattering; two excitations cannot reside on the same molecule: the molecules are hard-core exciton scatterers. Because single-exciton eigenstates are delocalized over a range of chromophores, Ψ_ee,f ≠ 0; thus, double excitations of single-exciton eigenstates are possible. Their energy, however, is different than 2ε_e. Therefore, they are soft-core exciton scatterers. We note that the system–bath interaction induces damping of density matrix coherences and have no significance for our conclusions.

The (Ω₂,Ω₁) signal presented in Fig. 3 shows interesting spectral dynamics with the delay t₃. Technically, this time dependence results from the interference of two Feynman diagrams (see Fig. 1 and Eq. 11). After the summation over exciton states e′ and f and in the absence of dephasing, the dynamics along t₃ will show modulations of the signal peaks. When ω_e′g ≈ ω_fe′ the modulation will be very slow; thus, the characteristic modulation time scale τ_m = ∣ω_e′g − ω_fe′∣⁻¹ determines the modulation period. Note that ω_e′g = ω_fe′, with τ = ∞ corresponding to a harmonic system (when the entire signal vanishes). In the paragraph above we related double-exciton delocalization in the PESE basis with the signal amplitude. It follows that shorter τ_m implies more delocalized double-exciton states. Both τ_m and the delocalization length χ_E depend on the nonlinear (anharmonic) part of the Hamiltonian and are signatures of exciton scattering.

The power of the signals proposed here and the quasiparticle analysis will become even more pronounced for large complexes such as PS1 (46), because the density of eigenstates in the energy interval grows rapidly with aggregate size. The localized nature of exciton scattering then becomes crucial for simulating their nonlinear optical response.