Inputs to directionally selective simple cells in macaque striate cortex

Abstract

It is clear that the initial analysis of visual motion takes place in the striate cortex, where directionally selective cells are found that respond to local motion in one direction but not in the opposite direction. Widely accepted motion models postulate as inputs to directional units two or more cells whose spatio-temporal receptive fields (RFs) are approximately 90° out of phase (quadrature) in space and in time. Simple cells in macaque striate cortex differ in their spatial phases, but evidence is lacking for the varying time delays required for two inputs to be in temporal quadrature. We examined the space-time RF structure of cells in macaque striate cortex and found two subpopulations of (nondirectional) simple cells, some that show strongly biphasic temporal responses, and others that are weakly biphasic if at all. The temporal impulse responses of these two classes of cells are very close to 90° apart, with the strongly biphasic cells having a shorter latency than the weakly biphasic cells. A principal component analysis of the spatio-temporal RFs of directionally selective simple cells shows that their RFs could be produced by a linear combination of two components; these two components correspond closely in their respective latencies and biphasic characters to those of strongly biphasic and weakly biphasic nondirectional simple cells, respectively. This finding suggests that the motion system might acquire the requisite temporal quadrature by combining inputs from these two classes of nondirectional cells (or from their respective lateral geniculate inputs, which appear to be from magno and parvo lateral geniculate cells, respectively).

Although there is considerable processing of motion information by the visual system in cortical areas (primarily MT) beyond the striate cortex, it is clear that the initial information about local image motion is extracted in the striate cortex. Many directionally selective cells are found in the striate cortex (1), neurons that respond to a pattern of a particular spatial frequency and orientation moving in one direction but are unresponsive to the same pattern moving in the opposite direction. Several closely related models can account for such directional selectivity (2–4) by postulating that the inputs to a directionally selective simple cell come from two or more neurons that have the same spatial frequency and orientation tuning, but that differ from each other in their spatial and temporal phases.

Primate striate cortex cells are almost all tuned for selective spatial frequency ranges (5), and most also have selective orientation tuning (1, 6). Furthermore, there is a columnar arrangement of cells with the same spatial frequency tuning (7–9) and orientation tuning (10, 11), so nearby cells are likely to have the same spatial frequency and orientation selectivity. By combining inputs from cells with the same spatial frequency and orientation tuning, the motion system would vastly simplify the correspondence problem, the problem of knowing what to compare with what at different times to determine whether a pattern had moved or not. Striate simple cells have receptive fields (RFs) with a variety of different spatial phases (12), so the requirement of motion models for an approximate quadrature spatial relation between inputs could be easily achieved within a local cortical region. However, direct evidence in primates for neurons with the different temporal properties required for inputs to the first stage of a motion system is lacking. We have addressed this problem by studying the spatio-temporal responses of a population of cells in the macaque monkey striate cortex.

MATERIALS AND METHODS

Macaque monkeys (Macaca mulatta and M. fascicularis) initially were tranquilized with ketamine HCl (10–15 mg/kg, i.m.). Anesthesia was maintained with a continuous i.v. infusion of sufentanil citrate (during surgery, 8–12 μg/kg per hr; during recording 5–8 μg/kg per hr). After surgery, paralysis was induced and maintained with pancuronium bromide (0.1–0.15 mg/kg per hr, i.v.). Electrocardiogram, electroencephalogram, body temperature, and expired CO₂ were monitored continuously. All of the procedures were in accord with National Institutes of Health guidelines and approved by the local Animal Care and Use Committee.

All of the single-cell recordings were within the central 5° visual angle. Action potentials (spikes) were recorded with a resolution of 1 msec. Visual stimuli were generated and controlled by a Sun/TAAC image processor (Sun Microsystems, Mountain View, CA). On-line data analysis also was performed by the Sun. The stimuli were presented on a NEC monitor (Nippon Electric, Tokyo) with a spatial resolution of 1,024 × 900 pixels, a 66-Hz refresh rate, and a mean luminance of 70 cd/m². An initial characterization of the cell’s properties was obtained with drifting sinusoidal gratings. Typically, we measured the spatial and temporal frequency, orientation, and chromatic tuning of the cell. Subsequently, the spatio-temporal RF structure was mapped by using a long continuous series of brief (30 msec) stimuli. Each stimulus consisted of 16 contiguous, optimally oriented black or white bars. Bar length was slightly longer than the cell’s classical RF, and bar width was 1/4 to 1/6 of the cell’s optimal spatial period (optimal spatial period = 1/optimal spatial frequency). The contrast of each bar was independently modulated in time by 16 signals generated from temporal shifts of a binary m-sequence (13, 14). The spike train was cross-correlated with each of these signals to obtain a temporal impulse response at each of the 16 spatial positions.

Because it takes some 40 msec or more for visual information to reach the cortex, there are no significant correlations between neuronal responses and stimuli presented for this period before each spike. But in the case, for example, of a cell that fires to luminance decrements in its RF center, at somewhat greater intervals before each spike there would be significant correlations between the spike train and negative portions of the temporal signal that controls the luminance at those locations. This correlation would reach a maximum at a delay corresponding to the cell’s peak response latency, say 60 msec. Furthermore, if the cell happens to have a biphasic temporal impulse response, there would be high correlations between the spike train and positive portions of the stimulus sequence at that location at, say, 90 msec. The ensemble of correlation functions resulting from some thousands of spikes evoked by such a stimulus sequence gives a quantitative estimate of the cell’s spatiotemporal RF, a map of how the cell responds to stimuli in different locations along its width, and how this response waxes and wanes, and perhaps reverses, in time.

Cells were categorized as directional or nondirectional on the basis of their responses to drifting gratings of different orientations. We define a directional index as (1 − R_np/R_p)*100, where R_p and R_np are the cell’s responses (spikes/sec) to gratings of the optimal orientation, drifting in the preferred and nonpreferred directions, respectively. As reported earlier (6) and confirmed in our present sample, there is a subclass of very directional cells, with directional indices of 70 or more, and these we categorize as directional cells.

RESULTS

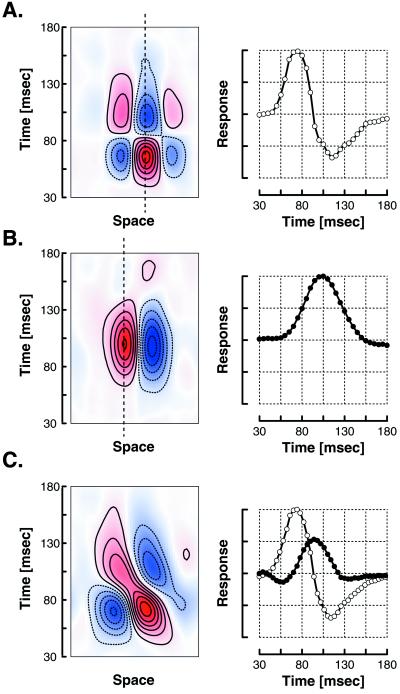
Spatio-temporal RF maps were obtained from 96 simple cells. Typical examples are illustrated as contour plots in Fig. 1 A–C. The cells shown in Fig. 1 A and B are nondirectionally selective because their temporal dynamics in all spatial locations across the width of their RFs are nearly identical; that is, their RFs do not change in position over time. The cell shown in Fig. 1A has a RF with three spatial subregions, all of which start developing at 50 ms after the stimulus, peak at 70 ms, go through a polarity reversal at 81 msec, and finally reach a secondary peak at 110 ms. This cell’s strongly biphasic temporal response (shown in profile in Fig. 1A, Right) indicates a preference for transient as opposed to sustained stimuli, a property reminiscent of magno lateral geniculate (LGN) cells. The cell shown in Fig. 1B is also a nondirectional cell, but its response has a longer latency (peaking at 106 ms) and does not reverse in time, indicating that this cell prefers sustained over transient stimuli. This property is reminiscent of parvo LGN cells.

Figure 1.

Spatiotemporal receptive fields for different classes of simple striate cortex cells. Shown are the cells’ temporal impulse responses, from 30 to 180 msec after stimulus onset, along the width dimensions of the RFs. Excitatory responses to light increments are shown in red, and excitatory responses to decrements in blue. (A) Spatio-temporal RF of a typical strongly biphasic simple cell. This cell responded to white bars in the RF center and black bars on the flanks, with the response reversing later. (Right) A time cross-section through the RF center (dotted line). This cell started responding at about 50 msec after stimulus onset; the response reached its peak at 70 msec and then reversed phase at 81 msec, with the second phase reaching its peak at 110 msec. (B) Spatio-temporal RF of a typical weakly biphasic simple cell. Note in the time cross-section (Right) that the initial response is considerably slower, with a peak at 106 msec, and that there is little if any reversed phase. (C) Spatio-temporal RF for a typical directionally selective simple cell. Note the leftward tilt in space-time of the RF subregions of this cell, which responded to patterns moving in one direction but not the other. (Right) The RF’s first and second SVD components. Note that the latency of the early component (open symbols) corresponds closely to that of the strongly biphasic nondirectional cell shown in A, and the latency of the later component (closed symbols) corresponds closely to that of the weakly biphasic cell shown in B.

The cell shown in Fig. 1C is directionally selective. It has increasing response latencies to stimuli in increasingly leftward locations, so it would respond best to a moving pattern that started on the left and shifted to the right in time. The waveforms shown in Fig. 1C (Right) correspond to the temporal profiles of the two strongest principal components obtained through a singular value decomposition (SVD) of its RF (see further discussion of this procedure below). A linear combination of these two components accounts for the oriented structure (in space-time) of this cell’s RF.

Strongly and Weakly Biphasic Cells.

An examination of the RF structure of nondirectional cells suggested to us that there might be two different classes of cells in terms of their temporal response characteristics: cells with very biphasic temporal impulse responses (Fig. 1A) and others with much less biphasic or even monophasic (Fig. 1B) temporal impulse responses, with few cells falling between these extremes. To quantify this observation, we measured the amplitude of the peaks of the first and second temporal parts of the impulse response through the RF center for each cell. We later refined this (with an improvement in the signal/noise ratio but without any change in the conclusions to be drawn) by performing a SVD or principal component analysis of each RF and analyzing the temporal profile of the strongest component. (The spatial RF of a nondirectional cell does not change with time and one principal component accounts for most of the RF structure.) Temporal profiles were fit with a damped oscillation, which gave an excellent fit to the time course of the response. We define a biphasic index as the ratio of amplitude of the second temporal peak to that of the first.

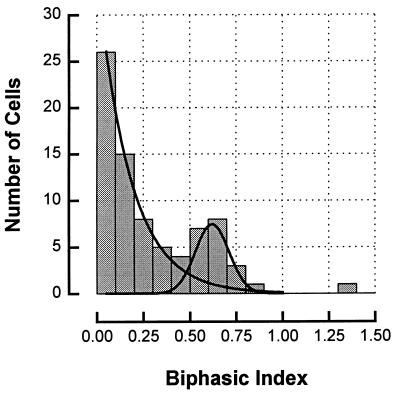
The biphasic index plotted for our whole population of nondirectional striate simple cells shows clear evidence for a bimodal distribution (Fig. 2). As can be seen, the distribution is well fit by the sum of an exponential for the weakly biphasic population and a gaussian for the strongly biphasic population. The large majority (50/79) of the cells showed only a small biphasic response, with a biphasic index of 0.3 or less. Many in this population were not biphasic at all, with a biphasic index of 0.0. A smaller subset of cells (20/79) was strongly biphasic, with the second phase being half or more as large as the first, thus with a biphasic index of more than 0.5. The few ambiguous cells (9/79) lying in the region of overlap between the two distributions, with indices between 0.3 and 0.5, were discarded from the analysis, although we found that including them in either one class or the other had an insignificant effect on the conclusions.

Figure 2.

Distribution of the biphasic index (amplitude of second temporal peak/amplitude of first) for all the nondirectional cells in our study. The distribution is biphasic and is well fit, as shown, by a sum of an exponential and a gaussian (solid line). Cells with biphasic indices of more than 0.5 (the second-phase half or more as large as the first) were categorized as strongly biphasic. Those with indices of less than 0.3 were categorized as weakly biphasic, and cells between 0.3 and 0.5 were not included in the analysis, as being ambiguous.

Latencies of Strongly and Weakly Biphasic Cells.

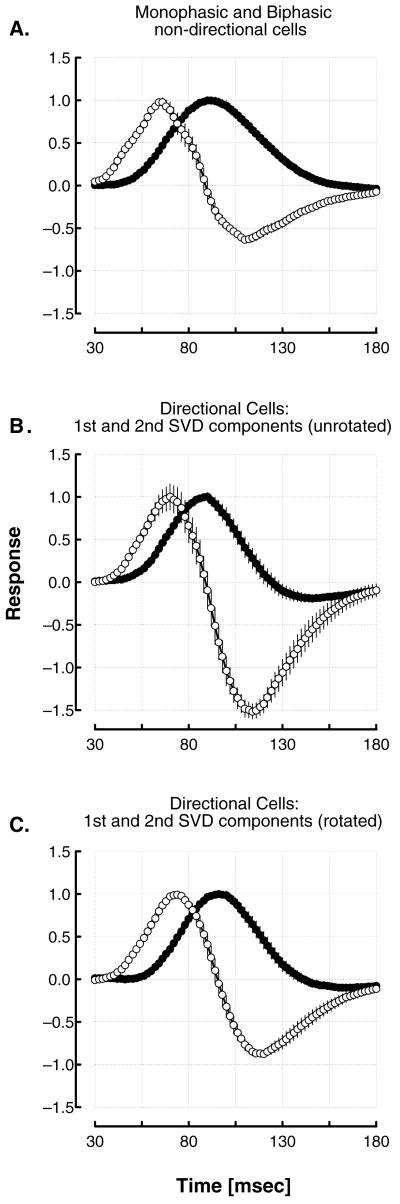
Of primary interest are the time courses of the responses of the strongly biphasic and weakly biphasic cells. Dividing the population of nondirectional cells purely on the basis of their biphasic index, we find that the strongly biphasic cells on average have a considerably shorter latency for both the first and second peaks of their response than do the weakly biphasic cells. The median latencies to the first and second peaks of the strongly biphasic cells are 68 and 111 msec, respectively; for the weakly biphasic cells the median latencies are 93 and 161 msec, respectively; see Table 1. The average, normalized temporal impulse responses of these two subpopulations are shown in Fig. 3A. It can be seen that on average the weakly biphasic cells reach their peak response at the point at which the strongly biphasic cells are at zero, crossing from the first to the reversed phase, so the responses of the two classes of cells on average are almost precisely in temporal quadrature.

Table 1.

Median times to peak for the first and second peaks of temporal impulse responses, measured from SVD components

Cell type	Median time to peak, msec
	Tpeak1/Tpeak2	Tpeak1/Tpeak2
Nondirectional	68/111 (strongly biphasic)	93/161 (weakly biphasic)
Directional	71/112 (early component)	90/145 (late component)

Note that the latencies of the early principal component of the directional cells correspond closely to that of the strongly biphasic nondirectional cells, and that the latencies of the late principal components of the directional cells correspond closely to that of the weakly biphasic nondirectional cells. 

Figure 3.

Average normalized temporal impulse responses across all of the cells. (A) Mean temporal profiles of the strongly biphasic (open symbols) and the weakly biphasic (closed symbols) nondirectional cells. Vertical lines represent ±1 SEM. A considerable latency difference can be seen between these two classes of cells, the weakly biphasic cells on average reaching their peak response at precisely the point at which the responses of the strongly biphasic cell population is at zero, as it is reversing phase. Thus these two types of cells are in quadrature temporal relation to each other. (B) Mean temporal profiles of the first and second SVD components of the directional cells’ RFs. Note that the time courses of the early (open symbols) and late (close symbols) components correspond to the time courses of the strongly biphasic and the weakly biphasic nondirectional cells, respectively. Note also that although directional cells are more biphasic overall, the early principal component is strongly biphasic, whereas the later component is much less biphasic. (C) Mean profiles of rotated SVD components of the directional cells. Here each pair is rotated so that one of the components is as monophasic as possible. Note that the time courses of the early (open symbols) and late (closed symbols) components of the directional cells are almost indistinguishable from those of the strongly biphasic and weakly biphasic nondirectional cells, respectively.

It is apparent that the differing time courses of the strongly biphasic and the weakly biphasic cells could provide the temporal quadrature relation required for inputs to a motion mechanism. That is, if one cell from each of these two classes (or from the LGN cells that provide the input to each of these classes, respectively) were spatially displaced with respect to the other and their outputs linearly summed, the result would be a directionally selective cell, one whose RF shifted position over time.

Directional Cells.

The question then arises whether directionally selective simple cells in the striate cortex actually might have the temporal properties that would be expected if they were constructed by summing signals from the two subpopulations of nondirectional cells we have identified. We examined this by analyzing the spatio-temporal RFs of all of the directional simple cells (17) in our sample, measured by the same RF mapping procedure. In a directional cell’s RF, the temporal impulse responses at different spatial locations have continuously changing latencies (Fig. 1C). SVD analyses of the RFs of our directional cells showed that in each case 80% or more of the ensemble of temporal impulse response shapes across the RF width could be accounted for by a linear summation of just two temporal impulse responses—the cell’s two principal components.

The temporal profiles of the two principal components for the directional cell shown in Fig. 1C (Left) are shown on the right of Fig. 1C. The principal component with the earliest latency (open symbols in the time slice) is categorized as strongly biphasic by the criterion we used for nondirectional cells. The principal component with the longer latency (closed symbols in the time slice) is much less biphasic. Similar results were obtained for each of our directional cells.

Using the same procedure as we had done for nondirectional cells, we then curve-fit the temporal profile of each of the two principal components for each cell and measured the time to peak of the first and second phases of each component’s profile. We also averaged the normalized data across all cells for each of the principal components (Fig. 3B). Not only did the early components of the directional cells resemble the strongly biphasic cells in being very biphasic, but the times to peak were very similar to our strongly biphasic nondirectional cell sample, as can be seen by comparing Fig. 3 A and B (open symbols), and examining the medians of the latencies in Table 1. The late components of the directional cells, in turn, closely resemble the weakly biphasic cells in being almost monophasic, and the times to peak were very similar to the weakly biphasic population, as can be seen by comparing Fig. 3 A and B (closed symbols), and the median latencies in Table 1. This result is just what one would predict if the earliest input to each directional cell were coming from one or more of the strongly biphasic nondirectional cells we have identified, and the later input were coming from one or more of the weakly biphasic nondirectional cells (or from their respective LGN inputs).

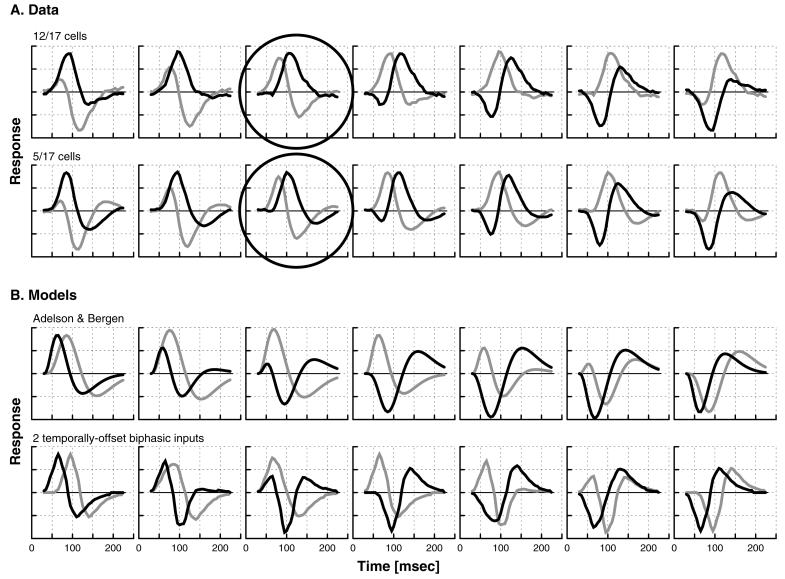
It should be noted, however, that the principal components found via SVD analysis do not provide a unique decomposition of a cell’s RF. Any rotation of these components (i.e., any linear combination of them) will account equally well for the same amount of variance in the temporal impulse responses across the width of a directionally selective cell’s RF. To determine whether various combinations of the principal components of directional cells might give an even better correspondence to the two nondirectional cell populations, we examined various component rotations for each of our directional cells (see Fig. 4A). For all of the directional cells, there was a rotation at which one component was very biphasic, and the other component was either monophasic (for 12 of the 17 cells, with biphasic index <0.1), or weakly biphasic (for the remaining five cells, with biphasic index <0.4). Picking that axis rotation in which one component was most monophasic, we again averaged the two rotated components of all of our directional cells. As seen in Fig. 3C, there is now an even closer resemblance between the temporal impulse responses of the two classes of nondirectional cells and the two components that together could account for the RFs of directional cells.

Figure 4.

Principal components of directional cells and inputs to two motion models, with various rotations (0°–180°, every 30°, left to right). (A, Upper) Example of a directional cell for which there was one particular rotation angle (circled) at which one of the components was totally monophasic (biphasic index <0.1). This result was seen in 12/17 cells. (Lower) Example of a directional cell for which at one rotation angle (circled) one component was minimally biphasic (index <0.4) but not totally monophasic. This result was seen for the remaining five cells. (B) Linear combinations of two components used in models of directional cells. (Upper) The pair of temporal profiles used in the Adelson–Bergen (2) model. (Lower) The pair of temporal profiles of a model that produces directional cells by combining two biphasic cells with identical temporal impulse response shapes (average waveform of the strongly biphasic cells in our sample) but different latencies. Note that for neither of these models is there a rotation angle at which the least biphasic component has a biphasic index of less than 0.45. Neither thus can account for any of our directional cells.

Thus both in terms of the biphasic index and of the time to peak, two components that can be linearly summed to account for the responses of directional cells have the same characteristics as the two subpopulations of strongly biphasic and weakly biphasic nondirectional cells we have found in the striate cortex. These observations are consistent with our suggestion that directional simple cells in the macaque striate cortex acquire the temporal quadrature offset required for local motion detection by a linear summation of outputs from one or more cells from each of these nondirectional cell classes (or from the LGN cells from which they respectively get their inputs).

DISCUSSION

Temporal Properties of Directional and Nondirectional Cells.

The temporal properties of the two populations of nondirectional cells we have identified closely resemble in several respects the two principal components of directional cells, which, linearly summed, can account for the RF structure of these cells. First, the latencies to peak of the early components of the directional cells correspond quite precisely to the latencies to peak of the strongly biphasic nondirectional cells regardless of rotation. The separations in peak latencies of the two components are around 20 msec for every rotation angle so the latencies of the late components of the directional cells also correspond quite closely to the latencies of the weakly biphasic nondirectional cells, regardless of axis rotation. Second, the early components of the directional cells are very biphasic, as are the fast, strongly biphasic nondirectional cells and the later components of the directional cells are monophasic or weakly biphasic, as are the slow weakly biphasic nondirectional cells.

In the classic motion models, the two temporal components that serve as inputs to directional cells are both biphasic. The upper row in Fig. 4B shows the temporal impulse responses of the inputs in the Adelson–Bergen (2) model on the leftmost panel and their various linear combinations to the right. It can be seen that there is no combination in which one of the components is monophasic. Such a model thus could not account for the characteristics of the 12/17 directional cells in which the later component is totally or almost totally monophasic (and even for the remaining 5/17 cells in which the later component is less biphasic than the earlier component). Our data also cannot be accounted for by a model based on summing two biphasic inputs displaced in time, each with the phasic characteristics of our strongly biphasic cell population (see Fig. 4B Lower). (This model is based on directional cells having inputs from temporally offset biphasic cells from the magno LGN pathway, see below.) So the fact that the directional cells we find in the striate cortex can be constructed from a strongly biphasic fast component and an almost monophasic slower component, similar to the properties of the two classes of nondirectional cells, is an unexpected finding that strongly suggests the functional relationship we propose.

Finally, we find that the temporal profiles of the two populations of nondirectional cells are in quadrature, as are the two components of directional cells. Principal component analysis, of course, specifies that the two components of the directional cell be in quadrature relationship, but there is nothing that requires the two populations of nondirectional cells to be in similar quadrature relationship to each other.

Combination of Magnocellular (M) and Parvocellular (P) Paths for Motion?

The accepted doctrine is that the motion system is based on the M geniculate population, with little or no P input (15–16). One basis for this conclusion is that directional cells are very common in layer IVcα of the cortex, where the M geniculate cells synapse (17), and this layer is the start of what is considered the IVcα-IVb-MT motion pathway. But there is ample anatomical evidence for vertical interactions within a cortical column (18–19) and direct evidence for P-cell input to cells in layer IVb (20). Another basis for the accepted doctrine that only M cells constitute the motion path is that psychophysical studies show that motion detection saturates at very low contrasts (21), and it has been shown that M geniculate cells have a much higher contrast gain than do P cells (22) and reach response saturation at low contrasts. However, there are situations in which motion perception improves up to quite high contrasts (23), like the output of P cells, and it has been argued on these grounds as well as from sampling considerations (24) that P cells must have an important role in motion perception.

We argue that one of the inputs to striate cortex directional cells, in most cases the strongest one, comes from the M path, but suggest that both inputs typically do not. Our data suggests that the two subpopulations of strongly biphasic and weakly biphasic V1 cells we have identified have primarily M and P inputs, respectively, and that directional cells get inputs with the different time courses required to extract motion information by summing together signals from M and P pathways.

Two aspects of our data support this position. First, the differing temporal characteristics of our two populations of nondirectional cells correspond to the properties that have been reported of P and M cells, respectively, in the LGN. A number of studies have shown that P cells give quite sustained responses to most stimuli, whereas M cells’ responses are much more transient (25–27). The sustained-transient distinction is consistent with the weakly versus strongly biphasic difference we find in the two classes of nondirectional cells and in the two components that could account for the responses of directional cells. There is also evidence for latency differences between P and M cells. Studies of electrical stimulation of the optic nerve consistently have found faster conduction velocity for M than for P cells (26, 28), and geniculate M cells have been reported to respond some 15–17 msec faster than P cells to comparable stimuli (26, 29). Thus, the short-latency, strongly biphasic component of the directional cells’ responses resembles the fast, transient, temporal properties that have been reported of cells in the M path, whereas the slower, weakly biphasic second component resembles in latency and in sustained character the temporal dynamics that would be expected from a P-cell input. Furthermore, we find no evidence for two classes of M-like biphasic cells in the striate cortex, one fast and one slow. Rather, the biphasic cells are all very fast, and the cells with longer latencies have the characteristics of P cells.

A second argument for directional cells getting their requisite temporal properties by summing signals from M and P geniculate cells comes from a consideration of the chromatic properties of the two nondirectional cell populations in our sample. We have data from RF mapping with cone-specific stimuli and from responses to isoluminant chromatic stimuli for most of the nondirectional cells in our study. Sixteen of the 18 strongly biphasic cells for which we have chromatic data had RFs in which the different cone (and geniculate) inputs were superimposed and in phase; that is, they are clearly nonopponent cells with the types of RFs expected from cells with M input. Only two of the 18 had a clear spectral opponency. On the other hand, 31 of the 35 weakly biphasic cells for which we had appropriate data had cone-opponent RFs and gave opponent responses to chromatic stimuli; the other four were nonopponent.

In conclusion, we find evidence for a bimodal distribution of nondirectional simple striate cortex cells on the basis of how biphasic their temporal responses are. The strongly biphasic cells turn out to have much shorter latencies than the weakly biphasic cells for both the initial and the reversed second phases, and these two classes of cells are on average in quadrature temporal relationship to each other. We find that the spatiotemporal RFs of directionally selective simple cells can be accounted for by two components that have almost exactly the same latencies and similar biphasic characters as do the strongly biphasic and weakly biphasic cells, respectively. This finding suggests that directional cells might acquire the linear component of their directional selectivity by integrating signals from cells of each of the two biphasic classes of nondirectional cells or their respective geniculate inputs. Furthermore, we postulate that these fast and slow inputs to the directional cells have their origin in cells of the M and P retinocortical paths, respectively.

ABBREVIATIONS

RF

receptive field

LGN

lateral geniculate

SVD

singular value decomposition

M

magnocellular

P

parvocellular