Systematic analysis of nucleation-dependent polymerization reveals new insights into the mechanism of amyloid self-assembly

Abstract

Self-assembly of misfolded proteins into ordered fibrillar aggregates known as amyloid results in numerous human diseases. Despite an increasing number of proteins and peptide fragments being recognised as amyloidogenic, how these amyloid aggregates assemble remains unclear. In particular, the identity of the nucleating species, an ephemeral entity that defines the rate of fibril formation, remains a key outstanding question. Here, we propose a new strategy for analyzing the self-assembly of amyloid fibrils involving global analysis of a large number of reaction progress curves and the subsequent systematic testing and ranking of a large number of possible assembly mechanisms. Using this approach, we have characterized the mechanism of the nucleation-dependent formation of β₂-microglobulin (β₂m) amyloid fibrils. We show, by defining nucleation in the context of both structural and thermodynamic aspects, that a model involving a structural nucleus size approximately the size of a hexamer is consistent with the relatively small concentration dependence of the rate of fibril formation, contrary to expectations based on simpler theories of nucleated assembly. We also demonstrate that fibril fragmentation is the dominant secondary process that produces higher apparent cooperatively in fibril formation than predicted by nucleated assembly theories alone. The model developed is able to explain and predict the behavior of β₂m fibril formation and provides a rationale for explaining generic properties observed in other amyloid systems, such as fibril growth acceleration and pathway shifts under agitation.

Self-assembly of misfolded forms of normally soluble and functional proteins or peptides into amyloid fibrils results in numerous human diseases (1). Understanding how amyloid self-assembly occurs, therefore, is of paramount importance for a molecular interpretation of amyloidosis and for the development of therapies against amyloid disease. Over the past decade, advances have been made toward a more complete description of amyoid fibril formation, including the determination of increasingly refined models of fibril structures (reviewed in ref. 1) and the identification of amyloid precursors and oligomeric states reviewed in ref. 2, one or more of which could be the culprits of cytotoxicity associated with several amyloid diseases (e.g., ref. 3). However, the molecular events occurring during the self-assembly process itself remain obscure because of the heterogeneity and the complexity of the early association events.

Amyloid fibril self-assembly reactions are generally accepted as a form of nucleated polymerization (4). These reactions are characterized by an initial lag phase where little or no change in fibril concentration can be detected. This is followed by an elongation phase where a large mass percentage of the starting protein material is converted into fibrils. A shared feature among amyloid formation and other nucleated processes is that the lag phase can be partly or entirely bypassed by the addition of seeds. In the case of amyloid fibrils, seeds are usually fragments of preformed fibrils. Traditionally, information regarding the species present during the lag phase, for example, the size of the so-called “critical nucleus,” are gained through analysis of the protein concentration dependence of the rate of fibril formation, determined for example by the time to reach 50% reaction completion (t₅₀), the length of the lag phase (t_lag), or the initial rate of fibril formation (4). This simple approach is based on nucleation-dependent polymerization theories and other similar and related models originally developed for actin and sickle cell haemoglobin assembly (4, 5) and dictates an increasingly strong concentration dependence of these parameters with an increase in the size of the “critical nucleus.” Many studies have applied this approach to amyloid assembly reactions, with the majority of cases showing a very small concentration dependence of the reaction progress (e.g., refs. 6–11), leading to the conclusion that the “critical nucleus” is monomeric or very small. Although simple to perform, mounting evidence indicates that this type of analysis is inadequate because of the presence of large populations of prenucleus oligomers (12, 13) and/or the use of mechanical agitation during fibril growth (8, 14), which can diminish the apparent concentration dependence of fibril growth leading to an underestimation of the nucleus size(s). Another drawback of such an analysis is that the sigmoidal shape of the progress curves are usually ignored, even though fibril formation most often displays a higher degree of apparent cooperativity than is typically theorised and observed in other nucleated reactions [supporting information (SI) Fig. S1], and upon which the amyloid assembly models were drawn (4).

Here, we provide a new strategy for the analysis of amyloid fibril formation by acquisition of >200 fibrillation progress curves under the widest possible range of protein concentration by defining nucleation in the context of both structural and thermodynamic aspects and by developing a generalized modular modeling approach that allows a variety of possible self-assembly mechanisms to be tested systematically. Using this approach, we have studied the assembly of β₂-microglobulin (β₂m) into amyloid-like fibrils at low pH (15, 16). Under these conditions, fibril formation occurs both rapidly and quantitatively, without visible formation of amorphous aggregates, providing an ideal system with which to develop theories of nucleated amyloid assembly.

Results

Experimental Measurement of the Concentration Dependence of Fibril Formation.

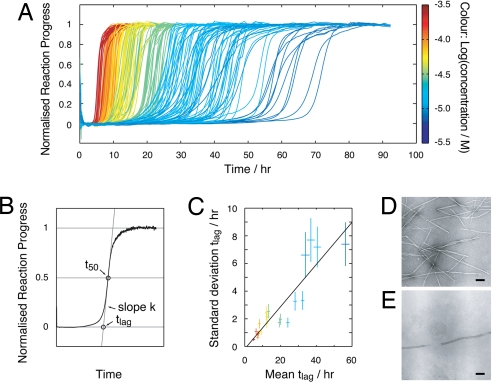
To obtain information regarding the nature of the nucleating species in β₂m amyloid formation, a large dataset consisting of 235 progress curves was obtained at monomer concentrations ranging from 8 to 244 μM monitored by the fluorescence of the amyloid-specific dye thioflavin T (ThT) (Fig. 1A). Twelve replicate reaction traces were typically collected at each protein concentration. In all cases, the samples were agitated (see Materials and Methods) to facilitate rapid fibril growth. Each curve displays lag-phase kinetics typical of nucleated growth. ThT fluorescence was chosen as the reporter to monitor the reaction progress because of its high sensitivity and signal to noise ratio (Fig. S2), which became particularly important at low protein concentrations. Control experiments, using intrinsic tryptophan fluorescence, light scattering, turbidity and EM, showed that the binding of ThT does not perturb the rate of assembly and confirmed that ThT reports on the same fibril formation process as the other detection methods (Fig. S2). Negative stain EM showed, in addition, that the fibrils formed under every condition used have a long-straight morphology typical of amyloid (Fig. 1 D and E). Principal parameters describing the transitional regions of the progress curves: The lag time (t_lag) and the transition slope (k) were extracted from the normalised progress curves (see Materials and Methods and Fig. 1B) for subsequent analysis.

Fig. 1.

Reaction progress curves of amyloid fibril formation of β₂m. (A) Reaction progress curves monitored by ThT fluorescence. A total of 235 traces are shown at 20 different protein concentrations ranging from 8 to 244 μM (color bar on the Right). (B) Representative illustration of the method by which t_lag and k are extracted from the reaction traces. (C) The variation in the replicates shown as the standard deviation of t_lag plotted vs. the average t_lag. The error bars represent the standard error of the standard deviation and the standard error of the mean, respectively. A free linear fit is also shown. (D and E) Negative stain EM images of samples after the reaction reached completion obtained at a protein concentration of 244 μM (D) or 8 μM (E). (Scale bars, 100 nm.)

As shown in Fig. 1A (as expected for a nucleated reaction), the length of the lag-time is increased as the protein concentration is decreased. However, at each protein concentration, a significant variation in the lag time is observed. This is particularly obvious at the lowest concentrations used (dark blue traces in Fig. 1A). The standard deviation of t_lag at each protein concentration is plotted against the average of t_lag in Fig. 1C. The plot shows that the variation in t_lag is linearly correlated with the average, with the fitted intercept close to zero, demonstrating the random nature of the variation, independent of the average. This suggests that the variations observed in the data are likely to originate from subtle experimental differences between the replicates, but may also reflect contributions from the stochastic nature of the nucleation mechanism (17, 18). Another important feature of the data is that all of the curves have steep transitions similar to the progress curves observed for the assembly of fibrils from other amyloidogenic proteins and peptides (e.g., refs. 8 and 11) but distinctively different from those predicted by nucleated assembly models alone (4, 5) (Fig. S1). The steepness of the transitions indicates the presence of a secondary process accelerating the reaction under the conditions used (4).

Construction of a Generic Mechanistic Modeling Approach for Fibril Self-Assembly.

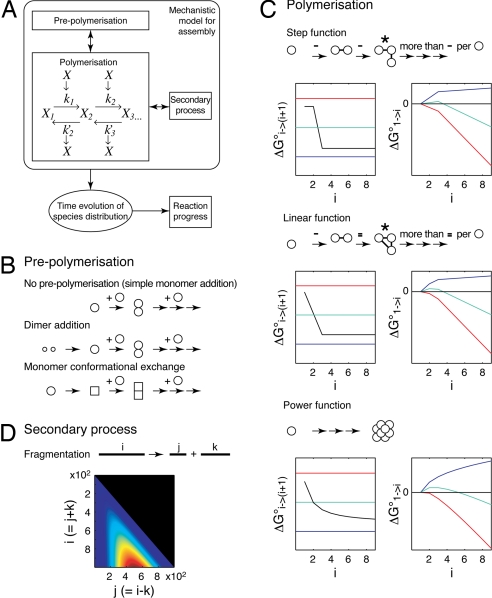
To gain new insights into the mechanism of amyloid formation, a model capable of describing the self-assembly process, including the progress curves and their concentration dependence, is required. Many different mechanistic models have been used to describe the assembly of amyloid and other self-assembled protein polymers (e.g., refs. 4, 5, 12, 14, and 19–23). Because of the complexity of the system and the consequent large number of different possibilities involved, a modular approach was used here to model amyloid assembly. We have rationalized the mechanism into three distinct modules: prepolymerization, polymerization, and secondary processes (Fig. 2). Each possible assembly model is then composed of a variant of each of the three modules (a full mathematical and thermodynamical description is given in SI Text and Table S1). Key features of the model design are: (i) The modular design enables a large number of different assembly mechanisms to be tested and ranked. (ii) The generic assembly reaction scheme used (Fig. 2A and SI Text, Eq. 1) does not itself constrain the assembly model but allows the assembly mechanism to be derived by the choice of functions describing the rate constants and reaction free energies for each step of the assembly (here step, linear, and power functions were tested, each corresponding to a distinct assembly scenario where different free energy contributions, such as specific interactions or translation/rotational entropies, dominate; see Fig. 2C and SI Text). (iii) The structural and thermodynamic aspects of assembly are separately and exactly defined, with the shape of the reaction free energies for each assembly step as function of the extent of assembly defining the structural nucleus size n_S (SI Text, Eq. 9). The free energy for each assembly species compared with the monomer (taking into account the contribution of translational entropy loss by reduction in the number of particles during assembly) then defines the thermodynamic nucleus size n_T (SI Text, Eq. 10). (iv) A secondary fragmentation process that includes a length and position-dependent rate of fragmentation is used (Fig. 2D, SI Text, and Eq. 13). (v) The progress curves for different possible mechanisms are calculated numerically, which eliminates the need for additional, potentially erroneous, assumptions used in analytical models such as negligible oligomer populations and irreversible steps (4, 12). In summary, the key idea behind our approach is that, instead of using a single model containing simplifications that are based on predetermined assumptions that may be difficult to justify or validate in the analysis of experimental data, we use a flexible approach that allows a large number of possible models to be tested against the experimental data.

Fig. 2.

Schematic illustration of the modeling strategy. (A) The overall model configuration consists of three modules: prepolymerization, polymerization, and secondary processes. The primary output is the distribution of species as a function of time. This distribution is then used to calculate reaction progress curves and other quantities that can be used to compare with the experimental data. (B) Diagram representation of the three different prepolymerization modules tested. (C) Different reaction free energy functions tested. For each case, the reaction free energy of each addition step as function of the extent of assembly are shown on the Left, and the free energy difference compared with the monomer is shown on the Right. Colored lines illustrate the reaction free energy ΔG%_i → (i + 1)° = 0 when the loss in translational entropy due to the reduction of particles at different concentrations is taken into account (Left), and the free energy of species compared with monomer (Right) at high (red), intermediate (green), or low (blue) initial monomer concentrations. A diagram describing the structural aspects of each variant tested is shown above each plot (−, interaction; *, structural nucleus in the case of step and linear functions). In the case of the power free energy function, which does not have a specific n_S, the intercept of the tangent to the initial slope and the value at i → ∞ are used to estimated n_S. (D) Illustration of the model used to describe the secondary process of fragmentation. The contour plot shows the dependence of the fragmentation rate constant on the total fibril length i and the breakage point in the fibril j for fibril lengths up to 1,000. The relative magnitudes of the fragmentation rate constant are shown from low (blue) to high (red).

Comparing Model Variants.

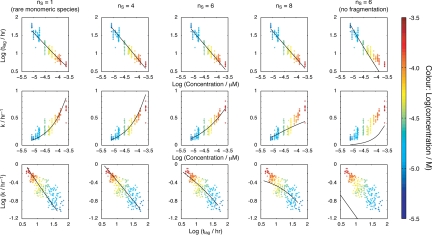
Next, we applied our modeling approach to the analysis of the experimental fibril growth curves for β₂m depicted in Fig. 1. The transitional regions described by the curve parameters t_lag and k were extracted from the numerical solutions of the models in the same way as for the experimental reaction progress traces shown in Fig. 1B. The resulting values were then compared with the experimental data through least-square analysis in order that the model(s) best representing the experimental progress curves can be determined. Key to this analysis were: (i) the acquisition of data over the largest possible protein concentration range (limited by the sensitivity of the assay and the need to avoid nonspecific aggregation); (ii) the collection of sufficient data to enable accurate statistical analysis; and (iii) the confirmation that fibrils with identical morphology were obtained under all conditions. Most importantly, global analysis of the entire dataset was carried out with the numerically calculated progress curves rather than analysis with any single kinetic parameter. A total of 21 different models, constructed through different combinations of variants of the three modules described above, were tested (numbered in Table S2). The pairwise relationship plots of the t_lag, k, and initial monomer concentration, together with representative examples of globally fitted models are shown in Fig. 3, with each 2D plot showing different representations of the dataset and the model. Although such a representations provide a useful means of displaying the data and the predictions of different models, the goodness of fit of the different models was quantified and ranked through the calculation of Akaike information criterion (AIC) scores (see SI Text) that take into account the quality of the global fit and the number of fitted parameters (Table S2).

Fig. 3.

The curve parameters t_lag and k representing the experimental data at different initial monomer concentrations shown in Fig. 1A (+) plotted as different pairwise combinations, together with selected global least-square fitted models shown in the same pairwise representations (black lines). (Top) log(concentration) vs. log(t_lag). (Middle) log(concentration) vs. k. (Bottom) log(t_lag) vs. log (k). All models shown involve monomer addition and a step nucleation polymerization mechanism and, with the exception of the rightmost plots, included fragmentation as a secondary process. Although each figure serves to represent the data and the predictions of different models, the best fit model was selected by global analysis and subsequent ranking of the goodness of each fit.

Through ranking of AIC scores of the 21 models tested, a single best-fit model was identified. This model involves monomer addition through a hexameric structural nucleus involving fragmentation as a secondary process (Fig. 3, column three, n_S = 6 and Table S2, model 5). Although significantly poorer in describing the experimental data, the models with the nearest best fits included a rarely populated monomeric species as the structural and thermodynamic nucleus (Fig. 3 leftmost column Table S2, model 21), and some models with n_S larger than one but with the n_T approaching one (Table S2, models 8–10). However, models without fragmentation as a secondary process are unable to describe the experimental data (rightmost column in Fig. 3 and Table S2, models 1, 12, and 20). Importantly, although a single model of the 21 tested emerged as best able to describe the data if the global picture is considered, analyses based solely on the concentration dependence of a single kinetic parameter, such as t_lag or t₅₀, are inadequate in distinguishing between different possible assembly mechanisms (Fig. 3 Top). This is especially true for amyloid assembly reactions displaying a high apparent cooperativity of assembly, which is indicative of the involvement of secondary processes, such as fragmentation (24).

To further distinguish the best-fit model from the other alternative possibilities, we next analyzed the size of species populated during the lag phase predicted by each model. The best-fit model involving step free energy function with n_S = 6 (Table S2, model 5) predicts a significant decrease in monomer concentration and a corresponding increase in the population of on-pathway oligomeric species preceding the hexameric structural nucleus in the lag phase (Fig. 4). Other models tested that have relatively good agreement with the data, such as the model involving a rarely populated monomeric species as the structural nucleus (Table S2, model 21), or n_S = 4 with linear free energy function (Table S2, model 8), predict monomer depletion that reflects the formation of fibrils and the absence of significant amounts of oligomers in the lag phase. Importantly, previous analysis of fibril growth under conditions very similar to those used here using ESI-MS demonstrated the presence of dimers, trimers, and tetramers in the lag phase, but no higher order species were found (25). The ESI-MS analysis also demonstrated a significant decrease in the monomer concentration in the lag phase, consistent with the predictions of the best-fit model (Table S2, model 5). Parallel experiments using sedimentation velocity AUC also revealed an equilibrium between 1 and 4 mers in the lag-phase, although rapid equilibrium between these species on the timescale of the experiments precluded determination of their relative populations (25). These experiments provide powerful independent information that mirrors the predictions made assuming the best-fit model with n_S = 6 (Fig. 4), but are inconsistent with the other models tested that fitted the fibril formation data less well. The best model able to describe all of the experimental data available, therefore, is that involving monomer addition to a hexameric structural nucleus in a step nucleating polymerization reaction with fragmentation as a secondary process.

Fig. 4.

Comparison of the calculated reaction progress (leftmost column), together with the population of monomer dimer, trimer and tetramer vs. time. (Upper) The best-fit model (monomer addition, step free energy function with n_S = 6, including secondary fragmentation) (Table S2, model 5). (Lower) Next-best model (monomer addition, rare monomeric structural nucleus and secondary fragmentation) (Table, model 21).

Testing the Model Predictions.

As a further test of the robustness of the above model, we next performed additional experiments and used the resulting information to test the predicted properties of the described system. First, we carried out fibril growth experiments in the absence of agitation but in the presence of fibril seeds. Fibrils used as seeds were formed at an initial monomer concentration of 63 μM exactly as described above. At the end of fibril growth (50 h), 2% (vol/vol) of the sample was added directly to freshly prepared protein solutions to seed growth. The rate of fibril growth was monitored at different initial monomer concentrations ranging from 1.5 μM to 12 μM. The resulting reaction progress curves showed traces without a detectable lag phase and the reaction reached completion within 5–10 h (Fig. S3A). Importantly, the model that best describes the experimental data for the unseeded agitated growth reactions shown in Fig. 1A (monomer addition, step nucleation at n_S = 6, with fragmentation as a secondary process) reproduces accurately the progress curves obtained in the absence of agitation through seeded fibril growth (Fig. S3B). However, if fragmentation is excluded during seed formation, the model is no longer able to describe the experimental data (Fig. S3B Inset), instead predicting that even under seeded conditions fibril formation would take >500 days to complete.

Second, if fragmentation is the dominating secondary process during agitated fibril growth, as the best-fit model suggests, the ability of fibrils to seed new reactions should depend on the number of fibril ends, determined by the extent of fragmentation. By contrast, if the secondary process involves heterogeneous nucleation on fibril surface (26), then the seeding efficiency should be independent of the number of fibril ends, because the total surface area of thin linear aggregates will be essentially independent of agitation. To determine whether this is the case, fibrils were formed in the absence of agitation but in the presence of the same amount seeds by weight that had been fragmented to different extents by vigorous agitation (see Materials and Methods). The seeding efficiency characterized by the initial slope of the seeded reaction progress curves was then monitored (Fig. S3C). The data show that the seeding efficiency increases as the extent of fragmentation is increased, precisely as predicted assuming that fragmentation is the dominant secondary process under nonquiescent conditions.

Discussion

Polymerization Free Energy Profile and Structural vs. Thermodynamic Nucleus.

In this work, we have developed a systematic approach for the analysis of the mechanism of nucleation-dependent assembly into amyloid fibrils. The approach described is generically applicable and enables the complexities of amyloid assembly mechanisms to be dissected. It also allows different oligomeric species to be identified and their population quantified, providing a structural and thermodynamic platform for the analysis of nucleated mechanisms and allowing rare oligomeric species to be predicted and their populations quantified. The approach involves comparing variants of a generic and modular mechanistic assembly model with a large number of experimental reaction progress traces. Using this approach, global analysis of the concentration dependence of the rate of fibril assembly over 200 reaction progress curves with 21 different possible models and subsequent ranking of the models tested suggests that nucleated amyloid assembly of β₂m under the conditions used is likely to involve the addition of monomers to form a structural nucleus approximately the size of a hexamer, despite displaying a relatively low dependence of the rate of assembly on the monomer concentration. Indeed, if the log(concentration) vs. log(t_lag) plot in Fig. 3 is fitted to a linear function, a slope of 0.8 results, suggesting a monomeric “critical nucleus.” One reason for this apparent discrepancy is that the concentration dependence of reaction times alone provides only an estimate of the approximate size of the thermodynamic nucleus n_T, that is to say, the highest free energy species along the assembly reaction coordinate (maximum in SI Text, Eq. 10), under the experimental conditions and initial monomer concentrations used. Also, for a multimolecular reaction, n_T depends on the monomer concentration, because the entropic cost of forming multimeric species varies with the initial monomer concentration, a feature that is masked when applying a standard concentration of 1 M. We define the structural nucleus size, n_S, however, using the shape of the reaction free energy for each assembly step as function of the extent of assembly (SI Text, Eqs. 8 and 9) that includes terms describing the interaction pattern of the earliest species (Fig. 2C). Accordingly, n_S does not depend on the initial monomer concentration, and its determination thus provides important new information about the assembly process. Here, by modeling the nucleation rate and free energy functions separately from the generic polymerization reaction scheme itself, n_S (calculated from the shape of the reaction free energy as a function of the extent of assembly) (SI Text, Eqs. 8 and 9) and the concentration dependence of n_T (calculated as the species with highest free energy compared with monomer) (SI Text Eq. 10) are defined separately, allowing relevant structural and thermodynamic information regarding the early assembly species to be obtained.

For the in vitro assembly of β₂m fibrils, we show that a nucleation mechanism described by a step free energy function, involving a sudden increase in the number of stabilizing interactions leading from the structural nucleus (Fig. 2C), fits the data better than the other functions tested. A similar step nucleation mechanism has also been successfully used to describe assembly of other linear protein aggregates but does not describe well the aggregation of sickle-cell haemoglobin (21). This may reflect the fact that the former cases involve specific sidechain–sidechain interactions, rather than the simple packing of “large sticky spheres” as in the case of sickle cell aggregates (19). Another feature of the step nucleation mechanism is that the step free energy functions describing this type of nucleation mechanism only allow thermodynamic nucleus sizes n_T of 1 (at high concentrations), n_S, or infinity (at low concentrations where polymerization does not take place). Therefore, at intermediate protein concentrations where n_T = n_S, significant oligomer populations may be present in the lag-phase, relatively large structural and thermodynamic nucleus sizes will result, and shallow enough free energy functions for early species will still ensure that the rate of the overall reaction shows a small concentration dependence on the monomer concentration. This is analogous to the properties seen for a comparable polymerization mechanism through analytical approaches (12). Thus, nucleated assembly processes displaying a low dependence on the protein concentration of the rate of assembly do not necessarily exclude the possible presence of multimeric nuclei preceded by on pathway, potentially toxic, oligomers.

Role of Fragmentation in Amyloid Fibril Assembly.

Mechanical agitation not only affects the rate of nucleated fibrillation reactions (8, 27), but may also affect other properties, such as the final fibril morphology (15, 27), cellular toxicity (28), and the phenotypic behavior of different prion strains (29). How agitation produces such a variety of effects, however, was not clear (14, 28). Here, we have shown that fragmentation is the dominating result of agitation in β₂m fibril formation under the conditions used, rationalizing the dramatic effect of agitation on the rate of fibril formation and the shape of the reaction progress curves.

We have shown that β₂m fibrils with different morphologies can be formed under exactly the same solution conditions, depending on the agitation condition used (15). This phenomenon has also been observed with other amyloidogenic sequences, such as Aβ_1-40 (27) and GNNQQNY from the yeast prion protein Sup35p (30). In the case of β₂m, short rod-like or worm-like fibrils are formed rapidly under some conditions without mechanical agitation (15). These species represent kinetically stable oligomers off-pathway to long-straight fibrils. If sufficient agitation is provided so that the rate of formation of long-straight fibrils is significantly accelerated through the fragmentation mechanism we propose, the assembly pathway can shift from being kinetically controlled to being thermodynamically controlled, favoring the formation of long-straight amyloid fibrils as experimentally shown. Because fibrils with different morphologies are likely to respond differently to mechanical stress (29, 31), the assembly pathway taken may be dominated by the brittleness of the fibrils and the amplitude of the agitation force. Because both the mechanical and solution conditions are critical in defining the overall assembly energy landscape, both conditions must be precisely controlled to define the structural molecular mechanism of amyloid formation, to delineate the origins of amyloid disease and to develop therapeutic agents able to control aggregation by decreasing the concentration of toxic species or the fibril load that, together, are the causative characteristics of amyloid disease.

Materials and Methods

De Novo Fibril Growth.

β₂m protein expression and purification were carried out as described in ref. 32. The purity of the final gel filtered samples was confirmed by SDS/PAGE, native PAGE, and MS. Lyophilized protein powder was dissolved directly into the reaction buffer containing 10 mM sodium phosphate (pH 2.0), 50 mM NaCl, 0.02% (wt/vol) NaN₃, and 10 μM ThT. The mixture was then immediately syringe-filtered (0.2 μm of MiniSart fast flow), and 100 μl was added into the wells of black 96-well plates (Corning). The plates were sealed with transparent film and put into a BMG FluorStar plate reader at 37°C to start measurement. The measurement program consisted of 1-min measurements between 5 min of orbital 1-mm diameter shaking at 600 rpm, giving a sampling frequency of 10 data points per hour. The dead time between dissolving the protein and the start of the measurement was usually 10 min, equivalent to <3% of the t_lag of even the fastest reactions. Under the mechanical agitation condition used here, we estimate that the maximum sheer stress (based on the flow speed along the wall of the wells with inner diameter of 6 mm) is several orders of magnitude lower than the sheer modulus of the fibrils (31). However, because the agitation also induces other deformations such as torsion and bending in addition to pure sheer of the fibrils during the continuous application of agitation, significant breakage of the fibrils results. Fibril samples were analyzed by negative stain EM as described in ref. 32.

Seeded Fibril Growth.

Seed solutions were made by dilution of fibril samples formed as described above. For the determination of the effect of fragmentation on seeding efficiency, the fibrils to be used as seeds were subjected to additional vigorous stirring for different lengths of time, using a 3 × 8 mm PTFE coated magnetic stirring bar in a 1.5-ml chromatography glass vial on a multipoint stirrer (custom made by the workshop of the School of Physics and Astronomy, University of Leeds) with an accurate rpm readout provided by a rev-counter on the rotor axis. The stirring speed was 1,500 rpm. Seeding solutions of 2% (vol/vol) were used. The reactions were initiated by adding protein monomers and fibril growth was monitored as described above, except no agitation was used. The dead time between mixing the protein solution with the seeds and start of the measurements was usually 2 min.

Data Analysis and Modeling.

All data analysis and modeling calculations, including numerical integration of ordinary differential equation systems and least-square optimizations, were carried out by using Matlab (Mathworks). For the reaction progress data, scripts enabling fully automated linear baseline normalization and transition parameter extraction were used to ensure objective extraction of the curve parameters t_lag and k. Calculated progress curves were obtained through numerical integrations of the ordinary differential equation systems presented by the reaction kinetics. The numbers of species explicitly expressed in the calculations were chosen (up to 2400-mer), so that the error introduced by ignoring species larger than the cut-off size used was <1%. t_lag and k values were obtained from the calculated curves as described for the experimental data and fitted globally to the experimental t_lag and k values. The residuals in the least-square analyses were weighted by the standard error of mean obtained from the experimental data to normalize them to the magnitude and the number of curves in the global analysis. The goodness-of-fit for tested models were evaluated by visual comparison of the fits and by comparing AIC_C scores (see SI Text).