Heart valve function: a biomechanical perspective

Abstract

Heart valves (HVs) are cardiac structures whose physiological function is to ensure directed blood flow through the heart over the cardiac cycle. While primarily passive structures that are driven by forces exerted by the surrounding blood and heart, this description does not adequately describe their elegant and complex biomechanical function. Moreover, they must replicate their cyclic function over an entire lifetime, with an estimated total functional demand of least 3×10⁹ cycles. As in many physiological systems, one can approach HV biomechanics from a multi-length-scale approach, since mechanical stimuli occur and have biological impact at the organ, tissue and cellular scales. The present review focuses on the functional biomechanics of HVs. Specifically, we refer to the unique aspects of valvular function, and how the mechanical and mechanobiological behaviours of the constituent biological materials (e.g. extracellular matrix proteins and cells) achieve this remarkable feat. While we focus on the work from the authors' respective laboratories, the works of most investigators known to the authors have been included whenever appropriate. We conclude with a summary and underscore important future trends.

1. Introduction

Heart valves (HVs) are cardiac structures that ensure unidirectional blood flow during the cardiac cycle. However, this description does not adequately describe their biomechanical function, which is multi-modal and their loading cycle is repeated every second. While they are primarily passive structures driven by forces that are exerted by the surrounding blood and heart, this description does not adequately describe their elegant and complex biomechanical function. The semilunar valves (pulmonary valve, PV and aortic valve, AV; table 1) prevent retrograde flow back into the ventricles during diastole, while the atrioventricular valves (tricuspid valve, TV and mitral valve, MV) prohibit reverse flow from the ventricle to the atrium during systole. They must replicate this feat with each heart beat; over a single lifetime, HVs will open and close at least 3×10⁹ times.

Table 1.

Nomenclature.

AV	aortic valve
AC	when referred to flexure, the direction against the natural curvature of the leaflet
AVEC	aortic valve endothelial cell
AVIC	aortic valve interstitial cell
CFD	computational fluid dynamic (modelling)
Δκ	change in valve cusp specimen curvature in flexure
E	effective stiffness in flexure
EC	endothelial cell
ECM	extracellular matrix
GAG	glycosaminoglycans
Hsp47	heat shock protein 47
I	second moment of inertia
M	applied bending moment
MV	mitral valve
MVAL	mitral valve anterior leaflet
MVPL	mitral valve posterior leaflet
PV	pulmonary valve
SMA	smooth muscle actin (intracellular)
TEHV	tissue-engineered heart valve
TV	tricuspid valve
TVP	transvalvular pressure
VIC	valvular interstitial cell
WC	when referred to flexure, the direction with the natural curvature of the leaflet

As in many physiological systems, one can approach HV biomechanics from a multi-length-scale approach, since mechanical stimuli occur and have biological impact at the organ, tissue and cellular scales (figure 1). For example, we have reported that valvular interstitial cells (VICs) from the AV and MV were significantly stiffer than VICs of the PV and TV (Merryman et al. 2006b). These findings suggest that VICs respond to local tissue stress by altering cellular stiffness through valvular remodelling and valvular pathologies. On the other hand, valvular endothelium, which is directly exposed to shear stress, responds to the local shear changes (Butcher et al. 2004). The fact that AV diseases preferentially occur in the aortic side (fibrosa) of the valvular leaflets, where they are exposed to unstable flow conditions, highlights the importance of shear in AV biology and pathobiology.

Figure 1.

A schematic of the role of biomechanics in HV function, which occurs at multiple structural levels. At each structural level, biomechanics plays a functionally critical role. This is especially true at the cell and tissue levels, which will control functional equivalence and determine long-term growth/durability.

Another important point is that valvular extracellular matrix (ECM) is composed of a dense network of collagen, elastin and glycosaminoglycans (GAGs), and is thus functionally and mechanically very different from other cardiovascular structures (e.g. blood vessels, myocardium; Schoen 1997; Sacks et al. 1998). In fact, valvular ECM behaves structurally and mechanically much more like the dense planar connective tissues of the musculoskeletal system (Sacks & Chuong 1992; Billiar & Sacks 2000a). It is unique, however, in that it must function within a blood contacting environment and is thus coated with an endothelial cell (EC) monolayer. Moreover, there is evidence for aortic valve endothelial cell/aortic valve interstitial cell (AVEC/AVIC) communication that may play an important role in valve ECM homeostasis. Yet, despite its clinical importance, the unique and demanding valvular biological/biomechanical environment is relatively unexplored, with most research focusing on valvular prosthetic design and development.

The focus of the present review is on HV functional biomechanics. Specifically, we refer to the unique aspects of valvular haemodynamics and how the mechanical properties and behaviours of the biological materials (e.g. ECM proteins and cells) achieve this remarkable feat. While we focus on the work from our laboratories, the works of most investigators known to the authors have been included whenever appropriate. We conclude with future aims to underscore important future trends. In addition, while the literature is extensive there are still many gaps. Therefore, in this review, we note that experimental data and theoretical models may exist only for certain valves (or even specific leaflets).

2. Biomechanical function at the organ level

(a) Heart valve haemodynamics

The mechanisms ensuring the proper function of the HVs are essentially controlled by the surrounding haemodynamic environment. Understanding the interactions between the HVs and the local haemodynamic environment is thus critical to better understand normal valve function and disease progression. Although the four HVs present profoundly different anatomical and functional (e.g. opening/closing) characteristics, they all essentially function to facilitate the unidirectional flow of blood while maximizing flow rate and minimizing flow resistance. Thus, in the following, we focus on AV haemodynamics as an example for all the HVs. We also note that the effects of valve size or effective orifice area will affect the specific flow behaviours. However, for the purposes of the present review, we focus on general behaviours common to valve function.

The AV opens during systole when the ventricle is contracting and then closes during diastole as the ventricle relaxes. In healthy individuals, blood flows through the AV accelerating to a peak value of 1.35±0.35 m s⁻¹ (Otto 2001). The valve closes near the end of the deceleration phase of systole with very little reverse flow through the valve. The adverse axial pressure differences cause the low inertial flow in the developing boundary layer along the aortic wall to decelerate and then to reverse direction, resulting in vortices in the sinuses behind the AV leaflets (Reul & Talukder 1989). This action is thought to facilitate movement of the AV cusps (leaflets) away from the sinus wall and towards the closed position. When this force is coupled with the vortices that push the leaflet surfaces towards the closed position, a very efficient and fast closure is obtained. In vitro studies have shown that the axial pressure difference alone is sufficient to close the valve (Reul & Talukder 1989).

Thus, without the vortices in the sinuses the valve still closes, but its closure is not as efficient as when the vortices are present. However, we note that the AV should functionally be considered as part of the entire left ventricular outflow track. Thus, while the presence of the aortic sinuses helps to induce local haemodynamic patterns that facilitate AV function, they may have other functions. For example, during the cardiac cycle, the AV annulus expands and contracts, which clearly alters how the AV leaflets function, possibly facilitating valve opening. Further, the tissue structures at the leaflet/sinus interface reveal a gradual transition from the collagen-rich leaflet tissue to the elastin-rich sinus wall (Thubrikar 1990). Thus, the sinus geometry may also help reduce the effects of flexural stresses at the leaflet/sinus interface. We should always thus keep in mind that various valvular components have multiple functions and interact in a complex but ultimately in a functionally efficient manner.

The velocity profile at the level of the AV annulus is relatively flat. However, there is a slight skew towards the septal wall (less than 10% of the centre-line velocity) caused by the orientation of the AV relative to the long axis of the left ventricle (Kilner et al. 1993). The flow patterns just downstream of the AV are of particular interest owing to their complexity and relationship to arterial disease. Highly skewed velocity profiles and corresponding helical flow patterns have been observed in the human aortic arch using magnetic resonance phase velocity mapping (Kilner et al. 1993).

The PV flow profile is similar to that of the AV, but the velocity magnitude is lower. Typical peak velocities at the valve outlet for healthy adults measured with two-dimensional and Doppler echocardiography are 0.75±0.15 m s⁻¹ (Oh et al. 1997). During acceleration, the peak velocity is observed inferiorly with this peak flow rotating counterclockwise throughout the remainder of the ejection phase (Sloth et al. 1994). The mean spatial profile is relatively flat, although there is a region of reverse flow that occurs in late systole, which may be representative of flow separation. Typically, there is only a slight skew to the profile, and the peak velocity is generally within 20% of the spatial mean throughout the cardiac cycle. Secondary flow patterns can also be observed in the pulmonary artery and its bifurcation. In vitro laser Doppler anemometry experiments have shown that these flow patterns are dependent on the valve geometry and thus can be used to evaluate function and fitness of the HV (Sung & Yoganathan 1990; Sung et al. 1990).

(b) Atrioventricular valve haemodynamics

We first consider the MV functional demands. During isovolumic relaxation, the pressure in the left atrium exceeds that in the left ventricle, causing the MV leaflets to open. Blood then flows through the open MV from the left atrium to the left ventricle during diastole. The initial filling is enhanced by the active relaxation of the ventricle, which helps to maintain a positive transmitral pressure. A peak in the flow curve occurs during the early filling phase with normal peak velocities ranging from 50 to 80 cm s⁻¹ (Weyman 1994). Following active ventricular relaxation, the fluid begins to decelerate and the MV partially closes. In late diastole, the atrium contracts and the blood accelerates through the valve again to a secondary, lower velocity peak. The major/minor velocity peak ratios range from 1.5 to 1.7 (Weyman 1994).

The TV flow profile is similar to that of the MV, although the velocities are significantly lower because it has a larger valve orifice. The peak early and late flow velocities across the TV valve have been measured with Doppler echocardiography to be 0.51 and 0.35 m s⁻¹, respectively (Pye et al. 1991). Therefore, the TV peak early/late flow velocity ratios are similar to those of the MV (Pye et al. 1991). In contrast, the timing of TV opening is slightly different when compared with the MV. Since the peak pressure in the right ventricle is less than that in the left ventricle, the right ventricular pressure falls below the right atrial pressure faster than the corresponding time for the left side of the heart. Thus, there is a shorter right ventricular isovolumic relaxation time causing the TV to open earlier. Additionally, TV closure occurs after the MV, since the electrical stimulation of the left ventricle precedes that of the right ventricle (Oh et al. 1997).

MV fluid dynamics studies using magnetic resonance imaging (MRI) have shown that a large anterior vortex is normally present at the onset of partial valve closure as well as following atrial contraction (Kim et al. 1995). Bellhouse & Reid (1969) first suggested in an in vitro model that vortices generated by ventricular filling aid the partial closure of the MV following early diastole, and that without the strong outflow tract vortices, the valve would remain open at the onset of ventricular contraction. However, later in vitro experiments suggested that both flow deceleration and partial valve closure were due to an adverse pressure differential in mid-diastole, even in the absence of a ventricular vortex (Reul et al. 1981). Thus, although the vortices may provide additional closing effects in the initial stage, the adverse pressure gradient appears to be dominant in MV closure. A more unified theory of valve closure includes the importance of chordal tension, flow deceleration and ventricular vortices, with chordal tension being a necessary condition for the other two (Yellin et al. 1981).

(c) Flow characteristics

The experimental characterization of the haemodynamic environment experienced by HVs is difficult to achieve on a native valve owing to limited optical access. Additionally, although other imaging techniques such as MRI and ultrasound could capture the flow patterns produced in the vicinity of a fresh valve, those techniques do not offer the spatial resolution required to quantify the flow characteristics at small scales. More recently, computational tools have been developed to simulate the flow in complex HV geometries. As compared to the experimental flow techniques described above, computational fluid dynamics (CFD) permits the flow characteristics to be resolved at the microscale, in the entire valve region. Although the complexity of the valve geometry and motion prevents accurate simulations under physiological conditions represented by a peak systole Reynolds number of 6000, flow predictions obtained at a lower Reynolds number successfully capture the characteristics already observed in vitro and provide some insight into the small-scale haemodynamics experienced by the valve leaflets.

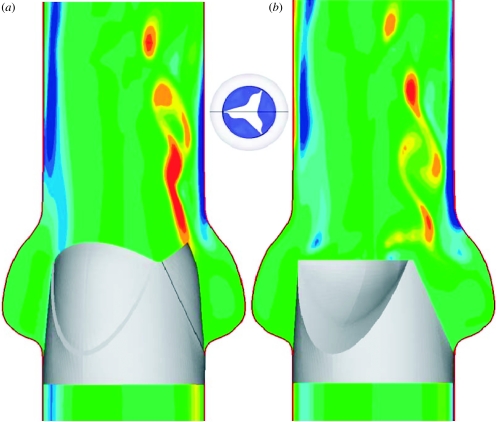
A CFD model was recently developed to simulate the flow through a tricuspid semilunar HV-like geometry. The kinematics of the valve was prescribed and the unsteady flow solution was computed for the case of a peak systole Reynolds number of 3000 (figure 2). The accelerating flow phase is dominated by the instability of the shear layers emanating from the leaflets, which gives rise to complex vortex shedding. The flow predictions provide evidence of the drastic difference between the haemodynamic stresses experienced by the aortic and ventricular sides. The limiting streamlines (i.e. lines tangent to the shear stress vector field) and the shear stress magnitude at two instants in time were computed on both the aortic and ventricular sides of the leaflets (figure 3). The ventricular stress field during the open phase suggests a fairly smooth, straight, accelerating flow, which is consistent with the favourable pressure gradient experienced by the flow as it is pushed by the contracting ventricle to pass through the leaflets. On the aortic side, however, the rapid cross-sectional area expansion in the sinus region imposes an adverse streamwise pressure gradient that gives rise to a very complex and disorganized flow. The stress field undergoes rapid changes as soon as the leaflets begin to close. On the ventricular side, the flow during the closing phase remains fairly straight, albeit less orderly than during opening. In addition to the drastically different flow patterns on the two sides of each leaflet, the computations also suggest significant differences in the magnitude of the shear stress field. In general, the aortic side is characterized by lower magnitudes but more complex patterns in the shear stress vector field than the ventricular side.

Figure 2.

Numerical simulation of unsteady, pulsatile flow in a tricuspid prosthetic HV. Contours of the out-of-plane vorticity are shown at two instants during the cardiac cycle: (a) fully open phase and (b) closing phase.

Figure 3.

Instantaneous friction streamline and shear stress magnitude plots on the aortic (a,c) and ventricular (b,d) sides of the leaflets during the fully open (a,b) and early closing (c,d) phases of the cardiac cycle.

(d) Diseased valve haemodynamics

AV pathology may be caused by inflammation or increasingly by degenerative valve disease, caused by increasing longevity coupled with rheumatic and infective endocarditis (Yacoub & Cohn 2004a,b). Current surgical interventions include valve repair or replacement, depending on the diagnosis. Tremendous progress has been achieved during the past century on the development and improvement of prosthetic valves but, to date, there is no ideal replacement valve available (Schoen 2005, 2006). Because knowledge of the haemodynamics could be invaluable in the treatment of such pathologies, studies have been done on the characterization of the fluid environment in the vicinity of diseased semilunar valves.

AV stenosis is a condition characterized by substantial calcification of the leaflet and often surrounding aortic tissues. This induces not only a reduction in the effective orifice area, but also a significant increase in leaflet stiffness and incomplete opening of the valve. Owing to the difficulty in obtaining diseased valve measurements, Yoganathan (1988) carried out some flow measurements on bioprosthetic valves mimicking different degrees of aortic stenosis in vitro. Under physiological conditions (heart rate of 70 beats min⁻¹, systolic duration of 300 ms and mean aortic pressure of 90–100 mmHg), flow visualization demonstrated that the fluid exits from the stenotic valve as an asymmetric, angulated jet. As the degree of stenosis increases, the jet diameter at the base of the aorta decreases and the flow field becomes more disturbed and chaotic. In addition, laser Doppler anemometry measurements showed that, as compared with the evenly distributed flow field obtained at peak systole in the normal AV (maximum axial velocity of 1.2 m s⁻¹), the stenotic valve is characterized by a jet-type flow field (maximum axial velocity of 7.0 m s⁻¹) with regions of separation located around the jet and highly turbulent shear layers (maximum r.m.s. axial velocity of 2.0 m s⁻¹). The elevated levels of turbulence measured downstream of the stenotic valves are high enough to cause damage to the blood elements (red blood cells and platelets) and the ECs lining the wall of the ascending aorta.

In the actually diseased AV, the situation is probably more complex, since calcification will occur non-uniformly over the leaflet, inducing irregular leaflet shapes and increasing the complexity of the flow patterns. Moreover, the surfaces of the leaflets will become more irregular, especially on the ventricular surface of the leaflet. While specific studies of these phenomena have not been undertaken to date, they should be considered in assessing actual clinical flow data from stenotic valves.

The haemodynamic characteristics of reconstructed bicuspid AVs have been investigated using Doppler echocardiography at rest and exercise (Schmidtke et al. 2005). At rest, patients with reconstructed bicuspid AVs demonstrate maximum and mean pressure gradients across the AV (14±5.5 and 7±2.6 mmHg, respectively) higher than those observed in controls (7±2.5 and 3.6±2.1 mmHg, respectively). Yet, the valvular resistance of the reconstructed valves was comparable to that of normal valves (13.4±4.8 versus 13.6±2.9 dyn s cm⁻⁵, respectively). At exercise, the haemodynamic differences between repaired valves and normal valves are not as significant.

The haemodynamics resulting from the Ross procedure that consists of the replacement of a diseased AV by a pulmonary autograft has been investigated using echocardiography (Xie et al. 2001). The study revealed a reduction of left ventricular diastolic volume. The ejection fraction does not change significantly in young patients, but decreases significantly in older patients (above 40 years old). Finally, pressure gradients across the valve remain within a normal range after the procedure.

Haemodynamically, pathologies of the MV can be characterized within two functional groups: stenosis and regurgitation. Stenosis describes the total or partial obstruction of the mitral orifice: the most common cause is rheumatic fever, but other causes may include endocarditis, ankylosing spondylitis, atrial myxoma and Lutembacher syndrome. In critically stenosed MV, pressures of up to 25 mmHg in the left atrium are required to maintain a normal cardiac output. In the case of severe mitral stenosis, mean pulmonary pressure may be raised significantly (greater than 60 mmHg; Umesan et al. 2000). In these severely stenosed valves, transmitral pressure gradients of up to 17.8±6.5 mmHg have been recorded (Umesan et al. 2000).

Mitral regurgitation is the most common functional abnormality of the MV, which may be caused by rheumatic fever, congenital abnormalities, ischaemic heart disease and cardiomyopathies among others. Mitral regurgitation occurs owing to malcoaptation of the MV leaflets during valve closure. This results in orifices in the coaptation line and subsequent regurgitation jets. Using M-mode echocardiography, mean regurgitant flow propagation velocities of 26.4±7, 43.3±7 and 60.3±7.3 cm s⁻¹ have been measured for mild, moderate and severe mitral regurgitation, respectively (Akdemir et al. 2005). Peak velocities within the jet are on the order of 4 m s⁻¹. The velocity, volume, direction and duration of the regurgitation jets are highly variable and pathology/patient specific. Mitral regurgitation is quantified by the ratio of the regurgitation volume to the stoke volume (regurgitation fraction). Regurgitation fractions of 20% are considered clinically significant and in severe cases of mitral regurgitation may be above 60%.

(e) Dynamic leaflet strains

Clearly, accurate diagnosis and treatment of valve disease, along with the development of improved surgical strategies/techniques, require a complete understanding of normal valve dynamics. As an example, investigators have undertaken the task of studying MV dynamics and left ventricular fluid mechanics (Bellhouse & Bellhouse 1969; Ormiston et al. 1981; Ming & Zhen 1986; Reul & Talukder 1989; Hartiala et al. 1993; Schwammenthal et al. 1994; Otsuji et al. 1997). However, due to the complexity of valve anatomy, it is difficult theoretically to determine the functional role and importance of each individual component (Arts et al. 1983). Computational models (Kunzelman et al. 1993, 1994, 1998) represent an exciting approach, but have not yet progressed to the point where fully dynamic function can be simulated. Moreover, simulations are currently difficult to fully validate in vivo with available imaging technologies.

Several approaches have been taken to attempt to quantify valvular dynamics. Early work by Thubrikar et al. (1982a–c) used biplane fluoroscopy to determine dynamic valve function. These experiments involved lead radiopaque markers sutured directly onto the valve leaflets. Leaflet radial length did not change significantly during maximum flow. Instead, it was observed that when the valve closes, the radial length increases during diastole (Thubrikar et al. 1986). Moreover, from the mid-diastole reference configuration, displacement of the circumferentially and radially oriented markers could be obtained throughout the cardiac cycle. The resulting in vivo strains of 10.1 and 30.8% in the circumferential and radial directions, respectively, were reported during valve closure over a period of approximately 20–25 ms. From these in vivo measurements, the corresponding circumferential and radial strain rates are 440±80.0 and 1240±160.0% s⁻¹, respectively. Although subtle variations between species are likely, it is reasonable to assume that comparable strain rates would be observed.

In these pioneering studies, because only two markers were used at the basal and belly region of the leaflet, they did not cover the free edge. Further, although the two markers were sutured directly to the leaflets and were spaced significantly apart, only straight distance measurements were possible. Thubrikar et al. (1982a–c) were thus not able to follow the entire leaflet surface and likely underestimated actual changes. More recently, using high resolution approaches, biplane X-ray imaging demonstrated significant regional complexities in valve motion and strain (Smith et al. 2000). However, in these studies, the number of markers used was small so that the spatial resolution was insufficient for detailed surface strain studies. This is considered critical as the high degree of structural and mechanical heterogeneity in HV leaflets (Sacks et al. 1998; Vesely 1998; Billiar & Sacks 2000a; Stella & Sacks in press) suggests an equally complex regional strain response over the cardiac cyclic.

As an example of the complex and subtle deformations of the HV leaflets, in several recent studies, we quantified both the in-surface strains of the MV anterior leaflet using both in vitro and in vivo techniques (Sacks et al. 2002, 2006; He et al. 2003, 2005). For the in vitro studies, we focused on an approximately 4×4 mm region of the centre portion of the anterior leaflet by tracking the three-dimensional motions of 16 surface markers. From the resulting marker motions, the complete in-surface strain tensor was computed, along with the corresponding strain rates. Relations of the principal strain directions to the underlying collagen fibre architecture were also quantified. Our key findings included

1. The anterior leaflet experienced large, anisotropic stretches during closure.

2. Once the valve is closed, further leaflet deformation ceases.

3. The closing deformation behaviour is essentially symmetrically reversed during valve opening.

4. The region of the anterior leaflet studied experienced relatively little shear throughout the cardiac cycle.

5. Peak stretch rates during the closing and opening phases were very high, reaching values of 500–1000% s⁻¹.

For the in vivo studies, a sheep model and sonomicrometry were used to compute, for the first time, the dynamic strains of the anterior leaflet over the cardiac cycle at varying afterloads (Liao et al. 2007). Specifically, the anterior leaflet of nine Dorsett sheep (35–45 kg) was instrumented with nine 1 mm hemispherical piezoelectric transducers in a 15 mm square array (figure 4a). Three-dimensional crystal spatial positions were recorded at 250 Hz over several cardiac cycles, with peak LV pressures being varied from 90 to 200 mmHg. The in-surface Eulerian strain tensor was computed from the crystal displacements. Surface strains were generally heterogeneous over the region delimited by the crystals. Since the central region demonstrated generally homogeneous strains, we elected to focus the present study on the results from this region.

Figure 4.

(a) A schematic of the MV anterior leaflet showing the nine transducer sonomicrometry array. (b) Representative time–areal strain traces, along with the corresponding areal strain rate data. Strain rates were quite high, on the order of 1000% s⁻¹, underscoring the highly dynamic nature of the MV. Moreover, once the valve had fully coapted there were no further deformations. (c) Mean principal strains for three pressures levels. Other than the differences between circumferential and mean radial peak strains, there were no significant differences with increasing LV pressure. Adapted from Sacks et al. (2006).

Peak stretch versus time responses demonstrated overall smooth deformations, with complete loading of the leaflet occurring in approximately 50 ms (figure 4b). Thus, as in our in vitro investigations (Sacks et al. 2002), we observed large anisotropic (i.e. directionally dependent) strains. Mean peak circumferential strains ranged from 2.5 to 3.3% and mean peak radial strains ranged from 16 to 22%. To quantify the net change in leaflet dimensions, an areal strain measure was defined as the change in the area defined by the sonocrystals expressed as per cent reference area. Corresponding areal strain ranged from 15 to 20% (figure 4b). Mean peak strain rates were approximately 300–400% s⁻¹ in the radial direction and 100–130% s⁻¹ in the circumferential direction (figure 4c). Interestingly, there was comparatively little effect of maximum pressure level on either the peak stretches or the peak strain rates (figure 4c).

Our leaflet deformation results were qualitatively consistent with our previous in vitro work. In particular, we noticed that the key deformation patterns of the MV leaflet were very consistent between the two studies. These include large, very rapid strains to the point of full coaptation, followed by an absolute cessation of any deformation during systolic ejection. The deformations during the final valve opening phase are basically a mirror reversal of loading phase. This function is reflected in the overall behaviour of the leaflet, where we observe an initial region with very large stiffness facilitating leaflet coaptation, followed by a rapidly stiffening region occurring once the leaflet coapts. However, despite the qualitative similarities with our previous in vitro work, the magnitudes of peak stretches and stretch rates were found to be smaller in vivo than in vitro. Although differences in species studied (the in vitro work was with porcine tissue) and strain measurement techniques used play a part, these differences more likely highlight the influence that a functioning left ventricle (including a deformable annulus and contracting papillary muscles) has on leaflet geometry and function. These studies should be viewed as only a first step; use of fiducial marker approaches, such as used by our labs, are intrinsically limited by the number of markers required for detailed regional studies. The highly dynamic motions, large anisotropic deformations, complex surface geometries and thin leaflets clearly put HV imaging beyond the forefront of what is possible with current imaging technologies. However, as imaging technologies advance, we anticipate not only being able to image and quantify normal and diseased HV motion, but also to use these in a clinical setting.

3. Biomechanical function at the tissue level

(a) Functional tissue structural elements relevant to heart valve tissue biomechanics

To achieve the demanding design goals using available biological materials (e.g. collagens, elastin, proteoglycans, etc.), nature has evolved a tri-layered leafletal structure. These layers are the ventricularis, spongiosa and fibrosa (Thubrikar 1990; Schoen 1997). As its name implies, the ventricularis layer faces the left ventricular chamber and is composed of a dense network of collagen and elastin fibres. The spongiosa layer contains a high concentration of proteoglycans. The fibrosa layer is composed predominantly of a dense network of collagen fibres and is thought to be the major stress-bearing layer. Interstitial cells (myofibroblasts) permeate the entire tissue structure, although they are generally more numerous in the spongiosa.

It is well known that collagen fibres can withstand high tensile forces, but have low torsional and flexural stiffness. Thus, directions in which the fibres are oriented can be identified with the directions in which the tissue is able to withstand the greatest tensile stresses. This is especially the case in the study of the structure of the aortic HV, which is uniquely suited for efficient transmission of mechanical stresses with the minimal use of material. To quantify the gross fibre architecture of the valve leaflet, we used small angle light scattering (SALS; Sacks et al. 1997). In SALS, laser light is passed through a tissue specimen and the spatial intensity distribution of the resulting scattered light represents the sum of all structural information within the light beam envelope. To simulate on the changes to AV leaflet structure with increasing transvalvular pressure (TVP), fresh porcine AVs were fixed at TVPs ranging from 0 to 90 mmHg. Overall, increasing TVP induced the greatest changes in fibre alignment between 0 and 1 mmHg, and past 4 mmHg there was no detectable improvement in fibre alignment (figure 5b–d).

Figure 5.

(a) A diagram of the AV cusp showing the locations of the belly, commissure and nodulus, regions of coaptation. SALS results for the AV cusp at (b) 0, (c) 4 and (d) 90 mmHg TVPs. Here, the lines represent preferred collagen direction and colour fringes the local degree of fibre alignment. Past approximately 4 mmHg, no further changes in fibre alignment were observed. This is consistent with histological-based observations were the per cent area of the tissue displaying collagen fibre crimp drops below 10% beyond TVPs of approximately 20 mmHg, as shown in (e). Adapted from Sacks et al. (1998).

Recently, we have quantified the amount of collagen fibre crimp in the native pulmonary and aortic HVs. Following the method of Hilbert et al. (1986, 1990), we represented the amount of collagen crimp as a percentage of the histological cross-sectional area containing observable crimp structures for each TVP level (Joyce et al. submitted). In this approach, cross-sectional regions displaying observable crimp were identified and the resultant areas measured, and expressed as a percentage of the total cross-sectional tissue image. It was found that at 0 mmHg, approximately 60% of the AV transverse cross-sectional area was occupied by crimp structure (figure 5b). As TVP increased, the per cent crimp decreased rapidly until 20 mmHg, with minimal decreases in per cent crimp thereafter.

Thus, we can see that for the AV much of the observed change in collagen structure is due to straightening of the collagen fibres. This is a finely tuned affair; straightening must occur at the right strain level and at the right rate to facilitate coaptation, yet not allow excessive tissue deformations that may lead to regurgitation. Further evidence of an adaptive structure is the unique structure of the commissure region, which approximately corresponds to the coaptation region. The coaptation region is under no TVP, but is loaded instead in a uniaxial-like manner due to tethering forces generated at the attachment of the commissures to the aortic root. Unlike the biaxially loaded belly region, the uniaxial loading of the commissures would tend to make their structure more highly aligned, i.e. more like a tendon. Like tendons, a highly aligned fibre network would have a very short transition region from low to high stiffness, as evidenced by rapid fibre uncrimping with stress. The highly aligned nature of the commissure region at unloaded state and the more rapid realignment with TVP in the commissure regions are consistent with the pre-transition strain level behaviour of tendon-like materials.

(b) How to approach the biomechanics of heart valve tissues

The results presented in §3a suggest a complex structure–mechanical behaviour and interactions for HV leaflets. It is useful to divide the study of the tissue-level biomechanics of HV leaflets into in-plane stretch and flexural deformation modes. These occur cyclically as the valve opens (flexure), experiences surface shear stress from the local blood flow, followed by closure (flexure), then coaptation and full loading (tension). Although common to all valves, the different valve geometries and effects of tethering by chordae tendineae in the TV and MV mean the magnitudes and rates of these loading modes will vary between the valves.

While there have been a few studies on MV tissue (May-Newman & Yin 1995, 1998), most of the research concerned with HV mechanics has been conducted on the AV (Vesely & Noseworthy 1992; Christie & Barratt-Boyes 1995a; Sacks et al. 1998; Vesely 1998; Vesely & Mako 1998; Billiar & Sacks 2000a,b; Adamczyk & Vesely 2002; Merryman et al. 2006b) and MV (Gorman et al. 1996; Sacks et al. 2002; Gorman et al. 2004; Stella & Sacks in press); however, interest in PVs has grown (David et al. 1994; Christie & Barratt-Boyes 1995c; Vesely et al. 2000; Stradins et al. 2004; Merryman et al. in press). The driving force behind this is likely due to the fact that these AV and MV are the most problematic valves and require surgical intervention or replacement more regularly. Additionally, many studies have been conducted with the valve in vivo under the full regime of loading required during normal (or pathological) function (Thubrikar et al. 1977a,b, 1979a,b, 1980a,b, 1981, 1986). Therefore, a complete understanding of the three individual loading modes is presented in the following.

(c) Planar biaxial tensile biomechanical behaviour of the aortic valve leaflet

In the following, we focus on the biomechanics of the native AV leaflet (also referred to as a ‘cusp’; however, we consider leaflet a better term to describe function rather than its shape). While we and others have made extensive examinations of other HV leaflets, we focus here on the native AV as an example of the intricacies of HV leaflet tissue biomechanics.

The mechanics of soft tissues are complex: they exhibit a highly non-linear stress–strain relationship, undergo large deformations, complex viscoelasticity and complex axial coupling behaviours that defy simple experiments and material models. Much of this behaviour is a direct result of changes in their internal structure with strain, which involves both straightening of highly crimped collagen fibres and rotation of these fibres towards the stretch axis. For valvular tissues, most previous work on the mechanical properties of the native and chemically treated AV has relied on uniaxial mechanical testing (Lee et al. 1984a,b; Vesely & Noseworthy 1992). These studies demonstrate that chemical fixation of intact valves, especially under pressure, alters the mechanical properties of the leaflets. Marked decreases in extensibility are generally attributed to ‘locking’ the collagen fibres in the uncrimped state (Broom & Christie 1982; Christie 1992). Tests on thin tissue strips, however, cannot mimic the heterogeneous multi-axial deformation fields, combined loading sequences and native fibre kinematics found in the physiological environment. Mayne et al. (1989) and Christie & Barratt-Boyes (1995a) have performed equibiaxial testing (i.e. equal levels of tension applied to each test axis) that overcomes many of the above limitations of uniaxial loading. However, derivation of a constitutive relationship solely from equibiaxial test data is limited due to multiple colinearities that confound the ability to obtain reliable, unique model parameter values (Brossollet & Vito 1995).

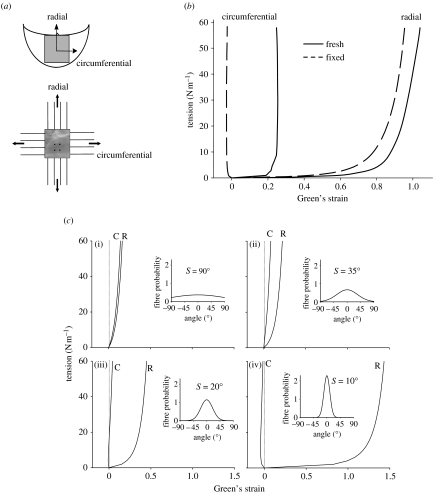
Billiar & Sacks (2000a) generated the first complete biaxial mechanical data necessary for constitutive modelling of AV leaflet. Owing to the small size and heterogeneous structure of the AV leaflet, testing methods were developed and validated. Leaflet specimens were subjected to biaxial tests (figure 6a) using seven loading protocols to provide a range of loading states that encompass the physiological loading state. The leaflets demonstrated a complex, highly anisotropic mechanical behaviour, including pronounced mechanical coupling between the circumferential and radial directions. Mechanical coupling between the axes produced negative strains along the circumferential direction and/or non-monotonic stress–strain behaviour when subjected to equibiaxial tension (figure 6b), a behaviour noted by Mayne et al. (1989) but was not explained. Moreover, Adamczyk & Vesely (2002) measured AV leaflet strains in situ and found that negative strains can occur in the non-coronary leaflet. Clearly, a constitutive model is needed to truly understand the aortic leaflet behaviour and its implications on the mechanics of the intact valve.

Figure 6.

(a) Schematic of the biaxial mechanical test configuration for the aortic valve leaflet. (b) Representative biaxial mechanical data taken for the native aortic valve under planar biaxial stretch. Note the large strains and dramatic degree of mechanical anisotropy, with the radial direction exhibiting much larger strains. (c) Simulations using the structural model of the effect of σ on the equibiaxial stress–strain behaviour. The insets provide a graphical representation of the fibre probability density distribution for each σ value: (i) σ=90° approximately isotropic, (ii) σ=35° response qualitatively similar to bovine pericardium, (iii) σ=20° the circumferential strains are negative at low equibiaxial tensions and (iv) σ=10° the material behaviour is highly anisotropic. The dotted lines indicating zero strain are included to highlight the ability of the model to simulate the crossover to negative strain observed in the pressure fixed cusps subjected to equibiaxial tension. Adapted from Billiar & Sacks (2000a,b).

The quantified fibre architecture (Sacks et al. 1998) and biaxial mechanical data (Billiar & Sacks 2000a) suggest that a structural approach is the most suitable method for the formulation of a constitutive model for the AV leaflet. Details of the model have been previously presented (Billiar & Sacks 2000b). In this approach, the tissue's total strain energy is assumed to be the sum of the individual fibre strain energies, linked through appropriate tensor transformation from the fibre coordinate to the global tissue coordinates. For the AV, we assume that the planar biaxial mechanical properties of the leaflet can be represented as a planar array of collagen fibres. Anatomically, these fibres most closely represent the dense, highly aligned collagen fibres in the fibrosa layer. Next, the angular fibre distribution and the density of the fibres are assumed constant throughout the tissue. Based on our SALS results for the AV leaflet (figure 5a; Sacks et al. 1998), we use the fact that the angular distribution of the collagen fibres, R(θ), can be represented by a Gaussian distribution,

$$R(\theta )=\frac{1}{\sigma \sqrt{2\pi }}\exp \left[\frac{-{(\theta -\mu )}^2}{2{\sigma }^2}\right],$$ (3.1)

where θ is the direction with respect to the x₁ or circumferential axis (figure 6a), σ is the standard deviation, and μ is the mean of the distribution. M was determined experimentally for each specimen using the preferred fibre directions as determined by SALS (Sacks et al. 1998). The ‘effective’ fibre stress–strain properties were represented using

$$S_{\text{f}}=A\left[\exp (B{E}_{\text{f}})-1\right],$$ (3.2)

where S_f is the second Piola-Kirchhoff fibre stress and E_f is the fibre Green's strain. This formulation for the fibre stress–strain law avoids detailed descriptions of complex crimp distributions.

For valvular tissue, it is more convenient to work with membrane stresses due to considerations such as variable total and layer thickness, and heterogeneous layer structure (Billiar & Sacks 2000a). Further, since the biaxial mechanical tests are run using membrane stress control using the specimen's unloaded dimensions, a Lagrangian membrane stress measure is used in the constitutive formulation. We also assume that inter-specimen variations in fibre volume fraction V_f and thickness h are negligible, so that the product hV_f can be conveniently absorbed into the material constant A. The resulting expressions for the Lagrangian membrane stresses T_ij are

$$\begin{array}{l}{T}_{11}={\int }_{-\pi /2}^{\pi /2}{S}_{\text{f}}^{*}(E_{\text{f}})R(\theta )\left({\lambda }_1{\text{cos}}^2\theta +{\kappa }_1\text{sin}\theta \text{cos}\theta \right)\text{d}\theta \\ T_{22}={\int }_{-\pi /2}^{\pi /2}{S}_{\text{f}}^{*}(E_{\text{f}})R(\theta )\left({\lambda }_2{\text{sin}}^2\theta +{\kappa }_2\text{sin}\theta \text{cos}\theta \right)\text{d}\theta \end{array}$$ (3.3)

where A^*=hV_fA and $S_{\text{f}}^{*}=A^{*}\left[\text{exp}(B{E}_{\text{f}})-1\right]$. λ₁ and λ₂ are the stretch ratios along the circumferential and radial directions, respectively, and κ₁ and κ₂ are the corresponding shear terms. The parameters A^*, B and σ were estimated by fitting equation (3.3) to the complete biaxial dataset (Billiar & Sacks 2000a).

An important aspect of the structural approach is that the two distinguishing aspects of the AV leaflet biaxial behaviour, namely the extreme mechanical anisotropy and the strong mechanical coupling between the axes, can be explained by the angular distribution of fibres. To more clearly demonstrate this effect, we generated simulations under equibiaxial loading for a given set of A^* and B values by letting σ vary (figure 6c). These simulations indicate that the value of σ is the primary determinant of the biaxial stress–strain response, as shown for (i) nearly random (σ=90°), (ii) moderately anisotropic (σ=35°), (iii) highly anisotropic, including contraction along one axis (σ=20°), and (iv) extremely anisotropic (σ=10°). Although we assumed a simplified tissue structure in the formulation of the model, the structural approach highlighted the importance of the angular orientation of the fibres in determining the complex anisotropic mechanical behaviour of the tissue.

While the above modelling approach worked well, it should be noted that the use of a membrane tension formulation ignores layer-specific mechanical contributions and the implicit non-uniformity of the transmural stress distribution. To begin to address these limitations, we recently conducted novel studies to quantify the biaxial mechanical behaviour of the two structurally distinct, load-bearing AV leaflet layers: the fibrosa and ventricularis (Stella & Sacks in press). A microdissection technique was developed based on previous methods (Vesely & Noseworthy 1992; Sacks et al. 1998) and modified to work with the biaxial test specimens rather than the intact leaflet. While keeping the specimen moist with PBS at all times, the ventricularis layer was gently lifted upwards with delicate forceps to expose the spongiosa layer (figure 7a). We found that the spongiosa contained numerous interconnecting fibrous structures that couple the fibrosa and ventricularis (figure 7b). In order to separate the outer fibrous layers, it was necessary to manually sever each interconnection. This was accomplished through the use of a low power dissection microscope and ophthalmic microscissors. For a bilayer tissue configuration, one would normally start with the individual layers in their separated, stress free reference configuration. Sequential deformations would then arise from coupling the layers in the intact configuration (accounting for any pre-strains) and the application of external loads. We define these states as

1. β₀. The separated, unconstrained configuration.

2. β₁. The intact unloaded configuration.

3. β_t. The current configuration of the intact tissue in response to external loads.

Figure 7.

(a) Microdissection of an aortic leaflet specimen, with the test specimen pinned to a cork dissection board such that the ventricularis can be gently lifted to expose the numerous collagen fibre connections coupling the fibrosa and ventricularis. (b) A magnified view of a partially separated leaflet showing the numerous connections found throughout the spongiosa. Each fibrous connection is severed manually enabling us to separate the fibrosa and ventricularis. Note, the markers shown were applied to the outer surface of the fibrosa and ventricularis prior to intact testing and subsequent separation. (c) The equibiaxial responses of the fibrosa and ventricularis computed with respect to both β₀ and β₁. When referenced to the intact conformation (β₀) substantial differences were seen between the radial contributions of each layer. The corresponding first Piola–Kirchhoff stresses were $P_{22}^{\text{v}}$=95.74 kPa while $P_{22}^{\text{f}}$=26.63 kPa at equivalent levels of stretch. These results suggest that the ventricularis layer makes profound contributions to the intact leaflet response in the radial direction. Adapted from Stella & Sacks (in press).

The equibiaxial responses of the fibrosa and ventricularis were computed with respect to both β₀ and β₁. Results indicated that both layers exhibited very different non-linear, highly anisotropic mechanical behaviours (figure 7c). When referenced to the intact conformation (β₀), substantial differences were seen between the radial contributions of each layer. Thickness measurements enabled us to calculate corresponding first Piola–Kirchhoff stresses: $P_{22}^{\text{v}}$=95.74 kPa while $P_{22}^{\text{f}}$=26.63 kPa at equivalent levels of stretch. These results suggest that the ventricularis layer makes profound contributions to the intact leaflet response in the radial direction. Thus, while the leaflet tissue mechanical response was dominated by the fibrosa layer, the ventricularis contributed double the amount of the fibrosa to the total radial tension, and experienced four times the stress level. Histological-based thickness measurements indicated that the fibrosa and ventricularis constitute 41 and 29% of the total layer thickness, respectively. Moreover, the extensive network of inter-layer connections and identical strains under biaxial loading in the intact state suggest that these layers are tightly bonded. In addition to advancing our knowledge of the subtle but important mechanical properties of the AV leaflet, this study provided a comprehensive database required for the development of a true three-dimensional stress constitutive model for the native AV leaflet.

In our laboratory and others (Mayne et al. 1989; Christie & Barratt-Boyes 1995b; May-Newman & Yin 1995), biomechanical tissue analyses were conducted at quasi-static (strain rates of 4–12% s⁻¹) experimental conditions. However, we have shown that the deformations of HV leaflets can reach strain rates in excessive of 300% s⁻¹ (figure 4c). These findings raised an important question: Are the quasi-static leaflet mechanical properties truly representative of their physiological behaviour?

The strain rate dependence of the mechanical properties of soft tissues has been extensively studied. Yet the literature indicates a wide range of findings which are very much a function of specific tissue composition and structure, as well as the specific testing methods used. Thus, the strain rate dependence of any one tissue needs to be properly investigated under realistic physiological loading states to model physiological functions. We explored, for the first time, the effects of strain rate (from quasi-static to physiological) on the planar biaxial mechanical properties of the MVAL (Grashow et al. 2006a,b). A novel high-speed biaxial testing device was developed, capable of achieving physiological strain rates. Porcine MVAL specimens were loaded to physiological load levels with cycle periods of 15, 1, 0.5, 0.1 and 0.05 s. The resulting loading stress–strain responses were found to be remarkably independent of strain rate (figure 8a). The hysteresis, defined as the fraction of the membrane strain energy between the loading and unloading curves, tension–areal stretch curves, was low (approx. 12%) and did not vary with strain rate.

Figure 8.

(a) The circumferential and radial stretches of the MV leaflet at the 90 N m⁻¹ equitension state, ${\lambda }_{\text{C}}^{\text{peak}}$ and ${\lambda }_{\text{R}}^{\text{peak}}$, revealed no significant differences among the prescribed set of loading time protocols in both the circumferential (p=0.987) and radial (p=0.996) directions. Stretches observed previously in mock flow loop (solid horizontal lines) ±s.e.m. (dotted lines) are plotted for the circumferential (black) and radial (grey) specimen axes. ${\lambda }_{\text{C}}^{\text{peak}}$ and ${\lambda }_{\text{R}}^{\text{peak}}$ exceeded those observed in vitro; however, the ratio of ${\lambda }_{\text{C}}^{\text{peak}}$ to ${\lambda }_{\text{R}}^{\text{peak}}$ (0.86±0.02) was very close to the ratio of peak circumferential and radial stretches observed in vitro (0.83). (b) Representative biaxial stress–relaxation data demonstrating continued relaxation throughout the 3 h time frame. (c) Representative stretch versus time curves for a typical biaxial creep experiment. Note the anisotropic leaflet behaviour exhibited by the higher radial stretch required to maintain the 90 N m⁻¹ membrane tension. Only very slight increases (at most 1%) in strain were observed past 1000 s.

These results suggest that valve leaflets can be modelled as ‘quasi-elastic’ biological materials. In a follow-up study, we expanded these results to provide a more complete picture of the time-dependent mechanical properties of the MVAL. To accomplish this, biaxial stress-relaxation and creep studies were performed on porcine MVAL specimens. Our primary finding was that the while the MVAL leaflet exhibited significant stress relaxation (figure 8b), it exhibited negligible creep over the 3 h test (figure 8c). These results furthered our assertion that the MVAL functionally behaves not as a linear or non-linear viscoelastic material, but as an anisotropic quasi-elastic material. These results appear to be unique in the soft tissue literature, suggesting that valvular tissues are unique in their ability to withstand significant loading without time-dependent material effects.

The underlying structural basis for this unique quasi-elastic mechanical behaviour is presently unknown. As collagen is the major structural component of the MVAL, we investigated the relation between collagen fibril kinematics (rotation and stretch) and tissue-level mechanical properties in the MVAL under biaxial loading using small angle X-ray scattering (SAXS; Liao et al. 2007). A novel device was developed and used to perform simultaneous measurements of tissue level forces and strain under a planar biaxial loading state. Collagen fibril D-period strain (ϵ_D) and the fibrillar angular distribution were measured under equibiaxial tension, creep and stress relaxation to a peak tension of 90 N m⁻¹.

Results indicated that, under equibiaxial tension, collagen fibril straining did not initiate until the end of the non-linear region of the tissue-level stress–strain curve. At higher tissue tension levels, ϵ_D increased linearly with increasing tension. Changes in the angular distribution of the collagen fibrils mainly occurred in the tissue toe region. Using ϵ_D, the tangent modulus of collagen fibrils was estimated to be 95.5±25.5 MPa, which was approximately 27 times higher than the tissue tensile tangent modulus of 3.58±1.83 MPa. In creep tests performed at 90 N m⁻¹ equibiaxial tension for 60 min, both tissue strain and ϵ_D remained constant with no observable changes over the test length. In contrast, for stress relaxation performed for 90 min, ϵ_D was found to decrease rapidly in the first 10 min followed by a slower decay rate for the remainder of the test. Using a single exponential model, the time constant for the reduction in collagen fibril strain was 8.3 min, which was smaller than the tissue-level stress relaxation time constants of 22.0 and 16.9 min in the circumferential and radial directions, respectively. Moreover, there was no change in the fibril angular distribution under both creep and stress relaxation over the test period. Our results suggest that:

1. valvular collagen fibrils do not exhibit intrinsic viscoelastic behaviour,

2. valve leaflet tissue relaxation results from the removal of stress from the fibrils, possibly by a slipping mechanism modulated by non-collagenous components (e.g. proteoglycans),

3. the lack of creep but the occurrence of stress relaxation suggests a ‘load-locking’ behaviour under maintained loading conditions.

These unique mechanical characteristics are clearly necessary for normal valvular function, and insight into these unique characteristics can help guide and inform efforts directed towards surgical repair and engineered valvular tissue replacements.

(d) Flexural response of native leaflets

Flexure of soft biological materials offers two distinct advantages over tensile mechanical testing: (i) the ability to discern slight changes in stiffness at low stress–strain levels that would not be appreciable in tension and (ii) the ability to assess the contributions and interactions of individual layers of multi-layered structures. Thus, multi-layered tissues like the AV leaflet should reveal a distinct bending response depending on the direction of bending. Thus, flexural mechanical testing techniques are sensitive ways to explore the effects of layer contributions.

To quantify the flexural properties, we have used circumferential strips of porcine AV leaflets taken from the belly region (figure 5a), with the experimental details previously reported in Gloeckner et al. (1999), Engelmayr et al. (2003) and Merryman et al. (2006a). It should be noted that in the unloaded state, the AV leaflet is curved in both the circumferential and radial directions (hence the often used term ‘cusp’). To account for the initial curvature of the test specimen, we use the change in curvature Δκ (in units of mm⁻¹) from the initial unloaded reference state. By applying bidirectional flexure, we can subject the fibrosa and ventricularis layers to alternate states of tension and compression (figure 9a). We refer to these flexural directions with respect to the with curvature (WC) and against curvature (AC) directions of the natural leaflet. Further, the effective stiffness measured in the WC direction is dominated by the tension in the ventricularis, with little contribution from the fibrillar collagen in the fibrosa, which is not designed to support compressive loads. Conversely, when the leaflet is bent in the AC direction, the fibrosa is in tension and the ventricularis is in compression. The resulting data show how the applied bending moment (M) changes with Δκ. From this relation, we can estimate the effective (i.e. total) bending stiffness using the Euler–Bernoulli equation M=EIΔκ (Frisch-Fay 1962), where E is the effective stiffness and I the second moment of inertia.

Figure 9.

(a) Schematic showing directions of bending for the AV with respective layers (V, ventricularis; S, spongiosa; and F, fibrosa). Note that respective layers are alternating tension and compression resulting from flexural directions. M versus Δκ relations in both the AC and WC directions for (b) specimens tested in 5 mM and 90 mM KCl, and (c) specimens flexed in 5 mM KCl and samples treated in 10 μM thapsigargin overnight and then flexed in 5 mM KCl. While the application of 90 mM KCl induced an increase in stiffness in the AC direction only, both bending directions experienced a loss of stiffness with the addition of thapsigargin to the bathing medium.

For the AV leaflet, we find a linear moment (M)–change in curvature (Δκ) response (figure 9b). This result contrasts with the highly non-linear in-plane tension tissue response (figure 6b). Not surprisingly, the micromechanical mechanisms underlying the flexural response are quite different from that of in-plane tension. This arises from differences on how the tissue layers are loaded, as mentioned above. Moreover, flexure induces small strains and possibly inter-layer sliding, and thus it is not a surprise that it produces profoundly different results. Continued work to provide insights into these mechanisms is clearly necessary to better understand native valve function. Moreover, improved knowledge of tissue micromechanics can provide the critical link to cellular function (figure 1), as discussed in §4.

4. Valve cell composition and function

(a) Valvular endothelial cells

The leaflets of all four HVs are sheathed by an ‘organ’ of single layer valvular endothelial cells (VECs) that have been shown to be morphologically different from aortic ECs (Butcher & Nerem 2004; Butcher et al. 2004). Additionally, VECs are aligned with the collagen architecture of the valve, which is circumferentially oriented (Deck 1986). The VECs are believed to regulate vascular tone, inflammation, thrombosis and remodelling, and their dysfunction has been linked with multiple disorders (Leask et al. 2003). Within the proximal third of the leaflets, where they are innervated, there is believed to be a feedback mechanism between the VECs and valvular interstitial cells (VICs; see below) wherein the nerves transmit information regarding released substances form the VECs (Marron et al. 1996). Primarily, release of cytokines has been shown to cause changes in interstitial cell structure and function (Davies & Tripathi 1993; Davies 1997). It has also been speculated that there exists some physical communication between the VECs and VICs. However, to date no direct junctions have been observed between the two cell populations (Filip et al. 1986).

To date, only studies on the effects of steady shear stress on AV biological response have been conducted. These studies reveal that steady shear stress alters the biosynthetic activity of AV cusps, and is unable to preserve the alpha-smooth muscle actin (αSMA) immunoreactive cells. Although the cellular mechanisms triggering this specific response to shear stress are not well understood, it is hypothesized that the valvular endothelium plays an important role. In fact, it is well established that AV ECs co-cultured with smooth muscle cells can affect the properties of smooth muscle cells through the release of paracrine factors. Ex vivo experiments demonstrate that valvular responses to shear in the absence of an endothelium are remarkably different from responses of intact leaflets (figure 10). Collagen synthesis in the intact leaflets is enhanced under shear stress, but not changed in the endothelium-denuded leaflets at the same shear stress; sulphated glycosaminoglycan (sGAG) content is not affected by shear stress in the intact leaflets, but is upregulated by shear stress in the denuded leaflets. These results indicate that AV interstitial cells respond to shear stress in the absence of AV ECs, but the presence of AV ECs alters these responses.

Figure 10.

Effects of steady shear stress on aortic valve biology. Collagen synthesis and sulphated glycosaminoglycan (sGAG) content in intact (a,b, respectively) and denuded (c,d, respectively) aortic valve leaflets under steady shear stress.

(b) Valvular interstitial cells

Within the three layers of the leaflet tissue, there resides a heterogenic population of interstitial cells (Filip et al. 1986; Messier et al. 1994; Mulholland & Gotlieb 1996; Taylor et al. 2003). The heterogeneity of the interstitial cells is made up of fibroblasts, smooth muscle cells and myofibroblasts, which have characteristics of both fibroblasts and smooth muscle cells. Studies of the interstitial cell population in both human and porcine subjects have revealed that the cell population was not localized to any one region or layer of the leaflet, but was present throughout the tissue (Bairati & DeBiasi 1981; Merryman et al. 2006b). Interest in the myofibroblast cells (typically referred to as valvular interstitial cells) has grown in recent years, as they are believed to be critically important in valve pathophysiology. Primarily, VICs serve to maintain the structural integrity of the leaflet tissue by remodelling via protein synthesis and enzymatic degradation (e.g. matrix metalloproteinases). Their phenotype (which ranges from fibroblast-like to myo-like) is believed to be plastic and reversible, as VICs of normal, healthy valves were quiescent, while in developing, diseased and remodelling valves, the VICs were activated and contractile (Rabkin et al. 2002; Rabkin-Aikawa et al. 2004). While their dualistic nature is not fully understood, the VIC's multifunctionality may be used for cell–cell communication, tissue remodelling, wound healing and contraction (Mulholland & Gotlieb 1996). Further, it is believed that when the phenotype of the resident VIC population is myo-like, the cells are actively remodelling the ECM. This indicates that the VIC phenotypic state at any given time is likely related to the current remodelling demands of the tissue (Rabkin et al. 2002).

Porcine AVIC contractility has been qualitatively studied with cultured cells on silicone substrates in the presence of multiple contractile chemical agents (Filip et al. 1986; Messier et al. 1994). In both studies, contraction occurred for most agents within 3 min and reached a plateau within 10 min. Additionally, Messier et al. (1994) found that the few cells with no initial basal tonus did not respond to the administered vasoconstriction drugs. Isoproterenol was used to elicit relaxation from active cells, from which all cells recovered their previous basal tonus within 25 min. While not quantitative, these findings were the first examples demonstrating an AVIC contractile response.

The flexural mechanical testing techniques described in §4a are also a sensitive way to explore the effects of cellular contraction on leaflet properties, as initially investigated by Chester et al. (2000, 2003). We have examined AVIC contractile behaviour within the intact leaflet tissue (Merryman et al. 2006a). As before, circumferential strips of porcine AV leaflets were mechanically tested under flexure, with the AVIC maintained in the normal, contracted and contraction-inhibited states. Leaflets were flexed in both the WC and AC directions, both before and after the addition of 90 mM KCl to elicit cellular contraction. In addition, a natural basal tonus was also demonstrated by treating the leaflets with 10 μM thapsigargin to completely inhibit AVIC contraction.

Results revealed a 48% increase in leaflet stiffness with AVIC contraction (from 703 to 1040 kPa, respectively) when bent in the AC direction (p=0.004), while WC direction resulted only in 5% increase (from 491 to 516.5 kPa, respectively—not significant) in leaflet stiffness in the active state (figure 9b). In addition, the loss of basal tonus of the AVIC population with thapsigargin treatment resulted in 76% (AC, p=0.001) and 54% (WC, p=0.036) decreases in leaflet stiffness at 5 mM KCl levels, while preventing contraction with the addition of 90 mM KCl as expected (figure 9c). Also, the loss of basal tonus of the AVIC population with thapsigargin treatment resulted in 76% (AC, p=0.001) and 54% (WC, p=0.036) decreases in leaflet stiffness at 5 mM KCl levels, while preventing contraction with the addition of 90 mM KCl as expected. We speculate that the observed layer-dependent effects of AVIC contraction are primarily due to varying ECM mechanical properties in the ventricularis and fibrosa layers. Moreover, while we have demonstrated that AVIC contractile ability is a significant contributor to AV leaflet bending stiffness, it most probably serves a role in maintaining AV leaflet tissue homeostasis that has yet to be elucidated.

(c) VIC deformation during physiological loading

While the extremely low AVIC forces generated make it unlikely that AVIC contraction directly affects valvular function, they are a dynamic cell source whose mechanical capabilities may serve a role in maintaining valve leaflet tissue homeostasis. Additionally, these cells may use their contractile elements to mechanically communicate with the local environment since the presence of vasoactive agents has been shown to increase in collagen synthesis in vitro (Hafizi et al. 2000). The local stress–strain fields in the vicinity of a cell are highly dependent on a number of factors, including cell shape, orientation and the relative properties of the cell and ECM (Guilak & Mow 2000). Thus, it is not clear how the pressures imposed on different sides of the heart translate into local stress on the VICs.

As a first step in understanding the mechanotransduction from the valve to the VICs (figure 1), we recently performed a study on the effects of TVP on the AVIC deformation (Huang et al. in press). This was accomplished by analysing histological sections taken from porcine AVs fixed under varying pressures (Sacks et al. 1998). Since cell deformation within intact tissues is complex and not well understood, we choose to use AVIC nuclear aspect ratio (NAR) as an index of overall cellular deformation. Moreover, since the AV leaflet layers consist of different structural components, variations in tissue layer stresses probably exist. We thus hypothesized that a relationship may exist between the valve tissue layer and the deformation experienced by AVIC nuclei under an applied TVP.

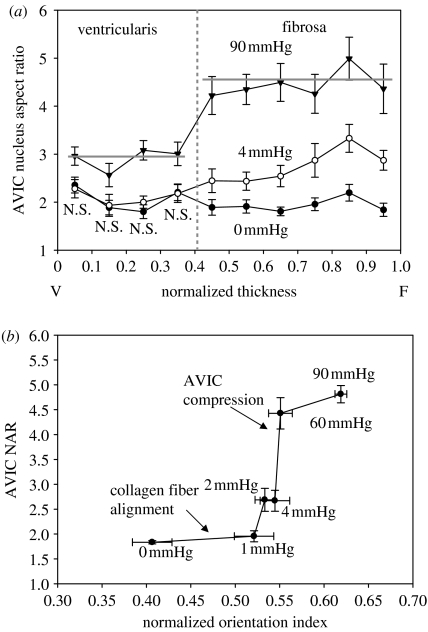
Results indicated that AVIC NAR versus normalized thickness indicated that under zero and low TVP (0 and 4 mmHg, respectively), the deformation of AVIC nucleus reached an almost constant level towards the ventricularis layer (figure 11a). In the fibrosa layer AVIC NAR slightly increased at 4 mmHg, while there were no detectable changes of NAR under 0 mmHg. In contrast, under high TVP (90 mmHg), the aspect ratios of AVIC nuclei were greater than those under the zero- and low-pressure levels. A clear demarcation in NAR at 90 mmHg was found in the fibrosa layer. In addition, statistically significant differences were found at all transmural locations by comparing the AVIC NARs at 90 mmHg to those at 0 and 4 mmHg pressure levels (p<0.05). Note well that the NAR approximately 5 at 90 mmHg, indicating profound cellular deformations under physiological pressure levels, is clearly dependent on the location in the valve leaflet. It should also be noted that these deformations occur very rapidly, within approximately 75 ms (figure 4).

Figure 11.

(a) The relation between AVIC NAR and TVP loading, with values reported over the leaflet thickness. Data were taken from native porcine aortic valves fixed from 0 to 90 mmHg pressure. Note clearly that while at 0 mmHg all AVIC have similar NAR, at 90 mmHg the ventricularis layer NAR is approximately 3 while the fibrosa is approximately 4.75. These data indicate that AVICs in the different leaflet layers are subjected to different effective external stresses. (b) AVIC NAR versus the normalized collagen fibre orientation index (NOI) at different TVP levels. Here, we observed that collagen fibre alignment with comparably minimal changes in NAR occur for TVPs up to approximately 4 mmHg. This was followed by the opposite trend for TVPs above 4 mmHg, where minimal changes in NOI were observed accompanied by large changes NAR. These results suggest that AVICs are not appreciably loaded until the collagen fibres fully straighten at TVPs above approximately 4 mmHg.

As discussed previously, AVICs are known to be in intimate contact with their surrounding collagenous ECM, and TVP-induced deformations of ECM should provide insight. To quantify the degree of fibre orientation, a normalized orientation index (NOI) was used by SALS technique (Sacks et al. 1998); studies showed that between 0 and 4 mmHg TVP levels, fibre network straightening occurred. A highly oriented fibre network has NOI→1, while a more randomly oriented network has a lower NOI→0. Figure 11 depicted the effects of increasing TVP on collagen fibre alignment and AVIC NAR for comparison. Gross visual comparisons yielded three distinct regions: (i) an asymptotic region between 0 and 1 mmHg: little change in AVIC NAR (+5%) with large increase in NOI (+25%), (ii) a transition region between 1 and 4 mmHg, and (iii) a region of steep behaviour between 4 and 60 mmHg: large increase in AVIC NAR but little change in NOI. Results suggested that for low pressure levels substantial fibre network straightening occurred, though it had little effect on changes in nucleus geometry. Yet the highly oriented fibre network observed at 4 mmHg and above, produced large changes in AVIC NAR. In the AV, TVPs above approximately 5 mmHg predominately result in ECM compaction as the collagen fibres become uncrimped and taut (Sacks et al. 1998). Due to this ECM compaction, significant changes in the AVIC nucleus aspect ratio were observed with increasing pressures (Huang et al. in press). At 90 mmHg, the AVIC nuclei aspect ratio increased from 2 : 1 (at 0 mmHg) to 4.8 : 1, demonstrating that valvular tissue stress is translated into large cell and subcellular deformations.

(d) VIC biomechanical behaviour

This measurable contraction of the cells at the tissue level is probably made possible by strong attachment of the AVICs to the ECM, which has been reported both in situ and in vitro (Mulholland & Gotlieb 1996; Taylor et al. 2003). The concerted cell contraction is believed to be mediated by cell communication through integrins with surrounding cells and the ECM (Taylor et al. 2003); AVICs demonstrate extended connecting processes that are believed to form a cellular network for communication (Filip et al. 1986). We speculated that the observed layer-dependent effects of AVIC contraction are primarily due to varying ECM mechanical properties in the ventricularis and fibrosa layers. Moreover, while we have demonstrated that AVIC contractile ability is a significant contributor to AV leaflet bending stiffness, it most likely serves a role in maintaining AV leaflet tissue homeostasis that has yet to be elucidated.

VICs also appear to be phenotypically plastic as they transdifferentiate into myofibroblasts during times of valve development, disease and remodelling (Rabkin-Aikawa et al. 2004). Under normal physiological conditions, the TVPs on the right and left side of the heart are vastly different. Hence, we have hypothesized that the higher left side TVPs impose larger local tissue stresses on VICs, which increase their stiffness through cytoskeletal composition, and that this relationship affects collagen biosynthesis. To evaluate this hypothesis, we require knowledge of the mechanical properties of VICs isolated from the surround ECM in order to decouple their responses (figure 1)

To begin to address this question, we have isolated ovine VICs from the four HVs and subjected them to micropipette aspiration to assess cellular stiffness, and cytoskeletal composition and collagen biosynthesis were quantified using surrogates smooth muscle α-actin (SMA) and heat shock protein 47 (Hsp47), respectively. Results revealed that VICs from the aortic and MVs were significantly stiffer (p<0.001) than the pulmonary and tricuspid VICs (figure 12). Additionally, left side isolated VICs contained significantly more (p<0.001) SMA and Hsp47 than the right side VICs. Mean VIC stiffness correlated well (r=0.973) with TVP; SMA and Hsp47 also correlated well (r=0.996) with one another. Moreover, assays were repeated for VICs in situ, and as with the in vitro results, the left side VIC protein levels were significantly greater (p<0.05; figure 12).

Figure 12.

(a) An example VIC under micropipette aspiration, with the vertical bar indicating aspiration length. (b) Functional correlations of effective cell stiffness E versus TVP, with the correlation coefficient (r) for this relationship of 0.973. (c) Linear correlation between Hsp47 versus SMA, showing a strong correlation between the two proteins (r=0.996) as one progresses from the right to the left side of the heart.

These findings suggest that VICs respond to local tissue stress by altering cellular stiffness (through SMA content) and collagen biosynthesis, and imply that VICs are responsive to their mechanical environment in order to maintain proper tissue homeostasis. Specifically, the increased SMA in left side VIC populations suggests that the cells are adapted for the stresses imposed on them, while the increased Hsp47 is necessarily expressed to synthesize larger amounts of collagen, the primary structural component of HVs. Furthermore, SMA and Hsp47 quantified from VICs in situ revealed a similar correlation, indicating that isolation of VICs hindered their normal function but was proportional among all populations. This functional VIC stress-dependent biosynthetic relationship may be crucial to maintaining valvular tissue homeostasis and also prove useful in understanding valvular pathologies.

5. Summary and future trends

(a) Summary

As in many physiological systems, one can approach HV biomechanics from an organ→tissue→cellular perspective, since mechanical function and stimuli occur and have biological impact on multiple length-scales. Biomechanics is ideally suited for the study of valve function as it takes an ‘integrated’ approach rather than a reductionist approach common to the biological sciences. While we do not as yet fully understand all the biomechanical aspects of valve development, function and disease, we can certainly conclude several key aspects as follows, following our cell/tissue/organ level approach (figure 1):

At the organ level:

1. HVs perform a basic, physiologically critical function to direct the flow of blood in the heart. While at first simple, this function clearly requires an extremely sophisticated valvular ‘biological device’ that permits the efficient flow of blood (i.e. with minimal gradients) and rapid directional control with minimal fluid loss (i.e. regurgitation).

2. One cannot think of HV function in terms of isolated components (e.g. cusps, leaflets, tendinae, annulus), but rather as an integrated functional unit that encompasses multiple components.

3. Valvular motions are extremely rapid and involve complex biofluid mechanical interactions with the surrounding blood. These interactions can induce large, spatially and time-varying flow patterns and fluid-induced shear forces on the valve surfaces.

At the tissue level:

1. Tissue level function is primarily dominated by the needs for:

   1. High tensile strength to resist high TVPs.
   2. Very low flexural rigidity to allow for passive interactions with the surrounding blood.
   3. Undergoing large, rapid, directionally dependent strain when in the process of closing.
   4. Allowing for rapid cessation of strain when closed.
2. The tissue functional requirements are met through a uniquely designed tissue structure that:

   1. Exploits the high tensile strength of type I collagen fibres.
   2. Uses a large amplitude but also synchronized collagen crimp waveform that allows for modest strains in the circumferential direction followed by a rapid stiffening.
   3. Exploits rotation of the collagen fibres to facilitate the very large radial strains. This is a critical design feature as collagen fibres typically fail at 8–10% strain once fully straightened.
   4. Uses a layered structure that facilitates low flexural rigidity and provides for additional structural support during closure.
   5. Elastin fibres in the ventricularis, while not a major structural component, do facilitate rapid retraction of the AV leaflet in the radial direction during opening.
   6. Elastin fibres also provide the mechanism for the pre-stress of the fibrosa by the ventricularis. The exact functional benefit for this pre-stress is as yet unclear, but is probably related to leaflet retraction as discussed above.

3. The high level of required durability is accomplished by a large redundant design (we estimate a failure stress approximately 20 times larger than functional stress levels), coupled to an interstitial cell population that maintains the collagen and other ECM components.

At the cell level:

1. VECs are believed to regulate vascular tone, inflammation, thrombosis and remodelling, and their dysfunction has been linked with multiple disorders.

2. Physical communication between the VECs and VICS may exist. However, to date no direct junctions have been observed between the two cell populations.

3. Changes in AVIC population stiffness can be measured at the tissue level, suggesting they are tightly bound to the surrounding ECM.

4. AVICs exhibit a significant basal tone, that is probably a result of the activated SMA.

5. AVIC contractile properties are likely related to their role in managing ECM formation, and are strongly influenced by the local stress environments of the valve leaflet.

6. AVICs are phenotypically plastic as they transdifferentiate into myofibroblasts during times of valve development, disease and remodelling.

7. The higher left side TVPs may impose larger local tissue stresses on VICs, which increase their stiffness through cytoskeletal composition (again mainly SMA), and this relationship affects collagen biosynthesis.

(b) The role of biomechanics in tissue-engineered heart valve development

Surgical replacement of diseased HVs by mechanical and tissue valve substitutes is now commonplace and enhances survival and quality of life for many patients. However, repairs of congenital deformities require very small valve sizes that are simply not commercially available. Further, in paediatric applications, growth of the replacement valve is essential to eliminate the need for reoperations as the patient grows. There are a variety of devices available for replacement of cardiac valves, but all current devices have significant limitations that result in a continuing risk for morbidity and mortality (Schoen & Levy 1999).

The ultimate HV replacement is characterized as a non-obstructive, non-thrombogenic living tissue valve substitute that lasts the lifetime of the patient, provides ongoing remodelling and repair of cumulative injury and potentially grows with the recipient, which is an important goal. Such a valve would be particularly useful in the treatment of the approximately 20 000 children with congenital heart disease born in the United States each year, and especially those with valvular disease. In this population, the anticoagulation required with mechanical valves is particularly dangerous and tissue valve substitutes undergo accelerated calcification. Moreover, the placement of oversized valves extra-anatomically in the right ventricular outflow necessitates multiple subsequent surgeries for these children, as valves and conduit devices repeatedly become stenosed over time. Thus, a fundamental problem inherent to the use of existing mechanical and biological prostheses in the paediatric population is their failure to grow, repair and remodel. Regardless of the design specifics of current prosthetic valve devices, none offers any potential for growth, and therefore paediatric patients requiring valve replacement will require reoperations to place larger devices to accommodate the growth of the patient (Kirklin et al. 1993).

As with the native valve, a complete understanding of the in vivo remodelling process requires multi-length-scale approaches (figure 1). For example, it has been reported that there is gradual development of a tri-layered structure, including variations in collagen, GAG and elastin, after 15–20 weeks post implantation (Rabkin et al. 2002). Yet, we do not know if these layers are functionally equivalent to the native valve, and even what mechanisms guide their formation in vivo. Further, we have no knowledge of the anisotropic mechanical properties of tissue-engineered heart valve (TEHV) leaflet tissue, and how well these compare with the native PV. In the principles of functional tissue engineering (Butler et al. 2000), it is stated that there is a need to establish the minimal functional parameters necessary to produce tissue equivalents. For HVs, this includes quantification of the anisotropic mechanical properties of TEHV leaflet tissue, which can only be achieved through multi-axial testing to determine if the developing tissue is a suitable valve replacement. Further, the degree of cellular function and similarity to the native valve have yet to be determined. Yet, despite the fundamental nature of these requirements, we currently have no knowledge of the TEHV functional similarity to the native PV at the tissue and cellular levels which will ultimately dictate functionality and long-term durability.

(c) The role of computational biomechanics in understanding valve function

This review has focused on the biomechanical behaviour and characteristics of HVs, mainly from an experimental perspective. These studies have been crucial in developing our understanding of HV function. However, in the authors' opinion, we are now entering a level of bioengineering knowledge of valvular function wherein computational approaches can begin to be applied realistically. For example, recent work from Einstein et al. (2004, 2005) on dynamic modelling simulated early acoustic detection of changes in MV properties, which may lead to the better management of MV disease. To model the transient vibrations of the MV apparatus bathed in a blood medium, they constructed a dynamic non-linear fluid-coupled finite element model of the valve leaflets and chordae tendineae. The gross movement and small-scale acoustic vibrations of the valvular structures result from the application of physiological pressure loads. Material changes that preserved the anisotropy of the valve leaflets were found to preserve valvular function. By contrast, material changes that altered the anisotropy of the valve were found to profoundly alter valvular function. These changes were manifested in the acoustic signatures of the valve closure sounds. Abnormally, stiffened valves closed more slowly and were accompanied by lower peak frequencies.

Recent work by Driessen et al. (2003, 2005) developed a finite-element model to relate changes in collagen fibre content and orientation to the mechanical loading condition within the engineered HV construct. They hypothesized that collagen fibres aligned with principal strain directions and that collagen content increased with the fibre stretch. The results indicate that the computed preferred fibre directions run from commissure to commissure and show a resemblance to experimental data from native aortic HVs. These models represent only a first step in developing physiologically realistic models of HV function. In particular, there is a need for thorough experimental validation and true dynamic models that couple tissue (solid) and blood (fluid). For example, Kim et al. (2006, 2007) have shown for pericardial bioprosthetic HVs the importance of including bending components together with in-plane material behaviour of the leaflets when attempting physiologically realistic valve simulations. Moreover, dynamic simulations with experimentally determined leaflet material specification can be potentially used to modify the valve towards an optimal design to minimize regions of stress concentration and structural failure.

Ultimately, we would like to connect the organ-scale simulations to evaluate our understanding of AVIC mechanotransduction; it would be beneficial to develop an AVIC phenotypic/biosynthetic model linked to organ-level deformations. In the AV leaflet, TVPs above approximately 5 mmHg predominately result in ECM compaction as the collagen fibres become uncrimped and taut. From this ECM compaction, significant AVIC nucleus aspect ratio has been observed with increasing pressures (figure 11). Even a phenomenological model could thus simulate the AVIC population with mechanical inputs (quantified by the deformation of the AVIC nuclei) and cytokine levels. It could then be possible to predict the phenotypic and biosynthetic response of AVICs after repeated loading cycles.