A generative, probabilistic model of local protein structure

Abstract

Despite significant progress in recent years, protein structure prediction maintains its status as one of the prime unsolved problems in computational biology. One of the key remaining challenges is an efficient probabilistic exploration of the structural space that correctly reflects the relative conformational stabilities. Here, we present a fully probabilistic, continuous model of local protein structure in atomic detail. The generative model makes efficient conformational sampling possible and provides a framework for the rigorous analysis of local sequence–structure correlations in the native state. Our method represents a significant theoretical and practical improvement over the widely used fragment assembly technique by avoiding the drawbacks associated with a discrete and nonprobabilistic approach.

Protein structure prediction remains one of the greatest challenges in computational biology. The problem itself is easily posed: predict the three-dimensional structure of a protein given its amino acid sequence. Significant progress has been made in the last decade, and, especially, knowledge-based methods are becoming increasingly accurate in predicting structures of small globular proteins (1). In such methods, an explicit treatment of local structure has proven to be an important ingredient. The search through conformational space can be greatly simplified through the restriction of the angular degrees of freedom in the protein backbone by allowing only angles that are known to appear in the native structures of real proteins. In practice, the angular preferences are typically enforced by using a technique called fragment assembly. The idea is to select a set of small structural fragments with strong sequence–structure relationships from the database of solved structures and subsequently assemble these building blocks to form complete structures. Although the idea was originally conceived in crystallography (2), it had a great impact on the protein structure-prediction field when it was first introduced a decade ago (3). Today, fragment assembly stands as one of the most important single steps forward in tertiary structure prediction, contributing significantly to the progress we have seen in this field in recent years (4, 5).

Despite their success, fragment-assembly approaches generally lack a proper statistical foundation, or equivalently, a consistent way to evaluate their contributions to the global free energy. When a fragment-assembly method is used, structure prediction normally proceeds by a Markov Chain Monte Carlo (MCMC) algorithm, where candidate structures are proposed by the fragment assembler and then accepted or rejected based on an energy function. The theoretical basis of MCMC is the existence of a stationary probability distribution dictating the transition probabilities of the Markov chain. In the context of statistical physics, this stationary distribution is given by the conformational free energy through the Boltzmann distribution. The problem with fragment-assembly methods is that it is not possible to evaluate the proposal probability of a given structure, which makes it difficult to ensure an unbiased sampling (which requires the property of detailed balance). Local free energies could, in principle, be assigned to individual fragments, but there is no systematic way to combine them into a local free energy for an assembly of fragments. In fact, because of edge effects, the assembly process often introduces spurious local structural motifs that are not themselves present in the fragment library (3).

Significant progress has been made in the probabilistic modeling of local protein structure. With HMMSTR, Bystroff and coworkers (6) introduced a method to turn a fragment library into a probabilistic model but used a discretization of angular space, thereby sacrificing geometric detail. Other studies focused on strictly geometric models (7, 8). For these methods, the prime obstacle is their inability to condition the sampling on a given amino acid sequence. In general, it seems that none of these models has been sufficiently detailed or accurate to constitute a competitive alternative to fragment assembly. This is reflected in the latest CASP (critical assessment of techniques for protein structure prediction) exercise, where the majority of best performing de novo methods continue to rely on fragment assembly for local structure modeling (5).

Recently, we showed that a first-order Markov model forms an efficient probabilistic, generative model of the Cα geometry of proteins in continuous space (9). Although this model allows sampling of Cα traces, it is of limited use in high-resolution de novo structure prediction, because this requires the representation of the full atomic detail of a protein's backbone, and the mapping from Cα to backbone geometry is one-to-many. Consequently, this model also cannot be considered a direct alternative to the fragment-assembly technique.

In the present study, we propose a continuous probabilistic model of the local sequence–structure preferences of proteins in atomic detail. The backbone of a protein can be represented by a sequence of dihedral angle pairs, φ and ψ (Fig. 1) that are well known from the Ramachandran plot (10). Two angles, both with values ranging from −180° to 180°, define a point on the torus. Hence, the backbone structure of a protein can be fully parameterized as a sequence of such points. We use this insight to model the angular preferences in their natural space using a probability distribution on the torus and thereby avoid the traditional discretization of angles that characterizes many other models. The sequential dependencies along the chain are captured by using a dynamic Bayesian network (a generalization of a hidden Markov model), which emits angle pairs, amino acid labels, and secondary structure labels. This allows us to directly sample structures compatible with a given sequence and resample parts of a structure while maintaining consistency along the entire chain. In addition, the model makes it possible to evaluate the likelihood of any given structure. Generally, the sampled structures will not be globular, but will have realistic local structure, and the model can thus be used as a proposal distribution in structure-prediction simulations. The probabilistic and generative nature of the model also makes it directly applicable in the framework of statistical mechanics. In particular, because the probability before and after any resampling can be evaluated, unbiased sampling can be ensured.

Fig. 1.

The φ, ψ angular degrees of freedom in one residue of the protein backbone. The ω dihedral angle can be assumed to be fixed at 180° (trans) or 0° (cis).

We show that the proposed model accurately captures the angular preferences of protein backbones and successfully reproduces previously identified structural motifs. Finally, through a comparison with one of the leading fragment-assembly methods, we demonstrate that our model is highly accurate and efficient, and we conclude that our approach represents an attractive alternative to the use of fragment libraries in de novo protein-structure prediction.

Results and Discussion

TorusDBN—A Model of Protein Local Structure.

Considering only the backbone, each residue in a protein chain can be represented by using two angular degrees of freedom, the φ and ψ dihedral bond angles (Fig. 1). The bond lengths and all remaining angles can be assumed to have fixed values (11). Even with this simple representation, the conformational search space is extremely large. However, as Ramachandran and coworkers (10) noted in 1963, not all values of φ and ψ are equally frequent, and many combinations are never observed because of steric constraints. In addition, strong sequential dependencies exist between the angle pairs along the chain. We define it as our goal to model precisely these local preferences.

We begin by stating a few necessary conditions for the model. First, we require that, given an amino acid sequence, our model should produce protein backbone chains with plausible local structure. In particular, the parameterization used in our model should be sufficiently accurate to allow direct sampling and the construction of complete protein backbones. Note that we do not expect sampled structures to be correctly folded globular proteins—we only require them to have realistic local structure. Secondly, it should be possible to seamlessly replace any stretch of a protein backbone with an alternative segment, thus making a small step in conformational space. Finally, we require that it is possible to compare the probability of a newly sampled candidate segment with the probability of the original segment, which is needed to enforce the property of detailed balance in MCMC simulations.

The resulting model is presented in Fig. 2. Formulated as a dynamic Bayesian network (DBN), it is a probabilistic model that ensures sequential dependencies through a sequence of hidden nodes. A hidden node represents a residue at a specific position in a protein chain. It is a discrete node that can adopt 55 states (see Methods). Each of these states, or h values, corresponds to a distinct emission distribution over dihedral angles [d = (φ,ψ)], amino acids (a), secondary structure (s), and the cis or trans conformation of the peptide bond (c). The angular emissions are modeled by bivariate von Mises distributions, whereas the ω dihedral angle (Fig. 1) is fixed at either 180° or 0°, depending on the trans/cis flag. Note that this model can also be regarded as a hidden Markov model with multiple outputs.

Fig. 2.

The TorusDBN model. The circular nodes represent stochastic variables, whereas the rectangular boxes along the arrows illustrate the nature of the conditional probability distribution between them. The lack of an arrow between two nodes denotes that they are conditionally independent. A hidden node emits angle pairs, amino acid information, secondary structure labels (H, helix; E, strand; C, coil) and cis/trans information. One arbitrary hidden node value is highlighted in red and demonstrates how the hidden node value controls which mixture component is chosen.

The joint probability of the model is a sum over each possible hidden node sequence h = {h₁, … , h_N}, where N denotes the length of the protein:

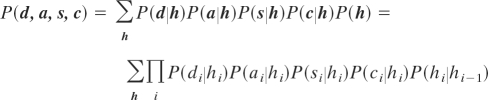The four types of emission nodes (d, a, s, and c) can each be used either as input or output. In most cases, some input information is available (e.g., the amino acid sequence), and the corresponding emission nodes are subsequently fixed to specific values. These nodes are referred to as observed nodes. Sampling from the model then involves two steps: (i) sampling a hidden node sequence conditioned on the set of observed nodes and (ii) sampling emission values for the unobserved nodes conditioned on the hidden-node sequence. The first step is most efficiently solved by using the forward–backtrack algorithm (12, 9) [see supporting information (SI) Text], which allows for the resampling of any segment of a chain. This resembles fragment insertion in fragment assembly-based methods, but the forward–backtrack approach has the advantage that it ensures a seamless resampling that correctly handles the transitions at the ends of the segment. Once a particular sequence of hidden node values has been obtained, emission values for the unobserved nodes are drawn from the corresponding conditional probability distributions (step ii). This is illustrated in Fig. 2, where the emission probability distributions for a particular h value are highlighted.

The parameters of the model were estimated from the SABmark 1.65 (13) dataset (see Methods). From the 1,723 proteins, 276 were excluded during training and used for testing purposes (test set).

We conducted a series of experiments to evaluate the model's performance. Throughout this article, we will be comparing the results obtained with our model (TorusDBN) to the results achieved with one of the most successful fragment assembly-based methods currently available, the Rosetta fragment assembler (3). Because our interest in this study is limited to modeling local protein structure, we exclusively enabled Rosetta's initial fragment-assembly phase, disabling any energy evaluations apart from clash detection. In all cases, as input to Rosetta, we used the amino acid sequence of the query structure, multiple sequence information from PSI-BLAST (14), and a predicted secondary structure sequence using PSIPRED (15).

Angular Preferences.

As a standard quality check of protein structure, a Ramachandran plot is often used by crystallographers to detect possible angular outliers. We investigated how closely the Ramachandran plot of samples from our model matched the Ramachandran plot for the corresponding native structures.

For each protein in the test set, we extracted the amino acid sequence, and calculated a predicted secondary structure labeling using PSIPRED. We then sampled a single structure using the sequence and secondary structure labels as input and summarized the sampled angle pairs in a 2D histogram. Fig. 3 shows the histograms for the test set and the samples, respectively. The results are strikingly similar. Although the experiment reveals little about the detailed sequence–structure signal in our model, it provides a first indication that a mixture of bivariate von Mises distributions is an appropriate choice to model the angular preferences of the Ramachandran plot.

Fig. 3.

Ramachandran plots displaying the distribution of the 42,654 angle pairs in the test set (Left), and an equal number of angle pairs from sampled proteins from the model (Right).

We proceeded with a comparison to Rosetta. For each protein in the test set, we created a single structure using Rosetta's fragment assembler and compared the resulting histogram to that of the test set. Also in this case, the produced plot is visually indistinguishable from the native one (plot not shown). However, by using the Kullback–Leibler (KL) divergence, a standard measure of distance between probability distributions, it becomes clear that the Ramachandran plot produced by the TorusDBN is closer to native than the plot produced by Rosetta (see SI Text and Table S1).

Structural Motifs.

The TorusDBN models the sequential dependencies along the protein backbone through a first-order Markov chain of hidden states. In such a model, we expect longer range dependencies to be modeled as designated high-probability paths through the model.

By manually inspecting the paths of length 4 with highest probability according to the model (based on their transition probabilities), we indeed recovered several well known structural motifs. Fig. 4 demonstrates how eight well known structural motifs appear as such paths in the model. Both the emitted angle pairs (Fig. 4) and the amino acid preferences (Fig. S1) have good correspondence with the literature (16, 17) (see SI Text). All reported paths are among the 0.25% most probable 4-state paths in the model (out of the 55⁴ possible paths).

Fig. 4.

Hidden node paths corresponding to well known structural motifs. The angular preferences for the hidden node paths are illustrated by using the mean φ (ψ) value as a circle (square), with the error bars denoting 1.96 standard deviations of the corresponding bivariate von Mises distribution. Because the angular distributions are approximately Gaussian at high concentrations, this corresponds to ≈95% of the angular samples from that distribution. In cases where ideal angular preferences for these motifs are known from the literature, they are specified in green. H, hidden node sequence; SS, secondary structure labeling (H, helix; E, strand; C, coil), with corresponding emission probabilities in parentheses.

Often, structural motifs will arise from combinations of several hidden node paths. By summing over the contributions of all possible paths [posterior decoding (18)], it is possible to extract this information from the model. To illustrate, we reversed the analysis of the structural motifs, by giving the ideal angles and secondary structure labeling of a motif as input to the model, and calculating the posterior distribution over amino acids at each position. Table 1 lists the top three preferred amino acids for each position in the different β-turn motifs. All of these amino acids have previously been reported to have high propensities at their specific positions (17).

Table 1.

Amino acid propensities for turn motifs calculated by using TorusDBN

Name	Position	Input		Output
		(φ, ψ)	SS	AA
β-Turn type I	1	(−60, −30)	C	P (3.2130)	S (1.5816)	E (1.3680)
	2	(−90, 0)	C	D (2.4864)	N (2.1854)	S (1.5417)
β-Turn type II	1	(−60, 120)	C	P (3.9598)	K (1.4291)	E (1.4234)
	2	(80, 0)	C	G (10.6031)	N (1.0152)
β-Turn type VIII	1	(−60, −30)	C	P (3.4599)	S (1.3431)	D (1.3290)
	2	(−120, 120)	C	V (1.9028)	I (1.8459)	F (1.3373)
β-Hairpin type I'	1	(60, 30)	C	N (5.9596)	D (2.3904)	H (1.6610)
	2	(90, 0)	C	G (12.4208)
β-Hairpin type II'	1	(60, −120)	C	G (11.2226)
	2	(−80, 0)	C	N (2.9914)	D (2.8430)	H (1.5844)

The propensity of a particular amino acid (columns 5–7) at a certain position (column 2) in a motif (column 1) is calculated as the posterior probability P(a∣d, s) divided by the probability of that amino acid according to the stationary distribution P(a) of the model. Angular and secondary structure input are listed in columns 3 and 4. The three most preferred amino acids (with propensities >1) are reported.

Sampling Structures.

We conclude with a demonstration of the model's performance beyond the scope of well defined structural motifs. In the context of de novo structure prediction, the role of the model is that of a proposal distribution, where repeated resampling of angles should lead to an efficient exploration of conformational space. In this final experiment, we therefore sampled dihedral angles for the proteins in our test set and investigated how closely the sampled angles match those of the native state.

For each protein in the test set, 100 structures were sampled, and the average angular deviation was recorded (see SI Text). This was done for an increasing amount of input to the model. Initially, samples were generated without using input information, resulting in unrestricted samples from the model. We then included the amino acid sequence of the protein, a predicted secondary structure labeling (using PSIPRED), and, finally, a combination of both. We ran the same test with Rosetta's fragment assembler for comparison.

Fig. 5 shows the distribution of the average angular distance over all proteins in the test set. Clearly, as more information becomes available, the samples lie more closely around the native state. When both amino acid and secondary structure information is used, the performance of the TorusDBN approaches that of the fragment assembler in Rosetta. Recall that Rosetta also uses both amino acid and secondary structure information in its predictions but, in addition, incorporates multiple sequence information directly, which TorusDBN does not. In this light, our model performs remarkably well in this comparison. The time necessary to generate a single sample, averaged over all of the proteins in the test set, was 0.08 s for our model and 1.30 s for Rosetta's fragment assembler. All experiments were run on a 2,800 MHz AMD Opteron processor.

Fig. 5.

Box-plots of the average angular deviation in radians (see SI Text) between native structures from the test set, and 100 sampled structures. From left to right, an increasing amount of information was given to the model: No input data, amino acid input data (Seq), predicted secondary structure input data (SS), and a combination of both (Seq+SS). The rightmost box corresponds to candidate structures generated by the fragment assembler in Rosetta.

To illustrate the effect of the different degrees of input, we include a graphical view of two representative fragments extracted from the samples on the test set (Fig. 6). Note how the sequence and secondary structure input provide distinct signals to the model. In the hairpin motif, the sequence-only signal creates structures with an excess of coil states around the hairpin, whereas the inclusion of only secondary structure input gets the secondary structure elements right but fails to make the turn correctly. Finally, with both inputs, the secondary structure boundaries of the motif are correct, and the quality of the turn is enhanced through the knowledge that the sequence motif Asp-Gly is found at the two coil positions, which is common for a type I′ hairpin (17).

Fig. 6.

Two representative examples of samples generated by TorusDBN on the proteins in the test set (1eeoA, position 2–14 and 1kzlA, position 46–56). Each image contains the native structure in blue and a cloud of 100 sampled structures. The sampled structure with minimum average distance to all other samples is chosen as representative and highlighted in red. From left to right, an increasing amount of input is given to the model. Note, that the leftmost structures are sampled without any input information and are therefore not specific to these proteins. They are included here merely as a null model. Figures were created by using Pymol (29).

Additional Evaluations.

We conducted several additional experiments to evaluate other aspects of the model. First, we performed a detailed evaluation of TorusDBN′s performance on local structure motifs using the I-sites library (19) (SI Text and Figs. S2–S4). Second, we compared TorusDBN directly to HMMSTR in the recognition of decoy structures from native (SI Text and Tables S2 and S3), and finally, the length distributions of secondary structure elements in samples were analyzed (SI Text and Fig. S5). All these studies lend further support to the quality of the model.

Potential Applications.

In closing, we list a few potential applications for the described model. First and foremost, it is in the context of de novo predictions that we expect the greatest benefits from our model. Seamless resampling and probability evaluations of proposed structures should provide a better sampling of conformational space, allowing calculations of thermodynamical averages in MCMC simulations (20). There are, however, several other potential areas of application. (i) Homology modeling, where the model is potentially useful as a proposal distribution for loop closure tasks; (ii) quality verification of experimentally determined protein structures, where it is likely that the sequential signal in our model constitutes an advantage over the current widespread use of Ramachandran plots to detect outliers; and (iii) protein design, where the model might be used to predict or sample amino acid sequences that are locally compatible with a given structure (as was demonstrated for short motifs in Table 1).

Methods

Parameter Estimation.

The model was trained by using the Mocapy DBN toolkit (21). As training data, we used the SABmark 1.65 twilight protein dataset, which for each different SCOP-fold provides a set of structures with low sequence similarity (13). Training was done on structures from 180 randomly selected folds (1,447 proteins, 226,338 observations), whereas the remaining 29 folds (276 proteins, 42,654 observations) were used as a test set. Amino acid, trans/cis peptide bond, and angle pair information was extracted directly from the training data, whereas secondary structure was computed by using DSSP (22).

Because the hidden node values are inherently unobserved, an algorithm capable of dealing with missing data is required. Here, we used a stochastic version of the well known expectation-maximization (EM) algorithm (23, 24). The idea behind stochastic EM (25, 26) is to first fill in plausible values for all unobserved nodes (E-step), and then update the parameters as if the model was fully observed (M-step). Just as with classic EM, these two steps are repeated until the algorithm converges. In our case, for each observation in the training set, we sampled a corresponding h value, using a single sweep of Gibbs sampling: in random order, all h values were resampled based on their current left and right neighboring h values and the observed emission values at that residue. Computationally, stochastic EM is more efficient than classic EM. Furthermore, on large datasets, stochastic EM is known to avoid convergence to local maxima (26).

The optimal size of the hidden node (i.e., the number of states that it can adopt) is a hyperparameter that is not automatically estimated by the EM procedure. We optimized this parameter by training models for a range of sizes, evaluating the likelihood for each model using the forward algorithm (18). Because the training procedure is stochastic in nature, we repeated this procedure several times. The best model was selected by using the Bayesian Information Criterion (BIC) (27), a score based on likelihood, which penalizes an excess of parameters and thereby avoids overfitting (see SI Text). As displayed in Fig. 7, the BIC reaches a maximum at a hidden node size of ≈55. The model, however, appears to be quite stable with regard to the choice of this parameter. Several of the experiments in our study were repeated with different h size models (size 40–80) without substantially affecting the results.

Fig. 7.

BIC values for models with varying hidden node size. For each size, four independent models were trained. The model used for our analyses is highlighted in red.

Angular Probability Distribution.

The Ramachandran plot is well known in crystallography and biochemistry. The plot is usually drawn as a projection onto the plane, but because of the periodicity of the angular degrees of freedom, the natural space for these angle pairs is on the torus. To capture the angular preferences of protein backbones, a mixture of Gaussian-like distributions on this surface is therefore an appropriate choice. We turned to the field of directional statistics for a bivariate angular distribution with Gaussian-like properties that allows for efficient sampling and parameter estimation. From the family of bivariate von Mises distributions, we chose the cosine variant, which was especially developed for this purpose by Mardia et al. (28). The density function is given by

The distribution has five parameters: μ and ν are the respective means for φ and ψ, κ₁ and κ₂ their concentration, and κ₃ is related to their correlation (Fig. 8). The parameters can be efficiently estimated by using a moment-estimation technique. Efficient sampling from the distribution is achieved by rejection sampling, using a mixture of two von Mises distributions as a proposal distribution (see SI Text).

Fig. 8.

Samples from two bivariate von Mises distributions, corresponding to two hidden nodes states. The red samples (h-value 20) represent a highly concentrated distribution (κ₁ = 65.4, κ₂ = 45.7, κ₃ = 17.3, μ = −66.2, ν = 149.6), whereas the blue samples (h-value 39) are drawn from a less concentrated distribution (κ₁ = 3.6, κ₂ = 1.9, κ₃ = −0.8, μ = 67.4, ν = 96.2).

Availability.

The TorusDBN model is implemented as part of the backboneDBN package, which is freely available at http://sourceforge.net/projects/phaistos/.