Order Parameters and Areas in Fluid-Phase Oriented Lipid Membranes Using Wide Angle X-Ray Scattering

Abstract

We used wide angle x-ray scattering (WAXS) from stacks of oriented lipid bilayers to measure chain orientational order parameters and lipid areas in model membranes consisting of mixtures of 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC)/cholesterol and 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC)/cholesterol in fluid phases. The addition of 40% cholesterol to either DOPC or DPPC changes the WAXS pattern due to an increase in acyl chain orientational order, which is one of the main properties distinguishing the cholesterol-rich liquid-ordered (Lo) phase from the liquid-disordered (Ld) phase. In contrast, powder x-ray data from multilamellar vesicles does not yield information about orientational order, and the scattering from the Lo and Ld phases looks similar. An analytical model to describe the relationship between the chain orientational distribution and WAXS data was used to obtain an average orientational order parameter, S_x-ray. When 40% cholesterol is added to either DOPC or DPPC, S_x-ray more than doubles, consistent with previous NMR order parameter measurements. By combining information about the average chain orientation with the chain-chain correlation spacing, we extended a commonly used method for calculating areas for gel-phase lipids to fluid-phase lipids and obtained agreement to within 5% of literature values.

INTRODUCTION

Incorporation of cholesterol into a phospholipid bilayer causes dramatic changes in the ordering of the lipid chains, as many investigations have shown. It has been proposed that the interaction of the rigid ring structure of cholesterol induces order in adjacent hydrocarbon chains of the lipid (1), but perhaps a better understanding of cholesterol/lipid interactions comes from considering hydrophobic interactions, as in the umbrella model (2). Increased chain order leads to increased hydrophobic thickness and a decrease in the area per lipid, the well-known “cholesterol-condensing effect” (1–5). Protein sorting into “rafts”, cholesterol-rich regions in the plasma membrane, may be related to differences in hydrophobic thickness and chain order properties (6). The liquid-ordered (Lo) phase in model membranes has been linked to these cell membrane rafts (7). Thorough structural characterization of different lamellar lipid phases in model membranes provides a foundation for understanding the structure-function relationships in cell membrane processes such as protein sorting.

This work addresses the quantitative structure of bilayers, particularly chain order, using wide angle x-ray scattering (WAXS) from oriented fluid phase membranes with and without cholesterol. With the use of digital charge-coupled device (CCD) detectors and synchrotron sources, it is now possible to obtain extensive WAXS data sets, as shown in Fig. 1. As is well known, the gel phase in Fig. 1 A has sharp wide angle reflections that are quantitatively related to arrays of well-ordered hydrocarbon chains (8–12). In contrast, the diffraction from the fluid phases shown in Fig. 1, B and C, is broad. Although this has been a good qualitative indicator that a phase has chains that are “melted”, i.e., conformationally disordered, the fact that there are distinct differences between the WAXS data in Fig. 1, B and C, indicates that there is more information in WAXS data that can be used to characterize different fluid-phase membranes. This difference is obscured in unoriented multilamellar vesicle (MLV) samples where the corresponding data consist of rotationally symmetrical broad rings which have lost orientational information. For fluid phases, such characterization must, of course, be of an average, statistical nature rather than the near crystallographic nature of gel-phase characterization.

FIGURE 1.

Grayscale CCD images show high intensity with white pixels. The spatial axes have been approximately converted to scattering vector components q_z along the normal to the bilayers and q_r in the plane of the bilayers. The scattering near q_r = 0 is LAXS lamellar scattering that is mostly absorbed by a beamstop extension. WAXS scattering is concentrated in the region with total q ∼ 0.8–1.8 Å⁻¹. (A) Gel-phase (Lβ′) DPPC at 25°C (indexing of two peaks described in Ruocco and Shipley (9) and Tristram-Nagle et al. (12)). (B) Fluid-phase DPPC at 45°C. (C) Lo phase DPPC + 40% cholesterol at 45°C. Instrumental background was subtracted as described in Materials and Methods.

With oriented samples, there are two kinds of information to be obtained from these data: 1), chain orientational order with respect to the membrane normal, and 2), lateral positional order with respect to neighboring chains. In this work, we apply a corrected form of an analytical method, often used in liquid crystal research (13,14), for quantitatively analyzing the angular distribution (φ in Fig. 1 C) of WAXS data to obtain chain orientational order parameters for liquid-phase 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC)/cholesterol and 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC)/cholesterol mixtures. Levine and Wilkins (3,15,16) used this approach for analyzing egg lecithin/cholesterol data, but a more thorough investigation as applied to model membranes is of current interest for the following reasons: 1), the availability of NMR order parameter data on purified lipids allows comparison to the WAXS method; 2), an x-ray sample chamber capable of full hydration of oriented lipid membranes allows us to characterize the effect of hydration on the WAXS data; and 3), the availability of CCD area detectors and synchrotron x-ray facilities improves the quality and digital usability of WAXS data.

Most quantitative x-ray studies of fluid-phase membranes have focused on low/small angle x-ray scattering (LAXS/SAXS). Although many WAXS results have been reported (3,15–23), many studies (17–19,23) simply report the position of the WAXS maximum and comment qualitatively on the width of the scattering. More quantitative analysis of fluid-phase WAXS has focused on lateral positional order, obtaining radial distribution functions and comparing them to simple models (24) and more recently to molecular dynamics (MD) simulations (20–22). Comparison to MD simulations has been shown to be valuable for determining the contribution to the scattering pattern from different parts of the lipid molecule (21,22). However, even for studies using oriented WAXS data (20,21), these analyses did not quantitatively relate the angular distribution of scattering to the chain orientational order. This work presents a quantitative approach for interpreting the angular distribution of scattering that is of particular value for comparing samples with very different orientational order (Fig. 1, B and C) or, as shown in the accompanying work (25), for analyzing WAXS data from ternary mixtures which are separated into a more orientationally ordered and disordered phase. Taken as a complement to studies emphasizing quantitative analysis of lateral positional ordering (20–22,24), our work shows that WAXS can be a powerful method for structural studies of fluid-phase lipid membranes.

MATERIALS AND METHODS

X-ray setup

Collection of WAXS data on oriented samples

Data such as those shown in Fig. 1 were obtained with the experimental geometry shown in Fig. 2. The oriented bilayers are supported by a solid silicon substrate tilted by an angle α relative to the incident x-ray beam. For x-rays (wavelength λ) undergoing elastic scattering through a total angle of 2θ, the magnitude of the scattering wave vector, q, is given by q = 4πsinθ/λ. The figure shows the detector coordinates with the beam at (x_b,z_b), scattering at (x,z), and the angle φ = tan⁻¹[(z − z_b)/(x − x_b)].

FIGURE 2.

Experimental geometry for the oriented WAXS setup. The bilayers in the oriented sample are parallel to the solid substrate with normal vectors n. Only one bilayer is shown, but the sample consists of a stack of ∼1800 bilayers. The angle of incidence of the x-rays (with incident wave vector k_i) is α. The x-rays (with final wave vector k_f) scatter through an angle of 2θ, and the scattering wave vector is q. The sample to detector distance is S. The angle φ is the angle measured from the x axis on the detector. The angle φ_L is complementary to the angle between the scattering wave vector q and the bilayer normal vector n.

X-rays were obtained at the Cornell High Energy Synchrotron Source (CHESS) at D-1 station (bending magnet beamline, flux ∼10¹⁰–10¹¹ photons/mm²/s) and G-1 station (wiggler beamline, flux ∼10¹²–10¹³ photons/mm²/s). Exposure times were typically 120 s at D-1 and <20 s at G-1. At D-1, two Mo:B₄C multilayers (APS Optics Lab, Argonne, IL), with 0.66% full width at half-maximum energy dispersion, were used to select x-rays with wavelength λ = 1.180 Å. At G-1, the monochromator used two W:B₄C multilayers (Osmic, Detroit, MI) with 1.1% full width at half-maximum energy dispersion to select x-rays with wavelength λ = 1.274 Å. Two beam defining slits and a set of guard slits set the beam size to 0.3 mm × 0.3 mm square for the D-1 experiments, and width = 0.25 mm × height = 0.6 mm for the G-1 experiments.

The detectors were 1 K (1024 × 1024 pixel) CCDs. The Medoptics CCD (Tucson, AZ) at D-1 has a pixel size of 0.04719 mm, and the Flicam CCD (built at Cornell) at G-1 has a pixel size of 0.06978 mm. Standard CCD image corrections, dezingering, dark background subtraction, and distortion and intensity corrections (26) were provided by CHESS. To collect a full quadrant of the scattering pattern in a single image, the detector was positioned so that the beam was aimed at the bottom corner of the detector as indicated in Figs. 1 and 2. A semitransparent molybdenum beamstop attenuated the full beam, allowing enough to be recorded on the detector to provide beam position, shape, and intensity throughout the experiments.

Full hydration of oriented multilayers requires sample chambers of special design (27). As has been described in detail elsewhere (28), the sample chamber provided a carefully regulated thermal environment that allowed the achievement of full hydration from the vapor for oriented samples. The use of a Peltier element under the sample allowed the temperature of the sample to be raised relative to the water vapor, thereby reducing the effective relative humidity of the sample to obtain smaller lamellar repeat (D) spacings or to be lowered relative to the water vapor to obtain the maximum D spacings more quickly. The chamber's exit windows are wider than they are tall, so the maximum q range was most limited in the q_z direction to 1.8 Å⁻¹. The sample-to-detector distance (S in Fig. 2) was chosen to record all the scattering on the CCD at the widest angle in the horizontal direction. The S distances, verified by calibration with silver behenate (spacing = 58.367 Å), were 115.7 mm for the experiments at D-1 station and 151.7 mm at the G-1 station. These choices recorded scattering in the vertical direction that was partially obscured by thermal insulation in the windows, which caused the fuzziness that is apparent at the top of the images in Fig. 1.

The incident angle α of the beam on the flat samples was adjustable with relative precision of 0.01° by a rotation stage inside the chamber. For the fluid-phase samples, we found that WAXS was insensitive to α in the range 0–0.5°, although some subtle differences were observed for gel-phase DPPC when α was smaller than the critical angle α_c = 0.12° for lipids at λ = 1.2 Å. When α < α_c, which produces an evanescent wave (29), it is customary to use the acronym GIWAXS, where GI connotes “grazing incidence”, although this term has been employed even for α as large as 0.5° (20). The upper surface of our fluid-phase samples may be too rough to support an evanescent wave, so we prefer to use the more conservative WAXS terminology. Nevertheless, it was desirable to work at small α to minimize blockage of scattering by the sample substrate at the smallest φ-angles. Our data were taken at α = 0.1° (D-1 data) and α = 0.15° (G-1 data).

Data collected as described in the preceding paragraph contain considerable scattering from the Mylar windows in the sample chamber as well as scattering of the beam from the water vapor and other gases in the sample chamber (air was replaced by helium as much as possible) that would make quantitative analysis impossible. This problem was solved by subtracting a “light background”, which consisted of immediately taking a CCD image after rotating the sample to −α. In this position, the substrate blocks the lipid sample from x-rays, but essentially the same Mylar window and gas background scattering is recorded. (See the Supplementary Material, Data S1, for details and raw data images.) The images in Fig. 1 have this light background subtracted.

Collection of lamellar repeat data on oriented samples

In addition to WAXS data, Fig. 1 shows LAXS data in the lower left corner of the CCD that is mostly blocked by a vertical portion of the beamstop to prevent the very strong lower orders from saturating the CCD during the relatively long exposure times advantageous for obtaining WAXS data with a good signal/noise ratio. To obtain the lamellar repeat spacing D that characterizes the hydration level of our oriented stacked samples, shorter (typically 1 s) exposures were taken with the beamstop moved to a position that exposed the strong lamellar orders. The D spacing measurements were taken while cycling the sample angle α between −3° and 7° at 20°/s to measure all of the Bragg angles, which results in more accurate D spacing measurements (this same procedure was used for the S calibration with silver behenate). The samples were symmetrically centered at the axis of the internal rotation so that no systematic displacement of the lamellar orders on the CCD occurred.

Samples

Mixture preparation

Mixtures of DOPC (Avanti Polar Lipids, Alabaster, AL; Lot No. 181PC-211), DPPC (Avanti Polar Lipids; Lot No. 160PC-270), and cholesterol (Chol) (Nuchek Prep, Elysian, MN; Lot No. CH-800-MA7-L and Lot No. CH-800-AU25-Q) were prepared from stock solutions in high-performance liquid chromatography grade chloroform (Fisher Scientific, Pittsburgh, PA). The molar concentrations of the phospholipid stock solutions were determined by phosphate assay (30). The DOPC and DPPC were each found to migrate as a single spot, as tested by thin-layer chromatography, using 65:25:4 chloroform/methanol/water (v/v) as a solvent system. The notation “DOPC + 40% cholesterol” indicates a sample composed of 0.6 mol fraction DOPC and 0.4 mol fraction cholesterol.

Oriented samples

Oriented samples consisting of ∼1800 bilayers (10 μm thick) were prepared using the rock-and-roll method (12,31). After evaporation of the chloroform, the lipid was redissolved in a nonaqueous solvent mixture; for the samples in this work, suitable solvent compositions for the rock-and-roll procedure varied for different lipids. For the DOPC/cholesterol mixtures, 1:1 chloroform/trifluoroethanol was used. For the DPPC/cholesterol mixtures, chloroform/methanol was used in the following volume ratios: 3:1 (0% cholesterol), 5:1 (10% cholesterol), 10:1 (15% cholesterol), and 20:1 (25% and 40% cholesterol). A total lipid amount of 4 mg dissolved in 150–200 μL of organic solvent was deposited onto a 15 × 30 × 1 mm Si wafer cleaned with methanol and chloroform. By gently rocking the wafer by hand, shearing action helps to align the lipid multilayers during solvent evaporation. After thorough drying, the samples were trimmed to a 5 mm strip occupying only the center of the 15-mm-wide silicon wafer. Oriented samples were annealed at 50°C in a water-saturated atmosphere for 4–8 h to improve sample orientation and to facilitate mixing of the components by lateral diffusion. After annealing, the samples were slowly brought to the initial temperature of the experiment, typically 25°C. It is important that the samples be well enough oriented that the angular spread in the oriented WAXS pattern reflect the orientational order of the chains and not the mosaicity, i.e., the angular distribution of bilayer normal vectors. Rocking curves obtained for samples prepared by the rock-and-roll procedure followed by annealing gave sample mosaicities below 0.03° halfwidth at half-maximum (HWHM) (see the Supplementary Material, Data S2). To limit radiation damage during the course of an experiment, the sample chamber was moved laterally along the 30 mm direction to expose fresh parts of the sample to the beam.

I(q) and I(φ) plots

Clearly, for oriented samples, the scattering intensity I in Fig. 1 is two-dimensional in q-space. We choose the basic independent variables to be 1), the angle φ defined in Fig. 1, and 2), the magnitude of the scattering vector, q = 4πsin(θ)/λ, where 2θ is the total scattering angle shown in Fig. 2. For our analysis, we extract one-dimensional I(q) and I(φ) plots from the two-dimensional I(q,φ) data, as illustrated in Fig. 3, A and C. The I(q) plots are obtained for each q value by averaging the intensity over φ-ranges of 10°, so there are eight I(q) plots shown in Fig. 3 B for the different φ-ranges from 5° to 85°. To produce I(φ) plots, such as the one shown in Fig. 3 D, a q range from 0.8 to 1.8 Å⁻¹ was selected to include most of the WAXS scattering as shown in Fig. 3 C, and then the scattering intensity was averaged within that q range that was also within φ-ranges of 1°. Note that the data from unoriented MLV samples are equivalent to a weighted average of the I(q) plots for all the angular ranges, which already loses considerable information. Most importantly, there is no I(φ) information from unoriented samples. MATLAB 7.1 (The MathWorks, Natick, MA) was used for data processing and analysis. The wide angle peak maximum (q₀) and HWHM were obtained from the I(q) plots for particular φ-ranges (see the Supplementary Material, Data S3). To avoid artifacts caused by high-q water scattering, the HWHM values reported were obtained using only the low-q portion of the peak and taking the intensity at q = 0.8 Å⁻¹ as a baseline value.

FIGURE 3.

A and C show the same CCD image for DOPC (T = 25°C, D = 60.0 Å). (A) Eleven constant q arcs for a Δφ = 10° range. (B) Eight I(q) plots obtained by averaging the intensities in the Δφ =10° range in (A) for φ centered at 10°, 20°, 30°, 40°, 50°, 60°, 70°, and 80°. The I(q) curve with the lowest maximum intensity corresponds to the largest value of φ. (C) Thin constant φ-slices, each with a q range of 0.8–1.8 Å⁻¹. (D) The average intensity within each slice in (C) as a function of φ.

Experimental resolution and artifacts

The relatively sharp (2,0) line seen for the gel phase in Fig. 1 A is resolution limited with a FWHM Δq/q ∼ 3% compared to a previously resolved intrinsic width of 0.02% (11). Experimental factors that affect the instrumental resolution are the energy dispersion (∼1.1% at G-1; 0.6% at D-1) and the beam divergence (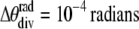); but these are negligible in comparison with geometric broadening due to the nonnegligible size of the sample in comparison with the sample to detector distance, which is estimated as ∼5% FWHM for our setup (as shown in detail in the Supplementary Material, Data S4). However, even this instrumental broadening is quite adequate for WAXS for fluid-phase samples which have intrinsic broadening of ∼20% FWHM.

In the I(φ) plot in Fig. 3 D, there is a peak in intensity near φ = 9°. The decrease in intensity observed for φ < 9° is due to increased absorption of scattered x-rays by the sample itself because x-rays scattered at small φ remain inside the sample longer than x-rays scattering at large φ. For φ = 1°, we calculate that ∼40% of the scattered x-rays are absorbed and this decreases to ∼10% for φ = 5°. In the analysis, data were not used below the φ-value where the maximum in intensity occurred (∼5–10°), so this artifact at small φ is <10%.

The total scattering comes from the lipid bilayers and also from water. Fig. 4 A shows that as the sample becomes more hydrated, more water scattering occurs, as shown by comparison with pure water scattering (32). Fig. 4 B shows that the pure water scattering curve can be reconstructed from normalized difference plots of the data shown in Fig. 4 A. The water scattering is roughly proportional to the increase in D except that the highest D shown has a disproportionately large increase in water scattering for an increase of only 1.2 Å in D spacing. This artifact is due to flooding the sample with a thick layer of water on top of the stack of bilayers. This occurs when the Peltier current is too high and the relative humidity at the sample exceeds 100% for too long a time. In principle, full hydration can be reached in the sample chamber without flooding, but hydration must be done slowly and very carefully. To avoid flooding, we typically took WAXS data at D = 2–5 Å less than the fully hydrated value that was determined from independent, nonsynchrotron experiments on unoriented MLVs immersed in water in capillaries. Although our oriented, less than fully hydrated lipid bilayers are under osmotic stress, bilayer structure changes negligibly when the D spacing is within 5 Å of full hydration. For example, at 98% relative humidity, the D spacing is ∼10 Å smaller than fully hydrated MLVs of DMPC at 30°C (33), although there is only 1% decrease in the area per molecule compared with 100% relative humidity (34,35).

FIGURE 4.

(A) I(q) plots averaged over a φ = 35–45° range for DOPC at various hydration levels (from top trace to bottom trace): D = 63.3 Å, 62.1 Å, 60.0 Å, and 51.1 Å. (B) The black line shows the integrated intensity for water from Table 1 in Hura et al. (32). The overlapping gray lines show the difference, ΔI(q) × q, for three different subtractions of the data in (A): I(63.3 Å) − I(62.1 Å); I(63.3 Å) − I(51.1 Å); and I(62.1 Å) − I(51.1 Å), each normalized to compare to the black line.

Determination of lamellar D spacings in MLVs in excess water

As noted in the previous paragraph, fully hydrated D spacings were required for the efficient study of oriented samples, and these are most easily obtained in unoriented MLV samples.

MLV preparation

Lipid mixtures were prepared in chloroform as described above for the oriented samples. After the removal of chloroform under vacuum (∼8 h), Millipore water was added to a water/lipid ratio of 5:1–10:1 (v/v) with a total lipid mass of 5 mg. The lipid/water mixtures were then taken through three freeze/thaw cycles between −20°C and 65°C and vortexed vigorously at each temperature. The samples were then annealed from 65°C to 25°C at 2°C/h in a temperature-controlled Neslab (Portsmouth, NH) water bath and then loaded into 1-mm-diameter glass capillaries (Charles Supper Company, Cambridge, MA).

Rotating anode setup

X-ray measurements were carried out using Ni-filtered Cu Kα x-rays (λ =1.5418 Å) from a Rigaku (The Woodlands, TX) RU3HR rotating anode x-ray source operated at 38 kV and 50 mA. X-rays were focused using orthogonal Franks mirrors. Tantalum slits at the sample stage trimmed the beam to ∼1 mm square, with an intensity of ∼3 × 10⁷ photons/s. Sample temperature was controlled with a water-cooled Peltier controller (Melcor, Trenton, NJ) and monitored with a 100 Ω platinum resistance temperature detector sensor (Omega, Stamford, CT). Images were collected on homebuilt CCD detectors (36) with 50 mm × 50 mm total area. The S distance (38.58 cm or 30.67 cm) was calibrated with silver behenate. Exposure times were 300 s, with a total of three to five exposures collected per measurement.

Even in excess water, full hydration of MLVs can be challenging since thermal history and small amounts of salt can affect hydration. An obvious sign of dehydrated lipid is the presence of two lamellar repeat spacings for a single-component lipid or for a mixture known to be in a single phase. However, observation of only a single D does not assure full hydration. The samples were first measured near or below room temperature (15°C or 25°C, depending on the sample) and then cycled to 45°C (above the DPPC melting temperature) and back again to 15°C or 25°C and remeasured. The capillary samples were equilibrated for at least 30 min at each temperature before data collection. These MLV results are shown in the Supplementary Material, Data S5, as well as the D spacings of the oriented samples.

THEORY AND ANALYSIS

For disordered fluid phases there is a distribution of acyl chain tilt angles and a distribution of interchain packing distances. We follow an approach commonly used in the liquid crystal literature for systems with fluid-like disorder (13,14) and used even earlier for lipid bilayers (3,15,16). Globally, the model assumes that the sample is composed of different local regions (“grains”) and that the scattering intensity adds incoherently from the different grains. Each grain consists of parallel straight rods of length L separated by a nearest-neighbor distance d_nn and packed in a hexagonal array. Locally, the rods are assumed to be well correlated. Each grain has a local director n_L, which is tilted by an angle β with respect to the z axis (Fig. 5 A), where the z axis is the normal n to the stack of bilayers shown in Fig. 2. The ensemble of grains with the same local director is rotationally symmetric about n_L, as shown in Fig. 5. For these grains, and in the limit of long chain length L, scattering is permitted only for values of the scattering vector, q, such that q is at right angles to n_L (q·n_L = 0) and q = 2π/d (where d = d_nn√3/2) as shown in Fig. 5 A. The distribution of local grain orientations n_L is described by the chain orientational distribution function f(β) such that the fraction of rods oriented at an angle between β and β + dβ (with regard to the sample normal) is given by f(β)sinβdβ. For a particular q, the total scattering is a sum of the scattering contributions from all grains with local directors n_L perpendicular to q (see Fig. 5 B). It is convenient to define the angle φ_L as the complement of the angle between q and the normal n to the stack of bilayers, as shown in Fig. 2. The scattering intensity I(φ_L) is then a weighted sum of the scattering from grains with tilt angles β in the range: φ_L ≤ β ≤ π/2. Note that fluid-phase samples are rotationally symmetric about the z axis so the observed scattering intensity depends only on φ_L and is independent of the azimuthal angle. The model scattering at a given angle φ_L for rods is then

(1)

where C is a constant that is proportional to the amount of sample, the incident beam intensity, and the length of the exposure (37). For the same model, a different formula for I(φ_L) that has the (secφ_Ltanβ) factor in the numerator of Eq. 1 replaced by (sec²φ_L sin β) was used in Levine's thesis (15), a derivation was given by Leadbetter and Norris (13), and that formula has been much used in the liquid crystal literature (14). That different formula is flawed, however, as has been emphasized recently and independently (38), where it was also pointed out that the correct formula can be attributed to much earlier work in the polymer field by Kratky (39). A fuller discussion of why Eq. 1 is correct and the Leadbetter and Norris formula is incorrect is presented in the Supplementary Material, Data S6.

FIGURE 5.

(A) In the chain scattering model, long thin rods are locally well aligned along the local director n_L, with orientation described by the angle β. For each grain (group of rods), scattering is permitted only at right angles to n_L. The membrane normal n points along the z axis. Note that the coordinate system is in the sample frame and is different from the experimental coordinate system shown in Fig. 2. (B) The scattering intensity for a given q is the sum of the scattering from all grains with directors lying on the ring q·n_L = 0.

For f(β) we use the Maier-Saupe orientational distribution function (40),

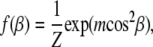(2)

where m > 0 is a parameter related to the width of the distribution, and Z is a normalization factor. This distribution function has been used to fit scattering data for a number of liquid-crystalline systems (13,14,41–43). Insertion of f(β) in Eq. 1 yields

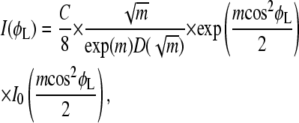(3)

where I₀ is a modified Bessel function of the first kind, D is Dawson's integral, and C can be adjusted to fit different amounts of sample with different exposure times. The derivation of Eq. 3 as well as the integral formulas for the special functions are given in the Supplementary Material, Data S6. The derivation of I(φ_L) is independent of the experimental scattering geometry used. For our experimental setup with small incident angle α, φ_L is nearly the same as φ defined in Fig. 1, as shown in Data S6, so Eq. 3 will be used with φ_L replaced by φ.

If this model were interpreted as having large grains consisting of very long rods packed together with uniform spacings d_nn, scattering would occur only for q = 2π/d (where d = d_nn√3/2). All these assumptions are relaxed for hydrocarbon chains in fluid-phase samples, so the chain scattering should occur over a range of q values, and this is incorporated into our protocol for obtaining I(φ) (see Fig. 3 and the section “I(q) and I(φ) plots” in Materials and Methods). There is also considerable scattering from nonchain components of the sample, namely, water, lipid headgroups, and cholesterol. Since the scattering intensity from these sources is likely to be more nearly isotropic and broader in both q and φ, following (42), we included a background fitting parameter, so our final fitting formula was

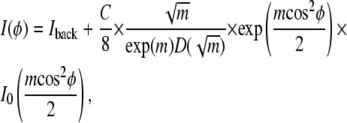(4)

which has three fitting parameters: 1), the constant background, I_back; 2), C, proportional to the amount of sample, beam intensity, and length of exposure; and 3), m, which describes the width of the Maier-Saupe distribution function (Eq. 2). Data were fit using the built-in MATLAB least-squares fitting routine “lsqcurvefit” using the “large-scale” algorithm based on the interior-reflective Newton method. The 95% confidence intervals were calculated from the covariance matrix at the solution using the MATLAB function “nlparci”.

The appropriateness of the background fitting can be judged from Fig. 6. Although I_back is a single number, the background subtraction can be represented by the shaded area shown in Fig. 6 A, which has an average value of I_back in the 1 Å⁻¹ fitted range. Note that the instrumental background has already been subtracted using data with no sample in the beam (using negative α). This remaining “background” is from the lipid sample. It may include diffuse scattering from the top surface of the sample as well as scattering from water and the lipid headgroups that give rise to broader scattering than the hydrocarbon chains, which are assumed to be responsible for the narrower scattering that remains after the subtraction of I_back. This is our justification for using the term “chain scattering” for this background-subtracted data.

FIGURE 6.

I(q) plots for (A) DPPC (T = 45°C) and (B) DPPC + 40% cholesterol (T = 45°C) obtained from Fig. 1, B and C, respectively. The gray boxes show the magnitude of the fitted I_back parameter (see Eq. 4) in comparison with the raw intensity data. The shape of the box is arbitrary, as the I_back parameter is a single number reflecting the nonchain background over the fitting range 0.8 < q < 1.8 Å⁻¹.

From the chain orientational distribution function (Eq. 2), quantities involving average values of the chain tilt angle β can be calculated, such as the chain orientational order parameter S_x-ray, defined as

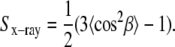(5)

Depending upon the value of m in Eq. 2, S_x-ray can take on values from 0 to 1, with S_x-ray = 1 (m = infinity) corresponding to all chains aligned along the bilayer normal and S_x-ray= 0 (m = 0) corresponding to all chain orientations being equally probable.

Fitting Eq. 4 to experimental I(φ) data is a simple way to obtain the chain orientational distribution function, from which average values involving β, such as the molecular order parameter S_x-ray, can be calculated. However, this approach makes several major assumptions, and so f(β) may not be the true orientational distribution function for the system. (Data S6 in the Supplementary Material provides a more thorough discussion of possible pitfalls when applying this approach to model membrane systems.)

Perhaps the largest problem with the model is that it assumes that the rods are infinitely long and thus it neglects the lengthwise form factor of the rods (13). The scattering from a rod of finite length L will contribute to the width of I(φ_L) by the factor Δφ_L ≈ d/(2L) (37), so the model overestimates the angular distribution of scattering by ∼6–11°, depending on the estimate of chain lengths (see Data S6). For more ordered samples, especially gel phases, the model breaks down due to the neglect of the finite length of the rods because this effect, and not the orientational disorder, begins to dominate the φ-width. For this reason, as well as for the nonrandom orientation of the chain packing lattice relative to the chain tilt that yields nonmonotonic I(φ) plots in gel phases, the model is appropriate only for liquid-phase lipids.

Although our treatment is designed to model systems with liquid-like ordering, in liquid phases a model consisting of rigid rods with orientation described by the single angle β is clearly a simplification. The methylene segments toward the middle of the bilayer have significantly more disorder than do segments closer to the surface (44). Levine and Wilkins (15,16) point out that if we think of the scattering domains as segments of chains, then application of such a simple model is more plausible. The model might be improved by treating the rods as flexible. (For an example of modification of Maier-Saupe mean-field theory for flexible rods, see Jähnig (45).) Since our data are well fit by using a simple Maier-Saupe distribution of rigid rods, we could not distinguish between this simple model and a more complicated model based on how well they fit the data.

Also, because we integrate over the width of the peak to obtain I(φ) plots, our analysis discards information about lateral positional order which is obtained from the details of I(q) plots. Radial distribution functions have been quantitatively interpreted by comparing to simple analytical models (24) or by comparing to MD simulations (20–22). (Note that in the model presented in Warren (24), the orientational information was discarded to model the radial distribution.)

RESULTS AND DISCUSSION

Fig. 1 shows that the scattering intensity I(q,φ) for oriented samples is a function of both the angle φ defined in Fig. 1 C and the magnitude 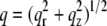of the scattering vector. The angular I(φ) plot defined in Fig. 3 D is sensitive to chain orientational order. The I(q) plots defined in Fig. 3 B report the position of the lipid WAXS peak, q₀, which gives the average spacing for molecular packing (d = 2π/q₀), dominated largely by the chain spacing, and the width of the peak gives information about disorder in the packing. Thus oriented WAXS data tell us about molecular orientational order (from the I(φ) plot) as well as information about molecular packing (from many I(q) plots). In contrast, for unoriented samples, the only information is a single I(q) plot because the scattering intensity I(φ) is constant.

Quantifying chain orientational order: fits to I(φ) data

Effect of cholesterol on the angular distribution of scattering

Fig. 7 shows I(φ) plots for two different fluid-phase lipids and two different cholesterol concentrations. The fits to pure DOPC and pure DPPC indicate that the background-subtracted scattering at φ = 90° is nonzero and at least 25% of its maximum value at φ = 0°. (Note that the trace for DPPC is offset by 0.3.) These values may seem rather large, but a similar result has been obtained for several lipids in the liquid-disordered (Ld) phase using a different background subtraction procedure (20). In contrast, Fig. 7 shows that the scattering intensity at φ = 90° is close to zero when 40% cholesterol is added to the pure lipids. In general the data in this study are all well fit to Eq. 4, although the DPPC + 40% cholesterol data shown in Fig. 7 are not as well fit as the other data. This is expected (13,14) because as the system becomes more ordered, additional details must play a role in determining I(φ). For example, for the gel-phase scattering in Fig. 1 A the I(φ) plot has two peaks because chains tilt specifically toward nearest neighbors. In contrast, the model assumes the tilt direction has a random distribution (also see Data S6 in the Supplementary Material).

FIGURE 7.

Normalized and background-subtracted I(φ) data are shown by gray data points for DPPC (45°C) and DOPC (25°C) with and without 40% cholesterol. Black lines show fits to Eq. 4. Data and fits were normalized by subtracting I_back from I(φ) and then dividing by the fitting parameter C. Each plot is offset from the one below by 0.15 normalized intensity units.

Table 1 gives the values of the parameter m that are obtained by fitting the Maier-Saupe angular distribution (Eq. 2) to the I(φ) data. Table 1 also gives the corresponding values of the x-ray order parameter S_x-ray calculated using Eq. 5. In comparison to pure lipid, the angular distribution of scattering f(β) is much narrower when 40% cholesterol is added to DPPC or DOPC, so m increases and S_x-ray more than doubles, as is shown in Fig. 8.

TABLE 1.

Chain order parameters

Sample	T (°C)	m (Eq. 2)	Sx-ray (Eq. 5)
DOPC*	25	1.83 ± 0.18	0.27 ± 0.03
DOPC + 10% Chol†	25	2.02 ± 0.08	0.30 ± 0.01
DOPC + 40% Chol†	25	5.52 ± 0.09	0.68 ± 0.01
DPPC†	45	3.03 ± 0.11	0.44 ± 0.01
DPPC + 10% Chol†	45	4.29 ± 0.06	0.59 ± 0.01
DPPC + 15% Chol†	45	5.97 ± 0.13	0.71 ± 0.01
DPPC + 25% Chol†	45	9.11 ± 0.32	0.82 ± 0.01
DPPC + 40% Chol†	45	11.26 ± 0.37	0.86 ± 0.01

^*Average values and standard deviations for data taken on three different samples (D = 59–61 Å).

^†Errors are 95% confidence intervals from the fits of a single sample.

FIGURE 8.

S_x-ray versus cholesterol is plotted for DPPC/cholesterol mixtures at 45°C with solid triangles and for DOPC/cholesterol mixtures at 25°C with solid circles. Open triangles show S_NMR (47) for DPPC/cholesterol, and the dashed curve shows the same S_NMR multiplied by 1.35.

Fig. 8 also compares values of S_x-ray for DPPC/cholesterol mixtures to values of S_NMR, sometimes referred to as S_mol = 2〈|S_CD|〉, where S_CD is the ²H-NMR segmental order parameter (46). S_NMR values were calculated from first moment (M₁) data (47) according to Eq. 11 in Ipsen et al. (4). At 45°C, both S_x-ray and S_NMR increase monotonically as a function of mol % cholesterol and begin to level off at ∼25% cholesterol. Obvious differences between the two techniques include assumption of the rigid chain model in the case of the x-ray analysis and time and motional averaging of deuterium NMR signals (48) that does not influence the x-ray measurements. Remarkably, in view of the considerable differences in quantities being measured and the differences in models, Fig. 8 shows that the qualitative trends in S_x-ray and S_NMR may be put into quantitative agreement if a simple factor of 1.35 is applied to S_NMR. At least for monitoring the effect of cholesterol, S_x-ray and S_NMR both report the orientational order of lipid bilayers.

Information about average chain order, as measured by ²H-NMR first moment data, is unavailable for DOPC. However, ²H-NMR measurements of DOPC selectively deuterated at the C-9 and C-10 positions show that the quadrupolar splittings almost double with 50% cholesterol content, evidence of significant increase in chain orientational order (49). Using a specialized two-dimensional NMR technique allowing the measurement of chain order parameters without deuteration, another study concluded that the addition of 30% cholesterol to DOPC results in a “lipid state analogous to the Lo phase” with a substantial increase in chain orientational order (50). These results are consistent with our x-ray results in Fig. 8, which show that S_x-ray more than doubles when 40% cholesterol is added to DOPC.

Liquid phases can have a broad range of properties, and a variety of techniques have been used to examine how these properties change as a function of temperature and composition in DPPC/cholesterol mixtures (23,51). Although it is customary to use the names Ld and Lo phases, these two fluid phases are clearly differentiated only in the case of Ld/Lo phase coexistence. The literature suggests that DOPC/cholesterol does not phase separate at any temperature or cholesterol composition (52), rather the properties of the single liquid phase change continuously from Ld to more Lo-like as cholesterol is added. There is disagreement over the DPPC/cholesterol system, with some reports suggesting that DPPC/cholesterol mixtures do separate into Ld and Lo phases above the DPPC melting temperature (53), whereas other reports claim that DPPC/cholesterol mixtures do not phase-separate (54). However, DPPC + 40% cholesterol at 45°C is generally considered to be in a single Lo phase, consistent with our fitting to the I(φ) data, which is satisfactory with only one distribution with one value of S_x-ray rather than a mixture of two distributions, which would indicate phase coexistence. For both DOPC and DPPC with 40% cholesterol, our large values of S_x-ray relative to the values for the pure lipids indicate that the chains are orientationally well ordered, which is consistent with the description of the Lo phase.

Effect of hydration on chain orientational order

For DOPC at different levels of hydration (nine D values ranging from 51.1 to 63.3 Å), the I(φ) plots were all well fit by Eq. 4, whereas Levine and Wilkins (15,16) required different distribution functions to fit their I(φ) data depending on the hydration level of the egg lecithin. The effect of hydration on chain orientational order was modest in comparison with cholesterol's large effects. S_x-ray as a function of D for DOPC was found to decrease with increasing hydration, with S_x-ray decreasing from 0.29 for D = 51.1 Å to 0.23 for D = 63.3 Å. This trend is consistent with increasing hydration causing increasing lipid area (34), which in turn decreases the hydrocarbon thickness (because hydrocarbon volume is nearly constant), which causes the hydrocarbon chains to become statistically shorter with more gauche bonds (conformationally more disordered).

Relationship between the angular distribution of scattering and angular distribution of chains

It has been assumed that the fraction of chains tilted in the range β₁ ≤ β ≤ β₂ is given by the fraction of scattering observed on the detector in the same angular range for φ (20), but it was noted in this same study that this interpretation is “too simplistic, since the scattering intensity at a given position on the detector is the sum over contributions of chains with different tilt angles, or a range of tilt angles”. Indeed in our model, these two quantities are not equal. F_chains(β₁ ≤ β ≤ β₂), the fraction of chains with orientation in the range β₁ ≤ β ≤ β₂, is calculated from the distribution function f(β). The fraction of scattering observed on the detector in a range φ₁ ≤ φ ≤ φ₂ is defined as

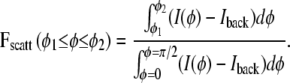(6)

For a distribution with m = 1.83 (which happens to be the value for DOPC at 25°C), F_scatt(0° ≤ φ ≤ 30°) = 0.50 and F_scatt(60° ≤ φ ≤ 90°) = 0.20, but F_chains(0° ≤ β ≤ 30°) = 0.31 and F_chains(60° ≤ β ≤ 90°) = 0.27, which are significantly different from the F_scatt values. Our values for F_scatt for DOPC in the fluid phase compare reasonably well with measurements for other fluid-phase phospholipids; depending on the lipid, F_scatt(0°≤ φ 30°) = 0.46–0.52 and F_scatt(60° ≤ φ ≤ 90°) = 0.19–0.24 have been reported (20). Since these scattering intensity fractions for the fluid-phase lipids are similar to ours, this suggests that our method for subtracting the isotropic nonchain scattering (I_back in Eq. 4) is effectively similar to a method that fits to a Lorentzian plus linear background (20) (See also Data S3 in the Supplementary Material).

Effect of undulation fluctuations on the angular distribution of scattering

In addition to chain order, the amplitude of undulations in the bilayer can affect the angular distribution of scattering I(φ) and thus our S_x-ray values. The magnitude of the undulation fluctuations depends on the elastic properties of the bilayer, which are known to change as a function of temperature and lipid composition. For example, cholesterol stiffens fluid-phase phosphatidylcholine bilayers (55,56). Higher chain order and smaller undulation amplitude (both generally expected for samples with more cholesterol) would result in a narrowing in I(φ). However, we now argue that the undulations have a small effect in comparison with chain orientational order on the angular distribution of scattering. A fluctuating bilayer can be divided into sections that are tilted at an angle β_F with respect to the average membrane normal. This angle is different from β, the angle of each chain with respect to the membrane normal. For DOPC at 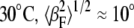(35). By comparison, from the fitted Maier-Saupe distribution function, we calculate 〈β²〉^1/2 ≈ 50° for DOPC at 25°C, which is much larger than for undulations. Similar conclusions have been reached regarding NMR order parameter data, which depend on the trans/gauche isomer ratio (conformational order) as well as changes in the orientation of the director caused by the tilting of the chains (as in the Lβ′ phase) and membrane surface undulations (57).

Lateral positional ordering

Table 2 summarizes our results obtained from the I(q) plots for the smallest φ-range that is free of absorption artifacts from the substrate (see Materials and Methods). The HWHM, which is inversely proportional to the correlation length, varied only slightly. This indicates that fluid phases, either orientationally ordered or disordered, have a similar distribution of nearest-neighbor distances. This contrasts strongly with our result in the previous section that cholesterol causes a significant increase in orientational order of the phospholipid chains; this “decoupling” of chain orientational order and lateral positional order is characteristic of the Lo phase (58).

TABLE 2.

Positions of maximal intensity for an I(q) slice with φ = 5–10°

Sample	T (°C)	q0 (Å−1)	d = 2π/q0 (Å)	HWHM (Å−1)
DOPC*	25	1.39 ± 0.01	4.53 ± 0.03	0.16 ± 0.01
DOPC + 10% Chol	25	1.36	4.60	0.16
DOPC + 40% Chol	25	1.28	4.91	0.17
DPPC	45	1.39	4.52	0.15
DPPC + 10% Chol	45	1.40	4.50	0.15
DPPC + 15% Chol	45	1.37	4.58	0.14
DPPC + 25% Chol	45	1.38	4.56	0.14
DPPC + 40% Chol	45	1.35	4.66	0.16

For φ = 5–10°, absorption is 10% or less. These values are the same (±0.01) for a radial slice with φ = 10–15°, for which absorption is <5%.

^*Average values and standard deviations for data taken on three different samples (D = 59–61 Å).

Cholesterol increases the wide angle spacing d for both DOPC and DPPC and for a variety of lipids (19). In addition to the effect of cholesterol, the effect of hydration on DOPC chain positional order was studied (see the Supplementary Material, Data S3). For lamellar repeat spacings of D = 51.1–63.3 Å, differences in d and HWHM were negligible, agreeing with a previous observation of the effect of hydration on fluid-phase WAXS data (18). Even though S_x-ray varies over the same D range, the invariance of d is expected because chain-packing distances are mostly dependent upon chain density, which does not vary much in liquid phases. As pointed out previously (20,22), d can easily be misinterpreted for the fluid phase because the acyl chains are not in a tightly packed lattice; however, it is a useful datum to report for comparison with other work, and we use it in the next section in combination with knowledge of the chain orientational distribution to obtain lipid areas from the WAXS data.

Calculation of lipid areas for fluid phases

Although WAXS data have often been used to obtain area per lipid A_L for gel phases (3,8,11,12), most x-ray methods for obtaining A_L for liquid phases are based on lamellar repeat (LAXS) data (35). In contrast, here we use WAXS data exclusively to obtain A_L.

For chains packed in a perfect hexagonal lattice, d = 2π/q₀ is the spacing between rows of chains from which the spacing between nearest neighbors is d_nn = 2d/√3. (For the Lβ′ phase there are usually two spacings: d₁₁ and d₂₀ (9), but this is a minor complication that is easily handled for gel phases.) Then, the area per chain A_c that is perpendicular to the chain is given by (17):

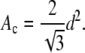(7)

The area per lipid is then given by (3,12)

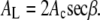(8)

where β is the chain tilt angle. In the fluid phase the average global chain tilt angle β is zero, but using A_L = 2A_c is flawed because the chains are not well ordered. The chains can even have upturns (59), and these would double the area/chain A_c but not affect d, so the A_L obtained from Eqs. 7 and 8 would be smaller than the actual A_L. This misuse of d is well known (15,16,20). An alternative formula

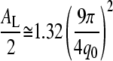(9)

has been proposed based on MD simulations (20). However, Eq. 9 predicts that if two lipids have the same q₀, they should have the same A_L. DOPC at 25°C and DPPC at 45°C do have the same q₀ (see Table 2), but they have quite different values of A_L (35). In a more recent work focusing on comparison of MD simulations and experimental x-ray scattering data for DMPC bilayers, it was proposed that the interchain correlation length (1/HWHM) could be quantitatively related to A_L (21). Our results show that the HWHM is similar for all the fluid-phase DOPC/cholesterol and DPPC/cholesterol bilayers (see Table 2), and yet cholesterol is known to cause a substantial decrease in A_L. Both the proposal of relating areas to q₀ as in Eq. 9 (20) and the proposal of focusing on the correlation length (21) ignore the chain orientational distribution, which has a major effect on A_L calculations, as we will show below. This failure to incorporate the orientational distribution into calculations of area make the methods presented in previous studies (20,21) dependent on obtaining MD simulations for the exact lipid (or mixture) of interest, without the ability to extend the approach to lipids where simulation data are unavailable.

Following Levine and Wilkins (3,15,16), our model treats the fluid phase as an assembly of local grains with chains locally packed in a hexagonal lattice and tilted with angle β. Then, just as in the gel phase, the local area is given by Eq. 8 using Eq. 7 for A_c. However, unlike the gel-phase, the grains in the liquid phase have a distribution f(β) of grains with orientation β, and so we take the average of the areas of the grains to obtain the final area per lipid, A_L. First, noting that the d value typically changes by <5% as a function of φ (see Data S3 in the Supplementary Material), we assume that d is independent of the angle β (or equivalently q₀ is independent of φ) and use the value of d for φ = 5–10° in Eq. 7. Then,

(10)

However, for the Maier-Saupe distribution, the average 〈secβ〉 cannot be computed because secβ becomes infinite as β approaches 90°. In our model, this corresponds to the unphysical artifact of a grain of infinitely long chains lying parallel to the surface of the bilayer.

Levine and Wilkins (15,16) pointed out this problem and did not attempt to approximate 〈secβ〉. The same 〈secβ〉 problem has been encountered in calculating areas from NMR data, and three approximations have been suggested (60). The two better ones are shown below:

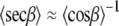(11)

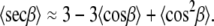(12)

These average values can be calculated from f(β).

Table 3 summarizes our A_L values calculated using Eq. 10 and the approximations in Eqs. 11 and 12, and compares these results with literature values. The agreement using either Eq. 11 or Eq. 12 is surprisingly good. This agreement with literature A_L values supports the underlying grain model, which was used to obtain a quantitative measure of orientational order. Although this is unlikely to be the preferred way to obtain lipid areas, the areas calculated in this way should reproduce trends. For example, our WAXS area determination reproduces the literature result that DPPC has a smaller area than DOPC. Also, the WAXS calculation shows that cholesterol addition causes an area decrease, in agreement with the well-known cholesterol-condensing effect (2–5). The observation of increased chain order and consequently decreased area of the lipid chains with cholesterol addition is consistent with the umbrella model (2): the reduced area of the lipid allows more space under the phospholipid headgroups to shield the cholesterol from water.

TABLE 3.

Area per lipid calculations using the following approximations in Eq. 10

		AL (Å2)
Lipid	2Ac (Å2)	Eq. 11	Eq. 12	Literature
*DOPC (25°C)	47.4	71.8 ± 2.5	72.6 ± 2.2	72.2 (30°C) (61,62)
DOPC + 10% Chol (25°C)	48.9	72.2	73.4	71.4 ± 1.0 (30°C) (63)
DOPC + 40% Chol (25°C)	55.7	63.6	64.7	64 ± 1.0 (30°C) (63)
DPPC (45°C)	47.2	62.5	64.3	64.3 (50°C) (64)
				64.0 (50°C) (66)†
DPPC +10% Chol (45°C)	46.8	56.4	57.9	60.5 (50°C) (66)†
DPPC + 15% Chol (45°C)	48.4	54.5	55.3	59.0 (50°C) (66)†
DPPC + 25% Chol (45°C)	48.0	51.3	51.6	55.5 (50°C) (66)†
DPPC + 40% Chol (45°C)	50.2	52.8	52.9	52.5 (50°C) (66)†

^*Average values and standard deviations for data taken on three different samples (D = 59–61 Å).

^†MD simulation results (66).

Table 3 also lists results for 2A_c, which are substantially different from A_L and show the effect of ignoring the orientational distribution (〈secβ〉) in calculating areas. Although 2A_c increases as a function of cholesterol content, A_L decreases because the chains become more orientationally ordered.

The DOPC/cholesterol and pure DPPC literature area values (61–64) were calculated by combining measurements of hydrophobic thickness from LAXS data with volume measurements. The lipid volume does not change with cholesterol addition (65), and so an increase in hydrophobic thickness corresponds to an area decrease. For the DOPC/cholesterol mixtures, LAXS and WAXS were performed on the same samples. The order parameter determination from WAXS and hydrophobic thickness determination from LAXS are complementary and provide consistency checks: for a particular lipid, if S_x-ray increases (e.g., by adding cholesterol), the hydrophobic thickness should also increase. A linear relationship between the average NMR chain order parameter and hydrophobic thickness (from scattering techniques) has been proposed (4). With the possibility of determining S_x-ray from WAXS, the relationship between chain order and thickness can be investigated using the same technique (x-ray scattering) on the same samples.

CONCLUSIONS

The angular distribution of scattering intensity I(φ) in WAXS images from oriented samples gives information about orientational order in liquid phases that is not available from unoriented samples. Even qualitatively, I(φ) shows dramatic differences between different fluid phases. Using an analytical method based on a simple model of independent grains, we calculated an orientational order parameter S_x-ray which reproduces the reported trends in the NMR order parameter as a function of cholesterol content for DOPC/cholesterol (25°C) and DPPC/cholesterol (45°C). In both of these systems, the addition of 40% cholesterol more than doubles S_x-ray, and yet the positional order remains as low as in the Ld phase, as indicated by the same width of the peaks in the I(q) plots. This decoupling of chain orientational order and lateral positional order is characteristic of the Lo phase.

Although both WAXS and NMR provide similar average orientational order parameters, there are other notable differences. NMR can provide order parameters for each methylene group, whereas S_x-ray averages over all the scatterers in the sample. WAXS has two advantages: 1) it provides a distribution function f(β) of the orientational angles instead of just the averages that are contained in the NMR order parameters, and 2) it provides a direct measurement of chain packing.

In addition to calculating S_x-ray values, we combined information about the orientational distribution function f(β) with the packing distance d to calculate areas for lipids in the liquid phase, based entirely on the experimental WAXS data. The results agree well with literature values of A_L, lending support to the independent grain model that we used to analyze the WAXS data. We perform WAXS and LAXS measurements at the synchrotron on the same oriented lipid multilayers at nearly the same time. Interpretation of both sets of data is complementary and provides consistency checks.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.