Gating Mechanisms of Mechanosensitive Channels of Large Conductance, I: A Continuum Mechanics-Based Hierarchical Framework

Abstract

A hierarchical simulation framework that integrates information from molecular dynamics (MD) simulations into a continuum model is established to study the mechanical response of mechanosensitive channel of large-conductance (MscL) using the finite element method (FEM). The proposed MD-decorated FEM (MDeFEM) approach is used to explore the detailed gating mechanisms of the MscL in Escherichia coli embedded in a palmitoyloleoylphosphatidylethanolamine lipid bilayer. In Part I of this study, the framework of MDeFEM is established. The transmembrane and cytoplasmic helices are taken to be elastic rods, the loops are modeled as springs, and the lipid bilayer is approximated by a three-layer sheet. The mechanical properties of the continuum components, as well as their interactions, are derived from molecular simulations based on atomic force fields. In addition, analytical closed-form continuum model and elastic network model are established to complement the MDeFEM approach and to capture the most essential features of gating. In Part II of this study, the detailed gating mechanisms of E. coli-MscL under various types of loading are presented and compared with experiments, structural model, and all-atom simulations, as well as the analytical models established in Part I. It is envisioned that such a hierarchical multiscale framework will find great value in the study of a variety of biological processes involving complex mechanical deformations such as muscle contraction and mechanotransduction.

INTRODUCTION

Overview and motivation

Many fundamentally important biological processes rely on the mechanical response of biomolecules and their assemblies to external stimuli (1). An important example is the gating of mechanosensitive (MS) channels, which are important in the transduction of signals related to touch, hearing, etc (2–6). Although the identities of MS channels responsible for specific physiological functions have been revealed at a rapid pace in recent years (7,8), the molecular mechanisms that dictate the gating properties of these channels are not well understood.

The most exciting aspect of mechanotransduction lies in the length scales that it spans: the mechanical stimuli can be introduced through macroscopic-scale contacts, which is transduced up to mesoscopic-scale (micron) distances and eventually leads to microscopic-scale (nanometer) conformational changes in membrane-bound protein or protein complexes (3,4,6,9,10). It is envisioned that under the guidance of an effective theoretical framework, a computational analysis of the gating mechanism of MS channels is a valuable supplement to experimental investigations, both in terms of better interpreting experimental data and stimulating new mechanistic hypotheses that can be tested experimentally.

A productive computational analysis of MS channels, however, requires the development of a novel simulation framework that cannot only treat the large length- and timescales implicated in the gating process, but also includes sufficient molecular details to faithfully capture the most important characteristics of a specific system. This is particularly important in biological systems where atomistic features are crucial to structure and function. In other words, the key challenge is to develop a flexible and reliable computational framework that complements the traditional bottom-up all-atom/coarse-grained simulations (which are most appropriate for studying nanoscale biological processes (11,12)), with a hierarchical approach that can efficiently treat large deformation at the macro/mesoscopic scale, while retaining key features and insights from the atomic scale.

Motivated by these considerations, we establish what to our knowledge is a new, top-down, continuum mechanics-based hierarchical framework to explore the working mechanisms of MS channels at multiple length and temporal scales. Molecular mechanics-based simulations such as molecular dynamics (MD) at the nanoscale are used to obtain critical insights into the physical properties of and interactions among proteins and lipid molecules. Effective continuum models are established to incorporate these atomistic features, which are then used to study the conformational responses of MS channel(s) upon various external mechanical perturbations with the finite element method (FEM). The proposed MD-decorated FEM (MDeFEM) approach is more versatile than those based on highly idealized geometries and properties (13,14), and sufficiently detailed for the purpose of probing the underlying gating mechanism without suffering from the limitations in the length- and timescales associated with all-atom simulations. From the key insights obtained from detailed MDeFEM simulations, the most important structural components that affect the gating process are identified, based on which simplified analytical theoretical models can be developed to further elucidate the essential gating mechanisms and conformational response of membrane proteins. Although we focus on the MS channels of large conductance (MscL), the frameworks established in this study are versatile and can be readily extended to other biomolecule systems, especially those with complex geometry and loads that are not accessible to conventional all-atom simulations.

The mechanosensitive channel of large conductance

Most cellular responses to force are due to MS channels (3,4,9). In bacteria, the gating of MS channels acts as a valve and facilitates the permeation of small ions and water molecules. In mammalian cells, MS channels play an important role in fundamental physiological functions such as touch and hearing. MS channels have been identified in more than 30 cell types and abnormality in their functions may contribute to serious health problems such as neuronal degeneration, hypertension, and glaucoma.

A considerable amount of research effort has been focused on the MscL, which are ubiquitous, diverse, and essential to the survival of bacteria. Compared with other types of MS channels, the structures of MscL are relatively simple and thus taken as the model system in this work to illustrate the effectiveness of the numerical and theoretical frameworks we develop.

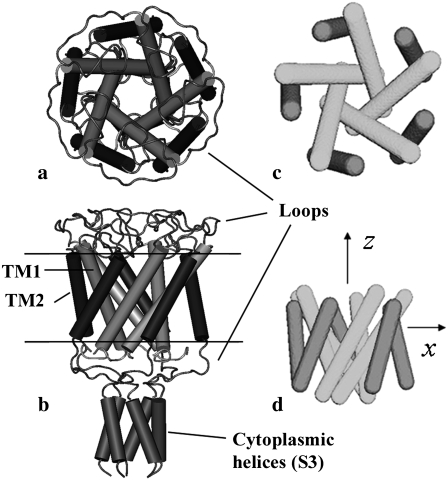
Although Escherichia coli-MscL (E. coli-MscL) is one of the most studied MS channels, the only available x-ray crystal structure in the literature is for the MscL from Myobacterium tuberculosis (Tb), which was captured in its closed state by the Rees lab (15). The Tb-MscL is a homopentamer with each monomer containing two types of transmembrane helices (TM1 and TM2), cytoplasmic S1 and S3 helices, and loops, Fig. 1, a and b. By retaining the main features of the crystal structure of Tb-MscL and based on experimental evidences, the atomic structure of E. coli-MscL was developed based on homology modeling (16), which is shown in Fig. 2, a and b, in its closed state.

FIGURE 1.

Tb-MscL: (a) top view and (b) side view of the closed crystal structure (15). (c) Top view and (d) side view of the continuum model used in the preliminary study (36) where only the transmembrane helices are taken into account.

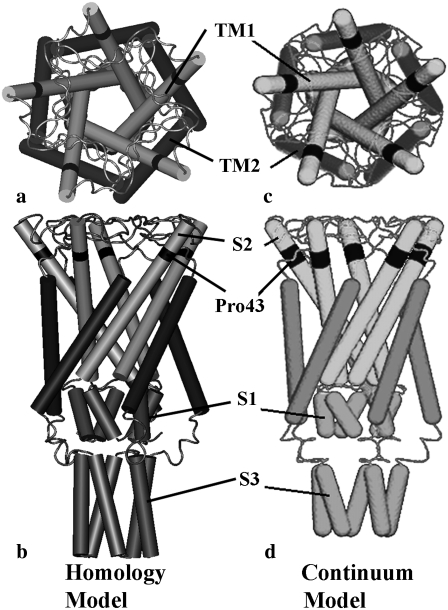
FIGURE 2.

E. coli-MscL: (a) top view and (b) side view of the closed structure of the homology model (16). (c) Top view and (d) side view of the full protein model in the refined MDeFEM approach in this article, where the cytoplasmic helices and loops are taken into account; the continuum model is developed based on the closed structure of the homology model (23).

As shown in Figs. 1 and 2, the structure of MscL is of fivefold symmetry, and the residues on top of the transmembrane helices are connected by periplasmic loops, whereas those at the bottom of the transmembrane helices are linked to cytoplasmic helices via cytoplasmic loops. The TM1 bundle consists of five longer subunits that form an inner gate (i.e., the MS channel), and the five TM2 subunits form the outer bundle. In E. coli-MscL (Fig. 2), for example, TM1 and TM2 helices correspond to residues Asn¹⁵-Gly⁵⁰ and Val⁷⁷-Glu¹⁰⁷, respectively. There is a break in TM1 due to Pro43 near the top of the TM1 helix, and in the literature, the segment above Pro43 is sometimes referred to as the S2 helices (16). The cytoplasmic domain is composed of gates formed by S1 helices and S3 helices, which correspond to residues Ile³-Met¹² and Lys¹¹⁷-Arg¹³⁵, respectively (16).

The size of the channel pore is a critical parameter, which determines the ion flux that passes through and can be estimated by measuring the electric current experimentally (17). In principle, three valves can be formed by the TM1 helix bundle, S1 helix bundle, and S3 helix bundle, respectively (Fig. 2 b). However, the transmembrane pore enclosed by the TM1 helix bundle is most important, and once its radius reaches a critical value, the conductive state is changed into one that allows ion entry (17). The transmembrane channel is of a pentagon shape when projected onto the membrane plane, and an effective radius of the MscL is defined as the radius of a circle with the same area as the pentagon-shaped TM1 pore enclosed by its principal axes, a = 6.5 Å for E. coli-MscL in the closed state.

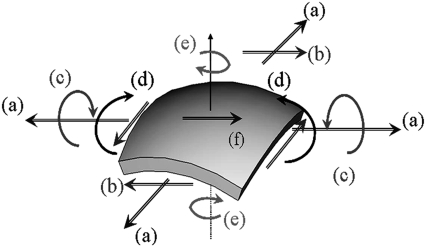
Despite the availability of an atomistic structure of MscL and extensive biophysical studies over the last few decades (3,4,6,9,10,18), much remains unknown regarding the detailed molecular mechanisms by which MscL senses the mechanical deformation. The challenge lies in the diverse forms of mechanical stimuli (1,3), which can include steady-state contacts, high-frequency vibrations, fluid shear stresses, osmotic and hemodynamic pressure, etc. All these external stimuli are present in the background of internally generated forces such as those that arise from hydrostatic pressure and cytoskeletal polymerization. Mechanotransduction pathways must therefore filter out irrelevant stimuli while at the same time responding efficiently to the relevant stimulus. In such a context, it has been established that the membrane, once considered only a passive cellular component, may play an important role (2,4,10,19,20). Nevertheless, several fundamental issues remain: What is the conformational transition pathway for MscL and what are the roles of various protein structural motifs in sensing and transducing the mechanical perturbation in the membrane? What are the special features of MscL that distinguish it from other transmembrane proteins as a mechanosensing system? Do different basic modes of membrane deformation (Fig. 3) impact the structure of MscL to a similar degree or is MscL sensitive to a specific type of perturbation? Is there significant cooperativity among MscL channels in the membrane? These questions are challenging from both experimental and theoretical perspectives, due to the highly heterogeneous features of protein structure and protein-lipid interactions as well as the multiscale nature of protein-membrane deformation. (Certain modes of the mechanical stimuli, such as bending and twisting of membrane (Fig. 3) and interaction among MscLs, involves substantially larger length scales than that accessible to the current all-atom simulations.) The continuum-based numerical and theoretical framework we develop is aimed to effectively fill the important technical gap and address these questions.

FIGURE 3.

Six basic deformation modes of a membrane (a) biaxial tension, (b) in-plane shear, (c) out of plane twisting, (d) bending, (e) torsion, and (f) membrane shear.

Previous experimental and modeling studies of MscL and their limitations

The relationship between channel opening probability and membrane tension force has been extensively studied using patch clamp methodology on a lipid vesicle containing E. coli-MscL (2,17). Since the cytoplasm and other membrane proteins were removed before patch clamp experiments, the measured channel opening indicated that the mechanical deformation of lipid membrane is essential for gating of MscL. A five-subconductance states model was established, which showed that the tension-dependent conformational transition is primarily attributed to the pore area variation that occurred between the closed state and the first subconductance state. A plausible gating mechanism of MscL at the molecular level was first developed by Sukharev and co-workers based on a homology model for E. coli-MscL and tested by cysteine cross-linking experiments (21). Later, the structural rearrangements in the large prokaryotic MscL has been determined by Perozo and co-workers (5,6,22) using electron paramagnetic resonance spectroscopy and site-directed spin labeling.

The importance of residues in different structural motifs has been probed with mutation studies followed by patch clamp measurements (16,23). Based on the experimental constraints and known structural features of membrane proteins, structural models for the gating transition of Tb-MscL and E. coli-MscL upon equibiaxial tension have been established (23). These models include 13 conformational states ranging from the fully closed state (when the effective pore radius a is ∼6.5 Å) to an opened conformation (when maximal conductance can be measured experimentally) with a = 19 Å. Although highly valuable, these structural models need to be evaluated for validity in a systematic and physical manner. For example, in the initial set of structural models (23), the S3 helices are intimately involved in the gating transition and eventually submerged into the membrane in the fully open state. In a revised model by the same authors (16), the cytoplasmic S3 helices are essentially static and remain closed during the gating transition, since the cytoplasmic helices are assembled as a stable bundle and the removal of S3 helices does not prevent opening (24,25). Which behavior is closer to reality can be studied using advanced simulation techniques.

There have also been theoretical efforts postulating the principles behind the gating transition of MscL. By considering possible deformation mechanisms (e.g., membrane tension and torque), a thermodynamics formulation was presented (26). Turner and Sens (27) proposed a gating-by-tilting model based on thermodynamics as an alternative mechanism to the dilatational gating. In a pioneering lipid-centric analytical work, Wiggins and Phillips (28) calculated the free-energy of the lipid bilayer deformation and found that it was on the same order as the energy barrier required for channel gating, thus confirming the critical role of lipid mechanics. Besides including the hydrophobic mismatch and tension, this model was further improved by incorporating other triggers, such as the membrane curvature change and midplane deformation and interactions between interfaces, in the transition from closed to opened states (20). The model was further expanded by Ursell et al. (29) to study cooperativity gating. Although these models provide useful insight into the common features of MS channels, their validity for a specific system is difficult to evaluate because these models do not contain sufficient structural details; for example, in Wiggins and Phillips (28) and Ursell et al. (29), the proteins were treated as simple objects with cylindrical symmetry, therefore the deformation energies of the protein were not considered. Moreover, key parameters in these models are usually not obtained from detailed simulations or experiments.

Current status of numerical simulation of MscL and their limitations

An effective numerical approach is a powerful alternative for exploring the fundamental principles of mechanobiology. Compared with lab experiments, the numerical experiments are easier to “control” where the biomolecules and their subunits may be manipulated in a precise way. Although all-atom MD simulations (e.g., Fig. 4 a) are generic and versatile (30), they are limited to phenomena at short timescales (<100 ns) and length scales (<100 nm), and are computationally intensive if the entire protein plus the surrounding solvent and lipid membrane are considered. All-atom MD simulations have been applied to study the gating of Tb-MscL (31). Not surprisingly, during a 3 ns simulation, the lipid membrane maintained a constant volume well before the conformation of MscL could be affected, and the increment of the pore radius was merely 4 Å. Even in the presence of an external steering force, which was estimated based on an analysis of the lateral and normal pressure profiles exerted by the deformed bilayer to the protein (32), the channel opened to a pore radius of only 9.4 Å after 12 ns of simulation, which is far from a fully opened pore and highlights the limit of atomistic MD simulations in the context of probing the channel-gating process. Moreover, due to the limit of pressure profiles accessible to all-atom simulations, the steered MD approach is restricted to the simplest loading mode of equibiaxial tension and a fairly high computational cost.

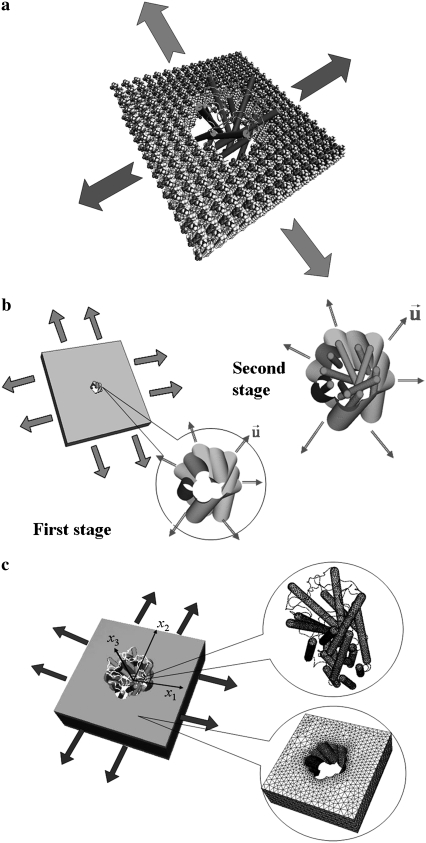
FIGURE 4.

Assembled protein/lipid system. (a) The “cartoon” representation of E. coli-MscL and all-atom representation of the lipid. (b) The preliminary “minimalist” model for Tb-MscL (36) where the simulation is divided into two stages. (c) The refined MDeFEM approach and continuum model for E. coli-MscL where concurrent coupling is realized between lipid and protein.

As an alternative approach to artificially accelerate the speed of the conformational transition, targeted MD was used (33). The lipid bilayer membrane was completely ignored and a holonomic constraint was used to drive MscL from the closed to the open state. Despite the guarantee of reaching the final target, the constraining force on the protein atoms can be extremely large compared to the realistic gating force exerted by the deformed membrane (34). This makes targeted MD simulations useful as a qualitative structural biology tool but inappropriate for the purpose of analyzing the membrane-mediated gating mechanism (33). Very recently, a coarse-grained model (35) was developed based on a thermodynamics parameterization, and the gating of MscL was simulated. However, the computational cost of such a particle-based model is still rather high and the model is difficult to be used for studying deformations involving large length scales, such as membrane bending/twisting that occur during cell-cell interactions. Moreover, further validation of the coarse-grained force field is still needed.

The limitations of those atomistic simulations motivated us to develop a continuum mechanics-based simulation model for MscL gating (36), which was essentially a phenomenological framework that incorporates certain key features from atomistic simulations. In the preliminary “minimalist” model, only the transmembrane helices of MscL were included since they are in direct “contact” with the membrane and therefore expected to be most crucial for gating (17); the cytoplasmic helices and the loops that connect helices were ignored. Since this preliminary “minimalist” model was only meant to illustrate the concept of a continuum mechanics-based framework, the helices were modeled by a cluster of homogeneous and isotropic elastic rods resembling the geometry of TM1/TM2 helices (Fig. 1, c and d, for the example of Tb-MscL). The effective Young's modulus of the helices was taken to be 100 GPa, which is the average value for several α-helices computed with atomistic MD simulations (37). The lipid membrane was modeled as a homogeneous and isotropic elastic sheet, for which the modulus was taken to be 100 MPa and thickness was taken to be 35 Å based on typical values in the literature (38,39). The transmembrane helix cluster is assembled in a cavity in the lipid with the equilibrium distance determined by the nonbonded interactions (Fig. 4 b for Tb-MscL). The nonbonded interactions among the protein helices (rods) as well as those between helices and the lipid were fitted based on atomistic simulations using a molecular mechanics force field.

The integrated system was discretized and its structural response to an external mechanical load was solved using the quasi-static FEM (Fig. 4 b). Under the assumption that the protein conformational transition is dominated by the membrane deformation (i.e., “one-way” coupling, which is consistent with that in steered MD (32)), the preliminary simulation was separated into two stages. During the first stage, the protein was not included, and an external load was applied on the outer boundary of the lipid. The nodal displacements of the cavity surface were recorded after each time step and transferred to the second stage as boundary conditions, where only the protein deformation was followed explicitly; through the nonbonded interactions between the lipid and the helix bundles, the MscL was gradually pulled open.

Despite the simplicity of this preliminary “minimalist” model, realistic gating behaviors were found during the subsequent quasi-static FEM simulations. The model channel opened up in an iris fashion, as proposed experimentally, upon equibiaxial tension in the membrane, and the intermediate structures along the gating pathway were qualitatively very similar to the structural models (23). The tension required to open the channel pore to reach the expected size was also quite similar to the experimental value. These results are significant, because the model was developed largely based on features of the closed x-ray structure. Moreover, it was found that pure bending of the membrane did not significantly open the channel, which not only emphasized the importance of specific mechanical perturbation in MscL gating but also nicely illustrated the unique power of the continuum-based simulation framework.

Although the proof-of-concept model (36) effectively captures the major physical properties and revealed some fundamental gating characteristics of MscL, a number of critical limitations need to be alleviated for more quantitative studies:

1. Only the transmembrane helices (TM1 and TM2) were included in the model; the S1 helices and the loops that connect TM1 and TM2 were ignored, although it is known that they contribute to the quantitative gating behavior of MscL (21,40,41); in addition, the major kink in the TM1 of the E. coli-MscL due to Pro43 was not accounted for.

2. Although the effect of curvature was incorporated, the lipid membrane was assumed to be isotropic and homogeneous, which ignored the distinct chemical nature of the headgroups and tail regions that are likely essential for gating (2,18,20,26).

3. The deformation of lipid and protein were decoupled in the two-stage approach, which is a reasonable approximation only if the strain energy of protein is much smaller than that of the membrane. As the membrane protein undergoes conformational changes, it tends to perturb the surrounding bilayer and the energy associated with such perturbation must be taken into account (19).

4. The preliminary numerical study in Tang et al. (36) only focused on membrane tension and bending, and it is important to explore the effects of other basic deformation modes of the membrane (Fig. 3) as well as other perturbations in the membrane such as that due to structural changes in nearby MS channels or suction pressure in patch-clamp experiments.

5. The mechanical properties of helices and lipid were obtained from averaged values in literature (on similar systems), which may not be sufficiently accurate and transferable. The protein was modeled as homogeneous and isotropic, and it may be useful to distinguish hydrophilic from hydrophobic groups and to include solvation contribution to the system free energy.

Organization of the article

We carry out a comprehensive and systematic numerical analysis on the detailed gating mechanisms of MscL under different forms of mechanical perturbations in the surrounding membrane. Based on insights from such numerical simulations (e.g., the more important factors governing the mechanochemical behaviors of biomolecules), simplified analytical models are developed so that qualitative insights can be gained toward the effect of different membrane deformations on membrane proteins in general. The article alleviates most limitations in our previous proof-of-concept study (36), except for the effects of heterogeneity in the protein materials properties and solvation, which require further developments and are left for future work. We focus on the conformation transitions of the MscL, and the surrounding lipid bilayer is simplified as a solid material in the current framework, which is an important approximation (see below and Part II for detailed discussions) that also requires revision in future studies.

In Part I, we describe the basic formulation of the continuum mechanics-based model, how it is connected to atomistic calculations, and the simulation framework that allows one to study the gating transition under external perturbation. Going beyond the proof-of-concept study (36) where only the transmembrane helices were taken into account, the full MDeFEM model also includes the cytoplasmic helices and loops so as to explore their contributions to the gating transition. In addition, a more sophisticated three-layer model is established for the lipid bilayer in which the lipid headgroup and tail regions are treated separately with different materials properties. Moreover, concurrent coupling between structural components are realized in the simulation instead of the two-stage protocol used in Tang et al. (36), so that lipid-protein interactions are treated in a more realistic manner. To help better define the limiting values and key components for the various mechanical perturbations that might induce the gating transition of MscL, an analytical effective coaxial continuum medium model and a linear response model are established; such a predictive, closed-form theoretical approach complements the numerical simulations.

In Part II, we analyze the detailed conformational transitions of E. coli-MscL under various basic deformation modes (see Fig. 3) and probe the contributions of various structural motifs to the gating characteristics. As illustrations of the unique value of the continuum mechanics framework, cooperativity among MscL channels as a function of their separation as well as the gating behaviors of MscL when the surrounding membrane is subjected to patch clamp and nanoindentation are also simulated; these phenomena are very difficult to study with current atomistic simulations. The results of these simulations are compared with previous all-atom simulations and experiments, wherever appropriate; in addition, the MDeFEM results are useful for evaluating the validity of the simplified analytical models, which are also developed in Part I.

ELEMENTS OF THE MDEFEM FRAMEWORK

As an illustrative example, we discuss in detail the construction and parameterization of a refined continuum mechanics model for E. coli-MscL as well as the finite element simulation protocol that probes the conformational response of the channel to external perturbation. We emphasize that the parameterization can, in principle, be very sophisticated, using state-of-the-art atomistic simulations. In this study, however, we limit ourselves to order-of-magnitude type of estimates based on potential energy scans and normal mode analysis. Keeping the parameterization simple helps highlight the fundamental physical principles that govern the gating process. Once the qualitative relative importance of different factors is understood, more sophisticated simulations can be used to establish more quantitative models.

Structural components

Protein components: helices and loops

To explore the effects of protein structural motifs, especially the S1 helices and the loops connecting TM1 and TM2 helices that may play an important role during gating (16,21,40,41), the preliminary continuum model of protein (36) is significantly expanded to become a complete model. The cytoplasmic helices are also taken into account as three-dimensional elastic cylinders and the loops as quasi-one dimensional springs (Fig. 2, c and d). Same as the previous model, the geometries of all continuum components are measured from the closed state structure (23); note that there is a small difference between the length of the S3 helix in the homology models in refs Sukharev et al. (23) and Sukharev and Anishkin (16); nevertheless as shown in Part II, the S3 helices play a minor role during the process of gating and thus such a difference is expected to be unimportant.

Each helix (TM1/TM2 helices or S1/S2/S3 helices) is modeled as an elastic cylinder with a diameter of 5 Å, a typical value for the dimension of the main chain of an α-helix (36). Spherical caps are imposed on both ends of the helices for numerical convergence purposes (36). The helix is taken to be homogeneous and isotropic, thus assuming that the mechanical properties of a helix vary little with respect to sequence and the elastic properties remain constant during the gating transition. (We note that in general, the properties of α-helices are inhomogeneous and environment-dependent. In this article, we take the simple approximation by neglecting these differences, and the materials properties of helices and other continuum elements should be considered as typical values. Further refinement of the MDeFEM model will be pursued in future studies as discussed in Part II.). The only exception is for the break between S2 and TM1 helices (Pro43, illustrated by the dark segment in Fig. 2, b and d), whose property is determined separately and is less stiff than the rest of the helix.

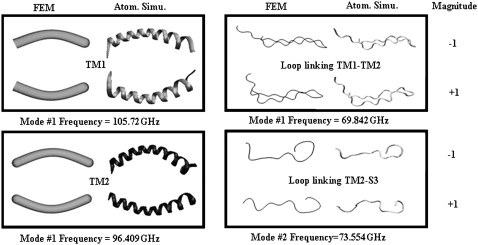
Instead of obtaining the properties from literature, the materials properties of the helices are calibrated by matching results of normal mode analysis (NMA) at the atomistic and continuum levels. The atomistic NMA is carried out using the CHARMM19 force field (42,43), which is more appropriate here because the calculations are done in the vacuum; the effect of solvation is approximated by adopting a distance-dependent dielectric constant in the electrostatic calculations, and no solvent damping effect is considered so as to be consistent with the continuum calculations. The Young's modulus is then varied such that the eigenvalues and eigenvectors for the three lowest-frequency modes computed at the continuum level best fit the results from the atomistic normal mode calculation. For example, the lowest eigenmode of a transmembrane helix is essentially flexural bending, whose continuum and atomistic configurations are shown in Fig. 5. For TM1 and TM2 helices, the lowest frequencies are 105.7 and 96.4 GHz, respectively, which lead to the fitting of their effective Young's moduli as 80 GPa and 117 GPa, respectively.

FIGURE 5.

Examples of several lowest eigenmodes and frequencies of helices and loops: comparisons between molecular mechanics and finite element simulations. Here the TM1 helix only corresponds to the segment below Pro43.

The loops (gray strings in Fig. 2) between the helical pairs TM1 and TM2, TM1 and S1, and TM2 and S3, are also incorporated in the continuum model to test hypotheses regarding their roles during the gating transition (23). For simplicity, the loops are modeled as elastic springs with key geometrical parameters directly measured from the homology model for the closed state (16). Their mechanical properties are also assumed to be homogeneous and obtained by the similar normal mode fitting at the atomistic and continuum levels as discussed for the helices. Selected examples are also given in Fig. 5.

The key geometrical and mechanical properties for the helices and loops are summarized in Table 1. The Young's moduli of helices fitted in this article are within the range for the α-helices (60–180 GPa) computed from atomistic MD simulations (37); the spring constants for the loops are rather stiff and also consistent with previous studies (31,32), supporting their possible importance during gating (see the discussions in Part II).

TABLE 1.

Geometry and fitted phenomenological material properties of the continuum components (helices, loops, membrane) used in the MDeFEM simulation

	Helices						Loops			Lipid membrane
Properties (E. coli-MscL)	TM1	TM2	Pro43	S1	S2	S3	TM1-TM2	TM1-S1	TM2-S3	Headgroups	Tails
Length (Å)	40.75	45.61	5.36	14.83	9.51	21.52	103	17.0	35.0	Large	Large
Thickness or diameter (Å)	5.0	5.0	5.0	5.0	5.0	5.0	—	—	—	5.0	25.0
Young's modulus E (GPa)	80	117	15	40	80	30	—	—	—	0.124	0.064
or spring constant Sl (N/m)							1.42	8.40	4.10
Poisson's ratio ν	0.3	0.3	0.3	0.3	0.3	0.3	—	—	—	0.50	0.50

Lipid membrane

In our previous study (36), the lipid membrane was modeled as a homogenous isotropic sheet (see Fig. 4 b). In the current study, a more sophisticated (refined) model that reflects the different materials properties for the lipid head and lipid tail regions is established, considering the importance of the membrane in transducing the mechanical stress to the channel (2,20,21). Specifically, a three-layer model is developed in which the lipid headgroup and tail regions are treated separately with different properties (Fig. 4 c for E. coli-MscL). This is motivated by the natural difference between the chemical and physical properties in these regions; e.g., it has been well established that the lateral pressure profile of lipid bilayers has distinct peaks at the interface (neck) between the head and tail regions (44), and that modifying the pressure profile can lead to different gating characteristics for the MS channels (2,18,20,26).

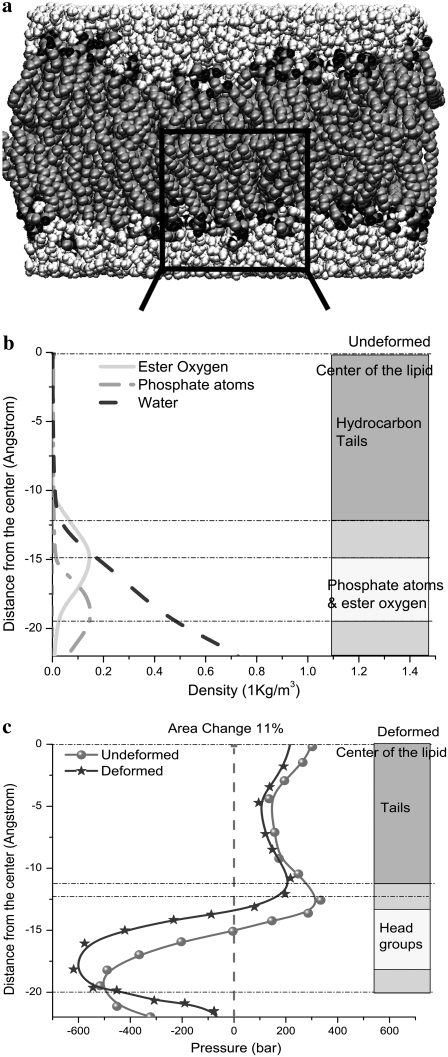
In the three-layer phenomenological continuum model for the lipid bilayer (Fig. 6 a), the effective elastic properties and effective thicknesses of headgroup layer and tail layer are derived from a previous MD simulation (44), where the density map of water and lipids (Fig. 6 b) and the lipid pressure profile (Fig. 6 c) elucidate the typical palmitoyloleoylphosphatidylethanolamine (POPE) lipid bilayer structure. In Fig. 6 c, one curve is the pressure profile of the undeformed lipid, whereas the other curve is the calculated pressure profiles of the deformed lipid with an area expansion of 10.8%, which corresponds to an equibiaxial strain of 5.4%; in addition, the overall thickness reduction of the membrane is 3.8 Å.

FIGURE 6.

POPE lipid membrane (44): (a) the atomistic structure, (b) the density map of a monolayer, and (c) the lateral pressure profiles of a monolayer for undeformed and deformed lipid.

With reference to Fig. 6 c, the small positive pressure peak corresponds to the interface between headgroup and tails; inside the hydrocarbon tail region, the water density is zero (Fig. 6 b) from which the thickness of the undeformed tail layer (t_tail) is ∼25 Å. The difference between the locations of the positive pressure peaks of the undeformed and deformed curves in Fig. 6 c indicates half of the thickness reduction of the tail layer after deformation, Denote the effective Young's modulus and Poisson's ratio of the hydrocarbon tail layer as E_tail and 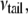respectively. Upon equibiaxial tensile stress σ, 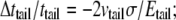the area expansion is 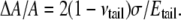Finally, v_tail = 0.5.

Half of the surface tension in the hydrocarbon tail can be estimated by integrating the pressure profiles in Fig. 6 c (from the center of the lipid to the small positive pressure peak). Between the undeformed and deformed configurations, the difference of their surface tension is 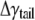= 17.4 dyne/cm. Thus, the effective area expansion modulus of the tail layer is 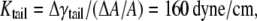and from Tang et al. (36),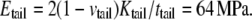

The properties of the headgroup layer can be derived through the same procedure. From the density map in Fig. 6 b, the region containing phosphate atoms and ester oxygen atoms is identified as the effective headgroup layer (which should also carry the majority of membrane load), with an undeformed thickness of t_head = 5 Å (on either side of the tail layer). Thus, the total membrane thickness is, 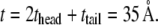For each headgroup layer, the thickness reduction after area expansion is 0.55 Å. Similar to the derivation for the tail layer, the effective Poisson's ratio of the headgroup layer is then v_head = 0.5, same as the tail layer. For the headgroups, the surface tension difference upon deformation is 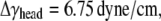the area expansion modulus 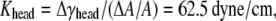and the effective Young's modulus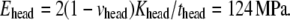

The effective mechanical properties and thickness of the continuum lipid layers are listed in Table 1. Note that the real lipid structure has a nonsmooth “surface” (Fig. 6 a), and thus the effective properties derived herein only serve to illustrate some of the most essential features from the continuum trilayer model. It is known that the lipid boundary adjusts for the channel (29) and the lipid property is different near the MscL; incorporating such features (e.g., inhomogeneity, local curvature, residual stress) will be carried out in future studies. It is expected that some of these features (e.g., local curvature) can help to reduce the membrane strain needed for full gating and thus are important for gating mechanisms.

In the middle of the membrane, a cavity with a 10-petal flower shape is created to host the MscL (the assembled MDeFEM system for E. coli-MscL-lipid bilayer is shown in Fig. 4 c, which is similar to the atomic structure in Fig. 4 a); the initial shape and size of the cavity surface conform to those of MscL transmembrane helices in the closed state with a distance of 5.5 Å (32). The nonbonded interactions between lipid and helices are discussed in the next subsection. In the absence of external forces, the system maintains equilibrium.

Interactions between continuum components

With a continuum-mechanics based representation, the interactions among atoms within each continuum component are not computed explicitly because the corresponding energy is implicitly represented via the phenomenological mechanical properties described in the last subsection; this is one reason that the computational cost associated with the continuum framework is substantially lower than all-atom simulations. The interactions among continuum components are calculated using pairwise terms following the standard cutoff schemes commonly used in atomistic simulations. Specifically, the nonbonded interactions between helices and those between helix and lipid are represented by a pairwise effective potential of the Lennard-Jones form (36),

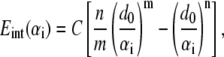(1)

where 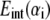is the nonbonded interaction energy (per area) between a pair of surface elements on two continuum components, which include contributions from both electrostatic forces and van der Waals interactions; computing the total interaction energy between two continuum components requires summing over all nearest pairs of surface elements between the two components. For any given pair of interaction, d₀ is the (shortest) initial equilibrium distance between the two surfaces, and α_i is the surface distance between two deformed surfaces (for the ith element). Both m and n are positive integers and account for repulsive and attractive terms, respectively, with 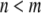in general. The value of d₀ depends on the different types of continuum components involved. For example, among the 10 interaction pairs between TM1 helices, d₀ is uniquely determined as the shortest distance between TM1 helices measured in the closed-state structure of E. coli-MscL. For other types of pairwise combinations, e.g., lipid-TM1, TM1-TM2, d₀ takes on different values (see Table 2).

TABLE 2.

Fitted parameters for the nonbonded interactions between helices and between helix and lipid for E. coli-MscL used in MDeFEM simulations

Interaction pair	Lipid -TM1	Lipid -TM2	Lipid -S1	TM1 -TM1	TM1 -TM2	S1 -TM1	S1 -TM2	S1 -S1	S3 -S3
d0 (Å)	5.5	5.5	7.0	1.5	5.0	4.0	5.5	4.0	7.0
ψ (GPa)	3.2	3.2	0.05	5.5	3.4	3.0	0.8	9.0	6.0
m	9	7	2	2	9	8	10	9	11
n	3	3	1	1	3	3	3	4	6

The parameters including the “well-depth”, C, and the exponents (n, m), are calculated based on fitting to energy calculations using an atomistic force field; more elaborate free energy (or potential of mean force) simulations are left for future studies, as emphasized in the beginning of this section. For each pair of helices, the interaction energy in the vacuum is calculated using the polar-hydrogen set of the CHARMM19 force field. Calculations are done for different combinations of helical pairs, which effectively sample many relative orientations; those between TM2-TM2 and between S3 and other helices have not been considered, since these structural components are very far apart. To estimate the helix-lipid interactions, the insertion energy profiles are computed when a single helix (TM1 or TM2) is gradually transferred in and out of an implicit membrane with varying orientations; an implicit dielectric model that includes both electrostatic and hydrophobic interactions (45) is used for the membrane to avoid the need of sampling a large set of lipid configurations. The fitted parameters are summarized in Table 2, where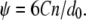

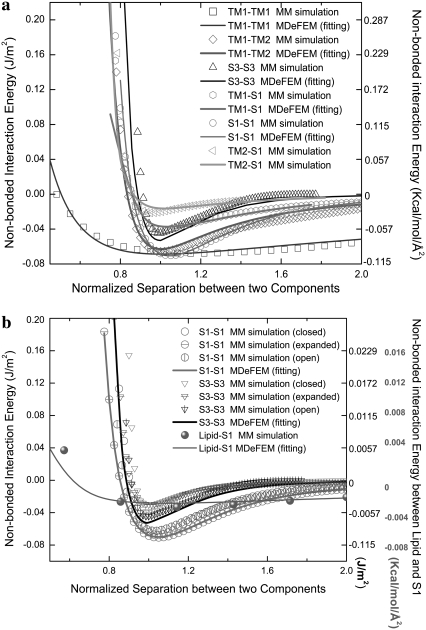
To illustrate the fitting procedure, Fig. 7 a shows the total nonbonded interaction energies of the primary helical interactions for E. coli-MscL as functions of the normalized distance between the helix-helix center of mass, where the initial configurations of the helices are taken from the closed structure. By inspecting results for different angles between the helical pairs, it seems that the fitted parameters (C, m, n) are fairly transferable to the close, intermediate, and open states; results are given in Fig. 7 b. (These parameters are meant to be order-of-magnitude estimates, and the relative importance of different parameters can be evaluated by systematically repeating the simulations with specific parameters modified (e.g., see the section “Comparison of continuum models of different sophistication” of Part II). Such studies suggest that, as expected, the most important parameter is the strength of protein-lipid interaction. For example, with a 50% reduction of the corresponding C value, gating of E. coli-MscL becomes more difficult. This implies that a quantitative parameterization of protein-lipid interactions should be an essential aspect for the refinement of the model in the future.)

FIGURE 7.

Example of fitting of the total nonbonded interaction energy (per area) between continuum components of E. coli-MscL. The x axis is the normalized separation between the center-of-masses (with 1.0 being the equilibrium spacing). (a) Comparison between FEM and molecular mechanics calculations for helical pairs in the closed structural model. (b) The fitted set of parameters is fairly transferable to other structural states (expanded/intermediate and opened). In b, the scale for the interaction between lipid and S1 helices is given on the right of the figure, whereas the scale for interaction between helices is given on the left.

Taking the first derivative of 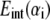with respect to α_i, the pressure-distance relationship between two surface elements is (by convention, the repulsive pressure is positive),

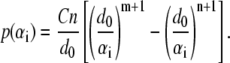(2)

Such stress, which is fully coupled with the deformation within each continuum component and the relative movement between the components, “integrates” the system such that upon external load, conformational transition of various structural motifs can be triggered together.

Estimation of load

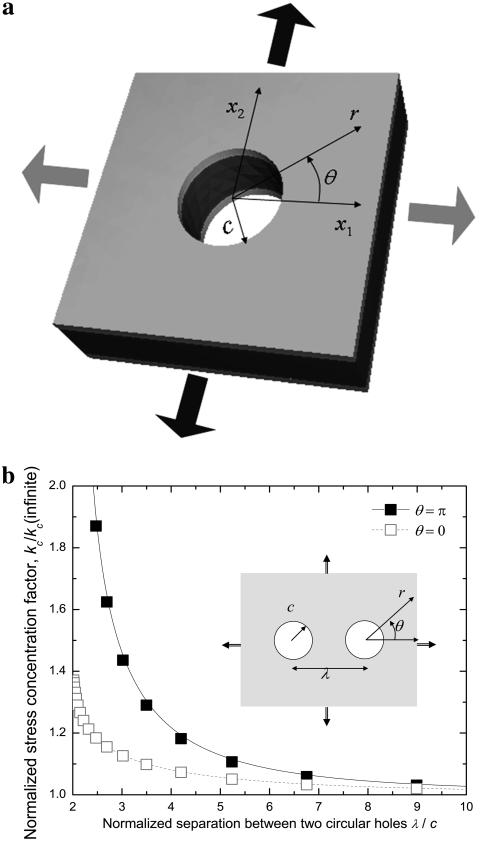
Previous experimental (2,17), theoretical (28), and numerical (32) studies have speculated the importance of lipid membrane deformation, which will be validated by the MDeFEM approach in this study (see Part II for details). In this subsection, we use a simple linear elastic membrane model to estimate the load needed to achieve gating of MscL. The lipid-protein interaction is neglected (i.e., MscL is absent), and the lipid cavity is simplified as a circular hole of radius c (∼22 Å for the averaged radius of the lipid hole of E. coli-MscL in the closed state (Fig. 4 a). The expansion of the lipid hole radius (which is correlated with the effective MscL radius) is explored when a three-layer lipid membrane of outer radius l (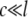) is subjected to several basic types of deformation, sketched in Fig. 8 a for nonequibiaxial in-plane tension.

FIGURE 8.

(a) Schematic of a continuum three-layer sandwich lipid membrane containing a circular hole. (b) The normalized stress concentration factor as a function of the normalized separation between two circular cavities (46,58,59) for a plane stress problem.

In-plane tension

For a three-layer “sandwich composite material” upon displacement-controlled loading, the in-plane strain components (with normal strains 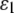and and 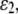shear strain 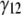) are related with the averaged stress components across the thickness (normal stresses 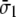and an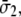d shear stress 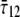), through the equivalent elastic constants of the whole lipid membrane, 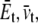and 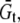and the constitutive relationships are

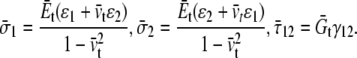(3)

The averaged stress conforms to the rule of mixture, e.g., 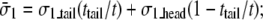by compatibility of in-plane deformation of the headgroup and tail layers:

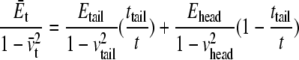(4)

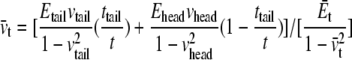(5)

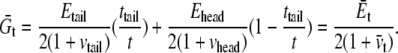(6)

When a membrane contains a hole of radius c, and under nonequibiaxial tension (Fig. 8 a), the radial displacement field is

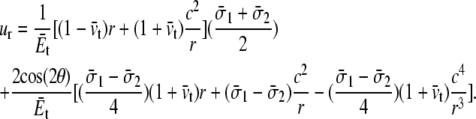(7)

Thus, the increment of lipid cavity radius is

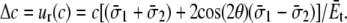(8)

Under equibiaxial tension,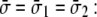

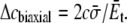(9)

For the POPE lipid bilayer with properties listed in Table 1, 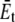and 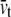are 81 MPa and 0.50, respectively. For E. coli-MscL, c = 22 Å. To enlarge the cavity radius by 17 Å for full gating (where channel radius a is increased by 12.5 Å), the required equibiaxial tension stress is estimated to be ∼31 MPa. Note that this is a rough estimation and in the nonlinear MDeFEM simulation (Part II), the actual load is adjusted until the desired MscL pore opening is reached.

Osmotic pressure

In the cellular context or liposome based measurements, one of the sources of in-plane tension in lipid membrane comes from osmotic pressure. Denote 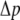as the net variation of osmotic pressure acting on the cell membrane, and the cell/liposome radius is R, with 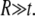Since the radius (typically microns) is much larger than that of a protein (such as MscL), the curvature effect can be neglected and the averaged in-plane tensile stress is 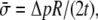and the lipid cavity radius increment is

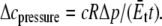(10)

For a typical liposome diameter of 5 μm, the estimated pressure for gating is 0.88 bar.

Axisymmetric pure bending

For a homogeneous layer, the relationship between the bending moment and inclination angle of axisymmetric pure bending was given in Tang et al. (36). For the three-layer lipid model, deformation compatibility requires the curvatures 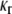and 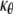in the cylindrical coordinates to be the same for headgroup and tail layers. The line moment applied on the cross section, M_r and M_θ, are related to the curvatures through the equivalent elastic constants

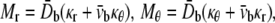(11)

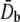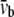where and are the equivalent bending stiffness and Poisson's ratio of the composite upon axisymmetric bending, which satisfy

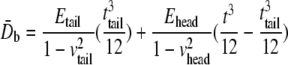(12)

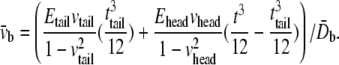(13)

When a large sandwich membrane contains a hole of radius c, and subjected to axisymmetric bending with radial line moment M_o, the gradient of deflection is

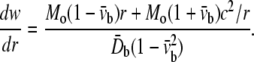(14)

The lipid cavity wall, which is normal to lipid surface before deformation, becomes inclined after bending, and the inclination angle is

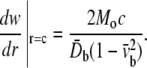(15)

For the POPE bilayer parameters in Table 1, the equivalent elastic constants for bending are 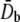= 487 pN·nm and 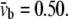According to the structural model (23), the averaged tilting angle of the TM1 helices in the closed state is ∼10° (with respect to the normal of lipid). Therefore, a distributed moment M_o ∼ 14.6 pN is expected to make the TM1 helices upright.

Protein interaction

The interaction between neighboring proteins dictates the cooperativity, which is of considerable interest in mechanotransduction. We consider the most fundamental case of interaction between two identical MscLs, when the lipid is subjected to an equibiaxial load. For a membrane containing two circular holes of radius c (with center-to-center distance λ), the stress concentration factor on the boundary of one of the circular holes is (46)

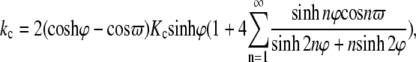(16)

where

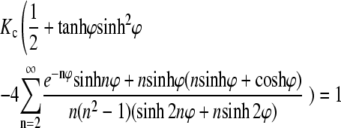(17)

with 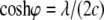and 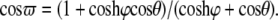Here, θ is measured as that shown in Fig. 8 b. The resulting k_c is plotted in Fig. 8 b, and it is normalized by 2 (the stress concentration factor when 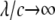). It follows that when 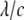is <∼4, the interaction between the two proteins becomes obvious under equibiaxial tension. These theoretical estimations will be examined in Part II of this study.

Simulation protocol and finite element analysis

In contrast to the two-stage simulation used in the preliminary study (36) (Fig. 4 b), in this study, both the lipid bilayer and the full protein model are coupled concurrently and simulated explicitly. While the lipid bilayer is deformed by applying external load, the lipid cavity is deformed and thus forces are transferred to the protein. Such force could also influence the local strain field of the lipid surrounding the channel. The configurations of lipid bilayer and protein are updated after every time step, via such “two-way” coupling (Fig. 4 c). The results of the concurrent simulation will be compared with those from the “one-way” (two-stage) approach used in our preliminary study (36), so as to reveal the quantitative influence of coupling.

Four-node tetrahedron elements are used to mesh the helices and lipid. The longest helix, TM1, contains ∼1800 nodes and ∼7000 elements, with all nodes roughly equal spaced. The lipid incorporates ∼23,000 nodes and 118,000 elements. The mesh of lipid is more refined toward the inner cavity where it interacts with the protein extensively. Two-node spring elements are used mesh the loops. The longest loop, connecting TM1 and TM2 helices, contains more than 100 nodes. An example of the mesh is given in the insets of Fig. 4 c for E. coli-MscL, where for the lipid, only the mesh near the cavity is shown. Finite element simulations are carried out using ABAQUS (47) with finite deformation. The nonbonded interactions (“Estimation of load” subsection) are implemented by a user interaction subroutine (UINTER) (36). The typical computational time for an equibiaxial gating simulation of E. coli-MscL is ∼7 h on a Dell work station with 3.2 GHz Intel Xeon CPU and 2 Gb RAM. The results of the MDeFEM simulations, which provide insights into various mechanistic issues, are presented in Part II.

ANALYTICAL MODELS

Although the MDeFEM framework can significantly reduce the computational cost compared to all-atom simulations, it still involves a large number of degrees of freedoms. Therefore, another important goal of this work is to explore the possibility of establishing closed-form and simple analytical models, as an alternative approach that can capture the most essential features of MscL gating, such as the evolution of the channel pore under different magnitudes of equibiaxial tension that might be broadly applicable to MS channels.

As discussed above, patch clamp experiments (17) on lipid vesicles showed that as the main carrier of force in a liposome, the lipid membrane is critical during the gating of MscL. Once stressed, the load is transferred to the protein (mostly through the transmembrane helices since they are in close “contact” with the lipid) and triggers major conformational changes in the channel (see Part II for detailed analyses). For a typical load applied on the membrane, the averaged deformation of the lipid cavity that holds the channel is derived in the “Estimation of load” subsection, which serves as the displacement boundary condition for the protein. The next key issue is to establish an effective analytical model for MscL, such that its conformational transition can be estimated upon a specified boundary condition. In the next two subsections, we develop continuum and “discrete” versions of such analytical models, respectively. The effectiveness of such models will be explored by comparing to results from MDeFEM simulations in Part II.

A linear effective continuum medium model

During gating, the deformation of the membrane cavity is mainly transferred to the closest TM2 helices via nonbonded interactions in the radial direction. The nonlinear interaction pressure-distance relationship (Eq. 2) is analogous to a nonlinear elastic medium between the lipid cavity and the TM2 bundle. After the TM2 helices are pulled open, the TM1/TM2 nonbonded interactions (another effective nonlinear medium) may perturb the MS channel radius, which is enclosed by the five TM1 helices (36). Therefore, a simple analytical model can be established in which the details of protein structures are ignored and the nonbonded interactions are described by effective elastic media.

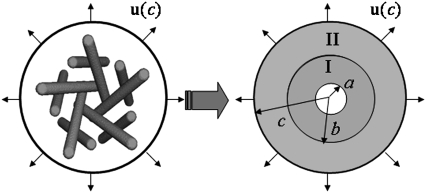
A schematic of such a plane stress effective continuum medium model (ECMM) is given in Fig. 9 with E. coli-MscL as an example. The inner effective annular medium I accounts for the TM1-TM1 interactions in the hoop direction and TM1-TM2 interactions in the radial direction, and the outer continuum medium II incorporates TM2-TM2 interactions in the hoop direction and TM2-lipid interactions in the radial direction. The inner radius, interface radius, and outer radius of the ECMM are denoted by a, b, and c, respectively. Here, a is the effective radius of the closed MscL (and consistent with the previous definition in the subsection “The mechanosensitive channel of large conductance”), which corresponds to the smallest “through” capacity of the TM1 bundle, and b is defined similarly for the TM2 bundle; c is the averaged radius of the lipid cavity surface (refer to the subsection “Comparison of continuum models of different sophistication”). From the closed homology structure of E. coli-MscL, a, b, c equals 6.5 Å, 17 Å, and 22 Å, respectively.

FIGURE 9.

Schematic of the linear effective continuum medium model (ECMM).

A boundary condition is applied on the ECMM, which is in general a function of angle θ, where the radial and hoop displacement components 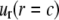and 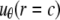can be obtained from in the subsection “In-plan tension”. The goal is to first determine the effective elastic moduli (in radial and hoop directions) of the annular media, and then estimate the radial displacement (MS channel radius evolution) at r = a using linear elasticity.

Elastic constants in the hoop direction

The plane-stress constitutive relationship of an orthotropic elastic material is

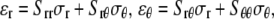(18)

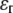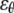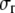where and and and 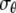are the strain and stress components in radial and hoop directions, respectively. S_rr, S_rθ, and S_θθ are the in-plane elastic (compliance) constants. Since the normal nonbonded interactions are more prominent than the lateral components, S_rθ is assumed to be zero in ECMM (which is also consistent with the current MDeFEM approach). The effective elastic constants, 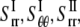and 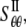for materials I and II, are estimated by letting the strain energy of the effective media to be equal to the potential energy change in molecular mechanics under the same deformation.

Among the elastic constants, 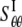is determined by the TM1-TM1 interaction. When the radial and hoop properties are decoupled and the TM2 bundle is removed, the potential energy difference of the TM1 helix bundle between the closed and the opened states can be obtained from molecular mechanics calculations as Consider the deformation of medium I only if a uniform radial displacement 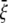is required to expand annulus I from the closed to opened structure (for E. coli-MscL, 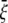= 13.1 Å, which is the averaged variation of the inner radius and interface radius), the hoop strain is 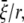and the strain energy is

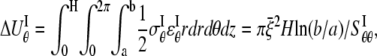(19)

where H is the height of the ECMM that equals to the membrane thickness (35 Å for the POPE bilayer). By letting the strain energy of ECMM to be equal to the potential energy change from molecular mechanics calculations, 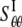can be estimated by

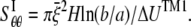(20)

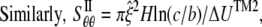(21)

where 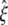is radial expansion of annulus II between the closed and opened states (15.4 Å for E. coli-MscL), and 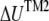is the relevant potential energy change of the TM2 helix bundle determined from molecular mechanics calculations.

Elastic constants in the radial direction

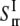is governed by the TM1-TM2 interaction. From molecular mechanics calculations, the nonbonded interaction energies between a pair of the nearest TM1 and TM2 helices are readily obtained in closed and opened structures (see Fig. 7). By summing up the contributions from the nearest neighbor interactions and ignoring those from further neighbors, the potential energy change in radial direction deformation, 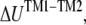can be estimated.

In ECMM, let 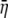to be the radial displacement difference at r = a and r = b, the radial strain can then be approximated as 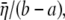with strain energy

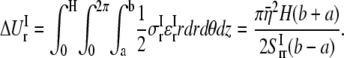(22)

By letting this term to be equal to 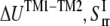can be estimated by

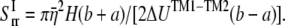(23)

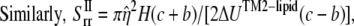(24)

where 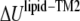is the nonbonded interaction energy between TM2 helix bundle and the lipid cavity surface, and 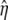is the radial displacement difference at r = b and r = c.

General axisymmetric solution

Upon equibiaxial tension (the most effective way of gating, as shown in Part II); the problem is axisymmetric. With 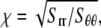the general solutions of the radial displacement component and stresses are

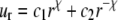(25)

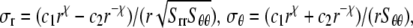(26)

where c₁ and c₂ are constants related with the boundary condition. In equibiaxial membrane tension, the resulting lipid cavity radial displacement 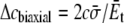is imposed at the outer boundary (r = c) (“In-plane tension” subsection); alternatively, from the variation of osmotic pressure, the boundary condition of ECMM can be 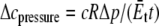(“Osmotic pressure” subsection). We use 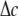to denote the lipid cavity radial expansion in this section. For material II, 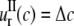and the inner surface (r = a) is traction free, 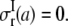Continuity of radial stress and displacement at the interface (r = b) requires 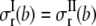and 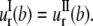By applying these boundary conditions, the MscL pore radius increment of ECMM is solved as

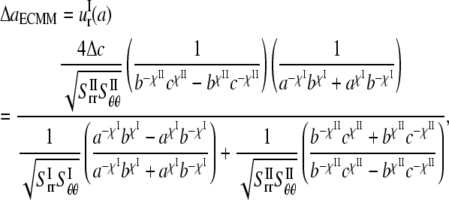(27)

which varies linearly with respect to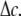

Closed-form solution for E. coli-MscL

In the first two subsections of this section, the energy difference between the closed and opened configurations of MscL is used to fit the elastic constants of the effective medium, which leads to 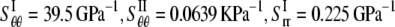and 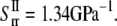From Eq. 27, 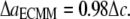Due to the nonlinear nature of nonbonded interactions, at a large deformation the fitted elastic stiffness should be smaller, i.e., the set of compliance constants should be regarded as the “upper-bound” of the ECMM.

One can also use the energy difference between the closed and a small deformation state of relevant helix bundles (based on the structural model (23)), which leads to the “lower-bound” of compliance constants 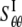= 0.221 GPa⁻¹ and 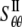= 15.2GPa⁻¹; the 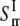and 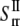are of similar magnitude as that of the upper bound. From Eq. 27, 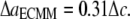Both bounds of the simple ECMM model are compared with the MDeFEM simulation results in Part II.

Although simple and explicit, the ECMM is subjected to severe limitations: 1), it can be applied to in-plane loading only, and 2), there is no detailed information regarding structural motifs. To overcome these disadvantages, we explore the elastic network model as described below.

Elastic network model

Basic formulation

Elastic network models (ENMs) have become popular in recent literature for exploring flexibilities of large macromolecules that undergo significant structural changes for function (48–50). In ENM, the atomic structure of a macromolecule is simplified to a network of elastic springs, where a harmonic spring is used to link any pair of atoms within a specified cutoff distance. Upon deformation, the displacement field of a complex system can be represented by the superposition of its lowest eigenmodes, which depend on the collective motion of atoms that can be effectively captured by the ENM. In its simplest form, the potential function of a macromolecule (V^M(x)) is written as that of a set of elastic springs (see Fig. 10 a):

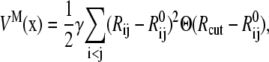(28)

where the sum goes over either all atoms in the system (all-atom ENM) or selected atoms (e.g., C_α atoms); 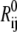is the equilibrium distance between atoms i and j, R_cut is a cutoff value that determines the number of elastic springs, and Θ is the Heaviside step function. The magnitude of the force constant, γ, is taken to be the same for all interactions, which is clearly a dramatic simplification but found to be a rather good approximation when only large-scale deformations are of interest. The optimal values of γ and R_cut, which are the only two parameters in the simplest ENM, can be determined based on matching the calculated atomic fluctuations via a normal mode analysis (NMA) using the ENM potential to either experimental data (e.g., the Debye-Waller factor in the x-ray crystal structure) or all-atom simulations based on a realistic force field (e.g., CHARMM (42,43)); see the next subsection for details. A number of variations have been proposed for ENM to make the interactions more heterogeneous and thus the elastic model for realistic. In this work, we take the slightly modified version in which the force constants for the covalently bonded interactions are taken to be substantially larger, i.e.,

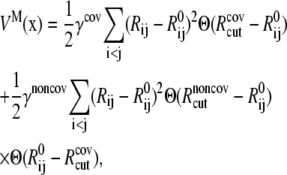(29)

where 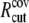and 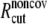are taken to be 1.7 and 5.0 Å in the current study, 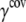taken to be 1000 kcal/(mol·Å²), and 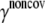is fitted against all-atom normal mode calculations (see next subsection). Previous studies (51) found that treating the covalent and noncovalent interactions separately gives a distribution of normal mode frequencies in ENM that better resembles that using more realistic potential functions (e.g., using an all-atom force field).

FIGURE 10.

ENM of E. coli-MscL: (a) Protocol 1, where only the protein is modeled. (b) Protocols 2 and 3, where the lipid is also taken into account.

Once the potential function of the system is given, we can explore the structural changes of the molecule induced by tension in the lipid membrane in several ways. In the simplest protocol (Protocol 1), we mimic the effect of membrane tension by attaching harmonic springs to a selected number of protein atoms (e.g., those exposed to the lipid atoms) and gradually pulling on the springs; i.e., the potential function of such a composite system is given as,

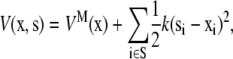(30)

where s_i indicates the end of the harmonic spring under tension, and k is the corresponding force constant. During the simulation, the values of s_i are changed gradually in a radially outward fashion (based on the estimated boundary condition derived in the “In-plane tension” subsection), which generates tension through the harmonic springs that pulls on the protein structure. The selection of the atoms to pull directly (i.e., set S) is not entirely straightforward and therefore several options have been tested (see Table 3 for three different selections).

TABLE 3.

Summary of calculations (protocols) using elastic network models

Notation	Model	Pulling set S*	Parameters†
ECO-1-1	United atom ENM	TM1 (16–40) & TM2 (77–106) backbone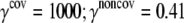
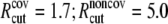			k = 0.41
ECO-1-2	United atom ENM	Backbone |z| < 20 Å	Same as ECO-1-1
ECO-1-3	United atom ENM	TM2 (77–106) backbone	Same as ECO-1-1
ECO-2-1	United atom ENM + elastic lipid	Outer membrane shell (2 Å); solving Eq. 31	Same as ECO-1-1, except
			k = 4.49;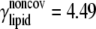
ECO-3-1	United atom ENM + elastic lipid	Outer membrane shell (2 Å); explicit minimization	Same as ECO-1-1, except k = 4.49;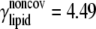

^*In all calculations, the ends of the external harmonic pulling springs are displaced in a radially outward fashion, and these pulling springs are free to move in the z-direction. The membrane center is at z=0.0 Å.

^†The force constants for the elastic springs (γ) and the harmonic pulling springs (k) are in kcal/(mol·Å²); the cutoffs (R_cut) are in Å.

In a more elaborate model (Protocols 2 and 3), the elastic protein is embedded in a lipid bilayer also described at the ENM level (see Fig.10 b); then the lipid molecules at the peripheral of the membrane are pulled using harmonic springs, and the distortion of the membrane is propagated to the membrane-protein interface in a way that is similar to the continuum framework. In this model, the elastic constant for noncovalent interactions within the lipid is taken to be slightly larger than that within the protein to ensure the structural integrity of the membrane under tension, which is consistent with an estimate based on NMA of a pure lipid bilayer with the materials properties specified in the MDeFEM (see below); the protein-lipid interaction is treated with the same elastic force constant as that within the protein (see Table 3). The relative position of the protein and the lipid bilayer is established in a similar fashion as in a typical MD simulation, which involves overlapping the closed state of MscL with a preequilibrated POPE bilayer and removing the lipids within 2.2 Å from the protein atoms.

The structural response of an elastic model under external tension (as represented by pulling the harmonic springs attached to certain protein or lipid atoms) can be derived in at least two ways. The more straightforward approach involves simply minimizing the total potential energy of the system that includes both the ENM and harmonic pulling springs (i.e., Eq. 30); we do this for the protein plus membrane model, referred to as Protocol 3-1 in Table 3. In a different approach (all other protocols in Table 3), which was motivated by recent studies of molecular motor proteins (52), we use a second-order expansion of the total potential energy to predict the structural response of the elastic system under pulling force. The result can be cast in a compact form using matrix notations,

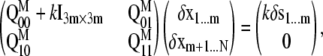(31)

where Q indicates the Hessian (second derivative) matrix of the molecular potential energy (V^M(x)), subscripts 0 and 1 indicate the set (including m atoms) and 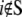(including N-m atoms), respectively, and δs indicates the displacements of the harmonic pulling springs based on the “In-plane tension” subsection. The displacements of the protein (and lipid) atoms are obtained by solving Eq. 31 using the LASPACK linear equation solver (53).

Given the quadratic form of the potential, the results from direct minimization and solving Eq. 31 are expected to be similar; see Part II (protocol 2-1 versus 3-1). If the potential energy function takes more complicated forms and therefore has many local minima, predicting the displacements using a quadratic approximation as in Eq. 31 can be advantageous because important contributions from collective (i.e., low-frequency) modes are explicitly included. Although we limit our attention to in-plane tension, the structural detail-enriched ENM can be readily extended to various types of loading modes (e.g., Fig. 3).

Noncovalent force constants (γ^noncov) in the ENM models

To estimate the noncovalent force constant (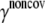) in the ENM model of E. coli-MscL, results from an all-atom NMA using the CHARMM19 force field and the EEF1 implicit solvation model are taken as the reference. Two protocols are used to explore the variation of the estimated value. In the first protocol, the value of 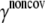is adjusted such that the two lowest frequencies from the ENM normal mode calculations best match those from the CHARMM19 results. In the second protocol, the value of 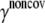is determined based on the best matching between root mean-square deviation fluctuations calculated from ENM and CHARMM19 normal mode analyses. In both the ENM and CHARMM19 calculations, the block normal mode (or translational-rotational-block) approximation (54) is used due to the large size of E. coli-MscL; for ENM, this is accomplished with the Elnemo program (55), whereas the implementation of (56) in CHARMM is used for the CHARMM19 calculations.

The estimated value for 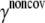using the two approaches is 0.30 and 0.41 kcal/(mol·Å²), respectively, which are rather close. In the pulling simulations, 0.41 kcal/(mol·Å²) is used for the protein. To estimate the value of 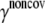for the lipid membrane model, an alternative reference is used because the normal modes of an all-atomic model of the lipid bilayer might be sensitive to the configurations. Instead, the reference is taken as a circular membrane plate of radius 60 Å with the elastic properties specified in the continuum model; for this system, the normal modes can be calculated analytically (57). For example, the first several normal modes are given by

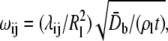(32)

where i is the number of nodal diameters, j the number of nodal circles, R_l the radius of the plate (60 Å), ρ_l the mass density of the plate (0.783 g/cm³), t the thickness of the plate (35 Å) and the equivalent bending modulus of the plate (the “Axisymmetric pure bending” subsection); λ_ij is a root of a frequency equation involving Bessel functions, and the numerical values are given in (57) (e.g., ).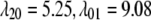

The value of 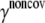for the lipid atoms is then adjusted such that the first two ENM normal mode frequencies for the lipid plate best match the analytical results according to Eq. 32 above; note that a scaling factor of 0.588 is used for the ENM frequencies because the block normal mode approximation is used (54). Such an estimated value for 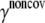of lipid is 4.49 kcal/(mol·Å²), which is much larger than the estimated value for protein atoms.

CONCLUSION

In this study, we establish the framework of what to our knowledge is a new top-down approach, MDeFEM, for studying biomechanical processes. It is a phenomenological continuum-based model decorated with the most important details from atomistic simulations, and the parameterization process for the MDeFEM makes a natural coupling between continuum and parallel all-atom simulations. The MDeFEM framework includes mechanical forces on long length scales while being faithful to local chemical details on short length scales. The flexibility of this framework enables its application to biological processes involving complex geometries/loads and systems with highly heterogeneous physical properties at a computational cost much lower than conventional all-atom simulations.

An E. coli-MscL is used as a model system to illustrate the MDeFEM approach. The representation of the continuum components and the parameterization of relevant materials properties have been chosen to be simple in this work to focus on the most fundamental physical principles of MscL gating. The transmembrane and cytoplasmic helices are modeled as elastic rods, and loops are taken to be elastic springs. The lipid is modeled by a three-layer structure to take into account the difference between headgroup and tails. The phenomenological mechanical properties of the continuum units are fitted from normal mode analysis. The interactions between the components of the integrated structure are derived from the nonbonded interactions between helices and lipid using molecular mechanics-based energy calculations, although more elaborate molecular simulations that include thermal fluctuations can also be carried out. The system is discretized and solved using the finite element method.

Since the MDeFEM continuum still involves a large number of degrees of freedoms, to envision the essential aspects in the gating of E. coli-MscL, ECMM and ENM are developed. These alternative models assume that the lipid deformation governs MscL conformation, which is imposed as a boundary condition on the channel and proper bounds (ECMM). The ENM model contains structural details for the approximate transition pathway.

In Part II of this study, the established MDeFEM protocol and analytical models will be used to study the detailed conformational transitions of E. coli-MscL, including the effects of different simulation protocols, structural motifs, loading modes, and protein interactions, as well as the simulation of patch clamp and nanoindentation experiments. The results will be validated via comparisons to all-atom simulations, structural models, and available experimental data. Furthermore, limitations of the current approach, especially the consequence of using a solid description for the membrane and neglect of solvation, will be discussed. It is envisioned that such a hierarchical multiscale framework will find great value in the study of a variety of mechanobiology problems.