Abstract
We have carried out a series of studies on the binding of a substrate mimic to the enzyme lactate dehydrogenase (LDH) using advanced kinetic approaches, which begin to provide a molecular picture of the dynamics of ligand binding for this protein. Binding proceeds via a binding-competent subpopulation of the nonligated form of the protein (the LDH/NADH binary complex) to form a protein-ligand encounter complex. The work here describes the collapse of the encounter complex to form the catalytically competent Michaelis complex. Isotope-edited static Fourier transform infrared studies on the bound oxamate protein complex reveal two kinds of oxamate environments: 1), a major populated structure wherein all significant hydrogen-bonding patterns are formed at the active site between protein and bound ligand necessary for the catalytically productive Michaelis complex and 2), a minor structure in a configuration of the active site that is unfavorable to carry out catalyzed chemistry. This latter structure likely simulates a dead-end complex in the reaction mixture. Temperature jump isotope-edited transient infrared studies on the binding of oxamate with LDH/NADH suggest that the evolution of the encounter complex between LDH/NADH and oxamate collapses via a branched reaction pathway to form the major and minor bound species. The production of the catalytically competent protein-substrate complex has strong similarities to kinetic pathways found in two-state protein folding processes. Once the encounter complex is formed between LDH/NADH and substrate, the ternary protein-ligand complex appears to “fold” to form a compact productive complex in an all or nothing like fashion with all the important molecular interactions coming together at the same time.
INTRODUCTION
Exactly how proteins bind small molecules to an interior location characterized by specific, typically noncovalent interactions is little understood. For example, the proper functioning of an enzyme requires that it undergo rather complicated and finely tuned dynamical processes to both bind substrate and release product. These dynamics involve events occurring over multiple timescales from picoseconds to milliseconds. The dynamical nature of the binding process has been hardly characterized because of the difficulties of performing both experimental as well as theoretical studies over such a wide time range.
Recently, we carried out a series of studies (1–4) on the binding of a substrate mimic to the enzyme lactate dehydrogenase (LDH) using advanced kinetic approaches, which begin to provide a molecular picture of binding for this protein. These studies established that the LDH/NADH binary complex samples multiple conformations, some of which are competent to bind substrate (a minority population) but most of which are not binding competent. The competent forms appear to expose the binding pocket to solvent and small molecules (3,4) with substrate able to reach near the binding pocket at diffusion limited speeds, probably via multiple pathways. The binding-competent form of the enzyme produces an encounter complex with substrate, which then “collapses” (1,2) to a LDH/NADH·substrate form that is able to bring about chemical catalysis (the so-called Michaelis complex). We investigate the nature of the structure(s) and evolution of structure in going from the encounter complex to the Michaelis complex in this study.
LDH catalyzes the direct transfer of a hydride ion from the pro-R face of the reduced nicotinamide group of NADH to the C2 carbon of pyruvate to produce NAD+ and the alcohol lactate, accelerating the solution chemical reaction by some fourteen orders of magnitude (5). Binding of substrate to LDH is ordered and follows the formation of the LDH/NADH binary complex. The substrate binding pocket lies somewhat deep, ∼10 Å, into the protein (6,7). Once the substrate reaches a position close enough to the enzyme's active site, the protein, including a surface loop of the polypeptide chain (residues 98–110, the so-called “mobile loop”) closes over the ligand to bring the bound substrate and NADH together in a proper geometry for reaction. These protein structural changes “activate” pyruvate and NADH for catalysis (8–10). It is believed that the rate-limiting step in the turnover of LDH is not the chemical hydride transfer step but rather the final closure of the mobile loop over the substrate binding pocket, occurring in a time of ∼1–10 ms (11). Important questions remain about how the substrate moves into this binding pocket and forms the polarizing interactions with the protein that activate it for hydride transfer. Oxamate (NH2(C=O)COO−) has long been used as a nonreacting surrogate for pyruvate. It is isoelectric and isosteric to pyruvate; its dissociation constant with LDH/NADH is close to that of pyruvate's Km; and it has been shown to have binding kinetics similar to that of pyruvate (12,13). Thus by using this nonactive substrate mimic, the atomic motion associated with the binding pathway can be separated from that associated with chemical steps occurring during catalysis.
Our previous studies on oxamate binding to the LDH/NADH complex by stopped-flow and laser-induced temperature-jump relaxation spectroscopy using NADH fluorescence as a probe of evolving structure revealed multiple intermediates along the substrate binding pathway (1,2). A kinetic model for oxamate binding with three detectable steps involving three bound oxamate species for the ternary LDH/NADH·oxamate complex was proposed. To come to better structural conclusions than can be provided by emission studies, we identify here several infrared (IR) marker bands in the LDH/NADH·oxamate complex associated with the formation of specific protein-ligand interactions at the active site using isotope-edited static Fourier transform infrared (FTIR) measurements. Isotope editing involves incorporating a stable isotope into a specific atom of the protein system so that assignments of bands in the IR spectrum associated with specific bond vibrations can be made (14). Such measurements on the LDH/NADH·oxamate complex reveal specific and unique marker bands indicating formation of the catalytically crucial strong hydrogen bonds between the substrate's carbonyl, C2=O, group and His-195 and Arg-109 of protein as well as marker bands of salt bridge formation between the substrate's charged carboxyl group and Arg-171. With the static infrared markers for substrate binding in hand, T-jump isotope-edited transient IR measurements were then conducted to determine the formation kinetics of these interactions along the binding pathway. This is a new, to our knowledge, and promising approach to define atomic motion in proteins over a large time range (10−10 −10+2 s): laser-induced temperature-jump relaxation methods to perturb the reaction equilibrium and isotope-edited IR spectroscopy to follow the accompanying structural relaxation dynamics. This report furthers and substantially completes a previous communication of IR transient studies (1) on this system.
MATERIAL AND METHODS
Pig heart LDH (as a suspension in ammonium sulfate solution), sodium oxamate, and NADH were obtained from Roche Scientific (Basel, Switzerland). The enzyme sample for IR experiments was first dialyzed against 50 mM TEA buffer in the presence of 0.15 M NaCl at pH 7.5 and then exchanged to the same buffer in D2O by a Centricon device (Millipore, Bedford, MA). The LDH concentration was determined using an extinction coefficient of 50 mM−1 cm−1 in terms of active sites (pig heart LDH is a homotetramer and all protein concentrations in this article are in terms of active sites). 13C1- and 13C2-labeled oxamate was prepared as described in the Supplementary Material, Data S1.
Static FTIR spectroscopy was performed on a Magna 760 Fourier transform spectrometer (Nicolet Instrument, Madison, WI) using an MCT detector. We used a two-position sample shuttle to alternate between the unlabeled sample and labeled sample positions; this procedure substantially decreases the spectral contribution of residual water vapor after subtraction. Both LDH/NADH·[12C]oxamate and LDH/NADH·[13C]oxamate sample solutions were simultaneously loaded into a dual cell shuttle accessory. CaF2 windows with 12 μm Teflon spacers were used for the protein sample cell. Typical sample volume was 10 μl. Spectra were collected in the range of 1100–4000 cm−1 with 2 cm−1 resolution. A Blackman-Harris three-term apodization and a Happ-Genzel apodization were applied, respectively. Omnic 4.1a (Nicolet Instruments) software was used for data collection and analysis.
The IR T-jump spectrometer has been previously described (15–17). We have modified the spectrometer in the following way to extend the length of the T-jump to resolve the millisecond binding dynamics described below. Since the sample cooling occurs primarily through diffusive heat transfer from the solution to the cell windows, the cooling time increases monotonically with the pathlength of the sample (18). Therefore the T-jump can be extended in time simply by increasing the pathlength of the sample. At pathlengths >100 μm, however, the absorption of the pump beam becomes significant, leading to a transverse temperature gradient (from the front to the back of the sample). We have overcome this limitation by splitting the pump beam using a 50:50 beam splitter and illuminating the sample from both the front and the back. This configuration produces even transverse excitation of the solution and eliminates the temperature gradient, provided the total absorbance of the pump beam is <∼50% of the initial intensity. Using this approach, we are able to increase the sample pathlength to 200–300 μm, and thereby increase the duration of the T-jump to more than 10 ms.
RESULTS
Oxamate IR spectra
The isotope-edited IR vibrational spectrum is the difference spectrum between the unlabeled form of a sample and the equivalent sample labeled with stable isotopes, where the label has been specifically incorporated into the bond of interest. The resulting difference spectrum then contains only vibrational modes whose frequencies are shifted by the label; all other modes subtract out of the difference spectrum.
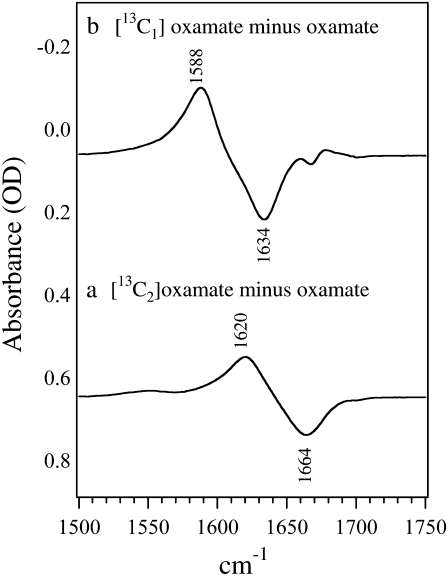
Fig. 1 shows the isotope-edited IR spectra between [12C1,12C2]oxamate and [13C2]oxamate in panel a and [13C1]oxamate in panel b. As shown in the figure, the 13C labeling on C2 causes a 44 cm−1 shift of the 1664 cm−1 band to 1620 cm−1; it can thus be assigned to oxamate's C2=O stretch mode. The 13C labeling on C1 causes a 46 cm−1 shift of the 1634 cm−1 band to 1588 cm−1 so that it is assigned to the asymmetric stretch mode of the C1 carboxylate group. The band width at half-maximum in these solution spectra is typically ∼30 cm−1.
FIGURE 1.
Difference FTIR spectra of (a) [12C2]oxamate minus [13C2]oxamate and (b) [12C2]oxamate minus [13C2]oxamate. The sample concentrations were 100 mM prepared in D2O at neutral pH. The temperature was kept at 25 C. The sample cell was composed of CaF2 windows with a 30 μm spacer.
Protein bound (LDH/NADH·oxamate) isotope-edited oxamate IR spectra
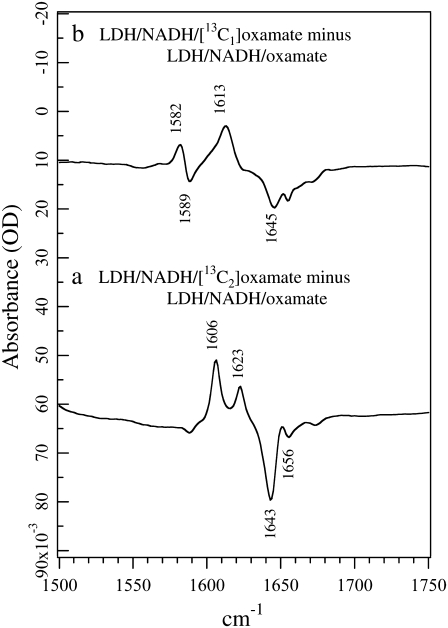
The corresponding isotope-edited IR spectra of oxamate in the ternary complex LDH/NADH·oxamate are shown in Fig. 2. Normal mode analyses on the oxamate bound in the LDH ternary complex suggest that the oxamate carboxyl and the oxamate amide motions are more likely to become coupled in 12C oxamate than in 13C-labeled oxamate, especially for 13C1 (H. Deng, K. Clinch, and R. Callender, unpublished results). Thus, vibrational bands arising from 13C oxamate are normally used as standards in subsequent discussions.
FIGURE 2.
(a) Difference FTIR spectrum between LDH/NADH·[12C2]oxamate and LDH/NADH·[13C2]oxamate. (b) Difference FTIR spectrum between LDH/NADH·[12C1]oxamate and LDH/NADH·[13C1]oxamate. All samples were prepared in 50 mM phosphate, 150 mM NaCl, pH 7.2 in D2O at 25 C. Sample concentrations were 4 mM (LDH):4 mM (NADH):4mM (oxamate). The sample cell was composed of CaF2 windows with a 12 μm spacer.
For 13C2-labeled oxamate, two IR bands arising from C2=O stretch are observed in the complex (Fig. 2 a): a major band at 1606 cm−1 and a minor band at 1623 cm−1. Their unlabeled counterparts can also be identified clearly at 1643 cm−1 and 1656 cm−1, respectively. The observation of two distinct C2=O stretch bands indicates that oxamate exists in two different forms in the complex. The C=O group of ligands bound to the active site of LDH typically exhibits a downward shift in frequency due to local hydrogen-bonding interactions (9). Thus, in the major form of the LDH/NADH·oxamate complex, the C2=O bond experiences stronger hydrogen bonding than in solution, as revealed by the 14 cm−1 red shift of its C2=O stretch frequency, from 1620 cm−1 in solution (Fig. 1 a) to 1606 cm−1 in the complex (Fig. 2 a). In the minor form, the hydrogen bond to the C2=O bond is similar or may be slightly weaker than that in solution, as indicated by the 3 cm−1 blue shift of the C2=O stretch, from 1620 cm−1 in solution to 1623 cm−1 in the complex. One noticeable difference compared to the solution spectra is that the band width at half-maximum decreases from ∼30 cm−1 to 6–7 cm−1, indicating well-defined, nonheterogeneous structures for the two conformations of bound oxamate.
A major band at 1613 cm−1 is observed in the 13C1-labeled isotope-edited spectra of the LDH/NADH·oxamate complex (Fig. 2 b). We assign this band to the −13C1OO− asymmetric stretch mode based on its 32 cm−1 shift compared to −12C1OO− (observed at 1645 cm−1). The upward frequency shift of 25 cm−1 relative to the solution value (from 1588 to 1613 cm−1) suggests a large environmental change near the −C1OO moiety. Upward shifts in the asymmetric carboxyl stretch mode are brought about by increases in hydrogen bonding (19), and it is believed that a carboxylate-guanidinium salt bridge is formed between oxamate's carboxyl and the guanidinium moiety of the Arg-171 side chain. Note that the free oxamate is hydrogen-bonded to water, therefore this upward shift in frequency represents a substantial increase in the hydrogen-bonding interaction in the protein. Like the isotope-edited IR spectrum of 13C2-labeled oxamate, two or more IR bands >1640 cm−1 in the unlabeled oxamate complex are observed (Fig. 2 b). However, in clear contrast with the results from 13C2-labeled oxamate (Fig. 2 a), only one IR band above 1600 cm−1 is associated with 13C1-labeled oxamate (negative going). This indicates that it is unlikely the oxamate carboxyl experiences different environments in the complex, in contrast to the results for the oxamate C2=O bond above. A likely explanation for this apparent discrepancy is that in the LDH/NADH·oxamate complex, the carboxyl asymmetric stretch is coupled with motions of other portions of the oxamate structure, particularly the C2=O stretch, and this coupling is removed upon 13C1 labeling. This suggestion is supported by our preliminary vibrational analysis based on ab initio normal mode calculations (H. Deng, K. Clinch, and R. Callender, unpublished results). Interestingly, another minor derivative feature at 1589/1582 cm−1 is also observed in Fig. 2 b. Since its 13C isotope shift is only 7 cm−1, it cannot be due to an isolated (localized) −C1OO− carboxyl stretch mode. Further studies revealed that this feature is a distributed vibrational mode unique for the carboxylate-guanidinium salt bridge, involving the motions from both oxamate carboxyl and the guanidinium moiety of the Arg-171 side chain. Thus, this mode can be used as a reporter for the formation of the salt bridge upon oxamate binding to the LDH complex, or the inverse process.
T-jump isotope-edited transient IR measurements
The IR kinetics studies were carried out by subjecting the chemical system
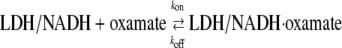 |
to a rapid change in temperature (induced by irradiating the protein solution with a pulse of near IR light; T-jumps of 15–20°C are typical). The change in infrared absorption as a function of time after the temperature changing pump pulse, typically ∼10 ns wide, is measured in real time using an IR beam tuned to a specific frequency (normally at the assigned IR bands shown in the static isotope-edited IR spectra) to monitor the relaxation process. T-jump isotope-edited IR transient studies were carried out for both 13C1- and 13C2-labeled oxamate within the LDH/NADH·oxamate complex. A difference measurement is made between these two transient IR absorbance responses and their 12C1 and 12C2 counterparts so that isotope-edited transients report only on the transient IR absorbance of vibrational modes affected by the isotope label. All other background components, mostly from protein and D2O solvent, subtract out.
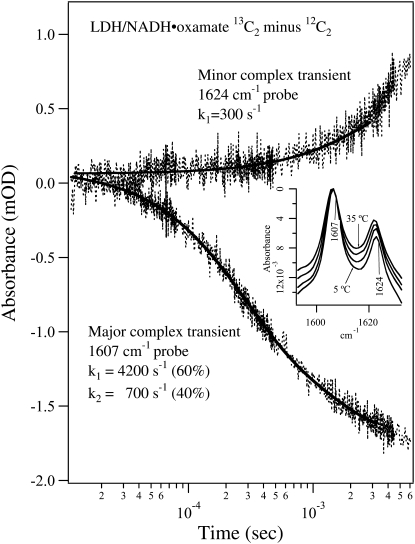
Fig. 3 shows the T-jump-isotope-edited IR transient absorbance probed at 1607 cm−1 (lower curve) and 1624 cm−1 (upper curve) obtained by subtracting the T-jump relaxation spectrum of the unlabeled LDH/NADH·oxamate complex from that of the 13C2-labeled complex. These transient IR absorbances report on the relaxation kinetics of the major and the minor oxamate components in the complex reported above, respectively, after the T-jump. The inset shows the corresponding temperature-dependent static IR difference spectra, and the probe frequencies are also indicated. Since the oscillator strengths as well as the band positions of the IR bands are hardly temperature dependent over this temperature range, as shown in the temperature-dependent data of Figs. 3 and 4 and unpublished studies, the changes in IR absorbance report directly on changes in concentration. These static difference spectra were used to estimate the expected final signal amplitude change due to the temperature jump in the transient measurements. Since the baseline in the static IR difference spectrum is difficult to determine accurately, we normalized these spectra at their maximum amplitude near 1606 cm−1 to show the relative intensity changes of the 1606 cm−1 and 1623 cm−1 band. It is clear from the inset in Fig. 3 that the 1623 cm−1 band intensity increases relative to the 1606 cm−1 band with increasing temperature. After an adjustment for the differences in sample concentration and sample path length between the static and transient experiments, we expect a final IR signal decrease of 1–2 mOD at 1607 cm−1 and/or a possible increase of 1–2 mOD at 1624 cm−1 for a 15–20°C T-jump.
FIGURE 3.
Transient IR isotope-edited absorbance of LDH/NADH·oxamate ternary complex (13C2 minus 12C2) after laser T-jump to 40°C at 1624 cm−1 (upper trace) and 1607 cm−1 (lower trace). The sample concentrations were (0.6:0.6:0.6 mM, LDH/NADH/oxamate, respectively) in D2O. A single exponential fit overlays the 1624 cm−1 transient, whereas a biexponential fit is shown for the 1607 cm−1 transient. The temperature-dependent static isotope-edited IR spectra are shown in the inset.
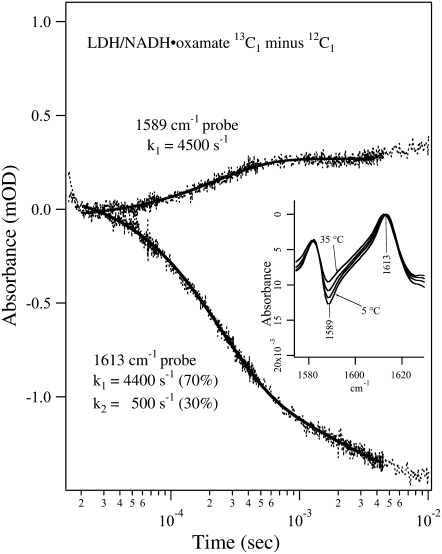
FIGURE 4.
Transient IR isotope-edited absorbance of LDH/NADH·oxamate ternary complex (13C1 minus 12C1) after laser T-jump to 40°C at 1589 and 1613 cm−1. Sample concentrations were (0.6:0.6:0.6 mM, LDH/NADH/oxamate, respectively) in D2O. A single exponential fit overlays the 1589 cm−1 transient and a biexponential fit overlays the 1613 cm−1 transient. The temperature-dependent static isotope-edited IR spectra are shown in the inset.
The transient difference IR absorbance probed at 1607 cm−1 can be fitted to a biexponential function with a fast phase (4200 s−1, 60% amplitude) and a slow phase (700 s−1, 40% amplitude, Fig. 3, lower curve). The signal decrease during relaxation indicates that the major form of the bound oxamate in the complex suffers a population loss after the T-jump pulse. The overall signal amplitude is ∼1.5 mOD, very close to that estimated from static IR data. Thus, the relaxation process for the major oxamate component reaches its equilibrium point on the millisecond timescale. The transient IR T-jump absorbance probed at 1624 cm−1 is adequately fitted with a single exponential function with a rate of 300 s−1 (Fig. 3, upper curve). At this frequency, no fast kinetics phase with significant amplitude is observed. These results clearly show that there is no direct population flow between the major and the minor components of the bound oxamate on the submillisecond timescale. Otherwise, the transient IR absorbance probed at 1624 cm−1 would appear as a mirror image of that probed at 1607 cm−1 on this timescale. Since the free 13C1-labeled oxamate also absorbs at this frequency (maximum at 1620 cm−1, Fig. 1 a), the relaxation signal should also contain its contribution. However, the much broader band width of the free oxamate limits its contribution to <20% of the total amplitude at a similar concentration. Thus, the small amplitude change in the spectrum probed at 1624 cm−1 during the submillisecond timescale cannot be used to rule out significant population change of the free oxamate. Signal increase in the millisecond and longer timescale may indicate a population increase of the minor form of the bound oxamate in the complex on this timescale or later. However, due to small variations of the cooling process between the sample and reference, the background cooling signal is imperfectly subtracted, therefore the time region longer than 2–3 ms is often obscured due to overlap of the transient signals from the C2=O stretch and sample cooling (17). Thus, our current data analysis of the transient spectra will be focused on the processes that occur faster than the millisecond timescale.
Fig. 4 shows the isotope-edited IR transient absorbance of the LDH/NADH·oxamate system, using 13C1-labeled and unlabeled oxamates, probed at 1589 cm−1 and 1613 cm−1. Due to the limited tuning range of the probe laser, we could not probe the band at 1582 cm−1 from the 13C1-labeled sample (Fig. 2 b), thus the signal increase in the transient absorbance with the 1589 cm−1 probe indicates a population decrease rather than increase, as would be the case if a 1582 cm−1 probe were used. The inset shows the corresponding temperature-dependent static IR difference spectra, and the probe frequencies are also indicated. According to the assignments of the IR bands in the static spectra, the kinetic trace observed at 1613 cm−1 reports on the total bound oxamate population change, whereas the kinetic trace observed at 1589 cm−1 predominantly reflects the change of the oxamate population that forms a salt bridge with Arg-171.
One relaxation process with a rate of 4500 s−1 was observed for the transient absorbance probed at 1589 cm−1 (Fig. 4, upper curve), suggesting that the salt bridge breaking/formation between oxamate's −C1OO− moiety and Arg-171 likely occurs in one step. The signal increase in this transient absorbance indicates that the concentration of the specie or species containing the guanidinium-carboxylate salt bridge diminishes with a temperature increase. The rate of the salt bridge decrease is very similar to the population decrease of the major oxamate structure in the complex (marker band at 1606 cm−1), suggesting these are simultaneous events. On the other hand, the transient absorbance probed at 1613 cm−1 shows two relaxation processes, one with a rate of 4400 s−1 and the other at 500 s−1. The faster process has a larger amplitude (70%) and seems to be associated with the salt bridge transient whereas the slower process with smaller amplitude (30%) may be associated with release of the bound oxamate or other processes.
Development of a kinetic model
Previous T-jump relaxation and stopped-flow mixing studies of oxamate binding to LDH/NADH monitoring the changes in fluorescence emission of bound NADH yielded the following kinetic scheme. Parameters given in this equation were obtained at 20°C, with those from 35°C in parentheses (2):
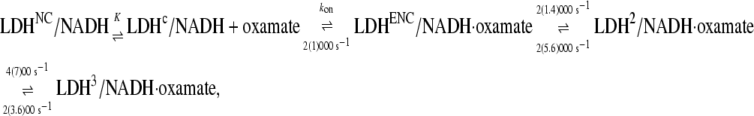 |
(1) |
where LDHNC/NADH and LDHC/NADH represent binary complexes that are not competent and competent to bind ligand, respectively, and 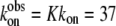 (20) μM−1s−1 (4). According to this kinetics model, an encounter complex is formed by the initial binding of oxamate to the LDHC/NADH complex followed by two subsequent unimolecular processes, resulting in a complex poised for catalysis, the putative Michaelis complex (LDH3/NADH·oxamate in the scheme). In LDH3/NADH·oxamate, it was speculated that all hydrogen bonds on the C2=O of the substrate are formed (1). In LDH1/NADH·oxamate and LDH2/NADH·oxamate, the “mobile loop” of the protein is still open and the hydrogen bonding on the substrate C2=O bond is incomplete. Thus, this model is consistent with the static IR data since the major form of the bound oxamate experiences a stronger C2=O bond polarization (corresponding to the 1606 cm−1 band in Fig. 2 a) whereas the hydrogen bonding to the C2=O bond of the minor form is weaker (the 1623 cm−1 band in Fig. 2 a).
(20) μM−1s−1 (4). According to this kinetics model, an encounter complex is formed by the initial binding of oxamate to the LDHC/NADH complex followed by two subsequent unimolecular processes, resulting in a complex poised for catalysis, the putative Michaelis complex (LDH3/NADH·oxamate in the scheme). In LDH3/NADH·oxamate, it was speculated that all hydrogen bonds on the C2=O of the substrate are formed (1). In LDH1/NADH·oxamate and LDH2/NADH·oxamate, the “mobile loop” of the protein is still open and the hydrogen bonding on the substrate C2=O bond is incomplete. Thus, this model is consistent with the static IR data since the major form of the bound oxamate experiences a stronger C2=O bond polarization (corresponding to the 1606 cm−1 band in Fig. 2 a) whereas the hydrogen bonding to the C2=O bond of the minor form is weaker (the 1623 cm−1 band in Fig. 2 a).
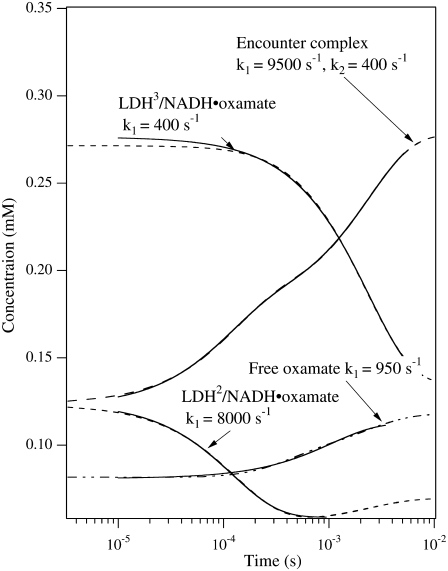
However, this interpretation is not consistent with the isotope-edited IR relaxation data of Fig. 3. First, the observed rate in the fast phase with the probe on the major oxamate component at 1606 cm−1, 4200 s−1, is too fast compared to the rate constants (400/200 s−1) leading to LDH3/NADH·oxamate formation. Second, there is no evidence for a direct population transfer, at the submillisecond timescale, between the major and minor forms of the bound oxamate in the IR T-jump measurements (Fig. 3) as predicted in Eq. 1. These qualitative considerations are supported by numerical simulations of the T-jump experiments using parameters from the three-step kinetic model (Eq. 1). In the simulations, the equilibrium concentrations of the oxamate-containing species were calculated using the parameters at 20°C. Then the kinetic parameters were changed to those at 35°C, and the time course of each species was calculated (Fig. 5). Single or biexponential fits for each simulated time-dependent concentration are shown, along with the apparent rate constants. Our simulations confirm that the concentration change of the LDH3/NADH·oxamate form does not have a fast phase in the submillisecond timescale, and the fast-phase kinetics can only occur in the concentrations of the encounter complex (LDHENC/NADH·oxamate) and LDH2/NADH·oxamate forms. Additionally, there are other features in the simulations that are not consistent with IR T-jump data. The predicted population increase of the encounter complex at 35°C is not observed, and the predicted population decrease of LDH2/NADH·oxamate is also not apparent in the experiments. Thus, either the kinetic parameters or the kinetic scheme require modification to explain our current IR data.
FIGURE 5.
Dashed lines are the simulated transient population of various oxamate forms after T-jump from 20°C to 35°C using the parameters for the three-step kinetic model given in Eq. 1 (McClendon et al. (2)). The total oxamate and LDH/NADH concentrations were 0.6:0.6 mM. The transient spectra start from the equilibrium concentrations of various species containing oxamate at 20°C and then the 35°C parameters for the kinetic model are used to simulate the time course of each species. The solid curves show the single or biexponential fitting for each simulated time-dependent concentration. The fitted rate constants are also indicated. For comparison to the experimental data of Fig. 3, the simulated kinetics for LDH3/NADH·oxamate should be compared to the kinetic results taken at 1606 cm−1, the marker band of the major species, whereas that for LDH2/NADH·oxamate would be compared to the results taken at 1624 cm−1, the marker band for the minor species. The simulated relaxation kinetics for the major species show only one relaxation rate of 400 s−1, in clear contrast to the two rates at 4200 s−1 and 700 s−1, respectively, observed in our experiments (see Fig. 3). The simulated relaxation for the minor species shows one rate at 8000 s−1, not consistent with the observed rate at 300 s−1. Furthermore, the populations of both major and minor species change in the same direction, also not consistent with our observations (see Fig. 3).
Alternative kinetics scheme
The simplest model that fits our current static and T-jump relaxation IR data as well as previous fluorescence data is the kinetics scheme shown in Eq. 2. After encounter complex formation, its conformation will change further in two different directions (Eq. 1), one to the major complex with a submillisecond rate constant and the other to the minor complex with a millisecond rate constant:
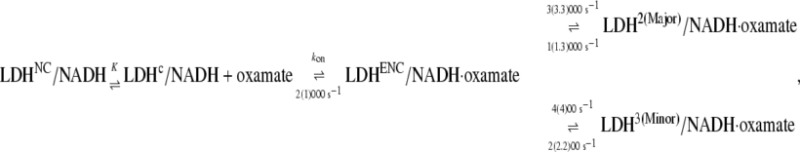 |
(2) |
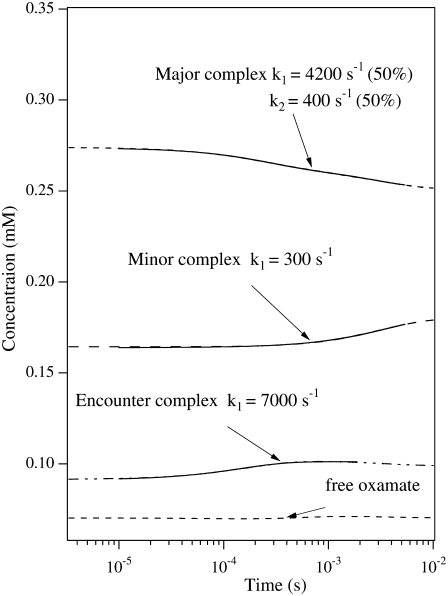
where, again, 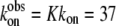 (20) μM−1s−1 was assumed in the modeling. Since no drastic population change in any bound oxamate form due to a temperature change was observed in our IR studies, only minor changes of the kinetic constants (shown in the parentheses in Eq. 2) were required to reproduce our IR T-jump relaxation data. The results of the T-jump relaxation simulation using this kinetic scheme are shown in Fig. 6, and they agree reasonably well with the data shown in Fig. 3.
(20) μM−1s−1 was assumed in the modeling. Since no drastic population change in any bound oxamate form due to a temperature change was observed in our IR studies, only minor changes of the kinetic constants (shown in the parentheses in Eq. 2) were required to reproduce our IR T-jump relaxation data. The results of the T-jump relaxation simulation using this kinetic scheme are shown in Fig. 6, and they agree reasonably well with the data shown in Fig. 3.
FIGURE 6.
Dashed lines are the simulated transient populations of various oxamate forms in the alternative kinetic model given by Eq. 2. Parameters similar to those from the three-step kinetic model given in McClendon et al. (2) were used, changed slightly to yield good comparison to experiment. The total oxamate and LDH/NADH concentrations were 0.6:0.6 mM. The solid curves show the single or biexponential fitting for each simulated time-dependent concentration. The fitted rate constants are also indicated. For comparison to the experimental data of Fig. 3, the simulated kinetics should be compared to the kinetic results taken at 1606 cm−1, the marker band of the major species, and to the results taken at 1624 cm−1, the marker band for the minor species. In this model, the simulated relaxation kinetics of both major and minor species agree well with experimental observations, and the population changes of the two species are opposite, also consistent with experiment.
DISCUSSION
Active site conformations of the LDH/NADH·oxamate complex
The isotope-edited IR difference studies of the ternary complex show that there are two forms of bound oxamate: a major form in which the hydrogen-bonding interactions with the oxygen of the C2=O moiety are significantly stronger than those in solution and a minor form, about half as populated, in which the hydrogen-bonding interactions with C2=O are similar to those found in solution. In previous isotope-edited Raman studies of this same complex (10,20), it was found that the bound reduced nicotinamide ring adopts a “half-boat” conformation. Furthermore, two conformations were found, also populated in a 2:1 concentration ratio. In the major form, the estimated angle of the C4 ring carbon with respect to the other carbon atoms is ∼10–15°, with the pro-R hydrogen (A side) in a pseudoaxial geometry and the pro-S hydrogen (B side) pseudoequatorial. In the minor form, the out-of-the-plane distortion of the C4 carbon is somewhat less and the pro-S hydrogen (B side) adopts a pseudoaxial geometry whereas the pro-R hydrogen (A side) is pseudoequatorial.
We can then conclude that there are two distinct active site LDH/NADH·oxamate complex conformations. The more populated conformation, which is shown as cartoon in Fig. 7, has relatively strong hydrogen bonding to oxamate's C2=O bond, presumably due to interactions with His-195 and Arg-109 (e.g., Deng et al. (9)); in this conformation, the reduced nicotinamide ring is puckered to force the pro-R hydrogen on C4 of the reduced nicotinamide ring of NADH to adopt an pseudoaxial geometry. This conformation is poised for catalysis since, in the first place, its ring structure is consistent with the transition state structure of the hydride transfer reaction predicted by theoretical calculations (21,22). Moreover, the polarization of the substrate C2=O bond found in the major conformation (based on the hydrogen-bonding induced downshift in the C2=O stretching frequency) is a crucial molecular factor in the catalytic power of LDH (9). LDH brings ∼14 orders of magnitude in rate enhancement, of which some six orders of magnitude are thought to arise from electrostatic effects of active site H-bonding environment to the substrate's C2=O moiety (9). Overall, the major populated structure of the LDH/NADH·oxamate complex apparently resembles an advanced stage of the true substrate LDH/NADH·pyruvate complex along the enzyme-catalyzed reaction path. In contrast, the minor populated conformation of the LDH/NADH·oxamate complex does not resemble one that is catalytically competent. The NADH ring puckering is toward the other face of the nicotinamide, forcing the pro-R hydrogen into a pseudoequatorial position, a wrong position for putative hydride transfer (21,22); and, even more importantly, the hydrogen bonding strength to C2=O is decreased substantially (based on the lack of a shift in the C2=O stretching frequency compared to water), possibly because the ring conformation increases the volume of the active site cavity.
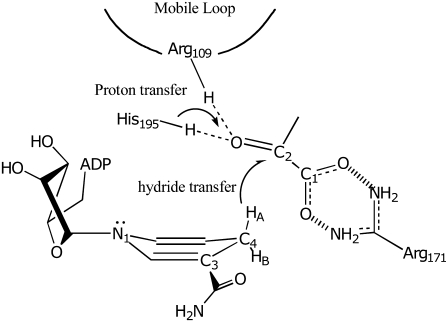
FIGURE 7.
Cartoon of the major active site structure in the LDH/NADH·oxamate complex. The hydrogen bonds between Arg-109 and His-195 with C2=O of substrate is shown as is the salt bridge between Arg-171 and the carboxyl of bound substrate. These interactions are crucial, respectively, for catalysis and for binding. The NADH is shown in a boat conformation bringing HA on its C4 carbon into a pseudoaxial geometry, believed to be important to catalyze hydride transfer of this hydrogen.
Although oxamate is a very good mimic for the substrate of LDH, pyruvate, and the majority form of the oxamate ternary complex is almost certainly an accurate structural model of the catalytically productive conformation, it is unclear if the minor populated oxamate ternary complex type species is populated with any substantial concentration in the LDH/NADH·pyruvate true Michaelis complex; there are no direct measurements at present that bear on this. Indirectly, no minor species similar in properties to those here were observed in vibrational studies of the LDH/NAD-pyruvate adduct complex (9). Also, we have not observed two branch kinetics in studies of pyruvate binding similar to that observed for oxamate binding as observed here (H. Deng, S. Brewer, D. M. Vu, K. Clinch, R. Callender, and R. B. Dyer, unpublished data).
Structural changes along the binding pathway
We do not know much about the structure of the encounter complex, called LDHENC/NADH·oxamate in Eqs. 1 or 2. The emission from the reduced ring of NADH is substantially quenched compared to its value in LDH/NADH, suggesting that the substrate mimic, oxamate, lies fairly close to the active site since bound oxamate (and pyruvate) quenches the emission of NADH in LDH ternary complexes (2). Our recent experimental and theoretical (3,4) studies on the formation of the encounter complex suggest that the binary complex, LDH/NADH, consists of a range of structures in dynamic equilibrium. Most are relatively closed and do not bind substrate well; these have been denoted collectively binding “not competent”, LDHNC/NADH above. Some, denoted LDHC/NADH, are relatively looser and bind ligand via “open” structures wherein the binding pocket is exposed to solvent. These studies also suggest that binding may take place along several distinct pathways so that the “encounter complex” may represent a range of conformations. According to our results, a number of structural changes take place in single exponential process that forms a complex poised for catalysis, LDH2/NADH·oxamate in Eq. 2, from the encounter complex. Strong H-bonds are formed between the substrate's carbonyl bond, C2=O, and the H-bond donors at the active site, His-195 and Arg-109 in this step. In addition, the salt bridge between the substrate's carboxyl, −C1OO−, group and Arg-171 is observed to form concomitantly during this step.
There are several interesting features of these dynamics that are worth noting. One is that this is an excellent example of the concept of “induced fit” (23), which says that that interaction between the protein and its substrate(s) leads to a binding pathway, dependent on the molecular nature of the substrate, whereby the ligand induces specific protein structural changes leading to the proper structure of the protein bound state(s). We also note that the production of the catalytically competent protein-substrate complex has strong similarities to kinetic pathways found in two-state protein folding processes. The binding competent LDHC/NADH protein complex(es) is believed to have a “loose” or open structure such that access of solvent to the active site is quite facile (3,4). Once the encounter complex is formed between this open structure and the substrate, the protein-ligand complex appears to “fold” to form a compact productive complex in an all or nothing like fashion with all the important molecular interactions coming together at the same time.
Another feature of note is that the catalytically poised complex is in dynamical equilibrium with a complex which would be nonproductive. This is expected, really; protein-substrate complexes are not the single structure pictured in textbooks. It is quite well established that a folded protein exists as a dynamic equilibrium of substates. Both stability and activity are controlled by a hierarchy of protein dynamics spread over a broad range of conformations and timescales, from femtoseconds to minutes (or longer). The vast majority of these will not be competent for the conversion of enzyme substrate to enzyme product. The goal of the enzyme in forming the bound enzyme-substrate complex is to reduce the number of conformations available to the enzyme-substrate complex so that, in what is a largely or completely a stochastic search through the available conformation space, with a “hunting” time on the femtosecond timescale (the time of bond vibrations or rotations), the correct atoms will all be aligned spatially just right along with their momenta, to give rise to chemical catalysis; this search takes place within about a millisecond, the typical time for enzymatic catalysis. On average, the protein will sample some 1010 conformations before alignment is just right for chemistry to occur. The structure of the nonproductive-like complex found in our study (LDH3(Minor)/NADH·oxamate in Eq. 2) suggests one that is quite far in configuration from the productive-like complex. Structures like this are typically suppressed. If there are too many of these long-lived conformations, the probability of catalysis taking place becomes small.
SUPPLEMENTARY MATERIAL
To view all of the supplemental files associated with this article, visit www.biophysj.org.
Supplementary Material
Acknowledgments
This work was supported by the Institute of General Medicine of the National Institutes of Health, program project grant No. 5P01GM068036 and by the Biomedical Imaging and Bioengineering Institute of the NIH, grant EB01958.
Editor: Heinrich Roder.
References
- 1.McClendon, S., D. Vu, R. Callender, and R. B. Dyer. 2005. Structural transformations in the dynamics of Michaelis complex formation in lactate dehydrogenase. Biophys. J. 89:L07–L09. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.McClendon, S., N. Zhadin, and R. Callender. 2005. The approach to the Michaelis Complex in lactate dehydrogenase: the substrate binding pathway. Biophys. J. 89:2024–2032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Pineda, J. R. E. T., R. Callender, and S. D. Schwartz. 2007. Ligand binding and protein dynamics in lactate dehydrogenase. Biophys. J. 93:1474–1483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Qiu, L., M. Gulotta, and R. Callender. 2007. Lactate dehydrogenase undergoes a substantial structural change to bind its substrate. Biophys. J. 93:1677–1686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Burgner, J. W., and W. J. Ray. 1984. Acceleration of the NAD-cyanide adduct reaction by lactate dehydrogenase: the equilibrium binding effect as a measure of the activation of bound NAD. Biochemistry. 23:3620–3626. [DOI] [PubMed] [Google Scholar]
- 6.Holbrook, J. J., A. Liljas, S. J. Steindel, and M. G. Rossmann. 1975. Lactate dehydrogenase. In The Enzymes, 3rd ed. P. D. Boyer, editor. Academic Press, New York. 191–293.
- 7.Griffith, J. P., and M. G. Rossmann. 1987. M4 Lactate Dehydrogenase Ternary Complex with NAD and Oxamate. Protein Data Bank 1LDM; www.rcsb.org.
- 8.Burgner, J. W., and W. J. Ray. 1984. On the origin of lactate dehydrogenase induced rate effect. Biochemistry. 23:3636–3648. [DOI] [PubMed] [Google Scholar]
- 9.Deng, H., J. Zheng, A. Clarke, J. J. Holbrook, R. Callender, and J. W. Burgner. 1994. Source of catalysis in the lactate dehydrogenase system: ground state interactions in the enzyme·substrate complex. Biochemistry. 33:2297–2305. [DOI] [PubMed] [Google Scholar]
- 10.Chen, Y.-Q., J. van Beek, H. Deng, J. Burgner, and R. Callender. 2002. Vibrational structure of NAD(P) cofactors bound to several NAD(P)-linked enzymes: an investigation of ground state activation. J. Phys. Chem. 106:10733–10740. [Google Scholar]
- 11.Dunn, C. R., H. M. Wilks, D. J. Halsall, T. Atkinson, A. R. Clarke, H. Muirhead, and J. J. Holbrook. 1991. Design and synthesis of new enzymes based upon the lactate dehydrogenase framework. Philos. Trans. R. Soc. Lond. B. Biol. Sci. 332:177–185. [DOI] [PubMed] [Google Scholar]
- 12.Parker, D. M., D. Jeckel, and J. J. Holbrook. 1982. Slow structural changes shown by the 3-nitrotyrosine-237 residue in pig heart[Try(3NO2)237] lactate dehydrogenase. Biochem. J. 201:465–471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Clarke, A. R., A. D. B. Waldman, K. W. Hart, and J. J. Holbrook. 1985. The rates of defined changes in protein structure during the catalytic cycle of lactate dehydrogenase. Biochim. Biophys. Acta. 829:397–407. [DOI] [PubMed] [Google Scholar]
- 14.Callender, R., and H. Deng. 1994. Non-resonance Raman difference spectroscopy: a general probe of protein structure, ligand binding, enzymatic catalysis, and the structures of other biomacromolecules. Annu. Rev. Biophys. Biomol. Struct. 23:215–245. [DOI] [PubMed] [Google Scholar]
- 15.Callender, R. H., and R. B. Dyer. 2006. Advances in time-resolved approaches to characterize the dynamical nature of enzymatic catalysis. Chem. Rev. 106:3031–3042. [DOI] [PubMed] [Google Scholar]
- 16.Gulotta, M., E. Rogatsky, R. H. Callender, and R. B. Dyer. 2003. Primary folding dynamics of sperm whale apomyoglobin: core formation. Biophys. J. 84:1909–1918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Gulotta, M., H. Deng, H. Deng, R. B. Dyer, and R. H. Callender. 2002. Towards an understanding of the role of dynamics on enzymatic catalysis in lactate dehydrogenase. Biochemistry. 41:3353–3363. [DOI] [PubMed] [Google Scholar]
- 18.Wray, W. O., T. Aida, and R. B. Dyer. 2002. Photoaucoustic cavitation and heat transfer effects in the laser-induced temperature jump in water. Appl. Phys. B. 74:57–66. [Google Scholar]
- 19.Gu, Z., R. Zambrano, and A. McDermott. 1994. Hydrogen bonding of carboxyl groups in solid state amino acids and peptides: comparison of carbon chemical shielding, infrared frequencies, and structures. J. Am. Chem. Soc. 116:6368–6372. [Google Scholar]
- 20.Deng, H., J. Zheng, D. Sloan, J. Burgner, and R. Callender. 1992. A vibrational analysis of the catalytically important C4-H bonds of NADH bound to lactate or malate dehydrogenase: ground state effects. Biochemistry. 31:5085–5092. [DOI] [PubMed] [Google Scholar]
- 21.Almarsson, O., and T. C. Bruice. 1993. Evaluation of the factors influencing reactivity and stereospecificity in NAD(P)H dependent dehydrogenase enzymes. J. Am. Chem. Soc. 115:2125–2138. [Google Scholar]
- 22.Wu, Y., and K. N. Houk. 1991. Theoretical evaluation of conformational preferences of NAD+ and NADH: an approach to understanding the stereospecificity of NAD+/NADH-dependent dehydrogenases. J. Am. Chem. Soc. 113:2353–2358. [Google Scholar]
- 23.Koshland, D. E. 1958. Application of a theory of enzyme specificity to protein synthesis. Proc. Natl. Acad. Sci. USA. 44:98–104. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.