Toward Resolution of Ambiguity for the Unfolded State

Abstract

The unfolded states in proteins and nucleic acids remain weakly understood despite their importance in folding processes; misfolding diseases (Parkinson's and Alzheimer's); natively unfolded proteins (as many as 30% of eukaryotic proteins, according to Fink); and the study of ribozymes. Research has been hindered by the inability to quantify the residual (native) structure present in an unfolded protein or nucleic acid. Here, a scaling model is proposed to quantify the molar degree of folding and the unfolded state. The model takes a global view of protein structure and can be applied to a number of analytic methods and to simulations. Three examples are given of application to small-angle scattering from pressure-induced unfolding of SNase, from acid-unfolded cytochrome c, and from folding of Azoarcus ribozyme. These examples quantitatively show three characteristic unfolded states for proteins, the statistical nature of a protein folding pathway, and the relationship between extent of folding and chain size during folding for charge-driven folding in RNA.

INTRODUCTION

Proteins generally display a globular conformation characterized by the presence of a surface with a distinguishable core often maintained by hydrophobic interactions (residue/residue interactions). The globular state can be of fixed structure associated with biological activity, the native state (N), or can be somewhat flexible in structure and display only limited functionality, the molten-globule state (MG) (1,2). Proteins can also display categories of unfolded states, such as the pre-moltenglobule (PMG), the unfolded state (U), and misfolded states (3) that display characteristics of synthetic polymers and mass fractal aggregates in that a discrete surface and distinguishable core are not observed. The nature of chemical interactions leading to unfolded states and PMG are not well defined but may be partly associated with solvation effects (residue/solvent interactions). RNA can also display a folding process reminiscent of protein folding though of a more rudimentary form and driven by ionic charge and hydrogen bonding. Native-state RNA enzymes (ribozymes) often do not display a fully globular structure by scattering in that a surface scattering regime is often not resolved. In this sense, ribozymes display some extent of unfolded structure in the native state parallel to natively unfolded proteins. Quantification of the degree of folding is important in understanding these biomolecules.

The unfolded state is the nascent state (4), but it is usually achieved in vitro through chemical, physical, or thermal denaturing (5,6) or by titration of counterions in ribozymes. In some cases, e.g., natively unfolded proteins, unfolded proteins can display biological activity (2,7–9). There is controversy concerning the extent of native secondary structure in the unfolded state and especially how the spectroscopic observation of secondary structure in the unfolded state is associated with folding (10–12). For instance, the PMG state shows secondary structure associated with the native state but displays variable density with molar mass for different PMG proteins (2,13), similar to the unfolded state.

The unfolded state has been described as a Gaussian structure (14,15), however, it has been pointed out that unfolded proteins are not expected to follow Gaussian scaling, since they exist in good solvents where a self-avoiding expanded coil is expected (2,15). Further, several different unfolded states are known for many proteins (2).

It would be helpful to quantify the extent of folding for various denatured states (16,17). Here, a quantitative, statistical description of folding is presented based on a mass-fractal model (18,19). The description associates branching/bridging in polymers and inorganic aggregates with folding in proteins, allowing a quantification of protein folding using a simple analytic method. The result of this approach is a quantitative definition of the unfolded state and a statistical description of the extent of folding.

A scaling model for protein and nucleic acid folding

There are subtle similarities between our understanding of random synthetic polymers, fractal aggregates of inorganic particles, and our understanding of the unfolded states of proteins and nucleic acids. Recently, advances have been made in our analytic understanding of these ramified fractal structures (18–20). This report seeks to apply these advances to quantify topological features of unfolded, misfolded, and PMG states in proteins (9) and unfolded, intermediate, and close-to-native structure in ribozymes. In the fractal model, a protein residue is represented by a particle of an aggregate (Fig. 1, circles) allowing a direct analogy between a protein chain and a branched mass-fractal aggregate. In this analogy, bridge sites reflect a variety of possible long-range enthalpic interactions such as hydrophobic interactions, hydrogen bonds, or disulfide bonds between residues at large sequence separations (Fig. 1) (2,14). In ribozymes these linkages are associated with hydrogen-bonded basepairs and ionic interactions. Such bridge/fold sites will lead to densification of the unfolded structure and might be seen as a quantifiable stage in the process of folding.

FIGURE 1.

Stylized model for protein structure. Schematic shows a rough two-dimensional cartoon of a protein chain, indicating the presence of a minimum path (gray circles) of p residues (circles) that differs from the protein's total residues (z) (gray and white circles) due to the presence of bridge/fold points. Fold points could be hydrophobic interactions, disulfide bonds, hydrogen bonds, or ionic bonds leading to association of the protein chain at large residue-index differences.

From a fractal view, the partially folded structure in Fig. 1 displays two “paths” or sequences of residues, the chain path, z, and the minimum path, p, that shortcuts the main path through long-range interactions, bridges (bold lines). The minimum path, p (Fig. 1, gray circles) is important to the static and dynamic mechanical response of the protein, since the stress-bearing path occurs along p (21) and because motion of the chain and the available conformations are dramatically restricted by shorter minimum paths. The chain path, z, is reflected by the total number of residues in a protein, the sum of the gray and white circles in Fig. 1. For an unfolded chain with no bridges, p = z. When folding bridges (18) are present, p < z. An unfolded protein is unambiguously defined by, p = z in this model.

We can relate the C-terminal to N-terminal separation distance of the partially folded protein, R, to p and the residue step length, b, through,

(1)

where d_min is the minimum dimension and represents the mass-fractal dimension of the minimum path (Fig. 1, gray circles). In a similar way, the whole protein can be described in terms of the number of residues, z, and the mass-fractal dimension, d_f,

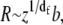(2)

where d_f is the mass-fractal dimension for the coil as a whole and is reported to be generally ∼5/3 in the denatured state by Kohn et al. (15), distinctly different from a Gaussian value of 2. Uversky (2) has given values of d_f ≈ 2.5 for PMG and values between ∼2 and 5/3 for U. For MG and N, d_f = 3 and d_min ≈ 1 (Table 1). As noted below, for some ribozymes the native state is not three-dimensional and the unfolded state may be Gaussian.

TABLE 1.

Dimensional description of objects

Object	c (≤df)	dmin (≤df)	df	φBr
Sphere/MG/N	3	1	3	1
Disk	2	1	2	(1 − 1/α)
Rod	1	1	1	0
Gaussian chain	1	2	2	0
Self-avoiding walk	1	5/3	5/3	0
Randomly branched chain	5/4	2	5/2	(1 − z−1/5)
PMG	≥3/2	≤5/3	5/2	(Eq. 4)
U	≥3/5 df	≤5/3	1–2	(Eq. 4)

c, d_min, d_f, and the extent of folding, φ_Br, are defined in the text. The d_f values for PMG and U are from Uversky (2); others are from Beaucage (18). Using Eq. 5, c and d_min ≤ d_f, as noted in the column title. α is the aspect ratio for a disk.

p can be directly related to z through the connectivity dimension c,

(3)

For a linear (unfolded) chain, the connectivity is c = 1 and d_min = d_f. This serves as an analytic definition for an unfolded protein. When d_min = 1 the path p is a straight line in at least one direction (for example, along the length of a rod/helix or the diameter of a disk or along the pleat of a β-sheet) and the structure is termed a regular object. We can consider a measure of the degree of folding, φ_Br, as the ratio of the residues in loops (z − p) to the total residues in the protein, z,

(4)

For a typical folded structure, there are many minimum paths through the structure, and φ_Br represents an average value for the fraction of the structural mass not used in the minimum path.

Table 1 shows the values for c, d_min, d_f, and φ_Br for various structures. Although there are a number of methods, including simulation, by which these statistical parameters might be determined for an unfolded or partially folded protein, a convenient method involves small-angle scattering of x-rays or neutrons from dilute solutions. All of the parameters in Table 1 can be determined from a single static scattering pattern (given sufficient angular range) just as they have been determined in studies of branched ceramic nanoaggregates and for branched synthetic polymers (18,20,21).

The scaling approach decomposes a complex structure of mass-fractal dimension d_f and mass z in terms of the tortuosity of the structure through d_min and p and the connectivity of the structure through c and the mass of an equivalently connected structure of mass s,

(5)

where s represents the mass needed to connect fold sites with straight lines.

Quantification of folding by small-angle scattering

Scattering under the Rayleigh-Gans approximation (x-ray and neutron scattering) is often reduced to generic scattering laws like Guinier's and power laws. Guinier's law (22,23) is given by

(6)

where I(q) is the scattered intensity, q = 4πsin(θ/2)/λ, θ is the scattering angle, and λ is the wavelength, is the mean-square radius of gyration, and G is a contrast factor. At higher q, the fractal power-law equation (23,24) is appropriate for U and PMG,

(7)

where B_f is the power-law prefactor. d_min can be calculated from scattering using features from Eqs. 6 and 7 to account for bridged structures (18),

(8)

where Γ() is the gamma function. Equation 3 can then be used to determine c. z can be considered the number of residues in the protein or can be experimentally measured from a high q observation of the protein persistence unit (18,25,26). In the latter case, we have

(9)

where G_per is the contrast factor for the persistence unit measured at high q and z is a weight-average value.

Using this approach, we can quantify the extent of folding in terms of the dimensions c and d_min. For example, for a fully unfolded structure, which folds to the native state, we should observe c = 1, d_min = d_f initially, with d_f close to 5/3 for a self-avoiding walk (15). The folding process should be characterized by an increase in c from 1 to d_f as the structure approaches a regular object. The folding process presumably involves densification of the structure, so an increase in d_f is also expected. The molar extent of folding, φ_Br, will show an increase from 0 to 1 during the folding process.

The scaling approach ignores local chemical structure and ionic charge, except as they affect tortuosity and connectivity of the molecule, as well as chain persistence. Moreover, it is expected that this scaling model will be most applicable to high z proteins and nucleic acids where scaling laws are most useful. However, in practice, even moderate-sized biomolecules seem to follow this scaling model, as shown below. This may be associated with stochastic averaging.

RESULTS AND DISCUSSION

An example using staphylococcal nuclease

Staphlococcal nuclease (SNase) is a protein excreted by Staphylococcus aureus bacterium that cleaves nucleic acids in the extracellular medium by hydrolyzing P-O bonds (26). SNase is a small monomeric protein, 17.5 kDa, z = 149 residues, and a single tryptophan residue with no disulfide bonds that has served as a model for protein folding studies (27,28). The native-state structure (grown at pH 8.15 in low salt buffer (28)) is composed of a five-member β-barrel and three α-helices (Fig. 2 d). The tertiary structure displays a nucleotide binding pocket with two flexible regions associated with biological function (29). Panick et al. (29) have studied the pressure dependence of small-angle x-ray scattering (SAXS) from SNase in 1% solutions at a pH of 5.5 (using a recombinant nuclease produced from Escherichia coli). A denatured state and a folded state were measured, as were defolding kinetics. Pressure-induced changes in the protein conformation are of particular interest due to the weak perturbation. Here, the SAXS data of Panick et al. (29) that was digitized is reanalyzed using the procedure described above.

FIGURE 2.

(a) Scattering from pH 5.5 100 bar SNase at 1% and 20°C (disklike regular object) (○) and 2800 bar, close to the unfolded state. Data is digitized from Panick et al. (29) and fit with the unified global function (solid lines) (18,23,25) that incorporates Eqs. 1. and 2, shown as dashed curves for the 2800-bar fit. (b) Fractal analysis of scattering for the transition from a PMG-like regular object (large rectangle) to a projected unfolded linear chain (large circle) at ∼4000 bar, where d_min = d_f and c = 1. (c) Minimum path, p; number of residues, z; and extent of folding, f_Br versus pressure, predicting the same pressure range for the purely unfolded state, where p = z and f_Br = 0. (Curves are empirical fits to 1 − k₀exp(k₁P²) and k₀exp(k₁P²).) (d) SNase in the native state (pH ∼7 atmospheric pressure) from PDB using King 1.39 viewer (28).

Fig. 2 a shows a low-pressure dilute solution scattering curve at pH 5.5 (100 bar) and a pressure denatured curve (2800 bar) for SNase. SNase displays a native state in SAXS at pH 7.5, as reported by Uversky et al. (30) and unfolds in the presence of acid at pH <4 (5,6,30). For this reason, Panick used a pH of 5.5 for these studies, just above the pH for acid unfolding. At 100 bar, the sample displays the characteristics of a regular object, that is, a low-dimensional solid object similar to a sheet. The low-dimensional regular structure at 100 Bar, pH 5.5, has not been previously reported, since the radius of gyration at pH 5.5 is indistinguishable from that at pH 7, though the structure is significantly different by this dimensional analysis. Such regular structures, displaying two-dimensional sheet structures, have been associated with misfolded proteins (e.g., (3)). The rounded rectangle in Fig. 2 b highlights a convergence of c and d_f, indicating this regular structure with d_f ∼2.2. This initial pH 5.5 structure, indicated in Fig. 2 b, may be related to the pH denatured states shown by Whitten et al. for SNase (32), associated with a framework model for folding where elements of secondary structure fluctuate around native tertiary locations (30). This is also reminiscent of the PMG described by Uversky (2). Similar molecular mobility was previously reported by Wall et al. (31) from x-ray diffraction measurements on SNase.

At higher pressure, c drops toward 1 for an unfolded, linear chain, as might be expected for the pressure-unfolding process. Simultaneously, d_min increases toward ∼1.8 and d_f drops toward the same value with a projected unfolded structure just below 4000 bar (Fig. 2 b, circle). The increase in d_min indicates that the minimum path becomes more convoluted and longer as the folds are released.

Although the dimensional analysis displays a gradual unfolding with pressure between an asymmetric regular-object, possibly misfolded (3) state (d_min = 1) and a totally unfolded state at high pressures (c = 1), R_g (Fig. 2 b), as well as p and φ_Br (Fig. 2 c), displays an exponential dependence on pressure that might be interpreted as a rapid transition such as that seen in a two-state model. This discrepancy is due to the exponential relationships between the dimensions of Fig. 2 b and R_g, p, and z.

An example using cytochrome c

SAXS studies of cyt c were first performed by Kataoka et al. (33). Kataoka studied acid-unfolded horse ferricytochrome c in an investigation of the unfolded-molten globule-native transition, as previously studied by CD and NMR (6,34). Cyt c has been used as a model protein for folding studies (35–38). Kataoka denatured cyt c by reducing the pH to ∼2 (acid-unfolded). He then induced folding from this acid-unfolded state by two methods: 1), addition of salt (NaCl), and 2), acetylation. Kataoka's SAXS data was digitized and fit using the unified function (18,19,23,25). Considering the acid-unfolded cyt c, SAXS shows a mass-fractal dimension of 2, a radius of gyration of 20.9 Å, and a connectivity dimension, c, of 1.1 (Table 2), indicating a near-linear chain with a sparse amount of folding (c would be 1 for unfolded) that leads to a fractal dimension slightly higher than the minimum path dimension of 1.9. The R_g of the coil is the largest measured by Kataoka (33), supporting an almost-unfolded structure. Cyt c has z = 105 residues, so the degree of folding for the acid-unfolded state is 0.34 using Eq. 4.

TABLE 2.

Unfolded and PMG states for cytochrome c

Sample	Rg (Å)	df	dmin	c	φBr	Description	Thermodynamic state
Acid unfolded	20.9	2.0	1.8	1.1	0.34	Weakly folded; good solvent	Expanded; coil dmin → 5/3
0.02 M NaCl	17.9	2.3	2.0	1.1	0.34	Weakly folded; nearly poor solvent	θ-state; dmin → 2
Acetylation	17.4	1.9	1.2	1.6	0.83	Misfolded	Sheetlike state; dmin → 1

Fit values using the published SAXS data of Kataoka et al. (33).

Two quite different mechanisms for collapse of the unfolded state are indicated by the fractal approach (Table 2):

1. The addition of salt (0.02 M NaCl) induces collapse by making the chain path more convoluted (d_min increases to ∼2), making d_f higher, whereas the chain folding is identical to the acid-unfolded state (c, φ_Br). This is essentially coil collapse driven by reduction in solvent quality (residue-solvent interactions), since d_min approaches 2 for θ-coils in a poor solvent, similar to solution phase separation in synthetic polymers.

2. For acetylation, the protein is misfolded in a sheetlike structure similar to pH 5.5 SNase above, with d_min ≈ 1 (a nearly linear path exists through the structure). Thus, despite a mass-fractal dimension, d_f, close to the acid-unfolded state, the structure is quite different and more compact reflecting an asymmetric, crumpled-sheet-like, misfolded structure. This is essentially coil collapse by formation of secondary structure (residue-residue interaction) similar to SNase.

All three results in Table 2 display what would appear to be Gaussian scaling in a Kratky plot of Iq² versus q, since d_f is ∼2, but none of these conditions produces truly random walks!

An example using a bacterial group I ribozyme

RNA folding shows parallels to protein folding and the scaling approach can be extended to consider structural development in RNA associated with changes in counterion concentration. For example, the 195-nucleotide group I ribozyme obtained from pre-tRNA^Ile of the bacterium Azoarcus is stable with rapid folding and no significant trapped intermediates. Folding of this ribozyme involves three states, unfolded (U) at low ionic strengths; more ordered intermediate states (I_c) at 0.5 mM Mg⁺²; and a native state (N) at ionic concentrations >2 mM Mg⁺². A complete set of scattering data was presented by Caliskan et al. (39) and Chauhan et al. (40) for variable Mg²⁺ concentrations for this intron (Fig. 3). At high Mg²⁺ concentrations, the intron collapses into a compact folded state, whereas at low counterion concentrations, an expanded state is observed. At very low counterion concentrations, <0.4 mM, small-angle x-ray scattering indicates two distinct structural size scales that may indicate two populations of structural conformations or the presence of a distinct substructure. In either case, a simple scaling analysis of the scattering at very low Mg²⁺ concentrations is not possible. For this reason, only Mg²⁺ concentrations >0.4 mM are considered here, though the radius of gyration, R_g, for the large-scale structure at low counterion concentrations has been given in the literature as ∼65 Å (39,40).

FIGURE 3.

Unified fits (18,19,23,25) to x-ray scattering data from Caliskan et al. (39) and Chauchan et al. (40) on the 195-nucleotide Azoarcus ribozyme for variable Mg²⁺ concentrations. (a) 4.26 mM (N). (b) 0.59 mM (I_c). (c) 0.47 mM (U).

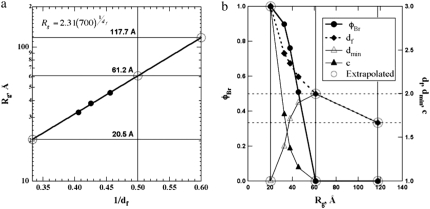
Scattering curves from three counterion concentrations are fit in Fig. 3. The 0.47-mM Mg²⁺ state is close to the unfolded (U) state in terms of R_g (Fig. 3 c). At 0.59 mM Mg²⁺, the structure is close to a proposed intermediate state (I_c) (39) (Fig. 3 b). The 4.26 mM Mg²⁺ state is close to the native state (N) (Fig. 3 a). The unified fits (18,19,23,25) result in a power-law regime (Eq. 7) that yields the mass-fractal dimension, d_f, as well as a Guinier regime (Eq. 6) that yields R_g. The molar mass of the RNA, z, is constant, so we can consider a logarithmic relationship between R_g and d_f, using Eq. 2, that suggests the plot of Fig. 4 a. This plot can be used to extrapolate to the three expected limiting scaling states at d_f = 3, for a fully collapsed chain; at d_f = 2, for Gaussian scaling where the chain is unfolded but near the solubility limit; and at d_f = 5/3, for good solvent scaling where the chain is fully solvated.

FIGURE 4.

Scattering-fit results and extrapolated values for the data from Fig. 3 (39,40) on Azoarcus ribozyme for variable Mg²⁺ concentrations. (a) R_g versus 1/d_f. Limits of d_f are 3, 2, and 5/3 for three-dimensional, Gaussian, and good-solvent (self-avoiding walk) states, respectively. From this plot, the limiting sizes (circles) can be determined and used to extend the measured dimensions and φ_Br in b. (b) Mole fraction folding (left), φ_Br, and three measured dimensions, with the limiting values (right) showing decreasing tortuosity, d_min, and increasing connectivity, c, with folding (lower R_g). (Circled values at R_g = 20.5, 61.2, and 117.7 Å are predicted for d_f = 3, 2, and 5/3, respectively.) Horizontal dashed lines indicate d_f = 2 and 5/3.

Fig. 4 a suggests that the fully solvated chain (right) is first reduced in size due to reduction in solubility reaching a Gaussian state, and then is reduced in size due to folding to a globular three-dimensional state. This is probably a gross simplification of the actual folding process and experimental data from Caliskan et al. (39) does not support the existence of either a fully expanded coil (right) or a fully collapsed chain (far left). Rather, the native state in this ribozyme displays R_g ≈ 31 Å both from x-ray crystallography and from previous SAXS calculations (39,40) at high Mg²⁺ concentrations using the distance distribution function. From the scaling analysis (Fig. 3 a), the native state contains a folded molar fraction of ∼0.9, indicating that the native state of this intron retains ∼10 mol % of disordered (unfolded) regions. If the chain could fully fold to a three-dimensional globular structure, a radius of gyration of ∼21 Å would be expected (Fig. 4 a). Similarly, the fully expanded ribozyme in experiments displays R_g ∼ 65Å (38,39), which is close to the extrapolated value of 61.2 Å for a Gaussian (d_f = 2) unfolded chain (Fig. 4 a). This may indicate that this ribozyme does not achieve good solvent behavior but can only achieve expansion to a θ-solvent condition near the thermodynamic limit for precipitation. If the coil could achieve good solvent conditions, a much more expanded chain is expected with R_g ≈ 120 Å (Fig. 4 a).

Fig. 4 b shows the behavior of φ_Br, d_f, d_min, and c with R_g for this ribozyme. The three measured scattering curves result in the second to fourth set of values (left to right), whereas the first and last two values that are circled are associated with 3, 2, and 5/3 dimension structures as extrapolated in Fig. 4 a. d_min increases with increasing R_g because chain unfolding causes a more tortuous minimum path through the structure, that is, fewer structural “short cuts” exist as the chain unfolds. At Mg⁺² concentrations of 0.59 and 4.26 mM, d_min is >5/3, indicating that the coil dimension for a fully unfolded chain may be approaching a Gaussian state where both d_f and d_min approach 2 (Fig. 4 b, upper dashed horizontal line). This is approximated at R_g = 61.2 in Fig. 4 b. This behavior indicates that at high counterion concentrations and at room temperature, this group I ribozyme may be marginally soluble and close to the θ-point, rather than displaying good solvent behavior.

CONCLUSION

Quantification of disordered, and especially partially disordered, states in biomolecules is important for the description of folding processes, misfolding diseases, and biomolecules that show enzymatic activity in the partially unfolded state. A scaling model has been proposed to quantify the molar degree of folding in biomolecules. The model also yields a dimensional description of the structure that can be used to extrapolate properties and to compare observed and theoretical conformations. The model can be applied to simulations and a variety of analytic techniques. The model is demonstrated through application to small-angle x-ray scattering data from two protein-folding studies and one RNA-folding study.

The SNase results indicate how the fractal model can view structural changes along a folding, or in this case, an unfolding pathway from a misfolded state. It is demonstrated that some structural measures can display a two-state model, although scaling parameters show a continuous transition. The cyt c results show three nonnative states: good-solvent expanded coil; poor-solvent coil; and a low-dimensional (sheet-structure), misfolded chain. A statistical interpretation of proteins can yield unique information concerning the extent of folding, and can define the unfolded state in terms of quantitative, statistical features. This information will be of use in understanding “natively” unfolded proteins, as well as folding pathways generally. Moreover, the statistical approach has promise for understanding structural transitions in other biomolecules, such as RNA. For the Azoarcus group I ribozyme, it was shown that residual disorder may exist in the enzymatically active, native state and that the unfolded state corresponds to a Gaussian structure reflecting close to theta conditions.