Darcy Permeability of Agarose-Glycosaminoglycan Gels Analyzed Using Fiber-Mixture and Donnan Models

Abstract

Agarose-glycosaminoglycan (GAG) membranes were synthesized to provide a model system in which the factors controlling the Darcy (or hydraulic) permeability could be assessed in composite gels of biological relevance. The membranes contained a GAG (chondroitin sulfate) that was covalently bound to agarose via terminal amine groups, and the variables examined were GAG concentration and solution ionic strength. The addition of even small amounts of GAG (0.4 vol/vol %) resulted in a twofold reduction in the Darcy permeability of 3 vol/vol % agarose gels. Electrokinetic coupling, caused by the negative charge of the GAG, resulted in an additional twofold reduction in the open-circuit permeability when the ionic strength was decreased from 1 M to 0.01 M. A microstructural hydrodynamic model was developed, based on a mixture of neutral, coarse fibers (agarose fibrils), and fine, charged fibers (GAG chains). Heterogeneity within agarose gels was modeled by assuming that fiber-rich, spherical inclusions were distributed throughout a fiber-poor matrix. That model accurately predicted the Darcy permeability when the ionic strength was high enough to suppress the effects of charge, but underestimated the influence of ionic strength. A more macroscopic approach, based on Donnan equilibria, better captured the reductions in Darcy permeability caused by GAG charge.

INTRODUCTION

The resistances of fibrous media to water flow influence transport across capillary walls and other biological barriers, and can have an important bearing on the distribution of nutrients, cytokines, and drugs within body tissues. In glomerular capillaries, for example, the hydraulic permeability of the vessel wall is a crucial property, as kidney function requires that a large volume of ultrafiltrate be produced daily. The structures that filtered water must traverse include the endothelial glycocalyx and the glomerular basement membrane. With regard to solute transport in other organs, the larger a molecule, the smaller its diffusivity, and the more likely it is that convection (transport via bulk flow) will control its extravascular distribution. Whether in the microvasculature or the interstitial spaces of tissues, the flow resistance is determined largely by gellike materials containing crosslinked mixtures of proteins, glycosaminoglycans (GAGs), and other biopolymers, and consisting mainly of water. The polymeric chains that act as fibers vary in hydrodynamic radius, net charge, spatial orientation, and other properties. Thus, a quantitative understanding of flow through such fiber mixtures is relevant to work ranging from the characterization of disease processes to the improvement of strategies for drug delivery.

The fluid velocity (〈v〉) in an isotropic fibrous medium is related to the pressure gradient (〈∇P〉) by Darcy's law,

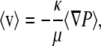(1)

where μ is the fluid viscosity and κ is the Darcy permeability. The angle brackets denote averaging over a length scale that is large compared to the interfiber spacing, but small relative to the system being modeled. The hydraulic permeability, k = κ/μ, is sometimes used as the material property. For uncharged, rigid fibers, κ depends solely on the microstructural geometry (fiber radii, volume fractions, and orientations); for charged fibers, it is affected also by the charge density and the ionic strength of the solution. Pressure-flow relationships in charged, porous, or fibrous media are influenced by electrokinetic coupling (1,2), making the apparent hydraulic permeability dependent on the macroscopic electrical constraints. Throughout this article, κ refers to the Darcy permeability under open-circuit conditions (no net current).

Whereas Darcy or hydraulic permeabilities have been reported for numerous materials with uniform fiber radii (3), data for flow through fiber mixtures are limited. Such information is available for glomerular basement membrane (4), cartilage (5), and other biological tissues (6), as well as for agarose-dextran hydrogels (7). It has been shown that low amounts of small-diameter fibers can greatly decrease the value of κ for a fiber mixture (7,8). Important effects of charge have been revealed by studies of charged poly(methacrylic acid) membranes (9), dextran sulfate matrices (10), and cartilaginous soft tissues (11,12). In each case, the permeability was decreased at lower ionic strengths or higher charge densities.

This study had two objectives. The first was to measure κ in synthetic gels that consisted of a mixture of neutral and charged fibers. The composite gels were designed to mimic biological materials, but could be made in more convenient form (as supported membranes) and with controlled composition. Glycosaminoglycans were attached covalently to agarose, the GAG (chondroitin sulfate) being a representative biological polyanion and the agarose selected because of its convenient properties. Agarose gels can be readily cast into membranes that exhibit little swelling or shrinkage in response to mechanical or osmotic pressures (13,14), the fibrils act as uncharged, rigid fibers with little Brownian motion (15), and the transport properties of pure agarose have been relatively well studied (16–18). The second objective was to test the ability of electrokinetic models, either microstructural or macroscopic, to explain the dependence of κ on the GAG concentration and the solution ionic strength. The microstructural approach was based largely on electrical double-layer calculations for arrays of parallel fibers, whereas the macroscopic model employed Donnan equilibria. Among the issues that had to be addressed were how to predict κ for a bimodal fiber mixture, given the mixture composition and the properties of the individual components, and how to account for spatial heterogeneity in materials such as agarose. As will be shown, either type of model was able to capture the main experimental trends, using few adjustable parameters.

EXPERIMENTAL METHODS

Membrane synthesis

Agarose-GAG membranes were synthesized as described previously (19). Briefly, agarose gels were cast on a polyester support mesh and compressed between two glass slides with spacers to a uniform thickness. The membranes were activated with 1-cyano-4-dimethylaminopyridinium tetrafluoroborate and exposed to a GAG (chondroitin sulfate) solution. The resulting membranes contained GAG which was covalently bound to the agarose by terminal amine groups. The bound GAG content of the membranes was adjusted by varying the conditions during activation and attachment. The mass of GAG in a membrane was measured by a toluidine blue dye assay (19). All gels used type VI agarose (Product #A3893, Sigma, St. Louis, MO) and chondroitin sulfate A from bovine trachea (Product # 230687, Calbiochem, La Jolla, CA).

Permeability measurements

The Darcy permeability of each mesh-reinforced gel was measured as described previously (7,14). The gel membrane was placed in a 10 mL ultrafiltration cell (Model 8010, Millipore, Bedford, MA). The cell reservoir was filled with a KCl-phosphate buffer solution at pH 7.4. The buffer was 0.01 M sodium phosphate with a balance of KCl to create solutions with an ionic strength of 0.1 M to 1 M. For ionic strengths <0.1 M, the buffer was 0.005 M sodium phosphate with the balance as KCl. All buffers contained ∼0.00015 M sodium azide to inhibit microbial growth.

The ultrafiltration cell was pressurized with nitrogen to achieve a transmembrane pressure drop of ∼10 kPa, unless otherwise noted. The pressure drop was monitored using a pressure transducer (Model CP379, Validyne Engineering, Northridge, CA), and corrections were made to account for hydrostatic pressure differences. Samples of the filtrate were collected over timed intervals and weighed to determine the steady-state volumetric flow rate (Q). The exposed area of the membrane (A) was 366 mm². The thickness of the gel (δ) was determined by confining the membrane between two microscope slides of known thickness and measuring the combined thickness with a micrometer. Gel thicknesses were generally 70–75 μm. The Darcy permeability was then calculated as

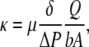(2)

where ΔP is the pressure drop across the membrane and b is a correction factor that accounts for the increased flow resistance due to the polyester mesh support. The mesh correction factor was evaluated via finite element calculations with COMSOL Multiphysics (COMSOL, Stockholm, Sweden), similar to what was done previously (14). Using mesh dimensions that we measured by light microscopy (fiber radius of 22.5 μm and center-to-center spacing of 88 μm), b = 0.363 for a 70-μm-thick membrane and increased for larger values of δ.

MODEL DEVELOPMENT

Overview

There are no simulations available in the literature for viscous flow through disordered mixtures of neutral and charged fibers, or even for a single type of charged fiber with random orientations. Thus, it was necessary to construct composite models based on results for simpler situations. Two types of models were used, differing mainly in how charge effects were described. The microstructural model made use of finite-element results for flow through arrays of parallel fibers, either parallel to the fiber axes (i.e., axial) or perpendicular to the axes (i.e., transverse). The calculations included the flow-induced distortion of the double layer surrounding each fiber. The macroscopic model ignored the details of the double-layer structure, employing instead an average concentration of fixed charges and applying Donnan equilibria at the boundaries. Common features of the two models are the use of neutral-fiber results to describe flow through pure agarose, mixing rules to combine results for two fiber types, and provisions for spatial heterogeneity within the gels. The two approaches are described now in turn.

Microstructural model

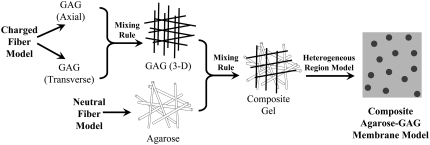
Information flow in the microstructural model is summarized in Fig. 1. To estimate the permeability of pure GAG, results for axial or transverse flow through parallel arrays of charged fibers were combined using a mixing rule that was designed to account for disorder in the orientation of the GAG chains. The permeability of pure agarose was predicted from available results for randomly oriented, neutral fibers. Then, the permeability of an agarose-GAG composite was calculated by applying another mixing rule. Finally, because there is evidence (discussed later) that agarose fibrils are not distributed homogeneously, provision was made for the presence of fiber-rich and fiber-poor regions within a gel.

FIGURE 1.

Elements of the microstructural model for the hydraulic permeability of an agarose-GAG membrane. Included were: a periodic, charged fiber model for GAG; a random, neutral fiber model for agarose; a mixing rule (applied twice) to average the permeabilities of differing fiber orientations or types; and a representation of agarose heterogeneity, as fiber clumps within a less dense matrix.

The double-layer calculations for parallel arrays of charged fibers were as detailed previously (2). Briefly, a commercial finite element package (COMSOL Multiphysics), was used to solve the continuity equation, Stokes' equation (with an electrical body force), and the conservation equations for mobile ions, via a regular perturbation scheme. The perturbation parameter (β), which is proportional to the applied velocity, may be interpreted as the strength of the flow-induced electric field relative to that in an equilibrium double layer. Both O(1) and O(β) terms were computed, the former corresponding to a static system. Open-circuit conditions were used to evaluate κ for either axial or transverse flow. For randomly oriented neutral fibers of uniform radius r and volume fraction φ, the Darcy permeability was calculated using

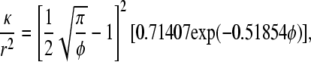(3)

as proposed by Clague et al. (20). This is the expression applied to pure agarose.

For a mixture consisting either of two fiber types or two fiber orientations, the overall permeability was computed as

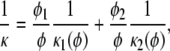(4)

where κ_i is the permeability of fiber type i, φ_i is its volume fraction, and φ is the total fiber volume fraction. As indicated, the individual permeabilities (κ_i) were each calculated by using the total volume fraction in the function appropriate for that type of fiber, and the resistivities (1/κ_i) were multiplied by volumetric weighting factors (φ_i/φ) to account for the relative amounts of the two types. Extensive comparisons showed this mixing rule to be the most reliable of several alternatives for neutral fibers of varying size or orientation and for mixtures of neutral and charged fibers (2). In using Eq. 4 to estimate κ for disordered arrays of GAG, the resistivities for axial and transverse flow were weighted as 1/3 and 2/3, respectively.

Heterogeneity within gels was accounted for by assuming that fiber-rich regions (fiber clumps) were distributed throughout a less dense matrix. For simplicity, the clumps were assumed to be spherical. Based on the formal analogy between Darcy flow and other processes in which the scalar field variable is governed by Laplace's equation, the effective permeability of such a composite was computed as given by Maxwell (21),

(5)

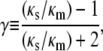(6)

where ɛ is the volume fraction of spheres and κ_m and κ_s are the permeabilities of the matrix and spherical inclusions, respectively. Although Eq. 5 was derived by assuming that ɛ → 0, for the conditions of interest here it yields values of κ_eff/κ_m that are within 2% of those obtained from extensions of Maxwell's analysis to more concentrated systems (22,23). Since GAG binds to active sites on agarose fibers, it was assumed that the GAG concentration in each region was proportional to the agarose concentration. Provided that the system dimensions greatly exceed the sphere-to-sphere spacing, κ_eff is independent of the sphere size and a function only of ɛ and γ (22). As will be discussed, heterogeneities within agarose gels appear to be fine enough to justify such an assumption.

The calculations with the charged fiber model were based on water at room temperature with ion diffusivities of 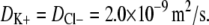The literature generally estimates the chondroitin sulfate charge as corresponding to one sulfate substitution and one carboxyl group per disaccharide, GAG radii as 0.5–1.0 nm, and length as 1 nm per disaccharide (corresponding to 105 nm for a 50 kDa chondroitin sulfate) (1,24–26). The properties of GAG fibers used here were r = 0.5 nm, a net charge of −2 per disaccharide, a length of 1 nm per disaccharide, and a disaccharide molecular weight of 457 Da. These properties resulted in a surface charge density (σ) of −100 mC/m², which is consistent with other values used in the literature (1,27). Some calculations were also performed for r = 1.0 nm, which corresponds to σ = −50 mC/m². Agarose fibers were modeled as being neutral, with r = 1.6 nm and a mass density of 1.025 g/mL (28). The volume fractions of agarose and GAG were known for each experiment (based on the measured masses of each). The only adjustable parameters in the model were the volume fraction of spherical clumps (ɛ) and the volume fraction of solid (agarose plus GAG) in the clumps divided by that in the surrounding matrix (φ_s/φ_m). A value of ɛ was selected arbitrarily (typically 0.1), and then the ratio φ_s/φ_m was chosen to fit the permeability measured in agarose blanks. If a higher value of ɛ was chosen, then a lower value of φ_s/φ_m was required to fit the blank permeability; the converse was true for lower values of ɛ. The model, with the fitted values of φ_s/φ_m and ɛ, could then be used to predict the hydraulic permeability of similar agarose gels with specified GAG contents. The results were found to be insensitive to the choice for ɛ, the value of κ_eff for the highest GAG content varying by <0.5% for clump volume fractions in the range 0 ≤ ɛ ≤ 0.5. In effect, then, adjusting the value of φ_s/φ_m provided just one degree of freedom in fitting the permeability data.

Macroscopic model

The information flow in the macroscopic model was similar to that depicted in Fig. 1, except that in this case the GAG chains were treated initially as uncharged fibers. Eq. 3 was applied once again to agarose. Then, the mixing rule in Eq. 4 was used to estimate the permeability of a mixture of agarose and neutral GAG, and Eqs. 5 and 6 used to account for spatial heterogeneity. (For some calculations, an experimental value of κ, obtained under conditions in which charge effects in the agarose-GAG gel were suppressed, was used instead to provide the permeability of the neutral composite.) Charge effects were added in the last step, in which the Donnan model was applied. In such a model all structural details are ignored, and the fixed charge is treated as if it were uniformly distributed throughout the membrane (as opposed to residing on fiber surfaces). Because no microstructural assumptions are involved in the description of charge effects, the Donnan model is independent of how the permeability for the uncharged membrane is obtained.

While Eq. 3 could be used to model a disordered array of neutral GAG fibers, we chose to employ results for axial or transverse flow through regular arrays of fibers, combining them using Eq. 4. This was done so that the neutral GAG permeability in the microstructural and macroscopic models would be the same. Thus, any differences in the predictions of the two models are attributable entirely to their treatment of charge effects, and are not influenced by errors in the mixing rules. The result used for axial flow through a square array of neutral fibers is (29)

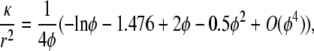(7)

and that for transverse flow is (30)

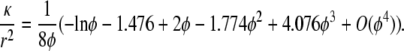(8)

The use of Eqs. 4, 7, and 8 gives results that differ by an average of 25% from Eq. 3.

The formulation of the Donnan model was similar to ones described previously (31,32). The Nernst-Planck equation was used to evaluate fluxes of univalent cations and anions within the membrane, and local electroneutrality (including fixed charges) was imposed. Donnan equilibria were applied at the boundaries, with equal salt concentrations in the two external solutions. Zero transmembrane current was assumed. The result was

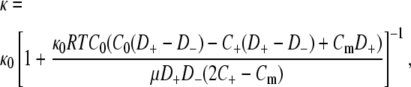(9)

where κ₀ is the permeability of an equivalent uncharged membrane, C₀ is the ionic strength of the bulk solution, C_m is the concentration of fixed negative charges, D_± are the diffusivities of the mobile anions, and RT is the product of the gas constant and absolute temperature. The cation concentration in the membrane (C₊) was given by

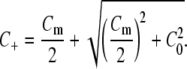(10)

Except for the replacement of σ by C_m, the parameters for the macroscopic model were the same as for the microstructural model. The concentration of fixed charge in the membrane (C_m) was calculated from the GAG volume fraction, surface charge density, and fiber radius. Alternatively, C_m could be estimated by fitting the experimental data.

RESULTS

The suitability of agarose-GAG gels for hydraulic permeability measurements was evaluated in preliminary experiments. To confirm that the composition of the gels remained constant, the GAG content and Darcy permeability were measured before and after 11 h of filtration with 0.1 M buffer. Both the Darcy permeability (253 ± 49 nm² initial and 240 ± 44 nm² final) and the GAG content (73 ± 6 mg GAG/g agarose initial and 70 ± 8 mg/g final) were unchanged. The permeability of agarose-GAG gels with 3 vol/vol % agarose and 129 mg GAG/g agarose showed a pressure dependence similar to that reported previously for pure agarose, decreasing on average by 1.0–1.2%/kPa over the range 0.5–20 kPa (8,14). However, most of this decrease occurred at very low applied pressures, such that the change above 5 kPa was negligible (<0.6%/kPa). This suggests that the 9 kPa pressure gradient applied during most permeability measurements did not significantly alter the fiber volume fraction.

To test whether electrostatic interactions among the GAG fibers changed the structure of the gels, two groups of 3 vol/vol % agarose gels with high GAG content (129 mg GAG/g agarose) were equilibrated overnight in 20–25 mL of buffers of differing ionic strength. With ionic strengths of either 0.01 M or 1 M, there was no change in the thickness of the agarose-GAG gels. Also, the permeabilities of two high-GAG gels measured for a random sequence of ionic strengths showed no evidence of hysteresis. Thus, the agarose-GAG gels had the same dimensional stability as pure agarose, the gel structure apparently being determined primarily by the physical cross-linking of the agarose fibers.

Once the preliminary experiments were complete, the permeability was measured for a range of ionic strengths and GAG contents. Six membranes were studied at each of three compositions, all with 3 vol/vol % agarose: no GAG; medium GAG (54 ± 0.3 mg GAG/g agarose or φ_GAG = 0.0017); and high GAG (129 ± 14 mg GAG/g agarose, or φ_GAG = 0.0039). The ionic strength was varied from 0.011 M to 1.0 M. As noted previously (14), there tends to be significant sample-to-sample variation in the permeability of pure agarose. Accordingly, before GAG binding, the agarose gels were prescreened to ensure that the mean permeability of each group of gels was the same (within experimental error). Although there was no evidence of hysteresis, the experiments at different ionic strengths were performed in a random order for each gel.

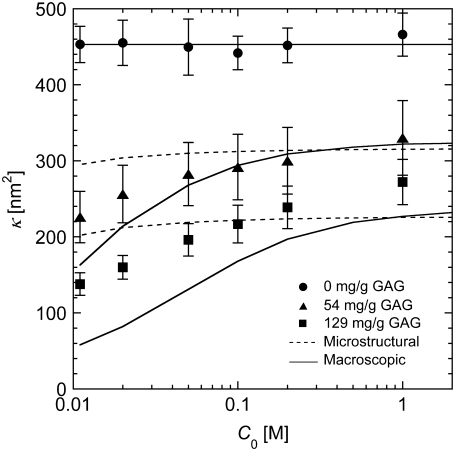
The Darcy permeabilities are plotted in Fig. 2 as a function of ionic strength, for each of the three GAG contents. The permeability of the blank gels was independent of ionic strength, confirming that pure agarose has negligible net charge. For the agarose-GAG gels, the permeability fell significantly as the ionic strength was reduced from 1.0 M to 0.011 M, decreasing by 32% and 49%, respectively, at medium and high GAG. Even at high ionic strengths, where charge effects were suppressed, the permeability was reduced significantly by the small amounts of GAG fibers (φ_GAG = 0.0017 and 0.0039, respectively, for medium and high GAG). At 1.0 M, the decreases for medium and high GAG were 29% and 41%, respectively, relative to pure agarose. Assuming fiber radii of 1.6 nm for agarose and 0.5 nm for GAG, the ratio of GAG fiber length to agarose fiber length was 0.57:1 and 1.35:1 for medium and high GAG, respectively. Slender body theory predicts that the permeability is primarily a function of the fiber length per unit volume (33). Thus, given the comparable total lengths of agarose and GAG chains, it is not surprising that the effects of GAG were significant, even in the absence of charge effects.

FIGURE 2.

Darcy permeability (κ) of agarose-GAG gels for a range of ionic strengths and GAG contents. The data are for 3 vol/vol % agarose and three GAG levels: agarose without GAG (•); 54 mg GAG/g agarose (▴); and 129 mg GAG/g agarose (▪). Error bars are one standard deviation for n = 6. The predictions of the microstructural and macroscopic (Donnan) models are shown by dashed and solid curves, respectively. The overall volume fractions corresponding to the three GAG contents are φ_GAG = 0, 0.0017, and 0.0039, respectively. The parameters used to describe gel heterogeneity were ɛ = 0.1 and φ_m/φ_s = 0.020.

Also shown in Fig. 2 are the theoretical predictions of the microstructural and macroscopic models. Recall that the parameters describing agarose heterogeneity (ɛ and φ_s/φ_m) were chosen to yield the correct permeability for pure agarose. It is seen that, without additional adjustable parameters, the predictions at high ionic strengths were quite accurate for each GAG content Also, both models correctly yielded decreases in permeability with decreasing ionic strength. However, the microstructural model tended to underestimate the effects of ionic strength, whereas the macroscopic model overestimated them.

As noted earlier, estimates of GAG radii in the literature are generally between 0.5 and 1.0 nm, and we chose the lower value. When a radius of 1.0 nm was used instead of 0.5 nm, the decrease in permeability from the addition of GAG was underestimated. For a GAG radius of 1.0 nm and an ionic strength of 0.1 M, the predicted permeability with high GAG was only 28% lower than that for pure agarose. By comparison, the reduction predicted using a GAG radius of 0.5 nm was 51%, closely matching the experimental reduction of 52%. Thus, the results in Fig. 2 support the use of a GAG radius of 0.5 nm, and the corresponding surface charge density for chondroitin sulfate of −100 mC/m². The performance of the models is discussed in greater detail in the next section.

DISCUSSION

Agarose-GAG membranes were synthesized to provide a model system in which the effects of fiber size, volume fraction, and charge on the Darcy permeability could be examined in composite gels of biological relevance. There were two key experimental findings. First, the addition of small amounts of GAG caused significant decreases in the permeability, even at ionic strengths high enough to suppress the effects of charge. At the highest GAG concentration, where the volume of GAG chains was still just 1/10th that of agarose fibrils, the permeability at high ionic strength was twofold lower than that of pure agarose. This result of adding small amounts of fine fibers to gels made up of coarser fibers, in the absence of charge effects, is similar to that seen previously with agarose-dextran gels (7,8). The second key finding is that the effects of charge on the open-circuit permeability were also very significant. For the highest GAG concentration, reducing the ionic strength resulted in an additional twofold reduction in the permeability, or roughly a fourfold reduction overall. Although the Darcy permeability of synthetic GAG-containing membranes seems not to have been studied previously, these effects of ionic strength are qualitatively consistent with the behavior of other charged gels (9–12).

Although the two-component gels that we studied are much simpler than those in basement membranes or the interstitial spaces of tissues, predicting their Darcy permeabilities from first principles is still a challenge. Results of hydrodynamic simulations for disordered mixtures of neutral and charged fibers have not been reported and, given the difficulty of such calculations, useful exact results are unlikely to be available soon. The only practical alternative at present is a multistep approach that assembles results for simpler situations. There were three main difficulties in constructing such models for agarose-GAG gels: 1), identifying a mixing rule that can predict the permeability of a fiber mixture from its composition and the properties of its individual components; 2), describing the effects of spatial heterogeneity in agarose; and 3), modeling the effects of GAG charge. The first issue was considered in detail previously (2), where it was concluded that Eq. 4 is the most reliable of several mixing rules that have been proposed. In comparing its predictions with exact results for a variety of mixtures, involving differences in fiber diameter, orientation, and/or charge, the root-mean-square error was 24%. In the remainder of this article we focus on the other two difficulties.

Spatial heterogeneity within pure agarose gels is suggested by both functional and structural observations. The Darcy permeability consistently exceeds predictions from models for random arrays of neutral fibers, by factors as large as 3–4 (7,14,33). As with a mixture of pore sizes, an inhomogeneous distribution of fibers will tend to increase the hydraulic permeability for a given void volume, the gain from large channels exceeding the loss from small ones. Sieving results for macromolecules in agarose membranes are also best explained by some form of spatial heterogeneity (8). Electron microscopy, dynamic light scattering, and turbidity measurements have provided more direct evidence of an uneven distribution of fiber spacings (34–36). It has been hypothesized that the agarose fibers tend to aggregate in cross-linked regions during gelation, leaving the surrounding regions fiber-depleted (37,38). The heterogeneities are microscopic, with estimated length scales ranging from 0.3 to 10 μm (35,38–40). As such lengths are much smaller than our membrane thicknesses (70 μm), the heterogeneities are too small to create membrane defects (e.g., pinholes). However, they are large enough to span many fibers, if one uses 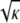(= 16 nm in 3 vol/vol % agarose) as an estimate of the interfiber spacing.

We chose to model the agarose heterogeneities as high-density spherical regions (fiber clumps) embedded in a less dense matrix. In such an approach, κ_s < κ_m. An alternative way to employ Eq. 5 would be to postulate fiber-poor voids surrounded by a fiber-rich matrix, in which case κ_s > κ_m. One might also assume regions of differing fiber density arranged either in series or in parallel, in which case

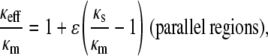(11)

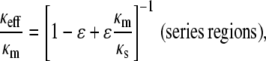(12)

where ɛ is the volume fraction of the region designated as s. (The m and s notations have been retained from Eq. 5, although no longer referring to “matrix” and “spheres”.) Schematics of these four configurations are shown in Fig. 3.

FIGURE 3.

Schematics of models for gels with regions of higher fiber density (shaded) and lower fiber density (open): (a) layers in series, (b) layers in parallel, (c) denser clumps, and (d) less dense voids.

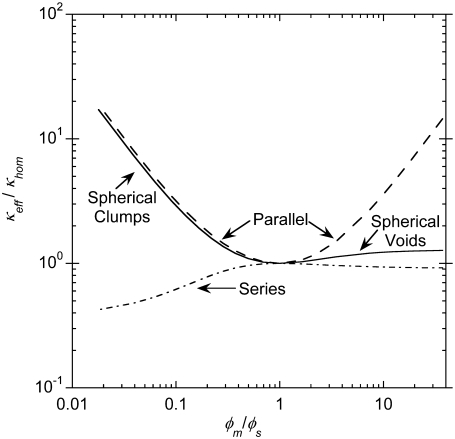
Results using the four models for heterogeneity (clumps, voids, parallel regions, series regions) are shown in Fig. 4. The effective Darcy permeability relative to that for a homogeneous material (κ_eff/κ_hom) is plotted as a function of the ratio of fiber volume fractions for the two regions (φ_m/φ_s). In each case the values of ɛ were adjusted so that the total number of fibers in the system remained the same, and Eq. 3 was used to compute κ_m and κ_s from the volume fractions and assumed fiber radius. As shown, the series model never yielded a permeability increase, whereas the void model gave only small increases. Only the clump and parallel models predicted values of κ_eff/κ_hom large enough to be consistent with the observed three-to-fourfold increase in agarose permeability. We preferred the clump model, as it seems more consistent with the structural observations mentioned above. Other ways to model heterogeneity have been proposed, such as a checkerboard-style arrangement of alternating unit cells (41,42), but they seem to have no inherent advantages over those we considered.

FIGURE 4.

Effective Darcy permeability of a two-region composite (κ_eff) compared to that for a homogeneous system with the same total fiber volume fraction (κ_hom). Permeabilities for various models are shown as a function of the ratio of the solid volume fractions in the two regions (φ_m/φ_s). In each case φ = 0.03 (overall volume fraction of solid) and ɛ = 0.1 (fraction of total volume occupied by region s). The results for spherical inclusions (clumps or voids), parallel regions, and series regions are based on Eqs. 5, 11, and 12, respectively; those for a homogeneous material are from Eq. 3.

The microstructural model, including the provision for agarose heterogeneity, can be applied also to agarose-dextran gels that were studied previously (7,8). Those gels were prepared by allowing a 500 kDa neutral dextran to equilibrate within an agarose gel, and using electron beam irradiation to create covalent bonds. In applying the model to these gels we assumed that the dextran concentration was uniform throughout the composite gel and that the dextran chains behaved as randomly-oriented neutral fibers with r = 0.33 nm. Equation 3 was used to calculate the permeabilities of both components (dextran as well as agarose), and then the mixing rule and heterogeneity correction were applied. Fig. 5 compares the predicted Darcy permeabilities with those measured for either 4 vol/vol % or 8 vol/vol % agarose gels with variable dextran content. In general, the model described well the decreases in permeability that accompanied increases in either the agarose or the dextran volume fraction. Thus, as seen already in Fig. 2 at high ionic strength, the microstructural model successfully captured the effect of adding fine fibers to the relatively coarse agarose fibrils. In that there was a wider variation in fiber volume fractions in the agarose-dextran gels, the data in Fig. 5 provide a more severe test of predictions for uncharged, composite gels than do the aforementioned results for agarose-GAG gels.

FIGURE 5.

Darcy permeability (κ) of agarose-dextran gels. The results are for 4 vol/vol % agarose (▪,□) or 8 vol/vol % agarose (▴,Δ), the open symbols representing data from Kosto and Deen (8) and the solid symbols data from White and Deen (7). (The results from the latter study are for 500 kDa dextran, with values of φ_dex corrected by using the binding efficiencies measured in the former study.) The curves are predictions obtained from a fiber-mixture model with r_a = 1.6 nm, r_dex = 0.33 nm, ɛ = 0.1, and φ_m/φ_s = 0.11 and 0.14 for 4 vol/vol % and 8 vol/vol % agarose, respectively. The heterogeneity parameters (ɛ and φ_m/φ_s) were chosen to fit the data of Kosto and Deen (8) for pure agarose.

Modeling the effects of charge presents its own set of challenges. Whereas the microstructural model gave good predictions for neutral gels or gels where charge effects were suppressed, it underestimated the reductions in Darcy permeability caused by decreases in ionic strength (Fig. 2). Although there are several possible sources of error, a clue concerning this failure is provided by results calculated for axial or transverse flow through regular arrays of a single type of charged fiber (not shown). For the microstructural results in Fig. 2, there was only a 9% decrease in the predicted permeability of the high GAG gels when the ionic strength was decreased from 0.1 M to 0.01 M. However, calculations for flow through an array having an equivalent volume of GAG fibers (φ = 0.004), but in the absence of agarose, yielded a 24% decrease. This suggests that the effects of ionic strength were minimized somehow by the way in which we modeled agarose heterogeneity. A likely problem is that, in our modular approach, a zero current condition was necessarily imposed separately within each region, matrix and spheres. In an actual heterogeneous material, zero overall current is all that is required under open-circuit conditions. Thus, flow in the two regions may be coupled electrically in ways that could be captured only by a more complex microstructural model. In one such model, the effect of charged inclusions within a neutral gel have been shown to have long-range effects on the electrokinetic coupling, even when Debye lengths are 1–2 orders of magnitude smaller than the charged inclusions (43). Other sources of error include the mixing rule and the assumption that the GAG concentration in each region was proportional to the agarose concentration.

In contrast, the macroscopic model overestimated the effects of ionic strength, when the average charge concentration (C_m) was based on the total GAG content (Fig. 2). However, the flow should have occurred mainly through the matrix, where the agarose and GAG concentrations were each lower than the average values. Thus, the appropriate C_m value for the macroscopic model may be lower than we had supposed. Fig. 6 shows results obtained by adjusting C_m to fit the permeability data (minimizing the relative least-square errors). To avoid errors stemming from calculations for neutral fibers, the neutral permeability used here was the experimental value at 1 M ionic strength. With C_m = 5.2 and 8.8 meq/L for medium and high GAG contents, respectively, the macroscopic model is seen now to represent the data quite well. As expected, these effective charge concentrations are lower than those based on the total GAG contents, 7.0 and 16.2 meq/L, respectively.

FIGURE 6.

Darcy permeability (κ) of agarose-GAG gels, compared to predictions of the macroscopic model. The data are as in Fig. 2, and the curves are now best-fit results obtained by adjusting the fixed-charge concentrations and neutral permeability. The best-fit charge concentrations were C_m = 5.2 meq/L for 54 mg/g and C_m = 8.8 meq/L for 129 mg/g. In calculations for GAG-containing gels, the permeability of the uncharged system (κ₀) was equated to the measured value at C₀ = 1 M.

A closer examination of the results in Fig. 6 reveals certain inconsistencies with the fiber models. For example, if ɛ = 0.1, a matrix charge concentration of 8.8 meq/L and average concentration of 16.2 meq/L imply a GAG concentration in the matrix that is 0.11 times that in the spherical regions. By assumption, this is the same as the ratio of agarose concentrations in the two regions. However, the neutral permeabilities were explained by a concentration ratio for both components equal to φ_m/φ_s = 0.020. Given the absence of structural information in the macroscopic model, such inconsistencies are not surprising. Indeed, the macroscopic model performed remarkably well, given that one of the usual requirements for smearing of charge was not met. That is, the experimental Debye lengths (ranging from 0.3 nm at 1.0 M to 3 nm at 0.011 M) did not exceed typical interfiber spacings (estimated as 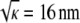for high GAG at 1 M).

In summary, agarose-GAG gels were synthesized to provide a model system that has some of the structural and functional complexity of biologically important materials. Two sources of complexity in these gels are the presence of a mixture of coarse fibrils (agarose) and fine polymer chains (GAG), and the presence of a negative fixed charge on the latter. A hydrodynamic model based on a mixture of rigid, cylindrical fibers was found to explain the measured Darcy permeabilities very well at high ionic strengths, where charge effects were negligible, provided that the heterogeneity of agarose gels was taken into account. Heterogeneity was modeled by postulating a structure consisting of fiber-rich spherical inclusions (fiber clumps) surrounded by a less-dense fiber matrix. A microstructural representation of charge effects was less successful, in that it underestimated the tendency of reductions in ionic strength to lower the open-circuit permeability. This deficiency may stem from practical limitations in applying the zero-current condition. Until more rigorous microstructural models can be developed, a macroscopic approach based on Donnan equilibria offers a reasonable alternative for describing the effects of charge on the Darcy permeability.