Abstract
We report on the x-ray absorption fine structure of the Fe2+ site in photosynthetic reaction centers from Rhodobacter sphaeroides. Crystallographic studies show that Fe2+ is ligated with four Nɛ atoms from four histidine (His) residues and two Oɛ atoms from a Glu residue. By considering multiple scattering contributions to the x-ray absorption fine structure function, we improved the structural resolution of the site: His residues were split into two groups, characterized by different Fe-Nɛ distances, and two distinct Fe-Oɛ bond lengths resolved. The effect of the environment was studied by embedding the reaction centers into a polyvinyl alcohol film and into a dehydrated trehalose matrix. Incorporation into trehalose caused elongation in one of the two Fe-Nɛ distances, and in one Fe-Oɛ bond length, compared with the polyvinyl alcohol film. The asymmetry detected in the cluster of His residues and its response to incorporation into trehalose are ascribed to the hydrogen bonds between two His residues and the quinone acceptors. The structural distortions observed in the trehalose matrix indicate a strong interaction between the reaction-centers surface and the water-trehalose matrix, which propagates deeply into the interior of the protein. The absence of matrix effects on the Debye-Waller factors is brought back to the static heterogeneity and rigidity of the ligand cluster.
INTRODUCTION
The primary photochemical events that initiate solar-energy conversion in photosynthetic bacteria take place in a membrane-spanning pigment-protein complex called the reaction center (RC). Within the RC from the purple bacterium Rhodobacter (Rb.) sphaeroides, a bacteriochlorophyll special pair, P, after light absorption, delivers an electron in ∼200 ps to the primary quinone acceptor, QA, located ∼25 Å away from P. The electron is then transferred from  to a secondary quinone molecule, QB, which acts as a two-electron, two-proton acceptor after successive turnovers of the RC photochemistry, as reviewed by Feher et al. (1). Independent experimental observations concur to indicate that the electron transfer from
to a secondary quinone molecule, QB, which acts as a two-electron, two-proton acceptor after successive turnovers of the RC photochemistry, as reviewed by Feher et al. (1). Independent experimental observations concur to indicate that the electron transfer from  to QB is conformationally gated, i.e., rate-limited by the dynamics of a conformational change of the protein (2,3). Elucidation of the structural basis for this gating is thought to be central for understanding the general mechanisms underlying electron-transfer coupled proton-uptake in energy-transducing proteins. Despite extensive experimental and theoretical efforts, the nature of the gating step(s) remains controversial. Based on the x-ray diffraction (XRD) structure of RCs frozen in the dark and in the light, a 4.5-Å displacement of QB from a distal-inactive to a proximal-active position, closer to QA, was proposed by Stowell et al. (4) as the gating process. This attractive model was subsequently questioned (5–7), and alternative gating events were suggested, including protonation or changes in hydrogen-bond pattern, protein relaxation, or a combination of these processes (8–10). The complexity of the energy landscape governing the
to QB is conformationally gated, i.e., rate-limited by the dynamics of a conformational change of the protein (2,3). Elucidation of the structural basis for this gating is thought to be central for understanding the general mechanisms underlying electron-transfer coupled proton-uptake in energy-transducing proteins. Despite extensive experimental and theoretical efforts, the nature of the gating step(s) remains controversial. Based on the x-ray diffraction (XRD) structure of RCs frozen in the dark and in the light, a 4.5-Å displacement of QB from a distal-inactive to a proximal-active position, closer to QA, was proposed by Stowell et al. (4) as the gating process. This attractive model was subsequently questioned (5–7), and alternative gating events were suggested, including protonation or changes in hydrogen-bond pattern, protein relaxation, or a combination of these processes (8–10). The complexity of the energy landscape governing the  to QB electron transfer is demonstrated by the strong influence of the RC environment on its kinetics (11,12).
to QB electron transfer is demonstrated by the strong influence of the RC environment on its kinetics (11,12).
The XRD structures of the RC show that QA and QB are located at near-symmetrical positions with respect to the ∼2-fold symmetry axis of the RC, which extends perpendicularly to the membrane plane. This axis connects the primary donor P with a nonheme Fe2+ atom, located between the two quinones. The XRD data (4,13–15) reveal that Fe2+ is ligated with four nitrogen atoms (Nɛ2) from four histidine (His) residues (His-L190, His-L230, His-M219, and His-M266), and with two oxygen atoms of a carboxylate group from a glutamic acid (Glu-M234). Two of the Fe-coordinating His residues are adjacent to QA and QB. Histidine residue M219 forms a strong H bond with QA, and when the secondary quinone is in proximal positions, His-L190 is H-bonded to QB. This arrangement gives rise to a quinone-His-Fe “bridge”, whose structural and functional significance has been the subject of extensive investigation (16–18).
Because of its position and tight coupling with its surroundings, the Fe2+ atom can serve as a probe for local structural changes associated with the final electron-transfer steps of the RC. The X-ray absorption fine structure (XAFS) represents the method of choice to detect subtle modifications of the Fe2+ site, because it can provide, in principle, local structural information at extremely high resolution (19,20). Nevertheless, relatively few XAFS studies have been performed on the RC Fe2+ site. Two pioneering works (21,22) revealed the presence of six atoms in the Fe2+ coordination shell, a result subsequently confirmed by XRD. These early analyses were based on a comparison with the spectra of model Fe compounds, and provided an average distance between Fe2+ and first-shell atoms. A more recent XAFS study aimed to resolve temperature-induced and light-induced structural changes in the Fe2+ site (23). This analysis, however, did not consider the multiple scattering contributions to the XAFS signal. Moreover, none of the three XAFS studies performed so far took explicitly into account possible heterogeneities in the first-shell distances, yielding at most a common distance between Fe2+ and the four His nitrogen atoms, and a single average distance for the two oxygen atoms of the Glu residue coordinating in a bidentate configuration (23).
It is evident that the usefulness of the XAFS spectrum as a reliable, sensitive probe of changes in the local Fe2+ structure rests heavily upon the development and validation of an XAFS analysis which provides the most detailed information in terms of structural and disorder parameters. In view of this, we performed an XAFS analysis of the RC Fe2+ site, based on a direct, multiparameter fitting of the XAFS function and ab initio simulations which take into account multiple scattering contributions. Although multiple scattering analysis was shown to yield essential information in the structural elucidation of metal sites in proteins (24–26), this approach has never been applied to the Fe2+ site of the RC.
We first studied RCs incorporated into a dried polyvinyl alcohol (PVA) film. The choice of this matrix, besides providing a practical, stable system well-suited for XAFS measurements in RCs (27), also allowed direct comparison with the early XAFS study by Eisenberger et al. (21), who introduced this approach. Moreover, local structures determined in PVA most likely well-approximate solution structures, as indicated by a comparative XAFS study performed on cytochrome (cyt) c in a liquid solution and in a dehydrated PVA film (28).
In a second step, we extended the investigation to RCs embedded in a dehydrated, glassy trehalose matrix. Glassy matrices of trehalose (α-D-glucopyranosyl-(1→1)-α-D- glucopyranoside) exhibit an outstanding ability to protect biostructures against adverse environmental conditions, such as potentially detrimental freezing, heating, and dehydration (29,30). Spectroscopic studies performed on soluble and membrane proteins (including the RC), as well as molecular dynamics simulations, showed that conformational protein dynamics are hindered in dried trehalose matrices, as reviewed by Cordone et al. (31). Among other hypotheses (32,33), the protective effect exerted by trehalose on isolated biological structures was suggested to stem from the formation of a water-mediated hydrogen bond network that anchors the biomolecule surface to the water-trehalose matrix, thus coupling the internal degrees of freedom of the biomolecule to those of the surroundings (31,34). In line with this proposal, in a recent XAFS study performed on the heme Fe of cyt c, we showed that the incorporation of this soluble protein into a dehydrated trehalose matrix gives rise to sizeable structural distortions and to a strong decrease of the conformational disorder (28).
Irrespective of the matrix, the analysis we applied was able to detect a splitting of the Fe2+ coordination shell: the Nɛ2 atoms of the four His residues are found at two different distances and there are two distinct Fe-O bond lengths, one for each oxygen atom of the coordinating Glu residue. When the protein was incorporated into the trehalose matrix, structural distortions were observed, compared with the RC-PVA film. The comparison between local structures determined in the two matrices is relevant to an understanding of the structural/dynamical coupling between the RC and the water-trehalose glassy matrix.
MATERIALS AND METHODS
Sample preparation and characterization
The RC was isolated and purified from Rb. sphaeorides R-26, a carotenoid-less spontaneous mutant, according to Gray et al. (35). In all buffers used during the reaction-center isolation, EDTA was present at 10 μM. To remove traces of exogenous proteins and metals, the purified RC suspension was additionally flowed through a DEAE-Sephadex (Sigma, St. Louis, MO) column, dialyzed for 15 h at 4°C against 10 mM Tris buffer, pH 8.00, 0.025% lauryl dimethylamine oxide, 10 μM EDTA, supplemented with 5 g Chelex resin (Chelex 100, Bio-Rad, Hercules, CA)/100 mL, and concentrated to 60 μM by ultrafiltration (50-kDa cutoff, Vivaspin, Vivascience, Hannover, Germany).
The magnesium/iron molar ratio in the RC final sample, determined by inductively coupled plasma atomic emission spectroscopy, was 4.9 ± 0.5. A previous, similar metal analysis, performed by atomic absorption spectroscopy on a highly purified RC preparation, yielded a Mg/Fe ratio equal to 5.2 ± 0.3 (36). Considering four bacteriochlorophyll molecules for each reaction center, the iron content of our preparation was slightly sub-stoichiometric with respect to the RC, indicating that no exogenous iron was present in the samples used for XAFS measurements.
Polyvinyl alcohol-RC films were prepared, starting from 1.4 mL of 24 μM RC and 2.5% PVA solution (PVA 130000 MW, Fluka, Buchs, Switzerland), dried under nitrogen flow into a 3.0 × 3.0 × 0.3 cm Teflon holder. The PVA-RC film was folded several times before exposure to the x-ray beam. Trehalose (>99% purity) was purchased from Sigma, and was used without additional purification. The RC-trehalose dried glasses were prepared as follows: 800 μL of 60 μM RCs were concentrated to 170 μL under nitrogen flow, raising the RC concentration to 282 μM. A sugar/RC molar ratio equal to 104 was achieved by direct addition of solid trehalose into the RC solution. The trehalose-RC solution was layered onto a sintered boron nitride support (Goodfellow Cambridge, Huntingdon, England, UK), and was extensively dried under nitrogen flow.
The content of residual water in the PVA and trehalose matrices can be evaluated by near-infrared (NIR) spectroscopy from the area of the combination band of water in the 1930–1960-nm spectral region, using the RC absorption band at 802 nm as an internal standard (12). In the case of the PVA sample, this estimate was performed directly on the sample used for XAFS measurements. For the trehalose sample, a direct determination was prevented by the boron nitride support. Parallel measurements on trehalose matrices of the same composition, layered on a transparent optical glass, showed that the extensive dehydration treatment resulted in a similar content of residual water in the PVA film and in the trehalose matrix, i.e., ∼4 × 103 water molecules per RC protein. Further desiccation under nitrogen flow at room temperature did not reduce the water content further, in agreement with previous determinations (11,12,31). To test the structural and functional integrity of the protein after XAFS measurements, both the PVA and trehalose samples were redissolved with the proper amount of water. For both samples, visible-NIR spectra taken after irradiation were indistinguishable from that of the RC solution before preparation of the dehydrated matrices. Moreover, no alteration of primary photochemistry was detected, as evaluated from the extent of the primary donor (P+) photo-oxidized by a laser pulse and from the unaffected lifetime of the primary  charge-separated state. The experimental details of these time-resolved optical spectroscopy measurements were given elsewhere (11,12).
charge-separated state. The experimental details of these time-resolved optical spectroscopy measurements were given elsewhere (11,12).
XAFS data collection and analysis
The Fe K-edge measurements were performed at the BM 8 General Purpose Italian Beam Line for X-Ray Diffraction and Absorption (GILDA) (37) of the European Synchrotron Radiation Facility (Grenoble, France). A Si(111) double-crystal monochromator employing dynamical sagittal focusing was used (38). The photon flux was on the order of 1011 photons per second, and the spot size was ∼1 × 1 mm2. Data were collected in fluorescence mode, using a 13-element hyperpure Ge detector equipped with fast digital electronics, and a peaking time equal to 1 μs (39). Samples were measured at room temperature in the energy range of 6900–7910 eV. The final spectra are given as the average of multiple scans, for a total integration time of 60 s/point for each sample. The molecular graphics program MOLDRAW (40) was used to build the structural model of the Fe2+ site.
The XAFS spectra were extracted from the raw data, using the AUTOBK algorithm (41) as implemented in the ATHENA package (42), using a linear function for the pre-edge region and a cubic spline to mimic the atomic background. Fits were performed using the ARTEMIS program, version 0.8.010 (42). Theoretical amplitudes and phase shifts were calculated using the ab initio code FEFF 8.2 (43), in which scattering potentials are calculated by overlapping the free atom densities in the muffin-tin approximation, and then adding the Hedin-Lundqvist form for the exchange potential. The amplitude reduction factor,  was estimated as 0.94 by running the program FEFF 8.2 for the starting model, and was kept fixed during the fitting procedure.
was estimated as 0.94 by running the program FEFF 8.2 for the starting model, and was kept fixed during the fitting procedure.
All of the multiple scattering signals constituted by up to five scattering paths involving atoms belonging to the same residue, and with an effective length ≤5 Å, were taken into account. The fits were performed directly in k-space, in the range of 2.5-10 Å−1 and with a k weight of 3, following a step-by-step procedure (28,44):
In a first step, only structural parameters (see Results for a detailed description) were varied in the fitting procedure, whereas the Debye-Waller (DW) factors were kept fixed. To assign initial values of the DW factors, we performed ab initio FEFF 8.2 simulations of the spectrum corresponding to the reference, starting structural model (see Results and Fig. 1). Using the ARTEMIS program, the effect of different sets of DW factors was tested by grouping the atoms of the cluster into three shells, depending on their distance from Fe2+. The values of the DW factors providing the oscillation amplitudes most similar to the experimental ones (i.e., 0.005 Å2, 0.009 Å2, and 0.007 Å2 for the three shells, respectively) were chosen.
Structural parameters were set to the best-fit values determined in step 1, whereas DW factors were allowed to vary.
The DW factors were fixed to the best-fit values of step 2, and the structural refinement was run again, to check whether the system converged with the previously determined values, and to improve the precision of structural results.
FIGURE 1.
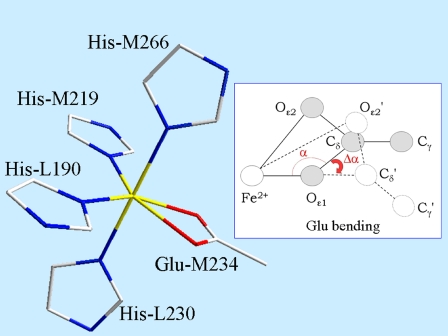
Reference structural model of the Fe2+ ligand cluster. (Inset) The bending of the Glu residue, i.e., a rigid rotation by an angle Δα around an axis through Oɛ1. The angle α was set to 94°, and the Fe2+-Oɛ1 distance was set to 2.12 Å; the Oɛ2 atom of Glu is thus placed at 2.34 Å from Fe2+. The two His residues in plane with the Glu residue are placed symmetrically, so that the angle between the two Fe2+-Nɛ2 bonds of the two His, and the angles between each Fe2+-Nɛ2 bond and the direction Fe2+-Cδ of the Glu, are equal (120°). The target Fe2+-Nɛ2 distance for the His residues was 2.16 Å (see text for details). The bond lengths of the His imidazole group are given in ref. 45.
RESULTS
The Fe2+ ion binds the Nɛ2 atoms of four His residues and the two oxygens (Oɛ1, Oɛ2) of a Glu residue in a bidentate configuration, as confirmed by several XRD studies (4,13–15). In the near-edge region, our spectra (not shown) are very similar to those reported in previous studies which indicated six ligands in the Fe2+ coordination shell (22). Qualitative inspection of the Fourier transform of the spectra acquired in PVA and trehalose (see the Supplementary Material, Fig. S1) shows similar, slightly displaced peaks in the two matrices. This indicates that a common structural model, characterized by the same ligands, possibly at different coordination distances, is likely to fit the two data sets. Interestingly, in both matrices, the presence of a minor peak, very close to the first shell peak, but at a slightly larger r value (see Supplemental Material), suggests the presence of a first-shell atom at a distance from Fe2+ significantly greater than the average coordination distance. On the basis of the XRD information (see above), the distorted octahedral cluster shown in Fig. 1 was built and used as a starting structural model. Structures of single amino acids were derived from a statistical survey (45) of x-ray structures of small compounds from the Cambridge Structural Database. The vertices of the basis of the octahedron are the Nɛ2 atoms of His-M219 and His-L190 and the two oxygen atoms of Glu-M234. The corresponding amino acids lie in the plane defined on this basis (see Fig. 1 for numeric values of the structural parameters). The two remaining vertices are occupied by Nɛ2 of His-M266 and His-L230. As first-shell distances, we chose the target distances based on combined analyses of the Cambridge Structural Database and Protein Data Bank, determined at or near atomic resolution (46). For Glu in bidentate conformation, a distribution of Fe-Oɛ distances was found, indicating a correlation between Fe-Oɛ1 and Fe-Oɛ2 bond lengths (see the database MESPEUS, MEtal Sites in Proteins at Edinburgh UniverSity, and Sheng et al. (47)). To build a reliable starting model, the coordination geometry of the Glu residue was parameterized, using the Fe-Oɛ1 distance and the angle α (Fig. 1, inset). To set their starting values, the Fe site for a number of XRD structures of photosynthetic RCs with resolution higher than 2.4 Å (Protein Data Bank codes 1DXR, 1E6D, 1EYS, 6PRC, and 1AIJ), found through a search of the Metal Data Bank (http://metallo.scripps.edu/), was considered, and the average values of Fe-Oɛ1 (2.12 Å) and α (94°) were set as the starting values. The Fe-Oɛ2 distance for the Glu residue follows from the Fe-Oɛ1 distance and α parameters, according to the equation:
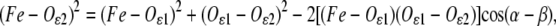 |
(1) |
where β (28°30′) is the  angle (Fig. 1, inset) that, as well as the
angle (Fig. 1, inset) that, as well as the 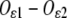 distance (2.194 Å) appearing in Eq. 1, is derived from the survey of amino-acid structures by Engh and Huber (45) and kept fixed throughout the analysis. To make the cluster as regular as possible, atoms belonging to the same residue were set to lie in a plane that also contains the Fe-residue bond. Moreover, no bending was considered for the His residues, i.e., the prolongation of the Fe-Nɛ2 bond bisects the Cɛ1-Nɛ2-Cδ2 angle of the imidazole.
distance (2.194 Å) appearing in Eq. 1, is derived from the survey of amino-acid structures by Engh and Huber (45) and kept fixed throughout the analysis. To make the cluster as regular as possible, atoms belonging to the same residue were set to lie in a plane that also contains the Fe-residue bond. Moreover, no bending was considered for the His residues, i.e., the prolongation of the Fe-Nɛ2 bond bisects the Cɛ1-Nɛ2-Cδ2 angle of the imidazole.
The XAFS oscillations measured in the PVA and in the trehalose matrices are shown as dotted lines in Figs. 2 and 3, respectively. The corresponding best-fitting XAFS functions are represented as continuous lines. Figs. 2 and 3 also show the main contributions to the best-fitting signal, coming from both single and multiple scattering (the two curves at the bottom of each figure describe the multiple scattering contributions with greatest amplitudes). In both spectra, three main oscillations are evident at 4, 6, and 8 Å−1, but their shape and relative amplitudes differ in the two cases, presumably as a consequence of a different arrangement of first-shell atoms in the two different matrices. The structural refinement was performed according to the rigid body refinement scheme (48), initially using as fitting structural parameters: 1), a common shift in the energy origin for all paths; 2), a distance variation for Fe-Oɛ1; 3), a Glu-bending angle Δα (Fig. 1, inset); and 4), a Fe-Nɛ2 distance variation for the four Fe-coordinating histidines. The fit was initially performed with a model in which only a single, common Fe-Nɛ2 average distance was considered for the four amino acids (this will be referred to as the 4 His model). The relatively poor results obtained with this approach (as testified by the high R factor of the fit; see Table 1) suggested the introduction of different Fe-Nɛ2 distances for the different coordinating His residues, i.e., heterogeneity in the His cluster. We considered in particular two fitting models in which two distinct Fe-Nɛ2 distances were introduced. In the first, which we call the 2 + 2 His model, we considered two groups, each composed of two His residues, and we assign to each group an independent distance from Fe2+ (Fe-Nɛ2(1) and Fe-Nɛ2(2)). In the second, which we call the 3 + 1 His model, the His cluster is divided into one group of three residues, for which we consider one common, average distance from Fe2+ (Fe-Nɛ2(1)), and one single His residue, which is allowed to move independently (Fe-Nɛ2(2)). The quantitative results obtained for each model, i.e., the first-shell distances, the bending angle Δα, and the first-shell DW factors, are reported in Table 1, together with the goodness-of-fit indicators, the R factor, and the reduced chi-square 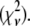 The fitting criterion relies, in fact, on the minimization of the R factor, defined as:
The fitting criterion relies, in fact, on the minimization of the R factor, defined as:
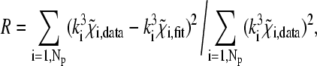 |
(2) |
where Np is the number of experimental points, k is the wave number, and 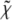 is the XAFS function. Table 1 shows that the introduction of heterogeneity in the Fe-Nɛ2 distances leads to an evident improvement of the fit, corresponding to a strong decrease in the R factor. We also note that, for both matrices (PVA and trehalose), when heterogeneity is allowed (models 2 + 2 His and 3 + 1 His), one of the two groups of His is situated much closer to the Fe2+ atom compared with the other one; the value of the first-shell DW factor is not affected (within the error) by the structural model used in the fit.
is the XAFS function. Table 1 shows that the introduction of heterogeneity in the Fe-Nɛ2 distances leads to an evident improvement of the fit, corresponding to a strong decrease in the R factor. We also note that, for both matrices (PVA and trehalose), when heterogeneity is allowed (models 2 + 2 His and 3 + 1 His), one of the two groups of His is situated much closer to the Fe2+ atom compared with the other one; the value of the first-shell DW factor is not affected (within the error) by the structural model used in the fit.
FIGURE 2.
Experimental k3-weighted XAFS functions measured in RCs embedded into the PVA film (dots), best fit to the 2 + 2 His model (solid bold line), and the corresponding dominating contributions coming from single and multiple scattering. The values of best-fitting parameters are given in Table 1.
FIGURE 3.
Experimental k3-weighted XAFS signal (dots), best fit to the 2 + 2 His model (solid bold line), and main contributions to the fit for RCs embedded into the dry trehalose matrix. The values of best-fitting parameters are given in Table 1.
TABLE 1.
Structural and dynamical parameters determined in the PVA and in the trehalose matrix
| Matrix | Model | Fe-Nɛ2(1) (Å) | Fe-Nɛ2(2) (Å) | Fe-Oɛ1 (Å) | Fe-Oɛ2 (Å) | Δα (°) | σ2 (10−3 Å2) | ΔE0 (eV) | R (%) | 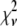 |
|---|---|---|---|---|---|---|---|---|---|---|
| 4 His | 2.14 (2) | 1.94 (3) | 2.42 (5) | 6 (2) | 6 (2) | 7 (2) | 34 (10) | 46 (14) | ||
| PVA | 2 + 2 His | 2.18 (4) | 1.99 (3) | 2.09 (3) | 2.43 (6) | 3 (2) | 4 (1) | 5 (3) | 18 (6) | 13 (4) |
| 3 + 1 His | 2.16 (3) | 1.97 (6) | 2.02 (3) | 2.43 (5) | 5 (2) | 5 (2) | 6 (2) | 25 (8) | 33 (11) | |
| 4 His | 2.16 (2) | 1.98 (3) | 2.42 (9) | 5 (3) | 6 (1) | 7 (2) | 29 (9) | 22 (7) | ||
| Trehalose | 2 + 2 His | 2.17 (5) | 2.04 (2) | 2.15 (7) | 2.41 (7) | 2 (2) | 5 (1) | 5 (2) | 21 (6) | 12 (4) |
| 3 + 1 His | 2.12 (2) | 1.98 (4) | 2.19 (5) | 2.41 (6) | 1 (2) | 5 (1) | 6 (2) | 23 (7) | 21 (7) |
The bending angle of the Glu residue is indicated by Δα, and the first-shell Debye-Waller factor by σ2. The Fe-Oɛ2 distance is calculated by inserting the best-fitting values of the Fe-Oɛ1 distance and α + Δα into Eq. 1. For each RC-matrix system, the fit was performed according to three structural models, characterized by a different grouping of the four His residues (see text for details). We report in parentheses the 1σ error on the least significant digit calculated by the fitting program. The 1σ error for the Fe-Oɛ2 distance was evaluated by considering the propagation of the errors associated with the best-fitting parameters inserted into Eq. 1.
To test the statistical significance of these effects, fits of the same experimental data to the different models were compared on the basis of the reduced chi-square, defined as:
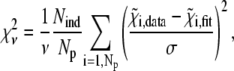 |
(3) |
where ν = Nind – p is the number of degrees of freedom in the fit, calculated as the difference between the number of independent points in the data set, Nind, and the number of fitted parameters included in the model, p. The number of independent points was evaluated (49) as:
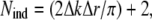 |
(4) |
where Δk and Δr are the intervals in real and reciprocal space in which the fit was performed. The noise of the experimental XAFS spectrum, σ, was estimated for each data set in the high-k region (k > 12 Å−1), where structural oscillations are no longer detectable. This value was found to be consistent with the square root of the number of counts, as predicted by Poisson statistics.
The calculated 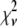 values (Table 1) are much larger than the theoretically expected value of 1, as commonly encountered in XAFS analysis. This is generally ascribed to small inadequacies of the model, and to systematic experimental errors (50). Therefore, to compare fits to the same data set performed on the basis of different structural models, the expected standard fluctuation in
values (Table 1) are much larger than the theoretically expected value of 1, as commonly encountered in XAFS analysis. This is generally ascribed to small inadequacies of the model, and to systematic experimental errors (50). Therefore, to compare fits to the same data set performed on the basis of different structural models, the expected standard fluctuation in 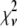 (which is equal to
(which is equal to 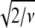 ) is multiplied by the minimum value of
) is multiplied by the minimum value of  obtained in the fit (49–51). Accordingly, fit b is considered significantly better than fit a, with a 95% confidence level (2σ), when
obtained in the fit (49–51). Accordingly, fit b is considered significantly better than fit a, with a 95% confidence level (2σ), when
 |
(5) |
Adopting this criterion, the statistical analysis revealed that the 2 + 2 His model is significantly better than the other two, both for RC embedded in PVA and in the trehalose matrices.
The distance of Glu Oɛ2 from Fe2+ is univocally determined by the values of the Fe-Oɛ1 distance and of Δα (see Eq. 1). By inserting into Eq. 1 the best-fitting values of these parameters for the 2 + 2 His model (Table 1), we obtain the Fe-Oɛ2 distance equal to 2.43 Å in PVA and 2.41 Å in trehalose. In both matrices, one of the two groups of His residues remains at or near the target distance from Fe2+ (i.e., 2.16 Å (46)), whereas the other group is placed much closer to Fe2+.
When the structural parameters obtained in the PVA and in the trehalose matrix are compared, it appears that incorporation into the latter matrix causes significant structural distortions. In particular (Table 1), the Fe-Nɛ2(2) and Fe-Oɛ1 bond lengths are sizably elongated in trehalose, whereas the Fe-Nɛ2(1) and Fe-Oɛ2 distances (see Table 1 and above) remain unchanged within the experimental error. As a consequence, the average first-shell distance of the Fe2+ ligands increases from a value of 2.14 Å in PVA to 2.16 Å in the trehalose matrix. At variance, no significant change is observed in the DW factors.
DISCUSSION
Removing degeneracy in the His coordination
The introduction of multiple scattering contributions allowed a better resolution of the structure of the histidine cluster in the Fe2+ coordinating shell, partially removing the degeneracy present in previous studies. Our analysis revealed, in fact, that the four His residues of the cluster can be split into two groups, each consisting of two histidines, characterized by a different average distance from Fe2+: 2.18 Å and 1.99 Å, respectively, for RCs embedded in a weakly interacting medium (PVA). In the crystallographic structure by Stowell et al. (4), the Fe-Nɛ2 distance is, on average, 0.16 Å larger for the two axial histidine residues (His-M266 and His-L230) than for the His residues (His-M219 and His-L190) acting as in-plane ligands, suggesting a heterogeneity related to the coordination geometry. Other XRD structures of the RC (14,15) do not confirm this systematic difference, which is close to the experimental uncertainty of the crystallographic data, even at the maximal resolution (1.87 Å) attained at present (15). However, all available crystallographic structures of the RC show differences and asymmetries in the environment experienced by the four His residues that coordinate the Fe2+ atom. In particular, His-M219 appears to be hydrogen-bonded to the primary quinone acceptor QA (bond length, 2.84 Å (15)). A second histidine (His-L190) is at hydrogen bond distance (2.71 Å (15)) from the QB molecule, when the quinone moves to the proximal configuration. These hydrogen bond interactions could be responsible for the heterogeneity resolved by us in the histidine Fe-Nɛ2 distances. In this respect, we observe that the occupancy of the proximal QB position appears to be 65%, even in the dark XRD structure at pH 8.0 (15), so that almost 2 of the 4 His residues may be expected to be hydrogen-bonded under our measuring conditions. The suggestion that the two different Fe-Nɛ2 distances observed stem from the interaction of two His residues with the bound quinones is in line with the observation that only one of the distances is changed when the RC is embedded in a strongly interacting matrix (trehalose glassy matrix), rather than in the weakly interacting PVA film (see below).
Our model also allowed us to remove degeneracy in Fe2+ coordination by the two oxygen atoms (23). According to the crystallographic model, a Glu residue (Glu-M234) is bonded to Fe2+ in bidentate configuration. For this residue, our analysis yields in PVA a coordination distance Fe-Oɛ1 = 2.09 Å with Δα = 3°, corresponding to Fe-Oɛ2 = 2.43 Å. The average of these two Fe-O distances (2.26 Å) differs markedly from the Fe-O distance of 1.88 Å determined in a previous XAFS study (23). We note that this latter value is hardly compatible with distances encountered in databanks for bidentate carboxylate groups (see the database MESPEUS and Sheng et al. (47)). An exploration of metal coordination by carboxylates in bidentate configuration revealed, in the case of Co, Cu, and Zn, an inverse proportionality between the O1 and O2 distances from the metal (46). Fig. 4 shows a correlation plot between the Fe-O1 and Fe-O2 distances, extracted from the MESPEUS database. Only distances obtained from XRD studies at a resolution higher than 1.5 Å were included. It appears that in the case of Fe, the two distances are inversely related. An average Fe-O distance of 1.88 Å (23) is clearly incompatible with the data clustering of Fig. 4, to which, at variance, the Fe-Oɛ1 and Fe-Oɛ2 distances obtained by fitting our data to the 2 + 2 His model nicely conform, both in trehalose and in PVA (solid symbols in Fig. 4).
FIGURE 4.
Relationship between the Fe-O1 and Fe-O2 distances in bidentate coordination with Asp and Glu residues. Data shown as open circles were extracted from the MESPEUS database, currently under development at Edinburgh University (47), selecting XRD protein structures at resolutions higher than 1.5 Å. Solid symbols correspond to distances determined in the PVA (circles) and in the trehalose matrix (squares) in this study (see Table 1 and text for details). The labels O1 and O2 can be permuted, so that each carboxylate group is shown twice in the plot, which is symmetrical about the diagonal line, d(Fe-O1) = d(Fe-O2).
Finally, we note that from the first-shell distances resolved in this work (Table 1), an average coordination distance of 2.14 ± 0.02 Å is obtained in the PVA film. Such a value is in excellent agreement with values determined in the pioneering studies of Eisenberger et al. (21) and Bunker et al. (22), i.e., 2.10 ± 0.02 Å and 2.14 ± 0.02 Å, respectively.
Matrix effect
In a recent study (28) performed on cyt c, we showed that XAFS is a sensitive tool in revealing both structural and dynamical local effects induced on protein metal sites by the incorporation of the protein in strongly dehydrated trehalose matrices. In the case of cyt c, such effects consist of 1), the induction of severe distortions of the metal-coordinating geometry, with respect to the local metal site structure observed in liquid solutions and in PVA films; and 2), a decrease of DW factors, indicating a strong reduction, at the local level, in the static or dynamical disorder of the protein.
In view of these results, in this work we performed a comparative analysis of the Fe2+ site in RCs embedded in PVA films and in extremely dehydrated trehalose matrices. The aim was to ascertain whether the trehalose effects observed on the local structure/dynamics of a small, soluble protein (such as cyt c) were also detectable in the case of a large membrane protein, such as RC. By analyzing the RC Fe2+ site, we found that two of the coordinating His residues are placed, on average, farther from the Fe2+ atom in the trehalose matrix, compared with the PVA film. The Fe-Nɛ2(2) distance, 1.99 Å in PVA, increases to 2.04 Å in trehalose (Table 1). Interestingly, the other two coordinating His residues do not change their average distance Fe-Nɛ2(1), strongly suggesting a tighter bond. We propose to identify these latter two His residues with His-M219 and His-L190, which are expected to be more rigid than His-M266 and His-L230, being also hydrogen bonded to the quinones QA and QB, respectively (4,13–15). In trehalose, the Glu residue also undergoes a sizeable displacement with respect to the position in PVA, as inferred from the stretching of the Fe-Oɛ1 bond (Table 1).
Although the elongations observed in the first-ligand distances are 3–4 times smaller in the RC Fe2+ site, compared with the cyt c iron, it is noteworthy that a detectable, local deformation occurs at a site of the RC which is well-shielded by the protein matrix from the surrounding water-trehalose matrix. In principle, the distortion of the Fe2+ local structure, observed in trehalose upon extensive dehydration, could be attributable to the loss of water molecules, located inside the protein between the quinone-Fe2+ region and the RC surface (15). This implies a larger extent of protein dehydration in trehalose than in PVA, even though extensive desiccation of the samples results in comparable concentrations of residual water in the two matrices (see Materials and Methods). We think it more likely that the deformations observed in the local iron structure of RC arise from a strong protein-water-trehalose interaction at the protein surface, as suggested by a number of spectroscopic studies and molecular dynamics simulations (31). In the case of RC, the structural effects of this tight coupling would propagate to the interior of the protein over a distance of at least 15 Å. This value is inferred from the minimum distance of His-M266 and His-L230 from the surface water molecules identified by XRD (15) (Protein Data Bank file 2J8C). These indications of long-range structural effects are consistent with the large effects induced on electron transfer by the incorporation of RC into a dried trehalose matrix (11,31) and with the much less severe effects observed in PVA films (12,31).
The first-shell DW factors determined in the PVA film and in the dehydrated trehalose matrix are the same (within the experimental error) (Table 1). This is in contrast with what was observed for the heme Fe of cyt c; in this case, in fact, the incorporation in trehalose leads to a dramatic decrease of DW factors (28). The behavior observed in RC can be rationalized when considering that both static (structural) and dynamical (vibrational) disorder contributes to the DW factors. Because incorporation into an extensively dehydrated trehalose matrix is expected to reduce protein dynamics drastically in the case of RC (31), the lack of trehalose effects on the DW factors suggests that the values of the DW factors are largely dominated in both matrices by the static (structural), local heterogeneity of the Fe2+ site. In line with this interpretation, Eisenberger et al. (21), by examining the temperature dependence of the DW factor, concluded that the disorder probed by their XAFS analysis was predominantly static (structural) in nature. They estimated a static disorder parameter ≥0.01 Å2. The DW factors we found (see Table 1) are even smaller than this estimate of the static component only, indicating that the vibrational contribution must be negligible.
This notion is further supported by a recent molecular dynamics study (52) in which a coarse-grained model of the wild-type Rb. sphaeroides RC was used to obtain a rigidity profile of the protein. The model was made up of force constants, describing the ease of displacements of each residue with respect to the rest of the structure. The result of this local flexibility study was that regions around the Fe2+ center exhibited the largest force constants, and that the Fe2+ ligands were among those yielding the highest values. It is not surprising, therefore, that the dominating contribution to the measured DW factors comes from static disorder and that, as a consequence, a possible reduction in dynamics, induced by incorporation in the trehalose matrix, has no effect on the measurable DW factors. At the same time, the high local rigidity of the Fe2+ coordinating residues, and of the surrounding protein region, can explain the sizeable structural distortions observed in the Fe2+ site when the RC is embedded in the trehalose matrix. The perturbation induced by straining of the RC surface in the dehydrated trehalose matrix, because of the rigidity of the interposed protein region, is expected to propagate to the buried Fe2+ site, and to be strong enough to distort the geometry of the Fe2+ site. Our suggestion that the two His residues that move farther from the Fe2+ atom in trehalose are His-M266 and His-L230 is consistent with the values of the force constants calculated by Sacquin-Mora et al. (52) for these residues (∼200 kcal mol−1 Å−2 and ∼306 kcal mol−1 Å−2, respectively), which are systematically lower than those evaluated for the other two His residues (i.e., ∼330 kcal mol−1 Å−2 for His-L190, and ∼540 kcal mol−1 Å−2 for His-M219, which forms a strong H-bond with QA). An extremely crude estimate of the energy involved in the distortion observed in trehalose can be performed, using the force constant values and considering the structure in PVA as the equilibrium configuration. Taking a force constant for Glu-M234 equal to 165 kcal mol−1 Å−2 (52), and an average force constant of ∼250 kcal mol−1 Å−2 for His-M266 and His-L230 (see above), we obtain, according to the displacements in Table 1, a total energy of ∼1 kcal mol−1, associated with the deformation of the site. This appears to be a reasonable value, and is at the lower end of the energy range for hydrogen bonding (53).
SUPPLEMENTARY MATERIAL
To view all of the supplemental files associated with this article, visit www.biophysj.org.
Supplementary Material
Acknowledgments
We thank M. M. Harding (University of Edinburgh, Edinburgh, Scotland, UK) for stimulating discussions, and for access to structural data of metallic sites during the development of the MESPEUS database. Measurements at the European Synchrotron Radiation Facility were performed within the public user program. We are grateful to the staff of the GILDA beamline of the European Synchrotron Radiation Facility for excellent support.
The financial support of MIUR of Italy is gratefully acknowledged (grant COFIN-PRIN 2005 No. 2005027011, and funds associated with the proposal COFIN-PRIN 2007 No. 2007WTJEY5). G.P. was partially supported by the Consorzio Interuniversitario per lo Sviluppo dei Sistemi a Grande Interfase (GSGI-Firenze).
Lisa Giachini's present address is the Institut de Chimie Moléculaire de l'Université de Bourgogne, LIMRES, UMR 5260 du Centre National de la Recherche Scientifique, 21078 Dijon cedex, France.
Editor: Jill Trewhella.
References
- 1.Feher, G., J. P. Allen, M. Y. Okamura, and D. C. Rees. 1989. Structure and function of bacterial photosynthetic reaction centres. Nature. 339:111–116. [Google Scholar]
- 2.Kleinfeld, D., M. Y. Okamura, and G. Feher. 1984. Electron-transfer kinetics in photosynthetic reaction centers cooled to cryogenic temperatures in the charge separated state: evidence for light-induced structural changes. Biochemistry. 23:5780–5786. [DOI] [PubMed] [Google Scholar]
-
3.Graige, M. S., G. Feher, and M. Y. Okamura. 1998. Conformational gating of the electron transfer reaction
 in bacterial reaction centers of Rhodobacter sphaeroides determined by a driving force assay. Proc. Natl. Acad. Sci. USA. 95:11679–11684. [DOI] [PMC free article] [PubMed] [Google Scholar]
in bacterial reaction centers of Rhodobacter sphaeroides determined by a driving force assay. Proc. Natl. Acad. Sci. USA. 95:11679–11684. [DOI] [PMC free article] [PubMed] [Google Scholar] - 4.Stowell, M. H. B., T. M. McPhillips, D. C. Rees, S. M. Soltis, E. Abresch, and G. Feher. 1997. Light-induced structural changes in photosynthetic reaction center: implications for mechanism of electron-proton transfer. Science. 276:812–815. [DOI] [PubMed] [Google Scholar]
-
5.Xu, Q., L. Baciou, P. Sebban, and M. R. Gunner. 2002. Exploring the energy landscape for
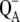 to QB electron transfer in bacterial photosynthetic reaction centers: effect of substrate position and tail length on the conformational gating step. Biochemistry. 41:10021–10025. [DOI] [PubMed] [Google Scholar]
to QB electron transfer in bacterial photosynthetic reaction centers: effect of substrate position and tail length on the conformational gating step. Biochemistry. 41:10021–10025. [DOI] [PubMed] [Google Scholar] - 6.Breton, J., C. Boullais, C. Mioskowski, P. Sebban, L. Baciou, and E. Nabedryk. 2002. Vibrational spectroscopy favors a unique QB binding site at the proximal position in wild-type reaction centers and in the Pro-L209→Tyr mutant from Rhodobacter sphaeroides. Biochemistry. 41:12921–12927. [DOI] [PubMed] [Google Scholar]
- 7.Breton, J. 2004. Absence of large-scale displacement of quinone QB in bacterial photosynthetic reaction centers. Biochemistry. 43:3318–3326. [DOI] [PubMed] [Google Scholar]
-
8.Li, J., D. Gilroy, D. M. Tiede, and M. R. Gunner. 1998. Kinetic phases in the electron transfer from
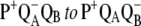 and the associated processes in Rhodobacter sphaeroides R-26 reaction centers. Biochemistry. 37:2818–2829. [DOI] [PubMed] [Google Scholar]
and the associated processes in Rhodobacter sphaeroides R-26 reaction centers. Biochemistry. 37:2818–2829. [DOI] [PubMed] [Google Scholar] -
9.Li, J., E. Takahashi, and M. R. Gunner. 2000. −ΔG°AB and pH dependence of the electron transfer from
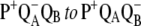 in Rhodobacter sphaeroides reaction centers. Biochemistry. 39:7445–7454. [DOI] [PubMed] [Google Scholar]
in Rhodobacter sphaeroides reaction centers. Biochemistry. 39:7445–7454. [DOI] [PubMed] [Google Scholar] -
10.Paddock, M. L., M. Flores, R. Isaacson, C. Chang, E. C. Abresch, and M. Y. Okamura. 2007. ENDOR spectroscopy reveals light induced movement of the H-bond from Ser-L223 upon forming the semiquinone (
 ) in reaction centers from Rhodobacter sphaeroides. Biochemistry. 46:8234–8243. [DOI] [PMC free article] [PubMed] [Google Scholar]
) in reaction centers from Rhodobacter sphaeroides. Biochemistry. 46:8234–8243. [DOI] [PMC free article] [PubMed] [Google Scholar] -
11.Francia, F., G. Palazzo, A. Mallardi, L. Cordone, and G. Venturoli. 2003. Residual water modulates
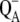 -to-QB electron transfer in bacterial reaction centers embedded in trehalose amorphous matrices. Biophys. J. 85:2760–2775. [DOI] [PMC free article] [PubMed] [Google Scholar]
-to-QB electron transfer in bacterial reaction centers embedded in trehalose amorphous matrices. Biophys. J. 85:2760–2775. [DOI] [PMC free article] [PubMed] [Google Scholar] - 12.Francia, F., L. Giachini, G. Palazzo, A. Mallardi, F. Boscherini, and G. Venturoli. 2004. Electron transfer kinetics in photosynthetic reaction centers embedded in polyvinyl alcohol films. Bioelectrochemistry. 63:73–77. [DOI] [PubMed] [Google Scholar]
- 13.Allen, J. P., G. Feher, T. O. Yeates, H. Komiya, and D. C. Rees. 1988. Structure of the reaction center from Rhodobacter sphaeroides R-26: protein-cofactor (quinones and Fe2+) interactions. Proc. Natl. Acad. Sci. USA. 85:8487–8491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Ermler, U., G. Fritzsch, S. K. Buchanan, and H. Michel. 1994. Structure of the photosynthetic reaction center from Rhodobacter sphaeroides at 2.65 Å resolution: cofactors and protein-cofactor interactions. Structure. 2:925–936. [DOI] [PubMed] [Google Scholar]
- 15.Koepke, J., E.-M. Krammer, A. R. Klingen, P. Sebban, G. M. Ullmann, and G. Fritzsch. 2007. pH modulates the quinone position in the photosynthetic reaction center from Rhodobacter sphaeroides in the neutral and charge separated states. J. Mol. Biol. 371:396–409. [DOI] [PubMed] [Google Scholar]
- 16.Debus, R. J., G. Feher, and M. Y. Okamura. 1986. Iron-depleted reaction centers from Rhodopseudomonas spaheroides R-26.1. Characterization and reconstitution with Fe2+, Mn2+, Co2+, Ni2+, Cu2+ and Zn2+. Biochemistry. 25:2276–2287. [DOI] [PubMed] [Google Scholar]
- 17.Hermes, S., O. Bremm, F. Garczarek, V. Derrien, P. Liebisch, P. Loja, P. Sebban, K. Gerwert, and M. Haumann. 2006. A time-resolved iron-specific X-ray absorption experiment yields no evidence for an Fe2+→Fe3+ transition during QA→QB electron transfer in the photosynthetic reaction center. Biochemistry. 45:353–359. [DOI] [PubMed] [Google Scholar]
-
18.Breton, J., J. Lavergne, M. C. Wakeham, E. Nabedryk, and M. R. Jones. 2007. The unusually strong hydrogen bond between the carbonyl of QA and HisM219 in the Rhodobacter sphaeroides reaction center is not essential for efficient electron transfer from
 to QB. Biochemistry. 46:6468–6476. [DOI] [PubMed] [Google Scholar]
to QB. Biochemistry. 46:6468–6476. [DOI] [PubMed] [Google Scholar] - 19.Konigsberger, D. C., and R. Prins. 1988. X-Ray Absorption: Principles, Applications, Techniques of EXAFS, SEXAFS and XANES. Wiley, New York.
- 20.Samar Hasnain, S., and K. O. Hodgson. 1999. Structure of metal centres in proteins at subatomic resolution. J. Synchr. Rad. 6:852–864. [Google Scholar]
- 21.Eisenberger, P., M. Y. Okamura, and G. Feher. 1982. The electronic structure of Fe2+ in reaction centres from Rhodopseudomonas sphaeroides. II. Extended x-ray fine structure studies. Biophys. J. 37:523–538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Bunker, G., E. A. Stern, R. E. Blankenship, and W. W. Parson. 1982. An x-ray absorption study of the iron site in bacterial photosynthetic reaction centers. Biophys. J. 37:539–551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Chen, L. X., L. M. Utschig, S. L. Schlesselman, and D. M. Tiede. 2004. Temperature and light-induced structural changes in photosynthetic reaction center proteins probed by X-ray absorption fine structure. J. Phys. Chem. B. 108:3912–3924. [Google Scholar]
- 24.Cheung, K. C., R. W. Strange, and S. S. Hasnain. 2000. 3D EXAFS refinement of the Cu site of azurin sheds light on the nature of structural change at the metal centre in an oxidation-reduction process: an integrated approach combining EXAFS and crystallography. Acta Crystallogr. D. 56:697–704. [DOI] [PubMed] [Google Scholar]
- 25.Di Cicco, A. 2003. Local structure in molecular complexes probed by multiple-scattering XAS. J. Sinchr. Rad. 10:46–50. [DOI] [PubMed] [Google Scholar]
- 26.Levina, A., R. S. Armstrong, and P. A. Lay. 2005. Three-dimensional structure determination using multiple-scattering analysis of XAFS: applications to metalloproteins and coordination chemistry. Coord. Chem. Rev. 249:141–160. [Google Scholar]
- 27.Giachini, L., F. Francia, A. Mallardi, G. Palazzo, E. Carpenè, F. Boscherini, and G. Venturoli. 2005. Multiple scattering X-ray absorption studies of Zn2+ binding sites in bacterial photosynthetic reaction centers. Biophys. J. 88:2038–2046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Giachini, L., F. Francia, L. Cordone, F. Boscherini, and G. Venturoli. 2007. Cytochrome c in a dry trehalose matrix: structural and dynamical effects probed by x-ray absorption spectroscopy. Biophys. J. 92:1350–1360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Crowe, L. M., D. S. Reid, and J. H. Crowe. 1996. Is trehalose special for preserving biomaterials? Biophys. J. 71:2087–2093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Crowe, J. H., J. F. Carpenter, and L. M. Crowe. 1998. The role of vitrification in anhydrobiosis. Annu. Rev. Physiol. 60:73–103. [DOI] [PubMed] [Google Scholar]
- 31.Cordone, L., G. Cottone, S. Giuffrida, G. Palazzo, G. Venturoli, and C. Viappiani. 2005. Internal dynamics and protein-matrix coupling in trehalose-coated proteins. Biochim. Biophys. Acta. 1749:252–281. [DOI] [PubMed] [Google Scholar]
- 32.Carpenter, J. F., and J. H. Crowe. 1989. An infrared spectroscopic study of the interactions of carbohydrates with dried proteins. Biochemistry. 28:3916–3922. [DOI] [PubMed] [Google Scholar]
- 33.Belton, P. S., and A. M. Gil. 1994. IR and Raman spectroscopic studies of the interaction of trehalose with hen egg white lysozyme. Biopolymers. 34:957–961. [DOI] [PubMed] [Google Scholar]
- 34.Giuffrida, S., G. Cottone, F. Librizzi, and L. Cordone. 2003. Coupling between the thermal evolution of the heme pocket and external matrix structure in trehalose-coated carboxy-myoglobin. J. Phys. Chem. B. 107:13211–13217. [Google Scholar]
- 35.Gray, K. A., J. W. Farchaus, J. Wachtveitl, J. Breton, and D. Oesterhelt. 1990. Initial characterization of site-directed mutants of tyrosine M210 in the reaction center of Rhodobacter sphaeroides. EMBO J. 9:2061–2070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Feher, G. 1971. Some chemical and physical properties of a bacterial reaction center particle and its primary photochemical reactants. Photochem. Photobiol. 14:372–387. [DOI] [PubMed] [Google Scholar]
- 37.D'Acapito, F., S. Colonna, S. Pascarelli, G. Antonioli, A. Balerna, A. Bazzini, F. Boscherini, F. Campolungo, G. Chini, G. Dalba, G. I. Davoli, P. Fornasini, R. Graziola, G. Licheri, C. Meneghini, F. Rocca, L. Sangiorgio, V. Sciarra, V. Tullio, and S. Mobilio. 1998. GILDA (Italian beamline) on BM8. ESRF Newslett. 30:42–44. [Google Scholar]
- 38.Pascarelli, S., F. Boscherini, F. D'Acapito, J. Hardy, C. Meneghini, and S. Mobilio. 1996. X-ray optics of a dynamical sagittal focussing monochromator on the GILDA beamline at the ESRF. J. Synchr. Rad. 3:147–155. [DOI] [PubMed] [Google Scholar]
- 39.Ciatto, G., F. D'Acapito, F. Boscherini, and S. Mobilio. 2004. Treatment of EXAFS data taken in fluorescence mode in non-linear conditions. J. Synchr. Rad. 11:278–283. [DOI] [PubMed] [Google Scholar]
- 40.Ugliengo, P., D. Viterbo, and G. Chiari. 1993. MOLDRAW: molecular graphics on a personal computer. Z. Kristallogr. 207:9–23. [Google Scholar]
- 41.Newville, M., P. Livins, Y. Yacoby, J. J. Rehr, and E. A. Stern. 1993. Near-edge x-ray-absorption fine structure of Pb: A comparison of theory and experiment. Phys. Rev. B Condens. Matter. 47:14126–14131. [DOI] [PubMed] [Google Scholar]
- 42.Ravel, B., and M. Newville. 2005. ATHENA, ARTEMIS, HEPHAESTUS: data analysis for X-ray absorption spectroscopy using IFEFFIT. J. Synchr. Rad. 12:537–541. [DOI] [PubMed] [Google Scholar]
- 43.Ankudinov, A. L., B. Ravel, J. J. Rehr, and S. D. Conradson. 1998. Real space multiple-scattering calculation and interpretation of x-ray-absorption near-edge structure. Phys. Rev. B. 58:7565–7576. [Google Scholar]
- 44.Scherk, C. G., A. Ostermann, K. Achterhold, O. Iakovleva, C. Nazikoll, B. Krebs, E. V. Knapp, W. Meyer-Klaucke, and F. G. Parak. 2001. The X-ray absorption spectroscopy Debye-Waller factors of an iron compounds and met-myoglobin as a function of temperature. Eur. Biophys. J. 30:393–403. [DOI] [PubMed] [Google Scholar]
- 45.Engh, R., and R. Huber. 1991. Accurate bond and angle parameters for X-ray protein structure refinement. Acta Crystallogr. A. 47:392–400. [Google Scholar]
- 46.Harding, M. M. 2006. Small revisions to predicted distances around metal sites in proteins. Acta Crystallogr. D Biol. Crystallogr. 62:678–682. [DOI] [PubMed] [Google Scholar]
- 47.Hsin, K., Y. Sheng, M. M. Harding, P. R. Taylor, and M. D. Walkinshaw. 2008. MESPEUS: a database of the geometry of metal sites in proteins. J. Appl. Cryst. In press.
- 48.Binsted, N., R. W. Strange, and S. S. Hasnain. 1992. Constrained and restrained refinement in EXAFS data analysis with curved wave theory. Biochemistry. 31:12117–12125. [DOI] [PubMed] [Google Scholar]
- 49.Stern, E.A., M. Newville, B. Ravel, Y. Yacoby, and D. Haskel. 1995. The UWXAFS analysis package: philosophy and details. Physica B. 208–209:117–120.
- 50.Kelly, S. D., K. M. Kemner, G. E. Fryxell, J. Liu, S. V. Mattigod, and K. F. Ferris. 2001. X-ray-absorption fine-structure spectroscopy study of the interactions between contaminant tetrahedral anions and self-assembled monolayers on mesoporous supports. J. Phys. Chem. B. 105:6337–6346. [Google Scholar]
- 51.Giachini, L., F. Francia, G. Veronesi, D.-W. Lee, F. Daldal, L.-S. Huang, E. A. Berry, T. Cocco, S. Papa, F. Boscherini, and G. Venturoli. 2007. X-ray absorption studies of Zn2+ binding sites in bacterial, avian and bovine cytochrome bc1 complexes. Biophys. J. 93:2934–2951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Sacquin-Mora, S., P. Sebban, V. Derrien, B. Frick, R. Lavery, and C. Alba-Simionesco. 2007. Probing the flexibility of the bacterial reaction center: the wild-type protein is more rigid than two site-specific mutants. Biochemistry. 46:14960–14968. [DOI] [PubMed] [Google Scholar]
- 53.Maréchal, Y. 2007. The Hydrogen Bond and the Water Molecule. Elsevier, Amsterdam.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.