Regional Difference in Dynamical Property of Sinoatrial Node Pacemaking: Role of Na⁺ Channel Current

Abstract

To elucidate the regional differences in sinoatrial node pacemaking mechanisms, we investigated 1), bifurcation structures during current blocks or hyperpolarization of the central and peripheral cells, 2), ionic bases of regional differences in bifurcation structures, and 3), the role of Na⁺ channel current (I_Na) in peripheral cell pacemaking. Bifurcation analyses were performed for mathematical models of the rabbit sinoatrial node central and peripheral cells; equilibrium points, periodic orbits, and their stability were determined as functions of parameters. Structural stability against applications of acetylcholine or electrotonic modulations of the atrium was also evaluated. Blocking L-type Ca²⁺ channel current (I_Ca,L) stabilized equilibrium points and abolished pacemaking in both the center and periphery. Critical acetylcholine concentration and gap junction conductance for pacemaker cessation were higher in the periphery than in the center, being dramatically reduced by blocking I_Na. Under hyperpolarized conditions, blocking I_Na, but not eliminating I_Ca,L, abolished peripheral cell pacemaking. These results suggest that 1), I_Ca,L is responsible for basal pacemaking in both the central and peripheral cells, 2), the peripheral cell is more robust in withstanding hyperpolarizing loads than the central cell, 3), I_Na improves the structural stability to hyperpolarizing loads, and 4), I_Na-dependent pacemaking is possible in hyperpolarized peripheral cells.

INTRODUCTION

Elucidation of the mechanisms of the sinoatrial (SA) node pacemaking is one of the most important subjects in cardiac electrophysiology. A large body of information on the ionic mechanisms of SA node pacemaking has been obtained from numerous experimental and theoretical studies (1). From the bifurcation analysis of a mathematical model for SA node primary pacemaker cells, we have elucidated the dynamical mechanisms of the natural SA node pacemaking and the roles of L-type Ca²⁺ channel current (I_Ca,L) and rapidly activating delayed-rectifier K⁺ current (I_Kr) in basal pacemaking (2). We have suggested that 1), the instability of an equilibrium point (EP) is essentially important for pacemaker generation; 2), I_Ca,L is responsible for EP instability and pacemaker generation, whereas I_Kr is not necessarily required for constructing a pacemaker cell system; and 3), I_Kr acts as an oscillation amplifier and frequency stabilizer as well as plays an important role in preventing bifurcation to quiescence of the system. Nevertheless, the pacemaking mechanism addressed in our previous article is for primary pacemaker cells in the central SA node. We expect that the same mechanisms underlie the pacemaking of transitional or peripheral SA node cells. However, previous reports suggest regional differences in pacemaker mechanisms, e.g., blocking I_Ca,L abolished spontaneous activity in central SA node tissues, but not in peripheral tissues (3). In the peripheral SA node, the Na⁺ channel current (I_Na), not present in the central SA node, might contribute to EP instability and pacemaker generation. Hyperpolarization-activated cation current (I_h) has also been suggested to play a predominant role in the subsidiary pacemaker mechanisms (4–6). Thus, regional differences in pacemaker mechanisms and roles of sarcolemmal currents, such as I_Na or I_h, remain to be clarified.

The aim of this study was to elucidate the regional differences in the mechanisms for basal pacemaking of SA node cells in terms of the nonlinear dynamical system theory. We particularly focused on the roles of I_Na in peripheral cell pacemaking, as well as the regional differences in the robustness of pacemaker activity to current blocks or hyperpolarizing loads. In previous studies, bifurcation structures (i.e., ways of changes in the number or stability of equilibrium and periodic states) of ventricular or SA node model systems were investigated for elucidating the mechanisms of normal and abnormal pacemaker activities (2,7–13). These theoretical works indicate that the initiation or cessation of pacemaker activity is considered as a bifurcation phenomenon, and that the mathematical approach—bifurcation analysis—provides a convenient way of understanding how individual currents contribute to pacemaker activities. In this study, therefore, we compared the bifurcation structures during current blocks or hyperpolarization of the central and peripheral SA node cells and also explored the ionic bases of the regional differences in bifurcation structures. Furthermore, we explored the manner in which I_Na contributes to the robustness of peripheral cell pacemaking and whether I_Na-dependent pacemaking is possible in the peripheral cell.

Local stability and bifurcation analyses were performed for the modified versions of our SA node model (14), as well as Zhang et al. models (15,16), for central and peripheral cells. We constructed bifurcation diagrams by calculating EPs, periodic orbits (POs), stability of EPs and POs, and bifurcation points as functions of bifurcation parameters such as the maximum current conductance. The structural stability of the model cells (robustness of pacemaker activity) was also evaluated by computing the stability and dynamics of the systems during applications of constant bias currents (I_bias) or acetylcholine (ACh), or during electrotonic modulations by the atrium.

A salient point of this study is that the theory of bifurcations of nonlinear dynamical systems was used to obtain significant insights into the region-dependent mechanisms of SA node pacemaking. Elucidating the regional differences in bifurcation structures of SA node cells would lead to a deeper understanding of the pacemaker mechanisms and may also provide a theoretical background for engineering a biological pacemaker (13,17,18). Definitions of the specific terms for the nonlinear dynamics and bifurcation theory are given at the end of the Theory and Methods section (see also (19–21)).

THEORY AND METHODS

Mathematical formulation

Base models for central and peripheral SA node cells

Zhang et al. (15) were the first to develop single-cell models for central and peripheral SA node cells of the rabbit that were based on the experimentally observed regional differences in action potential (AP) parameters, ionic current densities, and pharmacological responses. Their models are simplified versions that do not include intracellular Ca²⁺ dynamics or other intracellular factors. Nevertheless, we first chose to use their models, which have been corrected by Garny et al. (16), for the following reasons:

1. There was no other peripheral SA node model suitable for bifurcation analysis.

2. Their models could accurately reproduce the experimental data for the regional differences in AP dynamics and effects of various channel blockers, as summarized in Zhang et al. (15).

3. In our preliminary study, the bifurcation structures of their central cell model were essentially the same as those of our primary pacemaker model incorporating the dynamics of intracellular ion concentrations (2,14).

4. Their simple models are more suitable for bifurcation analyses than other more complex models.

5. Their cell models have been used for constructing SA node tissue models (16,22).

We found that EPs of their original models are stable, and thus they exhibit “bistability” (i.e., coexistence of stable steady and periodic states) under normal conditions. This implies that “annihilation” can easily occur in SA node cells; however, annihilation is seldom observed in SA node preparations (9). In the aspects of the nonlinear dynamics and bifurcation theory, pacemaker activity could be defined as a stable limit cycle (LC) around an unstable EP; thus, the most important dynamical property of the SA node cell system for robust pacemaking appears to be the instability of an EP (2). Other previous SA node models appear not to have a stable EP (2,23–26). Thus, we believe that EPs of SA node cell models must be unstable under normal conditions. To make the EPs unstable, therefore, the steady-state activation (d_L∞) and inactivation (f_L∞) curves for I_Ca,L were positively shifted by 5 and 10 mV, respectively, with the maximum conductance (g_Ca,L) being reduced by 5%; the shifts of d_L∞ and f_L∞ curves were determined so as to lie within the experimental ranges as shown in Fig. 2 of Zhang et al. (15). This modification only slightly altered the AP waveforms. A complete list of the equations and standard parameter values for their models has been provided in previous articles (15,16). The formulas for the modified I_Ca,L are given in Appendix A.

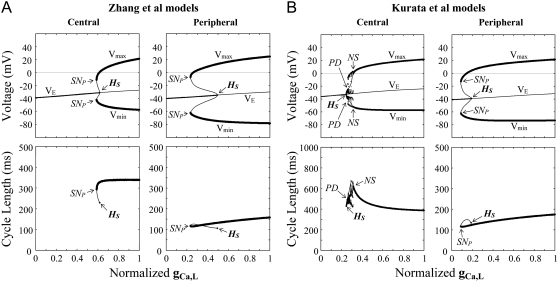
FIGURE 2.

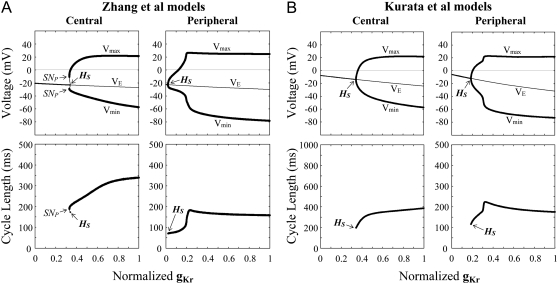
Effects of reducing g_Ca,L on the EP stability and oscillation dynamics of the Zhang et al. (A) and Kurata et al. (B) models for central and peripheral cells. One-parameter bifurcation diagrams for g_Ca,L with the steady-state branch as a locus of V_E and the periodic branches as the potential extrema of LCs (V_min, V_max) are shown (top); the CL of LCs is also plotted as a function of g_Ca,L (bottom). The steady-state and periodic branches consist of the stable (thick lines) and unstable (thin lines) segments. The normalized g_Ca,L value was reduced at an interval of 0.001 for calculations of EPs and stable LCs. The points of Hopf bifurcation of EPs, saddle-node bifurcation of LCs, period-doubling bifurcation of LCs, and Neimark-Sacker bifurcation of LCs are located, as labeled H_S, SN_P, PD, and NS, respectively: (A) H_S at g_Ca,L = 0.6178 (central) and 0.4912 (peripheral); SN_P at g_Ca,L = 0.5890 (central) and 0.2337 (peripheral). (B) H_S at g_Ca,L = 0.2457 (central) and 0.1891 (peripheral); SN_P at g_Ca,L = 0.085 (peripheral); PD at g_Ca,L = 0.257 (central); and NS at g_Ca,L = 0.312 (central).

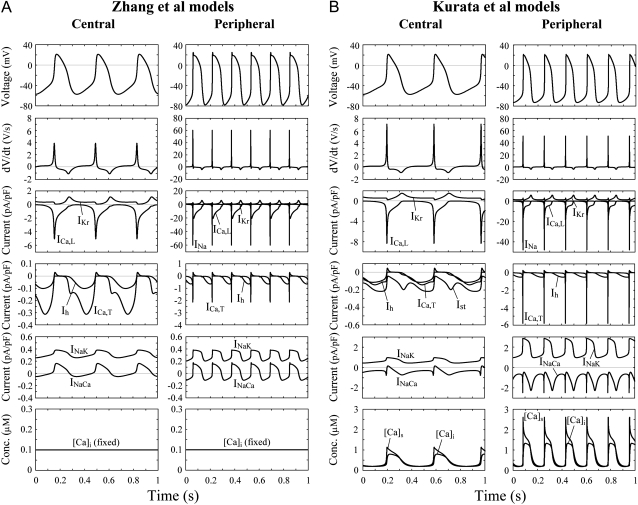
Intracellular Ca²⁺ dynamics is known to exert substantial effects on the dynamics of pacemaker cells and may also significantly affect the bifurcation structures of SA node cells. Therefore, we also used models that incorporated intracellular Ca²⁺ dynamics. On the basis of the Zhang et al. models (15) and related experimental data, we developed the central and peripheral versions of our SA node model (14). Although the expressions for individual components of our modified models (referred to as the Kurata et al. models) are essentially the same as in the previous article (14), the original formulas for I_Na and I_h were replaced by those of the Zhang et al. models for the following reasons: 1), the I_Na formulas of the Zhang et al. model yielded better fits to the experimental data for SA node I_Na kinetics (27,28), and 2), voltage dependence of the original formula for I_h activation (y²) was so steep that I_h became too large for the peripheral cell model and yielded irregular dynamics. Standard parameter values for the Kurata et al. models are provided in Table 1. Dynamics of the Kurata et al. models, as well as the Zhang et al. models, with the standard parameter values are shown in Appendix A (see Fig. 17).

TABLE 1.

Standard parameter values for the original and modified Kurata et al. models

Parameters	Units	Original central*	Modified central	Modified peripheral
Cm	pF	32	20	65
Vcell	pL	3.5186	2.19911	7.147123
Vsub	pL	0.0351	0.021936	0.0712925
Vi	pL	1.5835	0.98965	3.216384
Vrel	pL	0.0042	0.0026389	0.00857654
Vup	pL	0.0408	0.0255097	0.0829066
[K+]o	mM	5.4	5.4	5.4
[K+]i	mM	Variable	140	140
gCa,L	nS/pF	0.58	0.58	1.6008
gKr	nS/pF
gKs	nS/pF	0.0259	0.0259	0.0958818
gto	nS/pF	0.18	0.18	0.4194
gsus	nS/pF	0.02	0.02	0.0466
gNa†		0	0	1.204 × 10−15
gCa,T	nS/pF	0.458	0.458	0.458
gh†	nS/pF	0.375	0.05465	0.1565
gst	nS/pF	0.015	0.0075	0
gNa,b	nS/pF	0.0054	0.0054	0.0093312
gK,ACh	pA × mM−1 × pF−1
INaKmax	pA/pF	3.6	3.6	9.72‡
kNaCa	pF−1	125	125	187.5‡
Tdif,Ca	ms	0.04	0.01	0.01
Prel	ms−1	0.5	1.25	2.50
Pup	mM × ms−1	0.005	0.01	0.02
kτq§		1	0.670	0.670
kτr§		1	0.303	0.303

^*Parameter values used for the original Kurata et al. model (14) are given for comparison.

^†Values are shown in italic, because the formulas used in this study are different from those of the original model and thus direct comparison is impossible.

^‡Higher activities of Na⁺-K⁺ pump and Na⁺/Ca²⁺ exchanger were required to counteract the increased Ca²⁺ and Na⁺ influx via Na⁺ and Ca²⁺ channels.

^§Scaling factors for the activation and inactivation time constants of I_to and I_sus, which were determined for the peripheral model to reproduce the AP waveform experimentally observed in the periphery of SA node tissues (15).

FIGURE 17.

Steady-state behaviors of spontaneous APs, underlying transmembrane ionic currents, and intracellular Ca²⁺ dynamics simulated by the central and peripheral versions of the Zhang et al. (A) and Kurata et al. (B) models with the standard parameter values. Differential equations were numerically solved for 11 s (A) or 181 s (B) with initial conditions appropriate to an EP and a 1-ms stimulus of 1 pA/pF. Model cell behaviors during the last 1 s starting from maximum diastolic potential are depicted. Intracellular Ca²⁺ dynamics include the changes of Ca²⁺ concentrations in subspace ([Ca²⁺]_S) and myoplasm ([Ca²⁺]_i).

In our original or other SA node models, the contribution of sarcoplasmic reticulum (SR) Ca²⁺ cycling to pacemaker activity was small; the suppression of SR Ca²⁺ release did not slow pacemaking as dramatically as did the application of ryanodine or BAPTA in experiments (see Table 4 of Kurata et al. (14)). To examine how SR Ca²⁺ release affects the stability, dynamics, and bifurcation of SA node cells, we developed the modified versions of our SA node model for which SR Ca²⁺ cycling was enhanced by increasing the rate constants of Ca²⁺ uptake (P_up) and release (P_rel). The central cell model with increased P_up and P_rel could exhibit a 68.1–112.2% increase in CL on minimizing SR Ca²⁺ release, whereas a peripheral version of such a large response could not be developed, probably because of the presence of large I_Na (data not shown). Bifurcation structures of our original model and the modified models with enhanced SR Ca²⁺ cycling were essentially the same (data not shown). Thus, only the data from the models of the medium response (yielding 11.8–23.7% increases in CL) are shown in this article.

The standard models for the normal pacemaker activity include 13–14 membrane current components. The time-dependent change in the membrane potential (V_S) is described by

(1)

where I_Ca,L and I_Ca,T represent the L-type and T-type Ca²⁺ channel currents, respectively. The rapid and slow components of the delayed-rectifier K⁺ currents are denoted as I_Kr and I_Ks, respectively. The membrane current system also includes I_Na, I_h, the sustained inward current (I_st), four AP-sensitive currents consisting of transient (I_to) and sustained (I_sus) components, background currents carried by Na⁺ (I_b,Na), Ca²⁺ (I_b,Ca) and K⁺ (I_b,K), Na⁺-K⁺ pump current (I_NaK), and Na⁺/Ca²⁺ exchanger current (I_NaCa). All the currents charge the membrane capacitance (C_S).

Incorporation of ACh effects on ionic currents

To investigate the bifurcation structure of the model cells during applications of ACh, we incorporated the formulas of Dokos et al. (29) or Zhang et al. (30) for the muscarinic K⁺ channel current (I_K,ACh), as well as for the modifications of I_Ca,L and I_h by ACh, into the base models. Both the formula sets yielded qualitatively the same results; thus, only the results obtained with the formulas of Dokos et al. (29) are shown. It is unknown whether the density of the muscarinic K⁺ channel varies between the center and periphery of the SA node, whereas the density of the muscarinic M₂ receptor as well as vagal innervation may be greater in the center than in the periphery (31,32). In this study, therefore, it was assumed that the I_K,ACh density is the same in central and peripheral cells, as in Zhang et al. (30). Sensitivities to ACh of I_K,ACh, I_Ca,L, and I_h were also assumed to be independent of the regions. The expressions for these currents with the ACh modifications of Dokos et al. (29) are given in Appendix A.

Formulation of a coupled-cell model

To investigate the electrotonic influences of atrial myocytes on stability and dynamics of SA node cells, we used a coupled-cell model as introduced by Watanabe et al. (33). According to their method, a SA node cell was connected to a passive membrane model (resistance-capacitance (R-C) circuit) for an atrial myocyte via the gap junction conductance (G_C) of 0–20 nS. We used an atrial membrane capacitance (C_A) of 51 pF and an atrial membrane resistance (R_A) of 0.22 GOhm, as in Watanabe et al. (33), for the central cell (C_S = 20 pF). For the peripheral cell with a larger capacitance (C_S = 65 pF), the C_A and R_A values were scaled by multiplying 3.25 and 3.25⁻¹, respectively, to yield the same capacitance ratio (C_S/C_A) for the peripheral cell as for the central cell. An offset voltage, corresponding to a resting potential of the atrial myocyte, was set equal to −80 mV.

Time-dependent changes in the membrane potentials of the SA node cell (V_S) and atrial myocyte (V_A) were calculated by the equations

(2)

(3)

(4)

(5)

where I_total and I_A represent the sum of sarcolemmal ionic currents in the SA node cell (pA/pF) and the atrial membrane current (pA), respectively. I_C denotes the gap junction current (pA).

Bifurcation analysis

The model cells are 15- or 26-order autonomous continuous-time dynamical systems, each of which is described as a set of 15 or 26 first-order, nonlinear ordinary differential equations. Dynamical properties and bifurcation structures of a model cell system were determined by analytically and numerically handling the differential equations. Numerical computations were performed with MATLAB 7 for Windows XP (The MathWorks, Natick, MA) on Workstation HP xw9300 (Hewlett-Packard, Tokyo, Japan) and CELSIUS X630 (Fujitsu, Tokyo, Japan).

Locating EPs and LCs

In the model cell systems, 15 or 26 state variables define a 15- or 26-dimensional state point in the 15- or 26-dimensional state space. We calculated EPs and LCs (isolated POs) in the state space. An EP was determined as a point at which the vector field vanishes. A steady-state value of the state variable V_S (for dV_S/dt = 0) was calculated by the Newton-Raphson algorithm, practically with a nonlinear equation solver (fsolve) available in MATLAB 7 (optimization toolbox); then, steady-state values of the gating variables for individual currents were computed. A stable LC was located by the brute-force approach or autonomous shooting method (20) using the numerical algorithms available as MATLAB ODE solvers, i.e., 1), a variable time-step numerical differentiation approach selected for its suitability to stiff systems (ode15s) and 2), a fourth-order adaptive-step Runge-Kutta algorithm (ode45). When a stable LC appeared, the AP amplitude (APA) as a voltage difference between the local potential minimum (V_min) and maximum (V_max), as well as the cycle length (CL), was determined for each calculation of a cycle. Numerical integration was continued until the differences in both APA and CL between the newly calculated cycle and the preceding one became <1 × 10⁻³ of the preceding APA and CL values. To locate an unstable LC, we used CL_MATCONT, a continuation toolbox for MATLAB (34).

Constructing one-parameter bifurcation diagrams

To examine how the stability and dynamics of the model cells alter with changes in bifurcation parameters, we constructed one-parameter bifurcation diagrams in which values of a state variable at EPs and extrema of LCs are plotted as functions of the bifurcation parameters. Bifurcation parameters chosen in this study include 1), the maximum conductance of I_Ca,L (g_Ca,L), I_Kr (g_Kr), I_Na (g_Na), I_h (g_h), and I_Ca,T (g_Ca,T); 2), amplitude of I_bias; 3), ACh concentration ([ACh]); and 4), G_C. The maximum conductance is expressed as normalized values, i.e., ratios to the control value.

A single bifurcation parameter was systematically changed while keeping all other parameters at their standard values. The steady-state membrane potential (V_E) at EPs (steady-state branches) and local potential extrema (V_min, V_max) of LCs (periodic branches), as well as the CL of LCs, were determined and plotted for each value of the bifurcation parameter. When periodic behavior was irregular, model cell dynamics were computed for 60 s; all potential extrema and CL values sampled during the last 10 s were then plotted in the diagrams.

Detecting codimension-one bifurcations (determination of EP and LC stabilities)

The critical parameter value (bifurcation point) at which a codimension-one bifurcation occurs was determined by evaluating the existence and stability of EPs and LCs at each value of a relevant parameter (one-parameter bifurcation analysis). The asymptotic stability of an EP was determined by computing eigenvalues of a Jacobian matrix derived from the linearization of the nonlinear systems around the EP (for details, see Appendix B). The stability of an LC was determined by its characteristic multipliers, which were calculated as eigenvalues of the solution of the variational equation (for more details, see (9,12,20)).

The Hopf bifurcation point at which the stability of an EP reverses was determined by the stability analysis. The saddle-node (SN) bifurcation point at which two EPs coalesce and disappear was also detected as a point at which the steady-state current-voltage (I/V) curve and zero-current axis come in contact with each other. Moreover, the saddle-node, period-doubling, and Neimark-Sacker bifurcations were detected for LCs (for details, see “Definitions of Terms” at the end of this section and also (9,21)).

Constructing two-parameter bifurcation diagrams

We further constructed two-parameter bifurcation diagrams in which the path of codimension-one bifurcation determined by the one-parameter bifurcation analysis is traced in a parameter plane. The primary parameter was systematically changed with the secondary parameter fixed at a constant value. The critical value of the primary parameter at which Hopf or saddle-node bifurcations occur on the steady-state branch was determined for various different values of the secondary parameter. Bifurcation values for the primary parameter were plotted as a function of the secondary parameter. Codimension-two saddle-node bifurcation at which two loci of codimension-one (Hopf) bifurcation points coalesce and disappear was detected.

Definition and evaluation of structural stability

We also evaluated the structural stability of SA node cells, which is defined as the robustness of pacemaker activity to various interventions or modifications that may cause a bifurcation to quiescence or irregular dynamics (for details, see Kurata et al. (2)). In this study, we tested the structural stability against applications of hyperpolarizing (or depolarizing) I_bias or ACh and against electrotonic loads of an adjacent atrial myocyte.

The manner of evaluating the structural stability to I_bias is essentially the same as described in our previous articles (2,13). Changes in V_E and its stability during I_bias applications were depicted as the I_bias-V_E curve (for more details, see Fig. 4 in the Results section; see also Fig. 1 of Kurata et al. (2)). Hopf and saddle-node bifurcation points in the I_bias-V_E curve were determined as functions of bifurcation parameters and plotted on both the potential and current coordinates. Changes in EPs, LC dynamics, and their stability were also determined with increasing [ACh] or G_C; the Hopf bifurcation for EP stabilization, as well as the saddle-node, period-doubling, or Neimark-Sacker bifurcation causing cessation or destabilization of LCs, were detected.

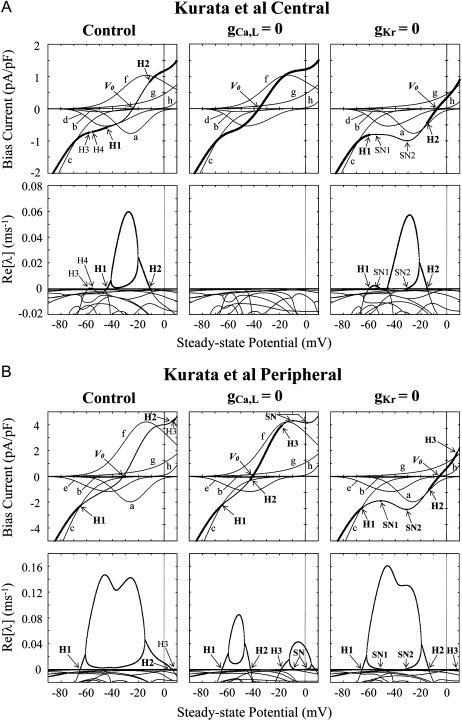
FIGURE 4.

Changes in EPs and their stability during I_bias applications of the normal (control), I_Ca,L-removed (g_Ca,L = 0), and I_Kr-removed (g_Kr = 0) versions of the Kurata et al. central (A) and peripheral (B) models. Shown are the I_bias-V_E curves illustrating how V_E and its stability changed when I_bias was applied (top). V_E was systematically changed by applying hyperpolarizing (negative) or depolarizing (positive) I_bias of various amplitudes; the resulting relationship between V_E (abscissa) and I_bias amplitude (ordinate) is depicted. Stability of EPs was evaluated by the stability analysis based on the linear stability theory (see Appendix B); real parts of eigenvalues (Re[λ]) of a Jacobian matrix for each EP (V_E) representing the rate constants (ms⁻¹) of a system to be attracted to or go away from an EP are shown (bottom). In the I_bias-V_E curve, the segments of thin lines designate the loci of unstable EPs with two positive Re[λ] values; those of thick lines are the stable EPs for which Re[λ] values are all negative. There are 2–4 Hopf bifurcation points (H1–H4), corresponding to the zero crossings of Re[λ]. Saddle-node bifurcation points are also located (labeled SN). Individual time-dependent current components in steady state are superimposed to show the contribution of each current to the stability of EPs: a, I_Ca,L; b, I_Ca,T; c, I_h; d, I_st; e, I_Na; f, I_Kr; g, I_to + I_sus; and h, I_Ks.

FIGURE 1.

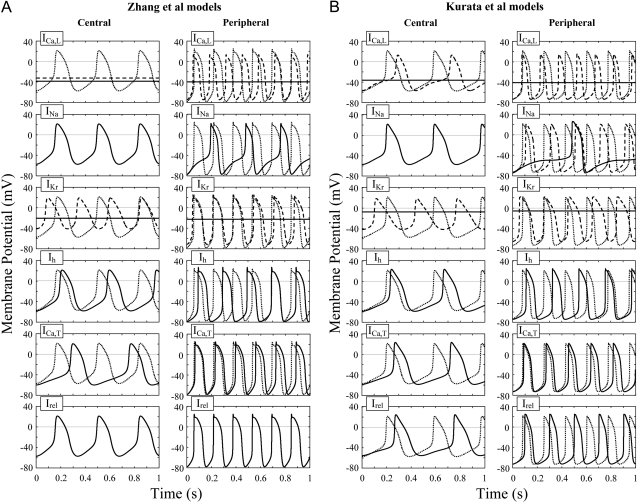
Simulated effects of blocking individual sarcolemmal currents or SR Ca²⁺ release on pacemaker activity of the Zhang et al. (A) and Kurata et al. (B) models for the central and peripheral cells. Membrane potential behaviors on decreasing one of I_Ca,L, I_Na, I_Kr, I_h, I_Ca,T, and the SR Ca²⁺ release current I_rel (from top to bottom) are shown. Effects of the complete block of each current (solid lines) and 50% block of I_Ca,L, I_Na, or I_Kr (dashed lines) were tested. The SR Ca²⁺ release rate (P_rel) was reduced to 1% of the control value. Control APs are superimposed in each panel (dotted lines). Differential equations of the model systems were numerically solved for 11 s (A) or 301 s (B), with an initial condition appropriate to an EP and a 1-ms stimulus of 1 pA/pF; the membrane potential behaviors during the last 1 s (starting from a maximum diastolic potential) were depicted.

In the unstable I_bias, [ACh] or G_C region, a system has an unstable EP only (no stable EP), generally exhibiting robust pacemaking (stable LCs) without annihilation. When the system removes to the stable I_bias, [ACh] or G_C region with a stable EP, it would, however, come to a rest at the stable EP via gradual decline of LCs, annihilation, or irregular dynamics (9). Thus, the larger the unstable I_bias, [ACh], or G_C range is, the more structurally stable the pacemaker system is.

Definitions of terms specific to nonlinear dynamics and bifurcation theory

Autonomous system

An nth-order autonomous continuous-time dynamical system is defined by the state equation, dx/dt = f(x), where the vector field f does not depend on time but depends only on the state variable x (20). A dynamical system is nonautonomous when the vector field f explicitly contains time t.

Limit set

The set of points in state space that a trajectory repeatedly visits in autonomous systems.

Equilibrium point

A time-independent steady-state point at which the vector field vanishes (i.e., dx/dt = 0) in the state space of an autonomous system, constructing the steady-state branch in one-parameter bifurcation diagrams. This state point corresponds to the zero-current crossing in the steady-state I/V curve, i.e., a quiescent state of a cell if it is stable.

Periodic orbit

A closed trajectory in the state space of a system, constructing the periodic branch in one-parameter bifurcation diagrams.

Limit cycle

An isolated periodic limit set onto which a trajectory is asymptotically attracted in an autonomous system. A stable LC corresponds to an oscillatory state—i.e., pacemaker activity—of a cell.

Bifurcation

A qualitative change in a limit set (i.e., in a solution of ordinary differential equations) caused by altering parameters, e.g., a change in the number of EPs or LCs, a change in the stability of an EP or LC, and a transition from a periodic to quiescent state. Bifurcation phenomena that can be observed in cardiac cells include a cessation or generation of pacemaker activity and occurrence of irregular dynamics such as skipped-beat runs (9).

Hopf bifurcation

This is a bifurcation at which the stability of an EP reverses with emergence or disappearance of a LC, occurring when the eigenvalues of a Jacobian matrix for the EP have a single complex conjugate pair and its real part reverses the sign through zero. It is supercritical when a stable EP becomes unstable with the emergence of a stable LC; it is subcritical when an unstable EP becomes stable with emergence of an unstable LC (21).

Saddle-node bifurcation

This is a bifurcation at which two EPs (steady-state branches) or two periodic solutions (periodic branches) coalesce and disappear, also called a fold or limit point bifurcation. The saddle-node bifurcation of EPs occurs when one of eigenvalues of a Jacobian matrix is zero; that of LCs occurs when one of characteristic multipliers becomes >1.

Period-doubling bifurcation

This is a bifurcation at which a stable period-K solution becomes unstable and spawns a stable period-2K solution (20), also referred to as a flip bifurcation. This occurs when one of characteristic multipliers becomes <−1.

Neimark-Sacker bifurcation

This is a bifurcation at which a stable LC becomes unstable with emergence of torus trajectories; it is thus also called a torus bifurcation. This bifurcation occurs when a complex conjugate pair of characteristic multipliers comes outside of a unit circle in the complex plane.

Codimension

The codimension of a bifurcation is the minimum dimension of the parameter space in which the bifurcation may occur in a persistent way (19,35). In other words, the codimension is the number of independent conditions determining the bifurcation (21). A bifurcation with codimension 1 is a point in one-parameter bifurcation diagrams or a line in two-parameter bifurcation diagrams, whereas a bifurcation with codimension 2 is a point in the two-parameter space.

Bistability

This means the coexistence of two stable structures in the phase space of a system. In the region of bistability, two stable EPs or stable LCs coexist, or a stable LC coexists with a stable EP (7,9,10,12). Thus, the system has two stable solutions at the same time in the bistable zone. Bistability links to the transition between two stable states; e.g., annihilation (transition from LC to EP) and single-pulse triggering (transition from EP to LC) could be achieved.

Annihilation

Permanent stable extinction of spontaneous activity, which depends upon the polarity, timing, and magnitude of the applied stimuli (9,10,12).

RESULTS

Regional differences in bifurcation structures of SA node cells

To elucidate the regional differences in pacemaker mechanisms and robustness of pacemaker activity, we compared the stability, dynamics, and bifurcation structures of the central and peripheral cells during sarcolemmal ionic current blocks or hyperpolarization.

Effects of blocking ionic currents or SR Ca²⁺ release on pacemaker activities

We first simulated the effects of blocking sarcolemmal ionic currents or SR Ca²⁺ release current (I_rel) on pacemaker activity by decreasing the current conductance. Dynamic behaviors of the central and peripheral cell models with normal and decreased conductance are shown in Fig. 1. When I_Ca,L or I_Kr was completely blocked, spontaneous activity ceased in both the central and peripheral cells. In contrast, the elimination of I_Na, I_h, or I_Ca,T, although slowing pacemaking, did not abolish pacemaker activity of either the central or peripheral cell. These simulated results are consistent with those shown in the original article of Zhang et al. (15), except that peripheral cell pacemaking ceased during the I_Ca,L block. Decreasing I_NaCa also abolished spontaneous oscillations in the Kurata et al. models, although it did not do so in the Zhang et al. models. This is a consequence of the Ca²⁺-dependent inactivation of I_Ca,L under Ca²⁺ overload conditions because pacemaker activities of the Kurata et al. models did not cease during the inhibition of I_NaCa when Ca²⁺-dependent inactivation of I_Ca,L was removed or when intracellular Ca²⁺ concentrations were fixed (data not shown). In the Kurata et al. models, spontaneous oscillations were slowed but not abolished by decreasing I_rel.

Comparison of bifurcation structures during inhibition of I_Ca,L or I_Kr

Blocking I_Ca,L or I_Kr, but not blocking other currents, abolished pacemaker activity in both the central and peripheral cells. Thus, we explored the stability, dynamics, and bifurcation structures of the model cells during the inhibition of I_Ca,L or I_Kr. Figs. 2 and 3 show the bifurcation diagrams constructed for g_Ca,L and g_Kr, respectively, depicting the V_E at EPs (steady-state branch), local potential extrema of LCs (periodic branches), and the CL of LCs as functions of g_Ca,L or g_Kr.

FIGURE 3.

Effects of reducing g_Kr on the EP stability and oscillation dynamics of the Zhang et al. (A) and Kurata et al. (B) models. One-parameter bifurcation diagrams for g_Kr with the steady-state branch (V_E) and the periodic branches (V_min, V_max) are shown (top); the CL of LCs is also plotted as a function of g_Kr (bottom). The normalized g_Kr value was reduced at an interval of 0.001 for calculations of EPs and stable LCs. The points of Hopf bifurcation of EPs (H_S) and saddle-node bifurcation of LCs (SN_P) are located: (A) H_S at g_Kr = 0.3384 (central) and 0.0228 (peripheral); SN_P at g_Kr = 0.3298 (central). (B) H_S at g_Kr = 0.3440 (central) and 0.1867 (peripheral).

During the block of I_Ca,L (decrease in g_Ca,L), the EP was stabilized via a Hopf bifurcation with emergence of an unstable LC or disappearance of a stable LC. In the Zhang et al. models and Kurata et al. peripheral model, stable and unstable LCs (periodic branches) abruptly disappeared via a saddle-node bifurcation, with the cells coming to quiescence. In the Kurata et al. central model, irregular dynamics emerged via a Neimark-Sacker bifurcation before cessation of spontaneous activity. It should be noted that the critical g_Ca,L values at the bifurcation points were smaller in the peripheral cell than in the central cell and that the Zhang et al. models and Kurata et al. peripheral model exhibited bistability, i.e., the coexistence of a stable EP and a stable LC.

The block of I_Kr (decrease in g_Kr) also caused EP stabilization via a Hopf bifurcation. Stable and unstable LCs of the Zhang et al. central model abruptly vanished via a saddle-node bifurcation, whereas the stable LC of the other model cells gradually contracted in size and collapsed at the Hopf bifurcation point. The critical g_Kr value at which the saddle-node or Hopf bifurcation to quiescence occurs was lower in the peripheral cell than in the central cell.

Influences of blocking I_Ca,L or I_Kr on stability and bifurcations during I_bias applications

We also examined the influences of blocking I_Ca,L or I_Kr on bifurcation structures (stability, dynamics, and bifurcations) during I_bias applications of the model cells. In Fig. 4, changes in V_E and its stability during I_bias applications are depicted as the I_bias-V_E curves for the normal, I_Ca,L-removed and I_Kr-removed versions of the Kurata et al. models. The control EP (V_E) at I_bias = 0 is unstable in the normal systems because two eigenvalues of a Jacobian matrix for the EP are positive real numbers; in contrast, those in the I_Ca,L- and I_Kr-removed systems are stable because all the real parts of eigenvalues (Re[λ]) are negative. There are 2–4 Hopf bifurcation points (labeled as H1–H4), where real parts of a pair of the complex conjugate eigenvalues go through zero and reverse their sign. In the whole interval between H1 and H2, the systems have no stable EP but have only one unstable EP, generating LC oscillations (Fig. 5). Saddle-node bifurcations at which multiple EPs emerge occurred in the I_Kr-removed systems.

FIGURE 5.

Oscillation dynamics during I_bias applications of the normal (control), I_Ca,L-reduced (g_Ca,L = 0.2 or 0), and I_Kr-removed (g_Kr = 0) versions of the Kurata et al. central (A) and peripheral (B) models. A bifurcation diagram for I_bias with the steady-state (V_E) and stable periodic (V_min, V_max) branches is shown; CL is also plotted against I_bias. Various amplitudes of hyperpolarizing (negative) or depolarizing (positive) I_bias were applied at an interval of 0.001 pA/pF. Hopf (H1–H3) or saddle-node (SN1, SN2) bifurcation of EPs, and saddle-node (SN_P), period-doubling (PD), or Neimark-Sacker (NS) bifurcation of LCs are located.

Figs. 6 and 7 show the displacement of Hopf and saddle-node bifurcation points in the I_bias-V_E curve, as well as the shift in the control V_E at I_bias = 0 (V₀), with decreases in g_Ca,L and g_Kr, respectively. Bifurcation points were plotted as functions of g_Ca,L or g_Kr on both the potential (V_E) and current (I_bias) coordinates. In the central cells, the unstable V_E and I_bias regions between H1 and H2 shrunk with decreasing g_Ca,L, and finally disappeared via a codimension-two saddle-node bifurcation. In contrast, the unstable regions of the peripheral cells did not vanish even when I_Ca,L was completely blocked. Reducing g_Kr did not significantly shrink the unstable V_E range in either the central or peripheral cells. The unstable I_bias regions did not disappear even when I_Kr was removed. The I_Ca,L-removed peripheral cells as well as the I_Kr-removed cells—quiescent at I_bias = 0—resumed spontaneous oscillations when an EP was destabilized by applications of hyperpolarizing I_bias (see Fig. 5).

FIGURE 6.

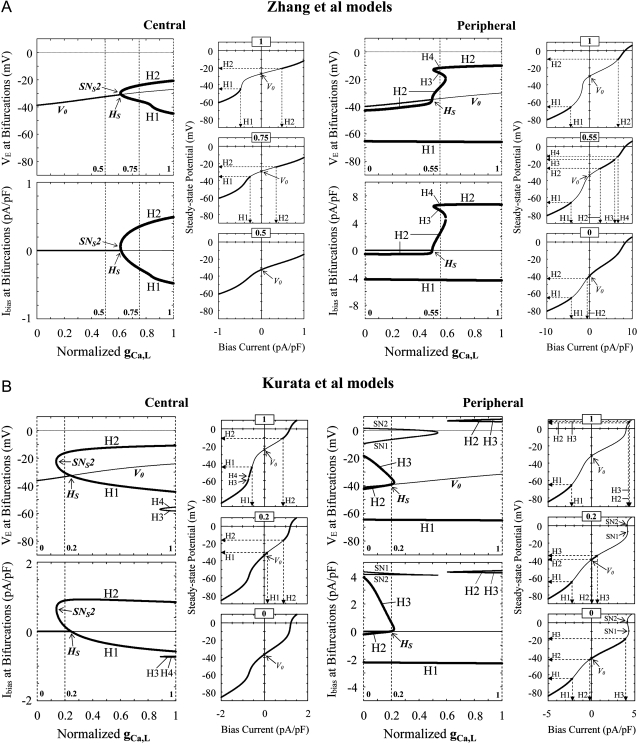
Effects of reducing g_Ca,L on bifurcation structures (stability and bifurcation of EPs) during I_bias applications of the Zhang et al. (A) and Kurata et al. (B) models for central and peripheral cells. Displacements of Hopf (H1–H4) and saddle-node (SN1, SN2) bifurcation points in the I_bias-V_E curve with decreasing g_Ca,L at an interval of 0.001 are shown on the potential (V_E) coordinates (top) and current (I_bias) coordinates (bottom). The path of the control V_E at I_bias = 0 is also shown on the potential coordinates (V₀), intersecting the locus of H1 or H2 at the Hopf bifurcation points (H_S) as shown in Fig. 2. In the insets, V_E and its stability, as well as bifurcation points, are shown as functions of I_bias for g_Ca,L = 1, 0.75, and 0.5 (A, central); g_Ca,L = 1, 0.55, and 0 (A, peripheral); or g_Ca,L = 1, 0.2, and 0 (B), as indicated by the dashed lines. The unstable regions where spontaneous oscillations occur are as follows: A, between H1 and H2 (or H3 and H4 in the periphery); B (central), between H1 and H2 (or H3 and H4); B (peripheral), between H1 and H2, or above H3 (or above H1 at g_Ca,L = 0.221–0.605). A codimension-two saddle-node bifurcation point at which the loci of H1 and H2 merge together, i.e., the unstable region disappears, is labeled SN_S2 (codimension-two saddle-node bifurcation of EPs) at g_Ca,L = 0.6131 (A, central) and 0.1382 (B, central).

FIGURE 7.

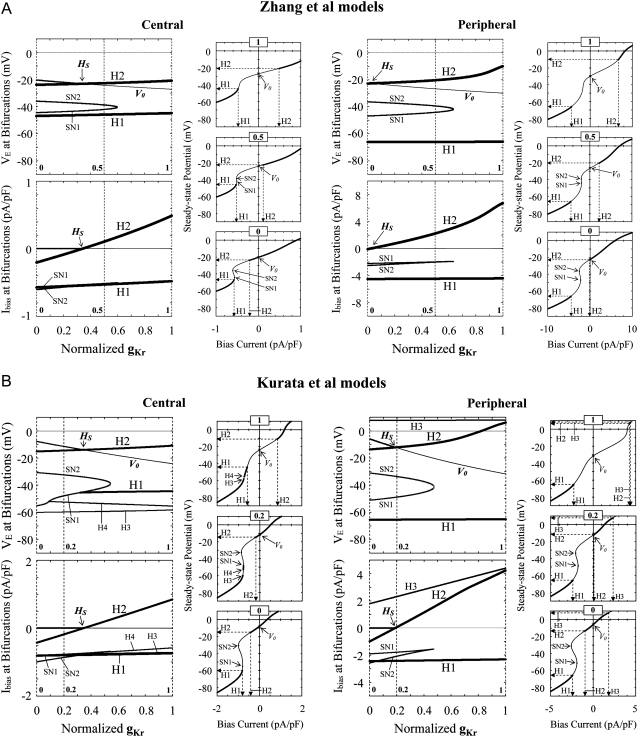
Effects of reducing g_Kr on bifurcation structures during I_bias applications of the Zhang et al. (A) and Kurata et al. (B) models. Displacements of Hopf (H1–H4) and saddle-node (SN1, SN2) bifurcation points in the I_bias-V_E curve with decreasing g_Kr at an interval of 0.001 are shown on the potential (top) and current (bottom) coordinates. The path of V₀ is also shown on the potential coordinates, intersecting the locus of H1 or H2 at the Hopf bifurcation points (H_S) as shown in Fig. 3. In the insets, V_E and its stability, as well as bifurcation points, are shown as functions of I_bias for g_Kr = 1, 0.5, and 0 (A) or g_Kr = 1, 0.2, and 0 (B), as indicated by the dashed lines. The unstable regions are as follows: A, between H1 and H2; B (central), between H1 and H2 (or SN1 and H2 at g_Kr < 0.318), and H3 and H4 (or H3 and SN1 at g_Kr < 0.090); B (peripheral), between H1 and H2, and above H3.

Bifurcation structures during ACh applications or electrotonic modulations

We further examined the regional differences in the structural stability against hyperpolarizing loads by comparing the bifurcation structures of the central and peripheral cells during ACh applications or electrotonic modulations. Figs. 8 and 9 show the stability, dynamics, and bifurcations of the model cells as functions of [ACh] and G_C, respectively.

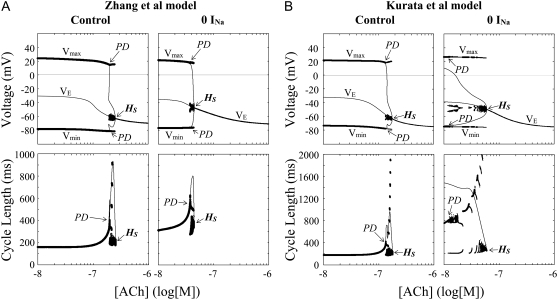
FIGURE 8.

Effects of ACh applications (increases in [ACh]) on the stability and dynamics of the Zhang et al. (A) and Kurata et al. (B) models. One-parameter bifurcation diagrams for [ACh] (log[M]) depicting a locus of V_E and the potential extrema of LCs (V_min, V_max) are shown (top); the CL of LCs is also shown as functions of log[ACh] (bottom). For calculations of EPs and stable LCs, the log[ACh] values were increased at the interval of 0.001. Hopf bifurcation points on the steady-state branches are labeled H_S: A, at log[ACh] = −7.3332 (central) and −6.6059 (peripheral); B, at log[ACh] = −7.2218 (central) and −6.7545 (peripheral). The points at which a saddle-node (SN_P) or period-doubling (PD) bifurcation of LCs occurs with disappearance of stable LCs are located on the periodic branches: A, SN_P at log[ACh] = −7.3239 (central); PD at log[ACh] = −6.7148 (peripheral); B, PD at log[ACh] = −7.329 (central) and −6.874 (peripheral). Potential extrema and CLs of the irregular dynamics emerging between PD and H_S are also superimposed.

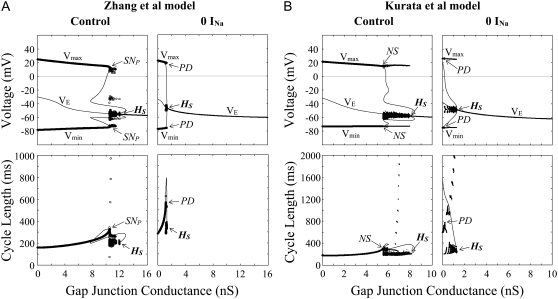
FIGURE 9.

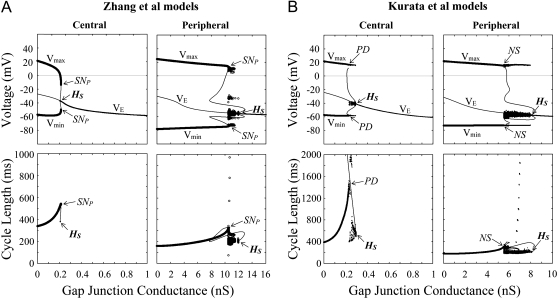
Effects of electrotonic loads of the atrium (increases in G_C) on the stability and dynamics of the Zhang et al. (A) and Kurata et al. (B) models. One-parameter bifurcation diagrams for G_C (nS) depicting a locus of V_E and the potential extrema of LCs (V_min, V_max) are shown (top); the CL of LCs is also shown as functions of G_C (bottom). G_C values for the central and peripheral cells were increased at the interval of 0.001 and 0.01 (nS), respectively. Hopf bifurcation points are labeled H_S: A, at G_C = 0.2067 (central) and 11.953 (peripheral); B, at G_C = 0.2925 (central) and 8.0688 (peripheral). The points at which a saddle-node (SN_P), period-doubling (PD), or Neimark-Sacker (NS) bifurcation of LCs occurs are located: A, SN_P at G_C = 0.2152 (central) and 10.484 (peripheral); B, PD at G_C = 0.230 (central); NS at G_C = 5.51 (peripheral). Potential extrema and CLs of the irregular dynamics emerging between the bifurcation of LCs and H_S are also superimposed.

During increases in [ACh], EPs of the central and peripheral cells were destabilized via Hopf bifurcations. In the Zhang et al. central model, a stable LC abruptly vanished via a saddle-node bifurcation, with the cell coming to a rest; in their peripheral model and Kurata et al. models, an LC became unstable via a period-doubling bifurcation with emergence of irregular dynamics between the period-doubling and Hopf bifurcation points. Destabilization of EPs via Hopf bifurcations was also observed during increases of G_C in the coupled-cell models. A stable LC of the Zhang et al. central cell abruptly vanished via a saddle-node bifurcation leading to quiescence; in their peripheral model and Kurata et al. models, an LC became unstable via a saddle-node, period-doubling, or Neimark-Sacker bifurcation with emergence of irregular dynamics. The critical [ACh] and G_C values at the bifurcations to quiescence were much greater for the peripheral cell than for the central cell.

Ionic bases of regional differences in bifurcation structures

Our results above suggest certain regional differences in bifurcation structures that can be summarized as follows: 1), the unstable V_E (EP) region determined by applications of hyperpolarizing I_bias was abolished by blocking I_Ca,L in the central cells but not in the peripheral cells (Fig. 6), and 2), the critical [ACh] and G_C values for the stabilization of EPs and abolition of stable LCs were much greater in the periphery than in the center (Figs. 8 and 9). To elucidate the ionic bases of these regional differences, we further explored how blocking individual sarcolemmal currents affects EP stability, oscillation dynamics, and bifurcation structures of the model systems. We particularly focused on the contributions of I_Na and I_h, the densities of which are much greater in the periphery than in the center.

Effects of blocking ionic currents on bifurcations during I_bias applications

To clarify the contributions of sarcolemmal currents to EP instability during applications of I_bias, we examined the effects of blocking I_Na, I_h or other time-dependent currents on the unstable V_E and I_bias regions in the I_bias-V_E curve. Hopf and saddle-node bifurcation points in the I_bias-V_E curve were determined with decreasing the maximum current conductance and plotted on the potential and current coordinates. The results after the I_Na and I_h blocks in the I_Ca,L-removed systems are shown in Fig. 10. The manner in which blocking each current shrinks the unstable V_E range where spontaneous oscillations occur should be noted; the more prominent the shrinkage in the unstable V_E region, the greater is the contribution of the current to EP instability.

FIGURE 10.

Effects of blocking I_Na or I_h on bifurcation structures during I_bias applications of the I_Ca,L-removed Zhang et al. (A) and Kurata et al. (B) peripheral models. Displacements of Hopf (H1–H4) and saddle-node (SN1–SN4) bifurcation points in the I_bias-V_E curve with decreasing g_Na or g_h at an interval of 0.001 are shown on the potential (top) and current (bottom) coordinates. The path of V₀ is also shown on the potential coordinates. In the insets, V_E and its stability, as well as bifurcation points, are shown as functions of I_bias for g_Ca,L = 1, 0.5, and 0, as indicated by the dashed lines. The unstable regions where spontaneous oscillations occur are as follows: A, between H1 and H2 (or H3 and H4); B, between H1 (or SN1) and H2, or above H3. A codimension-two saddle-node bifurcation point at which the loci of H1 and H2 merge together is labeled SN_S2 at g_Na = 0.4470 (A) and 0.388 (B).

The unstable V_E regions at negative potentials (between H1 and H2) shrunk with decreasing g_Na but not with decreasing g_h. In the I_Ca,L-removed systems, the unstable regions disappeared via a codimension-two saddle-node bifurcation; in contrast, reducing g_h did not shrink the unstable V_E range, not causing a saddle-node bifurcation. Decreases in either g_Na or g_h shrunk the unstable current region for hyperpolarizing I_bias. The effects of blocking other time-dependent currents were relatively small (data not shown).

Effects of blocking ionic currents on bifurcations during hyperpolarization

For further clarifying how sarcolemmal currents contribute to the relatively high structural stability of the peripheral cells to hyperpolarizing loads, we also examined the effects of blocking individual currents on bifurcation structures of the peripheral cells during ACh applications or electrotonic modulations. Figs. 8 and 9 indicate that a Hopf bifurcation point in the steady-state branch is just or close to the point at which spontaneous activity is abolished by hyperpolarizing loads. To assess the contribution of each current to the structural stability of the peripheral cells, we therefore focused on the changes in Hopf bifurcation points (unstable EP regions). In Figs. 11 and 12, the critical [ACh] or G_C values at which Hopf bifurcations occur are shown as functions of the maximum current conductance.

FIGURE 11.

Effects of blocking individual currents on bifurcations during ACh applications of the Zhang et al. (A) and Kurata et al. (B) peripheral models. Two-parameter bifurcation diagrams for the normalized maximum current conductance (abscissa) and log[ACh] (ordinate) are shown; the critical [ACh] values at Hopf bifurcation points were plotted as functions of the conductance, which was decreased at an interval of 0.001. The values of [ACh] (log[M]) were increased at an interval of 0.001 for searching for bifurcation points. In the insets, one-parameter bifurcation diagrams for log[ACh] used for construction of the two-parameter diagrams are shown for g_Na, g_h, and g_Ca,L at 1, 0.5, and 0, as indicated by the dashed lines in the two-parameter diagrams.

FIGURE 12.

Effects of blocking individual currents on bifurcations during electrotonic modulations of the Zhang et al. (A) and Kurata et al. (B) peripheral models. Two-parameter bifurcation diagrams for the normalized maximum current conductance (abscissa) and G_C (ordinate) are shown; the critical G_C values at Hopf bifurcation points were plotted as functions of the conductance, which was decreased at an interval of 0.001. The values of G_C (nS) were increased at an interval of 0.01 for searching for bifurcation points. In the insets, one-parameter bifurcation diagrams for G_C used for construction of the two-parameter diagrams are shown for g_Na, g_h, and g_Ca,L at 1, 0.5, and 0, as indicated by the dashed lines in the two-parameter diagrams.

The critical [ACh] and G_C values most dramatically reduced with decreasing g_Na; decreases in g_h or g_Ca,L also reduced the critical [ACh] and G_C, but their effects were relatively small. Thus, the robustness against hyperpolarizing loads was most dramatically attenuated by inhibiting I_Na. At lower g_Ca,L values, two Hopf bifurcation points (H1 and H2) appeared, with the unstable regions where LCs emerge lying between H1 and H2. It should be noted that the unstable regions did not disappear even when I_Ca,L was completely blocked. With decreases in g_Na, the unstable regions of the I_Ca,L-removed systems shrunk and finally vanished via codimension-two saddle-node bifurcations; in contrast, they were not significantly or only slightly shrunk by reductions of g_h or g_Ca,T (data not shown).

Bifurcation structures of I_Na- or I_h-removed peripheral cells

We compared the bifurcation structures during the I_Ca,L block of the normal, I_Na-removed, and I_h-removed peripheral cells (data not shown). In all the model cells, blocking I_Ca,L caused EP stabilization via a Hopf bifurcation. LCs of the I_Na-removed systems became unstable via a period-doubling bifurcation with emergence of irregular dynamics, which vanished at the Hopf bifurcation point. The critical g_Ca,L values for the bifurcations were higher in the I_Na-removed systems than in the control systems. The I_h-removed cells exhibited nearly the same stability, dynamics, and bifurcations during g_Ca,L decreases as the normal cells.

Figs. 13 and 14 show the bifurcation structures of the I_Na-removed cells as well as of the normal cells during increases of [ACh] and G_C, respectively. In the I_Na-removed systems, EPs were stabilized via Hopf bifurcations at smaller [ACh] and G_C values than in the control systems. Stable LCs of the I_Na-removed cells became unstable via period-doubling bifurcations, with irregular dynamics emerging between the period-doubling and Hopf bifurcations. The bifurcation values for irregular dynamics and quiescence were far smaller in the I_Na-removed systems than in the control systems. The critical [ACh] or G_C value for bifurcations of the I_h-removed cells was also smaller than that of the normal cells but much larger than that of the I_Na-removed cells (data not shown; see Figs. 11 and 12).

FIGURE 13.

Bifurcation structures during ACh applications of the normal (control) and I_Na-removed (0 I_Na) versions of the Zhang et al. (A) and Kurata et al. (B) peripheral models. One-parameter bifurcation diagrams for log[ACh] depicting the steady-state (V_E) and periodic (V_min, V_max) branches are shown (top); the CL of LCs is also shown as functions of log[ACh] (bottom). Procedures of the calculations are the same as for Fig. 8. Hopf (H_S) and period-doubling (PD) bifurcation points are located: A, H_S at log[ACh] = −6.6059 (control) and −7.3586 (0 I_Na); PD at log[ACh] = −6.7148 (control) and −7.4250 (0 I_Na); B, H_S at log[ACh] = −6.7545 (control) and −7.2241 (0 I_Na); PD at log[ACh] = −6.874 (control) and −7.930 (0 I_Na).

FIGURE 14.

Bifurcation structures during electrotonic modulations of the normal (control) and I_Na-removed (0 I_Na) versions of the Zhang et al. (A) and Kurata et al. (B) peripheral models. One-parameter bifurcation diagrams for G_C depicting the steady-state (V_E) and periodic (V_min, V_max) branches are shown (top); the CL of LCs is also shown as functions of G_C (bottom). Procedures of the calculations are the same as for Fig. 9. Hopf (H_S), saddle-node (SN_P), period-doubling (PD), and Neimark-Sacker (NS) bifurcation points are located: A, H_S at G_C = 11.953 (control) and 1.3152 (0 I_Na); SN_P at G_C = 10.484 (control); PD at G_C = 1.1380 (0 I_Na); B, H_S at G_C = 8.0688 (control) and 1.3170 (0 I_Na); PD at G_C = 0.15 (0 I_Na); NS at G_C = 5.51 (control).

Searching for I_Na-dependent pacemaking in peripheral cells

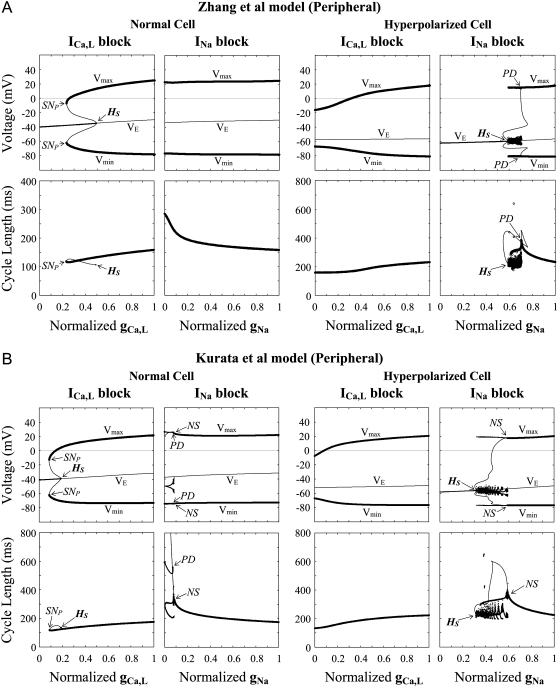
The I_Ca,L-removed peripheral cell has an unstable EP region during hyperpolarization (Figs. 4 and 5), which disappears by blocking I_Na (Fig. 10). As shown in Fig. 5 B, the application of hyperpolarizing I_bias to the I_Ca,L-eliminated peripheral cells yielded destabilization of an EP via a Hopf bifurcation, at which the cells resumed spontaneous activity. Increasing [ACh] or G_C also induced EP destabilization and emergence of a stable LC in the I_Ca,L-removed peripheral systems (data not shown). Under hyperpolarized conditions, therefore, I_Na may be responsible for EP instability and may possibly yield spontaneous oscillations independent of I_Ca,L. These findings further suggest that the “I_Na-dependent pacemaking” occurs in hyperpolarized peripheral cells. We assumed that pacemaker activity is I_Na-dependent when I_Na (not I_Ca,L) is responsible for the instability of an EP and, thus, an I_Na block (but not an I_Ca,L block) causes EP stabilization and cessation of spontaneous activity. To determine whether and how the I_Na-dependent pacemaking is possible, we further explored bifurcation structures of the hyperpolarized peripheral cells during the I_Na and/or I_Ca,L blocks.

Influences of hyperpolarization on bifurcations during inhibition of I_Ca,L and/or I_Na

We constructed two-parameter bifurcation diagrams in which the loci of Hopf bifurcation of EPs are plotted as functions of g_Ca,L and g_Na (Fig. 15). ACh was applied to the peripheral cells at various concentrations. The critical g_Ca,L value at which a Hopf bifurcation occurs was determined by the stability analysis with g_Na fixed at various different values, and was plotted as a function of g_Na (for more details, see Appendix C). Note that the right-top corner of the diagrams corresponds to the control condition. In the absence of ACh, an EP was stabilized by reducing g_Ca,L but not by reducing g_Na (with normal g_Ca,L). However, increasing [ACh] shifted the loci of Hopf bifurcation points, i.e., changed the stable and unstable regions, in the g_Na-g_Ca,L plane. With ACh at higher concentrations (Fig. 15, f–h), an EP was stabilized by decreasing g_Na but not by decreasing g_Ca,L (with normal g_Na).

FIGURE 15.

EP stability and bifurcation during decreases in g_Ca,L and/or g_Na of the Zhang et al. (A) and Kurata et al. (B) peripheral models in the presence of ACh at various concentrations. Each panel shows a two-parameter bifurcation diagram for g_Ca,L and g_Na, depicting the loci of Hopf bifurcation points. Values of [ACh] are shown at the top of each panel in log[M]. The normalized g_Ca,L value was decreased from 1 to 0 at an interval of 0.001 for searching for bifurcations, with g_Na fixed at various values; the g_Na value was decreased from 1 to 0 at an interval of 0.001 (see Appendix C). Critical g_Ca,L values at which Hopf bifurcations occurred were determined and plotted as functions of g_Na. The symbols S and US represent the stable and unstable EP regions, respectively.

Bifurcation structures of hyperpolarized peripheral cells during inhibition of I_Ca,L or I_Na

Fig. 16 shows the stability, dynamics, and bifurcations of the peripheral cells during I_Ca,L or I_Na block in the absence and presence of ACh at 1 × 10^−6.8 M (158.5 nM) for the Zhang et al. model and 1 × 10^−7.0 M (100 nM) for the Kurata et al. model. Under normal conditions at [ACh] = 0, reducing I_Ca,L stabilized an EP and abolished LCs, whereas reducing I_Na did not. Under the hyperpolarized conditions, however, blocking I_Na caused 1), LC destabilization to induce irregular dynamics via a period-doubling or Neimark-Sacker bifurcation, and 2), EP stabilization via a Hopf bifurcation below which quiescence occurred. In contrast, the abolition (or destabilization) of the stable LC or EP stabilization did not occur during the inhibition of I_Ca,L in the hyperpolarized cells.

FIGURE 16.

Bifurcation structures of the normal and hyperpolarized peripheral cells during the block of I_Ca,L or I_Na. Both the Zhang et al. (A) and Kurata et al. (B) models were tested. One-parameter bifurcation diagrams for g_Ca,L or g_Na depicting steady-state (V_E) and periodic (V_min, V_max) branches were constructed for the peripheral cells in the absence (left) and presence (right) of ACh (top); the CL of LCs is also shown as functions of g_Ca,L or g_Na (bottom). The [ACh] values for the Zhang et al. and Kurata et al. models are 1 × 10^−6.8 and 1 × 10^−7.0 M (158.5 and 100 nM), respectively. Procedures of the calculations are the same as for Fig. 2. Hopf (H_S), saddle-node (SN_P), period-doubling (PD), and Neimark-Sacker (NS) bifurcations are located: A, H_S at g_Ca,L = 0.4912 (normal) and g_Na = 0.5917 (hyperpolarized); SN_P at g_Ca,L = 0.2337 (normal); PD at g_Na = 0.7073 (hyperpolarized); B, H_S at g_Ca,L = 0.1891 (normal) and g_Na = 0.3178 (hyperpolarized); SN_P at g_Ca,L = 0.085 (normal); PD at g_Na = 0.074 (normal); NS at g_Na = 0.084 (normal) and 0.595 (hyperpolarized).

DISCUSSION

Regional differences in pacemaker mechanism and structural stability

Mechanisms of normal pacemaking are essentially the same for center and periphery

It has been reported that I_Ca,L is responsible for EP instability and spontaneous oscillations of the primary pacemaker cell in the rabbit SA node, i.e., natural pacemaking is I_Ca,L-dependent (2). In the center of the SA node, I_Ca,L would contribute to EP destabilization as a prerequisite for robust pacemaking, whereas other time-dependent currents are not necessary for basal pacemaking, rather playing pivotal roles in regulations of pacemaker activity. In this study, pacemaker activities of the peripheral cell models were abolished by blocking I_Ca,L but not by blocking I_Na or I_h, as in the central cell models (Fig. 1). Bifurcation structures during the I_Ca,L block of the central and peripheral cells were the same in that an EP was stabilized via a Hopf bifurcation, although the ways of abolishing automaticity were model-dependent (Fig. 2). These findings suggest that the dynamical mechanism of peripheral cell pacemaking is essentially the same as that of central cell pacemaking (2) and that basal pacemaking of the peripheral cell, as well as the central cell, is I_Ca,L-dependent.

Inconsistent with our simulated results, however, Kodama et al. (3) reported that applications of 2 μM nifedipine causing ∼99% block of I_Ca,L abolished spontaneous activity in the central region but not in the peripheral region, suggesting an I_Ca,L-independent pacemaker mechanism for the peripheral SA node. This inconsistency may reflect the relatively small g_Ca,L value for bifurcation to quiescence in the peripheral cell (Fig. 2), as well as the incomplete block of I_Ca,L or modulations of other currents by the agent in their preparations. Under hyperpolarized conditions, peripheral cell pacemaking was abolished not by blocking I_Ca,L but by blocking I_Na, i.e., I_Na-dependent (Fig. 16). Furthermore, eliminating I_Ca,L did not cause either stabilization of an EP (Hopf bifurcation) or cessation of pacemaker activity when relatively high [Na⁺]_i was assumed (data not shown). Thus, it is also possible that peripheral cell pacemaking was not I_Ca,L-dependent in their preparations due to hyperpolarization (outward shift in the net background current) or other unknown reasons. Previous reports also suggest that I_h plays a predominant role in the subsidiary pacemaker mechanisms (4–6). I_Na or I_h might contribute to EP destabilization and pacemaker generation in hyperpolarized peripheral SA node cells.

Structural stability to hyperpolarization of peripheral cell is greater than that of central cell

Our results suggest that the peripheral cell is considerably more robust than the central cell against hyperpolarizing loads such as applications of ACh (or hyperpolarizing I_bias) and electrotonic modulations by atrial myocytes (Figs. 6–9). Zhang et al. (30) also reported the lower sensitivity of the peripheral cell model to ACh. It should be noted that the structural stability of the peripheral cell against electrotonic loads was much greater than that of the central cell (Fig. 9). The higher structural stability of the peripheral cell is reasonable because in vivo peripheral cells are directly exposed to electrotonic loads of adjacent atrial myocytes, and thus must be more robust against hyperpolarizing loads than central cells.

The higher structural stability to hyperpolarization of the peripheral cell may be related to the pacemaker shift from the center to the periphery in SA node tissues under hyperpolarized conditions (36,37). Although it is not known whether there is a regional difference in the density of muscarinic K⁺ channels, that of muscarinic M₂ receptors as well as vagal innervation was reported to be greater in the center than in the periphery (31,32). As Shibata et al. (37) suggested, the pacemaker shift may be the result of the regional differences in the robustness against hyperpolarizing loads, M₂ receptor density, vagal innervation, and possibly I_K,ACh density as well.

Contribution of intracellular Ca²⁺ dynamics to regional differences

Lancaster et al. (38) reported that the effect of 2–30 μM ryanodine on CL was greater in peripheral cells (24 ± 6% increase) than in central cells (3.5 ± 2% increase). This may be related to heterogeneous expression of Ca²⁺ handling proteins (39), which might contribute to the regional differences in dynamical properties of pacemaker activities. Inconsistent with their experimental findings, our peripheral model could exhibit only a small increase in CL (10.7–14.0%) on minimizing the SR Ca²⁺ release, whereas a central version with a larger response (∼112.2% increase in CL) could be developed. The relatively small response of the peripheral model appeared to be due to the presence of large I_Na because the model cell with reduced I_Na exhibited much greater response, e.g., 34.3–39.6% increases in CL with g_Na = 0.3 (data not shown). In addition, ryanodine or BAPTA are known to affect sarcolemmal ion channel currents probably via decreasing intracellular Ca²⁺ concentrations (40); their secondary (or direct) effects on ionic channels may result in more dramatic responses of peripheral cells with higher densities of the channels.

To clarify whether SR Ca²⁺ cycling and intracellular Ca²⁺ dynamics substantially alter the dynamical properties of SA node cells and contribute to the regional differences in bifurcation structures, we explored their influences on stability and bifurcation of the Kurata et al. models (see Theory and Methods). Changes in SR Ca²⁺ uptake and release rates only slightly affected the stability and bifurcation of the model cells; bifurcation structures of the modified models with larger responses to the suppression of SR Ca²⁺ release were essentially the same as those of the original systems with smaller responses (data not shown). We therefore believe that neither SR Ca²⁺ cycling nor intracellular Ca²⁺ dynamics exerts substantial effects on the dynamical properties of SA node cells, not significantly contributing to the regional differences in bifurcation structures. This idea is also supported by the fact that the bifurcation structures of the Kurata et al. models incorporating the intracellular Ca²⁺ dynamics were essentially the same as those of the Zhang et al. models with fixed [Ca²⁺]_i.

Roles of I_Na in peripheral cell pacemaking

I_Na contributes to high structural stability of peripheral cell

The I_Na block most dramatically shrunk the [ACh] and G_C regions, as well as the I_bias region, of unstable EP where LCs emerge (Figs. 10–12), suggesting that I_Na mainly contributes to the relatively high structural stability of peripheral cells. This idea was further supported by the finding that the I_Na-incorporated system exhibited robust pacemaking over the broader ranges of [ACh] and G_C than the I_Na-removed system; spontaneous oscillations of the I_Na-removed system were unstable in frequency and ceased at relatively low [ACh] or G_C values (Figs. 13 and 14). Consistent with our result, Watanabe et al. (33) reported that an SA node cell with a relatively small maximum upstroke velocity (i.e., including only small I_Na) had a relatively low threshold G_C (0.58 nS) in causing bifurcation to quiescence or irregular dynamics. Thus, I_Na may dramatically improve the structural stability of peripheral cells, playing a pivotal role in preventing a bifurcation to quiescence or irregular dynamics, as well as an excess increase in CL, during hyperpolarization.

I_Na in peripheral cells is also suggested to help the SA node in driving the atrium, i.e., it plays an important role in the conduction of pacemaker activity to atrial myocytes. Reduction of I_Na in the peripheral SA node slows down the pacemaking rate (not only in the periphery but also in the center), decreases the conduction velocity, and causes exit block or sinus arrest (41,42). Thus, SA node dysfunctions in congenital sick sinus syndromes and aged hearts may be at least in part due to the I_Na decrease in peripheral cells (43,44). Our results and these reports suggest that I_Na is indispensable for the robust maintenance of SA node pacemaking and driving against electrotonic loads of the atrium.

Possible I_Na-dependent pacemaking in hyperpolarized peripheral cell

The I_Ca,L-removed peripheral cell resumed spontaneous activity when an EP was destabilized via a Hopf bifurcation by hyperpolarizing loads (Fig. 5). In the I_Ca,L-removed peripheral cell, the unstable I_bias, [ACh], or G_C region where stable or unstable LCs appear vanished via a codimension-two saddle-node bifurcation during I_Na inhibition, but not during I_h or I_Ca,T inhibition (Fig. 10). These results suggest that the spontaneous oscillation of the I_Ca,L-removed system is I_Na-dependent and that I_Na destabilizes an EP and induces spontaneous oscillations independent of I_Ca,L in hyperpolarized peripheral cells.

Our results further suggest that I_Na-dependent pacemaking is possible under hyperpolarized conditions (Figs. 15 and 16). An I_Na block by tetrodotoxin abolished pacemaker activity of the peripheral region of the intact SA node that suffers electrotonic loads of the atrium (41,42). Previous studies also suggest the requirement of I_Na for murine SA node pacemaking (41,42) and for pacemaking in human embryonic stem cell-derived cardiomyocytes that did not require I_Ca,L or I_h (45). Thus, I_Na-dependent pacemaking may actually occur in hyperpolarized peripheral SA node cells, as well as in other pacemaker cells.

Significance of applying bifurcation theory to pacemaker system analyses

In this study, we employed stability and bifurcation analyses to investigate the regional difference in the mechanisms and robustness of pacemaker activity, and also the roles of I_Na in peripheral cell pacemaking. Our work clearly shows that the nonlinear dynamical approach allows us to identify key variables or parameters responsible for pacemaker generation and to define the contribution of each current to pacemaking. As previous studies have indicated, bifurcation analyses of SA node or ventricular models are necessary for general understanding and systematic descriptions of the dynamical mechanisms of natural pacemaking (2), abnormal automaticity (7–13), and triggered activity (46).

Our study also suggests that exploring bifurcation structures of model cells can reveal the conditions and ways for oscillatory behaviors to emerge or disappear, and possibly allow us to accurately predict and properly control the dynamics and bifurcation structures of real cells. Thus, the mathematical approach based on the bifurcation theory possibly leads to the appropriate design of a structurally stable pacemaker cell system. As suggested previously, it may be applicable to the engineering of biological pacemakers from native cardiomyocytes in vivo (47–49) or human embryonic stem cells ex vivo (17,50,51) for gene or cell therapy of bradyarrhythmias (for review, see (13,17,18)). Our findings regarding the regional differences in bifurcation structures of SA node cells would be useful as a theoretical background for the engineering of biological pacemakers with robust pacemaking and driving similar to the SA node.

Limitations and perspectives of study

Possible disadvantage of using simplified models

Limitations of our study include incompleteness of the models. The model systems used in this study were constructed as base models to reproduce the normal pacemaker activities of central and peripheral cells under basal conditions (14–16). These simplified models could reproduce the experimentally observed regional differences in dynamic properties of the central and peripheral cell pacemaking (15). However, they do not include detailed descriptions for intracellular Ca²⁺ dynamics, SR Ca²⁺ handling, or activities of other modulating factors. These intracellular factors are known to exert substantial effects on ion channel functions and pacemaker dynamics (e.g., see (52–55)) and possibly affect bifurcation structures as well. Moreover, the regional differences in the activity of Ca²⁺ regulatory proteins including the Na⁺/Ca²⁺ exchanger, SR Ca²⁺ release channel, and SR Ca²⁺ pump were not taken into account or not based on detailed experimental data; the densities and activities of these proteins are probably greater in the periphery than in the center (38,39).

Another shortcoming of our models may be the use of the classical Hodgkin-Huxley formalism for the kinetic formulation of the time-dependent currents including I_Na. More general and realistic schemes, i.e., Markovian state models have been developed for the Na⁺ channel (56,57) as well as for other individual channels. However, we did not use these models for I_Na, because 1), no Markovian state scheme is available for the SA node Na⁺ channel, 2), more detailed experimental data from SA node cells are required for the Markov scheme-based formulation of the SA node I_Na kinetics, and 3), such complex models are less suitable for bifurcation analyses. Nevertheless, further sophisticated models based on Markovian state schemes, such as for ventricular myocytes (58), need to be developed and tested for SA node cells in future investigations.

Influences of lacking Ca²⁺ clock

The most serious drawback of the models may be the lack of a “Ca²⁺ clock” that is defined as the spontaneous rhythmic Ca²⁺ release from the junctional SR. Blocking the Ca²⁺ clock by ryanodine or BAPTA dramatically increased CL and finally abolished pacemaker activity (59–63); thus, the Ca²⁺ clock may exert substantial effects on the dynamical properties of SA node cells. Nevertheless, we assumed that the basal pacemaking of SA node cells is attributable to the interplay of sarcolemmal ionic currents such as I_Ca,L, I_Na, I_h, and I_Kr (i.e., “membrane clock”), for the following reasons:

1. Experimental reports on the effects of eliminating SR Ca²⁺ release or intracellular Ca²⁺ transient were controversial. In other experimental studies, ryanodine or BAPTA did not abolish, but only slowed, SA node pacemaking (38,64,65); thus, the Ca²⁺ clock is not necessarily required for pacemaker generation.

2. Ryanodine and BAPTA are known to affect not only the Ca²⁺ clock but also the membrane clock (40); their secondary (or direct) effects on the membrane clock, rather than the elimination of the Ca²⁺ clock, may result in the dramatic responses.

3. Spontaneous Ca²⁺ release was local (not global), stochastic, and transient in the pacemaker potential range (60); thus, the manner in which the Ca²⁺ clock contributes to the stability and bifurcation structures of SA node cells is unclear. In our opinion, the Ca²⁺ clock is not a prerequisite for basal SA node pacemaking, although it would significantly modulate pacemaker activity and is possibly involved in the regional differences in pacemaker dynamics (38).

As already mentioned, neither SR Ca²⁺ cycling nor intracellular Ca²⁺ dynamics exerted substantial effects on the stability and bifurcation of SA node model cells, with their effects being too small to alter our conclusions. The simplified models used in this study are therefore valuable and highly appropriate for exploring the bifurcation structures of pacemaker cells and essential mechanisms of basal SA node pacemaking. Nevertheless, our models do not incorporate the real Ca²⁺ clock defined as the spontaneous rhythmic Ca²⁺ release from the junctional SR to trigger the membrane clock. We could produce a model with the spontaneous SR Ca²⁺ release (and a transient increase in [Ca²⁺]_sub and the forward-mode I_NaCa) during phase 4 depolarization by further increasing SR Ca²⁺ uptake and release rates (data not shown). However, such a model was not used because an excess increase of the SR Ca²⁺ uptake and release rates resulted in very small CL (<150 ms in the peripheral model) and often induced irregular dynamics. Maltsev et al. (66) developed a modified version of the Kurata et al. model (14) to exhibit the spontaneous local Ca²⁺ release from the junctional SR during phase 4. However, their formulas were based on phenomenological representation to approximate the experimental pattern of Ca²⁺ signals in the subspace, which were not suitable for bifurcation analysis. More elaborate models incorporating detailed descriptions of the intracellular Ca²⁺ handling as well as other modulating factors need to be developed for future investigations regarding the role of the Ca²⁺ clock in SA node pacemaking in terms of nonlinear dynamics and bifurcation theory.

Requirement of multicellular models

We used the single-cell or coupled-cell systems to investigate the robustness of SA node pacemaking against hyperpolarization and the roles of I_Na in peripheral cell pacemaking. However, the real intact SA node has complex architectures to facilitate optimization of the electrical loading by the surrounding atrial tissue (36,67–69). Previous studies suggest that electrotonic interaction is involved in the pacemaker mechanisms of the intact SA node (5,69). Thus, multicellular models including central and peripheral SA node cells and also atrial myocytes are required for further investigating how electrotonic interactions, as well as I_Na, contribute to the pacemaking and driving ability of the intact SA node in vivo. Modeling SA node tissues would also be useful in exploring the mechanisms of pacemaker shifts (36,37), pacemaker synchronization (70), and abnormal rhythms such as the exit block and intranodal reentry (42).

Lack of experimental evidence

The conclusions in this study are, of course, the predictions from the model cell systems; thus they must be verified and supported by experimental works using real SA node cells. Fundamental properties of the model cell behaviors have been verified by Zhang et al. (15). Inconsistent with our result, however, pacemaker activity of the peripheral cell was not abolished by blocking I_Ca,L in either their simulation or in experiments (3). We could not find experimental evidence for the cessation of peripheral cell pacemaking by the inhibition of I_Ca,L as predicted by the models in Figs. 1 and 2, although the I_Na block was observed to abolish pacemaker activity of the peripheral SA node region with electrotonic loads of the atrium in mice (41,42). Whether an I_Ca,L blocker can abolish peripheral cell pacemaking should be reexamined in future experiments. To the best of our knowledge, there is no systematic study regarding the bifurcation structures of SA node cells to clarify the regional differences in the dynamical mechanism and the robustness of pacemaker activity. We hope that this study provides a stimulus to further experimentation on these issues.

APPENDIX A: MODEL EQUATIONS

Mathematical expressions, definitions of the symbols, and standard parameter values used in this study are essentially the same as those in the original articles (14–16). The formulas for I_Ca,L, I_h, and I_K,ACh with ACh modifications of Dokos et al. (29), as well as those for I_Na adopted from Garny et al. (16), are given below for convenience. Units are mV, pA, nS, ms, pF, mM, and L (pA/pF and nS/pF for ionic currents and conductance, respectively). Dynamics of the model cells with standard parameter values (for the Kurata et al. models; see Table 1) are shown in Fig. 17.

Na⁺ channel current (I_Na):

(A1)

(A2)

(A3)

(A4)

(A5)

(A6)

(A7)

L-type Ca²⁺ channel current (I_Ca,L) for modified Zhang et al. models:

(A8)

g_Ca,L=0.2752(central) or 0.9630 (peripheral)

(A9)

(A10)

(A11)

(A12)

(A13)

(A14)

(A15)

(A16)

(A17)

L-type Ca²⁺ channel current (I_Ca,L) for Kurata et al. models:

(A18)

(A19)

(A20)

(A21)

(A22)

(A23)

(A24)

(A25)

(A26)

Hyperpolarization-activated cation current (I_h):

(A27)

(A28)

(A29)

(A30)

(A31)

(A32)

Muscarinic K⁺ channel current (I_K,ACh):

(A33)

APPENDIX B: STABILITY ANALYSIS BASED ON THE LINEAR STABILITY THEORY

We evaluated the stability of EPs according to the linear stability theory, i.e., by linear approximation of a nonlinear system at an EP (see (71,72)). For simplicity, first consider the two-dimensional autonomous system of the form

(A34a)

or the vector form

(A34b)

(T denotes transpose). Suppose that the EP to be (x_1E, x_2E), so that f₁(x_1E, x_2E) = f₂(x_1E, x_2E) = 0. We can therefore write, by a Taylor series expansion of the vector field f_i(x₁, x₂) around the EP,

(A35)

where the symbol O stands for the term of higher order (tho). Thus, the linear approximation to Eq. A34 in the neighborhood of the EP is defined as the system for h₁(= x₁-x_1E) and h₂(= x₂-x_2E):

(A36a)

This linearized system is also written in the vector form

(A36b)

where Df(x_E) is the Jacobian matrix of first-order partial derivatives of f(x), denoted by:

(A37)

We can expect in most cases that the solutions of Eq. A36 will be geometrically similar to those of Eq. A34 near the EP. It is well known that there are solutions of Eq. A36 of the form

(A38a)

or the vector form

(A38b)

where λ₁ and λ₂ are the eigenvalues (roots of the characteristic equation) for the Jacobian matrix Df(x_E). C₁ and C₂ are arbitrary constants to be complex in general. The approximation h(t) describes the local behavior of the solution, indicating how the process evolves when the initial state deviates slightly from the EP. When λ_i is complex, represented as

(A39)

we obtain

(A40)

Here Re[λ_i] and Im[λ_i] are respectively the real and imaginary part of λ_i. For a more general case of an n-dimensional autonomous system of the form

(A41)

the linearized form around an EP of x_E = (x_1E, x_2E, …, x_nE)^T is

(A42)

Then, the solution of Eq. A42 is given by

(A43)

Thus, Re[λ_i] represents the rate constant of a solution beneath the EP to be attracted to or go away from the EP. The EP is stable if all of the Re[λ_i] values are negative because the system is asymptotically attracted to the EP; it is unstable if at least one of Re[λ_i] values is positive because the system goes away from the EP.

APPENDIX C: CONSTRUCTION OF TWO-PARAMETER BIFURCATION DIAGRAMS FOR G_CA,L AND G_NA

The two-parameter bifurcation diagrams for g_Ca,L and g_Na (Fig. 15) show how the stability of EPs reverses via Hopf bifurcations during the inhibition of I_Ca,L and/or I_Na. One-parameter bifurcation diagrams for g_Ca,L of 0–1 were first constructed with various g_Na values of 0–1 (with intervals of 0.001) by the stability analysis for EPs; those for g_Na = 1, 0.9, 0.8, 0.7, 0.65, 0.6, 0.4, 0.2, and 0 are shown in Fig. 18 (top-right). To construct the two-parameter bifurcation diagrams as shown in Fig. 15, the critical g_Ca,L values at Hopf bifurcations in the one-parameter bifurcation diagrams were plotted as functions of g_Na (Fig. 18 top-left). This two-parameter bifurcation diagram can also be constructed from one-parameter bifurcation diagrams for g_Na determined with various g_Ca,L values (see Fig. 18 bottom for g_Ca,L = 1, 0.9, 0.8, 0.7, 0.6, 0.5, 0.4, 0.2, and 0).

FIGURE 18.

How to construct the two-parameter bifurcation diagram for g_Ca,L and g_Na (Fig. 15) from one-parameter bifurcation diagrams for g_Ca,L or g_Na. (Left) The two-parameter bifurcation diagram for the Zhang et al. peripheral model with the [ACh] of 1 × 10^−7.32 M (47.863 nM). The point labeled C corresponds to the control condition. The leftward and downward shifts from C indicate the block of I_Na and I_Ca,L, respectively (shown by the arrows). Dashed lines designate the points of g_Na (top) or g_Ca,L (bottom) for the construction of the one-parameter bifurcation diagrams shown on the right. (Right) One-parameter bifurcation diagrams depicting V_E and its stability as functions of g_Ca,L (top) or g_Na (bottom). The normalized g_Ca,L (top) or g_Na (bottom) value as the first parameter was decreased from 1 to 0 at an interval of 0.001 for searching for Hopf bifurcations, with the second parameter g_Na (top) or g_Ca,L (bottom) fixed at various values as shown on the right of each panel. Critical values of the first parameter g_Ca,L (top) or g_Na (bottom) at which Hopf bifurcations occurred were determined by the stability analysis. The thick and thin segments are the stable and unstable V_E regions, respectively; the boundaries between the two segments correspond to the bifurcation points. The two-parameter bifurcation diagram can be constructed by plotting these bifurcation values of the first parameter g_Ca,L (or g_Na) as functions of the second parameter g_Na (or g_Ca,L).