Dynamics of Cellular Focal Adhesions on Deformable Substrates: Consequences for Cell Force Microscopy

Abstract

Cell focal adhesions are micrometer-sized aggregates of proteins that anchor the cell to the extracellular matrix. Within the cell, these adhesions are connected to the contractile, actin cytoskeleton; this allows the adhesions to transmit forces to the surrounding matrix and makes the adhesion assembly sensitive to the rigidity of their environment. In this article, we predict the dynamics of focal adhesions as a function of the rigidity of the substrate. We generalize previous theories and include the fact that the dynamics of proteins that adsorb to adhesions are also driven by their coupling to cell contractility and the deformation of the matrix. We predict that adhesions reach a finite size that is proportional to the elastic compliance of the substrate, on a timescale that also scales with the compliance: focal adhesions quickly reach a relatively small, steady-state size on soft materials. However, their apparent sliding is not sensitive to the rigidity of the substrate. We also suggest some experimental probes of these ideas and discuss the nature of information that can be extracted from cell force microscopy on deformable substrates.

INTRODUCTION

Focal adhesions (FAs) are micrometer-sized regions of proteins that connect the extracellular matrix (ECM) to the cellular cytoskeleton. Cytoskeletal stress fibers contain actin filaments and myosin II molecular motors and transmit force to their environment via the FAs. These highly organized adhesions play a crucial role in cell development and cell movement. One important feature of focal adhesions is their sensitivity to the compliance of the extracellular environment: FAs are only stable on substrates whose rigidity exceeds a certain critical value which may depend on cell type (1). Consequently, the mechanical properties of the substrate are an important determining factor of cell activity and viability (2). For example, for a given chemistry and geometry of the extracellular matrix, stem cells differentiate into different types of cells, depending on the stiffness of the ECM (2). The ability of the cell to probe the mechanical properties of its environment originates in the coupling of the FAs to the contractile stress fibers. An important probe of the mechanosensitivity of FAs is measurements of the forces cells exert on substrates. Several experiments have quantified the forces exerted by adhering cells by measuring the deformation of elastic substrates (patterned elastomers (3–5), deflection of elastomer pillars (6–8), and birefringence of an elastomer (9)). In all these experiments, it is observed that focal adhesions reach a steady-state value of the force and a steady-state area. On stiff substrates, focal adhesions of stationary fibroblasts were also observed to be highly motile (10).

The sensitivity of FAs to the elastic properties of the extracellular matrix has not yet been studied experimentally in a comprehensive manner. In this article, we investigate theoretically the impact of a deformable substrate on the growth dynamics of focal adhesions, and show that these dynamics are markedly different on very rigid surfaces compared with deformable ones. In a previous article, we proposed a model that accounts for the mechanosensitivity of focal adhesions (11). In that study, we assumed that focal adhesions contain a mechanosensitive, macromolecular unit that is activated by stress resulting from acto-myosin activity or from external, tangential applied stress (fluid flow, stretch of the substrate, micropipette-induced shear, etc.). With this model, we showed that the dynamics of focal adhesions is anisotropic, as opposed to the isotropic growth of protein domains in the usual, force-free, problem of protein surface adsorption; the adhesions grow in the direction of the stress: additional proteins join the adhesion at its front (the front and the back edges of the adhesion are defined relative to the direction of the stress), while proteins may (in some cases) dissociate from the back (11,12). A further analysis of the energetics (13) accounted for the observation that focal adhesions only form on ECM whose stiffness exceeds a certain threshold value (1). Finally, we predicted that on very thick elastic ECM, focal adhesions would reach a stationary size, whose value is proportional to the stiffness of the ECM. This implies that a focal adhesion deforms an elastic substrate with a total force that is proportional to the rigidity of the substrate. This result appeared to be consistent with the work by Saez et al. (6) that presented an alternative interpretation that did not take into account the adhesion size as a function of rigidity. Instead, those authors claim that the adhesions operate at a setpoint of fixed displacement or strain, rather than fixed force. This still-open question provides additional motivation for the analysis of our model for focal adhesion mechanosensitivity, and we show here that dynamics behavior is far from simple when the ECM has a finite compliance.

In Focal Adhesions: Two-Layer Model, we briefly review the framework of our model. The crucial assumption is that the dynamics of focal adhesions is driven by the exchange of energy of the anchoring/desorbing proteins including their coupling to cell contractility and hence to the resulting substrate deformation. The thermodynamic system under consideration therefore includes not only the adsorbing proteins as in the usual nucleation and growth or adsorption/condensation problems, but also includes the energetics of the processes that exert force on the adhesion and hence deform the substrate. When considering the situation of a fixed stress on soft substrates, one must account for the fact that part of the work done by cell contractility is used to deform the substrate. This results in an increase of the total free energy and therefore limits the growth of focal adhesions. (In the absence of cell contractility, condensation of adsorbing molecules in or on an elastic medium is, on the contrary, favored by the softness of the substrate (14).) In Dynamics of Focal Adhesions on a Rigid Substrate, we show that the dynamics of focal adhesions on a rigid substrate is characterized by several different regimes, depending on the stress exerted on adhesion. These results are a generalization of the predictions of Besser and Safran (12) that treated only the case of infinitely rigid substrates. Dynamics of Focal Adhesions on a Deformable Substrate predicts the dynamics of focal adhesions for the case of thick, elastic substrates. These new results show that adhesions saturate to a size that is proportional to the rigidity of the substrate with a characteristic time that is also proportional to the rigidity: adhesions on soft substrates reach small steady-state sizes on short timescales. In Discussion, we compare the predictions of our model to existing experimental results and finally conclude by discussing which physical quantities are accessible by cell force microscopy and which features must be studied using other techniques.

FOCAL ADHESIONS: TWO-LAYER MODEL

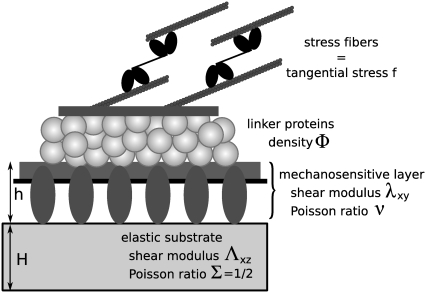
We model focal adhesions as a two-layer structure. The lower layer contains membrane-bound integrins and related proteins such as paxillin or zyxin that connect the cell to the ECM. The upper layer contains proteins such as vinculin or talin that link the lower layer to actin stress fibers (Fig. 1). This very schematic model highlights the different dynamical behaviors of the various components of FAs. The two layers refer to two distinct dynamical behaviors and not necessarily to a specific spatial organization. Although the limitation to only two dynamical classes is a simplification that is not yet supported by detailed experiments, the existence of different dynamics for various components of FAs is supported by recent high resolution fluorescence recovery after photobleaching (15) and total internal reflection fluorescence or fluorescence correlation spectroscopy (16) experiments. Atomic-force microscopy structural measurements have related these findings to some specific spatial arrangements (17), and show that stress fibers are localized above the FAs while paxillin lies close to the membrane. In the following, we assume that the lower layer is formed independent of, and prior to, the formation of the upper layer. This assumption, although crude at the molecular level, is inspired by the observation that integrin clustering in FAs requires neither force nor actin filaments (integrin clustering does require talin and PI(4, 5)P₂ (18)). This is in contrast to the assembly of the other components of the FAs that are only stable in the presence of acto-myosin force (18). In the following, we assume that the lower layer contains the mechanosensitive units, while the upper layer contains proteins, hereafter called linker proteins that transmit the stress from the stress fibers to the mechanosensitive, lower layer (Fig. 1). Our model assumes that once a linker protein anchors to the mechanosensitive layer, it instantaneously transmits a fixed and constant stress, 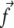(force per unit area); see Discussion for more about this assumption. Experiments have shown that the tangential component of the stress, 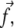plays a dominant role (19), and have quantified the stress that arises from actin contractility (3,7,5,9). We thus focus our analysis on the effect of the tangential component of the stress, 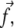which we denote as a scalar f. The direction of this component defines the direction x (Fig. 2), which we term the force direction.

FIGURE 1.

The two-layer model: linker proteins in the upper layer connect the acto-myosin stress fibers and the mechanosensitive, lower layer that is anchored to the substrate via integrins.

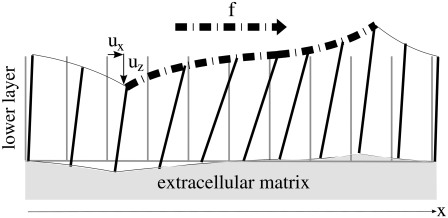
FIGURE 2.

The lower layer is deformed by the tangential component of the stress, 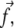that acts along the dash-dot line. The rods have no molecular significance but help to visualize the deformation of the molecular units. The stress-induced tilt is not uniform in the layer, giving rise to a nonzero gradient of tilt.

The dynamics of focal adhesions is controlled by the exchange of energy of the linker proteins coupled to the stress fibers

What causes a focal adhesion to grow? As detailed in previous publications (11,13), our model accounts for recent experiments if we assume that the dynamics of FAs is driven by the variation of energy of the linker proteins including their coupling to cell contractility and hence to the substrate deformation. Linkers bind to the lower layer and instantaneously connect this layer to the stress fibers, thus transmitting the forces of the stress fibers to the mechanosensitive layer. The force originates in the mechanical work performed by molecular motors in actin stress fibers and results in the elastic deformation of both the mechanosensitive layer and the elastic substrate. We assume that the assembly of FAs is limited by the kinetics of the various interactions among the proteins, while diffusion occurs on much faster timescales (12). Thus, the kinetics of the adsorption/desorption of the linker proteins results from the variation of the chemical potential of this coupled system (20),

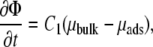(1)

where Φ is the concentration of linker proteins in the upper layer that transmit the stress from the actin stress fibers to the mechanosensitive layer: 0 ≤ Φ ≤ 1. The prefactor C₁ relates the variation of the chemical potential to the dynamics of the FAs: C₁ = Φ_bulkD/(k_BTa²), where D is the diffusion coefficient of the linker proteins, Φ_bulk is the bulk protein concentration, and a is the typical distance between two adsorbing sites in the mechanosensitive layer. The chemical potential difference between the linker proteins in the cell cytoplasm and those connecting the stress fibers to a focal adhesion, is μ_bulk – μ_ads. The free energy from which μ_ads is derived has two contributions:

1. The mechanical energy that originates in the work done by the stress fibers to maintain a constant stress (force per unit surface) as the adhesion grows. (The assumption that the stress is kept constant as the size of the adhesion varies is deduced from (3), but is questioned in another study (6), as discussed in the final section of our article.) The forces exerted by the stress fibers deform both the FAs and the substrate if indeed, the latter is deformable.

2. The chemical binding energy involved as additional linker proteins adsorb on the existing FAs. We showed in Nicolas et al. (11) that this energy must be exothermic (a lowering of the cellular energy) for our model to properly account for the observed, force-induced growth of FAs (19).

The total free energy that is relevant to the calculation of the linker protein chemical potential is obtained by starting with the following Hamiltonian:

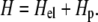(2)

The first term is related to the energy the molecular motors provide to maintain a constant stress on the focal adhesion; the contribution of this term becomes more important on deformable substrates. It is coupled to the concentration of linker proteins because the stress is only transmitted to the substrate via these proteins. When additional proteins adsorb, they connect the FAs to the cytoskeleton and the motors in the stress fibers must expend more energy (or must recruit additional motors with a consequent chemical potential energy cost) to maintain a constant stress on the deformable area, which has grown due to the presence of the additional linker proteins. The second term includes the energy that is released when additional linker proteins adsorb and enlarge the focal adhesion.

We treat the top of the lower layer as a two-dimensional lattice. Each site i may or not contain a linker protein, that connects the lower layer to the actin stress fibers (the site occupation variable Φ_i is then 1 or 0 whether there is or is not a linker protein at site i). For a given discrete distribution of linker proteins {Φ_i}, we write

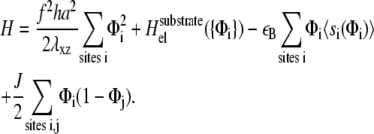(3)

The first term is the stress-induced deformation of the FAs, which is characterized by a Young's modulus Y, a Poisson ratio ν, and a shear modulus λ_xz = Y/(2(1 + ν)), as well as by the thickness h. The stress is denoted by f (see Table 1 for numerical values) and in Appendix B we present a detailed derivation of this term. The second term is the energy associated with the deformation of the substrate with shear modulus Λ_xz and Poisson ratio Σ. Since the linker proteins transmit the stress from the actin stress fibers to the substrate, this energy depends on the distribution {Φ_i} of the linkers: Φ_i = 0 if the site i is unoccupied, Φ_i = 1 otherwise. The functional form of 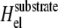also depends on the geometry of the substrate. A derivation of this term for a semiinfinite, elastic substrate is also presented in Appendix B. For the sake of simplicity and with no loss of generality, we limit our analysis to the case where Σ = 1/2. Coupling of the deformations of the adhesion and the substrate is a second-order correction in the limit where the substrate is much more rigid than the adhesion (λ_xz ≪ Λ_xz). The third term accounts for the energetics of adsorption of the linker proteins on the lower layer (the mechanosensitive layer); this adsorption is energetically favorable since it releases an energy ε_B > 0 if the lower-layer molecule (e.g., integrin) at position i is activated (s_i = 1) and is therefore in a conformation in which it can associate with a linker protein. If s_i = 0, the lower-layer molecule is not activated and cannot associate with the linker protein; no binding occurs in this case. The last term is the short-ranged, two-body attractive interaction between adsorbed linker proteins; this interaction is due to local effects and is independent of the acto-myosin force and substrate deformations. We assume J > 0, since experimentally it is observed that condensation of the adsorbed linker proteins is favored.

TABLE 1.

Mechanosensitive layer
a	Size of elementary mechanosensitive units.	0.02–0.06 μm (25)
h	Thickness of the mechanosensitive layer.	∼100 nm (17)
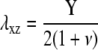	Shear modulus of the mechanosensitive layer.	∼1 kPa (28)
ΔG	Energy barrier between the inactivated and activated state for the mechanosensor.
τ	Lowering of the energy barrier associated with the gradient of tilt.
d	Molecular length scale associated with the change of conformation of the stretched mechanosensor.
s(x, y)	Degree of activation of the site located at (x,y).	0 ≤ s ≤ 1
Linker proteins
f	Magnitude of the tangential component of the actin induced or external stress.	3–6 nN/μm2 (3,4,7)
{Φi}	A particular realization of the occupation of the sites of the lower layer by the linker proteins.	Φi = 0, 1
Φ(x, y, t)	Linker proteins concentration averaged over all possible realizations {Φi}.	0 ≤ Φ(x, y, t) ≤ 1
ψ (x, y, t)	Small deviation from the average linker proteins concentration.	ψ = Φ – 1/2
εB	Energy of adsorption of a linker protein on an activated site.	εB > 0
J	Coupling coefficient for the short-ranged two body interaction.	J > 0
μbulk	Chemical potential of free linker proteins.
C1	Prefactor that relates the variation of the chemical potential to the dynamics.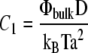
Extracellular matrix
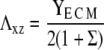	Shear modulus of the extracellular matrix.	Σ = 1/2

From this expression for H (Eq. 3), one can calculate the free energy of the system and hence the chemical potential of the linker proteins (including their coupling to cell contractility as described above),

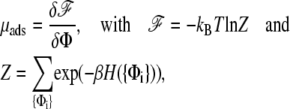where Φ(x, y, t) is the concentration of the adsorbed linker proteins averaged using the Boltzmann distribution. The expression Φ(x, y, t) is the continuum analog of the discrete variable 〈Φ_i〉 (see (12) for more details). The partition function Z is summed over all the realizations {Φ_i} of the site variables, Φ_i = 0, 1; β is the inverse of the thermal energy: β = 1/(k_BT).

The mechanosensitive layer is activated by two modes of deformation

To calculate μ_ads, we first calculate the probability, 〈s_i〉, that a site, i, in the mechanosensitive layer is activated and has changed its conformation in such a way so that association with the linker proteins is favorable. In the two-layer model that we use, the lower layer is composed of a uniform distribution of mechanosensitive units of size a. As discussed previously, linker proteins release an energy ε_B when they adsorb onto an activated site. In the following, we assume that activation is favored by two different modes of the mechanical deformation of the lower layer (12): 1), an in-plane shear, that results in both a tilt and an extension of every mechanosensitive unit; and 2), a gradient in tilt along the mechanosensitive layer (Fig. 2). Stretching of proteins is a common deformation that influences the molecular conformations and was suggested to induce a transition between very transient initial adhesions and the more force-resistant focal complexes (21). The gradient of the tilt is another possible, but less studied, way of inducing conformational change in proteins mainly because as a gradient of the molecular tilts, it is only applicable to protein aggregates. However, in the case of FAs, the assumption that the gradient of tilt induces a conformational change of the proteins leads to results that are consistent with observations. One major consequence of this assumption is that it is responsible for the nonuniform stress, and hence nonuniform activation of the lower layer in the direction of the stress 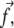which results in the directed growth of FAs. Further consequences of this assumption are presented in Nicolas et al. (11) and compared to experimental observations. It also accounts for the sliding of FAs that results from the simultaneous addition of new proteins at the edge of the FAs that is in the direction of the applied force and disassembly of the FAs at the opposite edge (22). In addition to the gradient of tilt, the in-plane shear of the mechanosensitive layer results in a uniform activation (12) of the entire FAs, consistent with experimental evidence for the disappearance of FAs when the force is removed. As already mentioned in Besser and Safran (12), this term is responsible for the switching from a shrinking FAs at small stress to a growing adhesion at larger stress. We therefore write the Hamiltonian that determines the probability, 〈s_i〉, that site i is activated and can associate with linker proteins as

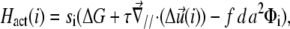(4)

where 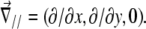In this expression, ΔG is the energetic barrier related to the changes in conformation of the mechanosensor that must occur for it to switch from an inactivated state (s_i = 0) (where it cannot associate with the linker proteins), to the activated one (s_i = 1) (where association can occur). The value 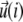is the displacement of the mechanosensitive layer, relative to its unstressed state (Fig. 2). The value 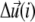is the relative displacement of the top of the mechanosensitive layer (where the acto-myosin force is applied) compared to its bottom (which is grafted to the substrate). 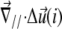therefore describes the gradient of tilt between neighbor mechanosensitive units: when 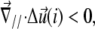the upper part of the units in the vicinity of site i are closer than their lower parts, as one can see at the front edge of the stressed region on Fig. 2; when 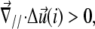the upper parts are farther away than the lower parts of these molecular units, as shown at the back edge of the stressed region on Fig. 2. We assume that a negative tilt gradient induces the change of conformation of the mechanosensitive units from deactivated to activated. We therefore take τ > 0, since it multiplies the gradient of tilt of the mechanosensor (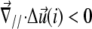) to determine the decrease of the energy barrier for the conformational change that arises from compression of the top of the units. The last term accounts for the lowering of the energy barrier for the conformational change that arises from the in-plane shear-induced stretching of the mechanosensitive units (21). Stress transmitted by the linker proteins (Φ_i = 1) causes stretching and hence a conformational change in the mechanosensitive units. The value d is the molecular length scale associated with the change of conformation. If one assumes that the lowering of the energy barrier, ΔG, by compression is perturbative (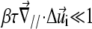), we can use Eq. 4 to estimate the probability that the site i is activated:

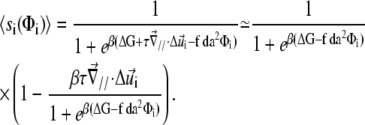(5)

We can now calculate the variation of the chemical potential of the linker proteins that adsorb onto the focal adhesion, including the work done by the stress fibers due to the deformation of the substrate.

DYNAMICS OF FOCAL ADHESIONS ON A RIGID SUBSTRATE

We first focus on the case of cells placed on an infinitely rigid substrate for which there is no substrate deformation. In this case, the stress transmitted by the cells due to their contractility only results in a deformation of the adhesion sites and not of the substrate: 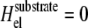in Eq. 3. In the situation where adhesions are grafted to an undeformable substrate (and hence cannot displace the ECM), the elastic energy H_el that determines the occupation probability, Φ_i, of linker proteins at site i is ((13); see also Appendix B)

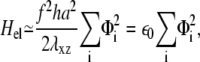(6)

where λ_xz is the shear modulus of the mechanosensitive layer and h its thickness. The Hamiltonian, Eq. 3, simplifies to

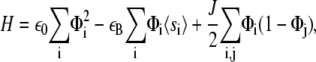(7)

where 〈s_i〉 is the average activation rate of the mechanosensitive layer at site i. Note that this expression differs from the one that was previously proposed by Besser and Safran (12) (see Eq. 13 in (12)) because we focus on the thermodynamic system that consists of the linker proteins coupled to the stress fibers and the substrate. Besser and Safran (12) focused only on the variation of the energy of the linker proteins. As was previously shown (11), we must include the coupling of the linker proteins to cell contractility to predict increased growth of FAs on rigid substrates compared with soft substrates (13).

This activation is caused by the elastic stresses in the lower layer, as explained above. Adsorption of new linker proteins at the activated sites influences the deformation of the layer, and therefore also changes the activation probability. However, the process of activation is much slower (of the order of seconds (24)) than the nearly instantaneous elastic deformation of the lower layer by the forces transmitted by linker proteins (the sound velocity in an elastic material with a Young's modulus of ∼1 kPa and with a density of ∼10³ kg/m³ is ∼1 m/s). This means that the activation probability, 〈s_i〉, averages over many attempts by many linker proteins to associate with the lower layer, so that 〈s_i〉 is a function of the local average linker concentration on the lower layer, Φ(x, y). (This can also include the effects of linker proteins that are adjacent to the location of a given, microscopic site, i.) This is in contrast to the terms in the Hamiltonian that directly account for the deformation and binding of a given linker protein; those terms depend on the instantaneous and local value of the site variable, Φ_i.

Taking into account the different timescales, and moving from a local to a coarse-grained description where the concentration is a continuous function of x and y, the chemical potential μ_ads of the adsorbing linker proteins is then (see (12) for detailed calculations)

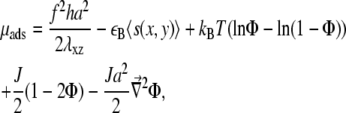(8)

where Φ(x, y) is the average adsorbed linker proteins concentration at position (x, y). Since the substrate is rigid, the stress-induced deformation of the mechanosensitive layer is short-ranged (12,13). For a force in the x direction, we write

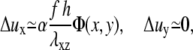(9)

where α is a coefficient that depends on the Poisson ratio of the mechanosensitive layer (13). The gradient of tilt-induced activation is therefore largest at the front of the domain, in the direction of the stress. The activation rate, that combines the effect on the activation of both the uniform and nonuniform deformations, is therefore written

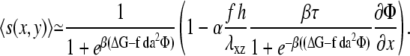(10)

Using the same procedure as in Besser and Safran (12), we consider the chemical potential Eq. 8 along with the (concentration- and gradient-dependent) activation rate Eq. 10 to obtain the dynamical equation for the linker protein concentration at the edges of the adhesion, where the concentration of linker proteins decreases from high to low values. Defining Φ = 1/2 + ψ with ψ ≪ 1, we find from Eq. 1 that

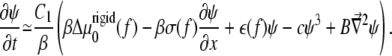(11)

Compared with the usual, isotropic condensation of a solute at an interface, Eq. 11 contains an additional term proportional to ∂ψ/∂x that accounts for the fact that the activation of the mechanosensitive layer is force-dependent and hence nonuniform; this term is responsible for the nonuniform condensation dynamics of linker proteins from solution, resulting in growth of the FAs in the direction of the force. The various coefficients are

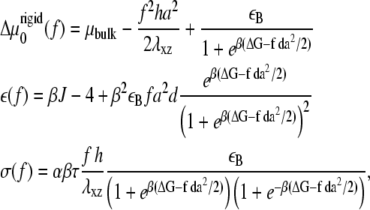(12)

and c = 16/3 and B = β Ja²/2. Equation 12 includes an additional term in the chemical potential difference, 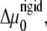compared with the chemical potential difference of Besser and Safran (12). This term, which is proportional to the square of the applied stress, accounts for the contribution of cell contractility that results in the deformation of the focal adhesion (for the case of an incompressible substrate). That is, the anchorage of each linker protein results in a deformation of the FAs and this modifies the chemical potential of these proteins. In the case of a soft substrate, as explained below, a similar term accounts for the elastic deformation of the substrate. The second line of Eq. 12 also shows that the dependence of the activation probability on the average, bound linker protein concentration results in an effective attraction among the linker proteins since the linkers bind to regions that are activated; those tend to be regions in which there was already a high concentration of linker proteins from previous binding events.

The solution of Eq. 11 yields the two-dimensional concentration profile of linker proteins ψ (x, y, t). However, because of the nonuniformity of the gradient of tilt-induced activation (the ∂ψ/∂x term), we expect that the concentration profile of the linker proteins varies nonuniformly with x but uniformly with y. For simplicity, we therefore consider the one-dimensional dynamics of FAs in which they grow only along the direction of the applied force (and hence the deformation and concentration gradients), which we take to be in the x direction. Within this simplified picture, the solution of Eq. 11 is a moving front (to first order in the small quantity 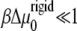(12)),

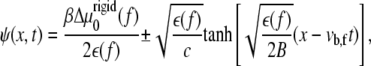(13)

where v_b and v_f are the velocities of the back and the front edges (defined relative to the force direction) of the cluster of linker proteins:

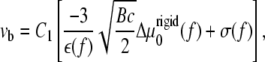(14)

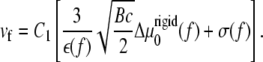(15)

For the case of a rigid substrate, the velocities of the front and back edges of the adhesion do not depend on the initial size, L₀, of the adhesion, as long as we assume that the stress, f is fixed. We therefore predict that in this case, the size, L, of the adhesion varies (in a decreasing or increasing manner, depending on the sign of 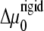) linearly with time:

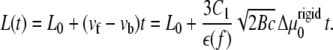(16)

Dynamics of focal adhesions on a deformable substrate

Cells that adhere to a deformable substrate form adhesions; but the acto-myosin force that stabilizes the FAs also stresses the substrate. In the case that the substrate is deformable but has a thickness that is smaller or of same order of magnitude as the thickness of the mechanosensitive (lower) layer of the FAs, the stress-induced deformation is short-ranged. This is because deformation must vanish on the bottom surface of the substrate. The acto-myosin force therefore acts on both the mechanosensitive layer and the relatively thin substrate in a similar manner. Thus, the range of deformation is the sum of the thickness of the mechanosensitive layer of the FAs and of the substrate. In this case, the dynamics of FAs can be extrapolated from the dynamics of FAs on infinitely rigid substrates by renormalizing the elastic moduli of the mechanosensitive layer in the expression for 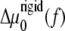or σ(f) (Eq. 12): 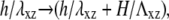where H is the thickness of the elastic substrate and Λ_xz its shear modulus (see Fig. 1).

However, in the case of an elastic substrate whose thickness is much larger than that of the mechanosensitive layer in the FAs, the deformation of the substrate is long-ranged; this introduces new physical features. In this situation where the substrate is much thicker than the size, L, of the adhesion, the substrate deformation decays slowly so that the contribution of the entire stressed region, as expressed by the size of the FAs, enters in the expression for its energy (13).

In this context, the deformability of the substrate or ECM has several effects. First, it modifies the nature of the deformation within the mechanosensitive layer and thereby influences the rate of activation (Eq. 5). To calculate this effect one must consider the true, three-dimensional elasticity of the adhesion; deformations along different directions are coupled by the elastic moduli. However, for simplicity, we focus here on substrates that are more rigid than the mechanosensitive layer (Λ_xz ≫ λ_xz) and adhesions whose size, L, is much larger that the thickness, h, of the mechanosensitive layer. In this limit, the contribution of the deformation of the substrate to the deformation of the FA, 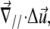is negligible (13).

Second, the deformability of the substrate induces an elastic interaction between the linker proteins. As shown in detail in Appendix A, this interaction is repulsive because we assume that the driving process for FA dynamics is the variation of the energy of adsorbing linker proteins coupled to the stress fibers. The elastic interaction between two adsorbed linkers separated by a distance, r, that transmit a stress f from the stress fibers to the lower layer of the FAs, is

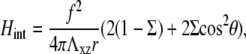where Σ is the Poisson ratio of the substrate and θ is the angle between 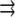and 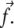This repulsion opposes the local, short-ranged two-body attraction as represented by the coupling coefficient J described above. For a material with Poisson ratio Σ = 1/2, condensation no longer occurs for forces that are too large, due to this repulsion. The crossover occurs when

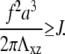(17)

In the following, we assume that the substrate is rigid enough (i.e., Λ_xz is large enough) so that this criterion is not obeyed; that is, we only consider the regime where linker proteins do condense and assemble in a dense plaque.

The last but major effect of the deformable substrate is its effect on the work that the stress fibers must perform to maintain a constant stress f on the adhesion, even while deforming the substrate. Because part of the work performed by the stress fibers goes into deforming the substrate, the molecular motors must invest additional energy, 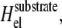to exert a constant stress, f, on the mechanosensitive, lower layer of the adhesion. This tends to effectively increase the free energy of the linker proteins and thus reduces the difference between the chemical potentials, μ_bulk and μ_ads. This results in a smaller driving force for adsorption which then slows down (and can even stop) the dynamics.

Unfortunately, the more complex expression of the elastic Hamiltonian 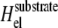for the case of the deformable substrate does not permit us to use the procedure we used to treat the rigid substrate; this is due to the long-range coupling between adsorbing, linker proteins (see Appendix B). We can, however, estimate the dynamics of the FAs by assuming a gate-shaped profile for the concentration, 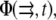of linker proteins, in which the concentration is nonzero and constant in a region whose extent is L and zero elsewhere. The deformation energy of the substrate then contributes a term to H_el that is proportional to the size, L, of the adhesion (13). (The modification of the activation rate by the substrate deformation energy is negligible, as discussed above.) We then assume that the FAs grow slowly, and adiabatically solve Eq. 11 keeping the adhesion size, L, constant. The velocities at the edges of the adhesion in the direction of the stress are given by expressions that are similar to those derived above, for the case of a rigid substrate (Eqs. 14 and 15), although the coefficient, Δμ₀, now includes the contribution of the substrate deformation energy. (We ignore the corrections of the substrate deformation in the expressions for σ(f), or for ε(f) since we showed above that these are negligible in the regime where the substrate is more rigid than the FAs, Λ_xz ≫ λ_xz.) We write the difference in chemical potentials as

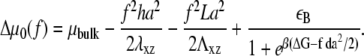(18)

For a thick, elastic substrate, the variation of the chemical potential in the absence of interactions, Δμ₀, now depends on the size, L, of the adhesion via the third term of Eq. 18. Consequently, the velocities v_b and v_f also exhibit a dependence on L. Up to now, we considered the adiabatic limit and calculated the velocities for instantaneous values of L. This relationship can now be used to derive an expression for the time dependence of the FA size, L(t), since the net velocity difference between the velocities of the front and back edges of the FAs cause the FAs to grow or shrink; this velocity difference is thus identified with dL(t)/dt,

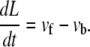(19)

Replacing the velocities v_b and v_f by their expressions Eqs. 14 and 15, which contain the length-dependent term Δμ₀ (Eq. 18), leads to an expression for the time evolution of the length, L(t), of the adhesion,

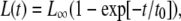(20)

where L_∞ is the saturation length and t₀ is the characteristic decay time (see Eq. 12):

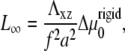(21)

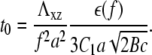(22)

We therefore conclude that on deformable, thick substrates, FAs reach a saturated size that is proportional to the rigidity of the substrate on a timescale that also scales with the elastic compliance of the substrate.

DISCUSSION

The major assumption of our model is that the dynamics of FAs is driven by the exchange of energy of the linker proteins as they adsorb from the bulk and assemble on the adhesion. These energies include the coupling of the linker proteins to the stress fibers that must perform more work to keep the stress exerted on the FAs constant, even as they deform the substrate. This couples the energies of the linker proteins to the substrate deformation energy and introduces a dependence on the adhesion size that modifies the growth law of the FAs. This model predicts that the linker proteins assemble into clusters above the mechanosensitive, lower layer of the FAs and that the edges of the cluster move with velocities v_f at the front and v_b at the back of the adhesion, where the front and back refer to the direction of the stress f. These two velocities differ because we assume that the mechanosensitive layer is activated, allowing a conformational change that induces association with the linker proteins, by two kinds of deformations:

1. A gradient of tilt, which leads to a nonuniform activation of the layer, with a strong maximum at the front edge (in the direction of the tangential stress). This nonuniform activation results in the apparent sliding of FAs, with a velocity (v_f + v_b)/2 ∝ τ, where τ is the lowering of the energy barrier for this conformational change when the mechanosensitive unit experiences compression of its upper part (see Eq. 4).

2. The second mode of activation is due to the in-plane shear-induced stretching of the mechanosensitive layer, which results in a uniform activation of this layer and is responsible for the overall growth of the adhesion with velocity v_f – v_b.

In the case of a rigid substrate, the velocities of the edges of the cluster are given by Eqs. 14 and 15, along with Eq. 12. Experiments show that FAs are not stable in the absence of stress. This constrains the parameters to satisfy: μ_bulk + ε_B /(1 + e^βΔG) < 0 (see Table 1). Moreover, to get a regime where the adhesion indeed grows in response to stress, the parameters must be chosen so as Δμ₀(f) > 0 for a certain range of stress f (see Eq. 16). Both conditions limit the range of accessible parameters and we finally extract two different possible regimes: 1), a regime where the back edge moves in the direction opposite to that of the stress (see Fig. 4, βτ = 0.5); and 2), a regime where the velocity at the back of the cluster is in the same direction as the stress (see Fig. 4, βτ = 2). In the first regime, there is a range of stress where the uniform, in-plane shear-induced activation of the mechanosensitive units dominates the nonuniform gradient of tilt-induced activation; FAs still show maximal growth at their front edges, in the direction of the stress, f; the back edge of the FAs moves in a direction opposite to that of the stress due to the activation from the uniform shear. The system switches from one regime to the other as the magnitude of the nonuniform activation of the mechanosensitive layer is varied relative to the uniform mechanism; in practice, this is done by varying τ. This last regime has not yet been reported in the literature, but may indeed exist (P. Heil, Heidelburg University, personal communication, 2007).

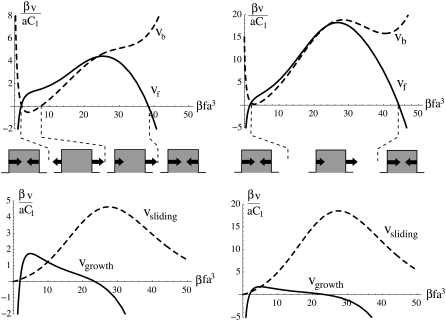
FIGURE 4.

Growth dynamics of FAs assuming a stiff substrate with velocities at the front (v_f) and back (v_b) edges of the cluster of linker proteins, together with the sliding velocity v_sliding = (v_f + v_b)/2 and the growth velocity v_growth = v_f – v_b, as a function of the stress f per unit of thermal stress 1/βa³. On the left-hand side, βτ = 0.5, is chosen so that the velocity at the back edge is in the direction opposite that of the stress. On the right-hand side, βτ = 2 and the back edge always moves in the direction of the stress. The sketches below the graph depict the direction of the velocities at the edges of a focal adhesion as a function of the stress, f. We have chosen μ_bulk = −2.7 k_BT, ΔG = 2.5 k_BT, ε_B = 30 k_BT, λ_xz = 40 k_BT/a³ (this corresponds to 0.7 kPa ≤ λ_xz ≤ 20 kPa for 20 nm ≤ a ≤ 60 nm (25), J = 4.2 k_BT, h = 2a, d = 0.23a).

For cells plated onto a rigid substrate, we predict that adhesions always continue to grow with time, with a constant velocity v_f – v_b (Fig. 3, and see Eq. 16); this quantity can be small or large. Smilenov et al. (10) reports that FAs in stationary fibroblasts slide with a velocity of 0.12 ± 0.08 μm/min but do not measurably get larger or smaller. Of course, this could be due to the fact that the linker proteins or motor proteins have become depleted and are no longer available to change the size of the FAs; however, we do not consider this possibility here. Alternatively, our model can account for such observation, with a choice of suitable parameters. We find that within a wide range of values of the parameters, our model can indeed reproduce a sliding velocity that is much larger than the growth velocity which may be so small as to be unobservable. For example, f = 20 k_BTa³, which corresponds to 0.3 ≤ f ≤ 10 nN/μm² for 20 nm ≤ a ≤ 60 nm (25), together with the parameters used in Fig. 4 leads to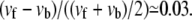

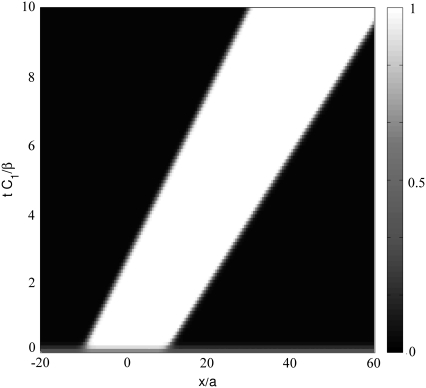
FIGURE 3.

Solution of Eq. 11 for the dynamics of the density profile of the linker proteins for a cell on a rigid substrate. The stress pulls on the FA from left to right. The FA grows and slides for this choice of parameters: μ_bulk = −2.7 k_BT, ΔG = 2.5 k_BT, ε_B = 30 k_BT, λ_xz = 40 k_BT/a³, J = 4.2 k_BT, h = 2a, d = 0.23a, and τ = 2 k_BT.

An important prediction of our model is the existence of a maximal stress above which the adhesion no longer grows, as illustrated in those regions of Fig. 4, where the growth velocity goes to zero. This threshold is a straightforward consequence of our assumption that the dynamics of FAs is determined, in part, by its coupling to the stress fibers and that these fibers must perform some mechanical work to keep the stress, f, constant when the substrate is deformed. Above a certain threshold of stress f, this deformation energy (which is a result of the large stress exerted on the FAs) cannot be compensated by the chemical energy released by the adsorption of the linker proteins; this is because the mechanical energy scales quadratically with f which, at large stress values, dominates the chemical energy that scales only linearly with f. This prediction—that the FAs cease growth at large values of the stress—has not yet been tested experimentally. It is, however, of importance since this feature distinguishes our model from other scenarios for focal adhesion mechanosensitivity (26).

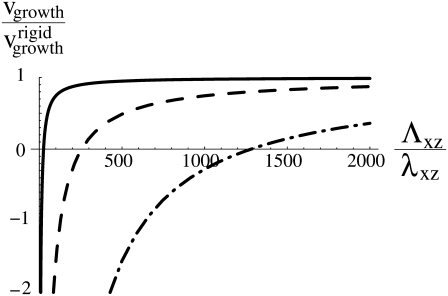
Our main result is that the deformation of the substrate causes the dynamics of FAs to depend on its elastic properties (Fig. 5). We showed that in this case, the adhesion size saturates to a finite value, L_∞, that is proportional to the elastic modulus of the substrate (Eq. 21). This effect originates from the term H_el in Eq. 2 that includes the long-ranged substrate deformations in the energetics and hence, the dynamics of the linker proteins that cause the FAs to grow. Since we assume that the cell pulls with a constant stress, f, on the adhesion, the linear relationship between the saturation length, L_∞, and the substrate rigidity, Λ_xz, also implies that the total force exerted by a single FA reaches a stationary value that is proportional to the rigidity of the substrate. (FAs grow mainly in one direction, so that the total force is proportional to L.) This scaling is observed in the experiments of Saez et al. (6). Here we have shown that even if the mechanosensitivity of the FAs is triggered by stress, the force may still be proportional to the rigidity because of the long-range nature of the substrate deformation (13). In addition, we have predicted that the timescale to reach this stationary regime is also proportional to the rigidity of the substrate. This implies that adhesions on a soft substrate reach a relatively small, stationary size, L_∞, on a timescale that is proportional to the substrate rigidity. Finally, we predict that the sliding velocity (v_f + v_b)/2 is, to a good approximation, independent of the rigidity of the substrate. To our knowledge, the dependence of the sliding velocity of focal adhesions on the mechanical properties of the extracellular matrix has not yet been discussed in the literature. Note that in the limit of a rigid substrate, where Λ_xz → ∞ in Eq. 20, the size of the adhesion grows linearly in time, as expected for simple growth driven by a constant difference between the velocities of the back and the front of the FAs (Eq. 16).

FIGURE 5.

Growth velocity for a stress f = 10 k_BT/a³ as a function of the rigidity of the substrate for three sizes, L, of the adhesion: L = 10a (—), L = 100a (– – –), and L = 1000a (– · –). The other parameters are the same as in Fig. 4. For a substrate with rigidity Λ_xz, the adhesion shrinks (v_growth < 0) when its size exceeds a threshold that is proportional to 1/Λ_xz (see Eq. 18).

Our model assumes that the cell exerts a constant stress, f, that is independent of the properties of the adhesion or the substrate. We account for the rigidity sensitivity of adhesions by the fact that additional work is required to maintain this stress on a deformable substrate as both the adhesion and substrate are deformed. We assume that this work results in additional forces that act on the linker proteins as they adsorb. Other detailed scenarios that also account for adhesion sensitivity to substrate rigidity are indeed possible. A possible, alternate model might consider constant cell energy as opposed to constant stress. In such a picture, the proteins are affected only by their mutual interactions and the binding to the lower layer of the FAs (this would be represented by Eq. 3 without the elastic terms). However, the stress exerted on the lower layer results in an energy that must be added to the energy cost of deforming the substrate. Since, in this model, the total cell energy is fixed, the stress is not constant and depends on the substrate deformation and hence, for soft and thick substrates, on the size of the FAs. Consequently, the protein binding probability, 〈s(x)〉, which is a function of the stress, depends on the substrate deformation. Although the details of this model differ from those of the theory presented in this article, both approaches share the common feature of the influence of cell contractility and substrate deformation on the dynamics of the linker proteins. This, we believe, is an important factor in determining the larger growth of adhesions on rigid substrates. Only experiments can discriminate between the different detailed models. For example, a theory that is consistent with experiment (6), must predict a linear relationship between the saturation length, L_∞, and the rigidity of the substrate, Λ_xz.

Our assumption of constant stress is consistent with the data in Balaban et al. (3), but has been questioned by other authors (6). In Balaban et al. (3), the authors combine static measurements of the area, the eccentricity, and the force exerted by single focal adhesions, and dynamic measurements of those quantities in response to 2,3-butanedione monoxime, or BDM treatment (BDM reduces the activity of the molecular motors, and therefore the stress, f). Dynamic measurements were done approximately every 25 s, faster than the expected timescale for the adhesion to reach a stationary state (of the order of several minutes). Both the static and dynamic measurements gave similar results, suggesting that the stress reaches a steady-state value on timescales that are much faster than the maturation of FAs. Transmission of stress from the stress fibers to the substrate through the protein plaque is also fast compared with the timescale for focal adhesion maturation. If we assume that the Young's modulus of the focal adhesion is ∼1 kPa (because focal adhesions are sensitive to the elasticity of the substrate when the compliance of the latter is of the order of a few kPa), and that the density, ρ, of the protein plaque is close to that of water, the velocity for stress transmission is of order of 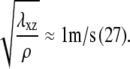Combining these estimates makes our assumption of constant stress fairly realistic.

Our results show that experiments whose goal are measurements of the absolute values of forces exerted by adhering cells through measurements of the magnitude of the substrate deformation should be considered with caution. The experimental force sensor indeed perturbs the measurement in an important manner, since it can change the size of the FA and hence the amount of force the FA transmits. The value of the measured forces is proportional to the elastic compliance of the substrate as is the dynamics of growth of the focal adhesion. Only the apparent sliding of the focal adhesion is, to a good approximation, independent of the rigidity of the substrate. Our analysis leads us to conclude that cell force microscopy on deformable substrates gives unambiguous results only for questions related to the magnitude of force, or to the dynamics required to reach this force by cells in the context of a given, specific, environment. In addition, the various velocities and steady-state quantities have a complex dependence on stress. (Stress seems to be a more tunable parameter compared with the use of drugs that inhibit the activity of the molecular motors.) This means that it may be difficult to extract molecular quantities, such as the energy of activation of the mechanosensor or mechanical properties of the adhesion itself, from force measurements on deformable substrates. Nevertheless, as a tool to quantify and understand the mechanical forces exerted in vivo, cell force microscopy on deformable substrates can give some valuable insights. However, such experiments should therefore be designed to use elastic probes whose rigidities are consistent within the in vivo environment of the cells.

APPENDIX A: REPULSIVE INTERACTION BETWEEN ADSORBING LINKER PROTEINS

When a protein adsorbs onto the lower layer of a focal adhesion, it immediately couples the adhesion to the cytoskeleton. An adsorbed protein is therefore equivalent to a point force that applies a surface stress 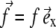(in the plane of the lower layer). We shall now consider the interaction between two such point forces.

In the case of the adsorption of physical point forces onto an elastic medium, one expects an attractive interaction since the driving force is the minimization of the energy of the elastic medium. This energy is written

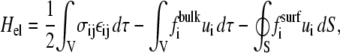(23)

where σ_ij is the stress tensor, ε_ij is the strain tensor, and 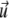is the displacement. The first term is the energy associated with the bulk deformations of the elastic solid. The second and third terms are the mechanical work performed by the external stresses (such as the point forces we consider). Note that this work is negative; the external stresses perform work on the elastic system and this work lowers the energy of the adsorbing bodies.

In the case of focal adhesions, we assume that the kinetics is driven by the minimization of the energy of the linker proteins coupled to the stress fibers. The stress fibers exert a fixed stress that results in the elastic deformation of the adhesion and the substrate. The deformation energy is the work exerted by the stress fibers:

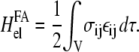(24)

We assume local equilibrium at each instant:

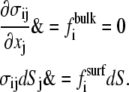(25)

Transformation of Eq. 24 with the expression of the strain tensor, integration by parts, and Eq. 25 leads to

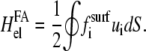(26)

This expression has the opposite sign compared with the case of physical defects, using Eq. 23. This originates from the assumption that we must account for the mechanical work performed by the cell in the energy of the linker proteins. Our thermodynamic system therefore includes the work done by cell contractility. This is in contrast to the negative work that is done by the forces in the case of physical defects that lower their energy (perform negative work on the medium) when they exert forces. In the case of focal adhesions, the cell expends energy and this must be accounted for as part of the thermodynamic system. The energy provided by the cell is partially expended, in the elastic deformation of the substrate, so that the Hamiltonian that drives the kinetics of the linker proteins includes the term 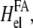as written in Eq. 24.

We now consider two proteins that adsorb on the lower layer of a focal adhesion. Each defect applies a stress f_α at position (α = 1, 2), so that the total external stress on the lower layer is 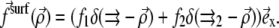Since we focus on linear elastic deformations, the total displacement is additive and we write 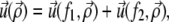with 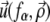the displacement at point 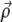due to the stress f_α alone. We replace 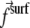and 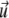by the respective expressions in Eq. 26. We find

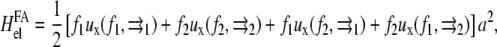(27)

with a² the area of the point force. The two first terms are the self-energies of the point forces. The two last terms are the interaction terms: for example, 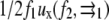is the elastic energy due to the action of the external stress f₁ at position 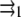that is deformed by f₂.

The elastic interaction is written in terms of the Green's function as

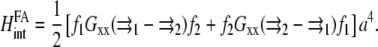(28)

Since G_xx is an even function of the distance, the interaction energy is simply written as

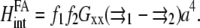(29)

In the case of a thin elastic medium with shear modulus Λ_xz and Poisson ratio Σ, which is anchored to an undeformable substrate,

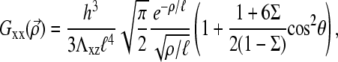(30)

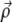where h is the thickness of the thin elastic solid and is the characteristic length of decay of the deformation. The value θ is the angle between and 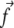(13); from that article, for a thick substrate, one finds

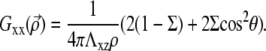(31)

In both cases, G_xx is positive as is the interaction energy. The interaction between adsorbed linker proteins is therefore repulsive. This is a straightforward consequence of our assumption that we must take into account the mechanical work performed by the cell in the energy of the linker proteins. This effect can be understood as follows: the deformation at point B due to the point force at point A is larger as B approaches A. The elastic energy stored in the solid is thus larger as the distance between the two point forces decreases. The cell must therefore invest more energy to maintain a fixed stress when the two point forces are close and less energy when they are far apart.

APPENDIX B: EXPRESSION FOR THE ELASTIC HAMILTONIAN H_EL

We solve the elastic force balance equation for two adjacent, elastically coupled layers. In this Appendix, we term the FA the upper layer, with index 1. The bottom layer, with index 2, is the substrate. (Note: In the main text the upper layer refers to the linker proteins and the lower layer to the mechanosensitive part of the FA.) In each layer,

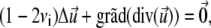(32)

where ν_i is the Poisson ratio of layer i. These equations are solved along with the boundary conditions

(33)

The displacements, 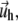on the top layer and 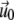at the interface between the two layers are obtained by minimizing the total elastic energy for a given stress f,

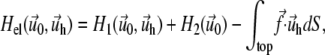(34)

where H₁ and H₂ are the elastic energies of the adhesion and the substrate respectively, integrated along their thickness:

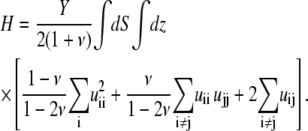Here, the values of the Young's modulus Y and the Poisson ratio ν are those of the elastic substrate (in which case, H is used to calculate H₂) or the adhesion (in which case, H is used to calculate H₁). In these formulae, u_ij is the (i, j) component of the strain tensor (27): u_ij = (∂u_i/∂x_j + ∂u_j/∂x_i)/2. The elastic layers are assumed to be infinite in the x and y directions. We use a Fourier transform to solve Eq. 32:

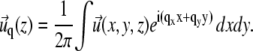(35)

Detailed calculations can be found in Nicolas and Safran (13). In this model, the stress that is transmitted to the mechanosensitive layer at a given position is proportional to the probability that a linker protein is present at that position. The surface stress to be considered in Eq. 34 is therefore the product of the force per unit area and the linker protein concentration, 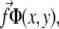where the stress, 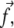is taken to be a constant. In Fourier space, this is written 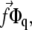where Φ_q is the Fourier transform of the linker protein concentration, Φ(x, y).

We first present the simpler situation of a rigid substrate: H₂ = 0 in Eq. 34. Identical calculations to those presented in Nicolas and Safran (13) yield

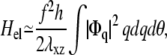(36)

where h is the thickness of the mechanosensitive layer whose shear modulus is λ_xz: λ_xz = Y₁/(2(1 + ν₁)). Using Parseval's theorem, we write H_el as an integral in real space as

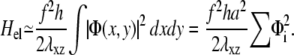(37)

In the case that the substrate has a finite compliance and a Poisson ratio ν₂ = 1/2, the former calculation yields

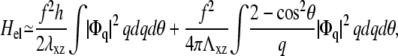(38)

where Λ_xz is the shear modulus of the substrate (Λ_xz = Y₂/(2(1 + ν₂)). The contributions of both elastic media simply add because we assume that Λ_xz ≫ λ_xz. As before, we can write the energy as an integral in real space using Parseval's theorem. The contribution of the substrate is now

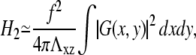(39)

where G(x, y) is the convolution of the concentration field, Φ(x, y), and the inverse Fourier transform of 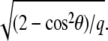The convolution introduces a coupling between the different locations (x, y) on the top of the mechanosensitive layer. This effect is expected since the elastic interaction is long-ranged and decreases like 1/r for a semiinfinite medium. However, we do not have any analytical expression for the inverse Fourier transform of 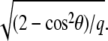This method therefore fails to give an analytical expression for the elastic Hamiltonian of the substrate in Eq. 3. We avoid this difficulty by assuming that the size of the adhesion varies slowly and adiabatically compared with the fast dynamics of the linker proteins as they move from solution (in the cytoplasm) to their adsorbed state on the adhesion, as presented in “Dynamics of focal adhesions on a deformable substrate”.