Extracting Intramural Wavefront Orientation from Optical Upstroke Shapes in Whole Hearts

Abstract

Information about intramural propagation of electrical excitation is crucial to understanding arrhythmia mechanisms in thick ventricular muscle. There is currently a controversy over whether it is possible to extract such information from the shape of the upstroke in optical mapping recordings. We show that even in the complex geometry of a whole guinea pig heart, optical upstroke morphology reveals the 3D wavefront orientation near the surface. To characterize the upstroke morphology, we use 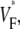the fractional level at which voltage-sensitive fluorescence, V_F, has maximal time derivative. Low values of 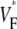(∼0.2) indicate a wavefront moving away from the surface, high values of 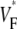(∼0.6) a wavefront moving toward the surface, and intermediate values of 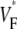(∼0.4) a wavefront moving parallel to the surface. We further performed computer simulations using Luo-Rudy II electrophysiology and a simplified 3D geometry. The simulated 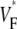maps for free wall and apical stimulations as well as for sinus rhythm are in good quantitative agreement with the averaged experimental results. Furthermore, computer simulations show that the effect of the curvature of the heart on wave propagation is negligible.

INTRODUCTION

Optical mapping with voltage-sensitive dyes has become the most widely used method for the study of excitation propagation in the heart (1–5). Although the largest contribution to the optical fluorescence signal comes from the cardiac surface, it is now well established that subsurface layers also contribute significantly to the optical signal (6–13). There is evidence that these subsurface contributions make it possible to determine the three-dimensional orientation of subsurface wavefronts from the optical signal. A theoretical study first pointed out that the transmural component of propagation velocity should have an impact on the optical upstroke (14), and a subsequent study predicted a one-to-one correspondence between upstroke morphology and wavefront orientation (15). In contrast, the first study to simulate optical signals in a whole rabbit heart did not find a significant correlation between the overall propagation direction and upstroke morphology (16).

The measure used to quantify the upstroke shape is the fraction of the action potential amplitude at which the V_F, the optically determined transmembrane potential, has its steepest slope. This fraction is called 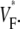An upstroke for which dV_F/dt is maximal close to its beginning would have 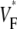∼ 0, whereas an upstroke for which dV_F/dt is maximal close to its end would have 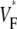∼ 1. In terms of 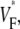the studies that predicted a one-to-one correspondence between upstroke morphology and wavefront orientation (15) described characteristic patterns of 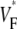for different types of wave propagation, whereas the simulation study in rabbit hearts (16) did not observe such characteristic patterns.

These conflicting results were discussed in Comments to the Editor in the Biophysical Journal (17,18), and both sides agreed that only experiments in whole hearts could determine whether a correlation exists between upstroke morphology and subsurface wavefront orientation. The main factors that might obscure these theoretically predicted correlations are the complex geometry of the heart, including its curved surface, and heterogeneities such as blood vessels.

In this article, we report the results of experiments designed to resolve the described controversy. The experiments were conducted using whole guinea pig hearts. We find that the upstroke morphology does indeed contain information about the transmural propagation direction. More specifically, the spatially averaged distributions of 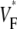determined experimentally closely follow theoretically predicted distributions. In particular, we studied three modes of activation: stimulation of the free ventricular wall, apical stimulation, and sinus rhythm. In computer simulations with a cylindrical cardiac geometry, we reproduce the experimentally observed morphologies. We also provide a computational analysis of the effect of the curved geometry of the heart on wave propagation.

MATERIALS AND METHODS

Experimental preparation

All experimental protocols conformed to the Guide for the Care and Use of Laboratory Animals (National Institutes of Health publication No. 85-23, revised 1996). Guinea pigs (n = 4) were injected with heparin (550 U/100 g), and euthanized by sodium pentobarbital (7.5 ml/kg), after which the heart was immediately excised and placed in ice-cold cardioplegic solution, composed of (in mmol/l) 280 glucose, 13.44 KCl, 12.6 NaHCO₃, and 34 mannitol. After removal of extraneous tissues, the aorta was cannulated (see Fig. 1 A) and Langendorff perfusion was started with a standard oxygenated Tyrode's solution (composed of (in mmol/l) 130 NaCl, 24 NaHCO₃, 1.2 NaH₂PO₄, 1.0 MgCl₂, 5.6 glucose, 4.0 KCl, and 1.8 CaCl₂, buffered to a pH of 7.4) at 80 mm Hg and 37°C. The whole, cannulated heart was put into a special transparent chamber and superfused with the same solution at a rate of 30–40 ml/min. Perfusion and superfusion temperatures were continuously monitored and kept at 37 ± 0.5°C by using two sets of glass heating coils and heated-refrigerated circulators.

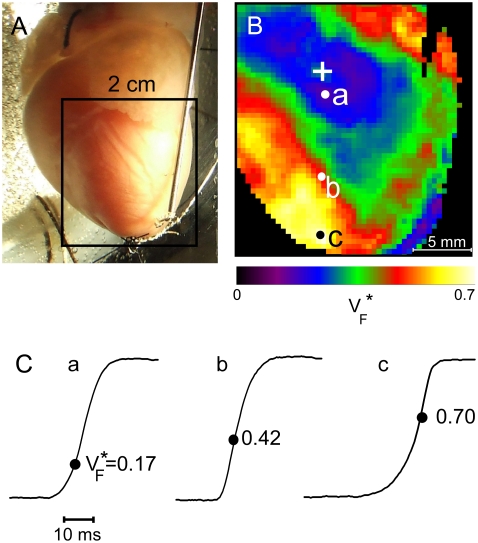
FIGURE 1.

Experimental setup and typical 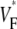recording. (A) Langendorff-perfused guinea pig heart. The black square indicates a typical field of view of optical mapping movies. (B) Experimentally determined 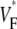map. Tissue was stimulated at the location marked “+”. (C) Upstrokes from locations a–c of B, as marked. The steepest point of the upstroke is marked and the fraction of the peak potential at the steepest point is indicated.

Electrodes were sutured to whole hearts to monitor the electric activity. All preparations were continuously paced at a basic cycle length of 300 ms. After a 30-min stabilization period during which the perfusion flow and electric activity were monitored, the excitation-contraction uncoupler diacetyl-monoxime was added to the Tyrode's solution (15 mmol/l) to stop contractions of cardiac tissue. Then the preparation was stained with a bolus injection of 1–2 ml of the voltage-sensitive dye Di-4-ANEPPS (from Molecular Probes (Eugene, OR), concentration 5 μg/ml), which was added into the perfusion flow.

Optical setup

The optical setup consisted of a 14-bit CCD video camera (“Little Joe”, SciMeasure, Decatur, GA) with a Computar H1212FI lens (focal length 12 mm, 1:1.2 aperture ratio; CBC, Commack, NY). We used a collimated beam from a 250-W tungsten halogen lamp to uniformly illuminate the left ventricular free wall. The light was heat filtered and then passed through 520 ± 40-nm bandpass excitation filters. Fluorescence was recorded at 640 ± 50 nm. The video images (80 × 80 pixels) were acquired from a 20 × 20-mm area of the preparation (see Fig. 1 A) at 2000 frames/s. The background fluorescence was subtracted from each frame to obtain the voltage-dependent signal.

Processing of optical recordings

In all experiments, 50–100 optical action potentials of each recording were ensemble-averaged to reduce noise while simultaneously avoiding the excessive use of spatial or temporal filters that might affect optical upstroke morphology. The alignment error of the optical action potentials was no more than one-half frame (0.25 ms). The ensemble averaged signal was filtered with a (rectangular) moving average filter of radius 2 in space and radius 2 in time.

To characterize the upstroke morphology, we used the fractional level at which the time-derivative of the voltage-sensitive fluorescence, 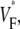is maximal (see Fig. 1 C). For example, 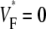means that 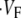is maximal right at the beginning of the upstroke, whereas 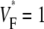means that 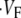is maximal at the end of the upstroke. Unlike in our previous study (15), we estimated 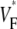not by cubic spline interpolation but simply using a centered second-order scheme; this was possible because the signal quality and temporal resolution are significantly improved with the better camera we now use. The 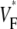maps shown have also been filtered with a spatial filter of radius 2 (see Fig. 1 B).

Computer simulations

To simulate electrical activity in the heart, we used the Luo-Rudy II dynamic model (19), specifically created for guinea pig ventricular myocytes. The geometry was a cylindrical tube with inner radius 10 mm, outer radius 15 mm, and length 30 mm. We implemented this geometry in 2D, using the gradient operator for cylindrical coordinates, 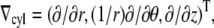and solved the standard reaction-diffusion equation:

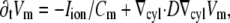(1)

where 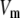is the transmembrane potential, 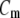the membrane capacity density, I_ion the total ionic current density of the membrane, and D the diffusivity tensor. The diffusivity tensor, D, was scaled to produce steady-state conduction velocities of 60 cm/s in the longitudinal and 20 cm/s in the transverse direction, consistent with our experimental measurements. The fibers were assumed to rotate at a linear rate with depth. The total transmural rotation was set to 100°, in accordance with our experimental determination of fiber rotation in guinea pig left ventricle (20). Our simulations used a spatial resolution dx = 100 μm and a temporal resolution dt =10 μs.

Stimulation was achieved by applying a double threshold stimulus for 2 ms. For free wall stimulation, this stimulus was placed on the epicardial surface, at half the cylinder's height. For apical stimulation, we stimulated the entire (ring-shaped) base of the cylinder (a good approximation of the situation after a point stimulation, when a ring-shaped front has developed). For sinus rhythm, we simultaneously stimulated a large number of endocardial surface points, which were distributed as follows: at the apex, we placed 10 equidistant stimulation points; at a height of 2.5 mm, 9 points; at 5 mm, 8 points; and so forth, up to a height of 22.5 mm, where we placed one stimulation point. This scheme approximates the distribution of the endpoints of the Purkinje fibers, which are most dense at the apex of the heart and thin out toward the base.

Optical model

To compare our simulation results to experiments, we further computed the optical signals corresponding to the electrical activity that we determined. We describe light propagation in cardiac tissue by the time-independent diffusion equation (14,21):

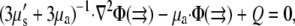(2)

where Φ is the photon density within the tissue due to a source Q, μ_s′ is the reduced scattering coefficient, and μ_a is the photon absorption coefficient. This approach assumes isotropic light propagation, and is justified by our previous work (14). We assumed Robin boundary conditions at all surfaces:

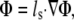(3)

where l_s is the so-called extrapolation distance (22) that accounts for refractive index mismatches at the boundary.

The electrical (Eq. 1) and optical (Eq. 2) models were coupled through the source function Q, in defined in Eq. 2, to account for the voltage-dependent fluorescence changes of the dye (14,21):

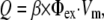(4)

where β represents the quantum yield of the dye and Φ_ex is the local photon concentration of the excitation light.

Equation 2 was solved analytically by using the method of images (23,24). The recorded surface distribution of voltage-dependent signals was calculated using Fick's law.

Our optical parameters are those previously reported (6,24). For the voltage-sensitive dye Di-4-ANEPPS that we use in our experiments, we have: μ_s′ = 1.5 mm⁻¹, μ_a = 0.35 mm⁻¹, and l_s = 0.8 mm for the excitation, and μ_s′ = 1.5 mm⁻¹, μ_a = 0.12 mm⁻¹, and l_s = 1.0 mm for the emission.

RESULTS

Free wall pacing

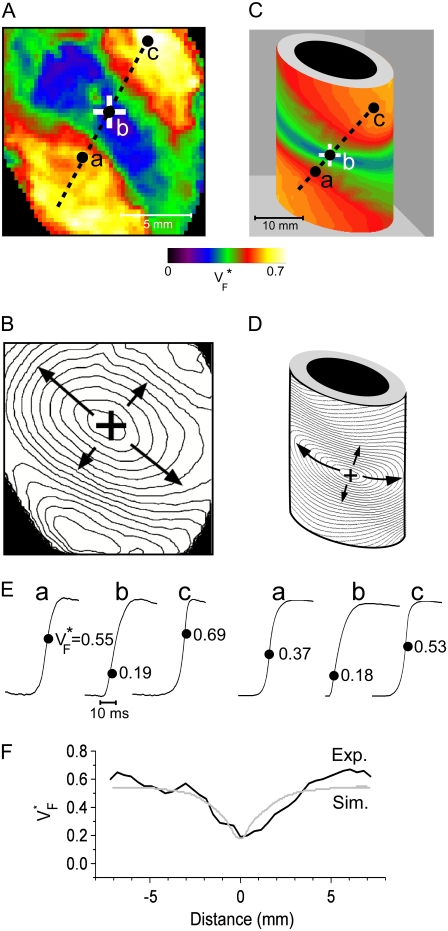
Fig. 2 compares maps and activation maps from experiments and simulations for free wall stimulation. Fig. 2 A shows the experimentally determined 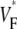map, and Fig. 2 B shows the corresponding activation sequence. This activation sequence reveals that in the vicinity of the stimulation site, the wavefront has an elliptical shape, with a direction of fastest propagation (long arrows) and a direction of slowest propagation (short arrows). In Fig. 2 A, we see that 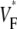is low (∼0.2) at the stimulation site. Moving along the direction of fastest propagation, 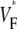remains at a low level, but in the direction of slow propagation, 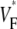increases rapidly, up to levels around 0.7. Thus, the 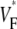pattern exhibits all the characteristic properties we previously found in simulations of a slab of tissue (15).

FIGURE 2.

Variation of upstroke morphology for free wall stimulation in experiment and simulation. (A) Experimental 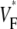map for point stimulation at the center of the left ventricle. The stimulation site is marked “+”, the dashed line marks a section of the surface that we use for comparison of profiles (see F). (B) Activation sequence for point stimulation experiment (same experiment depicted in A). Black lines are isochrones, spaced 1 ms apart; arrows indicate direction of wave propagation. (C) Simulated 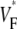map for point stimulation at the center of the left ventricle. (D) Activation sequence for point stimulation simulation; details are as in B. (E) Optical upstrokes from selected locations as marked in A and C. (F) Comparison of 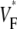profiles from experiment and simulation. Lines along which profiles are taken are marked by dashed black lines in A and C; the stimulation site corresponds to distance = 0.

Fig. 2 C shows the simulated 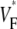map. It follows the characteristic pattern that we found in slab preparations (15) even more closely than the experimental data, and simulation and experiment (Fig. 2 A) are in good qualitative agreement. The simulated activation sequence (Fig. 2 D) is likewise in good agreement with the experimentally determined one (Fig. 2 B). The similar patterns in the 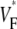map are also reflected in the similar shapes of experimentally determined and simulated optical upstrokes for corresponding locations, shown in Fig. 2 E. For a more quantitative analysis, we compared vertical profiles along the line that connects the stimulation site with the maxima of 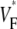(in simulations, both maxima of 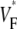lie on a line with the stimulation site due to symmetry, and in experiments, we fit the line to minimize the RMS of the deviations from the maxima). The comparison of profiles is shown in Fig. 2 F. Both profiles are close to symmetric with high values at the ends and a minimum in between. The plateaus on the left side are 0.57 experimental (average for x = −7 mm to x = −4 mm) and 0.54 simulated, the minimum is 0.19 experimental versus 0.18 simulated, and the right plateau (average for x = 7 mm to x = 4 mm) is 0.54 experimental versus 0.62 simulated.

To characterize the width of the minimum, we considered the half-width of the profile, which we define as follows. From the minimum (at distance 0), we determine at which distance to the left the value halfway between minimum and maximum (min + max_L)/2 is reached. In the same way, we determine the distance to the right where (min + max_R)/2 is reached. The sum of these distances is the half-width. The half-width of the minimum is 3.8 mm experimental and 3.0 mm in simulations. In short, there is good quantitative agreement between experimental and simulated 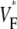maps.

Apical pacing

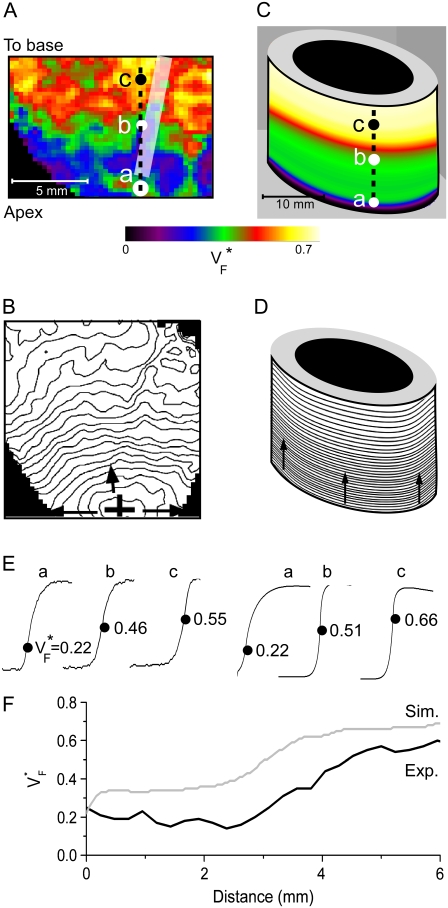
Fig. 3 compares 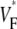maps from experiments (A) and simulations (B) for apical stimulation. The simulated 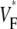has, by definition, perfect rotational symmetry, and the experimental map exhibits this symmetry approximately, although there is substantial local variation, especially in the upper part of Fig. 3 B. The activation maps from experiment (Fig. 3 C) and simulation (Fig. 3 D) agree on the most important characteristics: activation travels upward in a rotationally symmetrical way, and the conduction velocity increases significantly as the wave propagates upward. For both experiment and simulation, the change of upstroke shape in the axial direction is impressive, and similar for corresponding points (Fig. 3 E). The 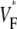profiles (Fig. 3 F) in the axial direction have a low plateau at the apex, then a steep rise for increasing x and finally a high plateau toward the base. The level of the low plateau is 0.2 in experiments versus 0.33 in simulations; that of the high plateau is 0.55 in experiments versus 0.67 in simulations. The width of the transition is ∼1.8 mm in experiments and ∼2 mm in simulations. The line a–c in Fig. 3 A was chosen so that it intersects the stimulation site and is vertical, but the profiles along other vertical lines give similarly good agreement. In summary, experimental and simulation 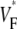-maps agree very well except for a general shift toward larger 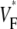in simulations. The shift may be caused by our approximation of linear transmural fiber rotation, which is valid in good approximation in free wall, but not close to apex. Despite the good qualitative agreement, it is apparent that the experimental data exhibit greater variability in 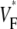than the simulated data, a fact that can be attributed to noise in our recording system or to small-scale heterogeneities in the tissue (see Discussion).

FIGURE 3.

Variation of upstroke morphology for apical stimulation in experiment and simulation. (A) Experimental 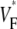map for point stimulation at the apex. The thick semitransparent white bar marks the position of the stimulation electrode; other details are as in Fig. 2 A. (B) Activation sequence for apical stimulation experiment (same experiment as in A), with details as in Fig. 2 B. (C) Simulated 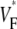map for apical stimulation. (D) Activation sequence for apical stimulation simulation. (E) Optical upstrokes from selected locations as marked in A and C. (F) Comparison of 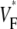profiles from experiment and simulation. Lines along which profiles are taken are marked by dashed black lines in A and C; the stimulation site corresponds to distance = 0.

Sinus rhythm

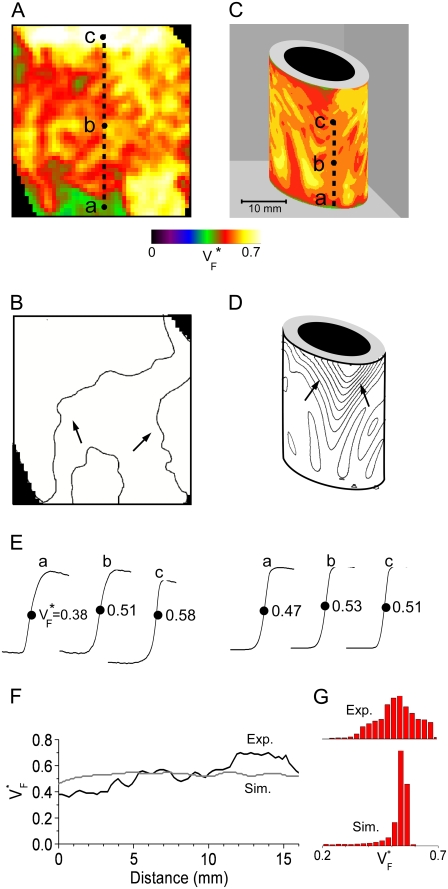
Fig. 4 compares 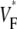maps from experiments (A) and simulations (C) for sinus rhythm. In both cases, 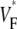varies much less than for free wall and apical pacing, and 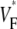is >0.4 almost everywhere. This should be expected for sinus rhythm, because during the ventricular activation, the Purkinje fibers at the endocardium are excited first, and from there the excitation travels outward. Only the experimental maps show a systematic, if small, increase of 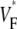from apex to base.

FIGURE 4.

Variation of upstroke morphology during sinus rhythm in experiment and simulation. (A) Experimental 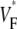map during sinus rhythm. The dashed line marks a section of the surface that we use for comparison of profiles (see F). Details are as in Fig. 2 A. (B) Activation sequence for sinus rhythm experiment (same experiment as in A), with details as in Fig. 2 B. (C) Simulated 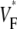map for sinus rhythm (same experiment as in A and C; the stimulation site corresponds to distance = 0. (G) Histograms comparing 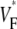distribution in simulations and experiments. Amplitudes have been normalized to achieve equal total histogram area.

The activation maps from experiments (Fig. 4 B) and simulation (Fig. 4 D) both show relatively synchronous activation. The only exception is the visible wave propagation in the upper middle of Fig. 4 D; this is a consequence of our relatively sparse stimulation on the endocardium. As Fig. 4 E shows, there is not much spatial variation in upstroke morphology in either experiment or simulation. The 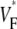profile (Fig. 4 F) shows that small-scale variations can be seen in experiment and simulation, with the average 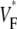from experiment (0.52) and simulation (0.52) matching closely. The line a–c was chosen vertically and in the center of the field of view, but profiles are similar along other vertical lines. Fig. 4 G compares the distributions of 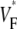in experiments and simulation. Both distributions have a maximum at 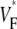= 0.54. The experimental distribution is significantly wider; this may be a consequence of small-scale tissue heterogeneities or of noise in the recording system (see Discussion).

Variability of V_F^* maps in different preparations

We compared 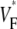maps for free wall stimulation in different preparations. All our preparations showed the characteristic pattern in Figs. 1 B and 2 A, with its three prominent features: 1), a low value of 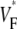(≈0.2) at the stimulation site, 2), a strip of low 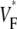around the stimulation site, oriented in the fiber direction at the stimulation site, and 3), rapidly increasing 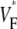when moving from the stimulation site in a direction orthogonal to fibers.

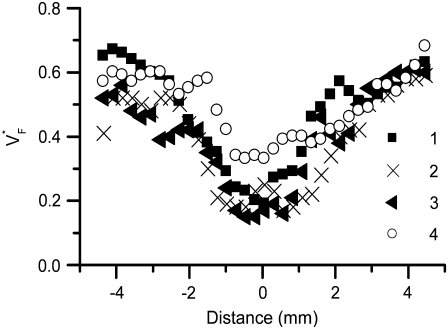
Fig. 5 shows profiles of 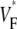through the point of stimulation and orthogonal to fiber direction. All profiles have a minimum at or near the stimulation points. The minimum value of 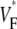is typically between 0.15 and 0.2, with one exception (preparation 4), where it is slightly above 0.3. At the left and right side, 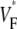goes up to between 0.55 and 0.7. The average the half-width (defined above) in our preparations was 3.50 ± 0.60 mm.

FIGURE 5.

Variability of 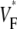profiles in different preparations. In all preparations, the stimulation site is at distance = 0. Profiles were measured in the direction perpendicular to fastest surface propagation.

Simulation study on the effect of curvature

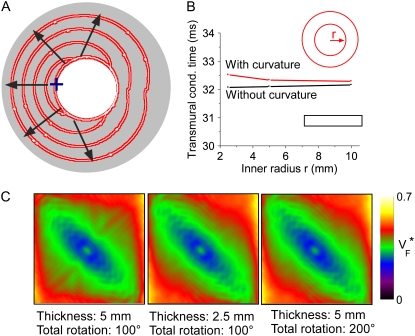
In the controversy that motivated this study (17,16,18), it was hypothesized that the complex geometry of the heart may obscure the 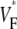patterns that had previously been observed in slab preparations (15). To address this question, we performed a series of simulations to assess the effect of curvature on propagation. The inner radius of the cylinder was 2.5 mm and the thickness 5 mm (see Fig. 6 A). Our simulations were done in polar coordinates in a cross section of the cylinder, with the regular Laplace operator (see Methods), as well as with a modified Laplace operator, 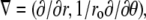where r_o is the (constant) outer radius. The modified operator corresponds to propagation in a rectangle rather than a slice of a cylinder.

FIGURE 6.

Effect of myocardial wall curvature on wave geometry and optical activation sequence. (A) Electrical activation sequence in a cross section of a cylindrical domain. The stimulation site is marked “+” and the direction of wave propagation is indicated by arrows. Red thick lines are isochrones (spaced 5 ms), computed in observance of wall curvature. White thin lines show the activation sequence as computed neglecting curvature (see text). (B) Transmural conduction times for endocardial stimulation with and without curvature term. (Insets) Geometry with curvature term (red) and without curvature term (black). (C) Effects of total fiber rotation and preparation thickness on the 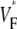pattern, obtained in a slab geometry.

Fig. 6 A shows that there is no visible difference in the activation sequences with and without the curvature term. From the stimulation to the point of time at which the whole medium is activated, the isochrones for propagation with and without the curvature term are nearly identical. We also computed 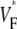maps for both cases and they are virtually indistinguishable (no picture shown).

We repeated simulations with and without the curvature term for a series of inner radii of the cylinder, keeping the thickness constant (Fig. 6 B). To assess the difference in propagation, we compared the transmural propagation time with and without the curvature term for all radii. The transmural propagation time was defined as the time between stimulation and the time where the first epicardial point reached 10% depolarization. In all cases, the difference in propagation time is <0.5 ms or ∼1.5%. Fig. 6 B shows that the transmural propagation time is independent of the radius if the curvature term is excluded, which is expected, because in this case, we are simulating propagation in slabs of different width, and curvature should not play a large role. When the curvature term is included, the conduction time is slightly larger, because in this case there is more surrounding medium around the stimulation site. The effect of curvature is diminished for large radii (small curvature). In summary, we find that the effect of curvature on propagation is minimal, even for curvatures that exceed those present in the guinea pig ventricles.

Effect of total fiber rotation and tissue thickness

Two other factors that could be thought to influence 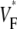maps are the total fiber rotation and thickness of the preparation. To assess their impact on 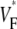maps, we compared three situations: 1), control conditions (as described in the Methods section); 2), doubled rate of fiber rotation over half the regular thickness (i.e., 100 degrees fiber rotation over 2.5 mm); and 3), doubled rate of fiber rotation, keeping the thickness constant (i.e., 200° fiber rotation over 5 mm). The resulting 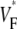maps are shown in Fig. 6 C. The maps for cases 2 and 3 are virtually identical, suggesting that the fiber structure in the superficial 2.5 mm almost entirely determines the subsurface wavefront orientation. Case 1 is still very similar but has slightly lower levels of 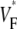everywhere. This reflects the fact that for a smaller rate of fiber rotation, it takes longer for the excitation to penetrate to a depth at which fiber orientation is significantly different from that at the surface, and subsurface wavefront orientation is altered by propagation in deeper layers only at a greater distance from the stimulation site.

Furthermore, we obtained one 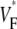map in a guinea pig right ventricle. Although the typical thickness is only 50–75% that of the left ventricle and the total fiber rotation is larger (119° vs. 106° in the left ventricle (20)), still the 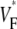map was not significantly different from those we showed for left ventricles.

DISCUSSION

The goal of this study was to establish whether in whole hearts, upstroke morphology can be used to assess the local intramural orientation of activation fronts. Tissue curvature and heterogeneities are the main factors that might distort theoretically predicted correlations. We discovered that for free wall and apical stimulation, the upstroke morphology shows characteristic patterns that should be expected if the morphology is correlated to subsurface wavefront orientation. For sinus rhythm, we observed little variation in 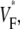consistent with wavefronts propagating from the endo- to epicardium, with near simultaneous wavefront breakthrough on the epicardium. Detailed quantitative comparisons with simulations of all three modes of stimulation further support the conclusion that the upstroke morphology correlates with the subsurface wavefront orientation as follows: low values of 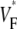(∼0.2) indicate a wavefront moving away from the surface, high values of 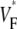(∼0.6) a wavefront moving toward the surface, and intermediate values of 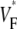(∼0.4) a wavefront moving parallel to the surface. In simulations we found that the curved geometry of the heart does not significantly influence 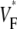maps.

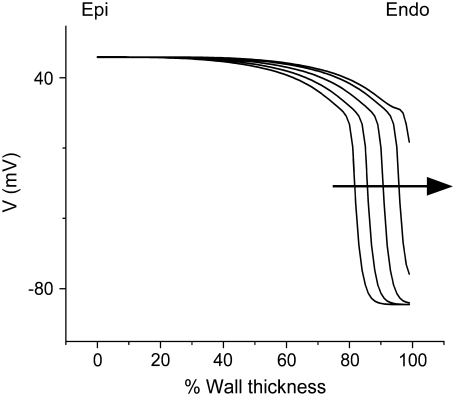
Interestingly, we never observed 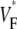> 0.8, not even in simulations of sinus rhythm, where excitation waves are oriented approximately parallel to the surface and one could expect 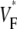to be close to 1. When studying this phenomenon, we found, however, that a traveling wave in the Luo-Rudy model has a voltage profile that explains the low maximum value of 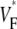(see Fig. 7). Indeed, the cells are not fully excited as the wavefront passes, but the wavefront only excites them by ∼80% of the action potential amplitude, whereas the last 20% of the excitation occurs slowly after the wavefront has passed. This explains why 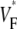does not go above 0.8, even for propagation directly toward the surface.

FIGURE 7.

Series of voltage profiles across the myocardial wall for a wave that is approaching the epicardial surface. Arrow indicates the direction of propagation.

Differences between predicted and experimental V_F^* maps

Although we report good qualitative and quantitative agreement of experimental and simulation results, experiments exhibit a higher degree of local variation in 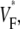as manifested in the more patchy color maps (see Fig. 3 A, for example). The most convincing explanation of this variation is in our opinion that tissue heterogeneities (e.g., blood vessels) locally perturb wave propagation. These heterogeneities were not included in our simulations, but they should effect wave propagation and therefore 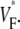Simulations that do include heterogeneities report similar variations in wavefront propagation (17) (although no 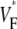maps have been published). Another contributing factor to the variation in 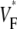is noise in our acquisition system. The relative contributions of noise acquisition and tissue heterogeneities cannot be determined based on the data presented here, but pose an important question for future studies.

Comparison to earlier studies

Our results are in good agreement with the only related experimental study (15), which was conducted in isolated right ventricular pig heart preparations. We find minimal values of 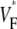at the stimulation site and a strip of low 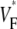around the stimulation site and extending in the direction of fastest preparation (as in the earlier study). For the most readily comparable stimulation mode, i.e., stimulation of the free ventricular wall, this strip has a typical half-width (defined above) of 3–4 mm in both studies.

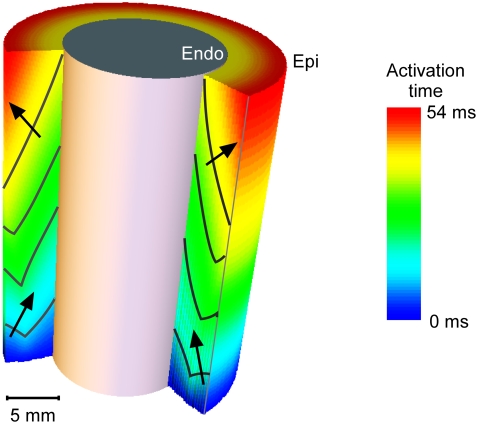
Careful analysis is needed when comparing our results to those of a detailed anatomical modeling study by Bishop et al. (16). It appears that their results disagree with ours, as the authors state that they cannot identify a significant correlation between upstroke morphology and intramural propagation direction. However, as we pointed out in a comment on their study (18), the key to resolving this apparent disagreement likely is to note that the intramural propagation direction close to the surface typically does not coincide with the macroscopic propagation direction. Indeed, the simulations of apical stimulation presented in earlier publications (25,26) clearly show that whereas the macroscopic wave propagation is from apex to base (orthogonal to the surface), the subsurface intramural propagation direction far from the stimulation site has a strong component toward the surface (see Fig. 8). Consequently, the intramural propagation direction in this situation is similar to that of sinus rhythm (endocardial stimulation), for simulations as well as for experiments (compare Figs. 3 and 4). In this light, it is not surprising that the upstrokes that Bishop et al. observed far from the apex are similar for apical and endocardial stimulation. Our experimental results obtained for different stimulation protocols highlight the distinction that should be made between macroscopic propagation direction and local subsurface wavefront orientation. In all cases, we find that 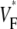is a good indicator of the latter.

FIGURE 8.

Activation map for apical stimulation in the computational model. A cross-section of the cylinder wall is shown to reveal the intramural wave propagation. The arrows denote the local normal to the wavefront beneath the epicardial surface.

Applications

Our findings show how important additional information can be extracted from optical mapping movies. Such movies can be equivocal with respect to which three-dimensional excitation pattern they project, and information about the transmural velocity of the wavefront will, in some cases, allow a definite determination. No modification of the standard optical mapping is needed and even previously acquired optical mapping data can be revisited to analyze transmural propagation of excitation.

Limitations

We proposed a method to assess the intramural propagation direction from 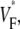but we can verify our assessment only in computer simulations, because experimental methods with sufficient accuracy are not yet available (15). Direct experimental validation would clearly be desirable and should be attempted once it is viable.

Since we filter our experimental results, the correspondence that we claim between 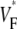and subsurface wavefront orientation need not be present for space and timescales smaller than those we filtered out (∼1 mm and 1 ms). Indeed, our raw data contain substantial small-scale noise that may be a result of the intrinsic noise in our camera, a result of tissue heterogeneities such as blood vessels, or both. In any case, our study shows that the filtered 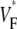maps agree well with those from simulations excluding heterogeneities; therefore, these heterogeneities do not substantially affect medium- and large-scale wave propagation.

In our computer simulations, we used a monodomain model of electrical propagation with simplified geometry and von Neumann boundary conditions. Thus, our model does not account for the tissue-bath interface present in our experiments. Bidomain models reported in the literature suggest that boundary conditions at the tissue-bath interface may affect wavefront orientation near the epicardium and may have an impact on the dynamics of scroll-wave reentry. Nonetheless, good agreement between our experiments and model predictions suggests that errors attributable to neglecting tissue-bath interface effects were small.

Our computer simulations also did not take into account tissue heterogeneities (e.g., fatty and connective tissue, electrical heterogeneities), tissue variations in voltage-sensitive dye staining, and dye photobleaching. It is important to note, however, that our experiments were performed in heart tissue possessing such heterogeneities, and these experiments were still in good agreement with computer simulations.