Molecular Motion at the Critical Point in Lipid Membranes

Abstract

It is shown that the calculated temperature dependence of the deuterium nuclear magnetic resonance (NMR) of labeled cholesterol-phospholipid bilayers is changed by magic-angle spinning. This makes it possible to distinguish different molecular motions at temperatures near a miscibility critical point, for motions with distinct temperature-dependent correlation times. In this way one finds that NMR line broadening due to critical point composition fluctuations can be distinguished from broadening due to the formation and dissociation of complexes.

In recent work, we have discussed the nuclear magnetic resonance (NMR) spectra of phospholipid bilayers containing cholesterol near a miscibility critical point (1–5). Two sources of line broadening were considered: 1), Composition fluctuations; and 2), formation and dissociation of putative complexes of cholesterol and phospholipid. The calculations found that, in general, both sources of line broadening were comparable in magnitude and consistent with the observed data. The calculated line broadening due to source 1 reached a peak at or very close to the critical temperature (5). The broadening due to source 2 was found to increase as the temperature T is lowered toward the critical temperature T_c (5). Here we revisit this problem, using an improved theoretical approach to source 1, and extending the calculation of source 2 to lower temperatures. We also take advantage of recent experimental work on correlation lengths in a ternary mixture of cholesterol (C), dipalmitoyl-phosphatidylcholine (DPPC), and dioleoly-phosphatidylcholine (DOPC) (6).

Consider the deuterium NMR of fatty-acid-labeled DPPC in the C/DPPC/DOPC ternary mixture, as described by Veatch et al. (3). In the absence of spinning, the NMR of this mixture exhibits the well-known Pake doublet spectrum, the splitting arising from quadrupole interactions of deuterium nuclei on the saturated fatty-acid chains of DPPC. This splitting depends on cholesterol concentration. At the miscibility critical point there is a broad, long-range distribution of cholesterol concentrations. Accordingly, as might have been expected, at the critical temperature and composition the Pake doublet shows a maximum in the temperature-dependent line-width (3). Magic-angle spinning (MAS) has two distinct effects on the deuterium NMR. One well-known effect of MAS is to eliminate the quadrupole splitting, and give rise to sidebands, the relative strength of which depends on the spinning frequency. A second effect, discussed here, is to increase the temperature of the maximum in the line-width.

We use the following model for our calculations of source 1. Fluctuations with correlation length ξ have lifetimes of the order of ξ²/D_g, where D_g is the gradient diffusion coefficient (5). Here, these fluctuations are treated as static for a labeled lipid molecule diffusing through the membrane with a tracer diffusion coefficient D. This picture is only strictly valid as long as D ≫ D_g. The gradient diffusion coefficient D_g approaches zero as the critical point is approached from higher temperatures. This calculation is thus most reliable close to the critical temperature. At present there are no experimental values for D_g for this mixture. The composition fluctuations are in a direction parallel to the tie lines that pass through the critical composition. Thus a single composition variable, such as the cholesterol mole fraction, is sufficient to describe the amplitude of the fluctuation. It is further assumed in source 1 that the deuterium NMR probe resonance frequency follows this cholesterol concentration along its random diffusion path.

It is known from the work of Waugh and collaborators that, in the case of deuterium quadrupole interactions, the MAS NMR line-width shows a maximum when ω_rτ ≈ 1, where ω_r is the spinning frequency in angular units, and τ is the effective correlation time of the molecular motion that affects NMR line-width (7). For a probe molecule diffusing in a membrane near a critical point with tracer diffusion coefficient D, we have τ ∼ ξ²/D, where ξ is the correlation length of composition fluctuations. Honerkamp-Smith et al. (6) have recently used fluorescence microscopy to measure the correlation length in mixtures of C, DPPC, and diphytanoyl-phosphatidylcholine. Above the miscibility critical temperature they find ξ = cst/(T−T_c), where the constant is ∼0.3 μm × degree. We assume the same value for this constant can be used for the C/DPPC/DOPC ternary mixture. It will be seen that with the Waugh condition (7) and with D ≈ 2 μm²/s, one estimates a maximum in the MAS NMR to be ∼10–20° above the critical temperature. In our model, τ → ∞ as T → T_c from above, and the deuterium powder spectrum is narrowed by spinning. At temperatures high above T_c, as 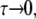the powder spectrum is narrowed both by spinning and by the diffusional averaging of composition fluctuations. At intermediate temperatures, the narrowing processes interfere with one another, leading to the Waugh maximum in line-width (7). Fig. 1 shows calculated deuterium NMR half-height line-widths (HHLW = 1/(πT₂)) using two assumptions concerning the structure factor S(k) for concentration fluctuations.

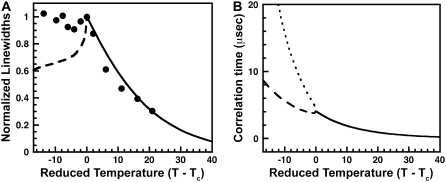
FIGURE 1.

(A) Calculated deuterium MAS NMR half-height line-widths (1/(πT₂)) as a function of temperature above the miscibility critical temperature (T–T_c) for a correlation function proportional to Exp[−r/ξ] and a correlation length taken from Honerkamp-Smith et al. (6), ξ = 0.3/(T–T_c) μm. (B) Half-height line-widths with peak widths normalized to one. The solid circles are data points from Veatch et al. (3), the solid curve uses the asymptotic Ising model structure factor (6), and the dashed curve uses the single exponential correlation function as in panel A.

When the spatial correlation function for concentration fluctuations is assumed to be a simple exponential, Exp(−r/ξ), the structure factor is 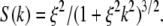From this, we calculate the HHLW shown in Fig. 1, A and B. Honerkamp-Smith et al. (6) report that their measured structure factors conform to the long-range asymptotic form for the Ising model, 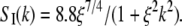With this Ising structure factor one obtains the normalized HHLW shown in Fig. 1 B. As mentioned earlier, the correlation length ξ and its temperature dependence are taken from Honerkamp-Smith et al. (6). In Fig. 1 B the two calculated line-widths are compared with the normalized experimental HHLW data of Veatch et al. (3), assumed here to be at or very near the critical composition.

In these calculations, we have adapted a theoretical formalism described by Kimmich and Weber (8). This leads to the following equation for the HHLW = 1/(πT₂):

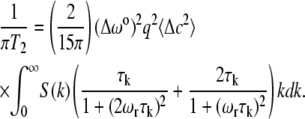The quantities Δω⁰, q, and 〈Δc²〉 have been defined previously (5), are relatively insensitive to temperature compared to ξ, and should play little role in the calculated relative normalized line-widths in Fig. 1 B. The quantity Δω⁰q Δc gives the change in deuterium resonance frequency for a Δc change in the mole fraction concentration of cholesterol. This factor was derived previously from a thermodynamic model for the phase diagram (5), but a purely empirical relation would do as well here. Except for Δω⁰, this equation also applies to the proton MAS NMR of DOPC in this ternary mixture, assuming that the broadening in that case is dominated by the dipole-dipole interaction between the two protons of the methylene group next to the carbon-carbon double bond (3). The important terms are then the known spinning frequency, ω_r = 2π × 10⁴, correlation time τ_k = 1/Dk², and the structure factor. The structure factors employed here are based on the experimental correlation lengths given in Honerkamp-Smith et al. (6). These experimental structure factors conform to the Ising structure factor S_I(k) to within a numerical constant, and are used for the line-width calculations shown by the solid curve in Fig. 1 B. Details of these calculations will be given elsewhere.

The maximum line-width in Fig. 1 A is similar in magnitude to the observed maximum. However, there is a marked discrepancy between the calculated and observed temperatures for the maximum, the observed maximum showing no shift (3). Unfortunately, our calculated temperature for the maximum may not be quantitatively accurate, in view of the assumption concerning the static nature of the composition fluctuations. However, it would be surprising if the calculations were not reasonable approximations within 5° of the critical temperature. Moreover, it is likely that our results are semiquantitatively accurate even at the higher temperatures, since composition fluctuations cannot have lifetimes <ξ²/D.

An earlier mean-field calculation of source 1 implicitly involves the correlation time 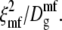Both this mean-field correlation time and the correlation time used here, ξ²/D, are proportional to (T–T_c)⁻². These correlation times can be made equal by adjusting the gradient energy parameter b (5), with the result that the mean-field Waugh peak is ∼5° above the critical temperature. Both calculations involve a distribution of fluctuation wavelengths and correlation times, of which the above correlation times are only representative.

It is seen that when the calculations are made consistent with the experimental correlation lengths (6), the shift of the line-width peak above the critical temperature is beyond the experimental error in Veatch et al. (3). Therefore we seek an alternative source of line broadening, which could yield the observed MAS maximum width at the critical temperature.

Thus consider the antithetical question: What line-widths are expected if there are no composition fluctuations? In source 2, the kinetics of formation and dissociation of a putative cholesterol-DPPC complex can lead to line broadening, which increases as the critical temperature is approached from higher temperatures (4,5). Normalized line broadening is shown in Fig. 2 A for the reversible reaction C + 2P ↔ CP₂, with a lifetime of the phospholipid bound state τ_off of ∼10 μs. The solid curve corresponds to the homogeneous phase above the critical temperature and has been described previously (5). Solid circles are normalized data points from Veatch et al. (3).

FIGURE 2.

(A) Normalized half-height line-widths for deuterium MAS NMR. The data points are from Veatch et al. (3) and the solid line is calculated for the effects of reaction kinetics due to the formation and dissociation of complexes of cholesterol and DPPC (5). The dashed curve below the critical temperature corresponds to the calculated line-width for the most abundant condensed phase. It is calculated that this phase would have the largest splitting in the absence of spinning, but the smallest line-width with spinning. The line-width is calculated as in Radhakrishnan and McConnell (5) except that the effect of the gradient energy term is omitted. (B) Correlation time associated with chemical reaction kinetics. The dashed line corresponds to the dominant phase, as in panel A. The dotted line corresponds to the less abundant phase. Calculated line-widths for this phase are omitted in panel A.

In this work we have extended the kinetic calculations in Fig. 2 A to lower temperatures. We use a thermodynamic model to calculate the compositions of the two coexisting phases below the critical temperature (5). The most abundant phase is the more condensed phase, with the larger splitting, and it is the line-width for this phase that is plotted in Fig. 2 A (dashed curve). The less abundant phase has smaller splittings, and much larger calculated line-widths, and so might escape detection. It is omitted from Fig. 2 A as it is not clear how the line-widths should be compounded. In any event, it is clearly possible that chemical kinetics might lead to an apparent line-width maximum at the miscibility critical point.

In general one might not anticipate that a reversible chemical reaction would lead to a significant maximum in NMR line broadening at a miscibility critical point. However, in the case of a kinetic mechanism for which the rates are concentration-dependent, an extremum in rates is expected at the critical point when the concentrations of the reactants begin to change rapidly due to the phase separation. Moreover, as discussed earlier, the immiscibility itself involves a product of this reversible reaction, the complex. The complex in turn undergoes a repulsive interaction with the third component (DOPC).

Thus there is an intimate relationship between the immiscibility and the reversible chemical reaction. Reaction kinetics can then be affected at the critical point. In obtaining the result given in Fig. 2 A, we use a correlation time for exchange, τ_e, which is related to the phospholipid on- and off-rate times by the equation 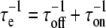(see Fig. 2 B).

Note that in these calculations the fluctuations in source 1 and kinetics in source 2 are treated as though they were independent. That is, in source 1, it is assumed that the NMR frequency of the probe follows perfectly the local instantaneous composition, which is only strictly true if the kinetics of complex formation and dissociation are rapid. In source 2, the fluctuations of source 1 are neglected, and only chemical kinetics are included. Clearly kinetic rates depend on local concentration. Despite this interdependence, for the parameters used it is reasonable to approximate the overall line-width by a sum of the contributions from sources 1 and 2. A related discussion applies to the proton MAS NMR of DOPC in these mixtures. The repulsive interaction between the complex and DOPC required to model the immiscibility implies that the proton NMR of DOPC show enhanced broadening at the critical point, since a DOPC molecule must sense changes in neighboring concentrations of complex.