A Coupled Diffusion-Kinetics Model for Analysis of Contact-Area FRAP Experiment

Abstract

Kinetic rates and binding affinity of receptor-ligand interactions are important determinants of cell adhesion. Measurements of these parameters in fluid phase using soluble molecules (i.e., three-dimensionial parameters) do not necessarily correlate with their counterparts measured when both binding partners are respectively anchored to two apposing surfaces (i.e., two-dimensional (2D) parameters). Moreover, 2D affinities measured by different methods can differ by orders of magnitude. Here we describe a coupled diffusion-reaction model for the fluorescence recovery after photobleaching experiment previously used to demonstrate the dynamics of adhesive bonds in the contact area. Applying the mathematical model to the contact area fluorescence recovery after photobleaching experiment enables in situ measurements of 2D kinetic rates of the adhesion molecules and their retarded diffusion in a stable contact area. The mathematical properties of the model are characterized in this article and its experimental validation will be presented in the companion article.

INTRODUCTION

Many important processes in cell adhesion and communication are mediated by receptor-ligand interactions at membrane interfaces (1). Kinetic rate and binding affinity constants of these interactions are important parameters for these processes (2,3). For example, the reverse-rate constant k_r (or the half-life, ln2/k_r) of the peptide-major histocompatibility complex ligand dissociation from the T cell receptor has been suggested to set a threshold between negative and positive selection of T helper cells (4) and to be a predictor for the responses of mature T cells upon their direct physical contact with an antigen presenting cell (5,6). Interactions among molecules of the immunoglobulin superfamily, including the CD28-CD58 pair and receptors for the common fragments of antibodies have also been intensively studied to gain insight into the relationship between molecular properties and adhesion (7–9). Molecular interaction parameters measured with at least one molecular species in solution, i.e., three-dimensional (3D) parameters, have provided significant insight, but there are still gaps in our understanding of how the same interactions operate when the receptors and ligands are spatially segregated and confined by two apposing membranes to which they are respectively anchored, i.e., two-dimensional (2D) binding.

Two classes of methods have been developed for measuring 2D binding parameters, which are based on either mechanical or fluorescent means. These methods differ both in the manner in which interactions are visualized and in the mechanism by which membranes are brought into apposition during the measurement.

The mechanical methods are based on the idea that binding results in receptor-ligand bonds that physically connect two cells or a cell to a surface. Cell binding can be quantified by various mechanical techniques, such as a flow chamber (e.g., Kaplanski et al. (10)), a micropipette (e.g., Chesla et al. (11)), a centrifuge (e.g., Piper et al. (12)), and an optical trap (13), which separate unbound from bound cells by pulling or shearing. Because it is difficult to directly quantify the number of bonds, the cell binding parameters are usually related to the desired receptor-ligand binding parameters via mathematical models that predict the bond number from the fraction of bound cells (14), which are based on a probabilistic theory for kinetics of small systems (15). As such, these experiments are designed to work in the regime of small numbers of bonds (a few, most likely one), which requires that the interactions be probed in short duration with low densities of receptors and ligands (compared to the 2D K_d) on the apposing surfaces, which are often rough and fluctuating. In these experiments, bonds form as two cells are put together mechanically. As such, the relative membrane positions are determined by the external forces (e.g., gravity) that push the cells into apposition, the repulsive forces between the apposed membranes (due to charges, steric effects, and thermal fluctuations), and the mechanical properties of the cells that transmit and distribute those forces.

The fluorescent method visualizes molecular interactions between receptor-expressing cells and a glass-supported lipid bilayer reconstituted with fluorescently labeled, lipid-anchored, freely mobile ligands at equilibrium (16,17). At physiological receptor and ligand densities, a large number (thousands) of bonds are typically observed. This high concentration of bonds enables quantitative measurements of the bond density from fluorescence intensity. Just like solution binding, the equilibrium bond density increases with the free ligand density in the bilayer when ligand density is low, but saturates after ligand density is sufficiently high. Fitting the equilibrium binding model to such a Langmuir isotherm or its linear transformation, i.e., the Scatchard plot or the Zhu-Golan plot, allows for evaluation of the 2D equilibrium dissociation constant, K_d (16,17). The formation of thousands of bonds at equilibrium is expected to distribute adhesion forces across many bonds and minimize the impact of force on the kinetics of individual bonds. The positioning of the apposed membranes is likely determined predominantly by the thousands of receptor-ligand interactions working against repulsive forces and thermal fluctuations, which smoothens the membrane wrinkles and minimizes membrane fluctuations. Thus, a major difference between the two methods is that the receptors and ligands themselves play a major role in assembling the interface across which they interact in the fluorescent method but not in the mechanical method.

It is remarkable that for identical receptor-ligand interactions or interactions of similar 3D K_d, the 2D affinities measured by the mechanical and fluorescent methods can differ by as much as five orders of magnitude (18). This may be due to the role, or lack thereof, of receptor-ligand interactions in defining the microtopology of the interface in the two methods. We refer to this as the self-assembly hypothesis, because it emphasizes the role of cooperative action of receptor-ligand interactions in establishing a membrane microtopology that favors efficient interaction. Increasing the smoothness and flexibility of the host cell surface in the mechanical method can result in a two-orders-of-magnitude increase in the effective 2D affinity and forward rate without changing the reverse rate (19,20). Thus, we can hypothesize that in the fluorescent method, self-assembly produces a more ordered contact area, thereby increasing effective forward rates by orders of magnitude compared to those measured under the conditions of mechanical methods; however, self-assembly would not decrease reverse rates. Testing this hypothesis requires a method to measure kinetic rate constants under the conditions of the fluorescent method.

The fluorescence recovery after photobleaching (FRAP, also termed fluorescence photobleaching recovery, or FPR) technique (21,22) has been used to demonstrate the rapid turnover of fluorescent bonds in the cell-bilayer contact area (completed in ∼10 min for the fast dissociating CD2-CD58 interaction (see Fig. 1)) (23). This experiment, termed contact-area FRAP, shows that the equilibrium of the receptor-ligand interaction in the contact area is dynamic rather than static, such that formation and dissociation of bonds occur simultaneously at equal rates along opposite directions. This allows the bound ligands to exchange place with the free ligands as long as their densities remain unchanged. Photobleaching eliminates the fluorescence of both the free and bound ligands, creating density gradients that drive diffusion of bleached free ligands away from and unbleached free ligands entering into the bleached zone. Over time, this leads to the replacement of the bleached bound ligands by the unbleached bound ligands as a result of the exchange between the free and bound ligands. In other words, the turnover of fluorescent bonds in the contact area is a result of dissociation of bleached bound ligands from the cell surface receptors and their rebinding by unbleached ligands. Thus, the contact-area FRAP time courses may contain both diffusion and kinetic information, which may be extracted if analyzed by a mathematical model for the reaction-diffusion process involved, which is the goal of this work. Theoretical development, solution methods, mathematical properties of the model, and strategy for parameter evaluation are described in this article. A refinement of the original contact-area FRAP assay, experimental tests of the model validity, and application to evaluate 2D kinetic rates will be presented in the companion article (24).

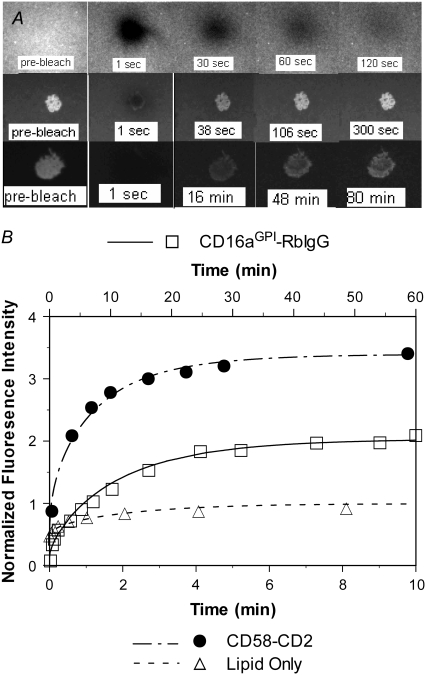
FIGURE 1.

(A) Fluorescence microscopic images at indicated time points from a conventional FRAP, showing nearly full recovery of the fluorescence intensity inside the lipid bilayer bleached spot to the prebleach level in ∼2 min (upper row), from a contact-area FRAP for the CD2-CD58 system, showing nearly full recovery in ∼5 min, despite the higher fluorescence intensity within the contact area (middle row), and from a contact-area FRAP for the CD16a^GPI-RbIgG system, showing a much slower time course of fluorescence recovery that is incomplete, although a steady state had apparently been reached (lower row). The gray-scale levels of different rows have been adjusted to accommodate their different dynamic ranges. See Tolentino et al. (24) for experimental methods. (B) Comparison between the measured (points) and predicted (curves) FRAP time courses. The fluorescence intensities were normalized by those of the free ligands outside of and far away from the contact area. The theoretical curves were fits of solutions of Eqs. 5–8 to the data. For the conventional FRAP problem, the only dependent variable of interest is m_l and the mathematical model is obtained from Eq. 5 by setting the kinetic rates to zero and ξ to unity. Note that the timescale of the CD16b^GPI-RbIgG case (upper abscissa) is six times that for the other two (lower abscissa).

MODEL

Underlying physical processes

Fluorescently labeled ligands can be thought of as “bright ligands”. After their fluorescence has been bleached by a high-intensity laser pulse, these molecules become “dark ligands”—a different species as far as diffusion is concerned. The conventional FRAP time course is governed by the diffusion of the bright ligands from outside into the bleached spot (with simultaneous diffusion of the dark ligands out from the bleached spot). As shown in Fig. 1 A (upper row) and Fig. 1 B (triangles, lower abscissa), the diffusion-driven fluorescence recovery occurred on a timescale of minutes, as expected from the 2D fluidic properties of the lipid bilayer. The contact-area FRAP involves placing a receptor-expressing cell on the ligand-coated bilayer and allowing contact-area formation to achieve a steady state, i.e., to become a stable contact area before photobleaching. Except for the occasional migration in some cases, the cell no longer deforms and the contact-area geometry becomes invariant in time. Moreover, binding between the receptors and ligands has reached equilibrium and the free receptors, free ligands, and bonds have achieved stable distributions. As shown in Fig. 1 A (prebleach, middle and lower rows), the fluorescence intensity inside the contact area is higher than outside because of the presence of the bound ligands in addition to the free ligands. Photobleaching created two new ligand species—dark free and dark bound ligands—in addition to the preexisting bright free and bright bound ligands. As in the conventional FRAP, this creates two steep gradients of the free ligands—higher density outside than inside the contact zone for the bright ligands but a reversed gradient for the dark ligands—which result in their diffusion across the perimeter of the contact zone (bright ligands in and dark ligands out). By comparison, binding remains in equilibrium, since it is assumed that the receptors bind identically to both bright and dark ligands. However, it is a dynamic equilibrium with equal (and nonnegligible) rates of bond formation and dissociation that proceed in opposite directions; only the net bond formation rate is zero. Although both the bright and dark ligands can form bonds with and dissociate from the cell surface receptors, their relative contributions to the forward and reverse reactions depend on their relative densities according to the mass action law, which changes due to diffusion. Thus, the receptor-ligand binding kinetics is coupled to diffusion. As diffusion brings more bright free ligands in and dark free ligands out, more bright bound ligands replace the dark bound ligands, resulting in the observed fluorescence recovery (Fig. 1 A, middle and lower rows).

Simplifying assumptions

Consider a coupled reaction-diffusion process in a circular contact area of radius r₀ and uniform gap distance separating the cell membrane and the lipid bilayer. Geometrical changes in the contact-area size, shape, and gap distance have been observed in “growing contact areas”, but are greatly reduced after the contact area becomes stable (25). Performing FRAP experiments with contact areas that have become stable minimizes impact on the reaction-diffusion processes by other mechanical processes of the cell, e.g., passive deformations and active motions, which occur during contact-area formation. Small deviations from the simple circular geometry (cf. Fig. 1 A) unlikely have significant effects on the determination of kinetic and diffusive parameters because they are estimated from fitting the model to the measured FRAP time courses that are averaged over the entire contact area. The simplification of uniform gap distance, which seems reasonable for contact areas mediated by single-species receptor-ligand interactions that have the same molecular lengths, allows us to assume uniform kinetic rate and diffusion constants with values independent of the spatial location inside the contact area in the length scale resolvable by optical microscopy. Outside the contact area, the problem can be treated as pure diffusion in an infinite 2D plane, as in conventional FRAP. In other words, the neighboring cells are assumed to be sufficiently far apart for their influence on the FRAP data of the cell in question to be negligible, and the bilayer is assumed to be sufficiently large for the ligand density outside the contact area not to be depleted by concentration of ligands inside the contact areas.

Let D_r, D_l, and D_b be the lateral diffusivities of the receptor on the cell membrane, the ligand on the lipid bilayer, and the bond on the contact area, respectively. They represent the diagonal terms of the full diffusivity matrix. The off-diagonal terms describing coupling among different species are assumed to be negligible, as they are typically much smaller than the diagonal terms. The presence of bonds (posts) and the apposing surfaces (narrow gap) inside the contact area may retard the lateral mobility of the free ligands by a (averaged) factor of ξ (0 < ξ ≤ 1), resulting in a step decrease in their diffusivity. In stable contact areas there should not be net diffusion for free receptors due to the lack of disturbance to their already stable density. However, bonds may diffuse because of the nonuniform distributions of the bright and dark bonds. Typically, lateral mobility of lipid-anchored molecules on artificial bilayers is orders of magnitude faster than on cell-surface proteins, D_l ≈ 1 μm² s⁻¹ ≫ D_r ≈ 10⁻² μm² s⁻¹ (26,27). Since D_b ≤ D_r, the bound ligands are treated as immobile compared to the free ligands that have respective diffusivities D_l outside and ξD_l inside the contact area.

It is assumed that neither the labeling of the ligand with a fluorescence tag nor the photobleaching of such label affects its reaction kinetics and lateral diffusion. Since only the bright free ligands and bright bound ligands (whose surface densities are designated m_l and m_b, respectively) are directly observed experimentally, the model is formulated for these two species only. The laser beam is assumed to have a uniform profile within a circle of radius r₀ identical to that of the contact area, although a different radius or a beam with a Gaussian profile can be similarly treated. Consequently, the densities of bright free ligands and bright bound ligands immediately after photobleaching are uniform within the contact area.

Governing equations

Under the above assumptions, the bright free ligands obey a reaction-diffusion equation:

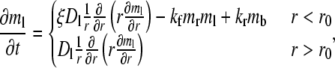(1)

where r is the polar coordinate originating from the center of the contact area and t is time starting immediately after photobleaching. k_f and k_r are, respectively, the forward- and reverse-rate constants. By neglecting D_b, the bright bound ligands can be described by just the kinetic equation:

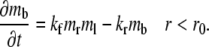(2)

The initial conditions are:

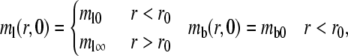(3a,b)

where the postbleach bright free (m_l0) and bright bound (m_b0) ligand densities and the steady-state bright free ligand density (m_l∞) are positive constants that satisfy m_l0 < m_l∞ and m_b0 = m_l0m_rk_f/k_r. The latter equation is obtained by assuming the same susceptibility of the ligand fluorophore to photobleaching regardless of whether the ligand is free or bound to a cell surface receptor. The boundary conditions are

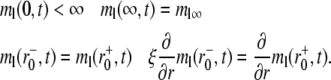(4a-d)

Setting k_f = k_r = 0 and ξ = 1 in Eqs. 1, 3a, and 4 reduces the problem to a conventional FRAP problem.

Defining respective dimensionless densities of bright free ligands and bright bound ligands as 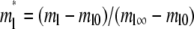and 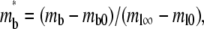a dimensionless time as 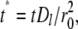a dimensionless polar coordinate as r* = r/r₀ inside but r* = 2 − r₀/r outside the contact area, Eqs. 1–4 can be nondimensionalized as

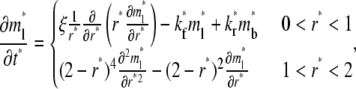(5)

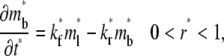(6)

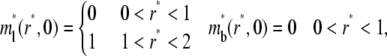(7a,b)

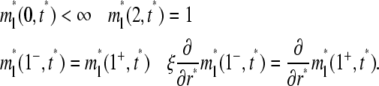(8a-d)

Data from contact-area FRAP experiments are commonly shown as a time series of normalized fluorescence intensity that is averaged over the entire contact area (Fig. 1 B), which correspond to

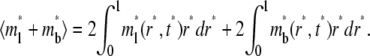(9)

The flux of bright free ligands entering the contact area is related to the rate of fluorescence recovery, which in nondimensionalized form is

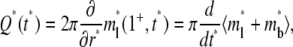(10)

where 1⁺ denotes the limit approaching from above.

Equations 5–8 were directly integrated numerically using a second-order Crank-Nicolson implicit finite difference scheme (28) that was implemented as an Excel (Microsoft) macro and run on a PC.

RESULTS

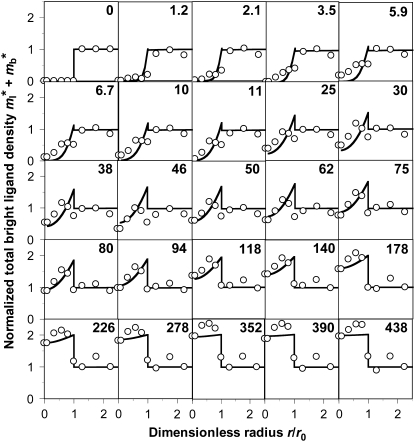
Application of this model involves fitting the theoretical solution to the experimental FRAP data, which is illustrated in Figs. 1 B and 2. The data in Fig. 2 (open circles) are obtained from the images shown in Fig. 1 A (lower row) and more from the same experiment, by measuring the average fluorescence intensities in a series of concentric annuli of increasing radii at the indicated times (numbers). The fluorescence intensities can be further averaged over the contact area to reduce the data to only a time sequence without the spatial variable. This is exemplified by the CD16a^GPI-IgG data in Fig. 1 B (squares, upper abscissa), which were obtained by averaging the data in Fig. 2 over the contact area. Spatially averaged time courses for a conventional FRAP experiment (triangles, lower abscissa) and a contact-area FRAP experiment for CD2-CD58 interaction (circles, lower abscissa) are shown in Fig. 1 B to match the images shown in Fig. 1 A (upper rows). Although systematic experimental tests of the model validity will be performed in the companion article (24), it is evident that the theory fits the data very well (curves). It is important to note that fitting the distribution in both space and time (Fig. 2) and fitting the spatially averaged time curve (Fig. 1 B, the CD16a^GPI-IgG curve) return very similar best-fit parameters, suggesting that the latter data contain sufficient information for estimation of model parameters.

FIGURE 2.

Solutions of Eqs. 5–8, the bright total ligands () that best fits the contact-area FRAP data (open circles) are plotted as functions of r/r₀ and t*. The data are from the same experiment as the CD16b^GPI-RbIgG experiment shown in Fig. 1.

The objective of curve-fitting is to extract diffusion and kinetic rate constants from analyzing the data with the model. Although we have not encountered a case where our model is unable to fit the data, we found that different fitting strategies, regardless of the goodness of fit, show different abilities to estimate the kinetic rates reliably. For example, fitting 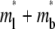to contact-area FRAP time courses in Fig. 1 B resulted in excellent fits in both CD16a^GPI-IgG and CD2-CD58 systems. However, kinetic rates can be reliably estimated for the former system only. To extract kinetic rates for the CD2-CD58 interaction requires a different fitting strategy, which is derived from how different aspects of the contact-area FRAP time course depend on the model parameters. The model is governed by three numbers: the fractional diffusivity, ξ; the dimensionless forward-rate constant, 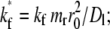and the dimensionless reverse-rate constant 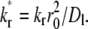Physically, these represent respective ratios of the timescale of diffusion outside the contact area to that of diffusion inside the contact area, to that of forward reaction under unit free-ligand density, and to that of reverse-reaction under unit bound-ligand density.

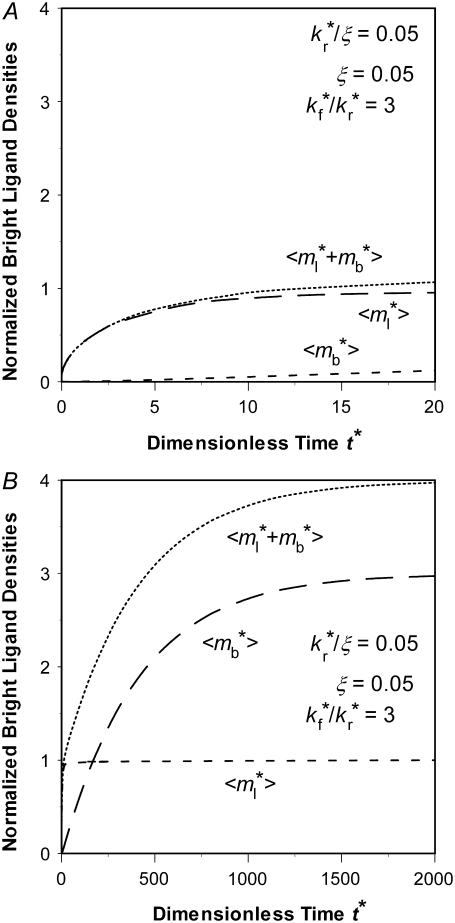
Slow kinetics results in two-phase recovery

Small values of 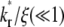indicate that the characteristic time for bond dissociation is much longer than that for diffusion inside the contact area. Under this condition, the contact area FRAP time course exhibits two phases, as shown in Fig. 3. In the diffusion timescale immediately after photobleaching, the receptor-ligand bonds would behave as if they were permanent. As such, diffusion is the dominant physical process that drives fluorescence recovery. However, only the free dark ligands are able to diffuse out of the contact area (with simultaneous diffusion of free bright ligands in to take their place), because the bound dark ligands are confined to the contact area by the cell-surface receptors with which they are associated. This is shown in Fig. 3 A for t* < ξ⁻¹ (20 in this case) during which time the average 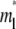rapidly increases to its plateau level (unity because of nondimensionalization), but the average 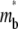remains small. Thus, the fluorescence can recover no more than the original fluorescence level outside the contact area. As this limit is approached, the density gradients of the bright and dark free ligands vanish, just as in the conventional FRAP case.

FIGURE 3.

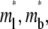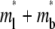Two-phase recovery of a reaction-limited case. (A) Phase I recovery in the short timescale is due to free ligand diffusion. (B) Phase II recovery is a result of bond dissociation and rebinding that occurs in a much longer timescale. The and values at any given time point have been averaged over the contact area, as indicated by the brackets. The dimensionless numbers are indicated.

As time extends to the timescale for dissociation, 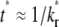(400 in this case), the receptor-ligand bonds have sufficient time to dissociate and reform. Once a dark bound ligand dissociates, however, it has to compete with the bright free ligand for rebinding to the free receptor. The dark free ligand is less likely to win in this competition because of its lower density relative to that of the bright free ligand. Moreover, once it becomes free, the dark ligand tends to diffuse out of the contact area where its density is lower, which further diminishes its density. By contrast, the reduced density in the bright free ligand resulting from its binding to a receptor is replenished by diffusion from outside, where its density is higher. Thus, the bright ligands gradually replace the dark ligands in the bound state, resulting in a fluorescence recovery level that is higher than that outside the contact area (i.e., the dimensionless 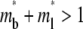(see Fig. 3 B)). This portion of the recovery time course can be approximated by a single exponential, 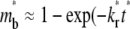). As such, the reverse rate can be readily estimated from the long-term behavior of the contact-area FRAP time course, i.e., 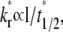where 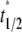is dimensionless time required for 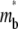to achieve half of the steady-state value, 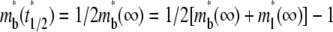(see Fig. 3 B).

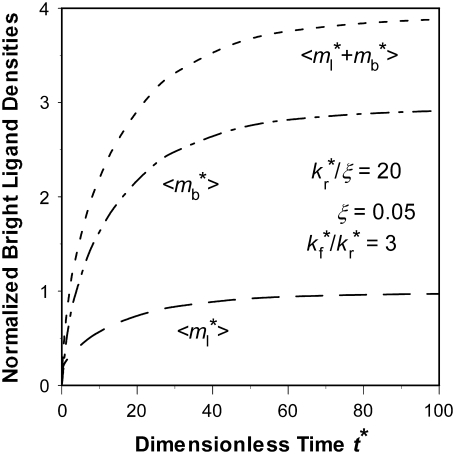
Fast kinetic rates are difficult to extract from contact-area FRAP time course alone

The other extreme is the case of 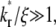i.e., the dissociation timescale is much shorter than the timescale of diffusion inside the contact area. Under this condition, the reaction is so fast that it may be considered as having reached equilibrium in the timescale of diffusion. As such, the dark bound ligands are being replaced almost at the rate of diffusion of bright free ligands into the contact area. The recovery time courses of free, bound, and total bright ligands are shown in Fig. 4, apparently controlled by the same timescale. Since diffusion is the rate-limiting process here, it may be difficult to extract kinetic information from the contact-area FRAP time course alone. Nevertheless, the data can be used to estimate diffusivity. In the conventional FRAP, the diffusion coefficient can be estimated from 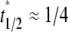where 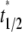is the dimensionless time required for 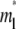to achieve 1/2, or D_l ≈ 0.25 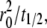where t_1/2 is the dimensional time required for the fluorescence intensity to recover half of the steady-state value (23,29). Likewise, the fractional diffusivity can be estimated from 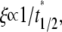or ξD_l ∝ 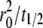where the half time should be estimated from the contact-area FRAP instead of the conventional FRAP time course.

FIGURE 4.

Recovery time courses of the averaged (over the contact area) bright free (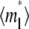), bound (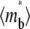), and total (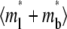) ligands for a diffusion-limited case. The dimensionless numbers are indicated.

The above two scenarios of slow and fast reactions resemble those of reaction-limited and diffusion-limited reactions, respectively. The difference is that the classical reaction-limited and diffusion-limited reaction cases involve local diffusion (in the vicinity of the reacting molecules), whereas the two scenarios discussed here involve diffusion over a long distance (across the perimeter of the contact area).

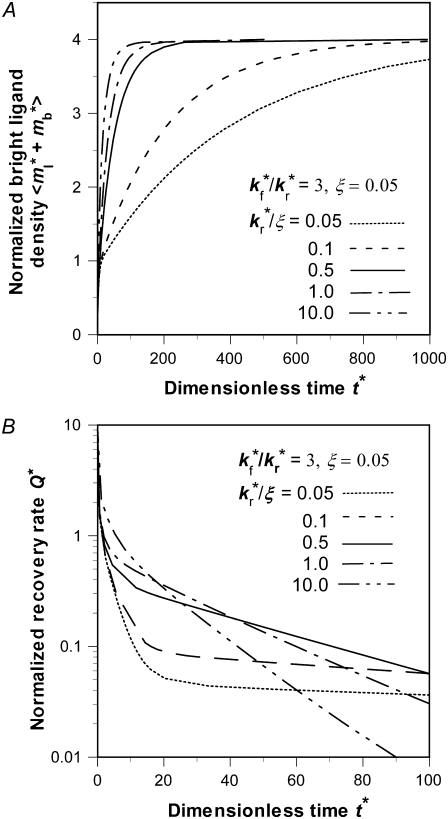
Effects of k_r^*/ξ on time courses of contact-area FRAP and recovery rate

The contact-area FRAP time courses are plotted in Fig. 5 A for a range of 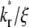values covering both extremes. As 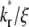increases from small to intermediate values, diffusion and dissociation timescales become comparable and the system behavior transitions from reaction-limited process to diffusion-limited process. Similar to the small 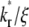case, the early and late phases of the contact-area FRAP time course are more sensitive to the ξ and 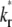values, respectively. However, there is not clear separation between the two phases. Therefore, fitting of the entire FRAP time course is required to estimate the ξ and 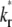values. This is the case for the CD16a^GPI-IgG interaction shown in Figs. 1 B and 2, where the best-fit 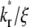value is 2.5.

FIGURE 5.

Time courses of recovery (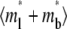) (A) and recovery rate (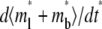) (B) in the full range of 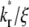for the indicated 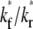and ξ values, as observed on a timescale relative to the time of free ligand diffusion outside the contact area.

Further increase in 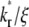increases the steepness of the ascending portion of the contact-area FRAP curve, which rapidly turns into a plateau (Fig. 5 A). Different curves become closer to each other and less sensitive to 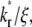making it difficult to extract the kinetic rates by fitting the contact-area FRAP time course alone. By contrast, the time course of recovery rate Q* becomes more sensitive to 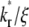(Fig. 5 B). Defined by Eq. 10, a recovery rate curve consists of a rapid declining segment and more gradual declining segment. In short times, faster-dissociating systems (with larger 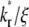values) have higher recovery rates because reaction can replace dark bound ligands with bright bound ligands more rapidly due to their faster dissociation. This in turn allows diffusion to replace dark free ligands with bright free ligands more rapidly, because depletion of the bright free ligands by binding results in their lower density inside the contact area relative to outside. However, the rapid declining phases of recovery-rate time courses turn into more gradually declining phases at earlier times for systems with larger 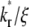values because diffusion takes over at earlier times in these systems (Fig. 5 B). For any two systems with different 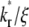values, there exists a time before which the system with the larger 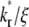has a higher Q* but after which the system with the lower 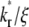has a higher Q*. Such a crossover phenomenon ensures that the Q* vs. t* curve remains sensitive to 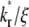even when it is large, suggesting that kinetic information can be extracted by fitting the recovery-rate data.

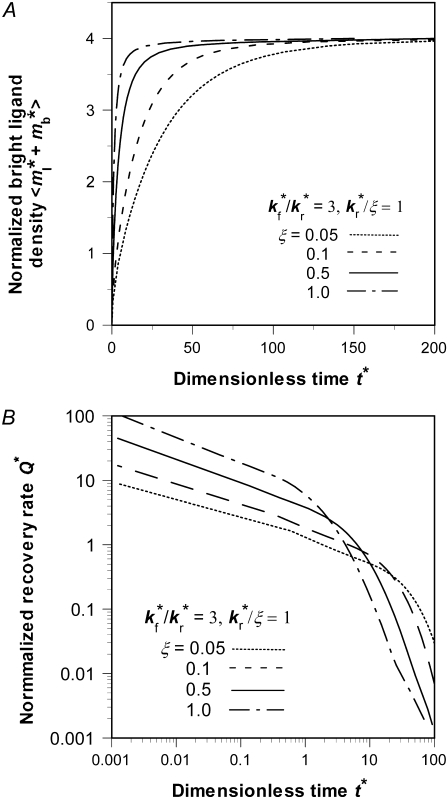
Effects of retarded diffusivity fraction ξ

Distinct dependencies on ξ of time courses of contact-area FRAP (Fig. 6 A) and recovery rate (Fig. 6 B) are similarly observed in numerical studies. Increasing ξ bends the elbow in the contact-area FRAP time course where the ascending phase turns into a plateau, which pushes curves of different ξ values toward each other, making it more difficult to extract kinetic information (Fig. 6 A). Concurrently, the position of the elbow shifts leftward toward shorter time. The elbow in the contact-area FRAP time course represents a period in which the recovery rate changes rapidly. This can be seen from Fig. 6 B where Q* is plotted versus t* in the log scale. Indeed, these curves consist of a slowly declining segment and a more rapidly declining segment connected by an elbow (Fig. 6 B) that corresponds to the elbow in the contact-area FRAP time course (Fig. 6 A). As ξ increases, the curve shifts leftward and upward toward lower t* and higher Q* rather than being pushed toward a limit like the contact-area FRAP curve, suggesting that the retarded diffusivity fraction, ξ, can be extracted by fitting the Q* vs. t* data.

FIGURE 6.

Time courses of recovery (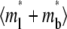) (A) and recovery rate (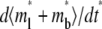) (B) in the full range of ξ for the indicate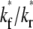d and 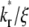values, as observed on a timescale relative to the time of free ligand diffusion outside the contact area.

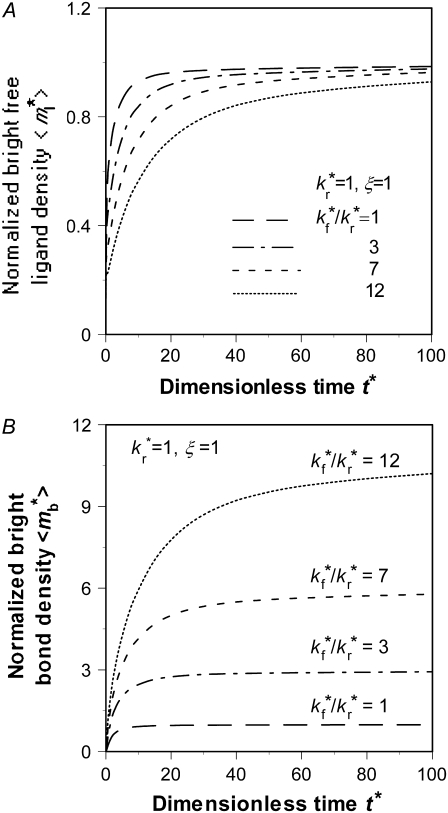
Effects of binding affinity and receptor density, m_rK_a

Although the ratio 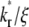controls the separation of the diffusion and dissociation timescales, the ratio 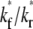determines the steady-state level of bound ligands, 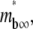as indicated in Fig. 7 B. This ratio equals the product of receptor density m_r (dimensional, in μm⁻²) and binding affinity K_a (dimensional, in μm²); it can be directly measured from the plateau level of the normalized fluorescence intensity inside the contact area minus one, regardless of the 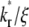value, because m_rK_a is an equilibrium property.

FIGURE 7.

Effects of 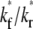on the recovery time courses of the averaged (over the contact area) bright free ligands (A) and bound ligands (B). The dimensionless numbers are indicated.

An effect of increasing 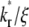(keeping 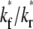and ξ constant) or increasing ξ (keeping 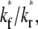and 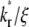constant) is to increase the sharpness of the elbow in the 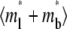vs. t* curves (Figs. 5 A and 6 A). In contrast, increasing 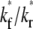(keeping 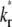and ξ constant) decreases the sharpness of the elbow of both the 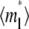vs. t* and vs. t* curves (Fig. 7). The reason is that, for the same 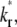the larger the 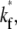the faster the bright ligands exchange with the dark ligands, thereby slowing down the recovery of bright free ligands. Although this enhances the rate of increase in bright bound ligands, the 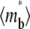vs. t* curve also has to climb up a higher steady-state level, resulting in a more gradual transition from rapid increase to plateau.

Strategy for evaluating model parameters

The preceding sections suggest that, as time increases, the contact-area FRAP time course becomes less and less sensitive to ξ and k_r*/ξ, whereas the recovery rate time course becomes more and more sensitive. This suggests that, for slow-reacting systems, it is better to extract these parameters from the contact-area FRAP time course, but for fast-reacting systems, it is better to extract them from the recovery-rate time course. We thus select the following χ² function to be minimized for curve-fitting:

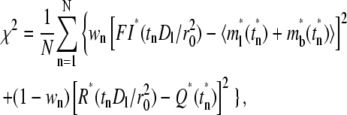(11)

where FI*(t_n) and R*(t_n) are, respectively, the normalized fluorescence intensity of the contact area and recovery rate measured at time t_n after photobleaching, 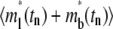and Q*(t_n) are their corresponding model solutions given by Eqs. 9 and 10, respectively, w_n (0 < w_n <1) is a weight function evaluating at the same time points, and N is the total number of time points. The choice of w_n is important, as it determines whether the model parameters can be successfully extracted, and if so, how fast the calculation is and how robust the parameters are. Choosing w_n > 0.5 implies more emphasis on the contact-area FRAP time course itself at time t_n, which favors slow-reacting systems. Choosing w_n < 0.5 implies more emphasis on the information embedded in the recovery-rate time course at time t_n, which is more suitable for fast-reacting systems. To strike a balance, we can chooose w_n > 0.5 for early time points, but w_n < 0.5 for later time points. We can also adjust the value of w_n progressively during the iterative curve-fitting process. For example, we first fix w_n = 0.5 and two parameters, allowing only one freely adjustable parameter in the iteration. Using the method of steepest descent to minimize χ², we first find an approximate value for the third parameter. Then we fix this parameter and let the next parameter be adjustable. We found that this worked well by following the sequence from ξ to k_r* to k_f*/k_r*. We used a minimum of 20 iterations with the following convergence criteria: |y_n+1 − y_n|/|y_n+1 + y_n| < 0.02, where y_n is the approximate value of any parameter at the nth iteration. To treat the singularity of the gradient of the free bright lights at time 0, we added a value to m_l*(1,0) = 0.5 in the numerical integration. This method was successful in extracting model parameters for both the CD16b^NA2-IgG and CD2-CD28 systems, including the data in Figs. 1 B and 2, and all data in the companion article (24).

DISCUSSION

In this article, we present a theoretical model for the contact-area FRAP experiment and examine its mathematical properties. The model describes a coupled reaction-diffusion process that is assumed to be in a simplest form. Some of the simplifying assumptions are nonessential and can be removed without affecting the physical basis of the model; only the mathematics becomes more involved. For example, the shape and size of the bleached spot need not be the same as those of the contact area. Other assumptions are made due to the lack of information regarding the underlying mechanisms. For example, the presence of bonds has been assumed to only retard diffusion of free ligands inside the contact area, but not to affect their equilibrium distribution across the contact perimeter. In early measurements of 2D K_d the density of free ligands was also assumed to be the same inside the contact area as outside the contact area. Recently, the density of free ligands in the contact area was estimated by measuring the density of a fluorescently labeled, lipid-anchored molecule in the contact area that does not interact with any receptors the cell expresses. In the case of both the CD2-CD58 and CD28-CD80 interactions, it was found that the free ligand densities in the contact area were reduced on the order of 20–40% (30). Thus, in addition to reduction in free ligand diffusivity, crowding in the contact area leads to free ligand exclusion, which can be treated by introducing a phenomenological parameter termed exclusion fraction.

Nearly full fluorescence recovery is expected for conventional FRAP performed on lipid-anchored molecules reconstituted in glass-supported synthetic bilayer membranes (26). By comparison, a substantial immobile fraction usually exists when protein mobility on a live cell surface is measured (21,22). Likewise, depending on the molecular systems examined we have found variable but significant fractions of nonrecoverable fluorescence in the contact-area FRAP experiment (24). This is mechanistically different from the immobile fraction in the conventional FRAP experiment, because here, all ligands are anchored to the lipid bilayer, which assumes uniform fluidic properties. It can also be treated by introducing a phenomenological parameter termed “nonrecoverable fraction”. In the conventional FRAP, the immobile fraction can be treated using nonideal diffusion models, e.g., anomalous subdiffusion (31). Such models may also find application in treating exclusion fraction and nonrecoverable fractions in the contact-area FRAP.

A proposed mechanism for the nonrecoverable fraction is that some bonds become much more stable, possibly due to clustering of some of the receptors (24). This nondissociable fraction of bonds can be treated using more complex reaction schemes, e.g., multimeric binding instead of the simplest monomeric binding model assumed here.

Despite its many simplifications, the model presented here appears to capture the basic features of the contact-area FRAP experiment, which, when analyzed by the model, enables in situ measurements of 2D binding kinetics and retarded diffusion in a model immunological synapse (24). In addition to the accumulation of adhesion molecules at the intercellular junction, the coupled reaction-diffusion mechanism described here may underlie other cellular process, e.g., the recruitment of signaling molecules in the cytoplasmic side of the immunological synapse.