Fast Fluorescence Laser Tracking Microrheometry, II: Quantitative Studies of Cytoskeletal Mechanotransduction

Abstract

Fluorescence laser tracking microrheometry (FLTM) is what we believe to be a novel method able to assess the local, frequency-dependent mechanical properties of living cells with nanometer spatial sensitivity at speeds up to 50 kHz. In an earlier article, we described the design, development, and optimization phases of the FLTM before reporting its performances in a variety of viscoelastic materials. In the work presented here, we demonstrate the suitability of FLTM to study local cellular rheology and obtain values for the storage and loss moduli G′(ω) and G″(ω) of fibroblasts consistent with past literature. We further establish that chemically induced cytoskeletal disruption is accompanied by reduced cellular stiffness and viscosity. Next, we provide a systematic study of some experimental variables that may critically influence microrheology measurements. First, we interrogate and justify the relevance of bead endocytosis as a method of cellular internalization of 1-μm probes in FLTM. Second, we show that as sample temperature increases, FLTM findings are elevated toward higher frequencies. Third, we confirm that relevant bead sizes (1 and 2 μm) have no effect on FLTM measurements. Fourth, we report the lack of influence of bead coatings (antiintegrin, antitransferrin, antidystroglycan, or uncoated tracers were surveyed) on their rheological readouts. Finally, we demonstrate the potential of FLTM in studying how substratum rigidity regulates cellular rheological properties. Interestingly, multiple, coupled strain relaxation mechanisms can be observed separated by two plateau moduli. Although these observations can be partly explained by rheological theories describing entangled actin filaments, there is a clear need to extend existing microrheology models to the cytoskeleton, including potentially important factors such as network geometry and remodeling.

INTRODUCTION

To gain insight in mechanotransduction and understand how the mechanical properties of cells are affected by environmental cues, we developed what we believe is a novel fluorescence-based passive microrheology technique: fluorescence laser tracking microrheometry (FLTM) (1). Although a consensual model of mechanotransduction has yet to be fully elaborated, it is now commonly believed that the cytoskeleton plays a crucial role in sensing and transmitting information regarding the physical environment of cells (2–5). In eukaryotic cells, the cytoskeleton (composed of an intricate mesh of actin microfilaments, intermediate filaments, microtubules, and their associated proteins) interacts dynamically with the plasma membrane, where it anchors via integrin receptors (among others), and with a variety of intracellular compartments, which it envelops. The cytoskeleton is not only viewed as the main stress-bearing component of the cell, it has also been observed to reorganize under mechanical stress (3,6–9) and is regarded as a scaffold for spatially organizing signaling molecules (3,10). The cytoskeleton thus lies at the crossroads of cell architecture and cell function; according to so-called “decentralized models”, its milieu-mediated remodeling likely participates in mechanotransduction by altering cellular rheology.

In our companion article (1), we describe FLTM, point out its design concepts and optimized constituents, and evaluate its performance in an assortment of viscoelastic materials. FLTM strengths are severalfold. First, being a passive microrheology technique, FLTM characterizes the local viscoelastic behavior of biomaterials (characterized by the frequency-dependent complex shear modulus G*(ω)) in the absence of an active mechanical perturbation to the sample. As with other passive methods, FLTM utilizes the thermal motion of embedded colloids to determine the viscoelastic properties of the surrounding medium (11,12). Second, FLTM speed (up to 50 kHz), owing to the white spectrum of the thermal energy, and spatial resolution of the bead probe's trajectory (∼4 nm) make this apparatus well suited to the study of heterogeneous and dynamic biological systems. Third, the extended frequency range (∼0.5 Hz–50 kHz) probed by FLTM allows appraisal not only of the macroscopic viscoelasticity of molecular networks at long timescales (on the order of seconds), but also the fast fluctuations of single filaments in the cytoskeleton at shorter timescales (13), which are important to understand fast transitions in cytosketetal dynamics. Fourth, the combination of fluorescence to a microrheometry system enables targeting of cellular structures with molecular specificity, and overcomes the shortcoming of the rarity of endogenous large particles to be tracked (14). Because of their spectral signatures, fluorescent probes are readily and categorically identified, and their detection is less sensitive to optical background effects than that of white-light probes.

In this article, and as a complement to the companion article (1), we concentrate on biological findings using FLTM. Specifically, we i), quantitatively assess the rheological consequences of cytoskeleton-disrupting drugs in fibroblasts, ii), test two options of tracer introduction into living cells for FLTM, iii), consider the effects of sample temperature on FLTM results, iv), evaluate the influence of bead size on FLTM measurements, v), report the effects of different choices in bead coating, and vi), show that substratum rigidity mechanically regulates subcellular viscoelasticity.

METHODS

Bead coating

Unless otherwise stated, chemicals were purchased from Sigma (Saint Louis, MO). Covalent coupling of antibodies to fluorescent polystyrene beads was achieved using a carbodiimide kit by Polysciences (Warrington, PA) and following the accompanying instructions. Briefly, 0.5 ml of a 2% suspension of carboxylated 1.0-μm microparticles (FluoSpheres F-8820, Molecular Probes, Eugene, OR, a subdivision of Invitrogen, Carlsbad, CA) were subjected to a series of centrifugation washes followed by pellet resuspension in either a carbonate or a phosphate buffer. A 2% carbodiimide solution was then added dropwise to the redispersed pellet before end-to-end mixing of the solution of microspheres for 4 h. To remove unreacted carbodiimide, another cycle of centrifugation washes was performed. Next, 400 μg of antibodies were added to the fluorescent beads resuspended in borate buffer. The antibodies used were rat anti-mouse antiintegrin α_V, or rat anti-mouse anti-CD71 transferrin receptor, or mouse anti-mouse anti-VIA4-1 α-dystroglycan monoclonal antibodies (Chemicon, Temecula, CA). Covalent coupling was allowed overnight at room temperature with gentle mixing. Unreacted sites on the microspheres were blocked using ethanolamine, and nonspecific binding sites on the antibodies were blocked using bovine serum albumin. For the two-color microrheology experiments, the same protocol was followed to coat orange beads (FluoSpheres F-8820, Molecular Probes; 540/560 nm) with antibodies against transferrin receptors, and fuchsia beads (TransFluoSpheres T-8882, Molecular Probes; 543/620 nm) with antibodies against integrin receptors.

Cell culture

NIH 3T3 fibroblasts were grown in standard 100 mm × 20 mm cell culture dishes (Corning, VWR, West Chester, PA) in Dulbecco's modified Eagle's medium (Cellgro, Mediatech, Herndon, VA) supplemented with 10% fetal bovine serum (Invitrogen) and penicillin-streptomycin (100 units of penicillin per ml media, and 100 μg streptomycin per ml media) (Invitrogen). Cells were cultured at 37°C in 5% CO₂. The day before the fluorescence laser tracking experiments, fibroblasts were plated on 35 mm glass-bottom cell culture dishes (MatTek, Ashland, MA) coated with collagen I (1 μg/cm², Cohesion Tech, Palo Alto, CA). On the day of the experiments, the cell confluency had reached ∼60%; 1-μm or 2-μm fluorescent beads (F-8820 or F-8825, Molecular Probes) coated with antibodies were mixed to the growth media (at a concentration of 5 × 10⁵ microspheres/ml) and added to the plated cells for a period of either 30 min (for attachment to the cell membrane via surface receptors) or 24 hr (for bead attachment and ensuing endocytosis). Before the microrheology experiments, nonadherent beads were washed off with two washes using culture media.

To assess the influence of cytoskeletal components on the rheology of living cells, we treated fibroblasts with either of two cytoskeleton-disrupting drugs: cytochalasin D and nocodazole. Both pharmacological agents were dissolved in dimethylsulfoxide to yield stock solutions of 200–1000 times the working concentration, and further diluted in Dulbecco's modified Eagle's medium before being applied to cell monolayers. Fibroblasts were exposed for 30 min either to 10 μM cytochalasin D or to 17 μM nocodazole. Cells were finally washed with culture media immediately before FLTM experiments.

To examine the contribution of endocytotic organelles to the rheological information presented by endocytosed beads, we subjected fibroblasts to 100 μM chloroquine, an endosome-disrupting agent, for 3 h. Treated cells did not show any alteration in morphology or excessive mortality after 24 h incubation with chloroquine.

Although culture medium acidity was not controlled per se during FLTM experiments, its influence on cell viability is deemed to be similar on average under all chemical conditions, since the duration of the FLTM data acquisition was limited to 1 h per dish in all cases.

Fluorescent labeling of the cellular cytoskeleton

NIH 3T3 fibroblasts were cultured on fibronectin (4 μg/ml) coated glass-bottom culture dishes (MatTek) at 37°C in 5% CO₂ for 24 h. At room temperature, cells were then fixed with 3.7% formaldehyde in phosphate-buffered saline (PBS, Mediatech) for 10 min, washed twice with PBS, and extracted with 0.1% Triton X-100 in PBS for 5 min. To reduce nonspecific background staining, fixed cells were then incubated in PBS containing 1% bovine serum albumin (Polysciences) for 20 min before adding the cytoskeleton-staining agents. For F-actin labeling, cells were then incubated with 165-nM AlexaFluor 568 phalloidin (Molecular Probes) for 20 min and washed three times with PBS. For microtubule labeling, cells were incubated with 40 μg/ml of fluorescein isothiocyanate-conjugated anti-β-tubulin monoclonal antibodies for 60 min and washed three times with PBS.

To illustrate two-color fluorescence microrheology (see Fig. 5 A), fibroblasts were prepared as above, with an overnight incubation with both antiintegrin fuchsia beads and antitransferrin orange beads, and with a final actin stain using 165-nM AlexaFluor 532 phalloidin (Molecular Probes).

FIGURE 5.

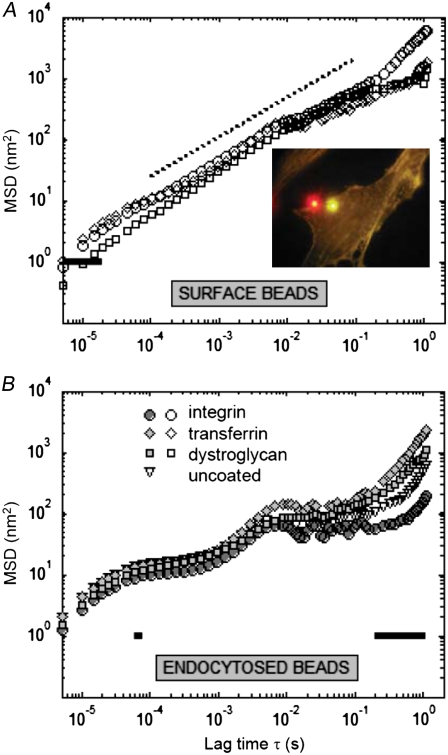
Influence of bead coating conditions on FLTM measurements depends on probe site on or in cells. Mean-squared displacements of surface (A) or endocytosed (B) 1-μm beads left uncoated (triangles) or coated with antibodies against integrin (circles), transferrin (diamonds), or dystroglycan (squares) receptors. Differences in MSDs were statistically quantified by the Kruskal-Wallis nonparametric test (P < 0.05, solid lines). Two distinct fluorescent tracers are clearly differentiated by eye (A, inset): NIH 3T3 fibroblasts were incubated overnight with both orange (540/560 nm) antitransferrin beads and fuchsia (543/620 nm) antiintegrin beads before being fixed and actin-stained with phalloidin Alexa Fluor 532.

Principles of FLTM

Both the principles of laser tracking microrheology and the instrumentation of these studies are explained in depth in the companion article (1). Briefly, the FLTM approach consists in monitoring the Brownian dynamics of a particle embedded in a viscoelastic material to probe the latter's rheology. From the trajectory of the particle, its mean-squared displacement can be calculated and the frequency-dependent complex shear modulus G*(ω) = G′(ω) + iG″(ω) deduced. G*(ω) characterizes both the solid-like (through its real part G′(ω), the storage modulus) and the liquid-like (through its imaginary part G″(ω), the loss modulus) behaviors of the material.

Instrument setup

Unless otherwise indicated, all measurements were performed at 37°C by means of a custom-made heating apparatus, and on vibration-isolating floating optical tables (TMC, Peabody, MA). All samples were ultimately prepared in cell culture dishes equipped with a glass bottom coverslip No. 1.0 of thickness 0.13–0.16 mm (MatTek). A schematic of the FLTM system is presented in Fig. 1 of the companion paper (1): A laser beam (1 in that figure) (532 nm from a Verdi Nd:YVO₄, Coherent, Santa Clara, CA) was collimated through a custom light path and a 100× NA 1.30 oil objective (2) (Olympus, Melville, NY) and illuminated a 100 μm × 100 μm area of sample positioned on the stage of an Olympus IX71 inverted microscope (3) and mounted on an xy piezoelectric nanopositioning system (Queensgate, Torquay, UK). The photons emitted by the fluorescent beads (4) contained in the excitation volume were filtered by a dichroic mirror-barrier filter combination (5) (Q560LP and HQ585/40m, Chroma Technology, Rockingham, VT) and detected after beam expansion (lenses from Thorlabs, Newton, NJ) by a quadrant photomultiplier tube (6) (Hamamatsu, Bridgewater, NJ). Position signals were inferred at the photomultiplier tube level from the difference in photocurrents between opposing pairs of quadrant elements, which were further amplified into digitized voltages by a 200 kHz 16-bit simultaneous four-channel analog-to-digital converter (ADC, Strategic Test, Stockholm, Sweden).

FIGURE 1.

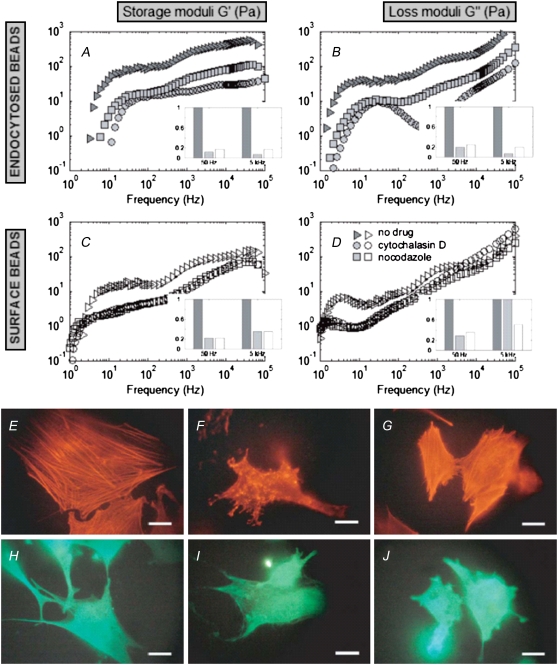
Effects of cytoskeleton-disrupting drugs on cellular rheology as evaluated by FLTM. From the MSDs of 1-μm fluorescent beads, either endocytosed by the cells (A and B) or attached to surface integrins (C and D), the fibroblasts' storage moduli G′(ω) (A and C) and loss moduli G″(ω) (B and D) were inferred. Fibroblasts were either left untreated (E and H, and triangles in A–D), or they were treated with cytochalasin D (F and I, and circles) or nocodazole (G and J, and squares). The four bar diagrams (insets A–D) reproduce G′ and G″ at ω = 50 Hz and ω = 5 kHz and illustrate the drop in cell stiffness and viscosity between untreated cells (dark shaded bars) and cells treated with either cytochalasin D (light shaded bars) or nocodazole (open bars); all heights are normalized to the untreated case. Fluorescent labeling of cytoskeletal networks after FLTM measurements (Alexa Fluor 568 phalloidin staining of F-actin, E–G, or fluorescein isothiocyanate-conjugated β-tubulin antibodies, H–J) confirmed that the drug cytochalasin D disrupted the actin filaments only (F and I), and that the drug nocodazole promoted depolymerization of the microtubules only (G and J). Scale bars are 20 μm.

Data acquisition and instrument calibration

Single fluorescent tracer particles of diameter 1 μm, trapped in viscoelastic samples, were positioned at the center of the detector's field of view. The centering procedure was fully automated by custom LabVIEW (National Instruments, Austin, TX)/C++/MATLAB (The MathWorks, Natick, MA) programs commanding and coordinating the Queensgate xy stage (for raster-scanning of successively smaller areas) and the ADC acquisition card (for fluorescent signal detection), and were carried out at very low illumination power (<5 × 10² W.m⁻², or 5 μW for the whole 100 μm × 100 μm excitation area) to avoid photobleaching of the probes. Once the bead was centered, its Brownian motion was monitored by FLTM for ∼1.5 s, under high illumination power (∼5 × 10⁵ W.m⁻²), at an ADC sampling rate of 200 kS/s. Calibration curves for FLTM (bead x- or y-position versus ADC signals) were obtained after each experiment for every bead. Calibration consisted in translating the bead along both detection axes (x, then y) using the high-resolution (0.5 nm) Queensgate xy stage and recording light distribution at each step. Tracking data acquired from the four photodetector quadrants were further analyzed and compared with the calibration data by a custom MATLAB code that established the beads' trajectories, mean-squared displacements (MSDs), and ultimately the viscoelastic materials' shear moduli G*(ω) using equations described in the companion article (1).

Statistics

The Wilcoxon rank sum test, or Mann-Whitney U test, was used to compare medians of distributions of i), MSDs of endocytosed beads with and without application of chloroquine, ii), MSDs of beads at 37°C versus room temperature, and iii), viscoelastic moduli as sensed by probes of diameter 1 μm vs. 2 μm. The significant differences between MSDs under different bead-coating conditions were assessed using the Kruskal-Wallis nonparametric test. These analyses were conducted with the MATLAB software, and P < 0.05 was considered statistically significant.

RESULTS

Subcellular mechanics under different chemical treatments

FLTM was used to probe living cells directly. Microrheological features were measured for NIH 3T3 fibroblasts plated at low confluence levels undergoing spontaneous migration. From the Brownian trajectory of 1-μm fluorescent beads either attached to integrins on the cells' plasma membrane or endocytosed by the cells, the MSDs of the probed particles were inferred and the cells' local shear moduli G*(ω), storage moduli G′(ω) (Fig. 1, A and C), and loss moduli G″(ω) (Fig. 1, B and D) deduced. For each of the two bead locations (on the cell surface or in endocytotic organelles) three conditions were examined: untreated fibroblasts (Fig. 1, triangles), fibroblasts treated with the actin-disrupting drug cytochalasin D (circles), and fibroblasts treated with the microtubule-disrupting drug nocodazole (squares). For these conditions, a total of 47 beads in 6 different dishes were analyzed for beads on the cell surface (17 beads in untreated cells, 14 beads in cytochalasin D-treated cells, and 16 beads in nocodazole-treated cells; Fig. 1, open symbols), and a total of 45 beads in 6 dishes were analyzed for endocytosed beads (14 beads in untreated cells, 14 beads in cytochalasin D-treated cells, and 17 beads in nocodazole-treated cells; solid symbols). Our sample preparation led to most cells containing a single fluorescent microsphere.

Untreated fibroblasts exhibit storage and loss moduli ranging between a few pascals and a few hundred pascals, for frequencies ω varying between 0.5 Hz and 50 kHz, regardless of the bead location (Fig. 1, triangles). (Explicit comparison of the rheological data yielded by beads positioned differently on the cytoplasmic membranes or within the cells will be addressed in a later paragraph.)

Disrupting F-actin with cytochalasin D or promoting microtubule depolymerization with nocodazole altered not only the cytoskeletal morphology (Fig. 1, E–J) but also the rheological profile of fibroblasts (Fig. 1, A–D). First, we verified that cytochalasin D disrupted the actin filaments but left untouched the microtubules of fibroblasts (Fig. 1, F and I), and that nocodazole affected the microtubules without affecting F-actin integrity (Fig. 1, G and J). Second, we found that disruption of the fibroblasts' cytoskeletal networks by either cytochalasin D or nocodazole resulted in less stiff (G′_drug < G′_untreated, Fig. 1, A and C) and less viscous (G″_drug < G″_untreated, Fig. 1, B and D) drug-treated cells as compared to untreated ones over the entire five-decade range of frequencies (0.5 Hz < ω < 50 kHz). These results were statistically significant (Mann-Whitney test, P < 0.05). The chemically induced viscoelastic alterations were more marked for endocytosed beads than for beads attached to cell surface receptors. More specifically, in the former case, a drop in cell stiffness by a factor varying between 4 and 20 across the frequency spectrum studied was accompanied by a fall in cell viscosity by a factor 4–50 (Fig. 1, A and B, respectively); and in the latter case the storage moduli decreased by a factor 2 at the high- and up to 9 at the low-frequency end of the spectrum, while the loss moduli diminished by a factor of 1–6 (Fig. 1, C and D).

Endocytosed beads directly probe the cytoskeletal mesh

To find out whether passive endocytosis of the probe particles was an adequate substitute for direct placement of the beads into the cytoplasm (by microinjection for instance), experiments were carried out with and without the endosome-disrupting agent chloroquine. In so doing, and basing our reflection on the assumption that large bodies (1 μm in diameter) would be enclosed extremely tightly in endocytotic vesicles after cellular uptake, we tested the hypothesis that endocytosed beads would yield a fair assessment of the local cytoskeletal properties, almost as if they were free of the extra organelle membrane wrapped around them.

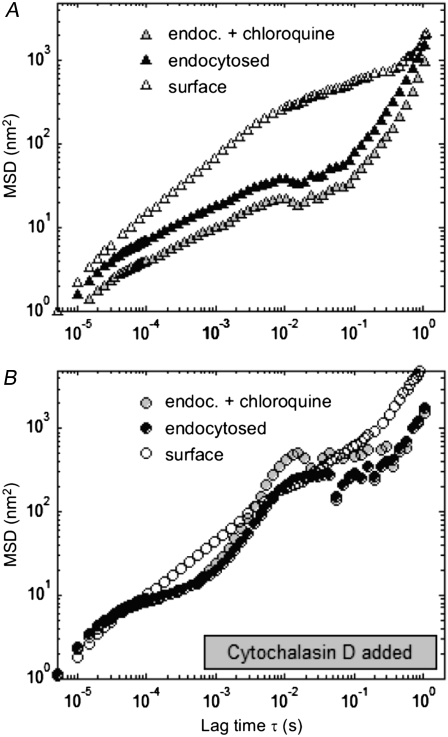
We looked at the displacements of 1-μm antiintegrin beads endocytosed overnight by fibroblasts, with or without the addition of chloroquine (Fig. 2, shaded and solid symbols, respectively). For reference, the MSD of surface beads attached to the cell's integrin receptors are also indicated (open symbols). Two cytoskeletal states were reviewed: either the cytoskeleton was left intact (9 endocytosed beads, 30 internalized beads in chloroquine-treated cells, and 41 surface beads, Fig. 2 A, triangles) or its actin microfilaments were disrupted by use of cytochalasin D (15 endocytosed, 25 internalized in chloroquine-treated cells, and 14 surface beads, Fig. 2 B, circles). In both cases, endocytosed beads exhibited similar behavior whether treated with chloroquine or not. In cells with undamaged cytoskeletons, the MSDs of internalized beads freed from endosomes after chloroquine treatment were lower on average, but of strikingly similar profile, than the MSDs of endocytosed beads (Fig. 2 A). After cytochalasin D treatment, the MSDs of the two types of beads inside the cells overlapped crudely at most time lags (Fig. 2 B). Under all these conditions, Mann-Whitney tests on the medians and t-tests on the averages of the data sets indicated that there were no statistically significant differences between the rheological parameters witnessed by the endocytosed beads and the internalized beads in chloroquine-treated cells (P > 0.05).

FIGURE 2.

Effect of the endosome-disrupting agent chloroquine on FLTM-based cytoskeletal rheology. Mean-squared displacements of 1-μm integrin-bound surface beads (open symbols), endocytosed beads (solid symbols), and beads having undergone endocytosis before being released into the cytoplasm by chloroquine (shaded symbols), in fibroblasts either left untreated (A) or subjected to the actin-damaging drug cytochalasin D (B). Mann-Whitney test-based statistics did not detect any significant differences between the profiles before and after chloroquine treatment (P > 0.05).

Effect of temperature on FLTM results

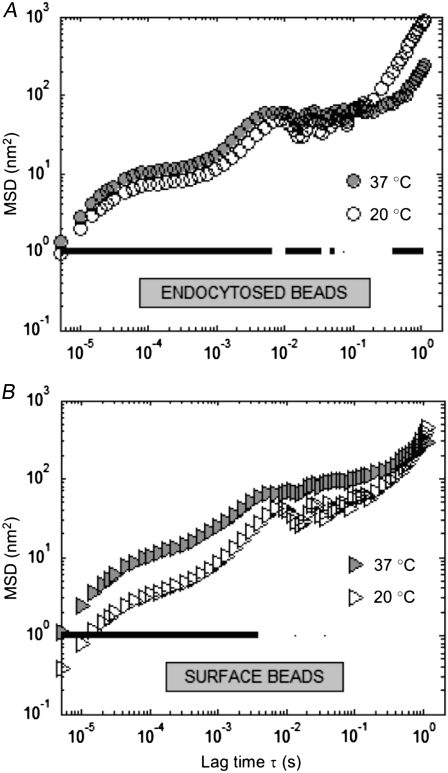
The effect of temperature on FLTM-probed microrheology was examined by measuring the Brownian motions of 1-μm fluorescent beads (coated with antiintegrin antibodies) in NIH 3T3 fibroblasts at room temperature (∼20°C) and at 37°C. The MSDs of 34 endocytosed beads in 2 dishes at 20°C, 34 endocytosed beads in 2 dishes at 37°C, 6 surface beads in 1 dish at 20°C, and 14 surface beads at 37°C were recorded. Fig. 3 presents the results, both for endocytosed probes (Fig. 3 A) and for probes attached to the cellular membrane via its anchored integrin receptors (Fig. 3 B). For both conditions and over an extended range of lag times (20 μs < τ < 0.1 s), particles exhibited larger motions at 37°C (Fig. 3, solid symbols) than at 20°C (open symbols). These differences in MSD profiles were found to be significant (P < 0.05) at most frequencies in the case of endocytosed beads, and for all lag times shorter than 5 ms in the case of beads on the cell surface (Fig. 3 A and B, thick solid lines). Working at the physiologically relevant temperature of 37°C was therefore proved to be important.

FIGURE 3.

Effect of sample temperature on FLTM measurements. Mean-squared displacements of 1-μm fluorescent beads either endocytosed by the cells (A) or attached to surface integrins (B) at 37°C (solid symbols) and 20°C (open symbols). Statistical comparison of the distributions' medians was performed using the Wilcoxon rank sum test, or Mann-Whitney U test (P < 0.05, solid line).

Effect of probe size on FLTM results

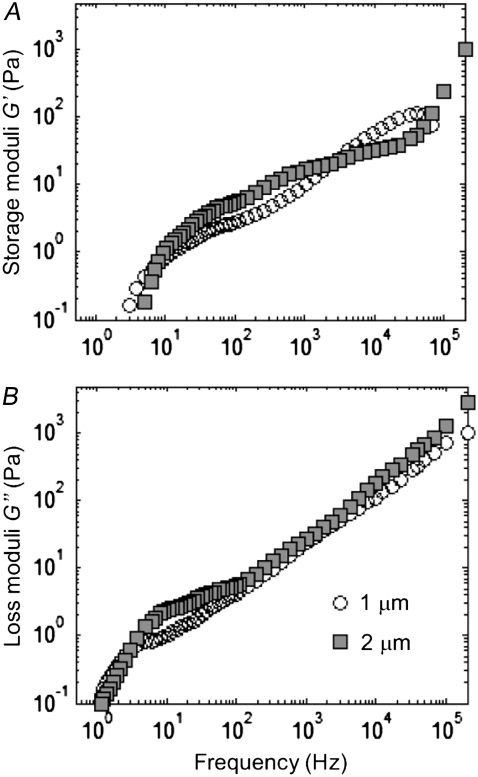
Laser tracking microrheology parameters (the storage and loss moduli G′(ω) and G″(ω)) should be independent of the diameter a of the spherical probe used, provided that it is much larger than the typical mesh size of the surveyed network (a ≫ ξ; see the Theory section in the companion article (1)). We checked this assertion in our FLTM queries by measuring cellular viscoelasticity using either 1-μm or 2-μm fluorescent beads, coated with antiintegrin antibodies and endocytosed by fibroblasts. Spheres of diameter a = 2 μm consistently displayed reduced MSDs as compared to 1-μm spheres (data not shown), but when processed to determine G′(ω) and G″(ω), these differences disappeared to give rise to statistically identical profiles for both the storage and the loss moduli (Fig. 4). Although the averages (over 13 1-μm and 12 2-μm beads, in a total of 4 dishes) differed somewhat across the five-decade frequency range assayed (Fig. 4 A and B, respectively), the two distributions of viscoelastic data were not observed to be statistically distinct.

FIGURE 4.

Effect of probe size on FLTM measurements. Fibroblasts' storage moduli G′(ω) (A) and loss moduli G″(ω) (B) were deduced from the MSDs of fluorescent surface beads of diameter 1 μm (open circles) or 2 μm (solid squares). Mann-Whitney tests did not disclose any statistically significant differences between the two data sets (P > 0.05).

Two-color fluorescence microrheology

To illustrate the benefits of a fluorescence implementation of a laser tracking microrheometer, we performed two-color experiments using two types of 1-μm fluorescent tracers: orange (excitation/emission maxima at 540/560 nm) beads coated with antibodies against the CD71 transferrin receptor and fuchsia (543/620 nm) beads coated with antibodies against the α_V integrin receptor. Both probes could be satisfactorily excited by the 532-nm laser, and a proper choice of barrier filter allowed for separate identification (Fig. 5 A, inset). The results from 27 antiintegrin beads (in 3 dishes) and 24 antitransferrin beads (in the same 3 dishes, on different cells) are presented in Fig. 5 A. The comparison of the average and standard deviation of the MSD of the two types of probes showed that beads attached to integrin and transferrin receptors exhibited very similar Brownian motions over a five-decade range of lag times (Fig. 5 A). Likewise, similar frequency-dependent storage and loss moduli G′(ω) and G″(ω) were observed, no matter what class of receptors was used to assess the cells' viscoelasticity. Both G′(ω) and G″ω) varied from ∼1 Pa at 1 Hz to 1 kPa at 50 kHz (data not shown).

Effect of bead coating on FLTM results

To further investigate the role played by bead coating in fibroblast rheology, we expanded the previous study and looked at i), uncoated beads, or beads coated with antibodies against ii), the α_V integrin receptor, iii), the CD71 transferrin receptor, and iv), the VIA4-1 α-dystroglycan receptor. This selection of coating proteins enabled us to test the hypothesis that FLTM conducted with probes targeted to cytoskeletally linked membrane receptors would show different cellular mechanical properties from the noncytoskeletally linked pool. Note that integrins and dystroglycans are directly and indirectly linked to the underlying intracellular cytoskeleton, whereas transferrins are not.

Microrheology was unaffected by bead coating when the beads were either attached to the cell surface or when the probes had undergone receptor-assisted endocytosis (Fig. 5). Fig. 5 A recounts the displacements of beads attached to the cell surface: 27 antiintegrin beads in 3 dishes (circles), 24 antitransferrin beads in 3 dishes (diamonds), and 8 antidystroglycan beads in 1 dish (squares); after 1 h incubation, uncoated beads were observed to adhere poorly to the cell membrane via unspecific interactions and were not monitored by FLTM. The MSDs of all these beads were found to exhibit a power-law scaling with MSD ∝ τ ^0.65 (Fig. 5 A, open symbols and dotted line). The Kruskal-Wallis nonparametric test confirmed that the minute differences between the “integrin”, “transferrin”, and “dystroglycan” curves bore no statistical significance except for lag times τ ∼ 10 μs (Fig. 5 A, solid black line). Therefore, 1-μm beads attached to the cell surface showed evidence of the same overall viscoelastic environment (cell's exterior and embedment region) regardless of the nature of the contact they had with the cell and through which they connected with the cell interior.

Likewise, endocytosed beads exhibited similar motions and FLTM outcomes regardless of their antibody coatings (Fig. 5 B). In these experiments, 27 antiintegrin (in 3 dishes), 10 antitransferrin (in 1 dish), 13 antidystroglycan (in 2 dishes), and 18 uncoated 1-μm beads were followed after being internalized by fibroblasts overnight. All four types of beads (“integrin”, “transferrin”, “dystroglycan”, and uncoated) displayed very similar Brownian motions over the frequency range considered (Fig. 5 B, circles, diamonds, squares, and triangles), except at its low end (∼0.5–5 Hz) where the discrepancies in MSDs were attested statistically significant (black solid line). Hence, it did not appear that bead coating had any influence over the manner in which the endocytotic vesicles interacted with the cytoskeleton.

Mechanotransductive effects of substratum rigidity

It is well known that the chemical properties of the substratum can regulate cellular responses (15). Moreover, recent studies have shown that substratum mechanical properties such as its geometry and rigidity also have profound effects on cell survival (16), differentiation (17), migration (18), morphology (19), and signaling (20,21). The importance of substratum and extracellular matrix mechanical properties in regulating a variety of physiological and pathological processes are being investigated (20,22). Recent advances in controlling substratum properties such as adhesion area and rigidity further provide important experimental handles for these studies (16,23,24).

It is not surprising that substratum mechanical properties also control intracellular rheological properties. Cellular shear modulus was found to be a biphasic function of substratum adhesion area with up to ∼5-fold changes in magnitude (25). Cells growing on tear-drop shaped substrata further adopt rheological characteristics of polarized cells, with the leading edge showing more than a twofold higher a modulus than the trailing edge (26). Recently, an interesting study systematically measured the modulus of fibroblasts on substrates with a wide range of stiffnesses and showed that fibroblasts adapt their cytoskeletal modulus to their environment such that they are always slightly less stiff than their substratum (27).

Although these studies are informative (25–27), these rheological measurements focus only on the low-frequency responses of the cellular cytoskeleton. The use of FLTM offers an opportunity to study the effects of substratum mechanical properties on cytoskeletal rheology over a broad frequency range elucidating strain relaxation mechanisms of the cytoskeleton and providing insights into the micromechanical reorganization of the cytoskeleton responsible for these responses.

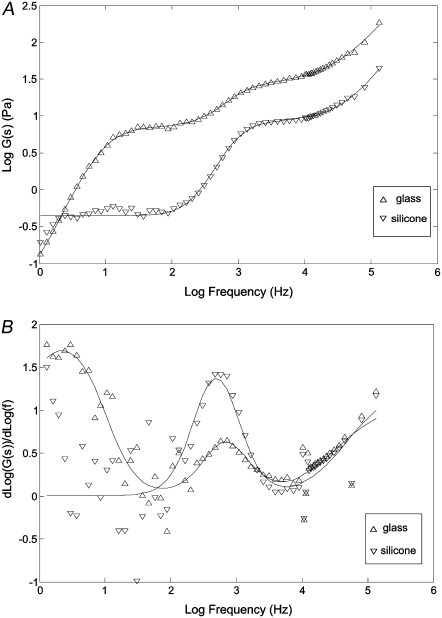
NIH 3T3 fibroblasts were plated on two substrates of very differing compliances: glass and silicone. One set of specimens was grown on glass coverslips of standard thickness No. 1.0 (or 0.13–0.16 mm, MatTek). Another set of specimens was grown on unstretched, flexible silicone membranes that were 0.005 inches in thickness (or 0.0125 mm, 40 duro gloss/gloss, material Q-7 4840, Specialty Manufacturing, Saginaw MI). Glass represents almost an ideal rigid substrate with a shear modulus on the order of 1–2 GPa significantly higher than the cellular modulus. The mechanical properties of the silicone substrate have been reported in the literature (28). Although the results of the measurements have fairly large uncertainties, the shear modulus of this material can be estimated to be between 1 and 5 kPa. The silicone membrane's modulus further can be modified by slight stretching but within a 1% strain, an upper experimental uncertainty in our measurements; the modulus uncertainty is easily within a factor of 2. Both surfaces were coated with collagen I (as described in the Cell culture section) before cell plating. Fig. 6 A represents FLTM findings in terms of shear modulus G(s), in the Laplace domain, as a function of frequency, extracted from data obtained from 30 beads in 3 different glass dishes, and 76 beads on 10 different silicone sheets. Due to the large distribution typically observed in cellular rheological properties (29,30), we reject outlier measurements by dropping 10% of the measurements in both glass and silicone specimens with the constraint of minimizing the standard deviations of the remaining data.

FIGURE 6.

Influence of substratum stiffness on FLTM measurements in fibroblast cells. (A) The shear modulus in the Laplace domain G(s) for cells grown on glass (triangles) and silicone (inverted triangles) substrates. The symbols are the actual data. The lines are fits to the model as described in the text and Table 1. (B) The derivative of the log shear modulus versus. log frequency for cells grown on glass (triangles) and silicone (inverted triangles) substrates. The symbols are the derivatives taken from the actual data points and the solid lines are the derivatives taken from the model fit.

The magnitudes of the shear modulus for these cells observed in lower frequency regime (100 Hz and below) are comparable to previous observations (31–34). As expected, significantly higher modulus is observed in cells on glass substrates than in cells attached to silicone surfaces at all frequencies inspected. At low frequencies (∼1 Hz), the shear modulus magnitude is almost 10 times larger than on silicone. The ratio of cellular cytoskeletal modulus, between ones grown on soft substrates and on glass, is comparable to the findings of Solon and co-workers (27).

The most surprising finding is the observation of multiple relaxation dynamics separated by two distinct plateau moduli for cells grown on the two types of substrate. For cells on glass substrates, the first plateau extends from 20 to 200 Hz with a second plateau extending from 1200 Hz to10⁴ Hz. For cells on silicone substrates, the first plateau extends from 2 to 200 Hz with a second plateau extending from 1600 Hz to 10⁴ Hz. The magnitude of the first plateau is 6 Pa for glass substrate and 0.6 Pa for silicone measured at 200 Hz. The magnitudes of the second plateau measured at 10⁴ Hz are 30 and 10 Pa for glass and silicone, respectively.

It is further interesting to observe the scaling behavior of the shear modulus as a function of frequency. Since the original data are quite noisy for accurate measurement, the data are fitted to a model of coupled relaxation processes characterized by stretch exponentials:

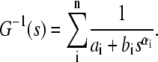(1)

The glass data are fitted to three coupled relaxation processes whereas the silicone is fitted to two relaxation processes. The calculated fits are superimposed onto Fig. 6 A. The fitted coefficients are shown in Table 1. The derivative of G(s) as a function of frequency is shown in Fig. 6 B. It should be noted that due to the presence of multiple relaxation mechanisms, the scaling coefficient never reaches a constant, even though G(s) was measured over five frequency decades. For the cells on the glass substrate, the shear modulus scales with frequency with a coefficient that reaches 1.75 before the first plateau; the transition region between the two plateaus has a maximum coefficient of 0.6; the scaling coefficient after the second plateau reaches ∼0.7. For the silicone membrane samples, we do not have sufficient low-frequency data to accurately measure the coefficient before the first plateau, but it appears to have a similar behavior as in the case of glass data; the transition region between the two plateaus has a maximum scale coefficient of 1.4 between the two plateaus; the scaling coefficient reaches 0.7 at high frequency.

TABLE 1.

Best fit parameters of shear modulus profile G(s) for cells grown on glass substrates versus silicone rubber substrates to a model of multiple coupled relaxation processes

Glass	ai	bi	αi
n = 1	0.02	1.08 × 10−1	1.88
n = 2	9.67	1.09 × 10−4	1.88
n = 3	28.5	1.84 × 10−4	1.10
Silicone	ai	bi	αi
n = 1	0.46	3.28 × 10−6	2.10
n = 2	8.52	4.65 × 10−6	1.34

This phenomenological fitting model, 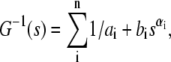has a simple explanation: the parameter n is the number of relaxation mechanisms, a_i sets the level of the plateau modulus, the ratio a_i/b_i approximately sets the critical frequency, and the parameter α_i sets the scaling coefficient. The number of relaxation mechanisms is set to 3 for glass specimens. This parameter is set to 2 for silicone specimens due to a lack of low frequency data. Since we are not fitting the low frequency data for the silicone specimens, that portion of the data is also not used for reduced chisq computation. The reduced chisq parameters for both fits are between 0.1 and 0.5. The reduced chisq values are lower than unity and this result is most likely due to correlation between data points and the non-Gaussian distribution of the variance at each frequency. It should be note that the chisq will worsen by an order of magnitude if α_i is fixed to 1, indicating that nonunity power law is an important feature of G(s).

DISCUSSION

FLTM is what we believe to be a novel method that can assess the local, frequency-dependent mechanical properties of living cells. This device overcomes the low light intensities inherent in fluorescence-based instrumentation and is capable of nanometer-scale spatial sensitivity at speeds up to 50 kHz (1). As a result, materials as stiff as several hundred pascals (measured by G*(ω)) can be accurately studied, which proves to be appropriate for cells in the frequency regime covered in typical FLTM experiments.

Our choice of fluorescent beads (1 μm in diameter) ensures that these probes are large enough to yield an adequate photonic signal, yet small enough to be easily endocytosed by cells. This bead size is also well suited for probing polymer networks of mesh size ∼1–10 nm (polyacrylamide gels) (1) as well as ∼10–100 nm (cellular cytoskeleton). Subdiffusive behavior of the probe particles was observed at all lag times between 20 μs and 0.2 s, supporting the assumption that 1-μm beads are effectively confined by a partially elastic solid network as opposed to freely percolating. At larger timescales (τ > 0.5 s), Brownian motion may not be predominant anymore and active transport poses some limit to single-particle tracking devices: directed motion by intracellular transporters is likely to be occurring (although this question has not been explored in this work), resulting in the tracer's superdiffusivity (e.g., Fig. 3). This likely explains the anomalous and variable behaviors seen in many of the results at long lag times (low frequencies). However, the whole cell migratory motion is believed to not influence significantly the particle's motion over the course of the FLTM experiments. Not only was spontaneous fibroblast migration speed observed to be on the order of a nanometer per second only (or a few microns per hour, that is to say too small to appreciably interfere with the probe's Brownian motion), but additionally, there was no manifest directional persistence standing out within the trajectories of tracked beads, which appeared instead generally compacted around their origin.

Since FLTM spans a widespread frequency range (∼0.5 Hz–50 kHz), the system provides considerable insight into frequency-dependent network dynamics. Evaluating over five decades of frequency the variations of cellular viscoelasticity against that of actin filament networks, one can estimate the total actin concentration (35), and its polymerized (36), cross-linked and bundled forms in cells (37). By acquiring data near 50 kHz, FLTM can measure the impact of individual chain motion on the polymeric mesh's rheology (13) and potentially help relate biological results to findings from reconstituted networks (14,29,34,38).

In NIH 3T3 fibroblasts, the values obtained by fluorescence laser tracking microrheology for viscoelastic moduli are similar to those reported in the literature: G′(ω) and G″(ω) vary from 1–10 Pa around 1 Hz to ∼100 Pa around 1 kHz and ∼500–1000 Pa around 50 kHz, which concurs with results in COS7 kidney epithelial cells by laser deflection single-particle tracking (14), in Swiss 3T3 fibroblasts by video-based multiple particle tracking (39), in neutrophils by optical trapping (40), in NIH 3T3 and SV-T2 fibroblasts by optical stretching (41), and in J774 macrophages by magnetic tweezers manipulation (42) and video-based multiple particle tracking (43). Twisting magnetocytometry using 4.5-μm magnetic beads and atomic force microscopy (AFM) tend to lead to higher moduli, for instance in alveolar epithelial cells and in aortic smooth muscle cells (44–47), a discrepancy that has yet to be fully explained. It has been conjectured that the micromechanics probed by magnetic twisting manipulation and cantilever poking in AFM may be different from those probed by passive microrheology (39,48,49). In the case of AFM, it has been suggested that the deformation of the cell's plasma membrane itself was responsible for additional cell stiffening upon cell thrusting in AFM assays (48). Another difference may lay in the fact that AFM measurements tend to focus on lamellipodia of cells that are oftentimes the stiffest regions. This difference between passive rheology measurements and AFM measurements is also seen when comparing our results with Solon and co-workers (27). Although we measure similar differences in modulus ratios between glass and soft substrates, the absolute magnitudes of the shear moduli measured are very different. As for magnetic twisting cytometry, uncertainty remains as to i), the accuracy of mechanical models and their parameters needed to calculate cellular rheology from the measured bead rotation, ii), the consequences, from a cell signaling standpoint, of applying to the cell an external force, and iii), the potential effects of artificially triggered clustering of signaling receptors and cytoskeletal elements by the attachment of such a large particle to the cellular membrane via its integrin receptors. This latter artifact could also affect the results reported here, but to a lesser extent due to the size of the bead.

Because it is a single-particle tracking microrheology technique with fluorescence-based molecular specificity, FLTM is well suited to study different regions within the cell and to detect local viscoelastic fluctuations possibly varying from site to site. In that respect, knowledge gained through FLTM is distinct from and complementary to the bulk rheology information bestowed by two-point microrheology modules. All single-particle methods have the distinct disadvantage, however, that they are influenced by active motions, as is likely responsible for the low-frequency behavior in Figs. 1 and 4. Another related limitation of FLTM should be mentioned: Because FLTM is a single-particle tracking method, there exists an inevitable dead time between tracking individual beads, which stems not only from the innate duration of a single given experiment, but also from the time to manually finding the next fluorescent bead to be monitored. Altogether, these intervals amount to ∼3 min elapsing between two tracking experiments. FLTM is therefore not optimally suited to follow in real time the kinetics of cells responding to sudden stimuli such as a bolus drug input or a step mechanical input. Further, similar to other single cell measurement methods, biological noise, defined as variance from cell to cell, is often significant. FLTM relies on averaging data from multiple probe particles on multiple cells; to account for this, biological noise and the typical data acquisition window are of 60–90 min for each experimental condition.

Our FLTM analysis of NIH 3T3 fibroblasts under diverse chemical treatments showed a clear frequency-dependent effect of cytoskeleton-disrupting drugs on cellular viscoelasticity (Fig. 1). These rheological modifications by cytochalasin D and nocodazole, respectively promoting depolymerization of F-actin and microtubules (as demonstrated by fluorescent imaging of fixed cells, Fig. 1, E–J) were consistent with changes in cell mechanics when the cytoskeleton was altered. They support the hypothesis that both actin and microtubule networks contribute to cellular rigidity. This statement is still controversial: some (50) allege that isotropic F-actin networks alone are sufficiently strong to withstand extracellular stresses and to stabilize cells, whereas others (35) reject this possibility and argue that F-actin acts in concert with other filamentous proteins and with actin-binding proteins to generate sufficient cellular rigidity.

With fluorescent microspheres linked to integrins at the cell surface or endocytosed by the cell, FLTM yielded findings in agreement with those from other rheological techniques, namely that the disruption of cytoskeletal filaments by cytochalasin D or nocodazole caused the viscoelastic moduli G′(ω) and G″(ω) to drop. FLTM via endocytosed beads saw the application of these drugs accompanied by a decrease in G′(ω) by a factor of 4–20, and in G″(ω) by a factor of 4–50, for frequencies 0.5 Hz < ω < 50 kHz (Fig. 1, A and B). FLTM via surface beads revealed only a slightly smaller decline on average (up to a factor 9) of these storage and loss moduli subsequent to chemical treatment (Fig. 1, C and D). To cite a few examples from the literature, Valentine et al. (30) reported that nocodazole, like latrunculin B, reduces G′(ω) 10 times in Xenopus laevis eggs; Yanai et al. (40) reported that nocodazole and cytochalasin D make both G′(ω) and G″(ω) drop by a factor 1.5–3 in leukocytes; Fabry et al. (44) reported that cytochalasin D reduces both moduli in human airway smooth muscle cells; Rotsch and Radmacher (49) reported that the Young modulus E of fibroblasts becomes smaller upon disturbance of F-actin by cytochalasin B or D, latrunculin A, or jasplakinolide.

The introduction of probe particles into cells has been a topic of concern to many: The probe should minimally impact the otherwise normal cellular activities and reactions, and the information it conveys should be well enough defined on the molecular level to tease out true cellular behaviors from probing artifacts. In the field of cellular microrheology, for instance, the parameter of interest is the viscoelasticity of the intracellular cytoskeleton, but it has primarily been characterized by techniques using extracellular probes interacting with the cell membrane (40–42,45,51–53). Intracellular probes used in the past were either endogenous but ambiguously identified lipid structures (14) or fluorescent polystyrene beads of very small size (∼10–100 nm) and thus weakly trapped in the cytoskeletal mesh (54). In this study, we used 1-μm fluorescent intracellular probes and compared their rheological readouts to those from beads attached to the cell surface. Note that direct injection of the beads into the cytoplasm would ensure direct probing of the cytoskeleton's viscoelastic properties. This option, although tedious, was attempted, but to no avail: Although intracellular delivery of 1-μm beads was achieved (custom capillaries of sufficient aperture were pulled and adapted into a commercial microinjection system), few of the injected fibroblasts survived.

Endocytosis was considered next. This route for transferring 1-μm beads into the cytoplasm is easy and harmless to cells, which are able to ingest the spheres within a few hours and continue to grow, migrate, and divide (data not shown). However, a drawback of endocytosis is the presence of a lipid enclosure around each individual bead once it has entered the endocytotic vesicle. Questions thus arise as to i), whether such endocytosed beads may be influenced by the viscoelastic milieu inside the endosomes in addition to the cytoskeleton, and ii), whether the tethering of such endocytotic organelles to microtubule and actin structures via motor or structural proteins might affect the beads' motions and compromise interpretation of cell rheological properties. Endocytosis appeared to be a satisfactory surrogate for direct injection. First, as confirmed by electron microscopy, 1-μm beads are large enough that they are tightly enveloped within the endosome. Thus, we anticipate that their Brownian motions would be minimally affected by the contents of the endosomes; instead, they more likely reflect interactions with the cytoskeletal network. Second, treating the cells with chloroquine bore out that these endocytosed particles undergo the same mean-squared displacements inside endocytotic pockets as they do once released in the cytoplasm (Fig. 2). The drug chloroquine alters the pH in endosomes where it tends to be sequestered and ultimately causes their contents to escape into the cytosol. We verified that the compound was efficient at rupturing the endosomic system by fluorescence imaging: Whereas untreated fibroblasts labeled with LysoTracker (Molecular Probes) showed numerous and bright endosomic structures, chloroquine-treated cells appeared much dimmer with sparse and diffuse fluorescence (data not shown). Fig. 2 demonstrates that endocytosed beads (solid symbols) and internalized beads in chloroquine-treated cells (shaded symbols) experience intracellular movements that are statistically equivalent over all timescales. The two types of beads yielded similar cytoskeletal rheologies in untreated as well as in cytochalasin D-treated fibroblasts (Fig. 2, A and B, respectively), thus reiterating the soundness of the endocytosis approach for FLTM experiments. Third, we perceived that active transport by molecular motors did take place in cells and influence the motions of the 1-μm probes (at τ > 100 ms), but this phenomenon occurred both with beads encapsulated in endocytotic vesicles and beads released into the cytoskeleton by chloroquine (subdiffusive behavior, or slope >1 in a log-log plot of MSDs versus lag times, in Fig. 2 A). On that note, we also verified that the intracellular location of the particles at time of measurement did not significantly affect FLTM results. For instance, beads located in the perinuclear region (where most probes are likely to be arrested after 24 h internalization and chloroquine treatment) showed statistically identical rheological profiles as beads spatially closer to the outer plasma membrane.

Surface beads coated with receptor antibodies showed displacement profiles distinct from those of intracellular beads (Figs. 2 and 5). More specifically, their motions were repeatedly reminiscent of constrained diffusion, with MSDs approximately following a power law trend (MSD ∝ τ ^0.65, Fig. 5 A). Analysis of cellular rheology using data gathered with membrane-tethered beads is complicated by several factors including the extent of bead-receptor adhesion, the influence of cell membrane, the nature of the receptor-cytoskeleton connections, and interactions with ambient media (55). The similarity in MSD of beads attached to integrin, transferrin, and dystroglycan receptors (Fig. 5 A) and their statistical equivalence suggest that this last actor may play a paramount role in dictating surface beads' motions. Effectively, neither the nature of the receptor protein nor its anchorage in the cytoskeleton seemed to matter (integrin and dystroglycan receptors are directly and indirectly bound to actin fibers; transferrin receptors are not); the viscous extracellular environment would determine predominantly the degree of movement of surface beads. Another factor that might influence the loss modulus is the transient formation and rupture of receptor-ligand bonds. Although the magnitude of this effect is not known, it would presumably introduce an additional dissipative mechanism since the energy stored in an extended receptor protein would be lost when the bond ruptures.

In Fig. 2 B, as well as in later instances (Figs. 3 and 5), oscillations in the MSD plots can be observed at ∼30 Hz (or τ = 3.3 × 10⁻² s) and ∼60 Hz (or τ = 1.7 × 10⁻² s, consistent with the first harmonic) were discovered that correspond to the mechanical vibrations observed in the building and its electronic components (see the Instrument Optimization section in Jonas et al. (56)). Although mechanical damping by floated optical table partially alleviated this problem, occasional large amplitude disturbances cannot be completely eliminated as they are transmitted acoustically. This artifact introduces some noises in the data at the aforementioned frequency range and can be eliminated by digitally filtering. However, since it does not affect the conclusions drawn from the data, we prefer to present the data in the least manipulated state.

Although experimental variables such as methods of tracer introduction, tracer size, tracer adhesion site, or temperature, may influence one-point microrheology measurements, to date their effects had not been evaluated. We provided in this article a systematic study of some of these key variables.

We were able to demonstrate the dependence of viscoelastic moduli on temperature and bead size. Both endocytosed and surface beads (coated with antibodies against integrins) exhibited larger displacements at 37°C than at 20°C (Fig. 3, A and B). This divergence was statistically significant at all lag times in the former case and for τ < 5 ms in the latter case. This observation emphasized the importance of conducting experiments at the physiological temperature of 37°C, which was accomplished by means of a homemade heating cap dipped in the sample holder. Likewise, we used statistical tools to compare the storage and loss moduli G′(ω) and G″(ω) measured by beads of diameter 1 μm and 2 μm. Fig. 4, A and B, show their behaviors to be similar, which was substantiated by the Mann-Whitney and the t-tests (P > 0.05). A correlate of the observed independence of FLTM on bead size is that attachment of a bead to the cell surface and the reorganized cytoskeleton beneath apparently had no perceptible effect on the measured cell rheology. Probe particles in the submicron range were not used in these studies. Not only did they not yield adequate fluorescence signals for FLTM tracking at the instrument's nominal speed of 50kHz, but most importantly, beads smaller than 500 nm in diameter were observed to diffuse notably and incessantly throughout the latticework inside the cell rather than be appropriately trapped within the cytoskeletal meshwork to effectively assess the latter's rheology.

Additionally, we demonstrated some of the advantages of this fluorescence laser tracking microrheometer over its white-light counterparts: because the spectral signatures of fluorescent beads of different colors could be readily distinguished (Fig. 5 A, inset), different membrane receptors could be studied on the same cell (Fig. 5 A). Naturally, similar studies could be conducted in white-light laser tracking microrheometers (for instance with beads of different diameters coated with different ligands) but the distinction of separate fluorescent colors makes FLTM more convenient in addition to ensuring identical experimental conditions (preparation chemistries, cellular treatments, and monitoring constraints). Using this method, we tested the hypothesis that rheological measurements critically depend on the specific receptor-probe linkages. Two-color FLTM agreed with previous findings (52) in so far as we found that integrin- and transferrin-mediated FLTM yielded similar viscoelasticity profiles in NIH 3T3 fibroblasts: the MSDs of the fuchsia and orange beads (Fig. 5 A), as well as the deduced storage and loss moduli, overlapped closely.

FLTM proved suitable for interrogating the dependence of rheological measurements on bead coating, a subject of concern to many researchers (29,57–60). As it tracks single particles, as opposed to multiple particle tracking methods, FLTM determination of cell rheology is based on probing local microenvironments and may be influenced by local perturbations such as adhesion effects. We used 1-μm fluorescent beads either uncoated or functionalized with one of three types of antibodies: against α_V integrin receptors, against CD71 transferrin receptors, or against VIA4-1 α-dystroglycan receptors. Integrins are a class of transmembrane glycoproteins, composed of a heterodimer of noncovalently linked α- and β-subunits (61,62). Integrins bind to components of the extracellular matrix (such as fibronectin, collagens, or laminins), and, through a short cytoplasmic domain, are connected to the intracellular actin microfilaments and interact with signaling cytoplasmic proteins. Transferrin receptors facilitate transport of iron-bound transferrin into the cell by clathrin-mediated endocytosis. They have been shown to circulate freely in the membrane over short time frames and to undergo hop diffusion according to a mosaic compartmentalization model of the cell membrane (63). Lastly, dystroglycans are laminin-binding receptors composed of two subunits, α- and β-dystroglycans, with the α-subunit located outside the cell and the transmembrane β-subunit linked indirectly to the cytoskeleton via dystrophin/utrophin molecules (64). Accordingly, this combination of bead coating conditions allowed us to test whether cytoskeletally linked probes would be subjected to viscoelastic milieus different from other probes'.

Different probe locations led to comparable answers regarding the influence of bead coating on FLTM results (Fig. 5). On the one hand, surface beads seemed to witness the same global rheological microenvironment regardless of their coating proteins (Fig. 5 A). Their respective MSDs overlapped considerably and were proportional to lag times to the power 0.65. As discussed above, this hinted at the preponderance of viscous effects from the extracellular medium (over those from probe-surface linkages and internal cytoskeletal networks). On the other hand, endocytosed beads reported similar rheological surroundings notwithstanding their coating molecules (Fig. 5 B): antiintegrin, antitransferrin, antidystroglycan, and uncoated probes underwent analogous MSDs. This last result concurs with the reported masking by endocytotic membranes of nanoparticles' surface chemistries and disparities in cytoskeletal binding (60). These FLTM data, even though they do not unearth the biochemical pathways at play, suggest that intracellular handling of the endocytotic vesicles ends up being independent of the receptors that initially mediated the engulfment and that these molecules may not remain anchored to the compartment membranes but rather be recycled or degraded.

Fig. 6 presents a plot of the shear modulus magnitude G(s) over a five-decade frequency range showing significant differences in rheology between cells grown on glass versus silicone. Fibroblasts demonstrate much higher stiffness and viscosity on the more rigid, glass substrate than on the more flexible, silicone rubber substrate. These data suggest that cells adjust their internal rheology to the mechanical properties of the surroundings they are presented. These results recapitulate some of the conclusions by Solon and co-workers (27) but at the same time provide important insight into the origin of this variation in mechanical properties.

The most interesting observation is the multiple modulus plateaus observed. Maggs (65) has suggested two plateau moduli should be seen in actin melts: One plateau would originate from the entropic confinement of the actin filament in the melt and the second plateau would be attributed to actin's longitudinal elasticity. This explanation is unlikely to account for our observations due to the highly cross-linked nature of the cytoskeleton and the differences in the expected timescales of these phenomena. Nonetheless, the coupling of multiple relaxation mechanisms occurring at very different timescales, as suggested by Maggs (65), may be responsible for the multiple plateau moduli observed in G(s).

Cells grown on glass substrates show a power law modulus increase at low frequency with a coefficient of up to 1.8. As for cells grown on silicone substrates, we do not have sufficient low-frequency data to accurately determine the coefficient of this scaling behavior, but it appears to be similar to the glass case. A low-frequency quadratic response is often associated with a Doi-Edward-type orientational relaxation process (66). However, for the cytosol, this relaxation mechanism is less likely because actin filaments are therein highly cross-linked. However, this timescale may be sufficiently long to allow dynamical binding and unbinding of actin cross-linking proteins, and this mechanism may enable some orientational reorganization of the actin filaments. Another, more likely, explanation may be that a single-particle tracking method is sensitive to the presence of cellular active dynamical processes such as transport by molecular motors, which may be responsible for this observation (67). An understanding of this low-frequency relaxation mechanism will require future experimental and theoretical investigations.

Focusing on the low-frequency plateau region, we observe that the plateaus for cells grown on glass and silicone substrates both terminate at ∼200 Hz with a subsequent power law scaling of the moduli close to the range between 0.75 and 1.25. Given the timescale and the scaling coefficient, one may suggest that this plateau and the subsequent power law scaling behavior are due to coupled transverse and longitudinal vibrational modes of the actin filament as suggested by Gitts et al. and Pasquali et al. (68,69). These theories suggest the presence of a low-frequency elastic plateau due to the elastic deformation of the actin filament. Beyond a critical frequency ω₁ (corresponding to the lowest vibrational mode of the actin filament clamped at both end by entanglement), the vibrational modes dissipate energy via viscous drag and show a power law scaling with increasing frequency. The Gitts theory predicts a ω^3/4 scaling accounting for only transverse modes whereas the Pasquali theory predicts a ω^5/4 scaling corresponding to a coupling of transverse modes with a longitudinal relaxation constraint. The greater-than-unity scaling coefficient is more consistent with the silicone data whereas the lower coefficient is more consistent with the glass data. Both theories predict the critical frequency ω₁ to occur at

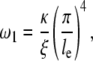(2)

where κ is the bending modulus, ξ is the drag coefficient, and l_e is the entanglement length. For actin filaments, many of these coefficients are known. The bending modulus is equal to kTl_p where l_p is the persistence length, ∼17 μm. The bending modulus is ∼7.3 × 10⁻²⁶ Nm². The drag coefficient is ∼0.0023 Nsm⁻² for a 5-nm diameter actin filament. The measured critical frequency of 200 Hz suggests an entanglement length of 2 μm. It is interesting to note that both cell types, either grown on glass or on silicone substrates, have very similar ω₁. Although parameters such as bending moduli may change due to actin bundling proteins, the simplest explanation of the result may be that actin's bending modulus, drag coefficient, and entanglement length are relatively independent of substrate choices.

Although the critical frequencies are almost identical for cells grown on either substrate, the magnitudes of the plateau moduli are different by a factor of almost 10. The plateau module, G_b, can be expressed as

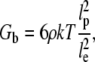(3)

where ρ is the spatial density of actin filaments (68). Besides the entanglement length that we assume to be constant between specimens of glass and silicone substrate (see the discussion about ω₁), the only free parameter in this equation is the spatial density. One would conclude that cells on glass substrates have a 10-fold higher actin spatial density. Since the actin spatial density is defined as the number of actin filaments per unit area, the actin mass density should scale approximately as 3/2 power with the actin filament spatial density. This predicts an increase in actin mass density by a factor of 30. The increase in actin content of cells is also reported in Solon et al. that found an actin mass increase by almost 50-fold for cells grown on 0.7 kPa vs. 15 kPa substrates (27). Since no three dimensional measurement of cell size is provided by Solon et al., a quantitative comparison is not possible. This result is also consistent with experiments showing that cellular shear modulus is correlated with intracellular filamentous actin concentration with a power law dependence (25,26).

This actin transverse bending relaxation mechanism is mechanically coupled to the lower frequency mechanism that exhibits almost quadratic power law scaling. At frequencies when the shear modulus due to the quadratic power law mechanism exceeds G_b, materials must relax via transverse bending of the actin filament resulting in an overall elastic plateau. Therefore, the difference in the onset frequencies for the plateaus in the glass and silicone rubber cases is rather trivial as it basically correlates with the change in the plateau magnitudes.

It is also interesting to consider the difference in scaling coefficients between the two plateaus for the glass and silicone specimens. The glass specimens exhibit almost 3/4 scaling whereas the silicone specimens appear to scale as 5/4 power. There may be two possible explanations for this difference. One possibility is that the glass specimen may experience less longitudinal constraint than the silicon specimen. However, given the similar entanglement lengths and higher actin density in the glass specimen, this possibility is deemed very unlikely. Another explanation may be that, in the glass case, the smaller magnitude difference between the first and second plateau moduli does not allow a sufficiently accurate measurement of scaling over a short transition region of less than two decades.

Gitts, Pasquali, and co-workers in a series of articles explored a second higher critical frequency, ω₂, above which longitudinal relaxation cannot occur and actin vibrations relax only transversely (69):

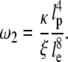(4)

This frequency corresponds to the spectral region of the second plateau and a transition where the scaling coefficient changes from 5/4 to 3/4. Using values of entanglement length obtained from considering the low-frequency plateau, ω₂ can be estimated to be ∼10 kHz, which corresponds to the location of the second plateau. This frequency is consistent with the observation that the shear moduli for both glass and silicon specimens scale with a coefficient of ∼0.75 above the second plateau. The existence of the second elastic plateau is, however, less well understood. The correlation with ω₂ suggests that this plateau may be related to mechanisms where strain is stored elastically, for instance through deformation of the cytoskeletal cross-linking proteins that restrict the longitudinal motion of filaments.

In conclusion, FLTM, benefiting from spatial and temporal sensitivities of 4 nm and 20 μs and sampling five decades of frequency (0.5 Hz–50 kHz), is a passive microrheology technique well suited to investigate biological problems, as illustrated here by its ability to quantitatively characterize i), the effect of cytoskeleton-disrupting drugs on cellular viscoelastic profiles, ii), the difference between intracellular and surface fluorescent probes, iii), the impact of bead-coating proteins on rheological results, and iv), the effect of substratum rigidity on cellular mechanical property. Most importantly, the extended frequency range of this instrument allows us to quantitatively study the different coupled strain relaxation mechanisms responsible for the rheology of the cytoskeleton. Although some features of the complex rheological profiles of the cytoskeleton appear to be well explained by existing theories, future experimental and theoretical investigations are required for a complete understanding of this important biological system.