Abstract
One of the most dominant methods cells use for a large class of cellular processes is reaction (or binding) diffusion kinetics, which are controlled by kinetic constants such as diffusion coefficients and on/off binding rate constants. Fluorescence recovery after photobleaching (FRAP) can be used to determine these kinetic constants in living cells. While an analytic expression for FRAP formulae for pure diffusion has been available for some time, an analytic FRAP formula for the binding diffusion model has not been reported yet. Here, we present an analytic FRAP formula for the binding diffusion model in an explicit form allowing for diffusion of the bound complex for either a uniform circle laser profile or a Gaussian laser profile.
The binding kinetics of proteins play important roles in biological processes such as cellular/nuclear signal transduction, cell regulation, transcriptional regulation, and the immune response depending on binding targets (1–2). Formally, these processes can be described by the equation
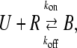 |
(1) |
where U and R denote unbound molecules and specific binding sites or receptors, and B denotes bound complexes (UR).
Fluorescence recovery after photobleaching (FRAP) provides an excellent way to study binding kinetics in vivo (3–7). For the case of pure diffusion, several analytic formulae have been derived that can be used to extract the diffusion coefficients (6,7). However, in reality, both binding kinetics and diffusion are responsible for the recovery in some cases, especially for the binding of soluble proteins to DNA or membranes (5,8). Thus, FRAP data also have to be interpreted as a combination of these two processes. Previously, several studies have computed binding rate constants from FRAP by data fitting (3–5). Some studies were devoted to simplification of the binding diffusion model depending on the size of the parameters (3,4). Although a Laplace transform of the solution of the binding diffusion model was reported (3), to our knowledge no analytic FRAP formula for the binding diffusion model in an explicit form has been reported so far. Moreover, the Laplace transform solution is limited to the case of a uniform circle laser profile, and also does not allow for diffusion of the bound complexes. Here, we present a closed-form analytic expression of the FRAP formula for the binding diffusion model.
To write differential equations for Eq. 1, let us consider the following a first-order reaction diffusion equation of ligand-receptor type binding. As is common in some classical articles (6,7), we assume that the bleaching spot size is small so that we can treat cells as an infinite plane and guarantee full recovery. We also assume that the receptor density is high enough so that a pseudo association rate constant 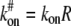 is constant. For typographical simplicity, we will drop the term # and use kon to represent
is constant. For typographical simplicity, we will drop the term # and use kon to represent  Now, for kon, koff, D1, D2 > 0, and D1 > D2, consider the following binding diffusion model in an infinite plane,
Now, for kon, koff, D1, D2 > 0, and D1 > D2, consider the following binding diffusion model in an infinite plane,
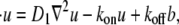 |
(2a) |
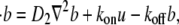 |
(2b) |
where u = ∂u/∂t and ∇2 = (∂2/∂x2 + ∂2/∂y2) with initial conditions,
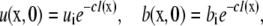 |
(3) |
where x is used to represent (x, y). In Eq. 3, for the laser parameter c, the laser I( ) can be either a uniform circle profile (6,7),
) can be either a uniform circle profile (6,7),
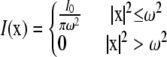 |
or Gaussian laser profile,
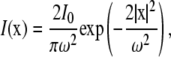 |
where I0 is the total laser power and ω is either the radius of the laser (uniform circle profile) or the half-width at e−2 height (Gaussian laser profile). Notice that in both cases, we have 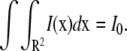
The solution to Eq. 2 for the initial conditions given by Eq. 3 has been found by Aifantis and Hill (9,10) as
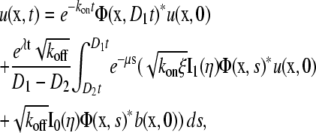 |
(4a) |
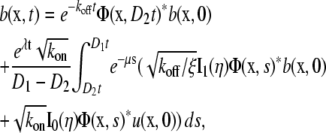 |
(4b) |
where
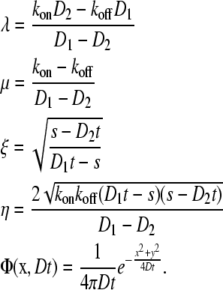 |
In Eq. 4, I0 and I1 are modified Bessel functions, and * represents convolution. Notice that Φ is the fundamental solution of the diffusion equation,
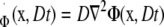 |
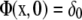 |
for Dirac delta function δ.
We now use this solution to derive the FRAP formula for the binding diffusion model. FRAP formulae for u and b are given by
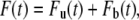 |
(5a) |
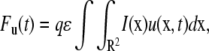 |
(5b) |
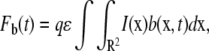 |
(5c) |
where Fu(t) and Fb(t) are fluorescence intensities of unbound and bound molecules. The parameter q is the product of all the quantum efficiencies of light absorption, emission, and detection and ɛ is the attenuation factor of the excitation laser beam (6).
By plugging Eq. 4 into Eq. 5, we obtain
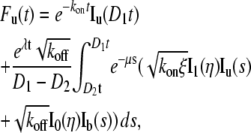 |
(6a) |
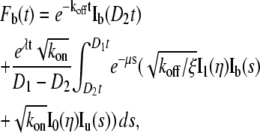 |
(6b) |
where
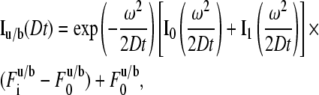 |
(7) |
for the uniform circle laser profile (7) where 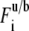 is prebleach fluorescence intensity of u and b and
is prebleach fluorescence intensity of u and b and 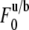 is postbleach fluorescence intensity of u and b.
is postbleach fluorescence intensity of u and b.
For the Gaussian laser profile (6),
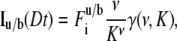 |
where 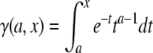 is the incomplete γ-function, ν = (8Dt/ω2+1)−1 and K is computed from the fraction of pre- and postbleach fluorescence intensities as
is the incomplete γ-function, ν = (8Dt/ω2+1)−1 and K is computed from the fraction of pre- and postbleach fluorescence intensities as
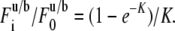 |
The value 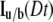 also can be represented as a series as shown in Axelrod et al. (6).
also can be represented as a series as shown in Axelrod et al. (6).
Finally, we can write the FRAP formula for the binding diffusion model as
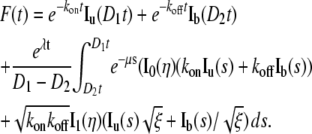 |
(8) |
Notice that the integral terms have a time-dependent integration domain [D2t D1t], which can be converted to [D2 D1] by a change of variable s = st (see Supplementary Material, Data S1 for details).
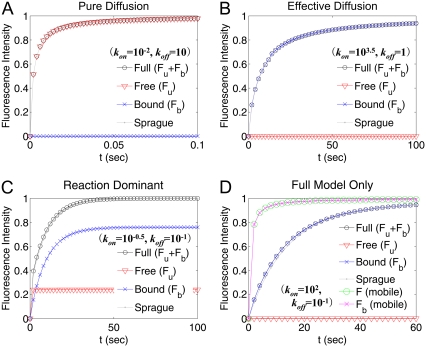
Having derived a FRAP formula for the binding diffusion model, we next plotted FRAP curves for four different regimes of parameters and compared our results with those of Sprague et al. (3). For computation and plotting, built-in functions of MATLAB 7 were used (see Data S1). In Sprague et al. (3), it was shown that the binding diffusion model can be categorized into four submodels:
Pure diffusion dominant.
Effective diffusion.
Reaction dominant.
Full model only, assuming D2 = 0.
When the free pool (u) is large (kon/koff ≪ 1), the pure diffusion dominant model is observed, while the reaction dominant model is observed when the bound pool (b) is large and the binding event occurs relatively slowly compared to diffusion (konω2/D ≪1). On the other hand, the effective diffusion model holds when the binding event occurs rapidly relative to diffusion (konω2/D ≫1).
Because the uniform circle laser profile was assumed in Sprague et al. (3), we used Eq. 7 and Eq. 8 for comparison. Since D2 = 0 was assumed in Sprague et al. (3), a very small value of D2 was chosen (D2 = 10−4 μm2/s) for our calculation. Fig. 1 demonstrates that the FRAP formula we derived can generate the four different subtypes of FRAP curves by the binding diffusion model.
FIGURE 1.
FRAP curves generated by Eqs. 5 and 6 for four different sets of parameters and comparison with the results of Sprague et al. (3). D1 = 30 μm2/s, D2 = 10−4 μm2/s, and ω = 0.5 μm were used. The values kon and koff are indicated in each figure. The FRAP curves from Sprague et al. (3) are denoted. (A–C) All the parameter values are from Sprague et al. (3). (D) the FRAP curve for D2 = 10−1 μm2/s (F (mobile), Fb (mobile)) was also plotted to study the role of diffusion of receptor-bound complexes.
Moreover, our results indicate that for submodels with a large binding pool (-x- in Fig. 1, B–D), diffusion of the bound complexes (∼0.1 μm2/s) can significantly contribute to the FRAP. To show this, D2 = 0.1 μm2/s was chosen and a FRAP curve was replotted in Fig. 1 D (F (mobile) and Fb (mobile)). Indeed, when diffusion of the bound complexes is included, the resulting FRAP curve recovers much faster than for an immobile complex.
In conclusion, we have derived a closed-form analytic FRAP formula of the binding diffusion model allowing for diffusion of bound complexes as well as free molecules. The FRAP curve generated by our formula exactly matches the existing FRAP formula (3). However, our formula has several advantages over Sprague et al. (3), not only from the mathematical point of view but also from a practical point of view. First of all, our formula provides solutions for both the uniform circle laser profile and the Gaussian laser profile. Secondly, it allows for diffusion of bound complexes, which may play an important role in FRAP in major cases of the binding diffusion model.
SUPPLEMENTARY MATERIAL
To view all of the supplemental files associated with this article, visit www.biophysj.org.
Acknowledgments
This work was supported by American Cancer Society-Institutional Research grant (No. IRG-58-009-48), the Sartain-Lanier Family Foundation, and grant No. RO1 GM07846.
Editor: Michael Edidin.
References
- 1.Eyster, K. M. 2007. The membrane and lipids as integral participants in signal transduction: lipid signal transduction for the non-lipid biochemist. Adv. Physiol. Educ. 31:5–16. [DOI] [PubMed] [Google Scholar]
- 2.Montell, C., and P. Devreotes. 2004. From protein dynamics to animal behavior: new insights into complex cell regulatory mechanisms. Curr. Opin. Cell Biol. 16:115–118. [DOI] [PubMed] [Google Scholar]
- 3.Sprague, B. L., R. L. Pego, D. A. Stavreva, and J. G. McNally. 2004. Analysis of binding reactions by fluorescence recovery after photobleaching. Biophys. J. 86:3473–3495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Carrero, G., D. McDonald, E. Crawford, G. de Vries, and M. J. Hendzel. 2003. Using FRAP and mathematical modeling to determine the in vivo kinetics of nuclear proteins. Methods. 29:14–28. [DOI] [PubMed] [Google Scholar]
- 5.Hinow, P., C. E. Rogers, C. E. Barbieri, J. A. Pietenpol, A. K. Kenworthy, and E. DiBenedetto. 2006. The DNA binding activity of p53 displays reaction-diffusion kinetics. Biophys. J. 91:330–342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Axelrod, D., D. Koppel, J. Schlessinger, E. Elson, and W. Webb. 1976. Mobility measurement by analysis of fluorescence photobleaching recovery kinetics. Biophys. J. 16:1055–1106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Soumpasis, D. M. 1983. Theoretical analysis of fluorescence photobleaching recovery experiments. Biophys. J. 41:95–97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Goodwin, J. S., K. R. Drake, C. Rogers, L. Wright, J. Lippincott-Schwartz, M. R. Philips, and A. K. Kenworthy. 2005. Depalmitoylated Ras traffics to and from the Golgi complex via a nonvesicular pathway. J. Cell Biol. 170:261–272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Aifantis, E., and J. Hill. 1980. On the theory of diffusion in media with double diffusivity. I. Basic mathematical results. Q. J. Mech. Appl. Math. 33:1–21. [Google Scholar]
- 10.Hill, J., and E. Aifantis. 1980. On the theory of diffusion in media with double diffusivity. II. Boundary-value problems. Q. J. Mech. Appl. Math. 33:23–41. [Google Scholar]