Morphological Transitions of Vesicles Induced by Alternating Electric Fields

Abstract

When subjected to alternating electric fields in the frequency range 10²–10⁸ Hz, giant lipid vesicles attain oblate, prolate, and spherical shapes and undergo morphological transitions between these shapes as one varies the field frequency and/or the conductivities λ_in and λ_ex of the aqueous solution inside and outside the vesicles. Four different transitions are observed with characteristic frequencies that depend primarily on the conductivity ratio λ_in/λ_ex. The theoretical models that have been described in the literature are not able to describe all of these morphological transitions.

Living organisms including ourselves are permanently exposed to electromagnetic fields of different strength and frequencies. These fields can be generated by various sources such as radio transmitters, power transmission lines, cellular phones, home appliances (e.g., bluetooth devices, remote controls, microwave ovens), etc. We investigate the effects of alternating electric fields on model membranes. The question “how cells respond to such fields?” has been addressed in several previous studies. In some of these studies, cells have been found to orient parallel or perpendicular to the field direction (1,2), others report that cells deform in electric fields (3,4). This difference is probably due to the membrane elasticity and coupling to the cytoskeleton as well as to the excess membrane area. The orientation of the cells in the field was found to depend on the solution conductivity (1,2). Similarly, the direction of elongation of the deformed cells is influenced by the external conductivity (4). In the following study, we aimed at drawing an overall picture of the spectrum of responses of model membranes to alternating electric fields at various field frequency and conductivity conditions. For this purpose, we used giant unilamellar vesicles.

When vesicles are subjected to electric fields, a transmembrane potential builds up across their membrane inducing an effective electrical tension (5,6). Consequently, spherical vesicles deform assuming ellipsoidal shapes. Initiated by the seminal work of Winterhalter and Helfrich (7), this effect has been studied theoretically by several groups (8–10). Lipid vesicles deformation was predicted to depend on the conductivity ratio x ≡ λ_in/λ_ex, where λ_in and λ_ex are the conductivities of the solutions inside and outside the vesicle, respectively. Only a few experiments with direct observation on vesicles have been carried out so far, and mainly in a small range of frequencies (between 2 × 10³ and 2 × 10⁵ Hz) and with x ≅ 1 (7,10). For various frequencies of the applied field, vesicles in pure water (x ≅ 1) have been observed to attain oblate and prolate shapes (9). Experiments with salt containing vesicles suspended in salt solutions, which is a biologically relevant condition, as well as the case x < 1 have not been explored so far. In contrast, we will consider conditions of various internal and external conductivities and investigate a wide range of alternating current (AC) field frequencies (i.e., from 10² Hz to 10⁸ Hz).

Giant unilamellar vesicles were prepared from egg yolk L-α-phosphatidylcholine (Avanti Polar Lipids, Alabaster, AL) using the electroformation method (11). The preparation procedure and the observation chamber were reported previously (6) and are described in detail in the Supplementary Material (Data S1). Vesicles made of other lipids such as dioleoylphosphatidylcholine and stearoyloleoylphosphatidylcholine, as well as diblock copolymers, showed similar behavior. The salt concentrations inside and outside the vesicles were varied between 0.01 and 100 mM corresponding to a large interval of conductivity ratios x = λ_in/λ_ex. The observation chamber with two parallel cylindrical electrodes was purchased from Eppendorf (Hamburg, Germany).

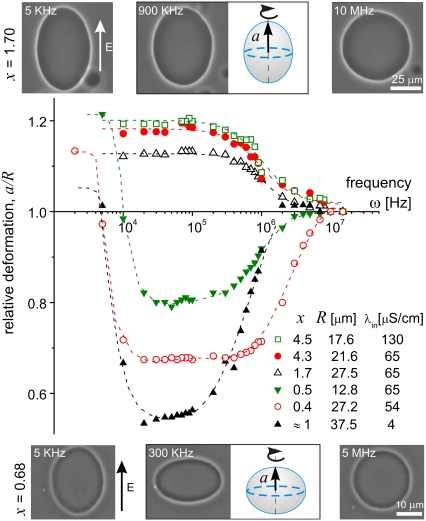
Before applying the field, the vesicles are spherical (tense) or quasispherical (with visible thermal fluctuations). Only the top view of the vesicles is accessible for observation but one can distinguish the various shapes taking into account the symmetry around the axis parallel to the field direction. The vesicle morphologies were characterized by the relative deformation, a/R, where a is the axis of the vesicle in the field direction (Fig. 1) and R is the radius.

FIGURE 1.

Deformation of vesicles subjected to AC fields (E = 0.2 kV/cm). For conductivity ratio x > 1, the vesicles undergo prolate to sphere transition with increasing field frequency. For x < 1, two successive, prolate to oblate and oblate to sphere transitions are observed. The size of the symbols reflects the measurement error. The dashed lines are guides to the eye. Snapshots of two vesicles with different x-values are given above and below the figure. Schematic drawing of the vesicle shapes at intermediate frequency are given with indication for the semi axis a. The field direction is indicated with an arrow.

Fig. 1 presents some examples for the dependence of the vesicle deformation as a function of the conductivity ratio x and the field frequency ω. For x > 1 the vesicles assume prolate shapes for low and intermediate frequencies, and above ≅3 MHz the vesicles become spherical. When x < 1 the vesicles again assume prolate shapes for low frequencies and spherical shapes for the high frequency region, but the vesicles have oblate shapes for intermediate values of ω between ∼5 KHz and 5 MHz. For ω < 2 KHz, observations are difficult because of vesicle movement due to dielectrophoretic forces (in this region the vesicle shape can be also influenced by the hydrodynamic flow). In the case x ≅ 1 for intermediate field frequencies, coexistence of prolate and oblate shapes is observed (examples for both cases are given in Fig. 1 (open circles) and in the Supplementary Material, Data S1).

Theoretical prediction for the dependence of the vesicle deformation on the field frequency has been reported earlier in the work of Winterhalter and Helfrich (WH) (7). The WH-model predicts only prolate deformations and considers only the case of symmetric conditions inside and outside the vesicle (x = 1). Vesicles of radius R = 1 μm were predicted to assume prolate shapes and the deformation was estimated to be ∼0.1 μm (yielding a/R = 1.1). However, the model gives unreasonably large deformations for larger vesicles because the deformation was predicted to scale with R⁴ (the analytical expression for the deformation and comparison with the experimental data are given in the Supplementary Material, Data S1). In addition, according to the WH model, the vesicle deformation monotonically increases with the frequency, which is not what one experimentally observes (Fig. 1).

Recently, the WH-model has been further extended to account for possible anisotropy in the dielectric constant of the membrane (10). This approach resulted in predicting the prolate to oblate transitions at low frequency and x ≅ 1 (Fig. 1, open circles). However, unusually high values for the membrane conductivity were needed to correctly explain the transition frequency. In addition, this model does not consider the dependence of the transition on the conductivity inside and outside the vesicles.

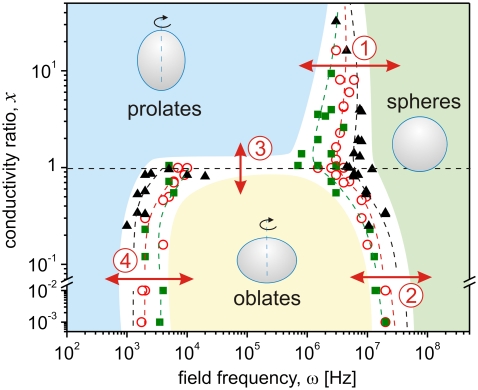
We observed more than 60 vesicles at different conductivity conditions to construct a morphological diagram of shapes subjected to AC fields of varying frequency. The vesicle radii ranged between 4 and 50 μm. The data were collected starting at ω = 20 MHz for decreasing frequency ω. The reverse type of measurement did not show hysteresis in the data. The data sets are grouped in Fig. 2 according to the conductivity of the internal solution (note that single value of x describes cases of both high and low internal conductivities as long as the ratio with the external one is the same). Whereas the transition from prolate to oblate for x < 1 is relatively sharp (it is completed within a couple of KHz; see Fig. 1), the transition to sphere, for arbitrary x, is smooth and covers an order of magnitude in the frequency scale. The frequency for the transition from sphere to prolate or oblate was determined from the onset of deviation from sphere scanning down from higher frequencies. Thus, the error of detecting this frequency is set by the optical resolution. To mimic physiological conditions we have explored a couple of cases where the external salt solution has been set up to ∼100 mM, expanding the range of x down to 10⁻³ (note the break in the ordinate in Fig. 2). The trend in the frequency dependence of the deformation was preserved.

FIGURE 2.

Morphological diagram of lipid vesicles subjected to AC fields of various frequency ω at different conductivity ratios x = λ_in/λ_ex. The internal conductivity λ_in in units μS/cm is: 15 (squares), 65 (open circles), and 130 (triangles). The dashed lines are guides to the eye, and the shaded areas indicate zones of specific morphology (see text for discussion on the four types of transitions).

Four types of transitions can be distinguished as indicated with arrows and numbers in Fig. 2. At high frequency and for arbitrary conductivity condition, the vesicles assume spherical shapes (transitions from prolate to sphere and from oblate to sphere, labeled by (1) and (2), respectively). The frequency of these transitions increases with increasing the internal (and external, for constant x) salt concentration because the pressure, and thus the vesicle deformation, increases with the ion concentration. A simple reasoning explaining the transition to a sphere at high frequency (several MHz) is that the ions in the solution can no longer follow the field oscillations and thus, the vesicles are no longer deformed. Such high frequencies correspond to travel distances of the ions of the order of nanometers, which is not enough to induce detectable deflection of the membrane.

The third type of transition we consider occurs at intermediate frequencies ω between a few KHz and several MHz when crossing the conductivity condition x ≅ 1 (see Fig. 2 (3) for transition). The vesicles assume prolate shapes for x > 1 and oblates for x < 1. Again, a simple interpretation for this type of transition can be given by considering the ionic pressure on the membrane. For x > 1, the pressure inside the vesicle exerted by the ions when the field is on, is higher than the external one, because the ion concentration inside is higher. This leads to a force elongating the vesicle along the direction of the field. In the opposite case, the higher ion concentration in the external media causes compression of the vesicle from the outside, thus leading to oblate deformation.

The fourth type of transition, which like the first one is also frequency induced, is observed only for x < 1 (indicated with (4) in Fig. 2). The vesicles undergo prolate to oblate shape changes at frequencies on the order of a few KHz. As discussed above, this frequency-induced shape transformation is least understood. It has been investigated by a few groups (9,10) but mainly vesicles in water solution were studied, where x ≅ 1. The transition has been interpreted as an effect due to a change of the water media from the conductive regime (low frequencies) to the dielectric regime (high frequencies) (9). Another attempt involved finding the steady-state solutions of the dynamical equations determined by the electric field inside and around a vesicle (8). The anisotropy in the dielectric constant of the membrane was also considered (10). However, none of the models is able to describe all four morphological transitions as a function of ω and x.

Finally, the reported morphological diagram calls for a novel and comprehensive theoretical approach, able to explain all observed behaviors. We envisage two possible approaches. One involves expanding the WH-model to include for conductivity asymmetry across the vesicle membrane and for frequency dependence of the conductivity. The second is based on calculating both the electric and hydrodynamic stresses exerted on the membrane. We currently pursue work in these directions. The interpretation of these shape transitions is relevant to the morphological changes observed in cells.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.