An Osmoregulatory Basis for Shape Oscillations in Regenerating Hydra

Abstract

The freshwater polyp Hydra has considerable regeneration capabilities. A small fragment of tissue excised from an adult animal is sufficient to regenerate an entire Hydra in the course of a few days. During the initial stages of the regeneration process, the tissue forms a hollow sphere. Then the sphere exhibits shape oscillations in the form of repeated cycles of swelling and collapse. We propose a biophysical model for the swelling mechanism. Our model takes the osmotic pressure difference between Hydra's inner and outer media and the elastic forces of the Hydra shell into account. We validate the model by a comprehensive experimental study including variations in initial medium concentrations, Hydra sphere sizes and temperatures. Numerical simulations of the model provide values for the swelling rates that are in agreement with the ones measured experimentally. Based on our results we argue that the shape oscillations are a consequence of Hydra's osmoregulation.

INTRODUCTION

The freshwater polyp Hydra (see Fig. 1 A) has captured the interest of the scientific community since J. Trembley discovered its astonishing regeneration capabilities in 1744. Since Hydra can be cultured in the laboratory and is accessible to various experimental procedures, it has become a standard model organism in developmental biology.

FIGURE 1.

(A) Adult Hydra vulgaris. (B and C) Example of the swelling-collapse oscillations during regeneration at T = 20°C. The snapshots in panel B show: 1), the initial fragment of tissue folding to form a sphere; 2), inflation stage; 3), critical inflation and rupture of the Hydra shell; and 4), collapse, healing, and beginning of a new inflation cycle.

The most remarkable feature in Hydra development is the animal's considerable regeneration potential. A small fragment excised from the body column of an adult animal (as small as 1–5% of the original tissue size) regenerates to form a complete animal in ∼48 h. Even an aggregate of previously dissociated Hydra cells regenerates successfully in the course of a few days (1,2). For a small fragment of tissue, a complex mechanism of tissue bending and healing leads to the formation of a hollow sphere made of a cell bilayer. During the subsequent development, the sphere breaks the initial spherical symmetry with the formation of a new body axis and, at later stages, the regeneration is completed with the formation of tentacles, mouth, and foot. In the case of aggregates, however, at first ectodermal and endodermal cells sort out according to their origin, then a hollow shell arises and regeneration is completed following the same process described above. If enough tissue is present, typically a unique head is formed; nevertheless, for large aggregates multiple heads and feet may appear.

During the last few decades, researchers have focused on the details of the molecular biology involved in Hydra regeneration and embryogenesis. A multitude of genes and peptides regulating development have been discovered and their interrelationship is starting to be understood (3–7). Furthermore, Hydra's unique biology has recently caught the attention of scientists from other disciplines. Among other topics, they studied body plan maintenance (8–11), minimal tissue size for regeneration (12), cavity formation (13,14), cell motility during embryogenesis (15), cell sorting (16–20) and axis formation (21) during regeneration, and regulatory networks involved in regeneration (22,23).

We are interested in a phenomenon occurring during regeneration of a small fragment of tissue and cell aggregates. After the hollow sphere has formed, the shell undergoes a series of cycles of steady inflation followed by a sudden collapse, as shown in Fig. 1, B and C.

These oscillations were first reported by Beloussov et al. (24). A more detailed experimental study was provided by Sato-Maeda and Tashiro (13). They described a sudden change in the amplitude of inflation and frequency of the oscillations during regeneration, which was followed by a change in shape toward an oblong cell ball at a later stage. Mombach et al. (14) described the formation of the hollow sphere and the subsequent oscillations with a numerical algorithm of the cellular Potts model type in two dimensions. Fütterer et al. (25) performed a Fourier analysis of the oscillating spheres and showed that a transition from elastic isotropy (where the cell ball becomes more spherical upon inflation) to elastic anisotropy (where the cell ball becomes more oblong upon inflation) starts simultaneously with the reported switch in the amplitude of inflation and frequency. Fütterer et al. (25) suggested that the elastic asymmetry could be a sign of axis formation, an idea that was later confirmed by Soriano et al. (21).

Despite these efforts, neither the mechanism nor the role of the oscillations has yet been clarified. This is even more puzzling if we consider that the oscillations consume energy at a time when Hydra cannot feed. Furthermore, it has not been explained why the sphere inflates almost linearly in time and with a remarkable periodicity, especially taking into account the significant increase in radius during swelling, which often exceeds 25% of the initial radius.

In this work, we propose that the oscillations are a by-product of Hydra osmoregulation. We will support this view by ideas from the literature, experiments with oscillating Hydra in different culture media, and a mathematical model. All relevant model parameters could be estimated from the literature. Experimental results and numerical simulations are consistent.

BIOLOGICAL BACKGROUND

Since Hydra lives in fresh water, it shares the osmotic problems of other fresh water animals (26), namely that the osmolarity of the tissue exceeds the osmolarity of the surrounding medium. Therefore, water constantly enters the tissue. This water must be removed to prevent swelling of the cells and subsequent rupture. The mechanism of water removal was studied by various authors (27–29). Benos et al. (27) found that osmoregulation is achieved by vacuoles in the cells that are connected by channels to the inner cavity of Hydra, the so-called enteron. The authors argued that Hydra constantly deposits ions in these vacuoles; consequently, water flows into the vacuoles and is transported to the enteron. If the vacuole fluid were ejected directly to the outside medium, the ions in the fluid would be lost. Since they are transported into the enteron, Hydra has the possibility to reabsorb some of the ions. This is indeed the case for potassium ions, which are present in the enteron fluid only in small amounts. Thus, the enteron fluid is hyposmotic to the tissue fluid. Sodium, on the other hand, is not reabsorbed, but constantly taken up from the outside medium, as shown by studies using radioactive sodium isotopes (29).

This mechanism leads to an ongoing flow of ions and water from the outer medium into the Hydra enteron. In a normal Hydra, the excess fluid in the enteron is removed by spontaneous contractions, ejecting the fluid through the mouth opening. It was shown in Benos et al. (27) that the frequency of these contractions decreases with increasing osmolarity of the outer medium.

In regenerating Hydra, a mouth opening and a functioning nervous system is still not present. Therefore, excess fluid in the enteron cannot easily be removed. Hydra continues to swell until rupture of the body wall tissue takes place. This way the fluid is ejected through the rupture, the Hydra ball collapses, the wound heals and the process starts anew. A similar behavior is observed in the so-called epithelial Hydra (animals that have a mouth but no nervous system) (30,31). These Hydra cannot contract and hence they also swell until the increased internal pressure is released through the mouth.

METHODS

Hydra culturing

All experiments were carried with strains of Hydra vulgaris. The animals were cultured at 18°C in Hydra medium (1.0 mM CaCl₂, 1.5 mM NaHCO₃, 0.1 mM MgCl₂, 0.08 mM MgSO₄, and 0.03 mM KNO₃), fed regularly four times a week, and starved for 24 h before manipulation for experiments.

Preparation of Hydra spheres

Fragments were prepared following the procedure described in the literature (21,25). Thin disks of tissue were cut from the body column of an adult Hydra. The disks were then split into 4–8 fragments to select different sizes. The fragments closed to form hollow spheres, with initial radius R₀ in the range 90–250 μm. Larger spheres were obtained from aggregates of dissociated Hydra cells, prepared as described in the literature (1,17).

To study the evolution of the spheres with different inner and outer concentrations 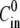and 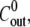each fragment was immersed, immediately after cutting, in a chamber containing the medium at the inner concentration and left for 4 h until the hollow sphere emerged. Since the sphere forms through a mechanism of tissue bending and healing, the medium inside the shell after closure is the same as the one at its surroundings. The sphere was next transferred to the recording chamber, consisting of a 30-mm-diameter petri dish that contained the medium at the outer concentration To ensure that variations in the outer concentration were negligible, the chamber contained 5 ml of outer medium (a volume ∼5 orders-of-magnitude larger than the typical volume of a Hydra sphere).

Experimental setup and data analysis

Between 5 and 10 spheres were placed together in the recording chamber, which was sealed to prevent evaporation. A thermal bath maintained the chamber at constant temperature T. The evolution of the spheres was monitored using a charge-coupled device camera mounted on an inverted microscope (Carl Zeiss, Oberkochen, Germany) with a 5× objective, and snapshots of the regenerating Hydra were obtained at 3 min interval with a spatial resolution of 1.8 μm/pixel. The images were later analyzed to extract the in-plane contour of the Hydra spheres, using the same procedure described in the literature (13,21).

The radius R of the sphere at time t was defined as the radius of the circle with the same area as the contour analyzed. To compare spheres of different sizes, we chose the radius at the beginning of the recording as the characteristic radius of the sphere, i.e., R₀ = R(t = 0).

The R(t) plots provided the basis for the analysis of the inflation-collapse oscillations under diverse experimental conditions. We explored different Hydra sphere sizes R₀, regeneration temperatures T (in the range 6–34°C), and a number of inner and outer initial concentrations and As a standard procedure, different initial concentrations were obtained by adding sucrose to Hydra medium (29). We explored concentration differences between −100 mM and 100 mM.

EXPERIMENTAL RESULTS

The R(t) plots were carefully studied and spheres that did not complete regeneration (typically those with μm) were excluded from further analysis. The study of the inflation-collapse oscillations was restricted to the isotropic phase only, i.e., before axis formation (Fig. 1 C).

Examples of inflation-contraction cycles at different concentrations 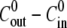are shown in Fig. 2 A. For clarity, data is shown only from the formation of the sphere to axis formation. Spheres continue to oscillate until they complete regeneration. In general, the qualitative behavior of the oscillations is the same for all combinations of inner and outer mediums. It is characterized by periodic cycles with swelling almost linear in time. The swelling rate strongly depends on the difference between the osmolarity of the inner and outer concentrations, and 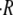gradually decreases as the concentration difference grows.

FIGURE 2.

(A) Examples of oscillations (from the beginning of regeneration to axis formation) at T = 20°C and for gradually higher osmotic difference showing that the slope 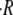decreases with (B) Values of the averaged swelling rate 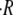along four consecutive cycles and for three different osmotic concentration differences. Each point is an average over four spheres with initial sizes R₀ in the range 150–200 μm. The cycles are limited to four since this is the maximum number of common cycles in all the spheres. The measured swelling rates for are approximately constant from cycle to cycle, while for the swelling rate of the first cycle is much higher than the rest. (C) Linear dependence of the swelling rate 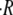on the initial radius of the sphere R₀. Each point is an average over four cycles. T = 20°C. (D) Dependence of the swelling rate 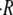on temperature. Each point is an average over six spheres of sizes in the range 130–150 μm, and over four cycles per sphere. The curve is an exponential fit. The experiments in panels C and D were carried out with Hydra medium as initial inner and outer concentrations. HM denotes Hydra medium and Suc sucrose solution in Hydra medium.

The swelling rate 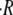was measured by fitting the inflation stages to straight lines, as shown in Fig. 2 A. We observed that for 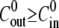the swelling rate is constant in the course of the oscillations and therefore 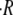can be averaged over all cycles (Fig. 2 B). On the other hand, for 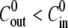sucrose is ejected out of the sphere after the first collapse. Hence, only the first cycle is actually driven by the strong concentration difference, as shown in the top panel of Fig. 2, A and B. The subsequent cycles have similar swelling rates, with values that approximate the ones measured for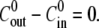

The swelling rate also depends on two other major parameters, namely the initial size of the sphere R₀ and the regeneration temperature T. As shown in Fig. 2 C, the dependence of 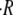on initial radius is well described by a linear relationship. The dependence of 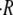on temperature is shown in Fig. 2 D. For spheres with similar initial radius R₀ = 130–150 μm and Hydra medium as inner and outer concentrations, we measured a swelling rate of 1.8 μm/h at 6°C, which increased to 6.8 μm/h at 20°C and to 30.5 μm/h at 28°C. We studied in total six different temperatures and observed that the variation of 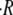with temperature followed an exponential growth. Hydra spheres did not regenerate at T < 6°C, and most of the spheres died for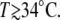

The observation that 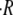varies linearly with the sphere size R₀ permits to define the relative swelling rate where 〈…〉 is average over sphere sizes. The dependence of the relative swelling rate on the concentration difference and for different sphere sizes is shown in Fig. 3 A. For 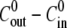< 0 mM, the analysis is limited to the first cycle only since the effect of 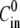disappears afterwards. As expected, 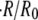strongly decreases with the concentration difference. For 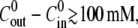no swelling was observed.

FIGURE 3.

(A) Relative swelling rate 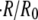as a function of the initial radius R₀ and for four different initial concentrations 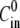and 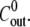The average 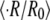is shown with straight lines. The accompanying values indicate the concentration difference. The relative swelling rate for = −50 mM corresponds to the first cycle only. For the other concentration differences, each point is an average over 2–5 cycles of the same sphere. HM denotes Hydra medium and Suc sucrose solution in Hydra medium. 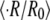(B) Dependence of the relative swelling rate on the concentration difference For 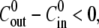the behavior of the first cycle (triangles, each point an average over 7–12 spheres) is different from the rest (circles, each point an average over 7–12 spheres and over 2–5 cycles per sphere). All experiments were carried out at T = 20°C.

The dependence of the relative swelling rate on 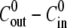and for eight different concentration differences is summarized in Fig. 3 B. For the cases with 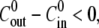the relative swelling rate of the first cycle is clearly much larger than the rest. From the second oscillation onwards, the values of 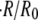are similar to the ones for 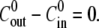The effect of the initial high inner concentration completely disappears after the first oscillation.

MODEL

Model development

We model the inflation-collapse oscillations in the simplest possible way. We assume that Hydra tissue is permeable to water and that the swelling is caused by the concentration gradient between the outside medium and the enteron fluid. Both assumptions are well supported by experimental observations. Then, the rate of change of total volume of water 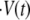inside the sphere at time t is given by a Darcy-type law

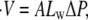where L_w is the water permeability coefficient, A the tissue area, and ΔP the pressure difference between enteron and outside medium (i.e., ΔP ≡ P_in – P_out). The pressure difference is the sum of the osmotic pressure and the elastic pressure of the shell on the enteron, i.e., ΔP = ΔΠ + ΔP_E. The osmotic pressure ΔΠ can be described by the van' t Hoff relation, ΔΠ(t) = k_BT[C_in(t) – C_out(t)], where C_in and C_out are the inner and outer concentrations, respectively. The elastic pressure ΔP_E can be easily calculated if we assume linear elasticity for the spherical shell although, as it will become clear later, this is not a significant restriction. This results in an evolution equation for the radius R of the shell, of the form

(1)

Here we have with E Young's modulus, h the thickness of the Hydra sphere, and μ Poisson's ratio. Furthermore, R₀ is the initial radius and k_B Boltzmann's constant. We further assume that the outer concentration remains constant, i.e., and that there is a constant influx of new ions into the enteron. Then where 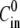is the initial concentration of solute in the enteron, V₀ and A₀, are, respectively, the initial volume and area of the shell, and U is the pumping rate per initial unit area. The combination of the above expressions yields an equation for the radius R of the form

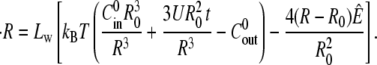For convenience, a more compact expression can be obtained by introducing the relative change in radius, r = (R − R₀)/R₀. This gives

(2)

where the constants 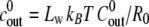and 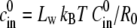are proportional to the initial ion concentration outside and inside the shell, respectively. The quantity u = 3L_w k_BT U/ 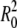is proportional to the ion pumping rate per initial unit area, and 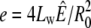is proportional to the elastic resistance of the shell.

The inflation process ends with the rupture of the Hydra sphere when the radius reaches a maximal value R_rup. This leads to a sudden collapse that resets the radius to R₀. The collapse results in an almost exponential decay of the relative radius change r to 0 (see Appendix A for details). Since the collapse is on the order of a few seconds, much faster that the inflation process (on the order of hours), we will replace the dynamics of the collapse by a direct resetting of r to 0 in the description of the oscillations.

It is generally accepted (32) that almost no cell divisions occur during Hydra regeneration and therefore we take R₀ constant in the model. This is also supported by our experiments. As shown in Fig. 1 A, the radius of the sphere after collapse is remarkably similar from cycle to cycle.

Analysis of the model

The magnitude of the parameters of the model can be estimated using data already available in the literature (see Appendix B for details). We used L_w = 0.9 × 10⁸ μm³ (N h)⁻¹, R₀ = 130 μm, and T = 293 K, to obtain the reduced concentrations 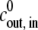= 1.7 × 10⁻³ 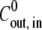(mM h)⁻¹, the reduced pumping rate u = 7.8 × 10⁻³ h⁻², and the reduced elastic resistance of the shell e = 3.3 × 10⁻³ h⁻¹.

The rupture of the Hydra shell is simulated by setting a critical radius r_rup above which the shell breaks. The value r is then set to zero and the swelling starts again. A value of r_rup = 0.25 is consistent with our experiments (compare Figs. 1 C and 2 A).

A numerical simulation for r(t) using these parameters is shown in Fig. 4 A. The analysis of the simulations provides three major conclusions.

1. The elastic resistance of the Hydra shell, which appears in the model through the quantity e, hardly contributes to the dynamics and thus can be neglected. Simulations with e = 0 are virtually identical to the simulations with our estimated e.

2. The swelling process is almost linear (Fig. 4 A).

3. The term in Eq. 2 that accounts for the concentration of ions inside the Hydra shell c_in(t) (see Eq. 2) does not change appreciably after the first few cycles, as shown in Fig. 4 B.

FIGURE 4.

Numerical simulations of the model and comparison with the experiments. (A and B) The time evolution of the relative radius r and, respectively, the inner concentration C_in is shown from a numerical integration of the model (the parameters of the simulation are described in the text, with and 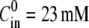). (B) The analytical approximation of 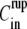of Eq. 4 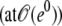is also shown. (C) Comparison among experiment, simulation, and analytical approximation of the relative swelling rate 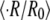as a function of the concentration difference (for 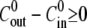) at T = 20°C. In this panel the experimentally measured values (circles) are compared with the ones measured in numerical simulations of the model (triangles). The solid curve shows the analytical approximation for the relative swelling rate (see main text and Eq. 4).

In fact, these observations are connected to each other, and the following analysis illustrates why this is the case. Furthermore, we can estimate the swelling rate 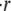analytically.

The observation that the inside concentration is almost constant greatly simplifies the analysis of the equations, because the time dependence and the nonlinearity of Eq. 2 are both contained in c_in. Indeed, Eq. 2 tells us that the inside concentration 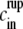in the shell at rupture time is given by

(3)

where only t_rup, the average time between ruptures, is unknown.

Assuming now that c_in(t) is almost constant (i.e., c_in ≈ 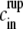), we can estimate t_rup. By solving Eq. 2 we get 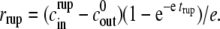And by isolating t_rup, inserting it into Eq. 3, expanding the logarithm and performing standard asymptotic techniques one obtains the following estimation 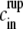for the internal concentration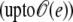

(4)

where v_rup = (1 + r_rup)³ – 1 is the relative volume change at rupture time. The correction term 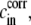proportional to e, is given by Because e is small the model equation simplifies to Its solution is trivially given by 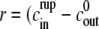) t.

Therefore, the analysis of the model shows that we obtain approximately linear swelling with slope This slope depends only on the outside concentration the pumping rate u, and the relative rupture radius r_rup.

Note that this analysis only applies for cycles with a steady-state regime where the inner concentration c_in does not change much. Therefore we cannot use the analysis to obtain quantitative values for the first cycle in the case 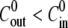because in this case the inner concentration decreases significantly.

Fig. 4 C shows a direct comparison between the relative swelling rate 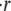measured experimentally, the results of numerical simulations of the model, and our analytical approximation. Here we plot 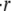as a function of the concentration difference 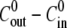with the parameter values estimated above.

DISCUSSION

The swelling behavior of the Hydra sphere obtained from the analysis of the model is in agreement with the one observed experimentally, and is best described in terms of the relative swelling rate 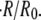The analysis of the model shows that is independent of time and of the initial radius R₀. The relative swelling rate has a weak dependence on the elasticity of the Hydra shell and a transient dependence on the initial concentration On the other hand, the relative swelling rate depends strongly on temperature through the pumping rate and on the outside concentration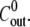

The time-independence of the swelling rate was verified experimentally for a wide range of sphere sizes, concentration differences, and temperatures (Fig. 2 A). It leads to a linear increase in radius of the Hydra shell followed by a sudden collapse, giving rise to the observed oscillations. This is in full agreement with our model.

The model also predicts that the relative swelling rate is independent of the initial radius R₀. This is indeed observed experimentally (Fig. 3 A). The experiments also show that the swelling rate increases exponentially with temperature, indicating that the pumping rate u is strongly temperature-dependent.

The initial inner concentration has a transient effect on the swelling rate. It only affects Hydra swelling for the first few oscillation cycles, after which C_in approaches an almost constant value 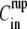(Fig. 4 B). The outside concentration, however, has a much larger impact on the swelling dynamics. As the concentration difference 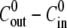is increased, the relative swelling rate 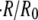decreases. This dependence in quantitatively captured by the proposed model for a significant range of 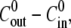up to 50 mM (see Fig. 4 C). At concentration differences 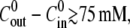the experimental values for 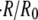are lower than the ones obtained from the simulations, and no swelling is observed at 100 mM. We conjecture that this deviation is due to the fact that the pumping rate depends on the outside concentration. Indeed, if the outside osmolarity is high the osmotic difference to the Hydra cells is small. Consequently, little water enters the tissue and little pumping is necessary to regulate osmotic balance.

Surprisingly, the analysis of the model shows that the elastic term e r in Eq. 2 is too small to have a significant contribution to the swelling and therefore it can neglected. If e is unrealistically large, our numerical simulations show that the swelling is no longer linear.

Although the model describes the swelling mechanism during the early stages of Hydra regeneration, it can be extended to the whole regeneration process. As shown in Fig. 1 C, the inflation-collapse events continue after axis formation. The rupture radius is significantly reduced, but the oscillations are periodic and the swelling linear with time. We can conclude that the inflation mechanism is the same. The reduced rupture threshold can be understood as a weak spot in the Hydra shell, possibly related to the formation of an early mouth, as suggested by Soriano et al. (21).

Finally, there are some experimental observations that cannot be explained with the model. For instance, the Hydra shell never shrinks, even in experiments using an outer concentration much larger than the initial inner concentration. This phenomenon is not predicted by the model, but understandable from Hydra's biology: even if the outside medium has a high osmolarity, the Hydra cells are still hyperosmotic compared to it. As excess water inside the cells is always transported into the enteron, shrinking cannot take place. This phenomenon could be captured using a more elaborated model that also takes other processes in the Hydra tissue into account. A second observation bears on the swelling behavior immediately after collapse. At that time, the swelling rate is often (but not nearly always) significantly larger, typically by a factor 2, than at later times during the swelling cycle. In that case, even the biological nature of this phenomenon is unclear.

CONCLUSIONS

We have presented a biophysical model to describe the mechanical oscillations in regenerating Hydra. The model is based on the idea that Hydra swelling is driven by the osmotic difference between the inner and outer concentrations of the Hydra shell. The analysis of the model provides two major conclusions: 1), the elastic forces of the Hydra shell during the swelling are negligible compared to the osmotic ones; and 2), the swelling rate 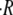is linear with time, with a slope that essentially depends on the difference between the outside and inside initial concentrations

The model is supported by experiments with regenerating Hydra spheres. The experiments show that swelling is linear with time in a wide range of concentration differences and sphere sizes, and that the relative swelling rate 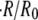decreases with

Unlike most models in biology, the magnitude of the parameters in our model could be directly estimated from the literature. Numerical integrations of the model using these parameters provided values of 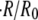in agreement with the experiments. Hence, our model captures the physical process of the oscillations, and confirms the osmoregulatory mechanism proposed by Benos et al. (27).

APPENDIX A: MODELING THE COLLAPSE OF THE SPHERE

The Hydra sphere collapses once the tension between the cells reaches a critical point and the sphere ruptures. The critical tension at the time of rupture can be estimated by the equation

where μ is Poisson's ratio and h the thickness of the Hydra sphere. From the tension we can calculate the critical force on a cell with a side surface A to be

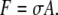Using μ = 0.25, h = 20 μm, r_rup = 0.25, 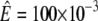N m⁻¹, and A = (10 μm)² we obtain F = 190 nN. This value is on the order of magnitude of the maximum force for cadherin-mediated adhesion as measured in Chu et al. (33).

To model the collapse of the Hydra sphere that occurs after a swelling period we first observe that the rupture point of the cell ball corresponds to a circular hole with a size of the order of a Hydra cell, as described in Fütterer et al. (25). Hence, we can assume that the water flow passing through the hole is laminar. Consequently, Poiseuille's law can be applied, leading to 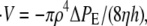where V is the volume of the sphere, ρ and h are the radius and depth of the hole, and η is the dynamic fluid viscosity. ΔP_E is the elastic pressure difference and is given by the second term of Eq. 1. Rewriting this equation for the relative radius of the sphere r we obtain 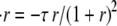where For small r this leads to an exponential decay of the radius with time, with a characteristic time constant given by 1/τ. For ρ = 5 μm, R₀ = 180 μm, and 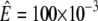N m⁻¹, we obtain 1/τ = 2.7 s, which is on the order of the characteristic deflation time observed in the experiments.

APPENDIX B: ESTIMATION OF THE PARAMETERS OF THE MODEL

The parameters of Eq. 2 can be obtained as follows. The water permeability coefficient L_w is given in Lilly (29) as L_w = 3.6 × 10⁸ μm³ (N h)⁻¹. This value can, however, only be seen as an order-of-magnitude estimation. The best correspondence between experiments and simulations was obtained using the value of L_w = 0.9 × 10⁸ μm³ (N h)⁻¹.We use R₀ = 130 μm as a typical value for the initial radius of the sphere in our experiments (see Fig. 2 C). The temperature is T = 293 K. Thus, for the quantities 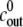and we obtain 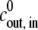= 1.7 × 10⁻³ 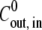(mM h)⁻¹.

For the estimation of e we need In Goidin (34) this quantity was estimated using two different methodologies giving values on the range If we use the upper limit of these estimations, we get E = 11 kPa and e = 3.3 × 10⁻³ h⁻¹.

More difficult is the estimation of the pumping rate per unit area U. This quantity is estimated from data in the literature using two different approaches. A first approach is based on the measurement of electric currents across the body column of an adult Hydra, providing a value of A = 58 nA (35). Hence, assuming that an adult Hydra is l = 1 cm long and has a diameter of d = 1 mm, we get U = π ldA/ε = 4.6 × 10⁷ h⁻¹ μm⁻² where E = 1.6 × 10⁻¹⁹ C is the elementary charge.

The second approach uses the observation that radioactive sodium is taken up from the medium by Hydra with exponential saturation (29). The measured half-time constant is γ = 2 h and the saturated concentration of sodium in the tissue is S = 17 mM. Assuming that S is constant we get a differential equation for the amount of radioactive sodium in the tissue T as follows: T ′ = K(1 – T/S). Here K is the pumping rate per Hydra volume. The equation has the solution T = S(1 − exp(−kt/S)). From this expression, we deduce K = S ln 2/γ, and finally (with h = 20 μm for the Hydra thickness) U = π ldhK = 7.1 × 10⁷ h⁻¹ μm⁻².

Considering the very different methodologies and the high systematic errors, these estimations are surprisingly close to each other. Experimentally, we know that the swelling rate depends strongly on temperature (see Fig. 2 D). This suggests that also the pumping rate is strongly temperature-dependent. For the simulations, we used the value U = 3 × 10⁷ h⁻¹ μm⁻², which best reproduces the swelling rate observed experimentally (for and T = 20°C). This leads to u = 7.8 × 10⁻³ h⁻².